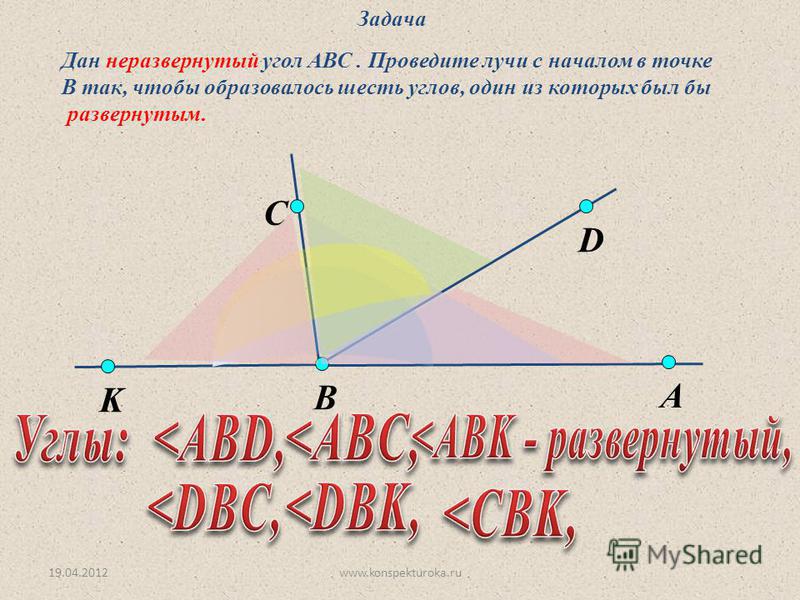
Три развернутых угла. Развернутый, тупой, вертикальный и неразвернутый: виды углов геометрии
В этой статье будет рассматриваться одна из основных геометрических фигур — угол. После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи.
Введение в понятие геометрического угла
В геометрии существует ряд объектов, которые составляют основу всей науки. Угол как раз относиться к ним и определяется с помощью понятия луча, поэтому начнем именно с него.
Также перед тем, как приступать к определению самого угла, нужно вспомнить о нескольких не менее важных объектах в геометрии — это точка, прямая на плоскости и собственно сама плоскость. Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью — поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии — это часть прямой, у которой есть начало, но нет конца.
Используя данные понятия, можем составить утверждение, что углом является геометрическая фигура, которая полностью лежит в некоторой плоскости и состоит из двух несовпадающих лучей с общим началом. Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Виды углов и геометрии
Мы знаем о том, что углы могут быть совсем разными. А потому немного ниже будет приведена небольшая классификация, которая поможет лучше разобраться в видах углов и их главных особенностях. Итак, существует несколько видов углов в геометрии:
- Прямой угол. Он характеризируется величиной в 90 градусов, а значит, его стороны всегда перпендикулярны между собой.
- Острый угол. К таким углам относятся все их представители, имеющие размер меньше 90 градусов.
- Тупой угол. Здесь же могут быть все углы с величиной от 90 до 180 градусов.
- Развернутый угол. Имеет размер строго 180 градусов и внешне его стороны составляют одну прямую.
Понятие развернутого угла
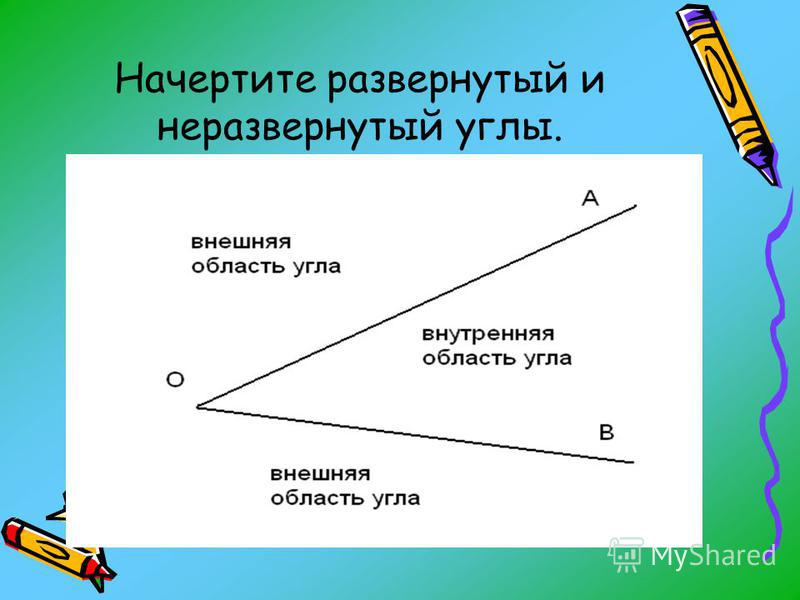
Теперь давайте рассмотрим развернутый угол более подробно.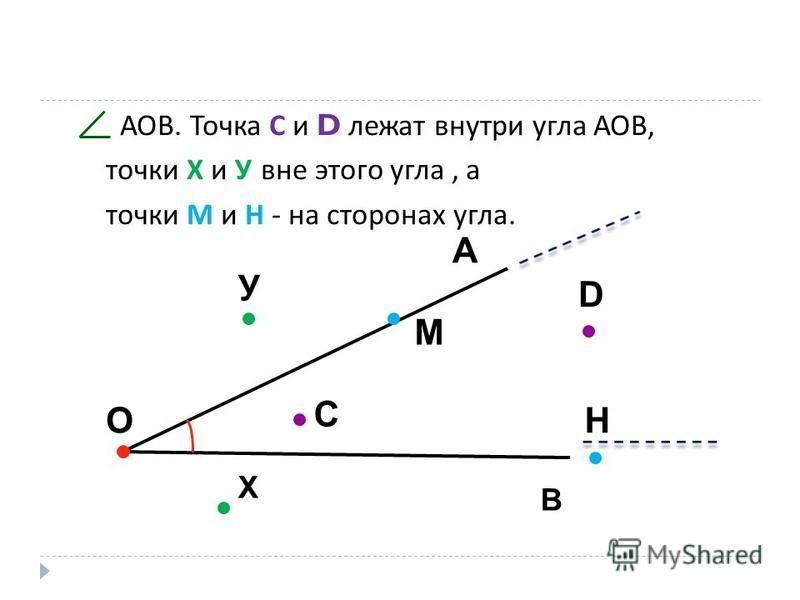 Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой.
Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой.
Стоит запомнить тот факт, что такой угол всегда можно разделить с помощью луча, который выходит из его вершины. В результате мы получим два угла, которые в геометрии называются смежными.
Также развернутый угол имеет несколько особенностей. Для того, чтобы рассказать о первой из них, нужно вспомнить понятие «биссектриса угла». Напомним, что это луч, который делит любой угол строго пополам. Что касается развернутого угла, то его биссектриса разделяет его таким образом, что образуется два прямых угла по 90 градусов. Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚.
Если же разделять развернутый угол совсем произвольным лучом, то в результате мы всегда получаем два угла, один из которых будет острым, а другой — тупым.
Свойства развернутых углов
Будет удобно рассматривать этот угол, собрав воедино все его главные свойства, что мы и сделали в данном списке:
- Стороны развернутого угла антипараллельны и составляют прямую.
- Величина развернутого угла всегда составляет 180˚.
- Два смежных угла вместе всегда составляют развернутый угол.
- Полный угол, который составляет 360˚, состоит из двух развернутых и равен их суме.
- Половина развернутого угла — это прямой угол.
Итак, зная все эти характеристики данного вида углов, мы можем использовать их для решения ряда геометрических задач.
Задачи с развернутыми углами
Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов.
- Чему равен развернутый угол, если его стороны составляют вертикальную прямую?
- Будут ли два угла смежными, если величина первого 72˚, а другого — 118˚?
- Если полный угол состоит из двух развернутых, то сколько в нем прямых углов?
- Развернутый угол разделили лучом на два таких угла, что их градусные меры относятся как 1:4.
 Вычислите полученные углы.
Вычислите полученные углы.
Решения и ответы:
- Как бы ни был расположен развернутый угол, он всегда по определению равен 180˚.
- Смежные углы имеют одну общую сторону. Поэтому, чтобы вычислить размер угла, который они составляю вместе, нужно просто прибавить значение их градусных мер. Значит, 72 +118 = 190. Но по определению развернутый угол составляет 180˚, а значит, два данных угла не могут быть смежными.
- Развернутый угол вмещает два прямых угла. А так как в полном имеется два развернутых, значит, прямых в нем будет 4.
- Если мы назовем искомые углы а и b, то пусть х — это коэффициент пропорциональности для них, а это значит, что а=х, и соответственно b=4х. Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚.
 Ответ: 36˚ и 144˚.
Ответ: 36˚ и 144˚.
Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии.
С понятием угол учащиеся знакомятся еще в начальной школе. Но как геометрическую фигуру, имеющую определенные свойства, начинают изучать его с 7-го класса в геометрии. Кажется, довольно простая фигура , что о ней можно сказать. Но, приобретая новые знания, школьники всё больше понимают, что можно узнать о ней довольно интересные факты.
Вконтакте
Когда изучаются
Школьный курс геометрии разделён на два раздела: планиметрию и стереометрию. В каждом из них немалое внимание уделяется углам :
- В планиметрии дается их основное понятие, происходит знакомство с их видами по величине. Более подробно изучаются свойства каждого вида треугольников. Появляются новые определения для учащихся – это геометрические фигуры, образованные при пересечении двух прямых между собой и пересечении нескольких прямых секущей.

- В стереометрии изучаются пространственные углы – двугранные и трехгранные.
Внимание! В данной статье рассматриваются все виды и свойства углов именно в планиметрии.
Определение и измерение
Приступая к изучению, первоначально определяют, что такое угол в планиметрии.
Если на плоскости взять определённую точку и провести от нее два произвольных луча, то получим геометрическую фигуру – угол, состоящую из следующих элементов:
- вершина – та точка, из которой и проводились лучи, обозначается заглавной буквой латинского алфавита;
- стороны – полупрямые, проведенные из вершины.
Все элементы, образующие рассматриваемую нами фигуру, разбивают плоскость на две части :
- внутренняя — в планиметрии не превышает 180 градусов;
- внешняя.
Принцип измерения углов в планиметрии
Важно! Угол называется развернутым, если полупрямые, выходящие из его вершины, образуют прямую линию. Неразвернутый угол это все остальные случаи.
Неразвернутый угол это все остальные случаи.
Если его разделить на 180 равных частей, то принято считать меру одной части равной 10. В таком случае говорят, что измерение производится в градусах, а градусная мера такой фигуры составляет 180 градусов.
Основные виды
Виды углов подразделяются по таким критериям, как градусная мера, характер их образования и представленные ниже категории.
По величине
Учитывая величину, углы разделяют на:
- развернутый;
- прямой;
- тупой;
- острый.
Какой угол называется развернутым, было представлено выше. Определимся с понятием прямого.
Его можно получить при делении развернутого на две равные части. В этом случае легко ответить на вопрос: прямой угол, сколько градусов составляет?
180 градусов развернутого делим на 2 и получаем, что прямой угол равен 90 градусам . Это замечательная фигура, так как многие факты в геометрии связаны именно с ней.
Имеет она и свои особенности в обозначении. Чтобы на рисунке показать прямой угол, его обозначают не дугой, а квадратиком.
Чтобы на рисунке показать прямой угол, его обозначают не дугой, а квадратиком.
Углы, которые получаются при делении произвольным лучом прямого, называют острыми. По логике вещей следует, что острый угол меньше прямого, но его мера отлична от 0 градусов. То есть, он имеет величину от 0 до 90 градусов.
Тупой угол больше прямого, но меньше развернутого. Его градусная мера варьируется в интервале от 90 до 180 градусов.
Данный элемент можно разбить на разные виды рассматриваемых фигур, исключая развёрнутый.
Вне зависимости от того, как разбивается неразвернутый угол, всегда пользуются базовой аксиомой планиметрии — «основное свойство измерения».
При разделении угла одним лучом
На уровне 7-го класса виды углов по их величине на этом заканчиваются. Но для повышения эрудиции можно добавить, что существуют и другие разновидности, которые обладают градусной мерой больше 180 градусов. Их называют выпуклыми.
Их называют выпуклыми.
Фигуры при пересечении прямых
Следующие типы углов, с которыми знакомятся учащиеся – элементы, образованные при пересечении двух прямых. Фигуры, которые размещаются друг напротив друга, называют вертикальными. Их отличительное свойство – они равны.
Элементы, которые прилегают к одной и той же прямой, называют смежными. Теорема, отображающая их свойство, говорит о том, что смежные углы в сумме дают 180 градусов .
Элементы в треугольнике
Если рассматривать фигуру как элемент в треугольнике, то углы подразделяют на внутренний и внешний. Треугольник ограничен тремя отрезками и состоит из трёх вершин. Углы, расположенные внутри треугольника при каждой вершине, называют внутренними .
Если взять любой внутренний элемент при любой вершине и продлить любую сторону, то угол, который образовался и является смежным с внутренним, называется внешним. Эта пара элементов имеет следующее свойство: их сумма равна 180 градусам.
Пересечение двух прямых секущей
Пересечение прямых
При пересечении двух прямых секущей также образуются углы , которые принято распределять по парам. Каждая пара элементов имеет свое название. Выглядит это следующим образом:
Каждая пара элементов имеет свое название. Выглядит это следующим образом:
- внутренние накрест лежащие:∟4 и ∟6, ∟3 и ∟5;
- внутренние односторонние: ∟4 и ∟5, ∟3 и ∟6;
- соответствующие: ∟1 и ∟5, ∟2 и ∟6, ∟4 и ∟8, ∟3 и ∟7.
В том случае, когда секущая пересекает две прямые, все эти пары углов имеют определённые свойства:
- Внутренние накрест лежащие и соответственные фигуры между собой равны.
- Внутренние односторонние элементы в сумме дают 180 градусов.
Изучаем углы в геометрии, их свойства
Виды углов в математике
Вывод
В этой статье представлены все основные виды углов, которые встречаются в планиметрии и изучаются в седьмом классе. Во всех последующих курсах свойства, касающихся всех рассмотренных элементов, являются основой для дальнейшего изучения геометрии. К примеру, изучая , необходимо будет вспомнить все свойства углов, образованных при пересечении двух параллельных прямых секущей. При изучении особенностей треугольников, необходимо вспомнить, что такое смежные углы.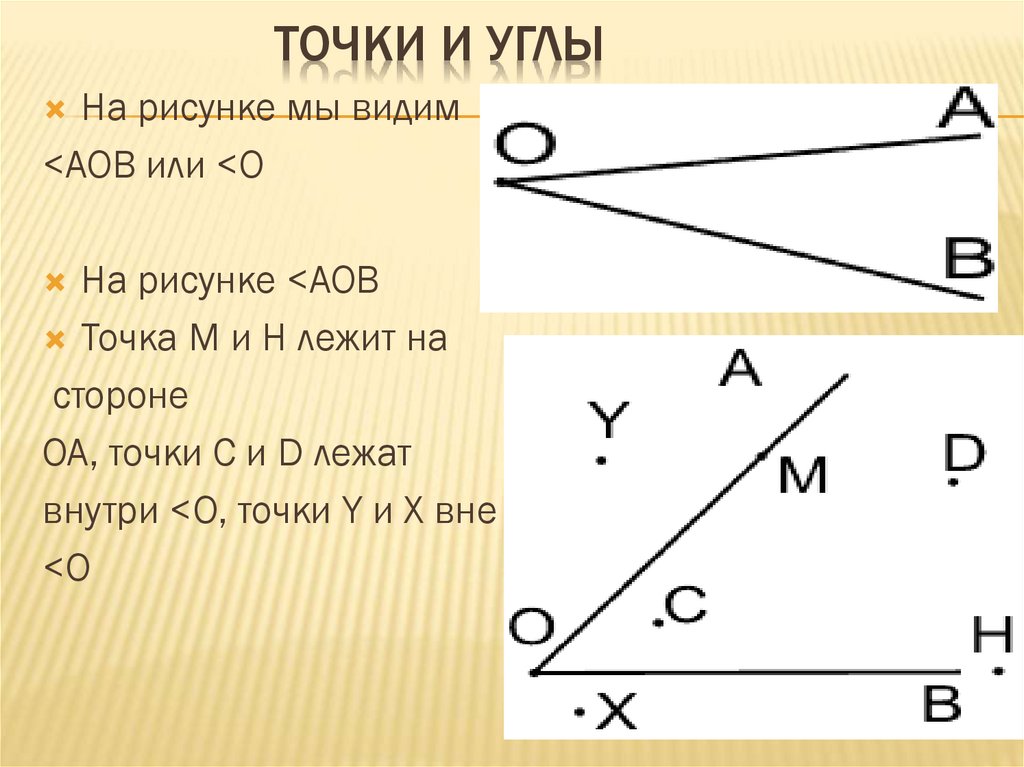 Перейдя в стереометрию, все объёмные фигуры будут изучаться и строиться, опираясь на планиметрические фигуры.
Перейдя в стереометрию, все объёмные фигуры будут изучаться и строиться, опираясь на планиметрические фигуры.
Давайте начнем с определения того, что такое угол. Во-первых, он является Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.
Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.
Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол.
Прямой
Он выглядит так:
Его градусная мера всегда составляет 90 о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.
Тупой
Он имеет такой вид:
Градусная мера всегда больше 90 о, но меньше 180 о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.
Острый
Он выглядит так:
Градусная мера острого угла всегда меньше 90 о. Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.
Развернутый
Развернутый угол имеет такой вид:
В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях.
Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
1. Нулевой
Он выглядит так:
Само название угла уже говорит о его величине. Его внутренняя область равняется 0 о, а стороны лежат друг на друге так, как показано на рисунке.
Его внутренняя область равняется 0 о, а стороны лежат друг на друге так, как показано на рисунке.
2. Косой
Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0 о, 90 о, 180 о, 270 о.
3. Выпуклый
Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла — от 0 о до 180 о.
4. Невыпуклый
Невыпуклыми являются углы с градусной мерой от 181 о до 359 о включительно.
5. Полный
Полным является угол с градусной мерой 360 о.
Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
1. Дополнительные
Это два острых угла, образовывающие один прямой, т.е. их сумма 90 о.
2. Смежные
Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении.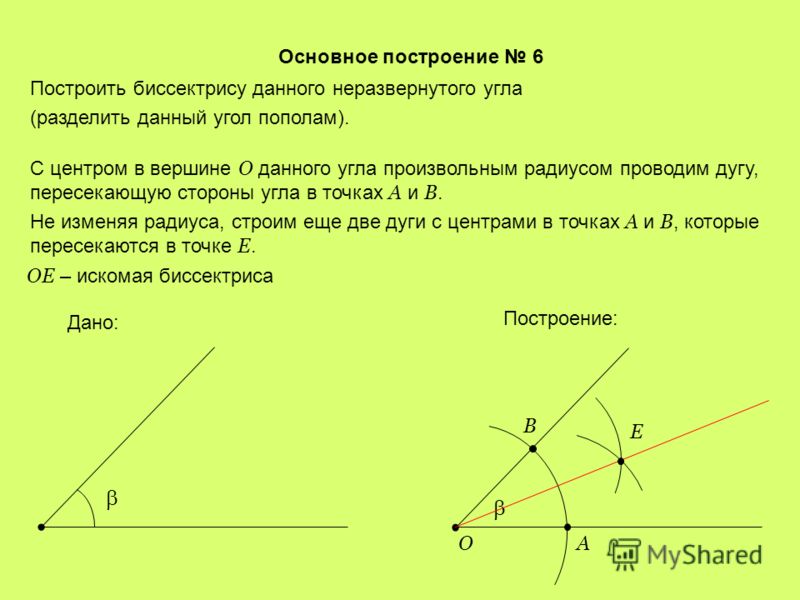 Их сумма равна 180 о.
Их сумма равна 180 о.
3. Вертикальные
Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны.
Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.
1. Центральный
Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.
2. Вписанный
Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.
Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
Угол
- Содержание
- Определение угла
- Обозначение угла
- Развернутый угол.
 Внутренняя и внешняя область угла
Внутренняя и внешняя область угла - Типы углов
- Сравнение углов
- Градусная мера угла
Определение угла
Определение 1. Угол − это геометрическая фигура,которая состоит из двух лучей, исходящих из одной точки.
Лучи называются сторонами угла, а их общее начало − вершиной угла.
Обозначение угла
На рисунке 1 изображен угол с вершиной O и сторонами m и n. Данный угол обозначают \( \small ∠mn \) или \( \small ∠O. \) Если на сторонах угла выбрать точки A и B, то угол можно обозачить так: \( \small ∠AOB \) или \( \small ∠BOA. \)
Развернутый угол. Внутренняя и внешняя область угла
Угол называется развернутым, если его стороны находятся на одной прямой. На рисунке 2 изображен развернутый угол с вершиной А и сторонами m и n.
На рисунке 2 изображен развернутый угол с вершиной А и сторонами m и n.
Любой угол разделяет плоскость на две части. Если угол неразвернутый, то меньшая из частей называется внутренней областью, а другая − внешней областью этого угла (Рис.3).
Если угол развернутый, то любую из двух частей, на которые разделяет угол данную плоскось можно считать внутренней областью угла.
Фигуру, состоящую из угла и его внутренней области также называют углом.
На рисунке 4 точки P и Q лежат внутри угла mn (т.е. во внутренней области угла), точки R и S лежат вне угла mn (т.е. во внешней области угла), а точки A и B на сторонах этого угла.
Типы углов
В зависимости от величин, углы бывают следующих типов (Рис.5):
- Нулевой угол (0°). Стороны угла совпадают. Его внутренняя область пустое множество.
- Острый угол (больше 0° и меньше 90°)
- Прямой угол (90°).
 Стороны прямого угла перпендикулярны друг другу.
Стороны прямого угла перпендикулярны друг другу. - Тупой угол (больше 90° и меньше 180°).
- Развернутый угол (180°).
- Невыпуклый угол (от 0° до 180° включительно).
- Выпуклый угол (больше 180° и меньше 360°).
- Польный угол (360°).
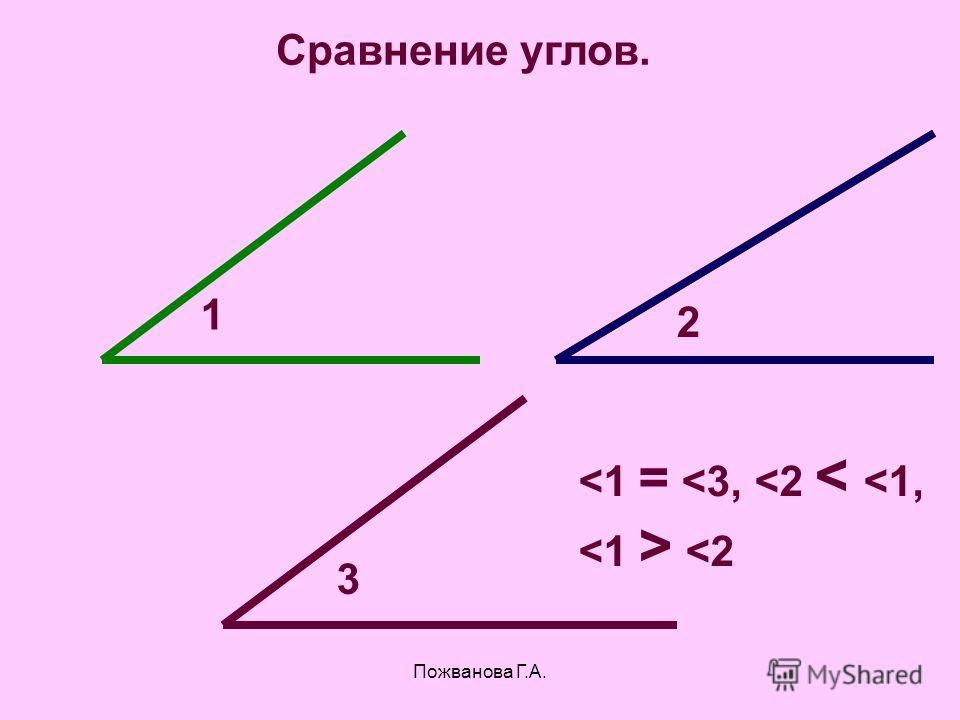
Сравнение углов
Углы можно сравнить, то есть определить равны ли они или какой угол меньше а какой больше. Чтобы определить равны ли углы или нет нужно наложить один угол на другой так, чтобы сторона одного угла совместилась со стороной другого угла а две другие оказались по одну сторону от совместившихся сторон. Если две другие стороны также совместились, то углы полностью совместятся и,следовательно они равны. Если же эти стороны не совместяться, то меньшим считается тот угол, который является частью другой.
На рисунках 6a и 6b представлены два угла: 1 и 2. На рисунке 7 угол 2 является частью угла 1, следовательно угол 2 меньше угла 1. Это пишется так: \( \small ∠2 \lt \angle 1. \)
Это пишется так: \( \small ∠2 \lt \angle 1. \)
Градусная мера угла
Измерение углов основана на сравнении их с углом, принятым за единицу измерения. За единицей измерения углов примнимают градус, которая является \( \small \frac {1}{180} \) частью развернутого угла. Положительное число, показывающая, сколько раз градус и его части помещаются в данном угле называвется градусной мерой угла. Для измерения углов используют транспортир (Рис.8).
Для угла AOB, градусная мера которого равна 120° говорят «угол AOB равен 120° » и пишут: \( \small ∠AOB=120 °. \) Очевидно, что градусная мера развернутого угла равна 180°. \( \small \frac {1}{60} \) часть градуса называется минутой и обозначается так: » ‘ «. \( \small \frac {1}{60} \) часть минуты называется секундой и обозначается так: » » «. Если градусная мера угла AOB равна 56 градусов 6 минут и 43 секунды, то пишут: \( \small \angle AOB=56°6’43». \)
\)
Отметим, что равные углы имеют равные градусные меры. Если углы разные, то меньший угол имеет меньшую градусную меру.
Как рассчитать развертку листового металла?
Первым шагом в процессе обработки листового металла является развертывание геометрии и связанного тела.
Качество детали напрямую зависит от правильности и аккуратности развертывания образца.
В прошлом из-за неразвитости средств расчета проекционным методом увеличивали образец на плоскости в соотношении 1:1 и измеряли реальную длину необходимой прямой линии.
Этот метод сложен и неэффективен и уже не может удовлетворить потребности общественного производства.
С развитием вычислительных инструментов, электронных калькуляторов и широкого применения компьютеров развертывание листового металла стало возможным с помощью расчетных методов.
В целях стандартизации метода расчета коэффициента разворачивания листового металла техническими специалистами, минимизации отклонения размеров изделий после гибки и облегчения самопроверки персонала цеха и повторной проверки инспекторов качества существует единый стандарт и основа для коэффициента развертывания, а стандарт расчета коэффициента развертывания листового металла имеет тенденцию к стандартизации.
В процессе изгиба внешний слой подвергается растягивающему напряжению, а внутренний слой подвергается сжимающему напряжению.
Существует переходный слой между напряжением растяжения и напряжением сжатия – нейтральный слой.
Длина нейтрального слоя во время гибки такая же, как и до гибки, поэтому нейтральный слой является эталоном для расчета длины изгибаемой детали в развернутом виде.
Положение нейтрального слоя зависит от степени деформации.
Когда радиус изгиба большой, а угол изгиба мал, степень деформации мала, а положение нейтрального слоя близко к центру толщины листа;
Когда радиус изгиба (R) становится меньше, а угол изгиба (θ) увеличивается, степень деформации увеличивается, и положение нейтрального слоя постепенно смещается к внутренней стороне центра изгиба.
Расстояние от нейтрального слоя до внутренней стороны листа обозначают λ, а толщину материала обозначают Т.
Основная формула для расчета длины в развернутом виде:
Длина в развернутом виде = внутренний размер материала + внутренний размер материала + сумма компенсации.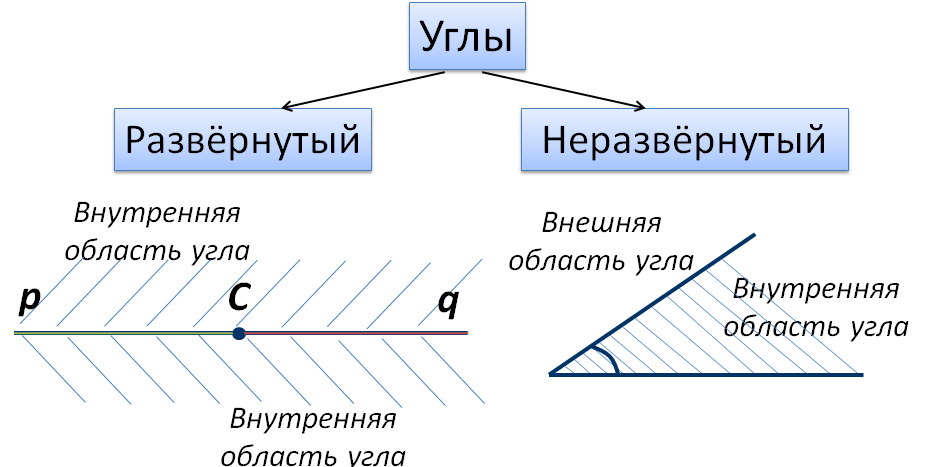
Вы также можете использовать следующий калькулятор для расчета длины развертки листового металла:
Далее последовательно описываются алгоритмы развертки различных элементов сгиба.
Общий изгиб IR = 0 мм, θ = 90° (Примечание: если R ≤ 1,0 мм, считается, что R = 0 мм).
L = A + B + K
- При 0 < T ≤ 3 мм, K = 0
- При 0,3 мм < T ≤ 5T, K = 0,4T
Обычно при гибке верхней части износ матрицы с углом R или угол R меньше 1 мм, или выбор нижнего V-образного паза матрицы велик, и по другим причинам, что приводит к небольшому коэффициенту изгиба.
Таким образом, в соответствии с фактическим эмпирическим значением коэффициент изгиба каждой толщины пластины материала показан в таблице 1.
Рис. 1 Схема общей гибки I
Общая гибка IIR ≠ 0 мм и θ = 90°
L = A + B + K длина дуги нейтрального слоя )
- При 0 < T ≤ 1,6 мм, λ = 0,5T
- При 0 < T ≤ 1,6 мм, λ = 0,5T
- При T > 1,6 мм, λ = 0,4T
9 Рис.
Общая гибка III 2 Схема общей гибки II
2 Схема общей гибки IIR = 0 мм, θ ≠ 90°
L = A + B + K’
- θ/90° )×K
Примечание: K — величина компенсации при 90°.
Общее изгиб I VR ≠ 0 мм, θ ≠ 90 °
L = A + B + K
(K принимает глюд Гейл -слои)
(K Принимает гидромагнитную длину. Рис. 4 Общая схема гибки IV гибки
Метод развертывания такой же, как и метод Z-сгиба с параллельными прямыми краями, а высота берется, как показано на рисунке 6.
Угол θ можно рассматривать как развертывание на 90°.
При 0
При T > 1,6 мм λ = 0,4T.
Z- изгибZ-сгиб, также известный как гибка со смещением, делится на гибку со смещением по прямой кромке и гибку со смещением со скошенной кромкой в соответствии с углом формования, а метод обработки зависит от высоты смещения .

- Если высота смещения h менее чем в 3,5 раза превышает толщину материала, для формовки используется смещенный штамп или сменный штамп.
- Когда высота смещения более чем в 3,5 раза превышает толщину материала, используется нормальная позитивная и негативная формовка.
- Если длина скошенной кромки менее чем в 3,5 раза превышает толщину материала, используйте штамп со смещением или сменный штамп.
- Когда длина скошенной кромки более чем в 3,5 раза превышает толщину материала, используется обычная фальцовка с одним положительным и одним отрицательным сгибом.
(1) Когда H < 3,5T, только тогда может быть выполнена гибка со смещением.
L = A + B + H
(если H ≤ T, компенсация 0,2 мм)
Рис. 5 Схема смещения линейки
(2) Непараллельное смещение линейки
Метод расширения такой же, как метод Z-образного сгиба с параллельной линейкой, а значение высоты показано на рис.
 6.
6.Угол θ можно рассматривать как разворот на 90°.
Рис. 6 Схематическая диаграмма непараллельного смещения прямой кромки
(3) Смещение прямой кромки — переходный сегмент касается двух дуг
Когда смещение прямой кромки развернуто в точке касания двух дуг окружности, вертикальная линия проводится в точке касания двух дуг окружности на внешней стороне подложки, а затем материал смещается на одну толщину материала внутрь, как показано на рисунке 7, для обработки, и разворачивается способом Z- сгиб 1 (смещение прямого края).
Рис. 7 Диаграмма смещения прямой кромки – переходный сегмент касается двух дуг окружности
Z-сгиб 2 (скос смещение )Когда H < 2T, алгоритм развертывания следующий: к офсетной обработке.
- При θ ≤ 70° L = A + B + C + 0,2
- При θ > 70° разворачивать согласно Z-сгибу 1 (смещение прямой кромки)
Рис.
Обратное складывание и сгибание 8 Схема скошенной кромки смещение
8 Схема скошенной кромки смещениеL = A + B – K
(1) При сплющивании подумайте, нужно ли нажимать на леску перед сгибанием в соответствии с реальной ситуацией.
Положение прессования линии находится в середине зоны деформации изгиба.
Рис. 9 Схема обратной фальцовки и правки
Обратная фальцовка и правка обычно выполняются в два этапа: сначала сгибают на 30° с помощью вставной матрицы, а затем расплющивают.
Следовательно, при выполнении линии сгиба развернутого чертежа необходимо провести линию сгиба по изгибу на 150°, как показано на рисунке 9.
Таблица 1 Коэффициент изгиба плит разной толщины под разными углами изгиба
N – foldAngle Thickness/mm 1 1.2 1.5 1.8 2.  5
545° 5.3 6.3 7.8 9.5 13 50° 4.5 5.4 6.8 8.1 11.25 55° 4 4.7 5.8 7.05 9.75 60° 3.4 4.1 5.1 6.15 8.5 65° 3 3.6 4.5 5.4 7.5 70° 2.65 3.2 4 4.75 6.6 75° 2.35 2.8 3.5 4.25 5.9 80° 2.1 2.5 3.1 3.75 5.25 85° 1.9 2.25 2.8 3.35 4.65 90° 1.  7
72 2.5 3 4.15 95° 1.5 1.8 2.2 2.7 3.75 100° 1.35 1.6 2 2.4 3.35 105° 1.2 1.4 1.75 2.15 3 110° 1.1 1.3 1.6 2 2.65 115° 1 1.25 1.4 1.7 2.35 120° 0.85 1 1.25 1.5 2.1 125° 0.75 0.9 1.1 1.35 1.85 130° 0.65 0.8 1 1.18 1.65 135° 0.55 0.  7
70.85 1.05 1.45 140° 0.5 0.6 0.75 0.9 1.25 145° 0.43 0.5 0.65 0.77 1.05 150° 0.35 0.43 0.55 0.65 0.9 155° 0.3 0.35 0.45 0.53 0.75 160° 0.23 0.27 0.35 0.4 0.6 165° 0.17 0.2 0.25 0.3 0.45 The N-fold processing method is shim refolding and flattening, and the unfolding algorithm это:
L = A + B + K
(K принимает длину дуги нейтрального слоя).

λ = 0,5T
Рис. 10 N-кратная диаграмма
Дуга (включая линейку с одной стороны)(1) Расширение дуги равно K, а длина дуги нейтрального слоя взят. λ= 0,5T
(2) Расширение прямой кромкой с одной стороны.
Д = А + K
(k — длина дуги нейтрального слоя)
Рис. легкая промышленность, автомобильная промышленность.
Развернутая форма деталей из листового металла является основной основой размера заготовки, которая определяет размер и форму заготовки.
В прошлом традиционные методы развертывания деталей из листового металла становились все более и более непригодными для современных требований проектирования из-за таких недостатков, как длительные циклы, низкая эффективность и низкое качество.
Чтобы преодолеть эти недостатки, в последние годы постепенно расширяются некоторые передовые CAD-системы.

Эти специальные системы проектирования деталей из листового металла имеют мощные функции и экономят много времени и рабочей силы для предварительного проектирования и развертывания деталей из листового металла.
BlueWalker-3 разворачивается, становится ярче в сто раз — Universe Today
После нескольких месяцев ожидания мы впервые можем взглянуть на полностью развернутый BlueWalker-3.
Теперь в небе над вами может быть виден новый крупный спутник. Недавно мы писали о новом спутнике AST Space Mobile BlueWalker-3 и о его потенциале стать одним из самых ярких объектов в ночном небе. Запущенный 10 сентября года года 2022 года на ракете SpaceX Falcon-9 вместе с партией Starlink Group 4-2, BlueWalker-3 является первым из запланированной компанией мега-группировки из 110 спутников BlueBird, которые должны быть развернуты к концу 2024 года для всемирной связи.
BlueWalker-3 настолько велик, что (как и космический телескоп Джеймса Уэбба) он был сложен в обтекателе полезной нагрузки для запуска.
Пол Мэйли сделал это изображение теперь уже сверкающего BlueWalker-3, пересекающего ночное небо. В развернутом виде отражающая антенна имеет размеры 8 на 8 метров (64 квадратных метра или 689 квадратных футов). Ожидается, что спутники BlueBird следующего поколения будут еще крупнее.
В развернутом виде отражающая антенна имеет размеры 8 на 8 метров (64 квадратных метра или 689 квадратных футов). Ожидается, что спутники BlueBird следующего поколения будут еще крупнее.Излишне говорить, что они могут стать самыми яркими искусственными объектами в ночном небе, соперничая с Международной космической станцией. Однажды BlueWalker-3 отделился от Falcon-9На верхней ступени охота шла полным ходом, так как добровольные «спутниковые корректировщики» дежурили, чтобы выследить BlueWalker-3. Ранние наблюдения перед развертыванием показали звездную величину спутника от +6 до +8, что ниже порога невооруженного глаза. Затем, утром 11 ноября -й -й, наблюдатели за спутниками забили тревогу: BlueWalker-3 наконец-то развернулся и стал намного ярче , увеличившись в сто раз до звездной величины +1. Это не совсем отрицательный диапазон звездной величины Международной космической станции, но все же довольно яркий… и мы не видели, насколько ярким может быть спутник на хорошем зенитном проходе под большим углом.
Почти Полная Луна сражается с BlueWalker-3. Изображение предоставлено: Paul Maley
Хуже того, BlueWalker-3 и ему подобные также могут иметь потенциальное влияние на радиочастотный спектр. Цель BlueWalker-3 — прямая связь между спутником и телефоном — также может помешать астрономическим радионаблюдениям.
BlueWalker-3 добавляет новую «звезду» к Большой Медведице. Изображение предоставлено: Мэтью Гудман/Exclosure/Космическая ситуационная осведомленность.Спутники прошлого, настоящего и будущего
Конечно, медленная деградация ночного неба из-за светового загрязнения не является чем-то новым, хотя растущее количество мегасозвездий, таких как SpaceX Starlink, экспоненциально увеличило количество искусственных спутников. на ночном небе мерцают звезды. В дополнение к ASTMobile, OneWeb и Swarm Technologies, SpaceBee, активно создают спутниковые группировки, и это еще не все.
Как упоминалось ранее, у нас есть детальное представление обо всем этом деле: если прямая спутниковая связь позволяет пользователю продолжать подключаться из палатки в дикой природе, это плюс… тем не менее, технология с потенциальным воздействием на окружающую среду должна не двигаться вперед без надзора.


 Вычислите полученные углы.
Вычислите полученные углы. Ответ: 36˚ и 144˚.
Ответ: 36˚ и 144˚.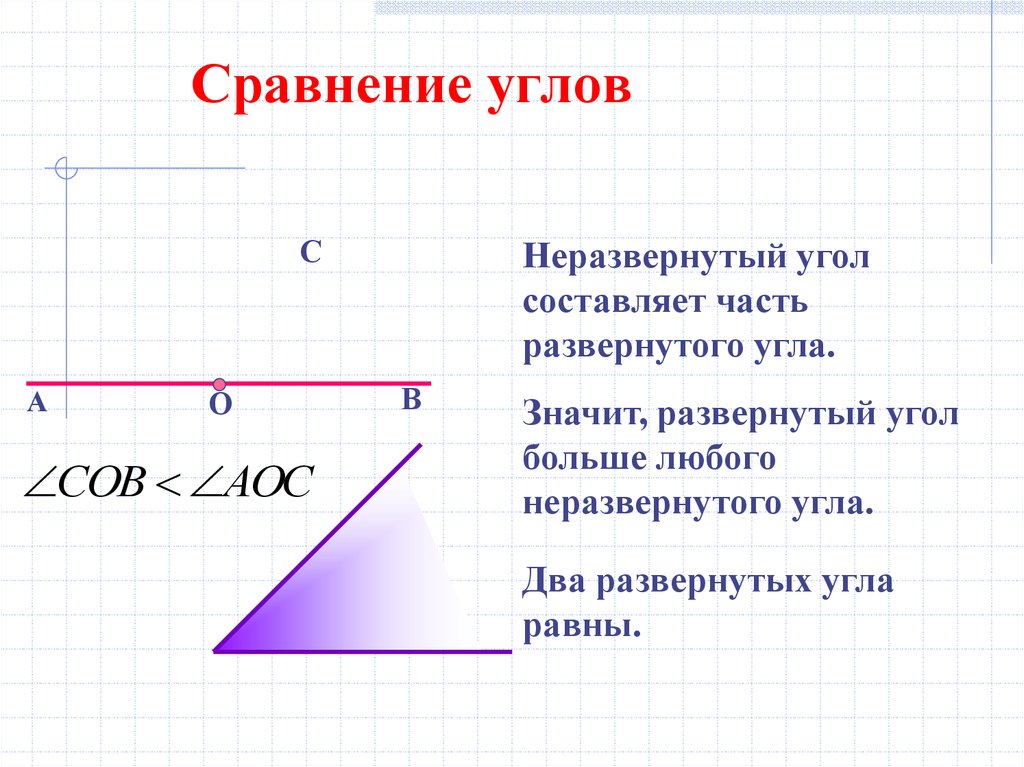
 Внутренняя и внешняя область угла
Внутренняя и внешняя область угла Стороны прямого угла перпендикулярны друг другу.
Стороны прямого угла перпендикулярны друг другу. 2 Схема общей гибки II
2 Схема общей гибки II
 6.
6. 8 Схема скошенной кромки смещение
8 Схема скошенной кромки смещение 5
5 7
7 7
7

 В развернутом виде отражающая антенна имеет размеры 8 на 8 метров (64 квадратных метра или 689 квадратных футов). Ожидается, что спутники BlueBird следующего поколения будут еще крупнее.
В развернутом виде отражающая антенна имеет размеры 8 на 8 метров (64 квадратных метра или 689 квадратных футов). Ожидается, что спутники BlueBird следующего поколения будут еще крупнее.