Y 2 x что это: Постройте график функции y=2x — ответ на Uchi.ru

Метод Монте-Карло — один из самых полезных алгоритмов в ИТ

Сегодня сложная тема, но мы объясним её просто и понятно. Разговор пойдёт про алгоритмы и немного про математику. 

Методы Монте-Карло — это набор методов в математике для изучения случайных процессов. Случайных — это когда что-то в них происходит непредсказуемым образом, например:

• подбрасываем монетку;
• кидаем кубик;
• опускаем жетоны в ячейки со столбиками;
• ловим элементарные частицы;
• считаем столкновения молекул;
• и что угодно ещё, что происходит полностью случайно и что нельзя предсказать заранее.

Смысл методов Монте-Карло в том, чтобы использовать данные случайных событий, чтобы на их основе получить более-менее точные результаты каких-то других вычислений. Они не будут идеально и математически точными, но их уже будет достаточно, чтобы с ними полноценно работать. Иногда это проще и быстрее, чем считать всё по точным формулам.

Пример такого вычисления — построение маршрута в навигаторе.

В исходном виде это задача коммивояжёра, которая требует колоссальных вычислительных ресурсов. Но благодаря приближённым методам с ней справится даже не самый мощный телефон. Один из таких методов — метод Монте-Карло.

Как автомобильный навигатор находит самый быстрый путь

Своё название метод получил в честь Монте-Карло — района Монако, где находится много казино с рулеткой, самым доступным источником случайных чисел в начале 20-го века.

В чём идея метода

Если совсем примитивно, то работает так: 

Вместо того чтобы строить сложную математическую модель, мы берём простую формулу и пуляем в неё случайные числа. Считаем результат по каждому числу и получаем результат с нужной нам точностью. Чем больше случайных чисел — тем точнее результат. 

Вот то же самое немного подробнее:

1. Выбираем, что мы хотим найти или посчитать — значение формулы, площадь, объём, распределение материала или что-то ещё.
2. Смотрим, как это считается в математике, и находим нужные формулы.
3. На основе формул составляем критерий проверки — если случайное значение попало в этот критерий, мы его учитываем как совпавшее число, а если не попало — как не совпавшее.
4. Запускаем алгоритм, который выдаёт случайные числа, и проверяем каждое по этому критерию.
5. Как наберётся достаточное количество случайных чисел — считаем результат. Обычно это соотношение чисел, которые попали в критерий и которые не попали.

Чем больше будет случайных чисел — тем точнее результат. 

Плюс этого метода в том, что нам не нужно запрягать весь математический аппарат для решения задачи — достаточно подставлять числа в формулу и смотреть, получилось верное значение или нет.

Как найти число пи методом Монте-Карло

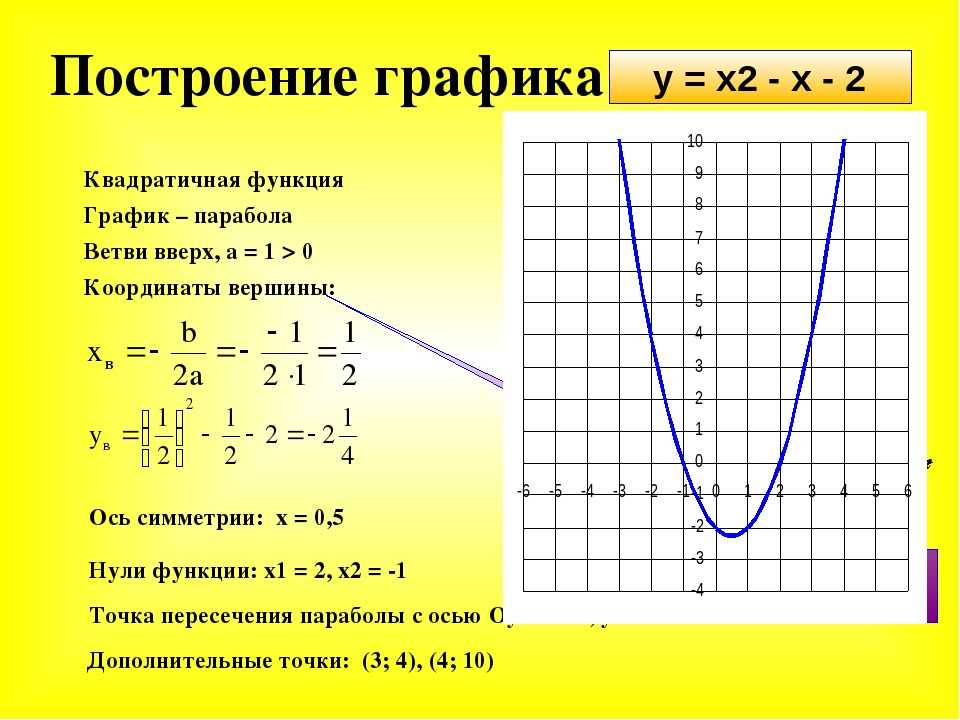
Для примера покажем классическое использование метода Монте-Карло — найдём число пи. Для этого нам понадобится круг, вписанный в квадрат, причём у круга радиус будет равен 1. Это значит, что сторона квадрата равна 2 — это диаметр (или два радиуса) круга:

В этот квадрат мы будем случайным образом кидать песчинки и смотреть, попадут они в круг или нет (но останутся в границах квадрата). Исходя из этого набора данных мы можем посчитать отношение всех песчинок, которые попали в круг, ко всем песчинкам.

Теперь смотрим на формулы: 

• площадь квадрата со стороной 2 равна четырём;
• площадь круга радиусом 1 равна πR² → π×1² = π.

Если мы разделим площадь круга на площадь квадрата, то получим π / 4. Но мы ещё не можем по условию посчитать площадь круга, потому что мы не знаем число π. Вместо этого мы можем разделить количество одних песчинок на другие — в этом и суть метода Монте-Карло. 

Это соотношение даст нам результат — π / 4. Получается, что если мы умножим этот результат на 4, то получим число π, причём чем больше песчинок мы кинем, тем точнее будет результат.

Кидать песчинки будем так: в качестве координат попадания X и Y будем брать случайные числа от 0 до 1. Это значит, что все числа попадут только в один квадрант — правый верхний:

Но так как в этом квадранте ровно четверть круга и ровно четверть квадрата, то соотношение промахов и попаданий будет таким же, как если бы мы бросали песчинки в целый круг и целый квадрат.

Чтобы проверить, попадает ли песчинка в круг, используем формулу длины гипотенузы: x² + Y² = 1 (так как гипотенуза — это радиус окружности):

Если длина гипотенузы меньше единицы — точка попадает в круг. В итоге мы посчитаем и общее количество точек, и точек, которые попали в круг. Потом мы разделим одно на другое, умножим результат на 4 и получим приближённое значение числа π.

Программируем поиск числа пи по методу Монте-Карло

Алгоритм на языке Python, читайте комментарии, чтобы лучше разобраться в происходящем:

# подключаем модуль случайных чисел
import random
 
# функция, которая посчитает число пи
def count_pi(n):
	# общее количество бросков
    i = 0
	# сколько из них попало в круг
    count = 0
    # пока мы не дошли до финального броска
    while i < n:
        # случайным образом получаем координаты x и y
        x = random.random()
        y = random.random()
        # проверяем, попали мы в круг или нет
        if (pow(x, 2) + pow(y, 2)) < 1:
			# если попали — увеличиваем счётчик на 1
            count += 1
		# в любом случае увеличиваем общий счётчик
        i += 1
    # считаем и возвращаем число пи
    return 4 * (count / n)
 
# запускаем функцию
pi = count_pi(1000000)
# выводим результат
print(pi)

Где ещё используется метод Монте-Карло

На методах Монте-Карло основано много полезного:

• моделирование облучения твёрдых тел ионами в физике;
• моделирование поведения разреженных газов
• исследования поведения разных тел при столкновении
• алгоритмы оптимизации и нахождения кратчайшего пути решения
• решение сложных интегралов (или когда их очень много)
• предсказание астрономических наблюдений
• поиск в дереве в различных алгоритмах
• алгоритмы работы некоторых функций квантового компьютера
• моделирование состояния приближённой физической среды

Без них изучать современный мир и совершать новые открытия было бы сложнее.

Что дальше

В следующей части поговорим про отжиг — интересное применение метода Монте-Карло, который имитирует физические процессы. Благодаря отжигу мы можем обучать нейросети и решать сложные комбинаторные задачи.

Текст:

Михаил Полянин

Редактор:

Максим Ильяхов

Художник:

Алексей Сухов

Корректор:

Ирина Михеева

Вёрстка:

Кирилл Климентьев

Соцсети:

Виталий Вебер

Словари (dict) и работа с ними. Методы словарей

Сегодня я расскажу о таком типе данных, как словари, о работе со словарями, операциях над ними, методах, о генераторах словарей.

Словари в Python — неупорядоченные коллекции произвольных объектов с доступом по ключу. Их иногда ещё называют ассоциативными массивами или хеш-таблицами.

Чтобы работать со словарём, его нужно создать. Сделать это можно несколькими способами. Во-первых, с помощью литерала:

>>> d = {}
>>> d
{}
>>> d = {'dict': 1, 'dictionary': 2}
>>> d
{'dict': 1, 'dictionary': 2}

Во-вторых, с помощью функции dict:

>>> d = dict(short='dict', long='dictionary')
>>> d
{'short': 'dict', 'long': 'dictionary'}
>>> d = dict([(1, 1), (2, 4)])
>>> d
{1: 1, 2: 4}

В-третьих, с помощью метода fromkeys:

>>> d = dict. fromkeys(['a', 'b'])
>>> d
{'a': None, 'b': None}
>>> d = dict.fromkeys(['a', 'b'], 100)
>>> d
{'a': 100, 'b': 100}

В-четвертых, с помощью генераторов словарей, которые очень похожи на генераторы списков.

>>> d = {a: a ** 2 for a in range(7)}
>>> d
{0: 0, 1: 1, 2: 4, 3: 9, 4: 16, 5: 25, 6: 36}

Теперь попробуем добавить записей в словарь и извлечь значения ключей:

>>> d = {1: 2, 2: 4, 3: 9}
>>> d[1]
2
>>> d[4] = 4 ** 2
>>> d
{1: 2, 2: 4, 3: 9, 4: 16}
>>> d['1']
Traceback (most recent call last):
  File "", line 1, in
    d['1']
KeyError: '1'

Как видно из примера, присвоение по новому ключу расширяет словарь, присвоение по существующему ключу перезаписывает его, а попытка извлечения несуществующего ключа порождает исключение. Для избежания исключения есть специальный метод (см. ниже), или можно перехватывать исключение.

Что же можно еще делать со словарями? Да то же самое, что и с другими объектами: встроенные функции, ключевые слова (например, циклы for и while), а также специальные методы словарей.

dict.clear() — очищает словарь.

dict.copy() — возвращает копию словаря.

classmethod

dict.fromkeys(seq[, value]) — создает словарь с ключами из seq и значением value (по умолчанию None).

dict.get(key[, default]) — возвращает значение ключа, но если его нет, не бросает исключение, а возвращает default (по умолчанию None).

dict.items() — возвращает пары (ключ, значение).

dict.keys() — возвращает ключи в словаре.

dict.pop(key[, default]) — удаляет ключ и возвращает значение. Если ключа нет, возвращает default (по умолчанию бросает исключение).

dict.popitem() — удаляет и возвращает пару (ключ, значение). Если словарь пуст, бросает исключение KeyError. Помните, что словари неупорядочены.

dict.setdefault(key[, default]) — возвращает значение ключа, но если его нет, не бросает исключение, а создает ключ со значением default (по умолчанию None).

dict.update([other]) — обновляет словарь, добавляя пары (ключ, значение) из other.

Существующие ключи перезаписываются. Возвращает None (не новый словарь!).

dict.values() — возвращает значения в словаре.

Для вставки кода на Python в комментарий заключайте его в теги <pre><code>Ваш код</code></pre>

БиоМатематика: Трансформация Графиков

Что такое горизонтальный перевод?

Горизонтальное перемещение графика эквивалентно смещению базового графика влево или вправо в направлении оси x . График перемещается на k единиц по горизонтали путем перемещения каждой точки на графике на k единиц по горизонтали.

Определение Для базовой функции f ( x ) и константа k , функция, заданная г ( х ) = ф ( х — к ), можно нарисовать, сдвинув f ( x ) k единиц по горизонтали.

 

Значение k определяет направление сдвига. В частности,

, если k > 0, базовый график сдвигается на k единиц вправо и , если k < 0, базовый граф сдвигается на k единиц влево.

Примеры горизонтального перемещения

Рассмотрим следующие базовые функции,

(1) ф ( х ) = 2 х ² ,

(2) г ( х ) = 5√ х .

Графическое представление функции (1), f ( x ), представляет собой параболу. Как вы думаете, график

у ₁ ( х ) = f ( х -3)

выглядит? Используя определение f ( x ), мы можем записать y ₁ ( x ) как

Y ₁ ( x ) = F ( x -3) = 2 ( x -3) ² = 2 ( x ² -6 x + + + 9) = 2 х ² -12 х + 18.

Однако в этом расширении нет необходимости, если вы понимаете графические преобразования. На основании определения горизонтального сдвига график y ₁ ( x ) должен выглядеть как график f ( x ), смещено на 3 единицы вправо. Взгляните на графики f ( x ) и y ₁ ( x ).

 

Функция (2), g ( x ), представляет собой функцию извлечения квадратного корня. Что бы график

г ₂ ( х ) = г ( х + 2)

выглядит? Используя наши знания о горизонтальных сдвигах, график y ₂ ( x ) должен выглядеть как базовый граф g ( x ) сдвинутый на 2 единицы влево. Мы можем записать y ₂ ( x ) как

Взгляните на графики g ( x ) и y ₂ ( x ).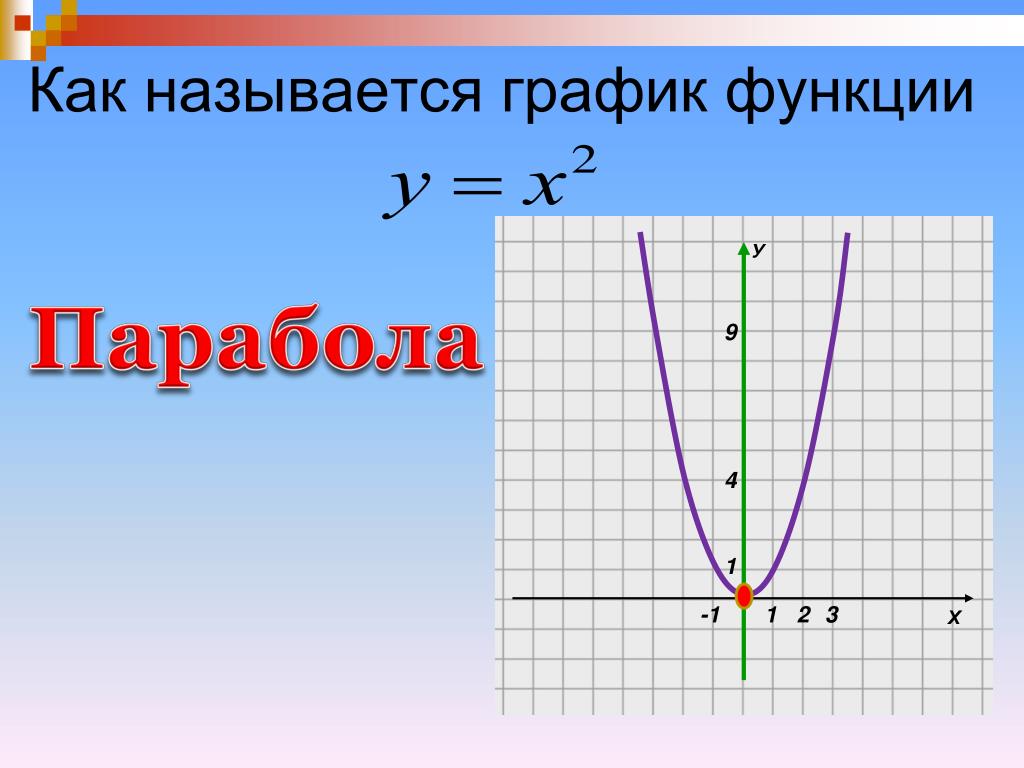

 

*****

В следующем разделе мы рассмотрим вертикальное растяжение и сжатие.

Вертикальные растяжения и сжатия

Операции над функциями: Переводы | SparkNotes

Переводы

График функции можно перемещать вверх, вниз, влево или вправо, добавляя или вычитание из вывода или ввода.

Добавление к выходу функции перемещает график вверх. Вычитание из вывода функции сдвигает график вниз. Вот графики y = f ( x ), y = f ( x ) + 2, и y = f ( x ) — 2. Примечание. что если ( x , y ₁ ) точка на графике f ( x ), ( x , y _{0 2 )9011 точка на график f ( x ) + 2, а ( x , y 3 ) является точкой на графике f ( x ) — 2, затем и 2 = y 1 + 2 и y 3 = y 1 — 2.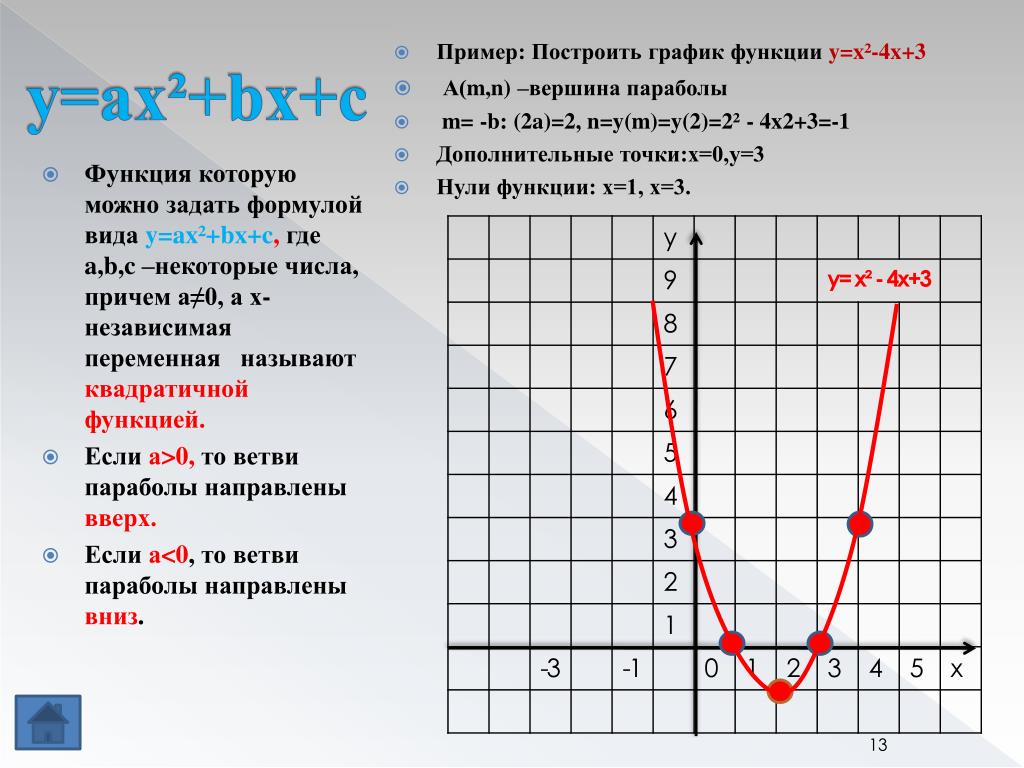 Например, (1, 2) находится на графике f ( x ), (1, 4) находится на графике f ( x ) + 2, а (1, 0) находится на графике из f ( x ) — 2. Графики f ( x ), f ( x ) + 2 и f ( x ) — 2}

При добавлении к входу функция увеличивается в и направление, добавление к вход уменьшает функцию в направлении x . Это потому что функция должна компенсировать добавленный ввод. Если функция выводит «7» когда вводится «3», и мы вводим x + 2, функция выводит «7», когда х = 1.

Таким образом, добавление к входу функции перемещает график влево, и вычитание из ввода функции сдвигает график вправо. Вот графики y = f ( x ), y = f ( x + 2) и y = f ( x — 2). Примечание что если ( x ₁ , y ) является точкой на графике f ( x ), ( x ₂ , 4 y) является точкой на 9025 график f ( x + 2) и ( x ₃ , y ) является точкой на графике f ( x — 2), тогда х ₂ = х ₁ — 2 и х ₃ = х ₁ + 2.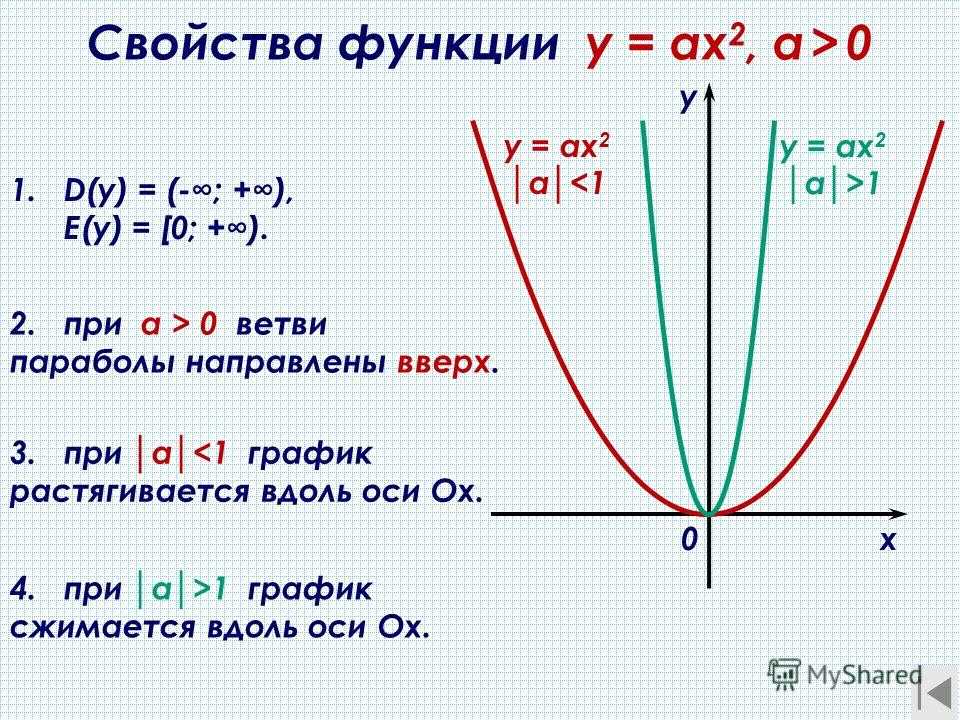 Например, (1, — 2) находится на график f ( x ), (- 1, — 2) находится на графике f ( x + 2), а (3, — 2) находится на график f ( x — 2). Графики f ( x ), f ( x + 2) и f ( x — 2)

Сдвиг графика вверх, вниз, влево или вправо без изменения формы, размера, или размеры графа, называется переводом.

Примеры : Если f ( x ) = x ² + 2 x , каково уравнение, если график перенесено:

a) 4 единицы вверх
b) 4 единицы вниз
c) 4 единицы влево
d) 4 единицы вправо

Решения:

а) ф ₁ ( x ) = f ( x ) + 4 = x ² + 2 x + 4
б) f ₂ ( x ) = f ( x ) — 4 = x ² + 2 x 402554
C) F ₃ ( x ) = F ( x + 4) = ( x + 4) ² +2 ( x + 4) ² +2 ( x + 4).

No related posts.