Наибольший общий делитель 42 и 63
Калькулятор «Наибольший общий делитель»
Какой наибольший общий делитель у чисел 42 и 63?
Ответ: НОД чисел 42 и 63 это 21
(двадцать один)
Нахождение наибольшего общего делителя для чисел 42 и 63 используя перечисление всех делителей
Первый способ нахождения НОД для чисел 42 и 63 — это перечисление всех делителей для обоих чисел и выбор из них наибольшего общего:
Все делители числа 42: 1, 2, 3, 6, 7, 14, 21, 42
Все делители числа 63: 1, 3, 7, 9, 21, 63
Следовательно, наибольший общий делитель для чисел 42 и 63 это 21
Нахождение наибольшего общего делителя для чисел 42 и 63 используя разложение чисел на простые множители
Второй способ нахождения наибольшего общего делителя для числе 42 и 63 — это перечисление всех простых множителей для чисел и перемножение общих.
Простые множители числа 42: 2, 3, 7
Простые множители числа 63: 3, 3, 7
Как мы видим, у чисел есть общие простые множители: 3, 7
Для нахождения НОД необходимо их перемножить: 3 × 7 = 21
Поделитесь текущим расчетом
Печать
https://calculat.io/ru/number/greatest-common-factor-of/42—63
<a href=»https://calculat.io/ru/number/greatest-common-factor-of/42—63″>Наибольший общий делитель 42 и 63 — Calculatio</a>
О калькуляторе «Наибольший общий делитель»
Данный калькулятор поможет найти наибольший общий делитель двух чисел. Например, он может помочь узнать какой наибольший общий делитель у чисел 42 и 63? Выберите первое число (например ’42’) и второе число (например ’63’). После чего нажмите кнопку ‘Посчитать’.
Наибольший общий делитель (НОД) для двух чисел - это наибольшее положительное целое число, которое делит каждое из целых чисел с нулевым остатком.
Калькулятор «Наибольший общий делитель»
Таблица наибольших общих делителей
| Число 1 | Число 2 | НОД |
|---|---|---|
| 27 | 63 | 9 |
| 28 | 63 | 7 |
| 29 | 63 | 1 |
| 30 | 63 | 3 |
| 31 | 63 | 1 |
| 32 | 63 | 1 |
| 33 | 63 | 3 |
| 34 | 63 | 1 |
| 35 | 63 | 7 |
| 36 | 63 | 9 |
| 37 | 63 | 1 |
| 38 | 63 | 1 |
| 39 | 63 | 3 |
| 40 | 63 | 1 |
| 41 | 63 | 1 |
| 42 | 63 | 21 |
| 43 | 63 | 1 |
| 44 | 63 | 1 |
| 45 | 63 | 9 |
| 46 | 63 | 1 |
| 47 | 63 | 1 |
| 48 | 63 | 3 |
| 49 | 63 | 7 |
| 50 | 63 | 1 |
| 51 | 63 | 3 |
| 52 | 63 | 1 |
| 53 | 63 | 1 |
| 54 | 63 | 9 |
| 55 | 63 | 1 |
| 56 | 63 | 7 |
Число 21
Свойства и характеристики одного числа
Все делители числа, сумма и произведение цифр, двоичный вид, разложение на простые множители.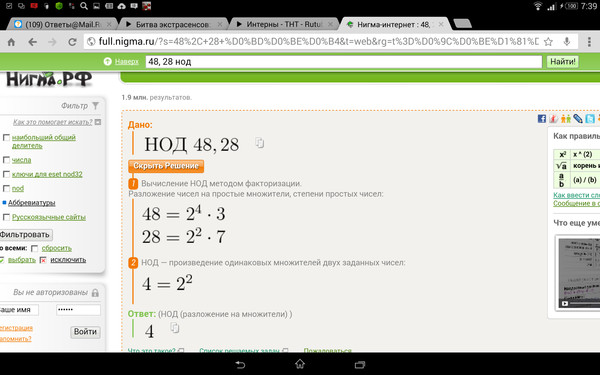 ..
..
Свойства пары чисел
Наименьшее общее кратное, наибольший общий делитель, сумма, разность и произведение чисел…
Сейчас изучают числа:
42 и 63 247882029 341211 21415955758 20960 2226 759 876593 532 201033 50000000000 346065 66 26640570 9332 2828619032160 8363 2950227975638 122666525 5308227108 846874 4122449 3156138558721 218362384
Двадцать один
Описание числа 21
Рациональное
нечетное
число 21
является составным.
Число 21 представляется произведением: 3 * 7.
Перевод числа в другие системы счисления: двоичная система: 10101, троичная: 210, восьмеричная: 25, шестнадцатеричная: 15. Конвертация из числа байтов — 21 байт .
Азбука Морзе для числа: ..— .—-
Число — число Фибоначчи.
Косинус 21: -0.5477, синус 21: 0.8367, тангенс 21: -1.5275. Логарифм натуральный: 3.0445. Десятичный логарифм числа: 1.3222. Если извлечь квадратный корень, получится 4.5826, а если кубический — 2.7589 Число 21 в квадрате это 441.00.
Число секунд 21 это 21 секунда .
В нумерологии это число означает цифру 3.
- ← 20
- 22 →
GCF, равный 42 и 63
GCF, равный 42 и 63, — это наибольшее возможное число, на которое 42 и 63 делятся точно без остатка. Множители 42 и 63 равны 1, 2, 3, 6, 7, 14, 21, 42 и 1, 3, 7, 9, 21, 63 соответственно. Существует 3 наиболее часто используемых метода нахождения НОК 42 и 63: алгоритм Евклида, разложение на простые множители и длинное деление.
| 1. | GCF 42 и 63 |
| 2. | Список методов |
| 3. | Решенные примеры |
| 4. | Часто задаваемые вопросы |
Что такое GCF 42 и 63?
Ответ: НГК 42 и 63 равно 21.
Объяснение:
НГК двух ненулевых целых чисел, x(42) и y(63), есть наибольшее натуральное число m(21) который делит и x (42), и y (63) без остатка.
Методы определения GCF 42 и 63
Методы определения GCF для 42 и 63 описаны ниже.
- Использование алгоритма Евклида
- Список общих факторов
- Метод длинного деления
GCF 42 и 63 по алгоритму Евклида
Согласно алгоритму Евклида, GCF(X, Y) = GCF(Y, X mod Y)
где X > Y, а mod — оператор по модулю.
Здесь X = 63 и Y = 42
- GCF(63, 42) = GCF(42, 63 mod 42) = GCF(42, 21)
- GCF(42, 21) = GCF(21, 42 mod 21) = GCF(21, 0)
- GCF(21, 0) = 21 (∵ GCF(X, 0) = |X|, где X ≠ 0)
Таким образом, значение GCF 42 и 63 равно 21.
GCF 42 и 63 путем перечисления общих факторов
- Коэффициенты 63: 1, 3, 7, 9, 21, 63
Существует 4 общих делителя чисел 42 и 63: 1, 3, 21 и 7. Следовательно, наибольший общий делитель чисел 42 и 63 равен 21.
GCF 42 и 63 путем длинного деления
GCF 42 и 63 — это делитель, который мы получаем, когда остаток становится равным 0 после повторного длинного деления.
- Шаг 1: Разделите 63 (большее число) на 42 (меньшее число).
- Шаг 2: Поскольку остаток ≠ 0, разделим делитель шага 1 (42) на остаток (21).
- Шаг 3: Повторяйте этот процесс до тех пор, пока остаток не станет равным 0.
Соответствующий делитель (21) — это НОД 42 и 63.
☛ Также проверьте:
- НОД 10 и 30 = 10
- GCF 56 и 72 = 8
- GCF 18 и 27 = 9
- GCF 4 и 9 = 1
- GCF 54 и 72 = 18
- GCF 27 и 30 = 3
- GCF 8 и 14 = 2
GCF 42 и 63 Примеры
Пример 1: Произведение двух чисел равно 2646. Если их GCF равен 21, какова их НОК?
Решение:
Дано: GCF = 21 и произведение чисел = 2646
∵ LCM × GCF = произведение чисел
⇒ НОК = Продукт/GCF = 2646/21
Следовательно, LCM равен 126.
Пример 2: Найдите наибольшее число, которое точно делит 42 и 63.
Решение:
Наибольшее число, которое точно делит 42 и 63, является их наибольшим общим делителем, т. е. НОД 42 и 63.
⇒ Множители 42 и 63:- Множители 42 = 1, 2, 3, 6, 7, 14, 21, 42
- Коэффициенты 63 = 1, 3, 7, 9, 21, 63
Таким образом, GCF чисел 42 и 63 равен 21.
Пример 3: Для двух чисел GCF = 21 и LCM = 126. Если одно число равно 63, найдите другое число.
Решение:
Дано: GCF (x, 63) = 21 и НОК (x, 63) = 126
∵ GCF × LCM = 63 × (x)
⇒ x = (GCF × LCM)/63
⇒ х = (21 × 126)/63
⇒ х = 42
Следовательно, другое число равно 42.
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Записаться на бесплатный пробный урок
Часто задаваемые вопросы о GCF 42 и 63
Что такое GCF 42 и 63?
GCF 42 и 63 равен 21 . Чтобы вычислить наибольший общий множитель (НОД) чисел 42 и 63, нам нужно разложить каждое число на множители (множители 42 = 1, 2, 3, 6, 7, 14, 21, 42; множители 63 = 1, 3, 7). , 9, 21, 63) и выберите наибольший множитель, который точно делит и 42, и 63, т. е. 21.
Какая связь между НОК и НОД 42, 63?
Следующее уравнение может быть использовано для выражения отношения между НОК и НОК 42 и 63, т. е. НОК × НОК = 42 × 63.
Как найти НОК 42 и 63 с помощью простой факторизации?
Чтобы найти НОК чисел 42 и 63, мы найдем простое разложение данных чисел, т. е. 42 = 2 × 3 × 7; 63 = 3 × 3 × 7,
⇒ Поскольку 3, 7 являются общими членами в простой факторизации 42 и 63. Следовательно, GCF(42, 63) = 3 × 7 = 21
Каковы методы нахождения GCF 42 и 63?
Существует три широко используемых метода нахождения GCF 42 и 63 .
- Путем перечисления общих факторов
- Длинным делением
- По простой факторизации
Как найти GCF чисел 42 и 63 методом деления в длину?
Чтобы найти НГК 42, 63 с помощью метода деления в длину, 63 нужно разделить на 42. Соответствующий делитель (21), когда остаток равен 0, принимается за НГК.
Если GCF 63 и 42 равен 21, Найдите его LCM.
GCF(63, 42) × LCM(63, 42) = 63 × 42
Так как GCF 63 и 42 = 21
⇒ 21 × НОК(63, 42) = 2646
.
Следовательно, НОК = 126
.
☛ Калькулятор GCF
Скачать БЕСПЛАТНО учебные материалы
GCF и LCM
Калькулятор модуля
Modulo Calculator помогает рассчитать модуль.
Операция по модулю находит остаток после деления одного числа на другое (иногда называемый модулем).
Для двух положительных чисел, a (делимое) и n (делитель), модуль n (сокращенно mod n) является остатком от евклидова деления a на n.


