Зная окружность как узнать радиус: Онлайн калькулятор радиуса круга. Как узнать радиус круга, окружности.

Шитье. Как рассчитать радиус и нарисовать окружность без циркуля — 3 способа!

загрузка…

Автор: Ольга Клишевская
Дорогие начинающие швеи-самоучки, сегодня я решила написать статью, которая нам поможет в будущем кроить детские панамки, взрослые пляжные шляпы, а также юбку-солнце, и естественно воланы. Как вы догадались, речь идет об умении рассчитать радиус окружности, и суметь нарисовать ее без циркуля. Потому что вполне возможно, что нам понадобится нарисовать окружности такого размера, для которого циркули и не продаются. Да и не у всех дома есть циркуль. Итак, на повестке дня следующее:

Расчет радиуса окружности, для панамки, волана и юбки-солнца.

Три способа нарисовать окружность без циркуля.

КАК РАССЧИТАТЬ РАДИУС ОКРУЖНОСТИ.

Для чего он нужен, этот расчет радиуса? Чтобы начертить окружность, нам надо знать радиус этой сомой окружности – то есть расстояние от одной ножки циркуля до другой.

Допустим нам надо нарисовать окружность донышка панамки, и все что мы знаем, это обхват головы ребеночка. Как широко надо раздвинуть ножки циркуля, чтобы в итоге получить окружность, совпадающую с размерами головы ребеночка?

Или нам нужно начертить окружность юбки-солнца, зная только то, что длина окружности должна идеально совпадать с обхватом нашей талии.

Сейчас, чтобы все было предельно ясно и понятно, разберем 2 конкретных случая, которые чаще всего встречаются в работе швей.

Это расчет радиуса донышка панамки. И расчет радиуса на выкройке юбки-солнца.

Итак, поехали…

Ситуация первая – нужно рассчитать радиус и начертить окружность дня панамки для девочки.

Эту история я красиво расписала в картинках прямо с текстом -рассуждением. Чтобы была понятна вся последовательность работы мозга. )))

 

 

Значит, чтобы узнать радиус – нам надо наш обхват головы ребеночка поделить на 6,28.

Берем мобильный телефон, находим в нем калькулятор и делим наши 42 см обхвата головы на 6,28 – получаем 6,68 см = то есть 6 см и 6 мм. Это и есть радиус.

Значит, нам надо раздвинуть ножки циркуля на расстояние 6 см 6 мм. И тогда нарисованная нами окружность будет равна 42 см – то есть ляжет ровненько по головке ребенка (только не забудьте ее обвесит отступив на 1 см для припусков на швы).

 

Ситуация вторая – нужно начертить окружность юбки-солнца. Все что мы знаем это обхват талии и длина юбки которую мы в итоге хотим получить.

В чертеже юбки солнца есть 2 окружности. Маленькая (внутренняя) должна лечь ровненько на нашу талию. То есть длина этой окружности должна совпасть с обхватом талии. Обхват талии 70 см, значит, и длина окружности должна быть 70 см (ну, разве что, там всякие сантиметры туда-сюда в виде припуска на швы, или еще какую дополнительную отделку в виде поясочка или кокеточки)

Значит нам нужно узнать, какого радиуса чертить круг, чтобы окружность в результате получилась длиной в эти нужные нам70 см.

На картинке ниже я все расписала и как рассчитать радиус маленькой окружности и как потом узнать радиус большой окружности.

И когда начерчена маленькая окружность. Все что нам нужно, это к маленькому радиусу прибавить желаемую длину юбки – и мы получаем большой радиус для большой окружности края юбки.

Вот с расчетами мы разобрались. Будем шить юбки и панамки – буду отправлять вас в эту статью.

Теперь давайте разберемся, как нарисовать окружность любого размера без циркуля.

КАК НАРИСОВАТЬ ОКРУЖНОСТЬ БЕЗ ЦИРКУЛЯ.

Вот здесь ниже я проиллюстрировала тремя картинками три способа. Надеюсь что все понятно нарисовано и прописано.

Да это быстрый способ – но надо следить за тем, чтобы карандаши не откланялись в сторону. Угол наклона карандаша изменяем радиус. Или надо чтобы один человек ровно держал один карандаш, а другой ровно перпендикулярно чертил вторым карандашом.

Вообще-то, чем ниже привязана нитка тем точнее будет окружность. Поэтому некоторые пользуются маленькими булавочками. Погрешность при отклонении булавки в сторону небольшая, и при шитье ею можно принебречь.

И все-таки самый вернейший способ начертить точный круг без циркуля, это при помощи обычной линейки и карандаша. Вот как это выглядит:

И далее по кругу, двигаем сантиметр (как часовую стрелку в часах) и отмечаем точки на одном и том же расстоянии – то есть на одной и той же цифре сантиметровой ленты. Вместо ленты можно использовать бечевочку с нанесенной на ней отметкой – главное убедитесь что бечевочка нисколько не тянется.

Ну вот и все – еще один пробел в знаниях устранен – теперь можно и на юбку-солнце замахнуться и на панамку – рассчитывать радиусы мы умеем .

Ольга Клишевская, специально для сайта “Женские разговоры”.

Как узнать окружность зная диаметр формула. Как найти и чему будет равна длина окружности

Чтобы написать, как найти диаметр круга, необходимо сначала определить, что это такое. Итак, диаметр круга — это прямая, которая проходит через центр круга и соединяет точки на окружности.

Ниже мы рассмотрим способы нахождения диаметра окружности через её длину, площадь вписанного круга, и через радиус.

Определение диаметра

Принято считать, что какой бы величины ни была окружность, отношение ее длины к диаметру — это постоянное число «Пи», которое примерно равно 3,14. Чтобы понять, как найти диаметр круга, следует привести формулы и на примере показать вычисления данной величины.

Радиус

Если известен радиус круга, то диаметр вычислить очень просто:

D = 2R, где D — это диаметр, а R — радиус. Получается, диаметр равен двум радиусам. Например, известно, что радиус равен 10 см, тогда диаметр вычисляем так: D=2*10, получается, что диаметр равен 20 см.

Длина окружности

В случае, если известна длина окружности, для вычисления может быть полезным число . Вот какой формулой можно воспользоваться: D = l/, где l — это длина круга. Получается, если длина окружности равна 18 см, то диаметр вычисляем так: D = 18 / 3,14 ≈ 5,73 см.

Площадь круга

Если известна только площадь круга, то это значение также можно применить. При этом площадь обозначается буквой S. Исходя из формулы S=R 2 , можно найти радиус, а значит, и диаметр. Итак, радиус R = √ (S / ). Для нахождения радиуса делим площадь на число Пи и извлекаем из этого значения квадратный корень. Таким образом, если площадь равна 25 см, то радиус вычисляется так: R = √ (25 / 3,14) ≈ √8 ≈ 2,8 см. Затем можно вычислить диаметр: D = 2R, D = 2,8*2= 5,6 см.

Таким образом, длину окружности (C ) можно вычислить, умножив константу π на диаметр (D ), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:

C = πD = 2πR

где C — длина окружности, π — константа, D — диаметр окружности , R — радиус окружности.

Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга.

Задачи на длину окружности

Задача 1. Найти длину окружности, если её диаметр равен 5 см.

Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:

C ≈ 3,14 · 5 = 15,7 (см)

Задача 2. Найти длину окружности, радиус которой равен 3,5 м.

Сначала найдём диаметр окружности, умножив длину радиуса на 2:

D = 3,5 · 2 = 7 (м)

теперь найдём длину окружности, умножив π на диаметр:

C ≈ 3,14 · 7 = 21,98 (м)

Задача 3. Найти радиус окружности, длина которой равна 7,85 м.

Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π

Площадь круга

Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга

:

S = πr 2

где S — площадь круга, а r — радиус круга.

Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:

Задачи на площадь круга

Задача 1. Найти площадь круга, если его радиус равен 2 см.

Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:

S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2)

Задача 2. Найти площадь круга, если его диаметр равен 7 см.

Сначала найдём радиус круга, разделив его диаметр на 2:

7: 2 = 3,5 (см)

теперь вычислим площадь круга по формуле:

S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2)

Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:

S = π	D 2	≈ 3,14	7 2	= 3,14	49	=	153,86	= 38,465 (см 2)
	4		4		4		4

Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .

Чтобы найти радиус круга по его площади, надо площадь круга разделить π , а затем из полученного результата извлечь квадратный корень:

r = √S : π

следовательно радиус будет равен:

r ≈ √12,56: 3,14 = √4 = 2 (м)

Число

π

Длину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно. Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге. В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.

Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:

Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. Это отношение и обозначается буквой π .

Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на

π . В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.

– это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.

Отрезок, который соединяет центр круга с точками его окружности, называется радиусом . В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром . Формула площади круга рассчитывается с помощью математической константы – числа π..

Это интересно : Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.

Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:

Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.

Площадь нашей окружности будет равна 50,24 кв. см.

Существует формула площади круга через диаметр . Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения .

Рассмотрим пример расчета площади круга через диаметр, зная его радиус. Пусть дана окружность с радиусом R = 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.

Теперь используем данные для примера расчета площади круга по приведенной выше формуле:

Как видим, в результате получаем тот же ответ, что и при первых расчетах.

Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.

Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности

Рассмотрим пример расчета площади круга через длину окружности. Пусть дана окружность с длиной l = 8 см. Подставим значение в выведенную формулу:

Итого площадь круга будет равна 5 кв. см.

Площадь круга описанного вокруг квадрата

Очень легко можно найти площадь круга описанного вокруг квадрата.

Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: отсюда .
После того, как найдем диагональ – мы сможем рассчитать радиус: .

И после подставим все в основную формулу площади круга описанного вокруг квадрата:

Множество предметов в окружающем мире имеют круглую форму.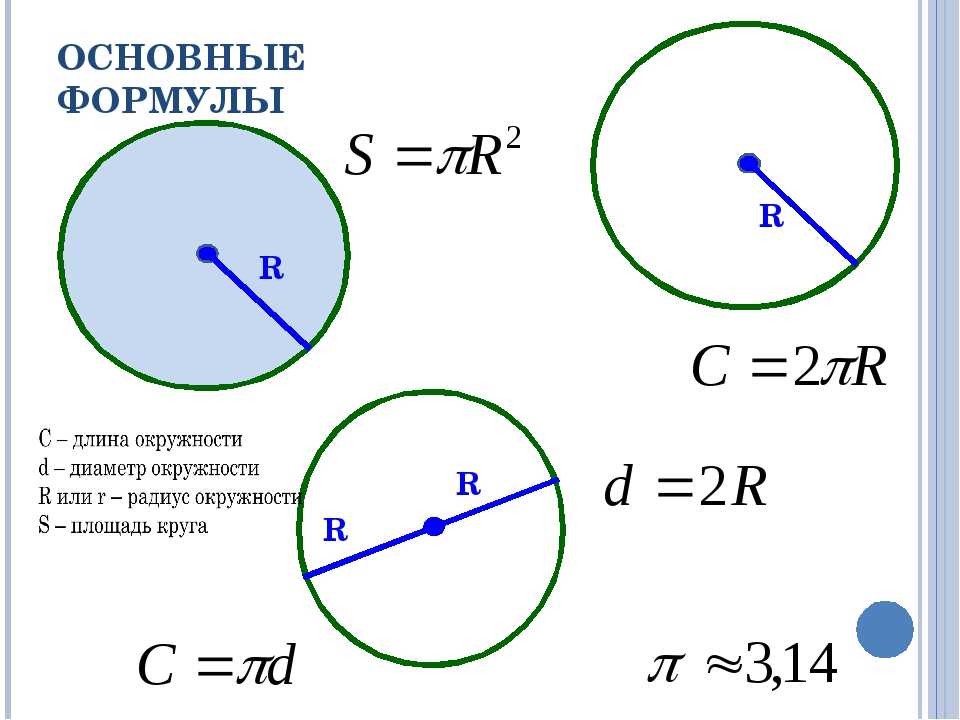 Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.

Существует несколько определений этой геометрической фигуры.

• Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
• Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом. При этом отрезок АВ – диаметр.
• Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
• Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка. Это определение выводится из теоремы Пифагора.

Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.

Определение окружности

Формулы

Как вычислить длину окружности через радиус? Это делается по простой формуле:

где L – искомая величина,

π – число пи, примерно равное 3,1413926.

Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.

Обозначения

Для нахождения через диаметр существует следующая формула:

Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.

Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда

L = 2πR = 2π√(S/π) = 2√(Sπ).

Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)

Резюмируя, можно сказать, что существует три основных формулы:

• через радиус – L = 2πR;
• через диаметр – L = πD;
• через площадь круга – L = 2√(Sπ).

Число пи

Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.

Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.

Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел.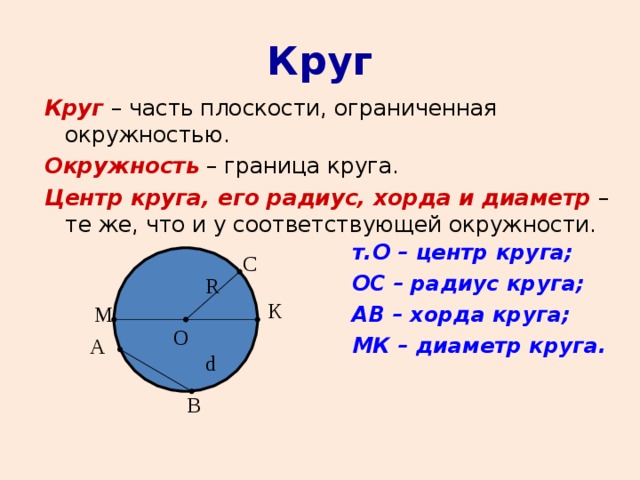 С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.

Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.

Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.

Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.

Полезное видео: длина окружности

Практическое применение

Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски:

L = πD = 3,14 * 20 = 62,8 см.

Другой пример: нужно построить забор вокруг круглого бассейна на определенном расстоянии. Если радиус бассейна 10 м, а забор нужно поставить на расстоянии 3 м, то R для полученной окружности будет 13 м. Тогда ее длина равна:

L = 2πR = 2 * 3,14 * 13 = 81,68 м.

Полезное видео: круг — радиус, диаметр, длина окружности

Итог

Периметр круга легко рассчитать по простым формулам, включающим диаметр или радиус. Также можно найти искомую величину через площадь круга. Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.

Как найти центр и радиус окружности из ее уравнения — Криста Кинг Математика

Какова стандартная форма уравнения окружности?

В этом уроке мы рассмотрим, как написать уравнение окружности в стандартной форме, чтобы найти центр и радиус окружности.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее. 92???

где ???r??? это радиус и ???(h,k)??? является центром.

Иногда, чтобы написать уравнение окружности в стандартной форме, вам нужно заполнить квадрат дважды, один раз для ???x??? и один раз для ???y???.

Приведение уравнения окружности к стандартной форме и определение ее центра и радиуса по стандартной форме

92=\фракция{19}{6}???

Центр круга ???(h,k)??? ???(-1,0)??? а радиус равен ???\sqrt{19/6}???. Исключить ???-\sqrt{19/6}??? потому что радиус не может быть отрицательным.

Получить доступ к полному курсу Алгебра 2

Начать

Изучение математикиКриста Кинг 30 мая 2021 г. математика, изучение онлайн, онлайн-курс, онлайн-математика, алгебра, алгебра 2, алгебра II, круг, уравнение окружности, центр и радиус, центр и радиус окружности, стандартная форма уравнение окружности

0 лайков

Как найти центр и радиус окружности (3 метода) – JDM Educational

Окружности используются в математике и в повседневной жизни. Однако знание того, как найти центр или радиус из другой заданной информации, также может быть полезным.

Итак, как найти центр и радиус круга? Чтобы найти центр и радиус окружности, запишите уравнение окружности в стандартной форме. Мы также можем использовать три точки на окружности (или две точки, если они находятся на противоположных концах диаметра), чтобы найти центр и радиус. Кроме того, мы можем использовать центр и одну точку на окружности, чтобы найти радиус.

Конечно, полезно ознакомиться со стандартной формой уравнения окружности, чтобы вы могли легко работать с этими различными ситуациями.

В этой статье мы поговорим о том, как найти центр и радиус окружности по информации о ней (например, ее уравнению или точкам на окружности). Мы также рассмотрим несколько примеров, чтобы прояснить концепции.

Начнем.

---

Проблемы с математикой?

Ищете репетитора?

---

Как найти центр и радиус окружности

Способ, которым мы находим центр и радиус окружности, зависит от информации, которую мы получили:

• Из уравнения : с уравнением в стандартной форме, мы можем легко найти центр и радиус круга. В противном случае нам нужно будет заполнить квадрат для переменной x или y (или обеих) для преобразования в стандартную форму.
• С двумя точками : по двум точкам на окружности на противоположных концах диаметра мы можем найти центр. Мы также можем найти радиус, учитывая центр и одну точку на окружности, используя формулу расстояния.
• С тремя точками : по трем точкам на окружности мы можем найти центр и радиус окружности, решив систему трех уравнений с тремя неизвестными (a, b и r).

В некоторых ситуациях мы можем найти центр и радиус круга, имея информацию о точках на круге.

Начнем с нахождения центра окружности по заданному уравнению.

Найти центр окружности из уравнения

Чтобы найти центр окружности из уравнения, мы всегда хотим преобразовать его в стандартную форму.

Как найти формулу экспоненты…

Включите JavaScript

Как найти формулу показательной функции

Помните, что уравнение окружности в стандартной форме задается как:

• ( x – a) ² + (y – b) ² = r ²

, где (a, b) – центр окружности, а r – радиус окружности.

Если нам дано уравнение не в стандартной форме, нам нужно сначала заполнить квадрат для одной или обеих переменных (x и y).

Пример 1: Центр окружности из уравнения в стандартной форме

Допустим, мы хотим найти центр окружности, заданной уравнением

• (x – 2) ² + (y + 4) ² = 9

Сравнивая это со стандартной формой выше, мы видим, что a = 2 и b = -4 (остерегайтесь этих отрицательных знаков: y — (-4) такое же, как y + 4 ).

Итак, центр окружности (a, b) = (2, -4).

Пример 2. Центр круга из уравнения путем заполнения квадрата одной переменной

Допустим, мы хотим найти центр окружности, заданной уравнением 004 Этот круг не стандартной формы, поэтому мы знаем, что нам нужно будет заполнить квадрат хотя бы для одной переменной.

Переставив члены таким образом, чтобы переменные сгруппировались, мы получим:

• (x ² + 6x) + (y ² + 10y + 25) = 27
9017 1

Легко видеть, что выражение с переменной y, y ² + 10y + 25, представляет собой трехчлен с полным квадратом, (y + 5) ² :

• (x ² + 6x ) + (y + 5) ² = 27

Теперь нам просто нужно дополнить квадрат выражения с переменной x, x ² + 6x. Помните, что для завершения квадрата мы берем половину коэффициента x и возводим результат в квадрат, а затем прибавляем его к обеим сторонам.

Здесь x-коэффициент равен 6, поэтому половина этого числа дает нам результат 3. Возведение результата в квадрат дает нам 3 ² = 9.

Итак, мы добавляем 9 к обеим частям уравнения, чтобы получить:

• (x ² + 6x + 9) + (y + 5) ² = 27 + 9 9 0034

Обратите внимание, что мы сгруппировали +9 слева с членами x. Это позволяет нам разложить на множители еще один идеальный квадратный трехчлен:

• (x + 3) ² + (y + 5) ² = 36

Теперь у нас есть уравнение окружности в стандартной форме. Сравнивая его с приведенным выше общим уравнением, мы находим, что a = -3 и b = -5.

Итак, центр окружности (a, b) = (-3, -5).

Пример 3: Центр круга из уравнения, заполнив квадрат для двух переменных

, скажем, мы хотим найти центр круга, заданный уравнением

• x ² + y ² + x ² + y ² + x ² + y ² + x ² + у 8x + 12y = 12

Этот круг не имеет стандартной формы, поэтому мы знаем, что нам нужно заполнить квадрат для обеих переменных.

Переставив члены так, чтобы переменные сгруппировались вместе, мы получаем:

• (x ² + 8x) + (y ² + 12y) = 12

Сначала нам нужно заполнить квадрат выражения с переменной x, x ^{2 9 0190 + 8х. Помните, что для завершения квадрата мы берем половину коэффициента x и возводим результат в квадрат, а затем прибавляем его к обеим сторонам.}

Здесь x-коэффициент равен 8, поэтому половина этого дает нам результат 4. Возведение результата в квадрат дает нам 4 ² = 16.

Итак, мы добавляем 16 к обеим частям уравнения, чтобы получить:

• (x ² + 8x + 16) + (y ² + 12y) = 12 + 16

Обратите внимание, что мы сгруппировали +12 слева с членами x. Это позволяет нам разложить как совершенный квадратный трехчлен:

• (x + 4) ² + (y ² + 12y) = 28

Теперь нам нужно завершить квадрат для выражения с переменная у, у ² + 12у. Помните, что для завершения квадрата мы берем половину коэффициента x и возводим результат в квадрат, а затем прибавляем его к обеим сторонам.

Здесь x-коэффициент равен 12, поэтому половина этого числа дает нам результат 6. Возведение результата в квадрат дает нам 6 ² = 36.

Итак, мы добавляем 36 к обеим частям уравнения, чтобы получить:

• (x ² + 8x + 16) + (y ² + 12y + 36) = 28 + 36

Обратите внимание, что мы сгруппировали +36 слева с у условия. Это позволяет нам разложить как совершенный квадратный трехчлен:

• (x + 4) ² + (y + 6) ² = 64

Теперь у нас есть уравнение окружности в стандартной форме. Сравнивая его с приведенным выше общим уравнением, мы находим, что a = -4 и b = -6.

Итак, центр окружности (a, b) = (-4, -6).

Найти центр окружности с двумя точками (на концах диаметра)

Имея две точки на окружности, мы можем найти центр. Если они не лежат на одном диаметре, то у нас недостаточно информации, и мы можем указать только все семейство окружностей, а не одну конкретную окружность.

Однако по двум точкам на окружности, лежащим на концах диаметра, мы можем найти центр окружности.

Центр круга будет в середине любого диаметра, нарисованного на круге.

Все, что нам нужно сделать, это найти середину отрезка между двумя точками на диаметре.

Помните, что для отрезка с концами (x ₁ , y ₁ ) и (x ₂ , y ₂ ) формула средней точки определяется как:

• (х _м , у _м ) = ((х ₁ + х ₂ ) / 2, (у ₁ + у _{2 904 06 ) / 2)}

В основном, x _m — это среднее значение координат x конечных точек, а y _m — это среднее значение координат y конечных точек.

Давайте попробуем на примере, чтобы увидеть, как это работает.

Пример: найти центр окружности с двумя точками на диаметре

Допустим, мы хотим найти центр окружности с точками (0, 0) и (6, -8) в качестве концов диаметра.

Использование формулы средней точки для нахождения центра окружности дает нам:

• (x _м , y _м ) = ((x ₁ + x ₂ ) / 2, (у ₁ + у ₂ ) / 2)
• (х _м , у _м ) = ((0 + 6) / 2, (0 + -8) / 2) 9016 2
• ( х _м , у _м ) = (6 / 2, -8/ 2)
• (х _м , у _м ) = (3, -4) 9016 2

Итак, центр этого круга находится в точке (3, -4).

Мы также можем найти радиус окружности, если захотим. Это просто половина диаметра, который определяется формулой расстояния:

• D = √((x ₂ – x ₁ ) ² + (y ₂ – y ₁ ) ² )
• D = √((6 – 0) ² + (-8 – 0) ² )
• D = √( (6) ² + (-8) ² )
• D = √(36 + 64)
• D = √(100)
• D = 10

Таким образом, диаметр равен 10, и радиус равен 5.

Помните, что диаметр Окружность — это длина самой длинной прямой линии, которую можно провести между двумя точками окружности. Радиус равен половине длины диаметра.

---

Проблемы с математикой?

Ищете репетитора?

---

Найти центр окружности по трем точкам

Чтобы найти центр окружности по трем точкам, мы можем просто подставить значения x и y из каждой точки в уравнение окружности.

Тогда мы можем установить все 3 уравнения равными друг другу (все они равны r ² , или квадрату радиуса).

Затем мы можем написать отдельные уравнения, упростить их и одновременно решать линейные уравнения.

Давайте рассмотрим пример.

Пример: найти центр окружности по трем точкам

Допустим, нам даны точки (-1, -3), (-2, 4) и (5, 5) на окружности.

Подставим каждую из этих точек по очереди в стандартную форму окружности:

• (x – a) ² + (y – b) ² = r ²

Для первой точки (-1, -3) получаем: 9000 5

• ( -1 – а) ² + (-3 – б) ² = r ²

Для второй точки (-2, 4) получаем:

• (-2 — а ) ² + (4 – б) ² = r ²

Для третьей точки (5, 5) получаем:

• (5 – а) ² + (5 – b) ² = r ²

Мы можем положить любые две левые части равными друг другу, поскольку все правые части равны r ² (независимо от значения р).

Приравняв первые две левые части, получим:

• (-1 – a) ² + (-3 – b) ² = (-2 – a) ² + (4 – b) ) ²
• 1 + 2а + а ² + 9 + 6б + б ² = 4 + 4а + а ² + 16 – 8б + б ²
• 1 + 2а + а ² + 9 + 6б = 4 + 4а + а ² + 16 – 8б [вычесть b ² с обеих сторон ]
• 1 + 2a + 9 + 6b = 4 + 4a + 16 – 8b [вычесть ² с обеих сторон]
• 10 + 2a + 6b = 20 + 4a – 8b  [объединить постоянные члены на обе стороны]
• -10 – 2a + 14b = 0  [собрать все термины на одной стороне и объединить подобные термины]
• 5 + a – 7b = 0 [разделить на -2 с обеих сторон]

Приравняв первую и третью левую части, получим:

•   (-1 – a) ² + ( — 3 – б) ² = (5 – а) ² + (5 – б) ²
• 1 + 2а + а ² + 9 + 6б + б ² = 25 – 10а + а ² + 25 – 10б + б ²
• 1 + 2а + а ² + 9 + 6б = 25 – 10а + а ² + 25 – 10b [вычесть b ² с обеих сторон]
• 1 + 2a + 9 + 6b = 25 – 10a + 25 – 10b [вычесть a ² с обеих сторон]
• 10 + 2a + 6b = 50 – 10a – 10b  [объединить постоянные члены с обеих сторон]
• -40 + 12a + 16b = 0  [собрать все члены с одной стороны и объединить одинаковые члены]
• -10 + 3a + 4b = 0 [разделить на 4 с обеих сторон]

Теперь мы можем решить следующую систему методом исключения:

• 5 + a – 7b = 0
• -10 + 3a + 4b = 0

Для этого умножьте первое уравнение на -3, чтобы получить:

• -15 – 3а + 21b = 0
• -10 + 3a + 4b = 0

Теперь сложите два уравнения, чтобы получить:

• -25 + 0a + 25b = 0
• 1 = б

Итак, при b = 1 находим:

• 5 + a – 7b = 0
• 5 + а – 7(1) = 0
• 5 + а – 7 = 0
• а – 2 = 0
• а = 2

Итак, центр окружность находится в точке (a, b) = (1, 2). Затем мы можем использовать центр и любую точку на окружности, чтобы найти радиус, используя формулу расстояния (подробнее об этом методе ниже).

Найдите радиус круга из уравнения

Чтобы найти радиус круга из уравнения, мы всегда хотим преобразовать его в стандартную форму.

Помните, что уравнение окружности в стандартной форме задается формулой:

• (x – a) ² + (y – b) ² = r ²
90 171

где ( a, b) — центр окружности, r — радиус окружности.

Если нам дано уравнение не в стандартной форме, нам нужно сначала заполнить квадрат для одной или обеих переменных (x и y).

Пример 1: центр окружности из уравнения в стандартной форме

Допустим, мы хотим найти радиус окружности, заданной уравнением приведение этого к стандартной форме выше мы видим, что r = 7 (поскольку r ² = 49 — не забудьте взять квадратный корень, чтобы найти r).

Итак, радиус окружности равен r = 7.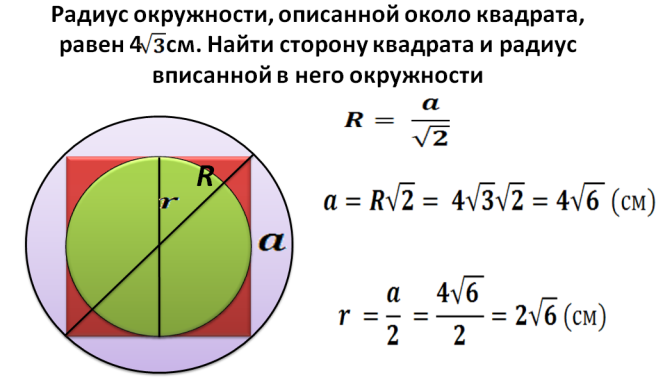

Пример 2. Радиус окружности из уравнения путем заполнения квадрата

Допустим, мы хотим найти радиус окружности, заданный уравнением

• x ² + y ² + 8x + 12y + 12 = 24

Этот круг не имеет стандартной формы, поэтому мы знаем, что нам нужно заполнить квадрат хотя бы для одной переменной.

Переставив члены таким образом, чтобы переменные сгруппировались, мы получим:

• (x ² + 8x) + (y ² + 12y) = 24 – 12
9015 9 (х ² + 8х) + (у ² + 12у) = 12

Чтобы завершить возведение в квадрат переменной x, x ² + 8x, мы возьмем половину от 8, чтобы получить 4, и возведем этот результат в квадрат, чтобы получить 16. Прибавим 16 к обеим частям:

• (x ² + 8x + 16) + (y ² + 12y) = 12 + 16
• (x ² + 8x + 16) + (y ² + 12y) = 28

Теперь нам нужно чтобы разложить выражение x на множители, x ² + 8x + 16.   Это идеальный квадратный бином: (x + 4) ² .

• (x + 4) ² + (y ² + 12y) = 28

половина из 12, чтобы получить 6 , и возведите этот результат в квадрат, чтобы получить 36. Добавим 36 к обеим частям:

• (x + 4) ² + (y ² + 12y + 36) = 28 + 36
• 90 033 (х + 4) ² + (y ² + 12y + 36) = 64

Теперь нам нужно разложить выражение y на множители, y ² + 12y + 36.  Это идеальный квадратный бином: (y + 6) ² .

• (х + 4) ² + (у + 6) ² = 64
• (х + 4) ² + (у + 6) 9 0189 2 = 8 ²

Мы также переписали 64 как 8 ² , так как это соответствует r ² в правой части уравнения окружности в стандартной форме.

Теперь мы знаем, что радиус окружности равен r = 8.

Найти радиус окружности по данным центра и точки

Если мы знаем центр окружности и одну точку на окружности, мы можем найти радиус с помощью формулы расстояния.

(Помните, что радиус — это расстояние между центром окружности и любой точкой на окружности.)

Давайте рассмотрим пример того, как это сделать.

Пример: нахождение радиуса окружности по центру и точке на окружности

Предположим, что вам дан центр окружности в точках (4, 3) и точка на окружности в точках (16, 12) . Используя формулу расстояния, мы получаем:

• D = √((х ₂ – х ₁ ) ² + (у ₂ – у ₁ ) ² )
• D = √((16 – 4 ) ² + (12 – 3) ² )
• D = √((12) ² + (9) ² )
• Д = √(144 + 81)
• D = √(225)
• D = 15

Итак, радиус окружности равен 15.

Найдите радиус окружности с двумя точками на окружности

В этом случае мы не можем решить для одного круга, так как у нас недостаточно информации. Вместо этого мы получили бы целое семейство окружностей, содержащих обе точки.

Если у нас также есть центр или третья точка на окружности, мы можем найти радиус (используя формулу расстояния с центром в качестве одной точки и одной из точек на окружности в качестве другой точки).

Затем мы можем использовать центр и радиус, чтобы записать уравнение окружности в стандартной форме.

Имея всего две точки на окружности, мы можем указать только семейство окружностей, а не конкретную. Нам нужно больше информации (например, центр или третья точка), чтобы дать конкретный круг.

Заключение

Теперь вы знаете, как найти центр и радиус круга в различных ситуациях. Вы также знаете, как использовать формулы средней точки и расстояния в качестве сокращений, чтобы сделать ваши вычисления немного проще.

Вы можете узнать о длине окружности и площади круга в моей статье здесь.

No related posts.