Ноль на бесконечность умножить на бесконечность: Неопределенность вида ноль умножить на бесконечность

Почему нельзя в математике делить на ноль и умножать бесконечность на 0 — правило

Очень часто многие задаются вопросом, почему же нельзя использовать деление на ноль? В этой статье мы очень подробно расскажем о том, откуда появилось это правило, а также о том, какие действия можно выполнять с нолем….

Ноль можно назвать одной из самых интересных цифр. У этой цифры нет значения, она означает пустоту в прямом смысле слова. Однако, если ноль поставить рядом с какой-либо цифрой, то значение этой цифры станет больше в несколько раз.

Число очень загадочно само по себе. Его использовал еще древний народ майя. У майя ноль означал «начало», а отсчет календарных дней также начинался с нуля.

Очень интересным фактом является то, что знак ноля и знак неопределенности у них были похожи. Этим майя хотели показать, что ноль является таким же тождественным знаком, как и неопределенность. В Европе же обозначение нуля появилось сравнительно недавно.

Также многим известен запрет, связанный с нолем. Любой человек скажет, что на ноль нельзя делить. Это говорят учителя в школе, а дети обычно верят им на слово. Обычно детям либо просто не интересно это знать, либо они знают, что будет, если, услышав важный запрет, сразу же спросить «А почему нельзя делить на ноль?». Но когда становишься старше, то просыпается интерес, и хочется побольше узнать о причинах такого запрета. Однако существует разумное доказательство.

Содержание

Действия с нулем

Для начала необходимо определить, какие действия с нулем можно выполнять. Существует несколько видов действий:

• Сложение,
• Умножение,
• Вычитание,
• Деление (ноля на число),
• Возведение в степень.

Важно! Если при сложении к любому числу прибавить ноль, то это число останется прежним и не поменяет своего числового значения. То же произойдет, если от любого числа отнять ноль.

При умножении и делении все обстоит немного иначе. Если умножить любое число на ноль, то и произведение тоже станет нулевым.

Рассмотрим пример:

0*5=0

Запишем это как сложение:

0+0+0+0+0=0

Всего складываемых нолей пять, вот и получается, что

0*5=0

Попробуем один умножить на ноль. Результат также будет нулевым.

Ноль также можно разделить на любое другое число, не равное ему. В этом случае получится дробь, значение которой также будет нулевым. Это же правило действует и для отрицательных чисел. Если ноль делить на отрицательное число, то получится ноль.

0:(-5)=0

Также можно возвести любое число в нулевую степень. В таком случае получится 1. При этом важно помнить, что выражение «ноль в нулевой степени» абсолютно бессмысленно. Если попытаться возвести ноль в любую степень, то получится ноль. Пример:

04=0*0*0*0

Пользуемся правилом умножения, получаем 0.

Это интересно! Свойства натуральных логарифмов: график, основание, функции, предел, формулы и область определения

Так можно ли делить на ноль

Итак, вот мы и подошли к главному вопросу. Можно ли делить на ноль вообще? И почему же нельзя разделить число на ноль при том, что все остальные действия с нулем вполне существуют и применяются? Для ответа на этот вопрос необходимо обратиться к высшей математике.

Начнем вообще с определения понятия, что же такое ноль? Школьные учителя утверждают, что ноль-это ничто. Пустота. То есть когда ты говоришь, что у тебя 0 ручек, это значит, что у тебя совсем нет ручек.

В высшей математике понятие «ноль» более широкое. Оно вовсе не означает пустоту. Здесь ноль называют неопределенностью, так как если провести небольшое исследование, то получается, что при делении ноля на ноль мы можем в результате получить любое другое число, которое не обязательно может быть нолем.

Знаете ли вы, что те простые арифметические действия, которые вы изучали в школе не так равноправны между собой? Самыми базовыми действиями являются сложение и умножение.

Для математиков не существует понятий «деление» и «вычитание». Допустим: если от пяти отнять три, то останется два. Так выглядит вычитание. Однако, математики запишут это таким образом:

Х+3=5

Таким образом, получается, что неизвестной разностью является некое число, которое нужно прибавить к 3, чтобы получить 5. То есть, не нужно ничего вычитать, нужно просто найти подходящее число. Это правило действует для сложения.

Немного иначе дела обстоят с правилами умножения и деления. Известно, что умножение на ноль приводит к нулевому результату. Например, если 3:0=х, тогда, если перевернуть запись, получится 3*х=0. А число, которое умножалось на 0 даст ноль и в произведении. Получается, что числа, которое бы давало в произведении с нолем какую-либо величину, отличную от ноля, не существует. А значит, деление на ноль бессмысленно, то есть оно подходит к нашему правилу.

Но что будет, если попытаться разделить сам ноль на себя же? Возьмем как х некое неопределенное число. Получается уравнение 0*х=0. Его можно решить.

Если мы попробуем взять вместо х ноль, то мы получим 0:0=0. Казалось бы, логично? Но если мы попробуем вместо х взять любое другое число, например, 1, то в конечном итоге получится 0:0=1. Та же ситуация будет, если взять любое другое число и подставить его в уравнение.

В этом случае получится, что мы можем как множитель взять любое другое число. Итогом будет бесконечное множество разных чисел. Порой все же деление на 0 в высшей математике имеет смысл, но тогда обычно появляется некое условие, благодаря которому мы сможем все-таки выбрать одно подходящее число. Это действие называется «раскрытием неопределенности». В обычной же арифметике деление на ноль снова потеряет свой смысл, так как мы не сможем выбрать из множества какое-то одно число.

Важно! На ноль нельзя разделить ноль.

Ноль и бесконечность

Бесконечность очень часто можно встретить в высшей математике. Так как школьникам просто не важно знать о том, что существуют еще математические действия с бесконечностью, то и объяснить детям, почему делить на ноль нельзя, учителя как следует не могут.

Основные математические секреты ученики начинают узнавать лишь на первом курсе института. Высшая математика предоставляет большой комплекс задач, которые не имеют решения. Самыми известными задачами являются задачи с бесконечностью. Их можно решить при помощи математического анализа.

К бесконечности также можно применить элементарные математические действия: сложение, умножение на число. Обычно еще применяют вычитание и деление, но в конечном итоге они все равно сводятся к двум простейшим операциям.

Но что будет, если попытаться:

• Бесконечность умножить на ноль. По идее, если мы попробуем умножить на ноль любое число, то мы получим ноль. Но бесконечностью является неопределенное множество чисел. Так как мы не можем выбрать из этого множества одно число, то выражение ∞*0 не имеет решения и является абсолютно бессмысленным.
• Ноль делить на бесконечность. Здесь происходит та же история, что и выше. Не можем выбрать одно число, а значит не знаем на что разделить. Выражение не имеет смысла.

Важно! Бесконечность немного отличается от неопределенности! Бесконечность является одним из видов неопределенности.

Теперь попробуем бесконечность делить на нуль. Казалось бы, должна получиться неопределенность. Но если мы попробуем заменить деление умножением, то получится вполне определенный ответ.

Например: ∞/0=∞*1/0= ∞*∞ = ∞.

Получается такой математический парадокс.

Ответ, почему нельзя делить на ноль

Мысленный эксперимент, пробуем делить на ноль

Вывод

Итак, теперь нам известно, что ноль подчиняется практически всем операциям, которые производят с обычными числами, кроме одной единственной. На ноль делить нельзя только потому, что в результате получается неопределенность. Также мы узнали, как производить действия с нолем и бесконечностью. Результатом таких действий будет неопределенность.

Это интересно! Как определить определенные интегралы от нуля, константы и с доказательством

«Можно ли бесконечность делить на ноль?» — Яндекс Кью

Популярное

Сообщества

На возможность деления на ноль меня натолкнула гипотеза Римана. Деление на ноль запрещено определением ноля.

Но мы получаем несоответствие.Основная система двоичная.Все остальные производные.Ноль определяеться как число, которое при прибавлении и отнимании ни какое число не изменяет.А когда оно приписывается справа или слева, через запятую.Оно изменяет его согласно разрядности системы счисления.Что соответствует такому же колличеству прибавлений и отниманий.Для обоснования создаеться целый аппарат математической логики.Но решить проблемму полность она не может.Гипотеза Римана регуляризирует натуральный ряд.Т.е.суммирует вещественный и комплексный ряд.Но эти ряды имеют разную силу.Комлексный ряд более слабый.

МатематикаНаука

Андрей Троицкий

20 сентября 2021  ·

807

ОтветитьУточнить

Maxim Vyalkov

Математика

1,4 K

Интересующие темы: история математики, история христианства, библеистика.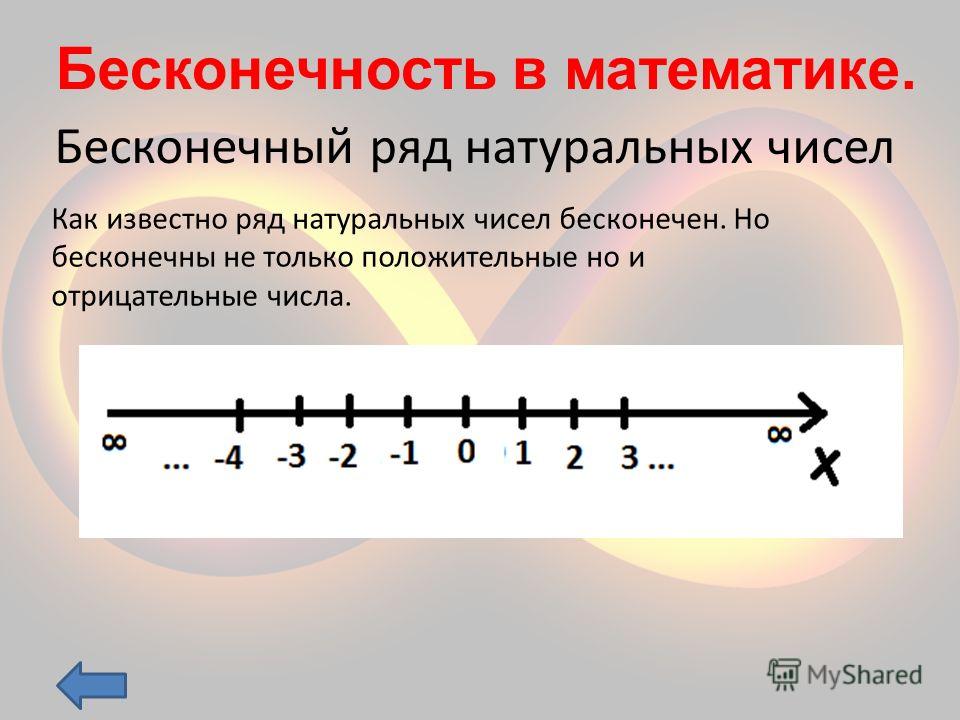   · 24 окт 2021

Это бессвязный набор тезисов. При чём тут написание нуля «слева» или «справа»? Что значит «сильнее» или «слабее» и применительно к чему? К теоретико-множественному подходу?

В рамках школьного курса запрет деления на ноль объясняется двояко:

1. Арифметически: потому что теряет смысл сама операция деления.
2. В рамках элементарной алгебры («школьной алгебры»): деление есть обратная операция к умножению, но не существует такого умножения, к которому деление на ноль чего-либо было бы обратным.

На чем вопрос деления на ноль в рамках школьного курса и вплоть до ТФДП можно считать закрытым.

Вопрос о «делении бесконечности на ноль» в рамках ТФДП лишен смысла, потому что «бесконечность это не число» и у Коши ∞ / 0 указано как неопределенность.

Прежде, чем задаваться вопросом о «делении бесконечности на ноль», нужно ответить на вопросы:

1. ЗАЧЕМ
2. С какой ситуацией мы работаем
3. ЧТО ИМЕННО Вы подразумеваете под «бесконечностью»?
4. ЧЕГО ИМЕННО Вы хотели бы достичь.

В общем, в такие моменты у меня просыпается «внутренний финитист» и сразу хочется «неистовствовать» по-Есенин-Вольпински, что называется.

Пока что Ваш вопрос не показывает, что Вы не владеете терминологии, выдумывая какой-то свой собственный язык, не имеющий к математике отношения. Начните с учебника Демидовича — с самого базового уровня. Потом учебники Эдмунда Ландау и Джеймса Стюарта. А потом можно уже и к Джерому Кислеру переходить. И вот тогда и поговорим.

Андрей Троицкий

25 октября 2021

Специальные методы суммирования, использующиеся в некоторых разделах математики, позволяют присвоить конечные… Читать дальше

Комментировать ответ…Комментировать…

Лучший

Elena E.

11

Физик и математик. Работаю в академическом институте, преподаю в университете  · 19 окт 2021

Честно сказать, в Ваших рассуждениях некий набор собственных измышлений, не имеющих ничего общего с математикой. В частности, за уши притянуто приписывание нуля справа и слева, да и с какой позиции комплексные числа более слабые? А гипердействительные — сильнее или слабее? В математике достаточно точно определяются операции деления и умножения на нуль и бесконечности… Читать далее

Андрей Троицкий

20 октября 2021

Спасибо за критику!!!Наконец нашел серьезного оппонента.Предлагаю встретиться здесь:http://mathhelpplanet.com/viewt… Читать дальше

Комментировать ответ…Комментировать…

Первый

fedor f.Федор трофименков

1

пенсионер  · 26 сент 2021

Вообще, если разумно представить , что в реальности ноль обозначает бесконечно малое число,то бесконечно большое число /т. е. бесконечность/ разделить на бесконечно малое,/ т. е. ноль/, даст нам в ответе бесконечность в степени два, а это в конечном итоге есть все та же бесконечность.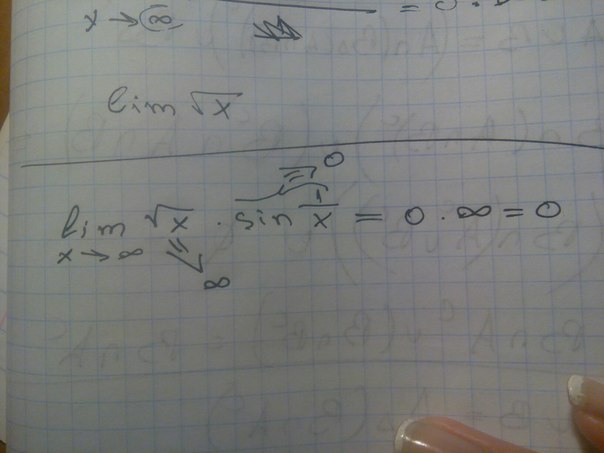

Комментировать ответ…Комментировать…

Первый

Алексей Онучин

Норм  · 26 сент 2021

Можно делать в жизни, что угодно, вопрос только для чего) скажите хоть одну ситуацию, когда вам такое может понадобиться? Алалаталалаьалалалаьал

Ber Strider

26 сентября 2021

Если мы бесконечность приравняем к некой переменной X, то с неким числом X мы можем выполнять любые допустимые опер… Читать дальше

Комментировать ответ…Комментировать…

мага магашка

2

Биолог  · 24 сент 2021

Если рассматривать натуральные числа, их можно расширить до чисел с бесконечностями, даже 2мя способами. В обычном смысле операция деления просто не определяется для знаменателя равного нулю . Мы не получаем ни чего, в том числе и бесконечности, имея в виду символическую запись предела частного числа и бесконечно малой функции.

Это все по отношению к бесконечности… Читать далее

Комментировать ответ…Комментировать…

Николай

Программирование на языке maxscript. Саморазвитие, философия.  · 27 сент 2021

Если число делить на очень, очень малое число, то в результате получится какое то огромное число. Но на ноль делить нельзя и линия нуля будет как асимптота, к которой будет бесконечно приближаться график функции деления на ноль, но никогда не пересечётся с линией нуля. Ну и логически если помыслить, что значит делить на ноль? Это что? Ты делишь яблоко не на троих, и не… Читать далее

Андрей Троицкий

29 сентября 2021

∞ ÷ 0 ≠ ∞2

Комментировать ответ…Комментировать…

Первый

Николай

Программирование на языке maxscript. Саморазвитие, философия.  · 27 сент 2021

Если число делить на очень, очень малое число, то в результате получится огромное число. Но на ноль делить нельзя и линия нуля будет как асимптота, к которой будет бесконечно приближаться график функции деления на ноль, но никогда не пересечётся с линией нуля. Ну и логически если помыслить, что значит делить на ноль? Это что? Ты делишь яблоко не на троих, и не на… Читать далее

Комментировать ответ…Комментировать…

Первый

Андрюха

-1

27 сент 2021

На нашей планете можно все что угодно если это не нарушает закон, и не причиняет вред жизни и здоровья людей и окружающей среде. Хотите бесконечность делить на ноль, пожалуйста делите. Это не запрещено.

Комментировать ответ…Комментировать…

Timothy Boltius

26 сент 2021

Можно ли «бесконечность» вообще делить и рассматривать такое значение как натуральное число ? Думаю нет и не стоит.
Но, если очень хочется, — то в итоге, думаю, ноль можно будет получить. Но это не точно.)

Комментировать ответ…Комментировать…

Вы знаете ответ на этот вопрос?

Поделитесь своим опытом и знаниями

Войти и ответить на вопрос

1 ответ скрыт(Почему?)

Нулевой раз Бесконечность | Superprof

В этой статье мы обсудим, как оценить заданную функцию, если ее предел приближается к бесконечности, и мы получаем неопределенный вид нуль умножить на бесконечность или бесконечность умножить на ноль. Но прежде чем приступить к обсуждению этого, сначала мы посмотрим, что такое пределы и правило Лопиталя, потому что оба эти понятия тесно связаны с нашей основной темой.

Что такое ограничения?

Пределы используются для представления того, как работает функция, когда ее независимая переменная x близка к определенному числу. Формальное определение предела дано ниже:

Предположим, f — функция, определенная на определенном открытом интервале, имеющем номер a, за исключением самого a. Мы можем заключить, что пределом f(x) при приближении x к a является L, и мы можем записать это в математической записи следующим образом:

когда угодно:

 

Лучшие репетиторы по математике

Поехали

Правило больницы

Предположим, что f и g — дифференцируемые функции, причем g'(x) не равно нулю в интервале вокруг a, за исключением самого a. В таком случае должно выполняться одно из следующих утверждений:

• Обе функции f(x) и g(x) имеют нулевой предел при приближении x к a
• Обе функции f(x) и g(x) имеют бесконечный предел (положительный или отрицательный) по мере того, как x приближается к соответствующую производную}, пока предел не существует или не станет бесконечным.

  Правило Лопиталя может применяться в одной из следующих форм предела:

  • , где и f(x), и g(x) приближаются к 0
  • , где и f(x), и g(x) ) приближение к бесконечности
  • , где f(x) стремится к бесконечности, а g(x) приближается к 0
  • , где и f(x) и g(x) стремятся к бесконечности
  • , где и f(x) и g (x) приближается к 0
  • , где f(x) приближается к бесконечности, а g(x) приближается к 0
  • , где f(x) приближается к 1, а g(x) приближается к бесконечности

   

  В этой статье мы обсудим, как применить правило Лопиталя  если , где f(x) стремится к бесконечности, а g(x) приближается к 0. Следовательно, мы можем назвать это нулем, умноженным на бесконечность, или бесконечностью, умноженной на нуль.

   

  В следующем разделе мы шаг за шагом решим пару примеров, которые объяснят, как применять рассмотренное выше правило, когда обе функции перемножаются друг с другом и ограничивают подходы к бесконечности.

   

  Пример 1

  Оценка

  Решение

  Вышеуказанная функция имеет неопределенную форму, поскольку

  равна, и

  равна 0.

  Функция может быть написана как:

  2

  . Когда мы применим ограничение к вышеуказанной функции, как показано ниже, мы все равно получим неопределенную форму или :

     

  Поскольку функция все еще имеет неопределенную форму, поэтому мы применим здесь правило Лопиталя. Чтобы применить правило Лопиталя, мы возьмем первую производную числителя и знаменателя отдельно. Первая производная от is и производная от is . Теперь подставим эти производные в функцию следующим образом:

  =

  Упрощение вышеуказанное выражение даст нам следующий результат:

  =

  Когда мы применим предел на вышеуказанной функции, мы получим следующий ответ:

  =

  Пример 2

  Вычислить

     

  Решение

  Приведенная выше функция имеет неопределенный вид, потому что

     

  равно , а

     

  равно 0.

  Функция может быть записана как:

  Когда мы применим ограничение к указанной выше функции, как показано ниже, мы все равно получим неопределенную форму или:

     

  Так как, функция по-прежнему имеет неопределенный вид, поэтому мы применим здесь правило Лопиталя. Чтобы применить правило Лопиталя, мы возьмем первую производную числителя и знаменателя отдельно. Первая производная от is и производная от is . Теперь подставим эти производные в функцию следующим образом:

  =

  Упрощение вышеуказанное выражение даст нам следующий результат:

  =

  Когда мы применим лимит на вышеуказанной функции, мы получим следующий ответ:

  =

  =

  Пример 3

  Вычисление

     

  Решение

  Приведенная выше функция имеет неопределенный вид, поскольку

     

  равно , и

     

  также равно \infty.

  Функция может быть записана как:

   

  Когда мы применим ограничение к вышеуказанной функции, как показано ниже, мы все равно получим неопределенную форму:

  =

     

  функция по-прежнему имеет неопределенную форму, поэтому мы применим здесь правило Лопиталя.

  Чтобы применить правило Лопиталя, мы возьмем первую производную числителя и знаменателя отдельно. Первая производная равна, а производная равна 2x. Теперь подставим эти производные в функцию следующим образом:

  =

  Применение предела к вышеуказанной функции даст нам следующий результат:

  =

  =

  Пример 4

  Оценка

  Решение

  Выше of потому что

     

  равно , а

     

  также равно \infty.

  Функция может быть записана как:

   

  Когда мы применим ограничение к вышеуказанной функции, как показано ниже, мы все равно получим неопределенный вид: Правило здесь. Чтобы применить правило Лопиталя, мы возьмем первую производную числителя и знаменателя отдельно. Первая производная равна, а производная равна 2x + 6. Теперь подставим эти производные в функцию следующим образом:

  =

     

  Применение предела к приведенной выше функции даст нам следующий результат:

  =

  =

  Задача бесконечности нулевого времени Есть два способа обезопасить себя во время скалолазания: Первый вариант — тщательно защитить себя с помощью веревок и снаряжения, чтобы в случае падения вы не упали слишком далеко или сильно.

  Второй вариант — не упасть. Я думаю, что вариант, который выбирают альпинисты, отражает их восприятие того, что мне нравится называть проблемой «ноль умножить на бесконечность», в которой вы умножаете почти нулевую вероятность на почти бесконечную потерю.

  Первая группа альпинистов думает: «Если бы у меня было неудачное падение, это было бы очень, очень плохо, поэтому я постараюсь сделать так, чтобы ни одно из моих падений не было таким». Эти люди фактически говорят, что ноль умножить на бесконечность — это бесконечность. Вторая группа альпинистов думает: «Давайте я просто позабочусь о том, чтобы не упасть, и тогда неважно, насколько плохо будет, если я упаду, потому что этого не произойдет». Эта группа принимает нуль, умноженный на бесконечность, чтобы быть нулем. Для протокола: я в первой группе по восхождению (но, конечно, во второй по теоретико-мерной интеграции!)

  Проблема нуля умножить на бесконечность имеет более общие приложения к планированию бедствий: вероятность возникновения какой-либо катастрофы очень мала, но потери, понесенные в случае катастрофы, будут очень большими.

  К сожалению, из-за самой природы этой проблемы трудно сделать разумные количественные выводы о ней: поскольку катастрофа случается очень редко, или, возможно, никогда еще не случалась, трудно оценить вероятность ее возникновения. А поскольку мы наблюдали лишь от нуля до нескольких стихийных бедствий, трудно оценить, сколько потерь вы понесете, когда или если это произойдет.

  И это имеет большое значение! Если годовая вероятность крупного бедствия в Чикаго составляет от 0,1% до 1%, а ущерб от этого бедствия составляет от 1 до 10 миллиардов долларов, то ожидаемые ежегодные убытки составляют от 1 до 100 долларов. миллионов, что определяет разницу между игнорированием возможности катастрофы и ее активным планированием.

  Чтобы понять, насколько сложна эта проблема статистически, предположим, что мы пытаемся оценить вероятность того, что какая-то катастрофа произойдет в данном году. Такого не было ни в один из последних 100 лет, и у нас нет данных до этого. давайте 9{1/100}] = [0, 0,0295]$. Таким образом, с достоверностью 95 % ежегодная вероятность стихийного бедствия может достигать 3 % в год, что достаточно для планирования, или всего 0, что означает, что у нас нет проблем.

  Другими словами, несмотря на данные за сто лет, мы до сих пор не знаем, стоит ли планировать катастрофу! Что мы можем с этим сделать? Вот три общие стратегии:

  Во-первых, иногда мы можем расширить количество имеющихся у нас данных, взглянув на «полупараллельные вселенные». Возможно, какой-то отдельно взятый город располагает данными о стихийных бедствиях всего за сто лет, но в совокупности городов мира их во много раз больше. Вероятно, эти вспомогательные данные можно использовать, например, для количественной оценки того, как летние температуры и плотность населения влияют на риск и стоимость крупных пожаров. Или вы можете просмотреть статистику лазания, чтобы определить, с какой скоростью падают сильные, осторожные альпинисты. Включение этих горизонтальных параллелей, по-видимому, хорошо работает для многих страховых проблем.

  Однако не у каждого вида катастрофы есть такие хорошие «горизонтальные» параллели, которые можно провести. Например, попробуйте вычислить вероятность крупной глобальной эпидемии и связанные с этим затраты. Мы не можем наблюдать параллельные миры, из которых можно было бы получить аналогичные данные, и (к счастью) не было крупной эпидемии с тех пор, как пандемия гриппа 1918 года унесла жизни 3-5% населения мира. Однако можно провести «вертикальные» параллели, анализируя частоту, размер и стоимость более мелких эпидемий и пытаясь экстраполировать эти цифры на более масштабные события.

  Наконец, мы также можем добиться прогресса в решении проблемы нулевого умножения на бесконечность, включив моделирование конкретных стихийных бедствий: например, для предварительных расчетов, приведенных выше, мы предположили, что стихийные бедствия происходят независимо друг от друга, что на самом деле неверно для стихийных бедствий, таких как лес пожары: Если какое-то время не было лесного пожара, я понимаю, что это повышает вероятность возникновения нового лесного пожара, потому что легко воспламеняющиеся кусты продолжают накапливаться.

  No related posts.