Ноль в степени два: Степень с показателем 0 — урок. Алгебра, 7 класс.

§ Что такое степень числа. Степень с натуральным показателем

Что такое степень числа Свойства степени Возведение в степень дроби

Обращаем ваше внимание, что в данном разделе разбирается понятие степени только с натуральным показателем и нулём.

Понятие и свойства степеней с рациональными показателями (с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.

Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.

Вместо произведения шести одинаковых множителей 4 · 4 · 4 · 4 · 4 · 4 пишут 4⁶ и произносят «четыре в шестой степени».

4 · 4 · 4 · 4 · 4 · 4 = 4⁶

Выражение 4⁶ называют степенью числа, где:

• 4 — основание степени;
• ⁶ — показатель степени.

В общем виде степень с основанием «a» и показателем «n» записывается с помощью выражения:

Запомните!

Степенью числа «a» с натуральным показателем «n», бóльшим 1, называется произведение «n» одинаковых множителей, каждый из которых равен числу «a».

Запись «aⁿ» читается так: «а в степени n» или «n-ая степень числа a».

Исключение составляют записи:

• a² — её можно произносить как «а в квадрате»;
• a³ — её можно произносить как «а в кубе».

Конечно, выражения выше можно читать и по определению степени:

• a² — «а во второй степени»;
• a³ — «а в третьей степени».

Особые случаи возникают, если показатель степени равен единице или нулю (n = 1; n = 0).

Запомните!

Степенью числа «а» с показателем n = 1 является само это число:
a¹ = a

Любое число в нулевой степени равно единице.
a⁰ = 1

Ноль в любой натуральной степени равен нулю.
0ⁿ = 0

Единица в любой степени равна 1.
1ⁿ = 1

Выражение 0⁰ (ноль в нулевой степени) считают лишённым смысла.

• (−32)⁰ = 1
• 0²⁵³ = 0
• 1⁴ = 1

При решении примеров нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в степень.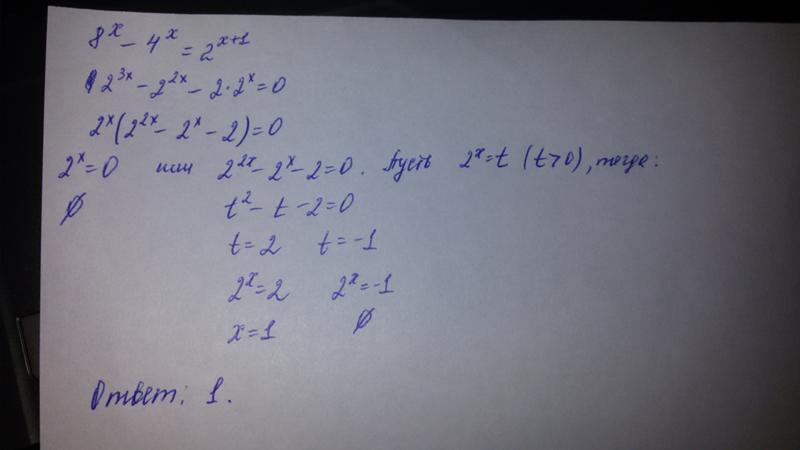

Пример. Возвести в степень.

• 5³ = 5 · 5 · 5 = 125
• 2,5² = 2,5 · 2,5 = 6,25
• ()⁴ = · · · =

  3 · 3 · 3 · 3

  4 · 4 · 4 · 4

  =

  81

  256

Возведение в степень отрицательного числа

Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.

Запомните!

При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Рассмотрим примеры возведения в степень отрицательных чисел.

Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.

Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.

Запомните!

Отрицательное число, возведённое в чётную степень, есть число положительное.

Отрицательное число, возведённое в нечётную степень, — число отрицательное.

Квадрат любого числа есть положительное число или нуль, то есть:

a² ≥ 0 при любом a.

• 2 · (−3)² = 2 · (−3) · (−3) = 2 · 9 = 18
• −5 · (−2)³ = −5 · (−8) = 40

Обратите внимание!

При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (−5)⁴ и −5⁴ это разные выражения. Результаты возведения в степень данных выражений будут разные.

Вычислить (−5)⁴ означает найти значение четвёртой степени отрицательного числа.

(−5)⁴ = (−5) · (−5) · (−5) · (−5) = 625

В то время как найти «−5⁴» означает, что пример нужно решать в 2 действия:

1. Возвести в четвёртую степень положительное число 5.
   5⁴ = 5 · 5 · 5 · 5 = 625
2. Поставить перед полученным результатом знак «минус» (то есть выполнить действие вычитание).
   −5⁴ = −625

Пример. Вычислить: −6² − (−1)⁴

−6² − (−1)⁴ = −37

1. 6² = 6 · 6 = 36
2. −6² = −36
3. (−1)⁴ = (−1) · (−1) · (−1) · (−1) = 1
4. −(−1)⁴ = −1
5. −36 − 1 = −37

Порядок действий в примерах со степенями

Вычисление значения называется действием возведения в степень.

Это действие третьей ступени.

Запомните!

В выражениях со степенями, не содержащими скобки, сначала выполняют вовзведение в степень, затем умножение и деление, а в конце сложение и вычитание.

Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.

Пример. Вычислить:

Для облегчения решения примеров полезно знать и пользоваться таблицей степеней, которую вы можете бесплатно скачать на нашем сайте.

Для проверки своих результатов вы можете воспользоваться на нашем сайте калькулятором «Возведение в степень онлайн».

Что такое степень числа Свойства степени Возведение в степень дроби

---

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».

Оставить комментарий:

Отправить

---

Артериальная гипертензия: стадии и риски

Слово «гипертензия» в буквальном смысле переводится с латинского как «сверхнапряжение». Какие стадии и степени есть у гипертензии и сколько факторов риска влияет на ее развитие — подробно в нашей статье.

Врачи различают три степени и три стадии заболевания. Эти понятия часто путают, однако между ними есть существенная разница.

Степени артериальной гипертензии

Это классификация по уровням артериального давления (АД): верхнего (систолического) и нижнего (диастолического).

Расширенная классификация уровней артериального давления (в соответствии с Национальными клиническими рекомендациями по лечению гипертонии). Считать кровяное давление «чисто техническим показателем» ошибочно: чем выше его постоянный уровень, тем серьезнее ситуация

Стадии артериальной гипертензии

Здесь деление на категории идет уже по серьезности изменений в организме: насколько выражены эти изменения и как сильно страдают органы-мишени — кровеносные сосуды, сердце и почки.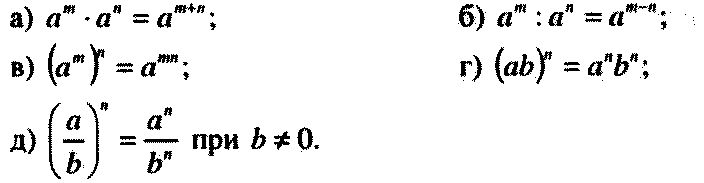 Их поражение — отдельный критерий для оценки риска.

Термин «гипертоническая болезнь» предложен Г.Ф.Лангом в 1948 г. и соответствует термину «эссенциальная гипертензия» (гипертония), который используется в зарубежных странах.

На любой из стадий заболевания давление также может соответствовать любой степени — от первой до третьей. Это очень индивидуально, поэтому, помимо показателей на тонометре, следует ориентироваться на данные обследования. Конкретные показатели всегда принимаются во внимание при назначении терапии, рекомендациях и прогнозах.

Артериальная гипертензия Ⅰ стадии

• При регулярном посещении врача и соблюдении правил жизни гипертоника не требует серьезного медицинского вмешательства, если нет ухудшения здоровья.

• Прогноз зависит от уровня АД и количества факторов риска: курение, ожирение, уровень холестерина и т.д.

Артериальная гипертензия Ⅱ стадии

• Если вовремя не скорректировать процесс лекарственными препаратами, болезнь может прогрессировать и перейти в третью стадию. Избежать этого можно лишь одним способом: контролировать состояние своей сердечно-сосудистой системы и регулярно проходить обследование.

Артериальная гипертензия Ⅲ стадии

• В этом состоянии требуются препараты не только для снижения давления, но и для лечения сопутствующих заболеваний. Рекомендация актуальна и для первых двух стадий гипертонической болезни, если у пациента диагностирован диабет, болезни почек или другие патологии.

Артериальная гипертензия — 4 группы риска

Чтобы уберечь сердце и сосуды от поражения и не пропустить состояние, когда будет уже поздно, нужно знать, от каких факторов зависит течение болезни.

4 группы факторов риска:

• низкий риск;

• умеренный;

• высокий;

• очень высокий.

Между факторами риска и классификацией по тяжести заболевания есть прямая связь. Наглядно она показана в Национальных Клинических Рекомендациях Минздрава РФ «Артериальная гипертония у взрослых».

Для определения своей группы риска нужно знать уровень АД и стадию заболевания.

Группы высокого и очень высокого риска

Эти состояния считаются самыми серьезными и требуют особого внимания.

При сочетании более трех факторов риска и артериальной гипертензии 2 степени пациент попадает в группу высокого риска. Также к ней относятся все, у кого существенно выражен хотя бы один показатель из следующих:

• повышение уровня общего холестерина от 8 ммоль/л (310 мг/дл),

• гипертония третьей степени (систолическое артериальное давление выше или равно 180 мм рт. ст., диастолическое — выше 110 мм рт.ст.),

• хроническая болезнь почек третьей стадии,

• гипертрофия левого желудочка,

• сахарный диабет без поражения органов-мишеней.

К группе очень высокого риска относят пациентов с любым из следующих факторов:

• Атеросклеротические заболевания сердца и сосудов, подтвержденные клинически или в ходе визуализирующих исследований (АССЗ). Это может быть стабильная стенокардия, коронарная реваскуляризация (аортокоронарное шунтирование и другие процедуры реваскуляризации артерий), инсульт и транзиторные ишемические атаки, ранее перенесенный острый коронарный синдром (инфаркт или нестабильная стенокардия), а также заболевание периферических артерий. Обязательно учитываются результаты визуализирующих исследований, значимые для прогноза клинических событий: значительный объем бляшек на коронарных ангиограммах или сканах компьютерной томографии (многососудистое поражение коронарных артерий со стенозом двух основных эпикардиальных артерий более чем на 50 %) или по результатам УЗИ сонных артерий.

• Сахарный диабет с поражением органов-мишеней, или наличием как минимум трех значимых факторов риска из указанных в следующей части статьи, сюда же приравнивается сахарный диабет первого типа ранней манифестации и длительного течения (более 20 лет).

• Тяжелая хроническая болезнь почек (рСКФ < 30 мл/мин/1,73 м2).

• Семейная гиперхолестеринемия с АССЗ или с другим значимым фактором риска.

Степень артериальной гипертонии при этом может быть первой, второй или третьей.

При любых провоцирующих факторах (например, при курении или злоупотреблении алкоголем) угроза для здоровья и жизни в таком состоянии возрастает.

Если вы обнаружили себя в группе высокого или умеренно высокого риска — стоит как можно быстрее обратиться к врачу-кардиологу

Общие факторы сердечно-сосудистого риска при гипертензии

• Мужской пол.

• Возраст более 55 лет у мужчин и более 65 лет у женщин.

• Курение и чрезмерное употребление алкоголя.

• Дислипидемии — повышенный уровень жиров в крови (принимается во внимание каждый показатель липидного обмена).

• Уровень общего холестерина более 4,9 ммоль/л (190 мг/дл).

• Альтернативные показатели: уровень холестерина липопротеинов низкой плотности свыше 3,0 ммоль/л (115 мг/дл) и/или уровень холестерина липопротеинов высокой плотности у мужчин менее 1,0 ммоль/л (40 мг/дл), у женщин менее 1,2 ммоль/л (46 мг/дл).

• Триглицериды более 1,7 ммоль/л (150 мг/дл).

• Повышенный уровень глюкозы в крови натощак: 5,6–6,9 ммоль/л  при исследовании натощак (101–125 мг/дл) или н.

• Нарушение толерантности к глюкозе: при проведении теста насторожить должны показатели глюкозы от 7,8 ммоль/л до 11,0 ммоль/л.

• Ожирение: индекс массы тела, равный 30 кг/м2 или выше, окружность талии более 102 см у мужчин, более 88 см у женщин.

• Наличие родственников, у которых сердечно-сосудистые заболевания проявились раньше 55 лет, если говорить о мужчинах, или раньше 65 лет, если говорить о женщинах.

По данным Европейского общества кардиологов, вероятность развития гипертонии у мужчин выше, чем у женщин — особенно после достижения 55 лет

Самые опасные состояния при артериальной гипертензии

• Диагностированные заболевания сердца: инфаркт миокарда, фибрилляция предсердий, сердечная недостаточность, стенокардия.

• Заболевания сосудов: острый коронарный синдром, коронарная реваскуляризация или артериальная реваскуляризация любой другой локализации, инсульт, транзиторные ишемические атаки, аневризма аорты, патологии периферических артерий.

• Наличие атеросклеротических бляшек в сосудах при визуализации.

• Сахарный диабет с поражением органов-мишеней или сочетание его с основными провоцирующими факторами.

• Тяжелая хроническая болезнь почек.

В любом из этих случаев пациенту нужна терапия под контролем врача

Если вы нашли себя в одной из категорий риска, необходимо:

• каждый день измерять артериальное давление и записывать результаты;

• даже при первой степени заболевания — обратиться к врачу, чтобы установить причины артериальной гипертензии;

• контролировать состояние здоровья — например, не нарушать принципы питания при диабете;

• проанализировать, какой образ жизни рекомендуется в вашем состоянии, и следовать этим правилам.

При выполнении всех рекомендаций врача и контроле своего самочувствия можно избежать критических последствий даже в группе высокого риска. Если исключить вредные привычки и пересмотреть образ жизни, давление может начать снижаться уже через 1-2 недели. {0}$, что тогда, не будет ли это $1 + 1$, поскольку все, что имеет степень $0 = 1$? Может быть я неправильно понял, но это то, что я получил. 90 = 1 $$

Вы сделали то, что делают многие изучающие элементарную алгебру, и думаете, что распределение показателей степени через бином допустимо. Это допускается только в более сложном смысле, когда $x$ и $y$ являются членами коммутативного кольца характеристики $p$ — простого числа. Конечно, это делается в абстрактной алгебре, курсе, который изучают математики на младших или старших курсах колледжа.

Дело в том, что все до нуля равно единице, и вы не можете распределять степени через бином (пока).

$\endgroup$

интуиция — Числа в степени нуля

Задавать вопрос

спросил 10 лет, 5 месяцев назад

Изменено 10 месяцев назад

Просмотрено 4к раз

9{0}$? Это не определено? Если да, то почему он не равен $1$?

Какое уравнение определяет показатели степени? Я могу легко написать для этого небольшую программу (см. ниже), но как насчет формата уравнения?

---

Я просто хочу немного обсудить числа в степени нуля, для некоторых пояснений.

---

Код для показателей: (псевдокод/Ruby)

 def int find_exp (int x, int n){
    общее количество = 1;
    n.times{всего*=х}
    общая сумма возврата;
}
 

• интуиция
• возведение в степень

$\endgroup$

29

$\begingroup$

В основном это просто вопрос того, что вы определяете для обозначения обозначения. Вы можете определять вещи так, как вам хочется, за исключением того, что если вы выберете определение, которое приводит к другим результатам, чем определения всех остальных, то вы несете ответственность за любую путаницу, вызванную тем, что вы используете знакомую нотацию для обозначения чего-либо. нестандартный. 9y$ не является непрерывным в $(0,0)$.

$\endgroup$

7

$\begingroup$

Изобретение чисел стало одним из крупнейших прорывов в истории математики. Это ознаменовало осознание того, что этот мешок с галькой $$\{ \blacktriangle\;\blacktriangle\;\blacktriangle\;\blacktriangle\;\blacktriangle \}$$ эта вереница узлов $$-\пуля-\пуля-\пуля-\пуля-\пуля-$$ и эта кость полна счетных отметок $$/\,/\,/\,/\,/$$ все воплощения одной вещи, абстрактной величины пять . Этот скачок абстракции стал для нас настолько обыденным, что даже кажется странным заниматься арифметикой, фактически считая вещи. Однако в некоторых случаях может оказаться полезным вернуться к основам — к тем дням, когда у нас не было чисел, и мы выполняли всю нашу арифметику, считая вещи. Ваш вопрос — один из таких случаев.

В дальнейшем я буду использовать заглавную букву, например $X$, для обозначения конечного набора вещей, например стада коз или кучи бус, и я буду использовать символ $|X|$ для обозначают количество вещей в наборе.

---

Возведение в степень — сложная операция, как вы уже ясно заметили, так что давайте разогреемся чем-нибудь попроще. Если у вас есть две стопки бусинок, $A$ и $B$, самое простое, что вы можете сделать с ними, — это сложить их вместе, чтобы получилась большая стопка, которую часто пишут $A \sqcup B$. Вы должны легко убедиться, что на уровне чисел $|A \sqcup B| = |А| + |В|$. Другими словами, конкретная операция сдвига двух кучек соответствует абстрактной операции сложения двух чисел. Сложение целых чисел часто определяется таким образом.

---

Вот немного более сложная разминка. Если у вас есть куча рубашек, $H$, и куча юбок, $K$, вы можете задаться вопросом, сколько разных нарядов можно составить, сочетая рубашку с юбкой. Набор нарядов обычно записывается $H \times K$. Вы должны быть в состоянии убедить себя, что $|H \times K| = |Н| \cdot |К|$. Другими словами, конкретная операция подсчета пар соответствует абстрактной операции умножения. Умножение целых чисел часто определяется таким образом. 90$ должен быть равен $1$, чтобы биномиальная теорема была верна. Даже эти странно выглядящие числа $\binom{n}{k}$ можно определить с помощью конечных множеств: если у вас есть $N$ игрушек и $K$ детей, $\binom{N}{K}$ — это множество способы, которыми вы можете выбрать достаточное количество игрушек, чтобы иметь по одной для каждого ребенка. (Обратите внимание, что вы не даете каждую игрушку конкретному ребенку: вы просто хотите, чтобы количество детей и игрушек было одинаковым.) Если вы достанете свой набор красок $C$ и еще один набор красок $D$ и начните раскрашивать различное количество детей и раздавать игрушки в зависимости от количества цветов детей, вы должны как-то быть в состоянии убедить себя в том, что биномиальная теорема верна, даже если в $C$ нет красок. Вот почему Андре Николя придумал те же правила для нулевых экспонент, что и мы. 90=1$$

$\endgroup$

1

$\begingroup$

Другой подход. ..

Можно показать, что существует бесконечно много функций, которые я называю «экспоненциальными функциями», которые могут быть определены на множестве натуральных чисел $N$. Под экспоненциальной функцией $f$ на $N$ я подразумеваю $f$ такую, что:

1. $f: N\times N\to N$

2. $f(x,0)=1$ для $x\ne 0$ 91}=1$

   $\endgroup$

   $\begingroup$

   [Этот ответ был перенесен из ответа в только что удаленной ветке Простой способ объяснить пустой продукт].

   Ниже я объясняю в простых терминах (абстрактную) алгебраическую мотивацию равномерного расширения степенных законов («закона показателей») с положительных степеней на нулевые и отрицательные степени. Большая часть поста элементарна, поэтому если вы встретите незнакомые термины, можете смело их пропускать. 9{\Bbb Z}.\,$ Поскольку отображение мощности на $\,\Bbb Z\,$ является расширением отображения на положительных степенях, мы гарантируем, что доказательства положительных степеней остаются верными, даже если в доказательстве используются отрицательные или нулевые степени, как и для доказательств положительных целых чисел, использующих отрицательные целые числа и ноль. n\,\Rightarrow\, a = b\,$ для целых чисел $a,b,\,$ Такие расширения до более богатых структур с $0$ и инверсии позволяют нам работать с объектами в более простых формах, которые лучше подчеркивают фундаментальную алгебраическую структуру (здесь циклические группы или главные идеалы)

   Этот принцип сохранения структуры является ключевым свойством, которое используется при расширении алгебраических структур, таких как группы и кольца. Если расширенная структура сохраняет законы (аксиомы) базовой структуры, то все, что мы выводим о базовой структуре, используя расширенную структуру, остается в силе в базовой структуре. Например, чтобы найти целые или рациональные корни квадратичных и кубических чисел, мы можем использовать хорошо известные формулы. Несмотря на то, что в этих формулах могут использоваться комплексные числа для нахождения целых, рациональных или действительных корней, эти результаты действительны в этих системах счисления с основными числами, поскольку в доказательствах использовались только (кольцевые) аксиомы, которые остаются действительными в базовых структурах, например.

   No related posts.