Содержание
Введение 3
Свойства тригонометрических функций на единичной окружности 4
Создание цифровой образовательной модели 5
Разработка внешнего интерфейса программы 5
Отрисовка основных элементов программы 6
Обеспечение реакции на управляющие кнопки 7
Организация пересчета значений функций 8
Тестирование получившейся программы 9
Заключение 11
Список литературы 12
Приложение 13
Введение
Образовательный
процесс в школьных учреждениях
несовершенен, усвояемость детьми
материала зависит не только от их
умственных способностей, но от качества
и способов подачи материала. На занятиях
от ученика требуется предельная
концентрация внимания, упущенный или
не до конца понятый учеником материал
может препятствовать дальнейшему
освоению установленной программы.
Программная среда Stratum 2000 позволяет разрабатывать как тестовые задания для проверки знаний ученика, так и интерактивные модели, позволяющие продемонстрировать учащимся учебный материал в понятной и интересной форме.
В данной работе поставлена цель: разработать интерактивную модель в среде Stratum, демонстрирующую определение тригонометрических функций (синуса, косинуса, тангенса и котангенса) на единичном круге.
Для достижения данной цели необходимо выполнять ряд задач:
1. Ознакомиться со средой моделирования и проектирования Stratum;
2. Ознакомиться с теоретической основой проекта;
3. Разработать модель единичного круга, реализовать вычисление и визуализацию значений тригонометрических функций:
создать единичный круг и радиус-вектор;
добавить элементы управления, определяющие отображаемую функцию и вид чертежа;
обеспечить изменение угла наклона радиус-вектора;
создать алгоритм пересчета значений, соответствующих выбранной функции и положению радиус-вектора;
протестировать разработанную модель.

Свойства тригонометрических функций на единичной окружности
Тригонометрический круг – основа тригонометрии. Он представляет собой окружность радиусом 1 с центром в начале координат. Тригонометрический круг позволяет нам:
пронаблюдать перевод градусов в радианы и наоборот;
найти значение синуса и косинуса;
убедиться, что синус и косинус принимают значения от -1 до 1;
увидеть, что синус и косинус – периодические функции с периодом 2π
вычислить тангенс и котангенс
увидеть знаки у синуса и косинуса, а также вычислить знаки тангенса и котангенса
Отсчет
углов начинается от положительного
направления оси OX
и идет против часовой стрелки. Полный
круг составляет 360°. Точка
с координатами (1;0) соответствует углу
0°. Точка
с координатами (-1;0) соответствует углу
в 180°,
тока с координатами (0;1) – угол 90°,
а точка с координатами (0; -1) — 270°.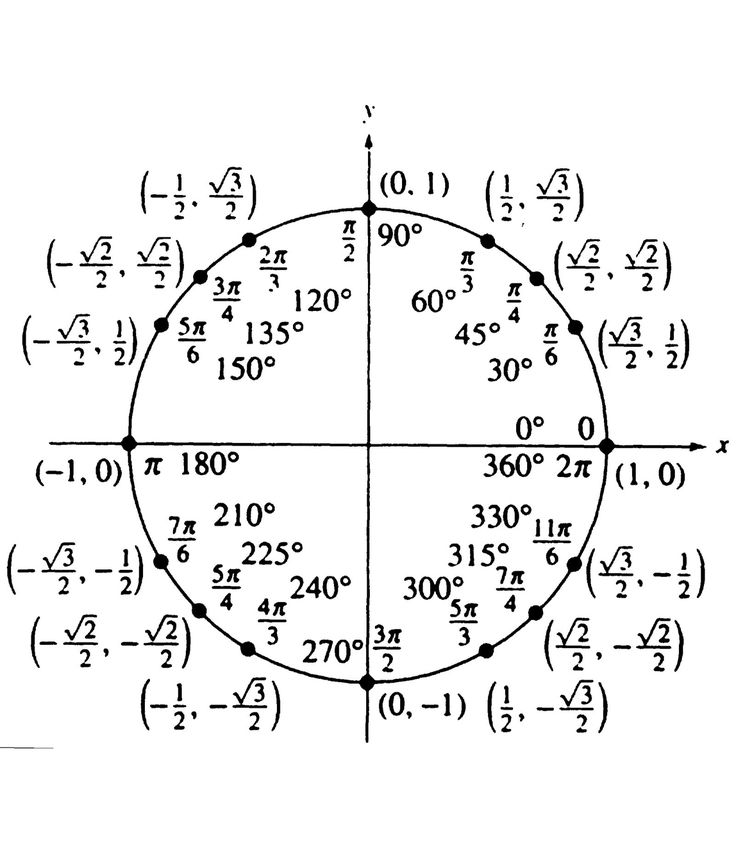
Синусом угла называется ордината (то есть значение на оси OY, соответствующее данному углу α). Также синус угла можно найти как отношение y к радиусу единичной окружности.
Косинусом угла называется абсцисса (то есть значение на оси OX, соответствующее данному углу α). Также косинус угла можно найти как отношение х к радиусу единичной окружности.
Для того, чтобы определить знак синуса или косинуса необходимо лишь поставить точку на окружности, соответствующую данному углу и посмотреть положительны или отрицательны у этой точки координаты.
Тангенс – отношение синуса к косинусу. Касательная к окружности в точке (1;0) называется осью тангенса. Для того чтобы графически определить чему равен тангенс, необходимо провести луч через начало координат и точку, соответствующую данному углу, до пересечения с осью тангенса. Y – координата точки пересечения и будет являться значением тангенса.
Котангенс
– отношение косинуса к синусу. Касательная
к окружности в точке (0;1) называется осью
котангенса. Для того чтобы графически
определить чему равен котангенс,
необходимо провести луч через начало
координат и точку, соответствующую
данному углу, до пересечения с осью
котангенса. X
– координата точки пересечения и будет
являться значением котангенса.
Касательная
к окружности в точке (0;1) называется осью
котангенса. Для того чтобы графически
определить чему равен котангенс,
необходимо провести луч через начало
координат и точку, соответствующую
данному углу, до пересечения с осью
котангенса. X
– координата точки пересечения и будет
являться значением котангенса.
Чтобы вычислить знаки тангенса или котангенса, необходимо найти знаки синуса и косинуса в данной точке и поделить их (для тангенса – синус на косинус, для котангенса – косинус на синус).
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град.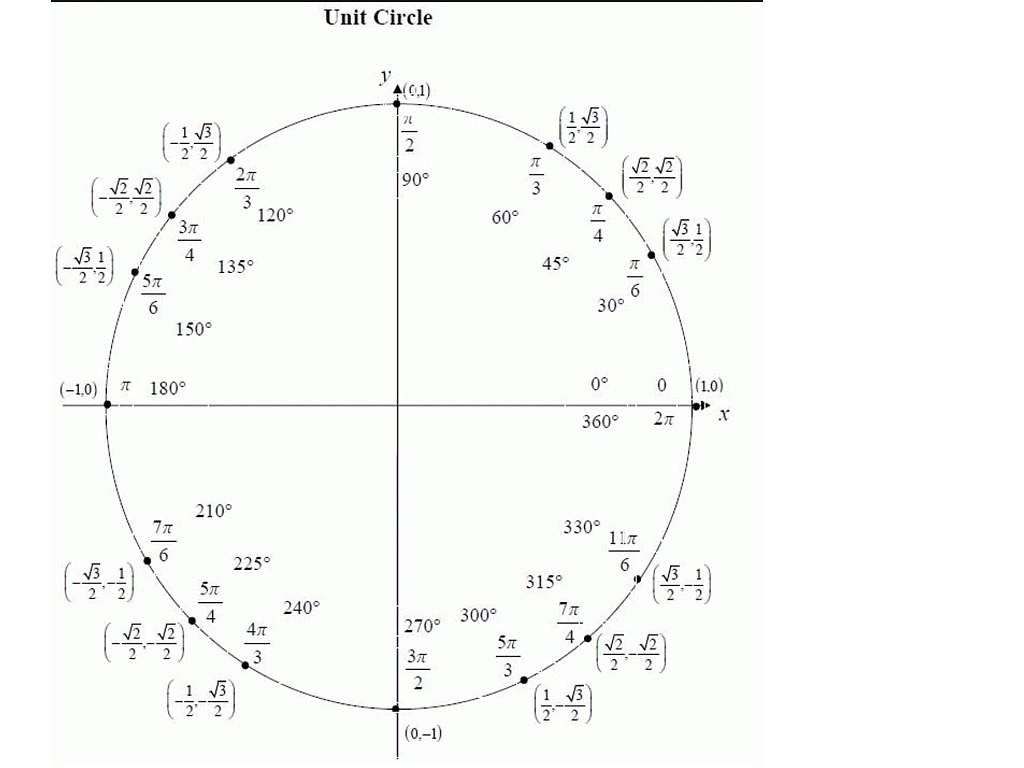 ) ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| Найти точное значение | csc(60 град. ) | ||
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.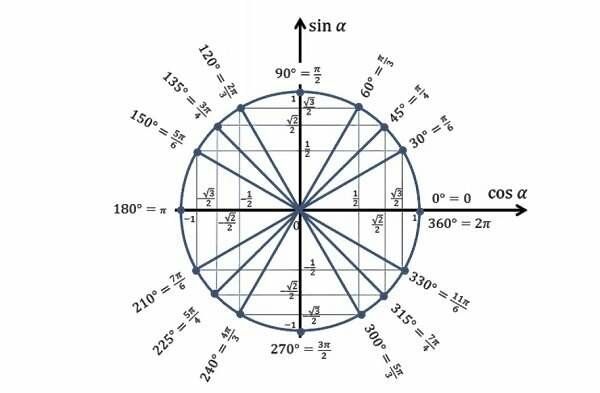 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град.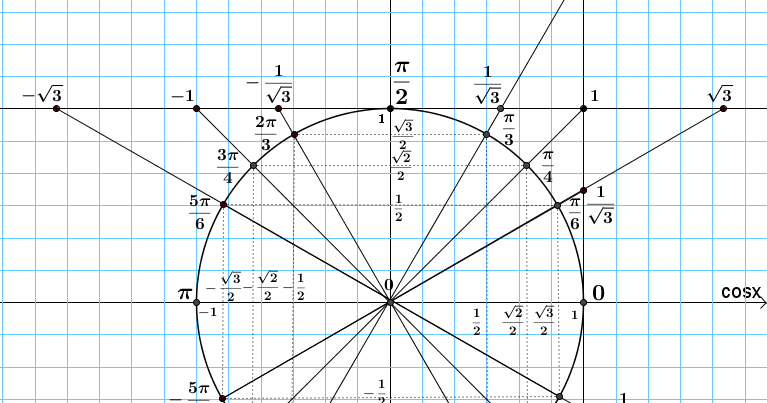 ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.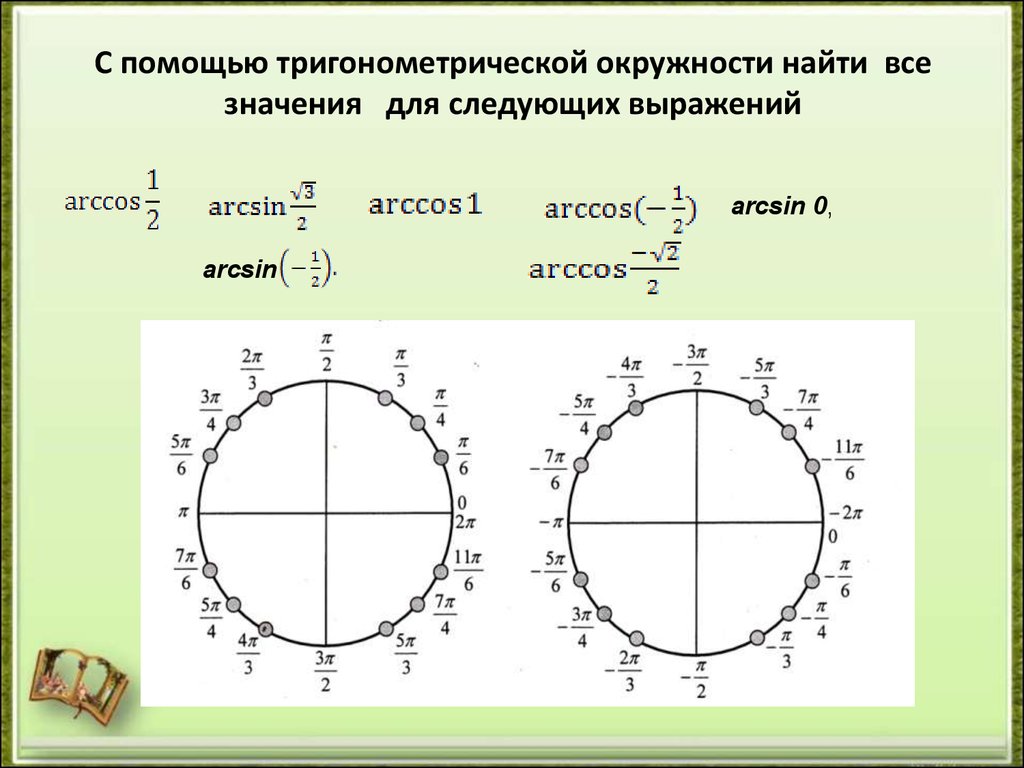 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град.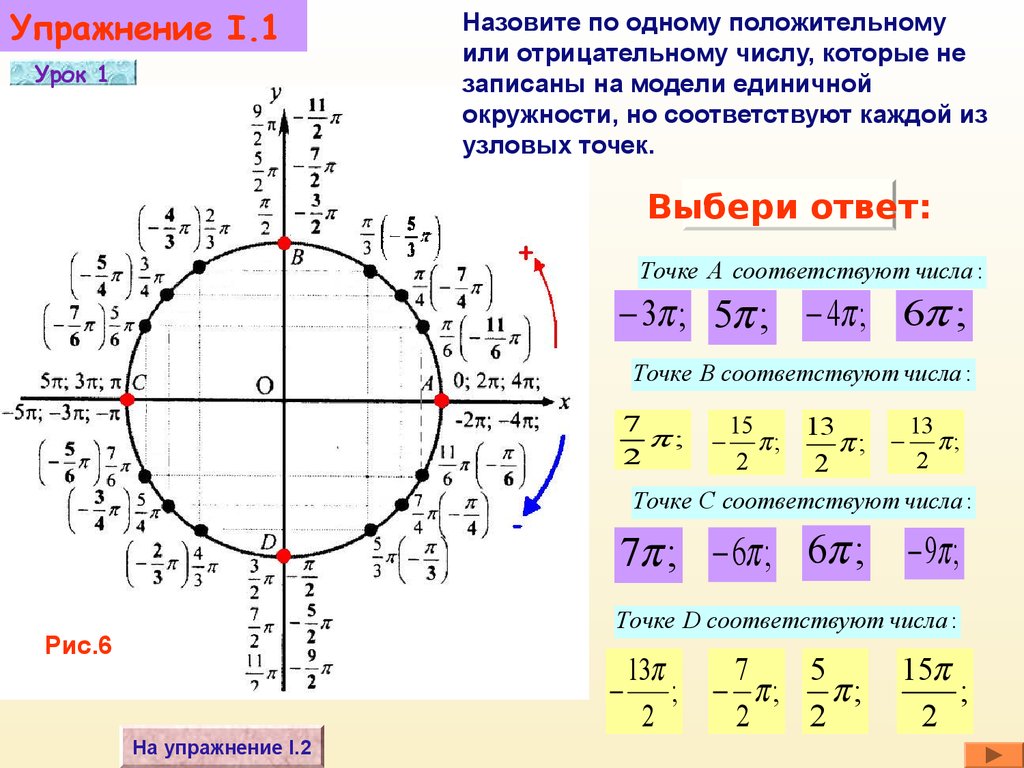 ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Объяснение урока: Тригонометрические отношения на единичной окружности
В этом объяснении мы узнаем, как связать 𝑥- и 𝑦-координаты точек на единичной окружности с тригонометрическими функциями.
Единичная окружность — это окружность радиусом 1, центр которой лежит в начале координат плоскости.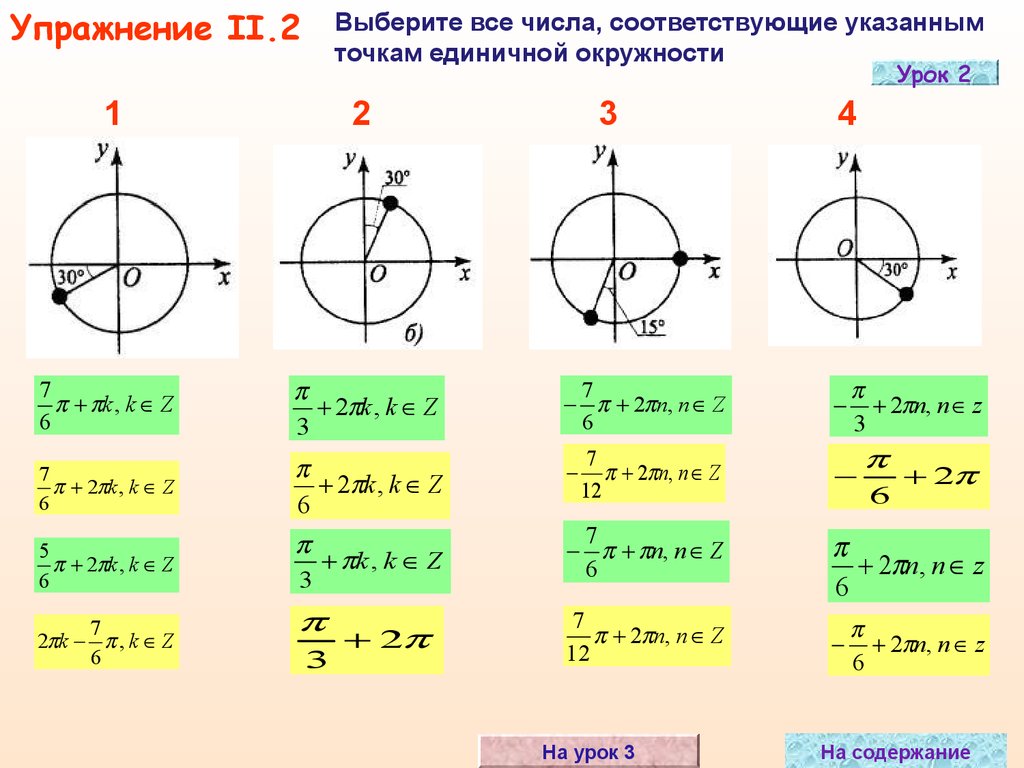 Для любой точки (𝑥,𝑦) на единичной окружности можно построить прямоугольный треугольник, как показано на следующей диаграмме. Гипотенуза этого прямоугольного треугольника образует угол 𝜃 с положительной осью 𝑥.
Для любой точки (𝑥,𝑦) на единичной окружности можно построить прямоугольный треугольник, как показано на следующей диаграмме. Гипотенуза этого прямоугольного треугольника образует угол 𝜃 с положительной осью 𝑥.
Используя тригонометрию прямоугольного треугольника, мы можем определить тригонометрические функции в терминах единичной окружности: sinoppositehypotenuseosincosadjacenthypotenusesocostanoppositeadjacentsotan
Отметим, что tan𝜃 не определен, когда 𝑥=0. Мы также замечаем, что, хотя мы получили эти определения для угла 𝜃 в квадранте 1, они справедливы для угла в любом квадранте.
Теорема: тригонометрические функции и единичная окружность
𝑥- и 𝑦-координаты точки единичной окружности, заданной углом 𝜃, определяются как0003
В нашем первом примере мы покажем, как мы можем использовать эти определения тригонометрических функций в единичном круге, чтобы найти точные значения, учитывая информацию о конечной стороне угла.
Пример 1. Нахождение значения тригонометрической функции угла по координатам точки пересечения конечной стороны и единичной окружности
Найти sin𝜃, если 𝜃 находится в стандартном точка 35,−45.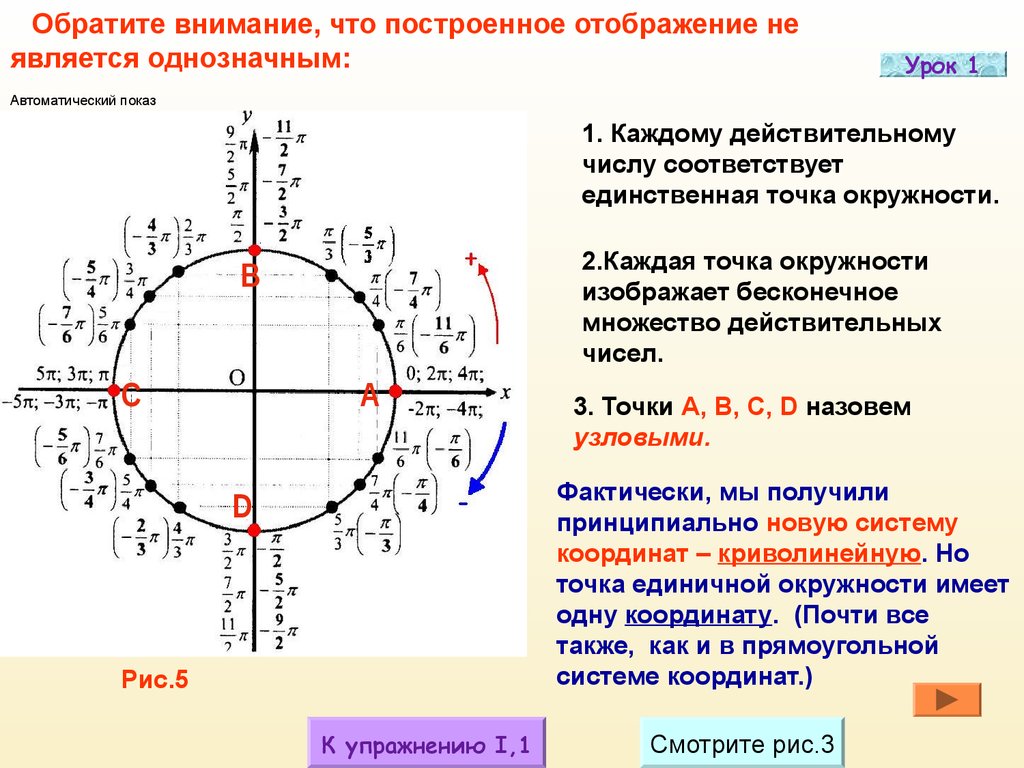
Ответ
Говорят, что угол находится в стандартном положении, если его вершина находится в начале координат, а начальная сторона лежит на положительной оси 𝑥. Угол измеряется в направлении против часовой стрелки от начальной стороны к конечной стороне. Следовательно, угол 𝜃 такой, как показано.
Мы рисуем прямоугольный треугольник со сторонами 35 единиц и 45 единиц, как показано ниже.
Теперь мы можем использовать теорему Пифагора для вычисления значения недостающего измерения в треугольнике: 35+45=𝑐,925+1625=𝑐,2525=𝑐.
Поскольку 𝑐=1, 𝑐=1. Это говорит нам о том, что точка 35,−45 лежит на единичной окружности. Напомним, что 𝑥- и 𝑦-координаты точки на единичной окружности, заданной углом 𝜃, определяются как что равно −45: sin𝜃=−45
В дополнение к стандартным тригонометрическим функциям также можно определить обратные тригонометрические функции (обратная величина число 𝑥 равно 1𝑥). Мы можем определить их следующим образом.
Определение: обратные тригонометрические функции
Для угла 𝜃∈ℝ обратные тригонометрические функции следующие:
- Функция косеканса: cos𝜃≠0
- Функция котангенса: cottan𝜃=1𝜃, for tan𝜃≠0
Поскольку мы можем записать стандартную тригонометрическую функцию в терминах единичного круга, мы также можем написать обратную
функции относительно единичного круга. То есть давайте еще раз рассмотрим точку (𝑥,𝑦) на единичной окружности,
под углом 𝜃 к положительной 𝑥-оси.
То есть давайте еще раз рассмотрим точку (𝑥,𝑦) на единичной окружности,
под углом 𝜃 к положительной 𝑥-оси.
Тогда обратные тригонометрические функции можно записать следующим образом: cscsinforseccosforcottanfor𝜃=1𝜃=1𝑦,𝑦≠0,𝜃=1𝜃=1𝑥,𝑥≠0,𝜃=1𝜃=𝑥𝑦,𝑦≠0.
Рассмотрим пример, в котором мы используем единичный круг, чтобы найти точное значение функции секанса.
Пример 2. Нахождение значения тригонометрической функции угла по координатам точки пересечения конечной стороны и единичной окружности
точка 45,35.
Ответ
Говорят, что угол находится в стандартном положении, если его вершина находится в начале координат, а начальная сторона лежит на положительной оси 𝑥. Угол измеряется в направлении против часовой стрелки от начальной стороны к конечной стороне. Следовательно, угол 𝜃 такой, как показано.
Чтобы вычислить значение sec𝜃, мы начнем с определения того, является ли точка с координатами
45,35 лежит на единичной окружности. Для этого рассмотрим прямоугольный треугольник со сторонами 45 единиц и 35
единицы, как показано ниже.
Для этого рассмотрим прямоугольный треугольник со сторонами 45 единиц и 35
единицы, как показано ниже.
Затем мы можем вычислить длину гипотенузы 𝑐, используя теорему Пифагора: 45+35=𝑐,1625+95=𝑐,2525=𝑐.
Следовательно, 𝑐=1, что означает 𝑐=1. Итак, мы показали, что точка 45,35 лежит на единичной окружности.
𝑥- и 𝑦-координаты точки на единичной окружности, заданной углом 𝜃, определяются как 𝑥=𝜃𝑦=𝜃.cosandsin
Напомним, что seccos𝜃=1𝜃. В случае единичного круга sec𝜃=1𝑥. sec𝜃=1=54.
Теперь мы покажем, как найти точное значение квадрантного угла, то есть угла, крайняя сторона которого лежит либо на оси 𝑥, либо на оси 𝑦.
Пример 3. Нахождение значений косинуса квадрантных углов
Найдите значение cos0.
Ответ
𝑥- и 𝑦-координаты точки на единичной окружности, заданной углом 𝜃, определяются как 𝑥=𝜃𝑦=𝜃.cosandsin
Следовательно, значение cos0 будет значением в точке, где крайняя сторона для 𝜃=0 радиан пересекает окружность единичного круга, как показано на диаграмме.
Конечная сторона угла 𝜃=0 радиан лежит на оси 𝑥, поэтому точка, в которой он пересекает единичную окружность, равна (1,0). 𝑥-координата и, следовательно, значение cos0 равно 1,9.0003
Значение cos0 равно 1.
В наших предыдущих примерах мы показали, как использовать определение единичного круга для нахождения точного значения тригонометрических функций. В нашем следующем примере мы продемонстрируем, как единичный круг подтверждает периодичность таких функций.
Пример 4. Изучение различных углов между 0 и 2𝜋, имеющих одинаковую тригонометрическую функцию
Предположим, 𝑃 — точка на единичной окружности, соответствующая углу 4𝜋3. Есть ли на единичной окружности другая точка, представляющая угол в интервале [0,2𝜋[ с таким же значением тангенса? Если да, укажите угол.
Ответ
Мы начнем с рисования единичной окружности и точки 𝑃, которая образует угол 4𝜋3 радиана с положительной осью 𝑥, измеренной против часовой стрелки. Поскольку 4𝜋3 находится между 𝜋 и 3𝜋2, мы знаем, что эта точка должна лежать в третьем квадранте. Поскольку и 𝑥-, и 𝑦-координаты этой точки отрицательны, мы определим ее как 𝑃(−𝑎,−𝑏) для некоторых положительных констант 𝑎 и 𝑏.
Поскольку и 𝑥-, и 𝑦-координаты этой точки отрицательны, мы определим ее как 𝑃(−𝑎,−𝑏) для некоторых положительных констант 𝑎 и 𝑏.
Теперь вспомним определение функции касательной к единичной окружности. Дан угол 𝜃 в стандартном положении, где координаты точки пересечения конечной стороны с единичной окружностью равны (𝑥,𝑦) и 𝑥≠0, 𝑦𝑥=𝜃.tan
Для точки 𝑃, загар4𝜋3=−𝑏−𝑎=𝑏𝑎.
Частное этих 𝑥- и 𝑦-координат положительно. Заметим теперь, что на единичной окружности должна быть вторая точка, для которой это имеет место. Это точка с координатами (𝑎,𝑏), которая лежит в первом квадранте.
Мы можем сопоставить точку 𝑃 с точкой 𝑄, выполнив один оборот на 𝜋 радиан. Найти значение 𝛼 такое, что tan𝛼=𝑏𝑎, 4𝜋3−𝜋=𝜋3.
Да, на единичной окружности есть еще одна точка, которая дает то же значение касательной, что и угол 4𝜋3. Угол равен 𝜋3.
В нашем последнем примере мы покажем, как использовать единичный круг для вычисления простой тригонометрической функции.
Пример 5. Нахождение значения тригонометрической функции по координатам точки пересечения единичной окружности с конечной стороной угла в стандартном положении
Конечная сторона ∠𝐴𝑂𝐵 в стандартном положении пересекает единичную окружность 𝑂 в точке 𝐵 с координатами 3√10,𝑦, где 𝑦>0. Найдите значение sin𝐴𝑂𝐵.
Ответ
Говорят, что угол находится в стандартном положении, если его вершина находится в начале координат, а начальная сторона лежит на положительной оси 𝑥. Поскольку ∠𝐴𝑂𝐵 находится в стандартном положении, а 𝐵 не лежит на оси 𝑥, точка 𝐴 должна лежать на положительной оси 𝑥. Поэтому мы можем нарисовать ∠𝐴𝑂𝐵=𝜃 на единичной окружности. Поскольку и 𝑥-, и 𝑦-координаты положительны, точка 𝐵 лежит в первом квадранте.
Мы знаем, что 𝑥- и 𝑦-координаты точки на единичной окружности, заданной углом 𝜃, определяются как 𝑥=𝜃𝑦=𝜃.cosandsin
Следовательно, значение sin𝐴𝑂𝐵 равно значению 𝑦-координаты точки 𝐵. Представив △𝐴𝑂𝐵 в виде прямоугольного треугольника, мы можем найти значение 𝑦, используя теорему Пифагора.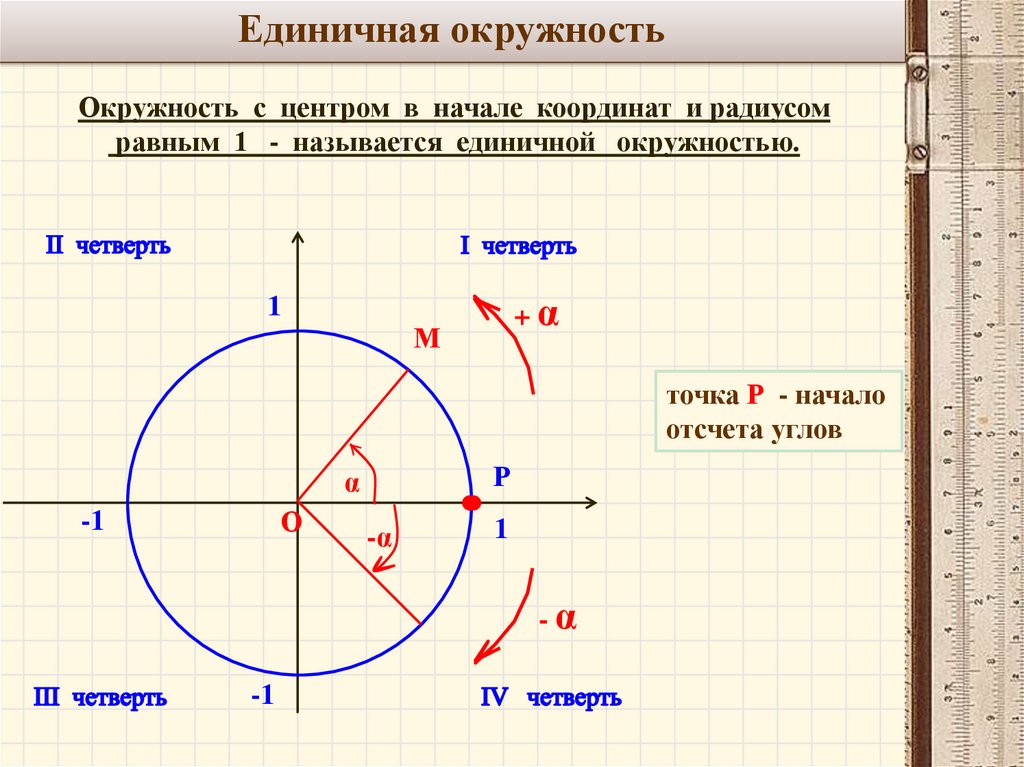
Имеем 1=𝑦+3√101=𝑦+910𝑦=110.
Поскольку в этом примере 𝑦>0, получаем 𝑦=1√10 единиц.
Значение sin𝐴𝑂𝐵 равно 1√10.
Давайте закончим повторением некоторых ключевых понятий из этого объяснения.
Ключевые точки
- Единичная окружность представляет собой окружность радиусом 1 с центром в начале координат плоскости.
- 𝑥- и 𝑦-координаты точки на единичной окружности, заданной углом 𝜃, определяются как ), где 𝑥≠0: tan𝜃=𝑦𝑥.
- Диаграмму CAST можно использовать для определения знаков тригонометрической функции для углов в каждом квадранте.
Как использовать единичный круг в тригонометрии?
Единичная окружность определяется как окружность, радиус которой равен 1 единице, центр находится в начале координат, а длина окружности равна 2π, поскольку r = 1. Здесь длина дуги эквивалентна величине центрального угла, пересекающего дуга. Тригонометрические функции, синус и косинус, имеют особое значение при рассмотрении единичного круга. Например, для любой точки на конце окружности угла в стандартном положении значение свойства синуса такого угла эквивалентно координате y точки. Кроме того, косинус такого угла эквивалентен координате x этой точки соответственно.
Например, для любой точки на конце окружности угла в стандартном положении значение свойства синуса такого угла эквивалентно координате y точки. Кроме того, косинус такого угла эквивалентен координате x этой точки соответственно.
Единица окружности в тригонометрии
Формула единичной окружностиНиже приводится общее уравнение для окружности:
(x – h) 2 + (y – k) 5 r 905 95 6 2 90 90
где,
- r — радиус окружности
- (h, k) — координаты центра круг можно лучше использовать для понимания тригонометрических функций. Для этого рассмотрим прямоугольный треугольник, помещенный внутри единичного круга в декартовой координатной плоскости. Если мы заметим, радиус этой окружности обозначает гипотенузу прямоугольного треугольника. Радиус окружности образует вектор. Это приводит к образованию угла, скажем, θ с положительной осью x. Предположим, что x — длина основания, а y — длина высоты прямоугольного треугольника соответственно.
Кроме того, координаты конечных точек радиус-вектора равны (x, y) соответственно.
Прямоугольный треугольник содержит стороны 1, x и y соответственно. Теперь можно вычислить тригонометрическое отношение следующим образом:
Теперь,
sin θ = y,
cos θ = x
Вычисления, tan θ = sin θ /cos θ = y/x.
Подставляя значения θ, мы также можем получить главные значения. Аналогично вычисляются значения всех остальных тригонометрических функций.
Тригонометрическое представление единичной окружности
Единичная окружность с отношениями Sin, Cos и TanЛюбая точка на единичной окружности с координатами (x, y), которые равны тригонометрическим тождествам (cosθ, sinθ). Координаты углов радиуса представляют собой косинус и синус значений θ для конкретного значения θ и линии радиуса. Имеем cos θ = x, а sin θ = y. Есть четыре части круга, каждая из которых лежит в одном квадранте, образуя углы 90°, 180°, 270° и 360°.
Единичные окружности и тригонометрические тождестваЗначения радиуса находятся в диапазоне от -1 до 1 соответственно. Кроме того, значения sinθ и cosθ лежат между 1 и -1 соответственно.
Тригонометрические тождества единичных окружностей для котангенса, секанса и косеканса можно вычислить, используя тождества для sin, cos и tan. В итоге получаем прямоугольный треугольник со сторонами 1, x и y соответственно. Вычисление тождеств единичного круга может быть выражено как
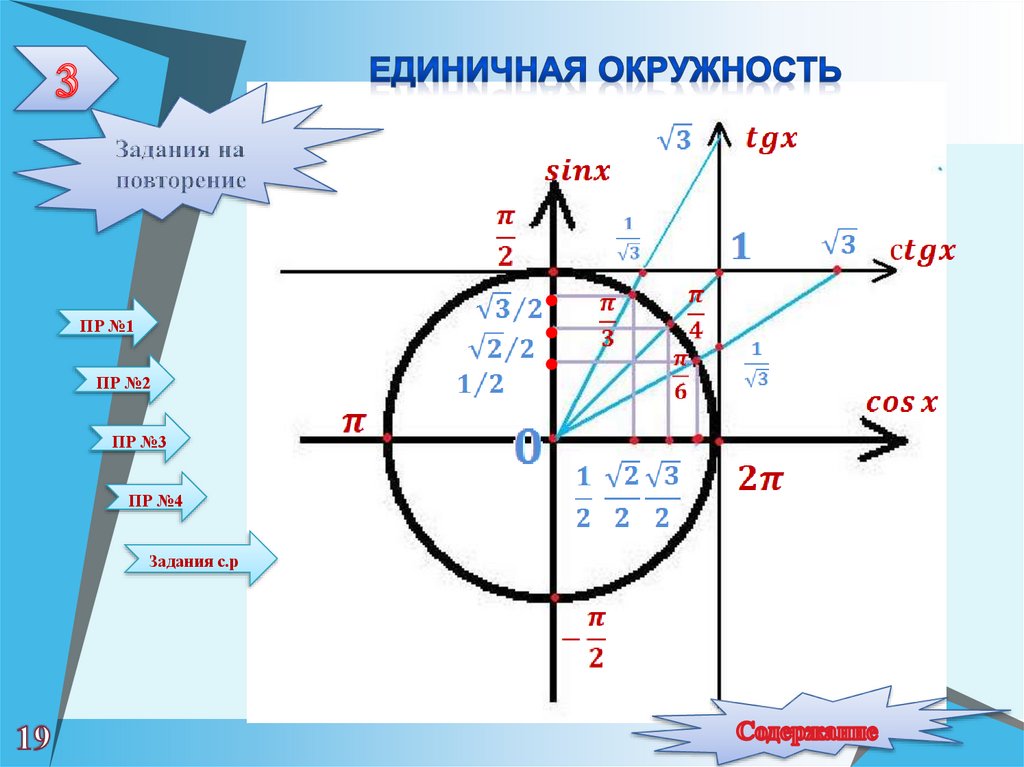
Таблица единичных окружностейsin θ =
cos θ =
tan θ =
sec θ =
cosec θ =
9θ0002 cot0003Тригонометрические соотношения, используемые в таблице единичных окружностей, используются для перечисления координат точек на единичной окружности, соответствующих общим углам.
Angles in Degree
0 o
30 o
45 o
60 o
90 o
sin
0
1
cos
1
0
7 9000 2 0236 0
1
Not Defined
csc
Not Defined
2
1
sec
1
\
2
Not Defined
cot
Not Defined
1
0
We can find the secant, cosecant , и функции котангенса, также использующие эти формулы:
secθ =
cosecθ =
cotθ =
Мы обсудили единичный круг для первого квадранта.
Решенные примеры для формулы единичной окружностиТочно так же мы можем расширить и найти радианы для всех квадрантов единичной окружности. Числа 1/2, 1/√2, √3/2, 0 и 1 повторяются вместе со знаком во всех 4 квадрантах.
Задача 1. Докажите, что точка Q лежит на единичной окружности.
Решение:
В соответствии с уравнением единичного круга, которое:
Отсюда заключаем, что точка Q не лежит на единичной окружности.
Задача 2: Вычислить tan 30 o , используя значения sin и cos единичного круга.
Решение:
Вычисление TAN 30 O Использование значений SIN и COS,
С.
,
,
SIN 30 O =
9000 2
9000 2 9000 2
o =
Следовательно,
Итого,
Tan 30 o =
Задача 3.
Проверить, лежит ли точка P(2/3, 3/2) на единичной окружности.
Решение:
В соответствии с уравнением единичного круга, которое равно:
x 2 + y 2 = 1
Здесь мы имеем
Подстановка значений x и y в уравнение (4*4)+(9*4))/36 = 1
= (16 +36)/36 = 1
= 52/36 = 1
= 13/9 = 1
Таким образом, 13/ 9≠ 1
Следовательно, точка P не лежит на единичной окружности.
Задача 4. Проверить, лежит ли точка Q(1/3, 1) на единичной окружности.
Решение:
Согласно уравнению единичного круга, то есть:
x 2 + y 2 = 1
Здесь мы имеем
x = 1/3
Y = 10003 Y = 10003 Y = 10003 Y = 10003 Y = 10003 Y = 10003 Y = 10003
.Теперь,
Подстановка значений x и y в уравнение
=> (1/3) 2 + (1) 2 = 1
=> 1/9 + 1 = 1
=> 10/9 = 1
Таким образом, 10/9 ≠ 1.

 Кроме того, координаты конечных точек радиус-вектора равны (x, y) соответственно.
Кроме того, координаты конечных точек радиус-вектора равны (x, y) соответственно.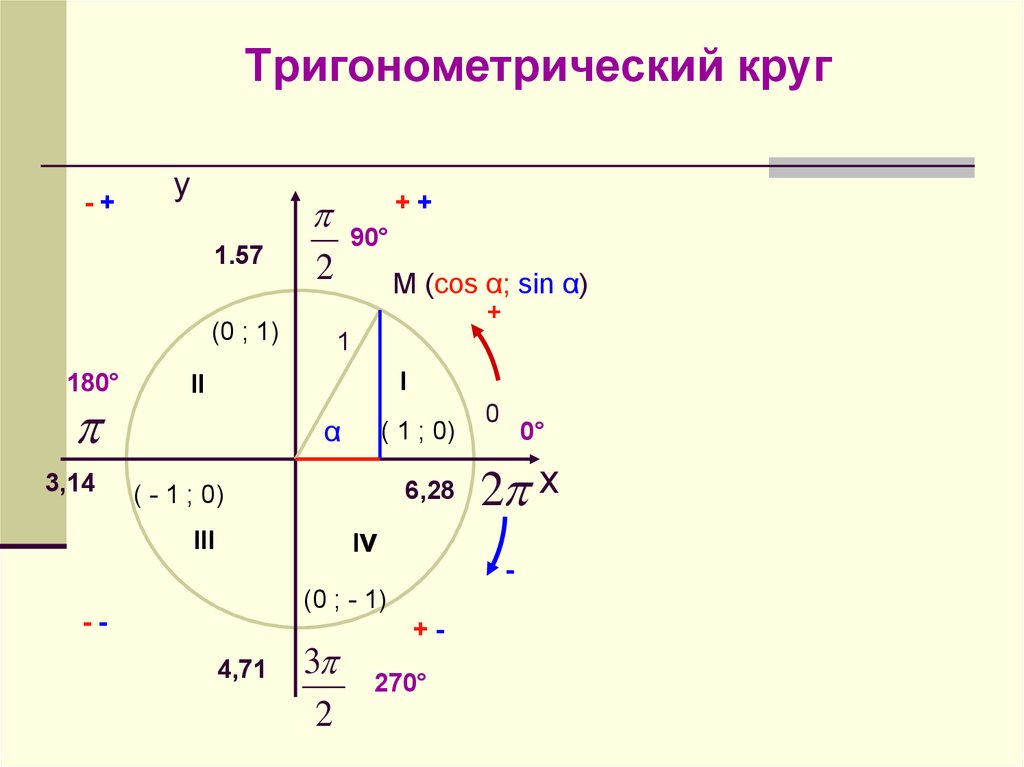 Значения радиуса находятся в диапазоне от -1 до 1 соответственно. Кроме того, значения sinθ и cosθ лежат между 1 и -1 соответственно.
Значения радиуса находятся в диапазоне от -1 до 1 соответственно. Кроме того, значения sinθ и cosθ лежат между 1 и -1 соответственно. Точно так же мы можем расширить и найти радианы для всех квадрантов единичной окружности. Числа 1/2, 1/√2, √3/2, 0 и 1 повторяются вместе со знаком во всех 4 квадрантах.
Точно так же мы можем расширить и найти радианы для всех квадрантов единичной окружности. Числа 1/2, 1/√2, √3/2, 0 и 1 повторяются вместе со знаком во всех 4 квадрантах. Проверить, лежит ли точка P(2/3, 3/2) на единичной окружности.
Проверить, лежит ли точка P(2/3, 3/2) на единичной окружности.