Нормальный закон распределения примеры решения задач: Нормальный закон распределения случайной величины. Правило трех сигм. Теория вероятностей и математическая статистика

8.8. Нормальный закон распределения

Непрерывная случайная величина Х имеет Нормальный закон распределения (закон Гаусса) с параметрами А и , если ее плотность вероятности имеет вид

.

Кривую нормального закона распределения называют Нормальной или Гауссовой кривой.

На рис. 8.14 приведены нормальная кривая Р(Х) с параметрами А и , т. е. , и график функции распределения случайной величины Х, имеющей нормальный закон

Рис. 8.14

Нормальная кривая симметрична относительно прямой Х = а, имеет максимум в точке Х = а, равный , и две точки перегиба с ординатой .

Для случайной величины, распределенной по нормальному закону, , .

Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(Х) по формуле

,

Где .

Вероятность попадания значений нормальной случайной величины Х в интервал Определяется формулой

.

Вероятность того, что отклонение случайной величины Х, распределенной по нормальному закону, от математического ожидания А не превысит величину (по абсолютной величине), равна

.

«Правило трех сигм»: если случайная величина Х имеет нормальный закон распределения с параметрами А и т. е. , то практически достоверно, что ее значения заключены в интервале

.

Асимметрия нормального распределения А = 0; эксцесс нормального распределения Е = 0.

Пример 8.23. Определить закон распределения случайной величины Х, если ее плотность распределения вероятностей задана функцией

.

Найти математическое ожидание, дисперсию и функцию распределения случайной величины Х.

Решение. Сравнивая данную функцию Р(Х) с функцией плотности вероятности для случайной величины, распределенной по нормальному закону, заключаем, что случайная величина

Х распределена по нормальному закону с параметрами А = 1 и .

Тогда , , .

Функция распределения случайной величины Х имеет вид

.

Пример 8.24. Текущая цена акции может быть смоделирована с помощью нормального закона распределения с математическим ожиданием 15 ден. ед. и средним квадратическим отклонением 0,2 ден. ед.

Найти вероятность того, что цена акции: а) не выше 15,3 ден. ед.; б) не ниже 15,4 ден. ед.; в) от 14,9 до 15,3 ден. ед. С помощью «правила трех сигм» найти границы, в которых будет находиться текущая цена акции.

Решение. Так как А = 15 и , то

По «правилу трех сигм» и, следовательно, . Окончательно .

Пример 8.25. Автомат изготавливает детали, которые считаются годными, если отклонение

Х от контрольного размера по модулю не превышает 0,8 мм. Каково наиболее вероятное число годных деталей из 150, если случайная величина Х распределена нормально с Мм?

Решение. Найдем вероятность отклонения при и

Считая приближенно Р = 0,95 и в соответствии с формулой

Где  — наивероятнейшее число, находим при

Откуда

Пример 8. 26. Размер диаметра втулок, изготовленных заводом, можно считать нормально распределенной случайной величиной с математическим ожиданием А = 2,5 см и средним квадратическим отклонением См.
В каких границах можно практически гарантировать размер диаметра втулки, если за вероятность практической достоверности принимается 0,9973?

Решение. По «правилу трех сигм» . Отсюда , т. е. .

Пример 8.27. Рост взрослых мужчин является случайной величиной, распределенной по нормальному закону. Пусть математическое ожидание ее равно 175 см, а среднее квадратическое отклонение — 6 см. Определить вероятность того, что хотя бы один из наудачу выбранных пяти мужчин будет иметь рост от 170 до 180 см.

Решение. Найдем вероятность того, что рост мужчины будет принадлежать интервалу :

Тогда вероятность того, что рост мужчины не будет принадлежать интервалу (170; 180) Q = 1 — 0,6 = 0,4.

Вероятность того, что хотя бы один из 5 мужчин будет иметь рост от
170 до 180 см равна

.

Пример 8.28. Браковка шариков для подшипников производится следу­ющим образом: если шарик не проходит через отверстие диаметром , но проходит через отверстие диаметром , то его размер считается приемлемым. Если какое-нибудь из этих условий не выполняется, то шарик бракуется. Известно, что диаметр шарика есть случайная величина с характеристиками и . Определить вероятность того, что шарик будет забракован.

Решение.

Так как , то

< Предыдущая		Следующая >

Примеры решения задач

Пример 1.

Пусть – количество очков при бросании игральной кости. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины.

Решение. Закон распределения имеет вид:

	1	2	3	6	5	6
							1

.

Дисперсию вычислим по формуле:

.

Закон распределения случайной величины имеет вид:

	1	4	9	16	25	36
							1

,

,

.

Пример 2.

Случайная величина – задана дифференциальной функцией распределенияв интервале. Вне этого интервала. Найти математическое ожидание величины.

Решение.

Для . Если.

Для

.

Пример 3.

Найти дисперсию случайной величины , заданной интегральной функцией

Решение.Найдем дифференциальную функцию распределения случайной величины:

.

.

Пример 4.

Дана функция

Определить, при каком значении функцияможет быть принята за плотность вероятности случайной величины. Определить это значение, найтии.

Решение.

– плотность некоторой случайной величины.

.

.

.

.

,.

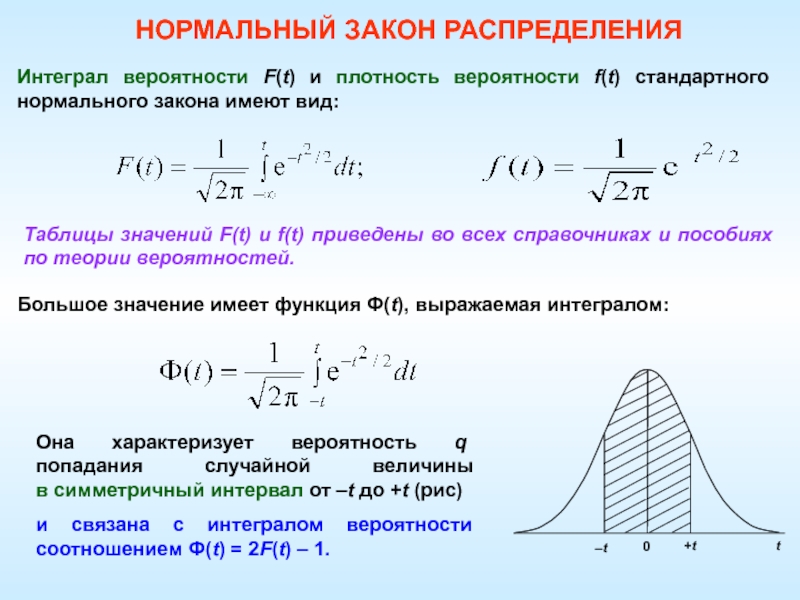
§ 3. Примеры распределения случайных величин

3.1 Биномиальное распределение

Определение. Распределение случайной величины, равной количеству появлений событияв схеме Бернулли изиспытаний, называется

биномиальным распределением.

В этом распределении значению случайной величинысоответствует вероятность, где– вероятность наступления событияв одном испытании, а.

Теорема. Пусть– случайная величина с биномиальным распределением. Тогда

,,.

Доказательство.

Т.к. биномиальное распределение дискретно, имеем:

Очевидно, что , где– случайная величина, равная количеству наступлений событияв-ом испытании. Всенезависимы и имеют закон распределения:

О

0	1

тсюда.

.

Согласно свойствам математического ожидания и дисперсии имеем:

,

,

.

3.2 Распределение Пуассона

Определение. Распределение случайной величины, принимающей значенияс вероятностями, где– некоторый параметр, называетсяпуассоновским распределениемилираспределением Пуассона.

Теорема. Пусть– случайная величина, подчиненная пуассоновскому закону распределения. Тогда

,,.

Доказательство.

Т.к. пуассоновское распределение дискретно, имеем:

.

.

.

3.3 Нормальное распределение

Определение. Распределение непрерывной случайной величины, заданное дифференциальной функцией распределения

, (1)

где и– некоторые параметры, называетсянормальным распределением.

Теорема.Если– нормально распределенная случайная величина с дифференциальной функцией распределения (1), то

,,.

Теорема устанавливает, таким образом, вероятностный смысл параметров нормального распределения.

Нормальное распределение (нормальная случайная величина) играет исключительно важную роль в теории вероятностей и в приложениях теории вероятности к практическим задачам.

Эта роль объясняется установленным фактом. Если известно, что изучаемая случайная величина складывается из большого количества случайных величин, каждое из которых оказывает лишь небольшое влияние на всю сумму, то можно считать, чтораспределена нормально.

Например, ошибка, допускаемая при измерении какой-либо физической величины, складывается, по-видимому, из большого числа ошибок, вызванных многочисленными причинами. Поэтому, как правило, случайная ошибка измерения имеет нормальное распределение.

Рассмотрим нормальное распределение более подробно.

График функции (1) изображен на рис. 14.1. Его можно получить из “стандартного графика” нормального распределения (,) сдвигом наединиц вправо, с последующим растяжением по горизонтали относительно оси симметрии враз. Функциятабулирована. Она упоминается в формулировке локальной теоремы Муавра-Лапласа. Криваясимметрична относительно прямой. Точкаявляется точкой максимума функции, а точки– точками перегиба. Чем больше, тем кривая положе.

Интегральный закон распределения, соответствующий дифференциальному закону (1), имеет вид:

. (2)

Интеграл (2) нельзя вычислить по формуле Ньютона-Лейбница. Однако удобно выразить через табулированную функцию Лапласа:

. (3)

Именно,

. (4)

По интегральной теореме Муавра-Лапласа имеем:

(5)

или

, где.

Пример.

Величина распределена нормально с параметрами,. Найти вероятность того, чтопримет значение в интервале.

Решение.

.

Функция быстро убывает при. Площадь под всей кривой равна 1. Площади криволинейных трапеций над интервалами,иравны соответственно,,. Таким образом, почти вся площадь под кривой сосредоточена над интервалом. Поскольку площадь криволинейной трапеции численно равна вероятности того, что случайная величина примет значение в соответствующем интервале, имеем

.

Это утверждение составляет содержание правила “трех сигм” для нормального распределения: практически достоверно, что нормальная случайная величина с параметрами ипринимает значения в интервале. Слова “практически достоверно” означают – с вероятностью.

Word Проблемы с нормальным распределением | Superprof

Что такое частота?

Когда люди думают о современной статистике, они часто думают об огромных достижениях в области машинного обучения и искусственного интеллекта. В то время как беспилотные автомобили и роботы представляют собой невероятное применение науки и математики, большинство статистических данных, которые используются ежедневно, на самом деле довольно просты. Частота, описательная статистика, является одним из примеров этого.

 

Частота определяется как количество раз, когда что-то происходит. Взгляните на несколько примеров ниже.

Как вы можете видеть выше, частота вычисляется простым подсчетом количества раз, когда что-то происходит. Информация, отображаемая на приведенной выше диаграмме, обычно резюмируется, как в таблице ниже.

 

	Частота	Частота
Люди 90 020	1 детский	3 взрослый
Шарики	2 синий	4 красный

 

Лучшие репетиторы по математике доступны

Поехали

Распределение частот

 

900 04 Частотное распределение может быть формулой, но чаще всего оно является визуальным представлением частоты. Независимо от того, как оно отображается, частотное распределение помогает нам лучше понять, как распределена переменная или как она выглядит. В следующей таблице указано количество пассажиров, ехавших на автобусе в каждый день недели.

 

9004 7

День	Частота
Понедельник	145
Вторник	205
Среда	199
Четверг	220
Пятница	250
Суббота	390
Воскресенье	405

 

Хотя иметь эту информацию в виде таблицы очень удобно, ее часто бывает трудно понять простыми числами. Отображение частотного распределения — это простой способ представить частоту в более понятной форме.

Что такое вероятность?

Чтобы дать определение вероятности, сначала нужно понять несколько основных определений. Эти определения вместе с примерами приведены ниже.

 

Концепция	Определение	Пример	Обозначение
Случайные переменные способный	Переменная, результат которой неизвестен	Результат подбрасывания монеты	Обычно заглавная буква как
Выборочное пространство	Все возможные результаты случайной величины	Орел и решка	S = {H,T}
Событие	Один или несколько результатов в выборке	Головы	A = H

 

9000 4 Вероятность определяется как шанс или вероятность того, что событие произойдет. Продолжая таблицу выше:

 

90 018 Обозначение

Концепция	Определение	Пример
Вероятность	Вероятность события	Вероятность выпадения орла (событие A)	P(A) = 0,5 (50%)

 

Вероятность Распределение

 

Вероятностное распределение — это визуализация, которая позволяет вам увидеть все возможные значения, которые может принимать случайная величина, а также вероятность возникновения каждого значения. Хотя это может показаться странным понятием, мы можем думать об этом с точки зрения роста людей в населении.

На изображении выше показан пример распределения вероятности роста, где средний рост составляет 175 см. Распределение показывает нам, что рост, который находится на нижнем и верхнем конце, например, 150 или 200 см, гораздо реже встречается в популяции. Другими словами, маловероятно, что чей-то рост находится на одном из этих концов.

 

Типы распределений

Как вы можете догадаться, разные переменные имеют разные распределения. Знание распределения переменной позволяет нам рассчитывать вероятности. Это потому, что каждое распределение имеет уравнение вероятности.

 

9002 6

Распределение	Параметры	Уравнение
Стандартный Нормальный	N(, )
Биномиальный	B(n,p )
Пуассона	Po()

 

9000 4 В приведенной выше таблице показаны три наиболее распространенных распределения вероятностей. Стандартное нормальное распределение весьма специфично. Одно из основных отличий состоит в том, что его вероятность можно найти только вместе с z-таблицей.

 

Нормальное распределение

Нормальное распределение — это непрерывное распределение вероятностей, которое является симметричным и имеет колоколообразную форму. Стандартное нормальное распределение похоже на нормальное. Вместо того, чтобы иметь интересующую переменную на оси X в виде необработанной оценки или простого числа, стандартное нормальное распределение показывает каждое значение случайной переменной в терминах стандартного отклонения. Каждое значение стандартизировано с использованием уравнения в приведенной выше таблице, в результате чего получается то, что известно как z-оценка.

 

9001 8 0,02 90 018 0,50000 90 018 0,58706

Z	0	0,01	0,03	0,04
0	0,50399	0,50798	0,51197	0,51595
0,1	0,53983	0 . 54380	0,54776	0,55172	0,55567
0,2	0,57926	0,58317	0,59095	0,59483
0,3	0,61791	0,62172	0,62552	0,62930	0,63307

 

В приведенной выше таблице показан пример z-таблицы. На изображении ниже показано, как найти z-оценку в z-таблице.

Задача 1

Нам интересно узнать, насколько вероятно, что один тип дерева вырастет до определенной длины. Длина этих деревьев имеет нормальное распределение. Дерево, которое вы измеряете, составляет 120 см. Учитывая следующую информацию, считаете ли вы, что такая длина дерева необычна для этого типа деревьев?

• Среднее значение: 100
• Стандартное отклонение: 10
• Формула:

Решение 1 . Помните, что стандартное нормальное распределение имеет среднее значение в центре с z-показателем, равным 0.

На изображении ниже представлены среднее значение и распределение высоты деревьев.

На данный момент мы знаем, что 120 см находится справа от 100 на распределении. Чтобы найти его точное местоположение, нам нужно найти z-показатель 120.

 

   

 

Z-показатель равен 2, что означает, что высота 120 на 2 стандартных отклонения выше средней высоты 100. Затем мы можем найти этот z-показатель в z-таблице.

Это дает нам вероятность 0,9772, что очень вероятно.

 

Задача 2

Вас интересует, насколько одинаковой длины носки, произведенные на фабрике. Вы измеряете распределение и видите, что существует нормальное распределение длины носков. Учитывая следующую информацию, насколько вероятно, что носок выше 25 см.

• Среднее значение: 20
• Стандартное отклонение: 10,5
• Формула:

 

Решение 2

На этот раз мы хотим узнать, насколько вероятно, что носок длина от 25 см и выше.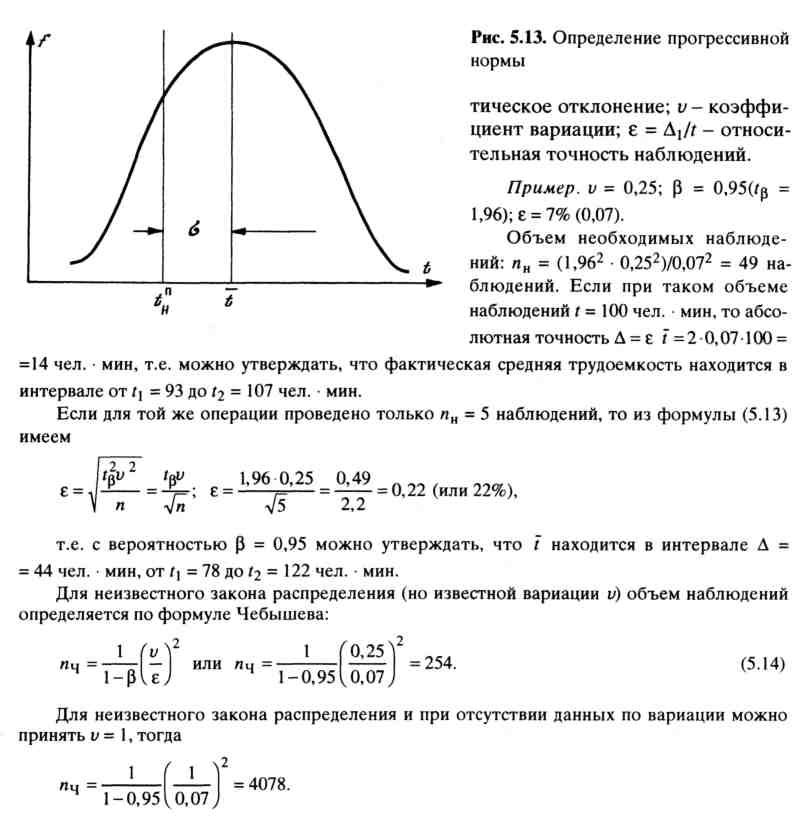 Это означает, что мы ищем вероятность правого хвоста вместо вероятности левого хвоста. Взглянув на дистрибутив, вы поймете, почему.

Сначала мы находим z-значение.

 

   

 

Затем мы смотрим на z-таблицу, чтобы найти вероятность.

Это дает нам вероятность 0,0004, что крайне маловероятно.

 

Нормальное распределение | Примеры, формулы и использование

Опубликован в 23 октября 2020 г. к Прита Бхандари. Отредактировано 9 января 2023 г.

При нормальном распределении данные распределяются симметрично без перекоса. При нанесении на график данные имеют форму колокола, при этом большинство значений группируются вокруг центральной области и сужаются по мере удаления от центра.

Нормальные распределения также называют распределениями Гаусса или кривыми нормального распределения из-за их формы.

Содержание

1. Почему нормальное распределение имеет значение?
2. Каковы свойства нормального распределения?
3. Эмпирическое правило
4. Центральная предельная теорема
5. Формула нормальной кривой
6. Что такое стандартное нормальное распределение?
7. Часто задаваемые вопросы о нормальном распределении

Почему нормальное распределение имеет значение?

Все виды переменных в естественных и социальных науках нормально или приблизительно нормально распределены. Рост, вес при рождении, умение читать, удовлетворенность работой или результаты SAT — вот лишь несколько примеров таких переменных.

Поскольку нормально распределенные переменные очень распространены, многие статистические тесты предназначены для нормально распределенных совокупностей.

Понимание свойств нормального распределения означает, что вы можете использовать статистику логического вывода для сравнения различных групп и делать оценки совокупности с использованием выборок.

Каковы свойства нормального распределения?

Нормальные распределения имеют ключевые характеристики, которые легко заметить на графиках:

• Среднее, медиана и мода точно такие же.
• Распределение симметрично относительно среднего — половина значений ниже среднего и половина выше среднего.
• Распределение можно описать двумя значениями: средним значением и стандартным отклонением.

Среднее значение — это параметр местоположения, а стандартное отклонение — параметр масштаба.

Среднее значение определяет центр пика кривой. Увеличение среднего значения сдвигает кривую вправо, а уменьшение — влево.

Стандартное отклонение растягивает или сжимает кривую. Небольшое стандартное отклонение приводит к узкой кривой, а большое стандартное отклонение приводит к широкой кривой.

Получение отзывов о языке, структуре и форматировании

Профессиональные редакторы вычитывают и редактируют вашу статью, уделяя особое внимание:

• Академический стиль
• Расплывчатые предложения
• Грамматика
• Согласованность стиля

См. пример

Эмпирическое правило

Эмпирическое правило , или правило 68-95-99,7, говорит вам, где находится большинство ваших значений в нормальном распределении:

• Около 68% значений находятся в пределах 1 стандартного отклонения от среднего.
• Около 95% значений находятся в пределах 2 стандартных отклонений от среднего.
• Около 99,7% значений находятся в пределах 3 стандартных отклонений от среднего значения.

Пример: Использование эмпирического правила в нормальном распределенииВы собираете баллы SAT от учащихся на новом курсе подготовки к экзаменам. Данные подчиняются нормальному распределению со средним значением ( M ) 1150 и стандартным отклонением ( SD ) 150.

Следуя эмпирическому правилу:

• Около 68% баллов находятся в диапазоне от 1000 до 1300, что на 1 стандартное отклонение выше и ниже среднего.
• Около 95% баллов находятся в диапазоне от 850 до 1450, что на 2 стандартных отклонения выше и ниже среднего.
• Около 99,7% баллов находятся в диапазоне от 700 до 1600, что на 3 стандартных отклонения выше и ниже среднего.

Эмпирическое правило — это быстрый способ получить обзор ваших данных и проверить любые выбросы или экстремальные значения, которые не соответствуют этому шаблону.

Если данные из небольших выборок не соответствуют этой схеме, то другие распределения, такие как t-распределение, могут быть более подходящими. Как только вы определите распределение вашей переменной, вы можете применить соответствующие статистические тесты.

Центральная предельная теорема

Центральная предельная теорема является основой того, как нормальные распределения работают в статистике.

В исследованиях, чтобы получить хорошее представление о среднем значении популяции, в идеале вы должны собирать данные из нескольких случайных выборок в популяции. Распределение выборки среднего значения — это распределение средних значений этих различных выборок.

Центральная предельная теорема показывает следующее:

• Закон больших чисел: по мере увеличения размера выборки (или количества выборок) среднее значение выборки будет приближаться к среднему значению генеральной совокупности.
• При наличии нескольких больших выборок выборочное распределение среднего имеет нормальное распределение, даже если исходная переменная не имеет нормального распределения.

Параметрические статистические тесты обычно предполагают, что выборки поступают из нормально распределенных совокупностей, но центральная предельная теорема означает, что это предположение не является обязательным, когда у вас достаточно большая выборка.

Вы можете использовать параметрические тесты для больших выборок из совокупностей с любым типом распределения, если выполняются другие важные предположения. Размер выборки 30 и более обычно считается большим.

Для небольших выборок предположение о нормальности важно, поскольку выборочное распределение среднего значения неизвестно. Чтобы получить точные результаты, вы должны быть уверены, что популяция распределена нормально, прежде чем вы сможете использовать параметрические тесты с небольшими выборками.

Формула нормальной кривой

Когда у вас есть среднее значение и стандартное отклонение нормального распределения, вы можете подогнать к вашим данным нормальную кривую, используя функцию плотности вероятности .

В функции плотности вероятности площадь под кривой говорит о вероятности. Нормальное распределение представляет собой распределение вероятностей , поэтому общая площадь под кривой всегда равна 1 или 100%.

Формула для нормальной функции плотности вероятности выглядит довольно сложной. Но чтобы использовать его, вам нужно знать только среднее значение генеральной совокупности и стандартное отклонение.

Для любого значения x вы можете подставить среднее значение и стандартное отклонение в формулу, чтобы найти плотность вероятности переменной, принимающей это значение х .

Формула плотности нормальной вероятности	Пояснение
	f ( x ) = вероятность x = значение переменной мк = среднее σ = стандартное отклонение σ 2 = дисперсия

Пример: использование функции плотности вероятностиВы хотите узнать вероятность того, что баллы SAT в вашей выборке превысят 1380.

На вашем графике функции плотности вероятности вероятность — это заштрихованная область под кривой, расположенной справа от того места, где ваш результат SAT равен 1380.

Вы можете найти значение вероятности этой оценки, используя стандартное нормальное распределение.

Что такое стандартное нормальное распределение?

Стандартное нормальное распределение , также называемое z -распределением , является особым нормальным распределением, где среднее значение равно 0, а стандартное отклонение равно 1.

Каждое нормальное распределение представляет собой версию стандартного нормального распределения, которая была растянута или сжата и перемещена по горизонтали вправо или влево.

В то время как отдельные наблюдения из нормального распределения обозначаются как x , они обозначаются как z в распределении z . Любое нормальное распределение можно преобразовать в стандартное нормальное распределение, превратив отдельные значения в z -баллов.

Z -счет показывает, на сколько стандартных отклонений от среднего лежит каждое значение.

 

Вам нужно знать только среднее значение и стандартное отклонение вашего распределения, чтобы найти z -оценку значения.

Z — формула счета	Пояснение
	x = индивидуальное значение мк = среднее σ = стандартное отклонение

Мы конвертируем нормальное распределение в стандартное нормальное распределение по нескольким причинам:

• Чтобы найти вероятность наблюдений в распределении выше или ниже заданного значения.
• Чтобы найти вероятность того, что среднее значение выборки значительно отличается от известного среднего значения генеральной совокупности.
• Для сравнения оценок по разным распределениям с разными средними значениями и стандартными отклонениями.

Нахождение вероятности с помощью

з -распределение

Каждая z -оценка связана с вероятностью, или p -значением, которая говорит вам о вероятности появления значений ниже этой z -оценки. Если вы преобразуете отдельное значение в z -показателей, вы можете затем найти вероятность того, что все значения до этого значения встречаются в нормальном распределении.

Пример: Нахождение вероятности с использованием распределения z 0557 z -счет.

Среднее значение нашего распределения равно 1150, а стандартное отклонение равно 150. Показатель z показывает, на сколько стандартных отклонений от 1380 от среднего значения.

Формула	Расчет

Для z -значения 1,53 значение p равно 0,937. Это вероятность того, что баллы SAT будут равны 1380 или меньше (93,7%), и это область под кривой слева от заштрихованной области.

Чтобы найти заштрихованную площадь, отнимите 0,937 от 1, что является общей площадью под кривой.

Вероятность x > 1380 = 1 – 0,937 = 0,063

Это означает, что только 6,3% баллов SAT в вашей выборке превышают 1380.

Часто задаваемые вопросы о нормальном распределении

Что такое нормальное распределение?

При нормальном распределении данные распределяются симметрично без перекоса. Большинство значений группируются вокруг центральной области, при этом значения сужаются по мере удаления от центра.

Меры центральной тенденции (среднее, мода и медиана) в нормальном распределении точно такие же.

Что такое эмпирическое правило?

Эмпирическое правило, или правило 68-95-99,7, говорит вам, где большинство значений находится в нормальном распределении:

• Около 68% значений находятся в пределах 1 стандартного отклонения от среднего.
• Около 95% значений находятся в пределах 2 стандартных отклонений от среднего значения.
• Около 99,7% значений находятся в пределах 3 стандартных отклонений от среднего значения.

Эмпирическое правило — это быстрый способ получить обзор ваших данных и проверить любые выбросы или экстремальные значения, которые не соответствуют этому шаблону.

Что такое t-распределение?

org/Answer»>

Распределение t — это способ описания набора наблюдений, где большинство наблюдений падают близко к среднему, а остальные наблюдения составляют хвосты с обеих сторон. Это тип нормального распределения, используемый для небольших выборок, когда дисперсия данных неизвестна.

Распределение t образует колоколообразную кривую при нанесении на график. Его можно описать математически, используя среднее значение и стандартное отклонение.

Процитировать эту статью Scribbr

Если вы хотите процитировать этот источник, вы можете скопировать и вставить цитату или нажать кнопку «Цитировать эту статью Scribbr», чтобы автоматически добавить цитату в наш бесплатный генератор цитирования.

Бхандари, П. (2023, 09 января). Нормальное распределение | Примеры, формулы и использование. Скриббр. Проверено 7 мая 2023 г., с https://www.

No related posts.