Нулевой вектор изображается: Недопустимое название | Математика | Fandom

Векторы в пространстве

Понятие вектора в пространстве. Равенство векторов.

1) С по­ня­ти­ем век­то­ра на плос­ко­сти мы уже стал­ки­ва­лись. Мы го­во­ри­ли, что есть такие ве­ли­чи­ны, для ко­то­рых важно не толь­ко чис­лен­ное зна­че­ние, но и на­прав­ле­ние, на­при­мер, сила, ско­рость и т. д. Такие ве­ли­чи­ны мы на­зы­ва­ли век­тор­ны­ми или про­сто век­то­ра­ми. В ма­те­ма­ти­ке век­тор изоб­ра­жа­ет­ся в виде на­прав­лен­но­го от­рез­ка. То есть, если задан от­ре­зок АВ и ска­за­но, что точка А – его на­ча­ло, а В – конец, то го­во­рят, что задан век­тор  или век­тор (рис. 1).

Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления. Нулевой вектор обозначает либо (рис. 1), либо .

Рисунок 1

Длина век­то­ра со­от­вет­ству­ет длине от­рез­ка, за­да­ю­ще­го этот век­тор. Длина вектора обозначается так: . длина нулевого вектора считается равной нулю: .

2) Два вектора называются коллинеарными, если изображающие их направления отрезки параллельны или лежат на одной прямой. Если два ненулевых вектора и коллинеарны и если при этом лучи АВ и CD сонаправлены, то векторы и называются сонаправленными (), а если лучи не являются сонаправленными, то векторы и называются противоположно направленными (). Нулевой вектор считают сонаправленным с любым вектором.

Пример.

По рисунку определить какие векторы являются сонаправленными, а какие противоположно направленными (рис. 2).

Рисунок 2

Сонаправленные: ,,,.

Противоположно направленные: , .

3) Рав­ны­ми на­зы­ва­ют­ся кол­ли­не­ар­ные со­на­прав­лен­ные век­то­ры, длины (мо­ду­ли) ко­то­рых равны. На рисунке 2 =, так как  и =, а , так как .

Если точка А – начало вектора , то говорят, что вектор отложен от точки А. нетрудно доказать, что от любой точки можно отложить вектор, равный данному, и притом только один. Для доказательства решим задачу: пусть — данный вектор, М – данная точка. Доказать, что через точку М можно провести вектор равный и притом только один (рис. 3).

Рисунок 3

Дано: , М.

Доказать: существование =, М , — единственный вектор.

Доказательство: проведем через начало и конец вектора и точку М плоскость и в этой плоскости построим =. из теоремы о параллельности прямых следует существование и единственность вектора =, где М.

4) Задача 1.

В тетраэдре ABCD точки M,N и K – середины ребер AC, BC и CD соответственно, АВ=3см, BC=4см, BD=5см. Найдите длины векторов

Дано: ABCD – тетраэдр, M,N и K – середины сторон AC, BC и CD соответственно, АВ=3см, BC=4см, BD=5см

Найти:

Решение: МК – средняя линия ∆ACD и NK – средняя линия ∆BCD (по условию).

=3см, =4см, =5см.

==1,5см.

==2см.

==2,5см.

Задача 2.

В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ стороны AD, AB и AA₁ равны 8см, 9 см и 12 см соответственно. Найти длины векторов ,,.

Задача 3.

На рисунке 4 изображен тетраэдр ABCD, ребра которого равны. Точки M,N,P и Q – середины сторон AB, AD, DC и BC соответственно. а) выпишите все пары равных векторов, изображенных на этом рисунке; б) определите вид четырехугольника MNPQ.

Рисунок 4

Домашнее задание:

Задача 4. Для рисунка из задачи 1 найти длины векторов

Задача 5. Дан правильный тетраэдр ABCD. Точки M,N,K – середины ребер AB, BC, CD соответственно. Найдите длину вектора , если

Действия над векторами.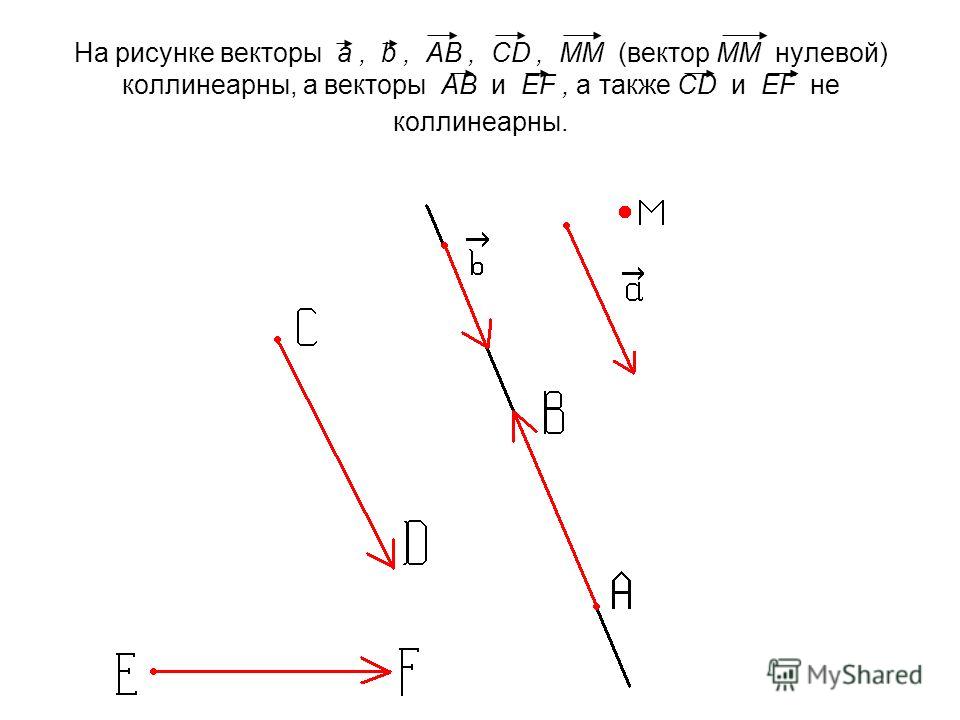

1. Сложение и вычитание векторов.

Введем правило сложения двух произвольных векторов и . Отложим от какой–нибудь точки А вектор (рис. 1), равный . затем от точки В отложим вектор , равный . Вектор называют суммой векторов и :. Это правило сложения векторов называется правилом треугольника. Его также можно сформулировать в такой форме: для любых трех точек А, В и С имеет место равенство: .

Рисунок 1

Для сложения неколлинеарных векторов также используется правило параллелограмма, знакомое вам из курса планиметрии (рис. 2).

Рисунок 2

Законы сложения векторов:

Переместительный закон	Сочетательный закон
=	=

Разностью векторов и называется такой вектор, сумма которого с вектором равна вектору (рис. 3).

, где вектор — противоположный вектору .

Рисунок 3

1. Умножение вектора на число

Произведением ненулевого вектора на число k называется такой вектор , длина которого равна , причем векторы и сонаправлены при k  0 и противоположно направлены при k  0. Произведением нулевого вектора на любое число считается нулевой вектор.

Законы умножения вектора на число:

Сочетательный закон	Первый распределительный закон	Второй распределительный закон
(kl)=k	k()= k+ k	(k+l)=k+l
Пример.	Пример.	Пример.

1. Задача 1.

Дан тетраэдр ABCD. Докажите что:

а) ;

б) ;

в) .

Задача 2.

Пусть ABCD – параллелограмм, а О – произвольная точка пространства. Докажите, что .

Задача 3.

Упростите выражение:

Задача 4.

Докажите, что в параллелепипеде ABCDA₁B₁C₁D₁ .

Домашнее задание:

Задача 5.

Нарисуйте параллелепипед ABCDA₁B₁C₁D₁ и обозначьте векторы соответственно через ,. Изобразите на рисунке векторы и .

Задача 6.

Векторы и коллинеарны. Докажите, что векторы и коллинеарны.

Компланарные векторы. Разложение вектора по направлениям

1. Компланарные векторы.

Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости. Любые два вектора компланарны; три вектора, среди которых два коллинеарны, также компланарны.

Пример.

На рисунке 1 изображен параллелепипед. Векторы – компланарны, так как, если отложить от точки О вектор, равный , то получится вектор , а векторы , и лежат в плоскости ОСЕ. – некомпланарны, так как вектор не лежит в плоскости ОАВ.

Рисунок 1

Признак компланарности трех векторов:

Если вектор можно разложить по векторам и , то есть представить в виде , (x,y – некоторые числа), то векторы , , – компланарны (рис 2).

Рисунок 2

1. Разложение вектора по трем некомпланарным векторам.

Если вектор представлен в виде , где x, y, z – некоторые числа, то говорят, что вектор разложен по векторам , и . Числа x, y, z называются коэффициентами разложения.

Теорема: любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.

Если векторы , компланарны, то z=0, и вектор оказывается фактически разложенным по двум векторам .

1. Задача 1.

Диагонали параллелепипеда ABCDA₁B₁C₁D₁ пересекаются в точке О.

Разложите векторы и по векторам .

Дано: ABCDA₁B₁C₁D₁ – параллелепипед: О – точка пересечения диагоналей.

Разложить векторы и по векторам .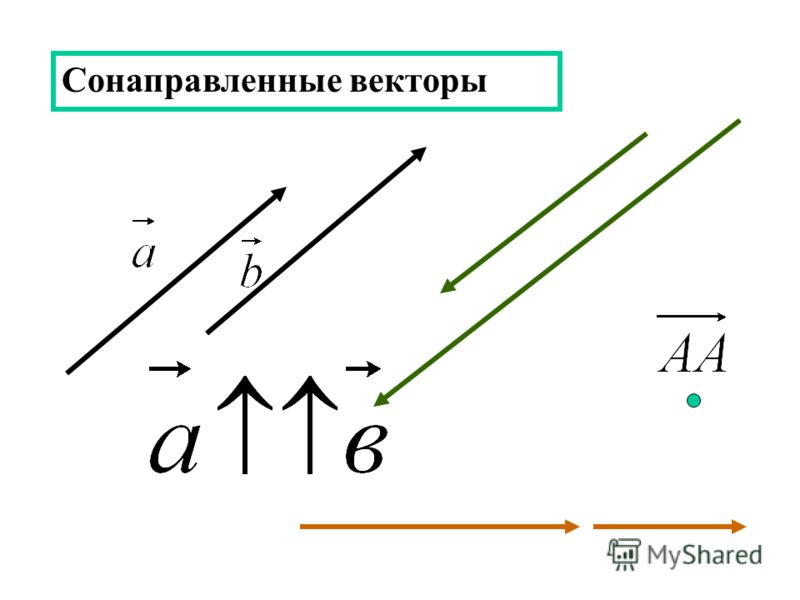

Решение: ;

;

;

Задача 2.

Основанием пирамиды с вершиной О является параллелограмм ABCD, диагонали параллелограмма пересекаются в точке М. Разложите векторы и по векторам

Задача 3.

Докажите, что если М – точка пересечения медиан треугольника ABC, а О – произвольная точка пространства, то:

Домашнее задание:

Задача 4.

Точка К – середина ребра В₁С₁ куба ABCDA₁B₁C₁D₁. Разложите вектор по векторам и найдите длину этого вектора, если ребро куба равно m.

Задача 5.

Вне плоскости параллелограмма ABCD взята точка О. точка М – середина АВ, а точка К – середина MD. Разложите вектор и по векторам

Нулевой вектор рисунок (49 фото) » Рисунки для срисовки и не только

Нулевой вектор

Понятие вектора. Нулевой вектор.

Скачать

Вектор изображается

Скачать

Изобразить векторы нулевой,

Скачать

Нулевой вектор в пространстве

Скачать

Понятие вектора на плоскости

Скачать

Координаты нулевого вектора

Нулевой вектор

Скачать

Нулевой вектор коллинеарен

Скачать

Нулевой впатор изображается

Скачать

Абсолютная величина вектора

Скачать

Определение нулевого вектора

Нулевой вектор изображается

Скачать

Нулевой вектор

Скачать

Нулевой вектор

Скачать

Нулевой вектор

Скачать

Нулевой вектор это в геометрии рисунок

Скачать

Нулевой вектор

Скачать

Нулевой вектор чертеж

Скачать

Определение нулевого вектора

Скачать

Координаты нулевого вектора

Скачать

Нулевой вектор пример

Скачать

Нулевой вектор

Скачать

Нулевой вектор изображается

Скачать

Понятие нулевого вектора

Скачать

Вектор нулевой вектор

Скачать

Как обозначаются коллинеарные векторы

Скачать

Сложение с нулевым вектором

Скачать

Определение нулевого вектора

Скачать

Вектор начало и конец которого совпадают называется

Скачать

Коллинеарные и неколлинеарные векторы на плоскости

Скачать

Нулевой вектор изображается

Скачать

Задачи на сложение и вычитание векторов

Скачать

Длина модуль вектора

Скачать

Модуль нулевого вектора

Скачать

Нулевой вектор в пространстве

Скачать

Построение векторов

Скачать

Нулевой вектор коллинеарен какому вектору

Скачать

Нулевой вектор изображается

Скачать

Которые из данных изображений соответствует сложения векторов

Скачать

Обозначение вектора

Скачать

Вектор ускорения тела

Скачать

Задание вектор

Скачать

Скачать

Нулевой вектор рисунок (49 фото)

Скачать

Скачать

Скачать

линейная алгебра — Что такое интуитивное определение нулевого вектора?

Задавать вопрос

спросил 9 лет, 4 месяца назад

Изменено 9 лет, 4 месяца назад

Просмотрено 10 тысяч раз

$\begingroup$

Сейчас я изучаю векторные пространства и подпространства, и одно из трех правил, определяющих, является ли что-то подпространством большего векторного пространства, состоит в том, что оно должно содержать нулевой вектор. {3}\;\middle|\; топор+by+cz=d\право\}$. Покажите, что $U$ является подпространством в $V$ тогда и только тогда, когда $d=0$. 92$. Это также не содержит нулевой вектор.

Мне кажется, что «нулевой вектор» используется как синоним «начала», но это не соответствует определению вектора, которое мне дали. Конечно, стрелка может начинаться в начале координат и выходить наружу, но не обязательно. Любая стрелка, представляющая вектор, такая же, как и любая другая, если она имеет одинаковую длину и направление, независимо от того, где находится основание стрелки, нулевой вектор все равно должен быть нулевым вектором.

Вот я и спрашиваю… Как может нулевой вектор не быть в 92$ — операция смещения с произвольной начальной точкой. Однако это не совсем так. Мы считаем два таких смещения существенно одинаковыми, если они имеют одно и то же направление и одинаковую величину. Это существенное тождество определяет отношение эквивалентности на множестве всех таких смещений. В этом контексте вектор является классом эквивалентности, а не просто его представителем.

Современный подход состоит в том, чтобы полностью отказаться от всех этих неудобств и принять аксиоматический подход. Векторное пространство — это множество с дополнительной структурой, удовлетворяющее определенному списку аксиом. Тогда вектор по определению является элементом векторного пространства. Тогда нулевой вектор является (доказуемо) уникальным вектором в данном векторном пространстве, который ведет себя нейтрально по отношению к сложению векторов. Это и есть нулевой вектор. Следует подчеркнуть, что точное имя нулевого вектора очень чувствительно к структуре векторного пространства. Например, $\mathbb R$ с его обычной структурой векторного пространства допускает $0$ в качестве нулевого вектора. Однако для каждого $a\in \mathbb R$ можно наделить $\mathbb R$ структурой векторного пространства так, что $a$ является нулевым вектором. Вот что происходит, когда мы переходим от определения того, что такое векторы (на котором в настоящее время зависит ваше понимание векторов), к тому, чтобы не заботиться о том, что они из себя представляют, и заботиться только о том, что вы можете с ними делать (это аксиоматический подход).

Есть веская причина, по которой последнее является преобладающим выбором в современной математике. Никто не заботится, и мы не должны заботиться о том, что есть что-то. Все, что имеет значение, это то, что мы можем с этим сделать. Если вы даже не пытаетесь определить, что такое что-то, а вместо этого просто прибегаете к перечислению того, что вы можете делать с этими вещами, это избавит вас от многих головных болей и бесконечных философских споров.

С учетом всего сказанного, за исключением упомянутых вами случаев, когда нулевой вектор не принадлежит данному множеству, рассмотрим пустое подмножество любого векторного пространства. Это никогда не векторное подпространство, поскольку оно не содержит нулевого вектора (или любого другого вектора).

$\endgroup$

1

$\begingroup$

«Дух» $0$-вектора таков: это элемент идентичности в операции «сложения», определенной в векторном пространстве.

Таким образом, вопрос о том, содержит ли ваш набор «тот» $0$-вектор, на самом деле зависит от того, как вы определили сложение: есть ли в вашем наборе элемент $\vec{0}$, такой что $\vec{x }+\vec{0}=\vec{0}+\vec{x}=\vec{x}$ для всех $\vec{x}$ в наборе?

$\endgroup$

$\begingroup$

Вы оперируете пониманием не просто векторного пространства, а аффинного пространства . Аффинное пространство — это в основном множество, на котором (транзитивно) действует векторное пространство. Векторы — это «направления», а аффинное пространство интуитивно состоит из точек в пространстве. Любые две точки определяют вектор смещения: уникальный вектор, который вы используете для перехода от одной точки к другой. Таким образом, вектор можно более или менее отождествить с классом эквивалентности пар точек с данным вектором в качестве вектора смещения.

Вы думаете: «Дано любое непустое подмножество аффинного пространства, в этом пространстве есть две точки с нулевым вектором смещения». 2$ — векторное пространство; это твой 92$. Важно отличать позиции (точки) от ходов (векторов).

Во многом это верно: «Дано непустое множество $S\subseteq A$ позиций, существует позиция $s\in S$, для которой у нас есть возможность не перемещаться». (Не двигаться эквивалентно смещению на $0\in V$.) Это соответствует тому, что вы думаете. Но идея подпространства — это

набора ходов , а не набор позиций, поэтому подмножество $M\subseteq V$. Действительно, в общем случае существуют наборы перемещений $M\subseteq V$, которые не содержат опции [идти в никуда]. Например, пусть $M=\{(0,1)\}$; это набор, содержащий движение [подняться на одну единицу]. Это не то же самое, что двигаться в никуда. Таким образом, даже несмотря на то, что все позиции допускают ход [никуда не ведут], не все наборы ходов содержат ход [никуда не идут]. 92}$. Линия, являющаяся подпространством, всегда будет натянута на один вектор. Если у нас есть линия в пространстве, которая не может быть натянута на один вектор, то является ли это векторным пространством (как может линия, не содержащая начало координат, рассматриваться как некоторая произвольная $(x,y)$)? Для подпространства $U$ имеется достаточно большое количество $x$ и $y$, где $x,y \in \mathbb{F}$ не удовлетворяют $x + y = 1$. n}$ не имеет решения $\mathbf{a}: \mathbf{x} + \mathbf{a} = \mathbf{x} $.

$\endgroup$

2

интуиция — Каково направление нулевого вектора?

спросил 12 лет, 5 месяцев назад

Изменено 1 год, 3 месяца назад

Просмотрено 29 тысяч раз

$\begingroup$

Чтобы быть более точным, мне интересно узнать , верно ли интуитивное предположение о том, что евклидов нулевой вектор не имеет определенного направления , и существует ли строгая формулировка, которая его поддерживает.

Записи Википедии о нулевом векторе вроде бы согласуются с этой интуицией, но, как всегда, не следует слепо доверять Википедии: в одном месте утверждается, что нулевой вектор »

ортогонален всем другим векторам с таким же количество компонентов, », а в другом утверждается, что « два вектора можно считать ортогональными тогда и только тогда, когда их скалярное произведение равно нулю и они имеют ненулевую длину. » Поправьте меня, если я ошибаюсь, но эти два утверждения противоречат друг другу.

Этот вопрос возник у меня в голове, когда я услышал, как кто-то утверждает, что, поскольку евклидов вектор определяется как геометрическая сущность, имеющая как величину, так и направление, а так как нулевой вектор является вектором длины 0, то нулевой вектор подходит только для того, чтобы иметь » направление 0. » Я лично склонен сказать, что нулевой вектор не имеет конкретного направления, но, как я уже сказал, я хотел бы знать, существует ли строгая формулировка, которая привела бы к такому выводу.

И к поставьте вопрос в менее «дискуссионной» форме: существует ли соглашение о направлении евклидова нулевого вектора? $\endgroup$

1

$\begingroup$

Нулевой вектор не имеет определенного направления; это согласуется с тем фактом, что он ортогонален любому другому вектору. (На самом деле не имеет смысла говорить, что он имеет « направление 0 », поскольку направление не является величиной; «направление 0» имеет не больше смысла, чем «направление 1». или «направление 5,873».)

В качестве альтернативы можно сказать, что он указывает во всех направлениях, но с нулевой величиной, так как если взять любой вектор и умножить его на ноль, вы получите нулевой вектор. «Каждый направление» — это то же самое, что «нет определенного направления»; это просто другой способ формулировки вещи.

Это недостаток традиционного описания вектора как пары, состоящей из величина и направление: для нулевого вектора величина равна нулю, но направление является произвольным.

$\endgroup$

2 9{n-1}$ путем определения противоположных точек.

$\endgroup$

$\begingroup$

Во-первых, нам нужно определение направления.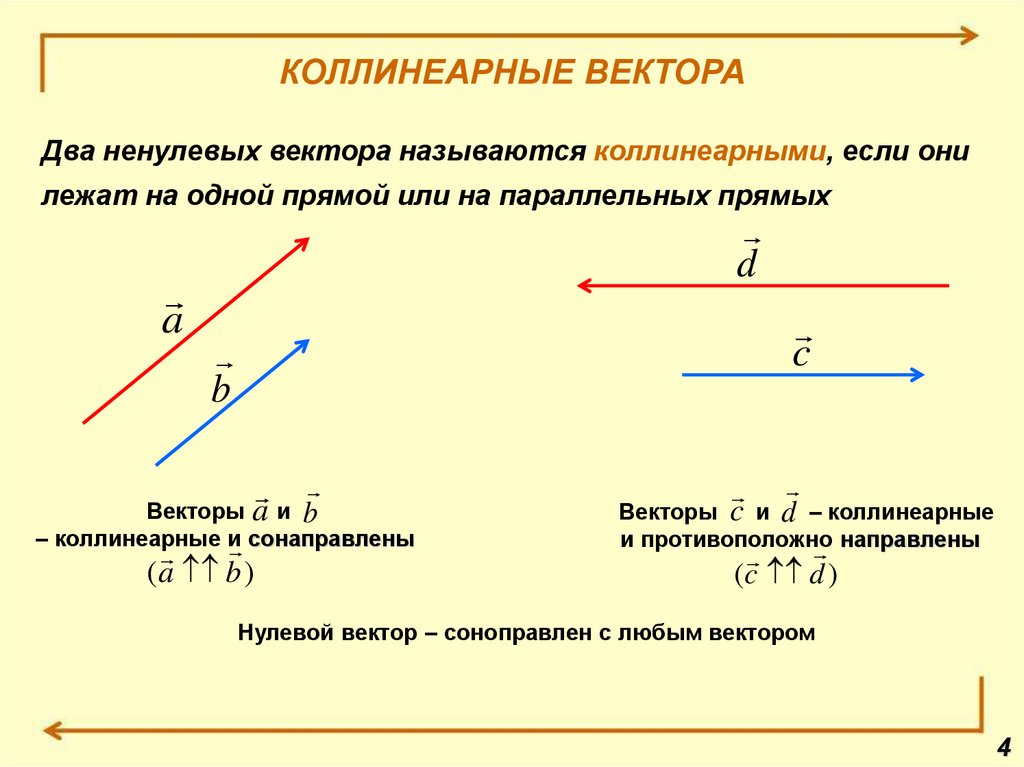

Как насчет этого: направлением вектора $x$ называется вектор $u$ единичной длины (то есть $|u| = 1$), такой что $cx = u$ для некоторого положительного действительного числа $c $.

Из определения ясно, что если $x = 0$, то не существует $c$ такого, что $cx$ — единичный вектор.

Также ясно, что направление $d(x)$ вектора $x$ есть функция, отображающая $x$ в единичный вектор. Для любого заданного $x$ коэффициент $c$ равен просто $\frac{1}{|x|}$, поэтому функция такова: $$d(x) = \frac{x}{|x| }$$.

Ясно, что функция не определена при $x = 0$, где она вызывает деление на ноль.

$\endgroup$

$\begingroup$

Вектор может иметь нулевую величину и направление. Выразите вектор как скаляр, умноженный на вектор единичной длины. Вектор единичной длины указывает направление, а скаляр представляет длину. Даже если длина стремится к нулю, у нас все еще есть направление. Это становится очевидным, если мы используем полярные или сферические координаты.

$\endgroup$

1

$\begingroup$

Я думаю, что вектор нулевой величины может иметь направление. Рассмотрим частицу, движущуюся по окружности с постоянной скоростью. Скорость переменная, потому что меняется направление. величина ускорения равна нулю, потому что скорость постоянна. Ускорение (направленное к центру) является переменным, потому что направление меняется каждое мгновение. Ясно, что ускорение присутствует с нулевой величиной.

$\endgroup$

3

$\begingroup$

Когда мы возьмем векторное произведение двух перпендикулярных векторов, мы получим вектор, имеющий нулевую величину.

No related posts.