Площади и периметры геометрических фигур: Площадь геометрических фигур — урок. Основной государственный экзамен 9 класс, Математика.

Нахождение площади и периметра геометрических фигур.

Муниципальное бюджетное общеобразовательное учреждение г. Владимира

«Средняя общеобразовательная школа № 32»

Ф.И.О. автора	Куликова Анастасия Юрьевна
Стаж работы	6 лет
Квалификационная категория	первая

Название УМК – «Гармония».

Название вариативного учебника, автора учебника – Н.Б. Истомина, Математика.

Название предмета – математика

Тема урока – нахождение площади и периметра геометрических фигур.

Класс, в котором проводился урок – 4 класс.

Математика

УМК – «Гармония»

Учебник «Математика» под редакцией Н.Б. Истоминой

Коллективный проект

Тема: «Площадь и периметр геометрических фигур»

Цель: формирование образовательных компетенций (информационных, проектировочных, коммуникативных, креативных) учащихся 4 «Б» класса в предметной области математики через включение учащихся в коллективный проект.

. Учебные задачи, направленные на достижение:

1) личностных результатов обучения:

—формирование уважительного отношения к иному мнению, иной точке зрения;

— развитие мотивов учебной деятельности и формирование личностного смысла учения.

2) метапредметных результатов обучения:

— развитие умения работать с информацией (сбор, систематизация, хранение, использование) – познавательные УУД;

— формирование начальных форм личностной рефлексии – регулятивные УУД;

—формирование умения слушать и слышать собеседника, вести диалог, излагать свою точку зрения и аргументировать её,

—формирование умения взаимодействия в статичных парах и группах – коммуникативные УУД.

3) предметных результатов обучения:

Закреплять знания учащихся по теме площадь и умение применять полученные знания на практике.

Формировать умение находить площадь и периметр, квадрата и прямоугольника, а также фигур неправильной формы.

Учить учащихся делать выводы, оформлять результаты.

Познакомить учащихся с примерами, связанными с практической необходимостью измерения площадей и периметров.

Научить работать в группе.

Научить производить расчёты.

Развивать навыки самостоятельной исследовательской деятельности.

Развивать умения использовать приобретенные знания и умения в практической деятельности.

Развивать мыслительную деятельность, творческие способности и логическое мышление учащихся при выполнении практической работы.

Формировать компетентности (информационные, проектировочные, коммуникативные, креативные)

Используемое оборудование: классная доска, карточки с нидивилуальным заданием, цветные карандаши, линейка, ручка.

Вопросы, направляющие проект

Основополагающий вопрос

Зачем нужно уметь находить площадь и периметр?

Проблемный вопрос

Площади: треугольника, фигур неправильной формы. Как составить алгоритм нахождения площади геометрической фигуры неправильной формы?

Самостоятельные исследования:

Вычисление площадей и периметров геометрических фигур.

Вывод формул для вычисления площади треугольника и неправильных фигур.

Учебные вопросы:

Площади каких фигур умеем находить?

Что для этого нужно знать и уметь?

Где в жизни нам пригодятся эти знания и умения?

Содержание взаимодействия педагога и учащихся

№ п/п	Этапы урока	Деятельность учителя	Деятельность учащихся	Формирование УУД
1.	Организационный момент	Учитель приветствует учащихся, проверяет их готовность к уроку.	Учащиеся готовы к началу работы.
2.	Мотивация к учебной деятельности	Сегодня у нас необычный урок, вы уже заметили. У каждого из вас в руках пропуск на этот урок. Что из себя представляет пропуск? Предположите, о чём пойдёт речь на уроке? Займите место за той партой, которая соответствует вашему пропуску. Будьте внимательны.	Геометрические фигуры О геометрических фигурах
	Осмысление учебной задачи (актуализация ранее изученного)	Посмотрите, как прекрасны эти сады. На весь мир известны королевский парк Версаль под Парижем, императорский Петергофский парк под Петербургом, легендарные сады Семирамиды. Над их созданием потрудилось много людей. Как думаете, с чего начиналась их работа? А начиналось всё с проектирования сада. Проектирование сада – старинное искусство. К нам обратилась фирма, занимающаяся ландшафтным дизайном, с просьбой сделать проект сада. Если мы правильно произведём расчёты площади и периметра объектов сада, торговая фирма «Наш сад» предоставит скидки на посадочный материал. Перед вами план этого сада.
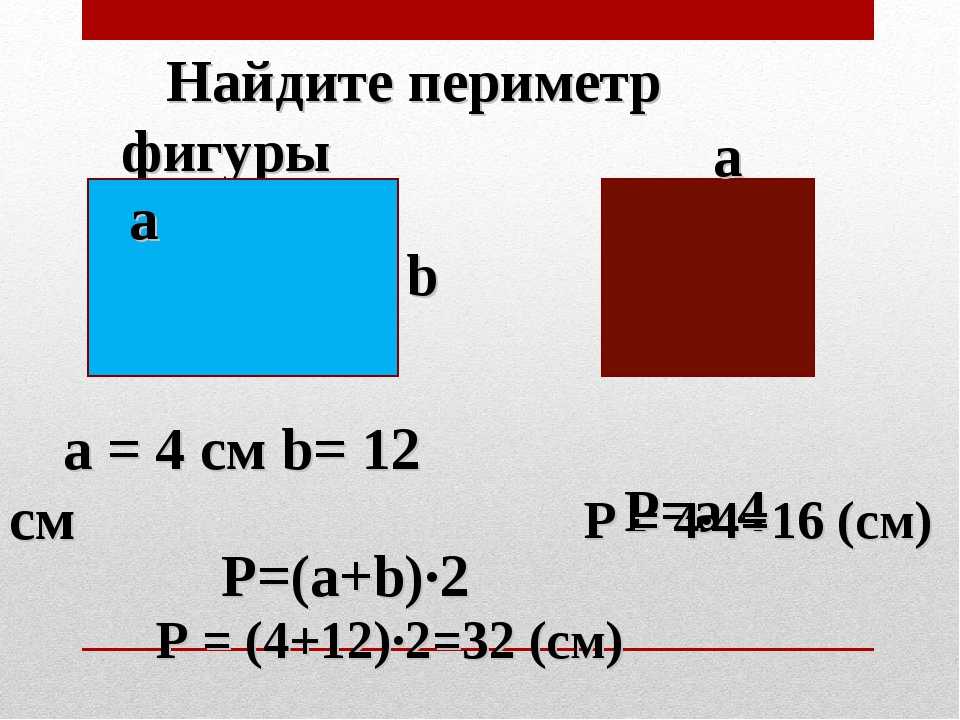
		Сначала надо рассчитать периметр сада, чтобы построить ограждение. Это задание предлагаю выполнить Злотович Георию и Белому Артёму.
		А мы в это время продолжаем знакомиться с планом сада. На нём есть: дом, газон, цветник, фруктовый сад. Формулу каких геометрических фигур имеют объекты сада? Площади каких фигур мы с вами умеем находить?	Треугольники, прямоугольники, шестиугольники. Квадрата, прямоугольника.
		Вспомните формулы нахождения. Среди предложенных мной формул нахождения площадей и периметров, найдите те, которые помогут нам найти площадь и периметр квадрата, площадь и периметр прямоугольника. Найдите их на доске. Формулы площадей каких фигур нам не знакомы?	Площадь треугольника.
	Открытие нового знания (изучение нового материала)	Как считаете, какова же тема нашего сегодняшнего урока? Чему будем на уроке учиться?	площадь треугольника Находить площадь треугольника, наблюдать, анализировать, работать по плану, в группе.	Регулятивные УУД
		Я предлагаю вам сегодня побыть математиками, исследователями и самостоятельно найти способ определения площади треугольника и попробовать самим создать формулу для нахождения площади треугольника. Поработайте в группе. Вспомните правила работы в группе.	Вежливо обращаться друг с другом, говорить тихим голосом, работать активно, серьёзно относясь к порученному заданию, умей слушать других.	Познавательные УУД

	Работа в группах	Распределите роли. Используя карточки с заданиями, произведите необходимые расчёты. А карточки с алгоритмами выступлений помогут вам сделать вывод о проделанной работе.		Коммуникативные УУД (постановка вопросов, инициативное сотрудничество в поиске и сборе информации)
	Рефлексия (итог урока)	Предоставит ли торговая фирма скидки на посадочный материал? Правильно ли мы произвели расчёты площади и периметра объектов сада? Чему учились на уроке? Что узнали?
		Оценить свою работу на оценочных листах.

Адрес публикации: https://www.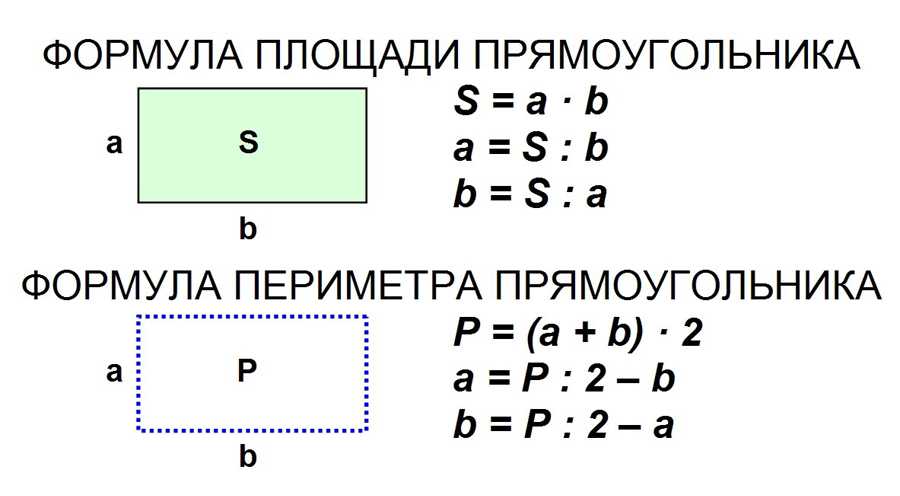 prodlenka.org/metodicheskie-razrabotki/439051-nahozhdenie-ploschadi-i-perimetra-geometriche

Задачи на площади и периметры геометрических фигур – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД

Запомнить

Восстановить пароль

Регистрация

Вопросы

1. По данным рисунка рассчитайте площадь фигуры.

    

2. По данным рисунка рассчитайте разность площадей двух частей фигуры.

    

3. Как изменится площадь фигуры, если ее периметр уменьшился на 30%, а ее форма осталась без изменений?

4. Если площадь фигуры уменьшилась на 36%, а ее форма осталась без изменений, то как изменится периметр этой фигуры?

5. По данным рисунка рассчитайте разность площадей закрашенной и не закрашенной частей фигуры.

    

6. Найти площадь заштрихованной части, если площадь большего треугольника равна \(40\), а стороны разделены на две и три равные части.

    

7. Найти площадь большего треугольника, если площадь заштрихованной части треугольника равна \(10\), а стороны разделены на две и три равные части.

    

8. Найти площадь заштрихованной части, если площадь большего треугольника \(60\), а стороны разделены на три равные части. 

    

9. Найти площадь большего треугольника, если площадь заштрихованной части \(10\), а стороны разделены на три равные части.

    

10. Найти площадь меньшего треугольника, если площадь заштрихованной части равно \(60\), а стороны разделены на три равные части.

     

Сообщить об ошибке

Обязательные

Математическая грамотность

Грамотность чтения

История Казахстана

Предметы по профилю

Биология

Химия

Английский язык

Французский язык

География

Немецкий язык

Информатика

Основы права

Русская литература

Математика

Физика

Русский язык

Всемирная история

Укажите предмет *

Скопируйте и вставьте вопрос задания *

Опишите подробнее найденную ошибку в задании *

Прикрепите скриншот

Объем файла не должен превышать 1МБ

Казахский

Русский

Обратите внимание! По выбранным Вами предметам ГРАНТЫ не предоставлены. В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.

1. Скачайте приложение iTest, используя QR-код или строку поиска в AppStore или Play Market

2. Авторизуйтесь в приложении и готовьтесь к экзаменам вместе с нами

8.G Площади геометрических фигур с одинаковым периметром ‹ OpenCurriculum

Ниже приведены изображения равностороннего треугольника, квадрата, правильного шестиугольника и круга с одинаковым периметром:

1. Найдите площадь равносторонний треугольник, периметр которого равен \(1\) единице.
2. Найдите площадь квадрата, периметр которого равен \(1\) единице.
3. Найдите площадь правильного шестиугольника, периметр которого равен единице.
4. Найдите площадь круга, периметр которого равен \(1\) единице.
5. Перечислите ответы на вопросы (а), (б), (в) и (г) в порядке возрастания. Как вы думаете, как площадь правильного восьмиугольника с единицей периметра \(1\) сравнима с площадью треугольника, квадрата, шестиугольника и круга?

Решения

Решение: 1

1. Чтобы использовать формулу Площадь = \(\frac{1}{2} \times\) Основание \(\times\) Высота треугольника, нам нужно выбрать основание, а затем определить высоту треугольника с этим основанием. Обозначив вершины треугольника \(A\), \(B\) и \(C\), пусть \(M\) будет точкой пересечения перпендикуляра из \(A\) с \(\overline{ до н.э.}\): 92 = \frac{3}{36}\) и $$ |AM| = \ гидроразрыва {\ sqrt {3}} {6}. $$ Теперь мы нашли высоту треугольника \(ABC\), используя \(\overline{BC}\) в качестве основания, поэтому площадь равна $$ \frac{1}{2}\times \frac{1 {3} \times \frac{\sqrt{3}}{6} = \frac{\sqrt{3}}{36}. $$

2. Квадрат с периметром, равным единице, имеет четыре конгруэнтные стороны, и, поскольку их длины в сумме составляют единицу, это означает, что каждая сторона равна \(\frac{1}{4}\) единице длины. Площадь квадрата равна длине, умноженной на высоту, так что это \(\frac{1}{4} \times \frac{1}{4} = \frac{1}{16}.\)

3. Правильный шестиугольник с периметром \(1\) можно разделить на \(6\) равносторонних треугольников, каждый из которых имеет длину стороны \(\frac{1}{6}\), как показано на рисунке ниже.

   В части (а) мы нашли площадь равностороннего треугольника, длина стороны которого равна \(\frac{1}{3}\) единице. Мы можем повторить рассуждения из части (а), чтобы найти площадь каждого из этих треугольников, и обнаружим, что она будет равна \(\frac{1}{4}\) ответа из части (а) в качестве основания и высота равностороннего треугольника из части (a) была увеличена с коэффициентом \(\frac{1}{2}\). Таким образом, площадь шестиугольника будет в \(\frac{6}{4}\) умножена на площадь равностороннего треугольника в части (a): $$ \text{Area(Hexagon)} = \frac{6}{ 4} \times \frac{\sqrt{3}}{36} = \frac{\sqrt{3}}{24}. $$ 92. $$ Умножение и упрощение дает \(\frac{1}{4\pi}\).

4. Поскольку \(\sqrt{3} \lt 2\) имеем $$ \frac{\sqrt{3}}{36} \lt \frac{2}{36} = \frac{1}{18} .
   2 = \frac{9{4}\). Итак, \(\frac{1}{16}\lt\frac{\sqrt{3}}{24}\). Наконец, чтобы сравнить \(\frac{\sqrt{3}}{24}\) с \(\frac{1}{4\pi}\), мы могли бы использовать тот факт, что \(\sqrt{3} \lt 1,8 \) поэтому \(\frac{\sqrt{3}}{24} \lt \frac{1.8}{24} = 0,075.\) С другой стороны, \(4\pi \lt 13\) и поэтому \( \frac{1}{4\pi} \gt \frac{1}{13} \gt 0,076\). Таким образом, $$ \ frac {\ sqrt {3}} {24} \ lt 0,075 \ lt 0,076 \ lt \ frac {1} {13} \ lt \ frac {1} {4 \ pi}. $$ Треугольник с периметром, равным единице, имеет наименьшую площадь, за ним следует квадрат, затем шестиугольник и, наконец, круг. Разумно предположить, основываясь на этом свидетельстве, что по мере увеличения числа сторон правильного многоугольника с периметром, равным единице, увеличивается и площадь. Это означало бы, что правильный восьмиугольник будет иметь большую площадь, чем правильный шестиугольник, но меньшую, чем круг.

Площади геометрических фигур с одинаковым периметром по иллюстративной математике, используемые в соответствии с CC-BY-NC-SA 3. 0

Формулы для площади периметра и объема

Формулы периметра, площади и объема

На этой странице мы будем учиться о различных формулах площади периметра и объема различных геометрических фигур и фигур. Насколько вам известно, периметр — это путь, который окружает или охватывает двухмерную форму.

Хотя Объем — это объем трехмерного пространства, заключенного в замкнутую поверхность.

А Площадь – это величина, выражающая размер двумерной фигуры или формы.

Формулы периметра, площади и объема для различных форм:-

• Геометрия — это раздел математики, который имеет дело с различными формами и размерами. Его можно разделить на два разных типа: плоская геометрия и сплошная геометрия
• плоская геометрия имеет дело с такими формами, как круги, треугольники, прямоугольники, квадраты.
• Объемная геометрия используется для расчета длины, периметра, площади и объема различных геометрических фигур и форм. Вот несколько основных формул, которые можно использовать для расчета длины, площади, объема и периметра различных форм и фигур.

Формулы для площади периметра и объема:-

• Формулы для площади

Здесь s = сторона 92}{2}

Длина окружности = 2πr

Длина окружности полукруга = πr

Длина дуги =\frac{2πrɵ}{360}

Площадь сектора = 1/2 (дуга*R) = πr²ɵ/360

• Parallelogram formulas
  • Perimeter: 2(a + b)
  • Area: b × h
  • Height of parallelogram = \frac{A}{b}

• Rhombus formulas 9{2}}

• Формулы трапеции
  • Периметр: a + b + c + d
  • Площадь: \frac{1}{2} × (сумма параллельных сторон) × расстояние между ними
  • Чтобы найти расстояние между параллельными сторонами, вам придется преобразовать трапецию в прямоугольник, а затем использовать ТЕОРЕМУ ПИФАГОРА .

    No related posts.