Чему равна площадь куба. Как найти площадь и объем куба
Куб обладает множеством интересных математических свойств и известен людям с давних времен. Представители некоторых древнегреческих школ считали, что элементарные частицы (атомы), из которых состоит наш мир, имеют форму куба, а мистики и эзотерики даже обожествляли эту фигуру. И сегодня представители паранауки приписывают кубу удивительные энергетические свойства.
Куб — это идеальная фигура, одно из пяти Платоновых тел. Платоново тело — это
правильная многогранная фигура, удовлетворяющая трем условиям:
1. Все ее ребра и грани равны.
2. Углы между гранями равны (у куба углы между гранями равны и составляют 90 градусов).
3. Все вершины фигуры касаются поверхности описанной вокруг нее сферы.
Точное количество этих фигур назвал древнегреческий математик Теэтет Афинский, а ученик Платона Евклид в 13-ой книге Начал дал им подробное математическое описание.
Древние греки, склонные с помощью количественных величин описывать строение нашего мира, придавали Платоновым телам глубокий сакральный смысл.
Итак, куб, называемый также гексаэдром (от греч. «hex» — 6), — это трехмерная правильная Его также называют или прямоугольным параллелепипедом.
У куба шесть граней, двенадцать ребер и восемь вершин. В эту фигуру можно вписать другие тетраэдр (четырехгранник с гранями в виде треугольников), октаэдр (восьмигранник) и икосаэдр (двадцатигранник).
Называется отрезок, соединяющий две симметричные относительно центра вершины. Зная длину ребра куба a, можно найти длину диагонали v: v = a 3.
В куб, как говорилось выше, можно вписать сферу, при этом радиус вписанной сферы (обозначим r) будет равен половине длины ребра: r =(1/2)а.
Если же сферу описать вокруг куба, то радиус описанной сферы (обозначим его R) будет равен: R= (3/2)a.
Довольно распространенный в школьных задачах вопрос: как вычислить площадь
поверхности куба? Очень просто, достаточно наглядно представить себе куб. Поверхность куба состоит из шести граней в форме квадратов. Следовательно, для того, чтобы найти площадь поверхности куба, сначала нужно найти площадь одной из граней и умножить на их количество: S п = 6а 2.
Аналогично тому, как мы нашли площадь поверхности куба, рассчитаем площадь его боковых граней: S б =4а 2.
Из этой формулы понятно, что две противолежащие грани куба — это основания, а остальные четыре — боковые поверхности.
Отыскать куба можно и другим способом. Учитывая тот факт, что куб — это прямоугольный параллелепипед, можно воспользоваться понятием трех пространственных измерений. Это значит, что куб, являясь трехмерной фигурой, имеет 3 параметра: длину (а), ширину(b) и высоту (c).
Используя эти параметры, вычислим площадь полной поверхности куба: S п = 2(ab+ас+bc).
Объем куба — это произведение трех составляющих — высоты, длины и ширины:
V= abc либо трех смежных ребер: V=а 3.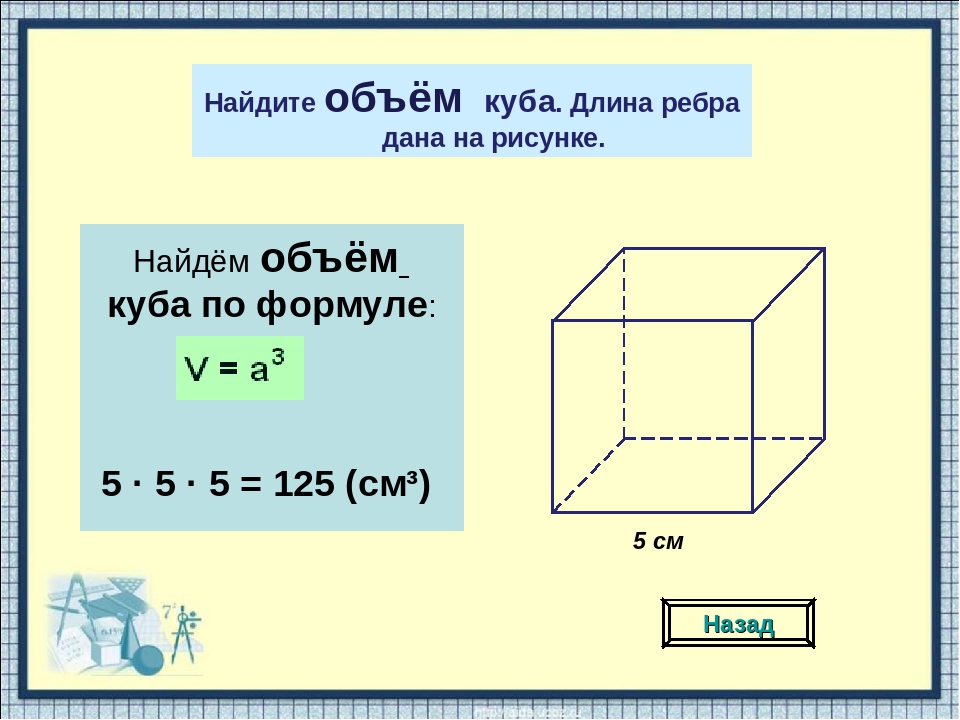
Это суммарная площадь всех поверхностей фигуры. Площадь поверхности куба равна сумме площадей всех его шести граней. Площадь поверхности является числовой характеристикой поверхности. Для вычисления площади поверхности куба, Вам необходимо знать определенную формулу и длину одной из сторон куба. Для того чтобы Вы могли оперативно вычислить площадь поверхности куба, вам необходимо запомнить формулу и сам порядок действий. Чуть ниже мы подробно разберем порядок вычисления полной площади поверхности куба и приведем конкретные примеры.
Выполняется по формуле SA = 6а 2 . Куб (правильный гексаэдр) — это один из 5 видов правильных многогранников, который является правильным прямоугольным параллелепипедом, куб имеет 6 граней, каждая из этих граней является квадратом.
Для вычисления площади поверхности куба Вам необходимо записать формулу SA = 6а 2 . Теперь давайте разберем почему данная формула имеет такой вид. Как мы говорили ранее, куб имеет шесть равных квадратных граней. Исходя из того что стороны квадрата равны, площадь квадрата составлять — a 2 , где а — сторона куба. Так куба имеет 6 равных квадратных граней, то для определения площади его поверхности, Вам необходимо умножить площадь одной грани (квадрата) на шесть. В итоге получаем формулу для вычисления площади поверхности (SA) куба: SA = 6а 2 , где а — ребро куба (сторона квадрата).
Исходя из того что стороны квадрата равны, площадь квадрата составлять — a 2 , где а — сторона куба. Так куба имеет 6 равных квадратных граней, то для определения площади его поверхности, Вам необходимо умножить площадь одной грани (квадрата) на шесть. В итоге получаем формулу для вычисления площади поверхности (SA) куба: SA = 6а 2 , где а — ребро куба (сторона квадрата).
Чему равна площадь поверхности куба.
Измеряется в квадратных единицах, к примеру, в мм 2 , см 2 , м 2 и так далее. Для дальнейших расчетов Вам необходимо будет измерить ребро куба. Как мы знаем, ребра у куба равны, поэтому Вам будет достаточно измерить только одно (любое) ребро куба. Выполнить такой замер Вы можете при помощи линейки (или рулетки). Обратите внимание на единицы измерения на линейке или рулетке и запишите значение, обозначив его через а.
Пример : а = 2 см.
Полученное значение возведите в квадрат. Таким образом, Вы возведите в квадрат длину ребра куба. Для того чтобы возвести число в квадрат умножьте его на себя.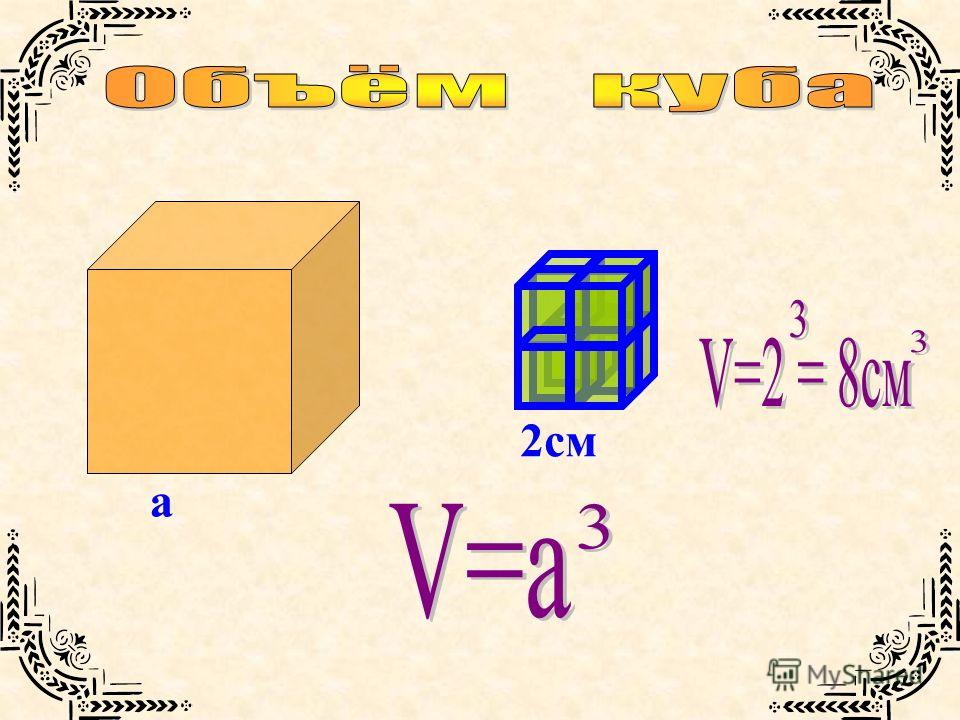 Наша формула будет иметь следующий вид: SA = 6*а 2
Наша формула будет иметь следующий вид: SA = 6*а 2
Вы вычислили значение площади одной из граней куба.
Пример : а = 2 см
a 2 = 2 х 2 = 4 см 2
Полученное значение умножайте на шесть. Не забывайте, что у куба 6 равных граней. Определив площадь одной из граней, умножьте полученное значение на 6, чтобы все грани куба участвовали в расчете.
Вот мы и пришли к конечному действию по вычислению площади поверхности куба .
Пример : а 2 = 4 см 2
SA = 6 х а 2 = 6 х 4 = 24 см 2
Куб — удивительная фигура. Он одинаковый со всех сторон. Любая его грань может вмиг стать основанием или боковой. И от этого ничего не изменится. А формулы для него всегда легко запоминаются. И неважно, что нужно найти — объем или площадь поверхности куба. В последнем случае даже не нужно учить что-то новое. Достаточно помнить только формулу площади квадрата.
Что такое площадь?
Эту величину принято обозначать латинской буквой S. Причем это справедливо для школьных предметов, таких как физика и математика. Измеряется она в квадратных единицах длины. Все зависит от данных в задаче величин. Это могут быть мм, см, м или км в квадрате. Причем возможны случаи, когда единицы даже не указаны. Идет речь просто о числовом выражении площади без наименования.
Измеряется она в квадратных единицах длины. Все зависит от данных в задаче величин. Это могут быть мм, см, м или км в квадрате. Причем возможны случаи, когда единицы даже не указаны. Идет речь просто о числовом выражении площади без наименования.
Так что же такое площадь? Это величина, которая является числовой характеристикой рассматриваемой фигуры или объемного тела. Она показывает размер ее поверхности, которая ограничена сторонами фигуры.
Какая фигура называется кубом?
Эта фигура является многогранником. Причем непростым. Он правильный, то есть у него все элементы равны друг другу. Будь то стороны или грани. Каждая поверхность куба представляет собой квадрат.
Другое название куба — правильный гексаэдр, если по-русски, то шестигранник. Он может быть образован из четырехугольной призмы или параллелепипеда. При соблюдении условия, когда все ребра равны и углы образуют 90 градусов.
Эта фигура настолько гармонична, что часто используется в быту. Например, первые игрушки малыша — кубики. А забава для тех, кто постарше, — кубик Рубика.
А забава для тех, кто постарше, — кубик Рубика.
Как связан куб с другими фигурами и телами?
Если начертить сечение куба, которое проходит через три его грани, то оно будет иметь вид треугольника. По мере удаления от вершины сечение будет все больше. Настанет момент, когда пересекаться будут уже 4 грани, и фигура в сечении станет четырехугольником. Если провести сечение через центр куба так, чтобы оно было перпендикулярно его главным диагоналям, то получится правильный шестиугольник.
Внутри куба можно начертить тетраэдр (треугольную пирамиду). За вершину тетраэдра берется один из его углов. Остальные три совпадут с вершинами, которые лежат на противоположных концах ребер выбранного угла куба.
В него можно вписать октаэдр (выпуклый правильный многогранник, который похож на две соединенные пирамиды). Для этого нужно найти центры всех граней куба. Они будут вершинами октаэдра.
Возможна и обратная операция, то есть внутрь октаэдра реально вписать куб.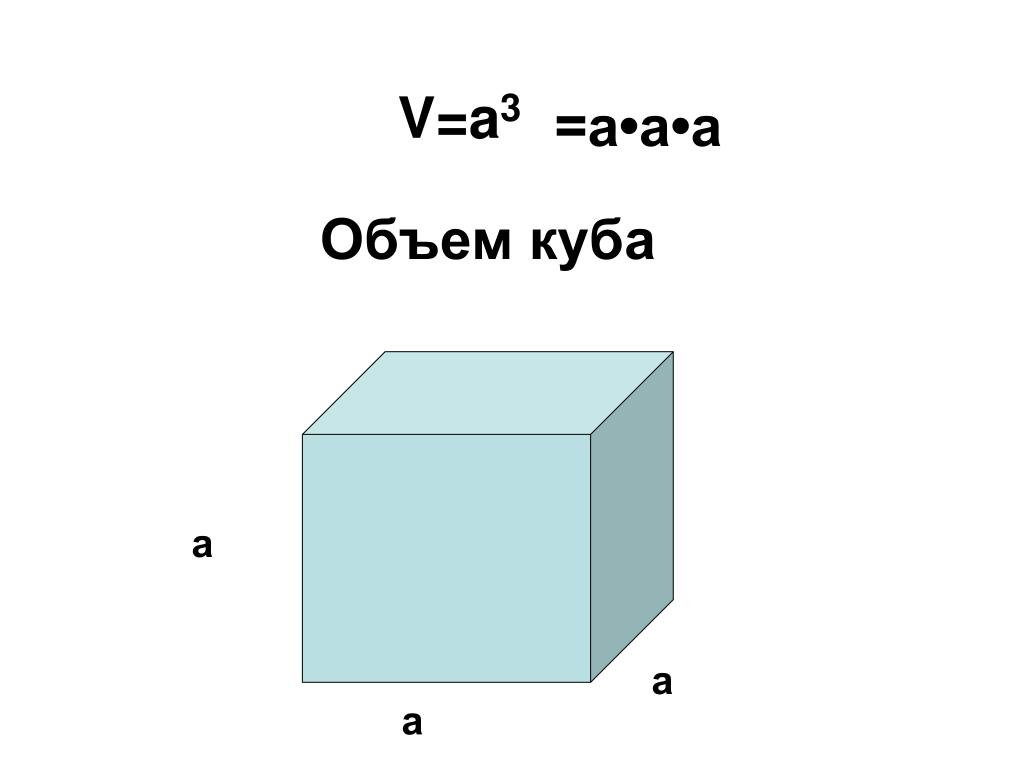 Только теперь центры граней первого станут вершинами для второго.
Только теперь центры граней первого станут вершинами для второго.
Метод 1: вычисление площади куба по его ребру
Для того чтобы вычислить всю площадь поверхности куба, потребуется знание одного из его элементов. Самый простой способ решения, когда известно его ребро или, другими словами, сторона квадрата, из которого он состоит. Обычно эта величина обозначается латинской буквой «а».
Теперь нужно вспомнить формулу, по которой вычисляется площадь квадрата. Чтобы не запутаться, введено ее обозначение буквой S 1 .
Для удобства лучше задать номера всем формулам. Эта будет первой.
Но это площадь только одного квадратика. Всего их шесть: 4 по бокам и 2 снизу и сверху. Тогда площадь поверхности куба вычисляется по такой формуле: S = 6 * a 2 . Ее номер 2.
Метод 2: как вычислить площадь, если известен объем тела
Из математического выражения для объема гексаэдра выводится то, по которому можно сосчитать длину ребра. Вот она:
Нумерация продолжается, и здесь уже цифра 3.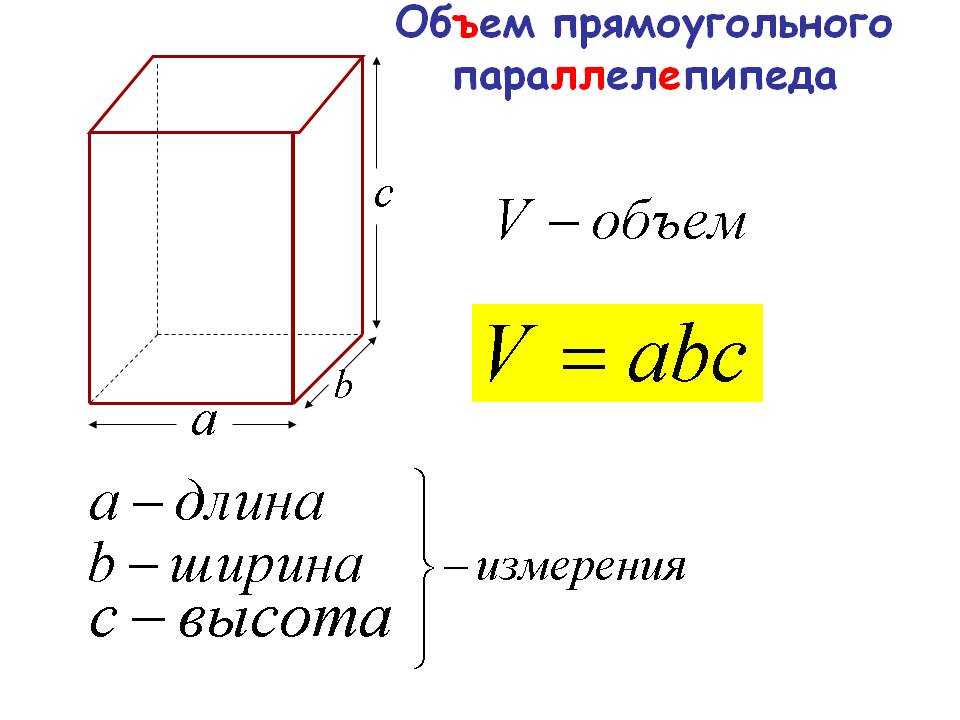
Теперь его можно вычислить и подставить во вторую формулу. Если действовать по нормам математики, то нужно вывести такое выражение:
Это формула площади всей поверхности куба, которой можно воспользоваться, если известен объем. Номер этой записи 4.
Метод 3: расчет площади по диагонали куба
Это формула №5.
Из нее легко вывести выражение для ребра куба:
Это шестая формула. После его вычисления можно снова воспользоваться формулой под вторым номером. Но лучше записать такую:
Она оказывается пронумерованной цифрой 7. Если внимательно посмотреть, то можно заметить, что последняя формула удобнее, чем поэтапный расчет.
Метод 4: как воспользоваться радиусом вписанной или описанной окружности для вычисления площади куба
Если обозначить радиус описанной около гексаэдра окружности буквой R, то площадь поверхности куба будет легко вычислить по такой формуле:
Ее порядковый номер 8. Она легко получается благодаря тому, что диаметр окружности полностью совпадает с главной диагональю.
Обозначив радиус вписанной окружности латинской буквой r, можно получить такую формулу для площади всей поверхности гексаэдра:
Это формула №9.
Несколько слов о боковой поверхности гексаэдра
Если в задаче требуется найти площадь боковой поверхности куба, то нужно воспользоваться уже описанным выше приемом. Когда уже дано ребро тела, то просто площадь квадрата нужно умножить на 4. Эта цифра появилась из-за того, что боковых граней у куба всего 4. Математическая запись этого выражения такая:
Ее номер 10. Если даны какие-то другие величины, то поступают аналогично описанным выше методам.
Примеры задач
Условие первой. Известна площадь поверхности куба. Она равна 200 см². Необходимо вычислить главную диагональ куба.
1 способ. Нужно воспользоваться формулой, которая обозначена цифрой 2. Из нее будет несложно вывести «а». Эта математическая запись будет выглядеть как квадратный корень из частного, равного S на 6. После подстановки чисел получается:
а = √ (200/6) = √ (100/3) = 10 √3 (см).
Пятая формула позволяет сразу вычислить главную диагональ куба. Для этого нужно значение ребра умножить на √3. Это просто. В ответе получается, что диагональ равна 10 см.
2 способ. На случай если забылась формула для диагонали, но помнится теорема Пифагора.
Аналогично тому, как было в первом способе, найти ребро. Потом нужно записать теорему для гипотенузы два раза: первую для треугольника на грани, вторую для того, который содержит искомую диагональ.
х² = а² + а², где х — диагональ квадрата.
d² = х² + а² = а² + а² + а² = 3 а². Из этой записи легко видно, как получается формула для диагонали. А дальше все расчеты будут, как в первом способе. Он немножко длиннее, но позволяет не запоминать формулу, а получить ее самостоятельно.
Ответ: диагональ куба равна 10 см.
Условие второй. По известной площади поверхности, которая равна 54 см 2 , вычислить объем куба.
Пользуясь формулой под вторым номером, нужно узнать значение ребра куба.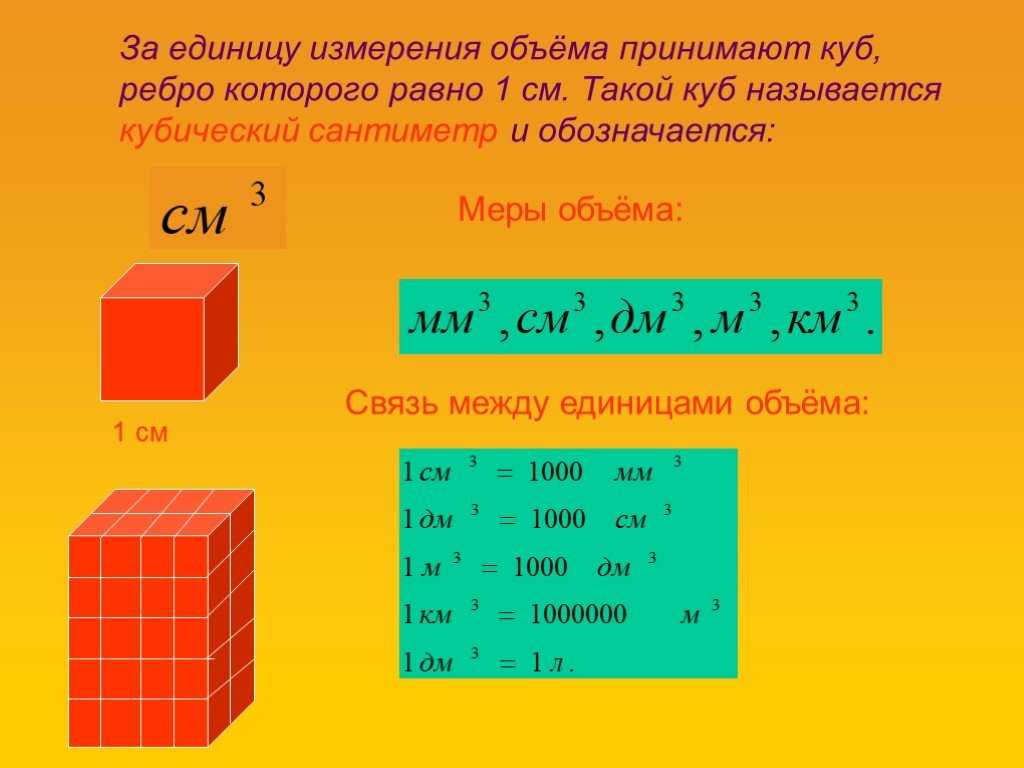
Теперь нужно воспользоваться формулой для объема куба, в которой длина ребра возводится в третью степень. Значит, объем будет считаться так: V = 3 3 = 27 см 3 .
Ответ: объем куба равен 27 см 3 .
Условие третьей. Требуется найти ребро куба, для которого выполняется следующее условие. При увеличении ребра на 9 единиц площадь всей поверхности увеличивается на 594.
Поскольку явных чисел в задаче не дано, только разности между тем, что было, и тем, что стало, то нужно ввести дополнительные обозначения. Это несложно. Пусть искомая величина будет равна «а». Тогда увеличенное ребро куба будет равно (а + 9).
Зная это, нужно записать формулу для площади поверхности куба два раза. Первая — для начального значения ребра — совпадет с той, которая пронумерована цифрой 2. Вторая будет немного отличаться. В ней вместо «а» нужно записать сумму (а + 9).
6 * (а + 9) 2 — 6 * а 2 = 594.
Нужно провести преобразования. Сначала вынести за скобку 6 в левой части равенства, а потом упростить то, что останется в скобках. А именно (а + 9) 2 — а 2 . Здесь записана разность квадратов, которую можно преобразовать так: (а + 9 — а)(а + 9 + а). После упрощения выражения получается 9(2а + 9).
Теперь его нужно умножить на 6, то есть то число, что было перед скобкой, и приравнять к 594: 54(2а + 9) = 594. Это линейное уравнение с одной неизвестной. Его легко решить. Сначала нужно раскрыть скобки, а потом перенести в левую часть равенства слагаемое с неизвестной величиной, а числа — в правую. Получится уравнение: 2а = 2. Из него видно, что искомая величина равна 1.
Площадь поверхности куба в чем измеряется. Как найти площадь и объем куба
Это суммарная площадь всех поверхностей фигуры. Площадь поверхности куба равна сумме площадей всех его шести граней.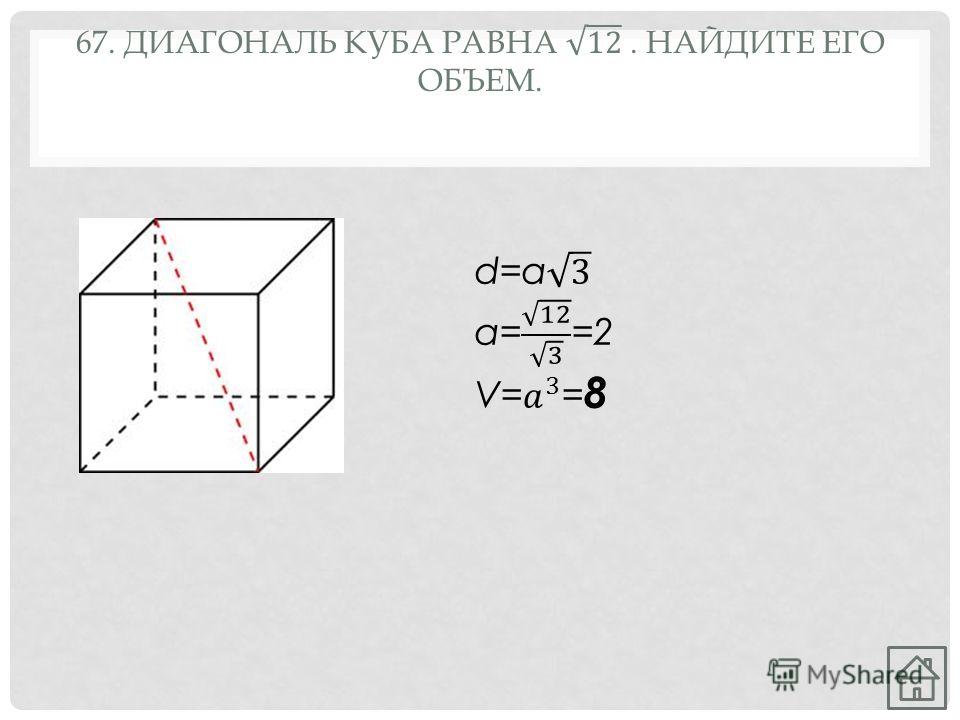 Площадь поверхности является числовой характеристикой поверхности. Для вычисления площади поверхности куба, Вам необходимо знать определенную формулу и длину одной из сторон куба. Для того чтобы Вы могли оперативно вычислить площадь поверхности куба, вам необходимо запомнить формулу и сам порядок действий. Чуть ниже мы подробно разберем порядок вычисления полной площади поверхности куба и приведем конкретные примеры.
Площадь поверхности является числовой характеристикой поверхности. Для вычисления площади поверхности куба, Вам необходимо знать определенную формулу и длину одной из сторон куба. Для того чтобы Вы могли оперативно вычислить площадь поверхности куба, вам необходимо запомнить формулу и сам порядок действий. Чуть ниже мы подробно разберем порядок вычисления полной площади поверхности куба и приведем конкретные примеры.
Выполняется по формуле SA = 6а 2 . Куб (правильный гексаэдр) — это один из 5 видов правильных многогранников, который является правильным прямоугольным параллелепипедом, куб имеет 6 граней, каждая из этих граней является квадратом.
Для вычисления площади поверхности куба Вам необходимо записать формулу SA = 6а 2 . Теперь давайте разберем почему данная формула имеет такой вид. Как мы говорили ранее, куб имеет шесть равных квадратных граней. Исходя из того что стороны квадрата равны, площадь квадрата составлять — a 2 , где а — сторона куба. Так куба имеет 6 равных квадратных граней, то для определения площади его поверхности, Вам необходимо умножить площадь одной грани (квадрата) на шесть. В итоге получаем формулу для вычисления площади поверхности (SA) куба: SA = 6а 2 , где а — ребро куба (сторона квадрата).
Так куба имеет 6 равных квадратных граней, то для определения площади его поверхности, Вам необходимо умножить площадь одной грани (квадрата) на шесть. В итоге получаем формулу для вычисления площади поверхности (SA) куба: SA = 6а 2 , где а — ребро куба (сторона квадрата).
Чему равна площадь поверхности куба.
Измеряется в квадратных единицах, к примеру, в мм 2 , см 2 , м 2 и так далее. Для дальнейших расчетов Вам необходимо будет измерить ребро куба. Как мы знаем, ребра у куба равны, поэтому Вам будет достаточно измерить только одно (любое) ребро куба. Выполнить такой замер Вы можете при помощи линейки (или рулетки). Обратите внимание на единицы измерения на линейке или рулетке и запишите значение, обозначив его через а.
Пример : а = 2 см.
Полученное значение возведите в квадрат. Таким образом, Вы возведите в квадрат длину ребра куба. Для того чтобы возвести число в квадрат умножьте его на себя. Наша формула будет иметь следующий вид: SA = 6*а 2
Вы вычислили значение площади одной из граней куба.
Пример : а = 2 см
a 2 = 2 х 2 = 4 см 2
Полученное значение умножайте на шесть. Не забывайте, что у куба 6 равных граней. Определив площадь одной из граней, умножьте полученное значение на 6, чтобы все грани куба участвовали в расчете.
Вот мы и пришли к конечному действию по вычислению площади поверхности куба .
Пример : а 2 = 4 см 2
SA = 6 х а 2 = 6 х 4 = 24 см 2
Куб — удивительная фигура. Он одинаковый со всех сторон. Любая его грань может вмиг стать основанием или боковой. И от этого ничего не изменится. А формулы для него всегда легко запоминаются. И неважно, что нужно найти — объем или площадь поверхности куба. В последнем случае даже не нужно учить что-то новое. Достаточно помнить только формулу площади квадрата.
Что такое площадь?
Эту величину принято обозначать латинской буквой S. Причем это справедливо для школьных предметов, таких как физика и математика. Измеряется она в квадратных единицах длины. Все зависит от данных в задаче величин. Это могут быть мм, см, м или км в квадрате. Причем возможны случаи, когда единицы даже не указаны. Идет речь просто о числовом выражении площади без наименования.
Это могут быть мм, см, м или км в квадрате. Причем возможны случаи, когда единицы даже не указаны. Идет речь просто о числовом выражении площади без наименования.
Так что же такое площадь? Это величина, которая является числовой характеристикой рассматриваемой фигуры или объемного тела. Она показывает размер ее поверхности, которая ограничена сторонами фигуры.
Какая фигура называется кубом?
Эта фигура является многогранником. Причем непростым. Он правильный, то есть у него все элементы равны друг другу. Будь то стороны или грани. Каждая поверхность куба представляет собой квадрат.
Другое название куба — правильный гексаэдр, если по-русски, то шестигранник. Он может быть образован из четырехугольной призмы или параллелепипеда. При соблюдении условия, когда все ребра равны и углы образуют 90 градусов.
Эта фигура настолько гармонична, что часто используется в быту. Например, первые игрушки малыша — кубики. А забава для тех, кто постарше, — кубик Рубика.
Как связан куб с другими фигурами и телами?
Если начертить сечение куба, которое проходит через три его грани, то оно будет иметь вид треугольника. По мере удаления от вершины сечение будет все больше. Настанет момент, когда пересекаться будут уже 4 грани, и фигура в сечении станет четырехугольником. Если провести сечение через центр куба так, чтобы оно было перпендикулярно его главным диагоналям, то получится правильный шестиугольник.
По мере удаления от вершины сечение будет все больше. Настанет момент, когда пересекаться будут уже 4 грани, и фигура в сечении станет четырехугольником. Если провести сечение через центр куба так, чтобы оно было перпендикулярно его главным диагоналям, то получится правильный шестиугольник.
Внутри куба можно начертить тетраэдр (треугольную пирамиду). За вершину тетраэдра берется один из его углов. Остальные три совпадут с вершинами, которые лежат на противоположных концах ребер выбранного угла куба.
В него можно вписать октаэдр (выпуклый правильный многогранник, который похож на две соединенные пирамиды). Для этого нужно найти центры всех граней куба. Они будут вершинами октаэдра.
Возможна и обратная операция, то есть внутрь октаэдра реально вписать куб. Только теперь центры граней первого станут вершинами для второго.
Метод 1: вычисление площади куба по его ребру
Для того чтобы вычислить всю площадь поверхности куба, потребуется знание одного из его элементов. Самый простой способ решения, когда известно его ребро или, другими словами, сторона квадрата, из которого он состоит. Обычно эта величина обозначается латинской буквой «а».
Самый простой способ решения, когда известно его ребро или, другими словами, сторона квадрата, из которого он состоит. Обычно эта величина обозначается латинской буквой «а».
Теперь нужно вспомнить формулу, по которой вычисляется площадь квадрата. Чтобы не запутаться, введено ее обозначение буквой S 1 .
Для удобства лучше задать номера всем формулам. Эта будет первой.
Но это площадь только одного квадратика. Всего их шесть: 4 по бокам и 2 снизу и сверху. Тогда площадь поверхности куба вычисляется по такой формуле: S = 6 * a 2 . Ее номер 2.
Метод 2: как вычислить площадь, если известен объем тела
Из математического выражения для объема гексаэдра выводится то, по которому можно сосчитать длину ребра. Вот она:
Нумерация продолжается, и здесь уже цифра 3.
Теперь его можно вычислить и подставить во вторую формулу. Если действовать по нормам математики, то нужно вывести такое выражение:
Это формула площади всей поверхности куба, которой можно воспользоваться, если известен объем. Номер этой записи 4.
Номер этой записи 4.
Метод 3: расчет площади по диагонали куба
Это формула №5.
Из нее легко вывести выражение для ребра куба:
Это шестая формула. После его вычисления можно снова воспользоваться формулой под вторым номером. Но лучше записать такую:
Она оказывается пронумерованной цифрой 7. Если внимательно посмотреть, то можно заметить, что последняя формула удобнее, чем поэтапный расчет.
Метод 4: как воспользоваться радиусом вписанной или описанной окружности для вычисления площади куба
Если обозначить радиус описанной около гексаэдра окружности буквой R, то площадь поверхности куба будет легко вычислить по такой формуле:
Ее порядковый номер 8. Она легко получается благодаря тому, что диаметр окружности полностью совпадает с главной диагональю.
Обозначив радиус вписанной окружности латинской буквой r, можно получить такую формулу для площади всей поверхности гексаэдра:
Это формула №9.
Несколько слов о боковой поверхности гексаэдра
Если в задаче требуется найти площадь боковой поверхности куба, то нужно воспользоваться уже описанным выше приемом. Когда уже дано ребро тела, то просто площадь квадрата нужно умножить на 4. Эта цифра появилась из-за того, что боковых граней у куба всего 4. Математическая запись этого выражения такая:
Когда уже дано ребро тела, то просто площадь квадрата нужно умножить на 4. Эта цифра появилась из-за того, что боковых граней у куба всего 4. Математическая запись этого выражения такая:
Ее номер 10. Если даны какие-то другие величины, то поступают аналогично описанным выше методам.
Примеры задач
Условие первой. Известна площадь поверхности куба. Она равна 200 см². Необходимо вычислить главную диагональ куба.
1 способ. Нужно воспользоваться формулой, которая обозначена цифрой 2. Из нее будет несложно вывести «а». Эта математическая запись будет выглядеть как квадратный корень из частного, равного S на 6. После подстановки чисел получается:
а = √ (200/6) = √ (100/3) = 10 √3 (см).
Пятая формула позволяет сразу вычислить главную диагональ куба. Для этого нужно значение ребра умножить на √3. Это просто. В ответе получается, что диагональ равна 10 см.
2 способ. На случай если забылась формула для диагонали, но помнится теорема Пифагора.
Аналогично тому, как было в первом способе, найти ребро. Потом нужно записать теорему для гипотенузы два раза: первую для треугольника на грани, вторую для того, который содержит искомую диагональ.
Потом нужно записать теорему для гипотенузы два раза: первую для треугольника на грани, вторую для того, который содержит искомую диагональ.
х² = а² + а², где х — диагональ квадрата.
d² = х² + а² = а² + а² + а² = 3 а². Из этой записи легко видно, как получается формула для диагонали. А дальше все расчеты будут, как в первом способе. Он немножко длиннее, но позволяет не запоминать формулу, а получить ее самостоятельно.
Ответ: диагональ куба равна 10 см.
Условие второй. По известной площади поверхности, которая равна 54 см 2 , вычислить объем куба.
Пользуясь формулой под вторым номером, нужно узнать значение ребра куба. То, как это делается, подробно описано в первом способе решения предыдущей задачи. Проведя все вычисления, получим, что а = 3 см.
Теперь нужно воспользоваться формулой для объема куба, в которой длина ребра возводится в третью степень. Значит, объем будет считаться так: V = 3 3 = 27 см 3 .
Ответ: объем куба равен 27 см 3 .
Условие третьей. Требуется найти ребро куба, для которого выполняется следующее условие. При увеличении ребра на 9 единиц площадь всей поверхности увеличивается на 594.
Поскольку явных чисел в задаче не дано, только разности между тем, что было, и тем, что стало, то нужно ввести дополнительные обозначения. Это несложно. Пусть искомая величина будет равна «а». Тогда увеличенное ребро куба будет равно (а + 9).
Зная это, нужно записать формулу для площади поверхности куба два раза. Первая — для начального значения ребра — совпадет с той, которая пронумерована цифрой 2. Вторая будет немного отличаться. В ней вместо «а» нужно записать сумму (а + 9). Так как в задаче идет речь о разности площадей, то нужно вычесть из большей площади меньшую:
6 * (а + 9) 2 — 6 * а 2 = 594.
Нужно провести преобразования. Сначала вынести за скобку 6 в левой части равенства, а потом упростить то, что останется в скобках. А именно (а + 9) 2 — а 2 . Здесь записана разность квадратов, которую можно преобразовать так: (а + 9 — а)(а + 9 + а). После упрощения выражения получается 9(2а + 9).
После упрощения выражения получается 9(2а + 9).
Теперь его нужно умножить на 6, то есть то число, что было перед скобкой, и приравнять к 594: 54(2а + 9) = 594. Это линейное уравнение с одной неизвестной. Его легко решить. Сначала нужно раскрыть скобки, а потом перенести в левую часть равенства слагаемое с неизвестной величиной, а числа — в правую. Получится уравнение: 2а = 2. Из него видно, что искомая величина равна 1.
Куб — одна из простейших трехмерных фигур. Каждому знакомы кубики льда, квадратные коробки или кристаллы соли – все они являются такими фигурами. Площадь поверхности куба — это общая площадь всех сторон на его поверхности. Все шесть его граней соразмерны, поэтому, зная длину одной из них, можно рассчитать боковую площадь и площадь поверхности любой фигуры.
Как найти площадь куба — что собой представляет фигура?
Куб — это трехмерная фигура, которая имеет одинаковые размеры. Его длина, ширина и высота идентичны, а каждое ребро встречает другие края под одним углом. Поиск площади поверхности куба быстрый и удобный, поскольку он состоит из конгруэнтных или соразмерных квадратов. Итак, как только вы найдете размер одного из квадратов, вы узнаете площадь всей фигуры.
Поиск площади поверхности куба быстрый и удобный, поскольку он состоит из конгруэнтных или соразмерных квадратов. Итак, как только вы найдете размер одного из квадратов, вы узнаете площадь всей фигуры.
Как найти площадь куба — грани фигуры
Из иллюстрации видно, что куб имеет переднюю и заднюю грань, две боковые и верхнюю с нижней стороны. Площадь любого куба будут составлять шесть конгруэнтных квадратов. Фактически, если развернуть его, можно четко увидеть шесть квадратов, которые составляют общую поверхность фигуры.
Как найти площадь куба
Площадь куба состоит из площади шести граней. Поскольку все они равны, достаточно знать площадь одной из них и умножить значение на 6. Площадь фигуры также находят по простой формуле: S = 6 x а², где «а» — одна из сторон куба.
Как найти площадь куба — установите площадь стороны
- Предположим, что высота куба составляет 2 см. Поскольку его поверхность состоит из квадратов, все его края будут иметь одинаковую длину.
 Поэтому, исходя из размеров высоты, его длина и ширина будут составлять 2 см.
Поэтому, исходя из размеров высоты, его длина и ширина будут составлять 2 см. - Чтобы найти площадь одного из квадратов, вспомните базовые знания геометрии, где S = а², где а — длина одной из сторон. В нашем случае, а = 2 см, так что S = (2 см)² = 2 см х 2 см = 4 см².
- Площадь одного из квадратов поверхности составляет 4 см². Не забудьте указать свое значение в квадратных единицах.
Как найти площадь куба — пример
Поскольку вся поверхность фигуры состоит из шести соразмерных квадратов, нужно умножить площадь одной стороны на 6, следуя формуле S = 6 x а². В нашем случае S = 6 х 4 см² = 24 см². Площадь трехмерной фигуры составляет 24 см².
Находим площадь куба, если сторона выражена в дробях
Если вам сложно работать с дробью, конвертируйте ее в десятичную.
Например, высота куба 2 ½ см.
- S = 6 х (2½ см) ²
- S = 6 х (2,5 см) ²
- S = 6 х 6,25 см ²
- S = 37,5 см ²
- Площадь поверхности куба — 37,5 см ².

Зная площадь куба, находим его сторону
Если площадь поверхности куба известна, можно определить длину его сторон.
- Площадь куба составляет 86,64 см². Необходимо определить длину грани.
- Решение. Поскольку известна площадь поверхности, нужно считать в обратном порядке, разделив значение на 6, а затем извлечь квадратный корень.
- Сделав необходимые вычисления, получаем длину 3,8 см.
Как найти площадь куба — онлайн измерение площади
Используя калькулятор на сайте OnlineMSchool , можно быстро вычислить площадь куба. Достаточно ввести нужное значение стороны и сервис выдаст детальное пошаговое решение задания.
Итак, чтобы знать площадь куба, вычислите площадь одной из сторон, затем умножьте результат на 6, так как фигура имеет 6 равных сторон. Можно при подсчете использовать формулу S = 6а². Если задана площадь поверхности, возможно определить длину боковой части, проделав обратные шаги.
Геометрия является одной из основных математических наук, базовый курс которой изучается даже в школе. На самом деле польза от знаний различных фигур и законов пригодится в жизни каждому. Очень часто встречаются геометрические задачи на нахождение площади . Если с плоскими фигурами особых проблем у учащихся не возникает, то вот объемные могут вызвать определенные трудности. Вычислить площадь поверхности куба бывает не так просто, как кажется на первый взгляд. Но при должном внимании решается даже самая сложная задача.
Необходимо:
Знания основных формул;
— условия задачи.
Инструкция:
- В первую очередь надо определиться, какая формула площади куба применима в конкретном случае . Для этого нужно посмотреть на заданные параметры фигуры . Какие данные известны: длина ребра , объем , диагональ , площадь грани . В зависимости от этого выбирается формула.
- Если по условиям задачи известна длина ребра куба , то достаточно применить простейшую формулу для нахождения площади.
 Известно практически каждому, что площадь квадрата находится умножением длин двух его сторон. Грани куба — квадраты, следовательно, площадь его поверхности равна сумме площадей этих квадратов. У куба шесть граней, поэтому формула площади куба будет выглядеть так: S=6*х 2 . Где х — длина ребра куба .
Известно практически каждому, что площадь квадрата находится умножением длин двух его сторон. Грани куба — квадраты, следовательно, площадь его поверхности равна сумме площадей этих квадратов. У куба шесть граней, поэтому формула площади куба будет выглядеть так: S=6*х 2 . Где х — длина ребра куба . - Допустим, что ребро куба не задано, но известен. Так как объем данной фигуры вычисляется возведением в третью степень длины его ребра , то последнюю можно получить достаточно легко. Для этого из числа, обозначающего объем, необходимо извлечь корень третей степени. Например, для числа 27 корнем третей степени будет число 3 . Ну а что делать дальше, мы уже разбирали. Таким образом, формула площади куба при известном объеме также существует, где вместо х стоит корень третей степени из объема.
- Бывает, что известна только длина диагонали . Если вспомнить теорему Пифагора , то можно легко вычислить длину ребра.
 Здесь достаточно базовых знаний. Полученный результат подставляется в уже известную нам формулу площади поверхности куба: S=6*х 2 .
Здесь достаточно базовых знаний. Полученный результат подставляется в уже известную нам формулу площади поверхности куба: S=6*х 2 . - Подводя итог, стоит отметить, что для правильных вычислений нужно узнать длину ребра. Условия в задачах встречаются самые разные, поэтому следует научится выполнять сразу несколько действий. Если известны другие характеристики геометрической фигуры, то с помощью дополнительных формул и теорем можно вычислить ребро куба. И уже на основании полученного результата посчитать результат.
Под кубом подразумевается правильный многогранник, у которого все грани образованы правильными четырехугольниками — квадратами. Для того, чтобы найти площадь грани любого куба, не потребуется тяжелых расчетов.
Инструкция
Для начала стоит заострить внимание на само определение куба. Из него видно, что любая из граней куба представляет собой квадрат. Таким образом, задача по нахождению площади грани куба сводится к задаче по нахождению площади любого из квадратов (граней куба). Можно взять именно любую из граней куба, так как длины всех его ребер равны между собой.
Можно взять именно любую из граней куба, так как длины всех его ребер равны между собой.
Для того, чтобы найти площадь грани куба, требуется перемножить между собой пару любых из его сторон, ведь все они между собой равны. Формулой это можно выразить так:
S = a?, где а — сторона квадрата (ребро куба).
Пример: Длина ребра куба 11 см, требуется найти ее площадь.
Решение: зная длину грани, можно найти ее площадь:
S = 11? = 121 см?
Ответ: площадь грани куба с ребром 11 см равна 121 см?
Обратите внимание
Любой куб имеет 8 вершин, 12 ребер, 6 граней и 3 грани при вершине.
Куб — это такая фигура, которая встречается в быту невероятно часто. Достаточно вспомнить игровые кубики, игральные кости, кубики в различны детских и подростковых конструкторах.
Многие элементы архитектуры имеют кубическую форму.
Кубическими метрами принято измерять объемы различных веществ в различных сферах жизни общества.
Говоря научным языком, кубический метр — это мера измерения объема вещества, которое способно поместиться в куб с длиной ребра 1 м
Таким образом, можно ввести и иные единицы измерения объема: кубические миллиметры, сантиметры, дециметры и т. п.
п.
Помимо различных кубических единиц измерения объема, в нефтяной и газовой промышленности возможно применение иной единицы — баррель (1м? = 6.29 баррелей)
Полезный совет
Если у куба известна длина ее ребра, то, помимо площади грани можно найти и другие параметры данного куба, например:
Площадь поверхности куба: S = 6*a?;
Объем: V = 6*a?;
Радиус вписанной сферы: r = a/2;
Радиус сферы, описанной вокруг куба: R = ((?3)*a))/2;
Диагональ куба (отрезок, соединяющие две противоположные вершины куба, который проходит через его центр): d = a*?3
Куб обладает множеством интересных математических свойств и известен людям с давних времен. Представители некоторых древнегреческих школ считали, что элементарные частицы (атомы), из которых состоит наш мир, имеют форму куба, а мистики и эзотерики даже обожествляли эту фигуру. И сегодня представители паранауки приписывают кубу удивительные энергетические свойства.
Куб — это идеальная фигура, одно из пяти Платоновых тел. Платоново тело — это
Платоново тело — это
правильная многогранная фигура, удовлетворяющая трем условиям:
1. Все ее ребра и грани равны.
2. Углы между гранями равны (у куба углы между гранями равны и составляют 90 градусов).
3. Все вершины фигуры касаются поверхности описанной вокруг нее сферы.
Точное количество этих фигур назвал древнегреческий математик Теэтет Афинский, а ученик Платона Евклид в 13-ой книге Начал дал им подробное математическое описание.
Древние греки, склонные с помощью количественных величин описывать строение нашего мира, придавали Платоновым телам глубокий сакральный смысл. Они считали, что каждая из фигур символизирует вселенские начала: тетраэдр — огонь, куб — землю, октаэдр — воздух, икосаэдр — воду, додекаэдр — эфир. Сфера же, описанная вокруг них, символизировала совершенство, божественное начало.
Итак, куб, называемый также гексаэдром (от греч. «hex» — 6), — это трехмерная правильная Его также называют или прямоугольным параллелепипедом.
У куба шесть граней, двенадцать ребер и восемь вершин. В эту фигуру можно вписать другие тетраэдр (четырехгранник с гранями в виде треугольников), октаэдр (восьмигранник) и икосаэдр (двадцатигранник).
Называется отрезок, соединяющий две симметричные относительно центра вершины. Зная длину ребра куба a, можно найти длину диагонали v: v = a 3.
В куб, как говорилось выше, можно вписать сферу, при этом радиус вписанной сферы (обозначим r) будет равен половине длины ребра: r =(1/2)а.
Если же сферу описать вокруг куба, то радиус описанной сферы (обозначим его R) будет равен: R= (3/2)a.
Довольно распространенный в школьных задачах вопрос: как вычислить площадь
поверхности куба? Очень просто, достаточно наглядно представить себе куб. Поверхность куба состоит из шести граней в форме квадратов. Следовательно, для того, чтобы найти площадь поверхности куба, сначала нужно найти площадь одной из граней и умножить на их количество: S п = 6а 2.
Аналогично тому, как мы нашли площадь поверхности куба, рассчитаем площадь его боковых граней: S б =4а 2.
Из этой формулы понятно, что две противолежащие грани куба — это основания, а остальные четыре — боковые поверхности.
Отыскать куба можно и другим способом. Учитывая тот факт, что куб — это прямоугольный параллелепипед, можно воспользоваться понятием трех пространственных измерений. Это значит, что куб, являясь трехмерной фигурой, имеет 3 параметра: длину (а), ширину(b) и высоту (c).
Используя эти параметры, вычислим площадь полной поверхности куба: S п = 2(ab+ас+bc).
Объем куба — это произведение трех составляющих — высоты, длины и ширины:
V= abc либо трех смежных ребер: V=а 3.
Куб – одна из простейших трехмерных фигур. Каждому знакомы кубики льда, квадратные коробки или кристаллы соли – все они являются такими фигурами. Площадь поверхности куба – это общая площадь всех сторон на его поверхности. Все шесть его граней соразмерны, поэтому, зная длину одной из них, можно рассчитать боковую площадь и площадь поверхности любой фигуры.
Как найти площадь куба – что собой представляет фигура?
Куб – это трехмерная фигура, которая имеет одинаковые размеры. Его длина, ширина и высота идентичны, а каждое ребро встречает другие края под одним углом. Поиск площади поверхности куба быстрый и удобный, поскольку он состоит из конгруэнтных или соразмерных квадратов. Итак, как только вы найдете размер одного из квадратов, вы узнаете площадь всей фигуры.
Его длина, ширина и высота идентичны, а каждое ребро встречает другие края под одним углом. Поиск площади поверхности куба быстрый и удобный, поскольку он состоит из конгруэнтных или соразмерных квадратов. Итак, как только вы найдете размер одного из квадратов, вы узнаете площадь всей фигуры.
Как найти площадь куба – грани фигуры
Из иллюстрации видно, что куб имеет переднюю и заднюю грань, две боковые и верхнюю с нижней стороны. Площадь любого куба будут составлять шесть конгруэнтных квадратов. Фактически, если развернуть его, можно четко увидеть шесть квадратов, которые составляют общую поверхность фигуры.
Как найти площадь куба
Площадь куба состоит из площади шести граней. Поскольку все они равны, достаточно знать площадь одной из них и умножить значение на 6. Площадь фигуры также находят по простой формуле: S = 6 x а², где «а» – одна из сторон куба.
Как найти площадь куба – установите площадь стороны
- Предположим, что высота куба составляет 2 см.
 Поскольку его поверхность состоит из квадратов, все его края будут иметь одинаковую длину. Поэтому, исходя из размеров высоты, его длина и ширина будут составлять 2 см.
Поскольку его поверхность состоит из квадратов, все его края будут иметь одинаковую длину. Поэтому, исходя из размеров высоты, его длина и ширина будут составлять 2 см. - Чтобы найти площадь одного из квадратов, вспомните базовые знания геометрии, где S = а², где а – длина одной из сторон. В нашем случае, а = 2 см, так что S = (2 см)² = 2 см х 2 см = 4 см².
- Площадь одного из квадратов поверхности составляет 4 см². Не забудьте указать свое значение в квадратных единицах.
Как найти площадь куба – пример
Поскольку вся поверхность фигуры состоит из шести соразмерных квадратов, нужно умножить площадь одной стороны на 6, следуя формуле S = 6 x а². В нашем случае S = 6 х 4 см² = 24 см². Площадь трехмерной фигуры составляет 24 см².
Находим площадь куба, если сторона выражена в дробях
Если вам сложно работать с дробью, конвертируйте ее в десятичную.
Например, высота куба 2 ½ см.
- S = 6 х (2½ см) ²
- S = 6 х (2,5 см) ²
- S = 6 х 6,25 см ²
- S = 37,5 см ²
- Площадь поверхности куба – 37,5 см ².

Зная площадь куба, находим его сторону
Если площадь поверхности куба известна, можно определить длину его сторон.
- Площадь куба составляет 86,64 см². Необходимо определить длину грани.
- Решение. Поскольку известна площадь поверхности, нужно считать в обратном порядке, разделив значение на 6, а затем извлечь квадратный корень.
- Сделав необходимые вычисления, получаем длину 3,8 см.
Как найти площадь куба – онлайн измерение площади
Используя калькулятор на сайте OnlineMSchool , можно быстро вычислить площадь куба. Достаточно ввести нужное значение стороны и сервис выдаст детальное пошаговое решение задания.
Итак, чтобы знать площадь куба, вычислите площадь одной из сторон, затем умножьте результат на 6, так как фигура имеет 6 равных сторон. Можно при подсчете использовать формулу S = 6а². Если задана площадь поверхности, возможно определить длину боковой части, проделав обратные шаги.
Как найти объём куба 5 класс?
Как найти объём куба 5 класс?
Формула вычисления объема куба
- Через длину ребра Объем (V) куба равняется произведению его длины на ширину на высоту. Т. к. …
- Через длину диагонали грани Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√2.
Чему равна сторона куба?
Как мы говорили ранее, куб имеет шесть равных квадратных граней. Исходя из того что стороны квадрата равны, площадь квадрата составлять — a2, где а – сторона куба. Так куба имеет 6 равных квадратных граней, то для определения площади его поверхности, Вам необходимо умножить площадь одной грани (квадрата) на шесть.
Как найти сторону куба через площадь его поверхности?
Вот формула: 6 x s2, где «s» это сторона куба. Найдите площадь одной из сторон куба, то есть «s», длину стороны куба, а затем нужно найти s2.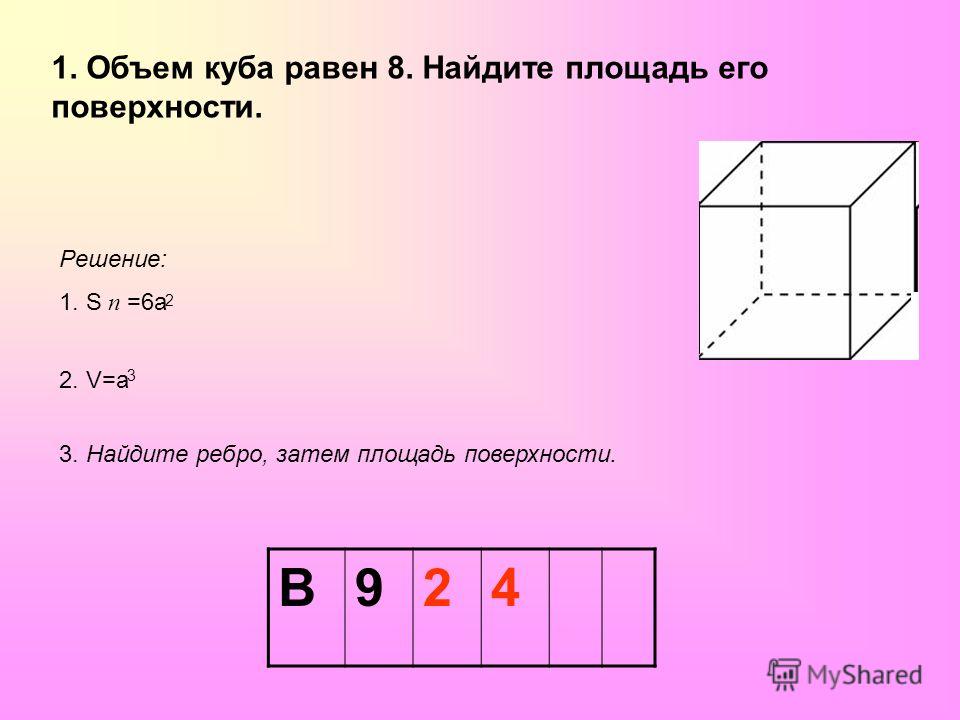 То есть, длина стороны куба в квадрате – это площадь, поскольку длина и ширина равны между собой.
То есть, длина стороны куба в квадрате – это площадь, поскольку длина и ширина равны между собой.
Как найти периметр куба?
Формулы
| Периметр куба (общая длина ребра) | O = | 12 × a |
|---|---|---|
| Площадь одной стороны | P = | a × a = a² |
| Площадь куба (поверхность) | Q = | 6 × P1 = 6 × a² |
| Объем куба | V = | a × a × a = a³ |
| Диагоналная (стороны/стены) | u2 = | a √2 ≈ a × 1,41 |
Как узнать площадь куба формула?
Площадь поверхности куба равна квадрату длины его грани умноженному на шесть (куб имеет шесть одинаковых граней). где S — площадь куба, a — длина грани куба.
Как найти площадь и объем куба?
Чтобы его найти, необходимо знать размеры рёбер: высоту, ширину и длинну. по формуле, размеры граней куба необходимо перемножить три раза, то есть возвести в третью степень.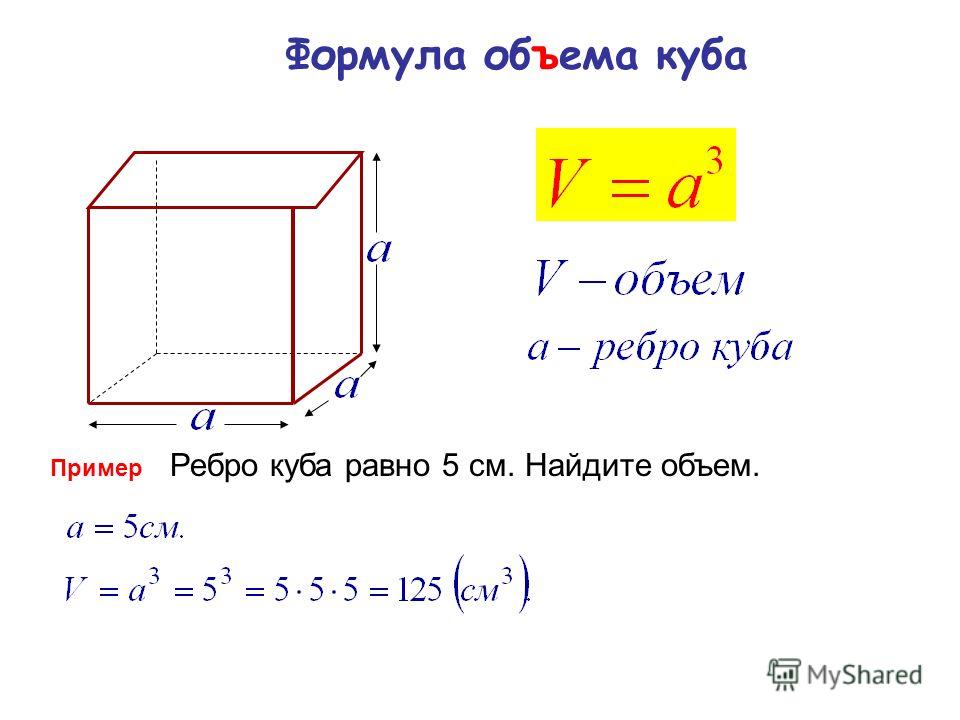 Объём куба равен длине ребра ‘в кубе‘ ))).
Объём куба равен длине ребра ‘в кубе‘ ))).
Что такое площадь поверхности у куба?
Площадь куба Площадь поверхности куба равна квадрату длины его грани умноженному на шесть. где S — площадь куба, a — длина грани куба.
Как найти площадь поверхности куба зная его ребро?
Формула вычисления площади куба
- Через длину ребра Площадь (S) поверхности куба равна произведению числа 6 на длину его ребра в квадрате. S = 6 ⋅ a2 …
- Через длину диагонали грани Сторона любой грани куба (ребро) может быть рассчитана через длину ее диагонали по формуле: a=d/√2.
Что такое площадь поверхности прямоугольного параллелепипеда?
Площадь поверхности прямоугольного параллелепипеда равна двойной сумме площадей трех граней прямоугольного параллелепипеда. где a,b,c — длины ребер параллелепипеда. Чтобы найти площадь поверхности прямоугольного параллелепипеда, введите значения ребер параллелепипеда и нажмите кнопку «ВЫЧИСЛИТЬ».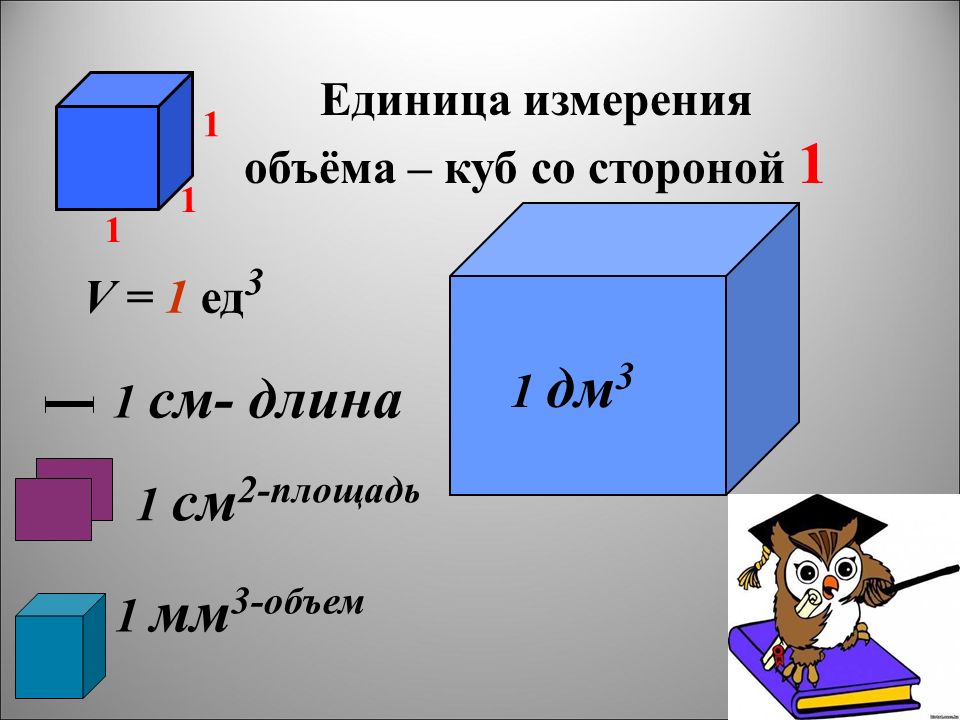
Как найти объем и площадь поверхности прямоугольного параллелепипеда?
Формула вычисления площади
- Гранями прямоугольного параллелепипеда являются прямоугольники, причем противоположные грани равны между собой: два основания: со сторонами a и b; …
- Сложив площади всех граней, каждая из которых равна произведению сторон разной длины, получаем: S = ab + ab + bc + bc + ac + ac = 2 (ab + bc + ac).
Как найти площадь поверхности в физике?
Чтобы определить площадь тела, используют формулы: площадь прямоугольника S можно рассчитать, умножив длину прямоугольника на ширину прямоугольника. S = l 1 ⋅ l 2 . Площадь треугольника S = ah 2 , где a — сторона, h — высота, проведённая к данной стороне.
Как найти площадь поверхности цилиндра формула?
Площадь полной поверхности цилиндра равна площадь верхнего основания цилиндра + площадь нижнего основания цилиндра + площадь боковой поверхности цилиндра или S = πr2 + πr2 + 2πrh = 2πr2 + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).
Иногда это выражение записывается идентичной формулой 2πr (r + h).
Как высчитать площадь поверхности?
Перемножьте двойку, число Пи, радиус и высоту. Сложите полученные значения. Сложите площади двух оснований и площадь цилиндрической поверхности (между двумя основаниями), чтобы вычислить общую площадь поверхности цилиндра. Обратите внимание, что при сложении этих величин получится исходная формула: SA = 2π*r2 + 2π*rh.
Как найти площадь поверхности прямоугольного параллелепипеда?
Наш онлайн калькулятор рассчитывает площадь прямоугольного параллелепипеда по формуле: S = 2(ab + bc + ac). Будьте осторожны и не путайте прямой параллелепипед с прямоугольным.
Нахождение объема и площади поверхности куба (видео и практика)
TranscriptPractice
Привет, добро пожаловать в это видео об объеме и площади поверхности куба!
Мы видим эту форму повсюду, чаще всего с кубиками и кубиками. А еще есть красочная головоломка, известная как кубик Рубика, которая представляет собой куб, который, кажется, состоит из более мелких кубиков.
А еще есть красочная головоломка, известная как кубик Рубика, которая представляет собой куб, который, кажется, состоит из более мелких кубиков.
В математике куб — это особый вид прямоугольной призмы. В большинстве прямоугольных призм длина, ширина и высота формы могут быть разными. Но в кубе они все одинаковые. То есть все ребра имеют одинаковую длину.
Объем куба
Куб имеет два важных измерения. Первый – это объем. Объем куба или любого другого трехмерного объекта является мерой того, сколько места он занимает. Мы измеряем это в кубических единицах, таких как кубические дюймы или кубические сантиметры. Это легко представить с помощью куба. Только представьте, что у нас есть набор маленьких кубиков высотой один сантиметр, шириной один сантиметр и длиной один сантиметр. Каждый из этих кубов равен одному кубическому сантиметру. Это наша единица измерения.
Теперь давайте соберем что-нибудь из этих маленьких кубиков. Давайте построим что-то похожее на кубик Рубика. Начнем с верхнего уровня. Нам нужно сделать сетку из кубиков три на три. Каждый куб имеет один сантиметр в высоту и один сантиметр в ширину. Как только мы закончим с этим слоем, мы увидим, что мы использовали девять кубов. Далее строим средний уровень, используя еще девять кубиков. Все вместе 9 и 9 составляют 18 кубических сантиметров. Наконец, мы строим нижний уровень, снова используя еще девять кубиков. Все вместе у нас есть 27 кубических сантиметров. 93\), что имеет смысл, так как нам нужно было использовать 27 маленьких кубиков, чтобы построить наш куб. Помните, что очень важно указать единицы измерения при ответе.
Начнем с верхнего уровня. Нам нужно сделать сетку из кубиков три на три. Каждый куб имеет один сантиметр в высоту и один сантиметр в ширину. Как только мы закончим с этим слоем, мы увидим, что мы использовали девять кубов. Далее строим средний уровень, используя еще девять кубиков. Все вместе 9 и 9 составляют 18 кубических сантиметров. Наконец, мы строим нижний уровень, снова используя еще девять кубиков. Все вместе у нас есть 27 кубических сантиметров. 93\), что имеет смысл, так как нам нужно было использовать 27 маленьких кубиков, чтобы построить наш куб. Помните, что очень важно указать единицы измерения при ответе.
Площадь поверхности куба
Другой основной мерой куба является площадь поверхности. Это измерение площади, так что оно в двух измерениях. Представьте, что мы делаем бумажную оболочку для куба, который построили ранее. Сколько бумаги нам понадобится в квадратных сантиметрах? Если мы посмотрим на куб, который мы построили ранее, и просто посмотрим на одну его сторону, мы увидим кучу этих квадратов размером в один сантиметр. Если мы посчитаем их, то увидим, что на самом деле их девять. Итак, одна сторона состоит из девяти квадратных сантиметров. 93\).
Если мы посчитаем их, то увидим, что на самом деле их девять. Итак, одна сторона состоит из девяти квадратных сантиметров. 93\).
Скрыть Ответ
Вопрос № 5:
Если не учитывать единицы измерения, какова разница между объемом и площадью поверхности куба со стороной 7?
49
23
17
64
Показать ответ
ответ:
и площадь поверхности, а затем вычтите два значения. Сначала найдите объем куба. 92=6(49)=294\)
Наконец, вычтем из объема площадь поверхности.
\ (343-294 = 49 \)
HIDE Ответ
Возвращение к геометрическим видео
664455
Том калькулятор куба
, созданный в Phlvaro Díez
, рассматриваемый на доминированном кандинтии, а также Phlvaro Díez
. Джек Боуотер
Джек Боуотер
Последнее обновление: 27 сентября 2022 г.
Содержание:- Что такое куб?
- Каков объем куба?
- Как рассчитать объем куба (вручную)?
- Как использовать калькулятор объема куба Omni?
- Расширенные возможности калькулятора Omni: найдите объем куба, не зная стороны.
- Почему формула объема куба такая простая?
- Кубики в мире от Ice Cube до IceCube и далее
Добро пожаловать в Omni том калькулятора кубов . Вы когда-нибудь задумывались, что такое объем куба или почему формула для объема куба так проста? Да, мы это сделали, и у нас есть ответы. Здесь мы объясним, как рассчитать объем куба, а также посмотрим, что делает куб такой популярной формой.
🔎 С помощью нашего калькулятора объема вы можете найти объем многих других трехмерных фигур.
Что такое куб?
Начнем с самого начала. Куб — это 3D-объект , состоящий из 6 граней, каждая из которых представляет собой квадратов одинакового размера . Если вы хотите спуститься в эту конкретную кроличью нору, мы можем сказать, что квадраты также являются обычными объектами, на этот раз в 2D-пространстве, состоящими из 4 сегментов одинаковой длины, встречающихся в 9углы 0 градусов.
Если вы хотите спуститься в эту конкретную кроличью нору, мы можем сказать, что квадраты также являются обычными объектами, на этот раз в 2D-пространстве, состоящими из 4 сегментов одинаковой длины, встречающихся в 9углы 0 градусов.
Куб является одним из основных трехмерных объектов, наряду с тетраэдром (правильная треугольная пирамида) и сферой. Вы уже должны быть знакомы с его формой; если вы когда-нибудь видели кубик Рубика (подсказка в названии, верно?), кубик льда (не рэпер) или игральные кости, вы видели кубик.
Из этого раздела следует, что куб — это трехмерный объект; следовательно, имеет объем . Он также очень регулярен, что означает, что найти объем куба несложно.
Каков объем куба?
Объем — это мера трехмерного пространства, занимаемого объектом. Но если вас не интересуют абстрактные понятия и вы просто хотите узнать объем куба, есть простой ответ на вопрос Каков объем куба?
объем = л³
где л длина сторон куба.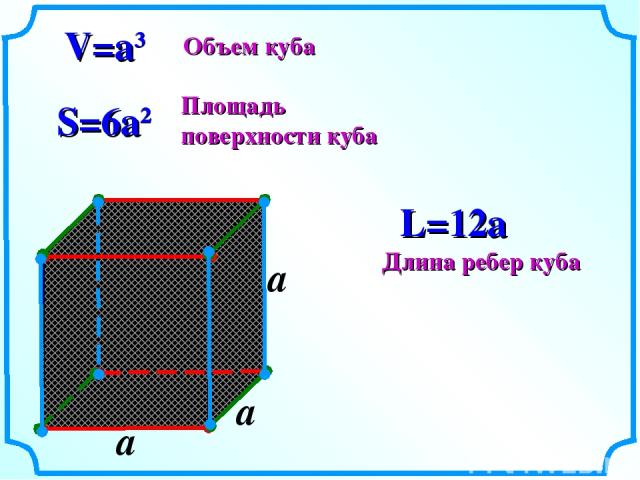 Это просто еще один способ сказать, что вам нужно умножить длину каждой стороны
Это просто еще один способ сказать, что вам нужно умножить длину каждой стороны l на себя три раза: l × l × l = l³ , или, другими словами, возведение в третью степень (узнайте больше о степени в калькуляторе степени)
Предыдущая формула исходит из того, что объем куба (в 3D) равен аналогично площади квадрата (в 2D). Подобно тому, как вы вычисляете площадь квадрата, умножая длины каждой стороны на , вы можете умножать три стороны куба, поскольку все они одинаковы.
Если все это звучит для вас очень просто, просто знайте, что есть еще формулы объема куба на случай, если вы не знаете длины сторон . Это сложнее и, вероятно, сделает вас счастливее. Если вас устраивает текущий уровень сложности, давайте двигаться дальше.
Теперь, когда мы увидели и поняли формулу объема куба, мы перейдем к объяснению того, как вычислить объем куба. Сначала мы вычислим объем куба вручную, а позже воспользуемся омни-калькулятором , чтобы найти объем куба, вообще не имея дело с формулой.
Как рассчитать объем куба (вручную)?
В истинном папском стиле , мы научим вас делать вещи старомодным способом , прежде чем вы отправитесь в будущее. Для этого есть веская причина; это поможет вам лучше понять, как вычислить объем куба. Вернемся к формуле и используем ее на простом примере : объем = л³ . Предположим, у нас есть куб со стороной l = 5 см . Единицы на самом деле не имеют значения, но мы сохраним их, чтобы отслеживать размеры.
Возьмите лист бумаги и начните атаковать формулу объема куба, умножив сначала l × l = 5cm × 5cm = 25cm² . Мы вычислили площадь квадратов, составляющих каждую из шести сторон нашего куба. Мы находимся в одном измерении (то есть в одном умножении) от нахождения объема куба , так что просто снова возьмите ручку и давайте сделаем это!
объем = л³ = л² × л = 25 см² × 5 см = 125 см³ . И с этим у нас получилось — мы вычислили объем куба и ушли целыми и невредимыми.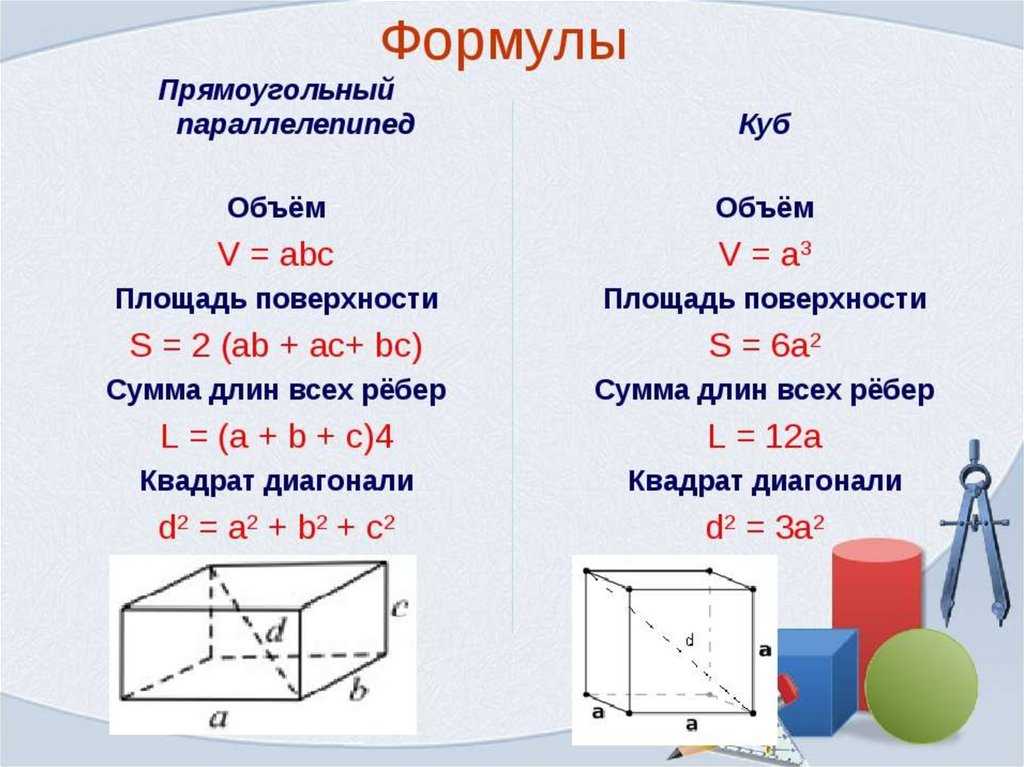 Поздравляем!
Поздравляем!
Теперь позвольте нам рассказать вам секрет об инструменте , который живет слева от этого текста и позволяет вам вычислить объем куба за один простой шаг. Что ты говоришь? Вы хотите знать больше? Конечно!
Как пользоваться калькулятором объема куба Omni?
Вы пришли сюда за этим. Калькулятор для решения всех ваших задач по объему куба: Калькулятор объема куба Omni . Здесь, в Omni, мы подготовили простой калькулятор, который использует формулу объема куба для автоматического вычисления объема без всяких усилий с вашей стороны.
Все, что вам нужно сделать, это ввести длину стороны в поле с именем Сторона , и он автоматически рассчитает объем куба. Никогда еще не было так просто ответить на вопрос: Каков объем куба? Кроме того, вы также можете вычислить длину стороны куба, если вы уже знаете его объем. Просто введите громкость в соответствующее поле и наблюдайте, как происходит волшебство (на самом деле это математика, но магия звучит круче).
Калькулятор также выполняет обратное вычисление почти так же, как это сделали бы вы сами. Возьмите формулу объема куба и переверните ее: объем = l³ => l = ³√объем , где ³√ — кубический корень.
Расширенные возможности калькулятора Omni: найдите объем куба, не зная стороны.
Если вы не заметили, у этого калькулятора Omni есть «Расширенный режим». Он расширяет функциональные возможности калькулятора, позволяя вычислять объем куба по чему-то другому, кроме длины его сторон. Вы можете ввести площадь поверхности, диагональ грани или диагональ куба.
Разница между диагональю грани и диагональю куба может быть не совсем ясна, поэтому давайте объясним ее немного подробнее. Диагональ куба — это трехмерное расстояние между любыми двумя противоположными углами. Это наибольшее расстояние между любыми двумя углами куба. Говоря о диагонали грани, мы имеем в виду двумерное расстояние между двумя самыми дальними углами любого из квадратов, составляющих шесть граней куба.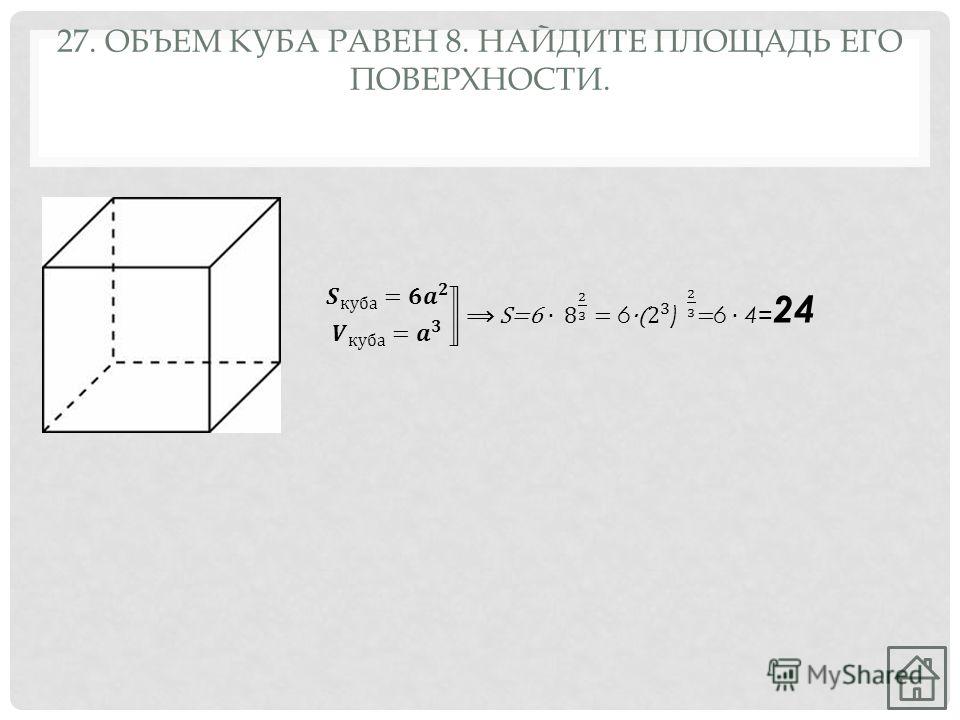 Все диагонали грани имеют одинаковую длину.
Все диагонали грани имеют одинаковую длину.
Почему формула объема куба такая простая?
Как и было обещано, теперь мы рассмотрим, почему формула объема куба такая простая и почему состоит всего из двух переменных и двух математических символов. Основная причина, на которую мы могли бы указать, — это простота куба. Куб очень правильный и, самое главное, его очень легко определить. Если подумать, сфера или тетраэдр даже правильнее куба, но вычислить их объем или площадь намного сложнее. Отчасти это можно объяснить тем, что трудно математически смоделировать поверхность сферы при использовании типичных декартовых координат.
Куб, однако, следует именно этому образцу. Стороны куба всегда выровнены с единичными векторами, которые создают трехмерное декартово пространство. Это делает вычисление объема таким же простым, как нахождение векторного произведения трех унитарных декартовых векторов (векторное произведение), каждый из которых умножается на длину сторон куба .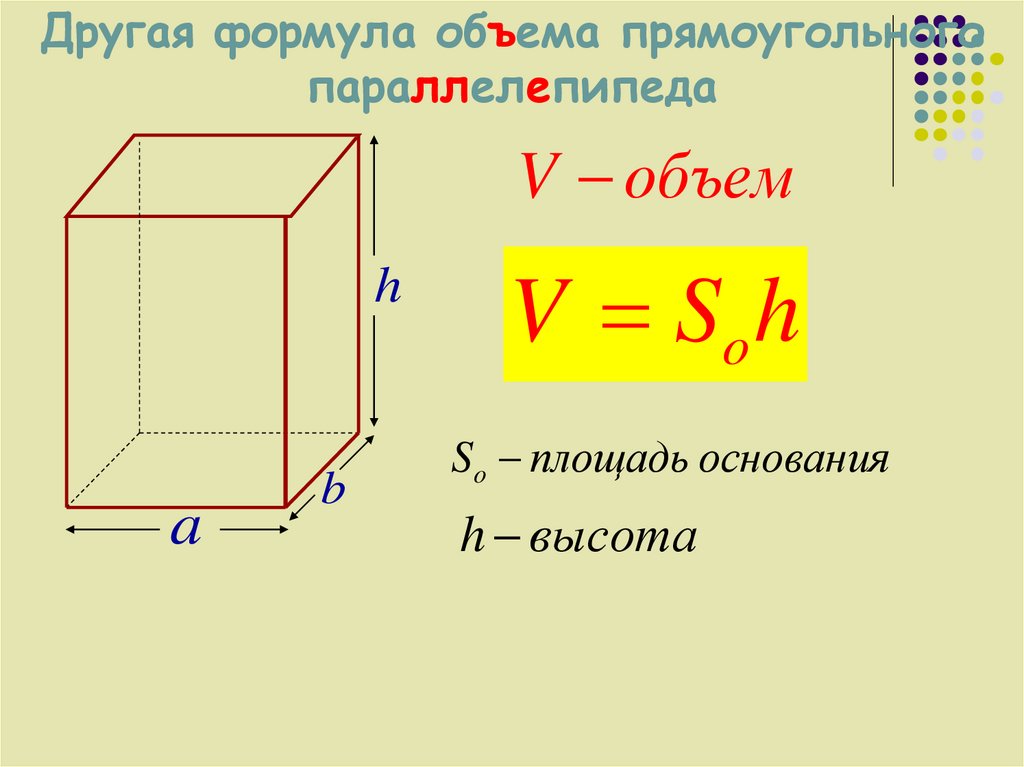
Проверив математические формулы, вы можете увидеть, что квадратные формы предпочтительнее округлых. Если вы не верите, взгляните на формы калькулятора прямоугольной призмы и калькулятора цилиндра и скажите мне 9.0037 какой из них вы бы предпочли вычислить вручную.
Кубики в мире от Ice Cube до IceCube и далее
Предпочтение кубическим формам, вероятно, связано с их простотой конструкции и, что более важно, с упаковочными свойствами. Как и квадраты и шестиугольники в двумерном пространстве, кубы могут полностью заполнять трехмерные пространства сами по себе, если их правильно сложить. Это может показаться не таким уж особенным, но существует очень мало форм, способных заполнить пространство 9.0037, не оставляя между ними пробелов .
Преимущество? Эффективность. Если вы сделаете контейнеры в форме кубов (прямоугольные призмы также подойдут), вы можете быть уверены, что используете все доступное пространство и не оставите между ними мертвого пространства. Только это свойство определяет формы контейнеров, ящиков и шкафов.
Только это свойство определяет формы контейнеров, ящиков и шкафов.
По этой причине кубиков льда являются кубиками , а не сферами, несмотря на то, что последние более энергоэффективны. На что мы действительно не можем найти хороший ответ, так это на то, почему и рэперам, и физикам нравится название «ледяной куб», но они не могут договориться о написании. Природа работает таинственным образом .
ALVARO Díez
Сторона (A)
Площадь поверхности
Диагональный (D)
Диагональный (F)
Объем
. Проверьте 20 аналогичных 3D GEOMETRY. a semisphereCubeCube Calc: найти v, a, d… еще 17
Калькулятор объема куба
GENERATE WORK
сообщить об этом объявлении
GENERATE WORK
Калькулятор объема куба и площади поверхности использует длину стороны куба и вычисляет площадь поверхности и объем куба. Это онлайн-инструмент геометрии, для которого требуется длина стороны куба. С помощью этого калькулятора мы найдем площадь поверхности и объем трехмерного тела, ограниченного шестью квадратными гранями.
Это онлайн-инструмент геометрии, для которого требуется длина стороны куба. С помощью этого калькулятора мы найдем площадь поверхности и объем трехмерного тела, ограниченного шестью квадратными гранями.
Необходимо выполнить следующие шаги:
- Введите в поле длину стороны куба. Значение должно быть положительным вещественным числом или параметром. Обратите внимание, что длина сегмента всегда положительна;
- Нажмите кнопку «СОЗДАТЬ РАБОТУ» , чтобы произвести расчет;
- Калькулятор площади поверхности и объема куба вычислит площадь поверхности и объем куба.
Ввод: Положительное вещественное число или параметр в виде длины стороны куба;
Вывод: Два положительных действительных числа или переменных как площадь поверхности и объем куба и соответствующие единицы после этого.
Формула куба:
Площадь поверхности формулы куба: 93$$
где $a$ — длина стороны куба.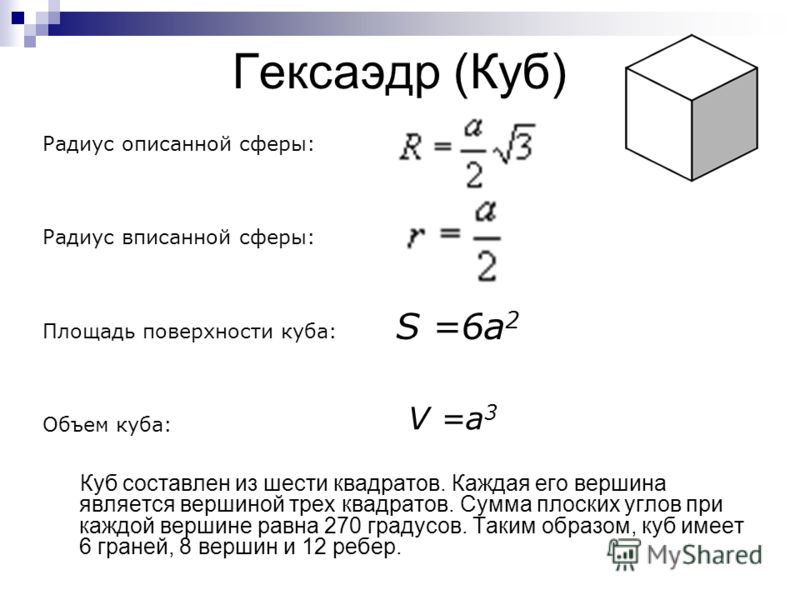
Многогранник представляет собой трехмерный геометрический объект, ограниченный многоугольниками. Эти многоугольники называются его гранями. Общая сторона двух соседних граней многогранника называется ребром или стороной многогранника. Три или более граней сходятся в одной вершине, которая называется вершиной многогранника. Многогранник является правильным многогранником, если все его грани являются правильными конгруэнтными многоугольниками и все ребра конгруэнтны. Существует пять выпуклых правильных многогранников, известных как Платоновые тела: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.
Тетраэдр, куб, октаэдр, додекаэдр, икосаэдр
Призма – это многогранник с двумя параллельными конгруэнтными гранями, называемыми основаниями. Остальные грани — параллелограммы. Призмы обычно называют по форме их оснований. Правильная призма – это призма с основаниями из правильных многоугольников. Куб является примером правильной призмы. У куба $6$ граней, $8$ вершин и $12$ ребер, и все грани куба являются квадратами.
Если картонную коробку разрезать по краям и положить в плоскость, то получится выкройка или сетка для кубика. В общем, для каждого твердого тела можно построить сеть. Сеть очень полезна для нахождения площади поверхности твердых тел. Сетка для куба показана ниже. Площадь поверхности куба равна сумме площадей каждой грани куба. Итак, площадь поверхности куба равна 92$$
Объем куба — это мера объема пространства, которое добавляет куб. Если мы умножим длину, ширину и высоту куба, то получим формулу объема куба. Так как длина, ширина и высота куба равны друг другу, например $a$, объем куба равен
$$V=a\times a\times a$$
Удвоение куба , известная как задача Делоя, является одной из трех самых известных геометрических задач в античный период (H. Dorrie, it 100 Great Problems Of Elementary Mathematics, Dover Publications, NY, 193)$ и т.д.
Работа с объемом и площадью поверхности куба с шагами показывает полный пошаговый расчет для нахождения площади поверхности и объема куба с длиной стороны $5\;in$ с использованием площади поверхности и объема формулы. Для любого другого значения длины стороны куба просто укажите положительное действительное число и нажмите кнопку СОЗДАТЬ РАБОТУ. Учащиеся начальной школы могут использовать этот калькулятор объема куба и площади поверхности для создания
работать, проверять результаты площади поверхности и объема трехмерных тел или эффективно решать домашние задачи.
Для любого другого значения длины стороны куба просто укажите положительное действительное число и нажмите кнопку СОЗДАТЬ РАБОТУ. Учащиеся начальной школы могут использовать этот калькулятор объема куба и площади поверхности для создания
работать, проверять результаты площади поверхности и объема трехмерных тел или эффективно решать домашние задачи.
Реальные задачи с использованием объема и площади поверхности куба
Вычисление объема и площади поверхности куба играет очень важную роль в математике и реальной жизни. Кубики льда, игральные кости, кубик Рубика, кубики сахара, подарочные коробки — вот некоторые примеры кубиков.
Многие реальные ситуации можно смоделировать и проанализировать с помощью площади поверхности и объема куба. Например:
- Если мы хотим обернуть подарочную коробку куба, мы должны обеспечить достаточное количество обертки для упаковки;
- Если мы хотим сделать аквариум, мы должны рассчитать количество стекла, необходимого для его изготовления;
- Если исключить пол, стоимость покраски стен кубической комнаты или кубического дома можно рассчитать по формуле площади поверхности;
- Если мы хотим построить комнату, то мы используем объем куба в концепции площади поверхности дизайна вышивки или рисунка;
- Количество образовавшейся воды равно объему кубика льда и т.
 д.
д.
В арифметике и алгебре куб числа равен его третьей степени. Это понятие можно связать по формуле объема куба. После возведения любого числа в куб мы получим число, которое называется совершенным кубом. Кубы четных чисел всегда четные. Кубики с нечетными числами всегда нечетны. 92$, найдите его объем.
Практическая задача 2:
Кубический аквариум заполнен на $\frac 27$. Когда мы добавляем $16$ литров воды, аквариум заполняется на $\frac 23$. Найдите объем воды, который может быть найден в этом аквариуме
Калькулятор куба, формула, пример расчета (работа с шагами), реальные задачи и практические задачи были бы очень полезны для понимания учащимися начальной школы (образование K-12). понятие объема и площади поверхности куба и призмы. Это понятие может иметь значение в геометрии, чтобы найти объем и площадь поверхности куба и других тел, которые можно получить из двух или более кубов. Изучив эту концепцию, учащийся сможет применять решение реальных задач к решению аналогичных математических задач, связанных с кубом.

 Поэтому, исходя из размеров высоты, его длина и ширина будут составлять 2 см.
Поэтому, исходя из размеров высоты, его длина и ширина будут составлять 2 см.
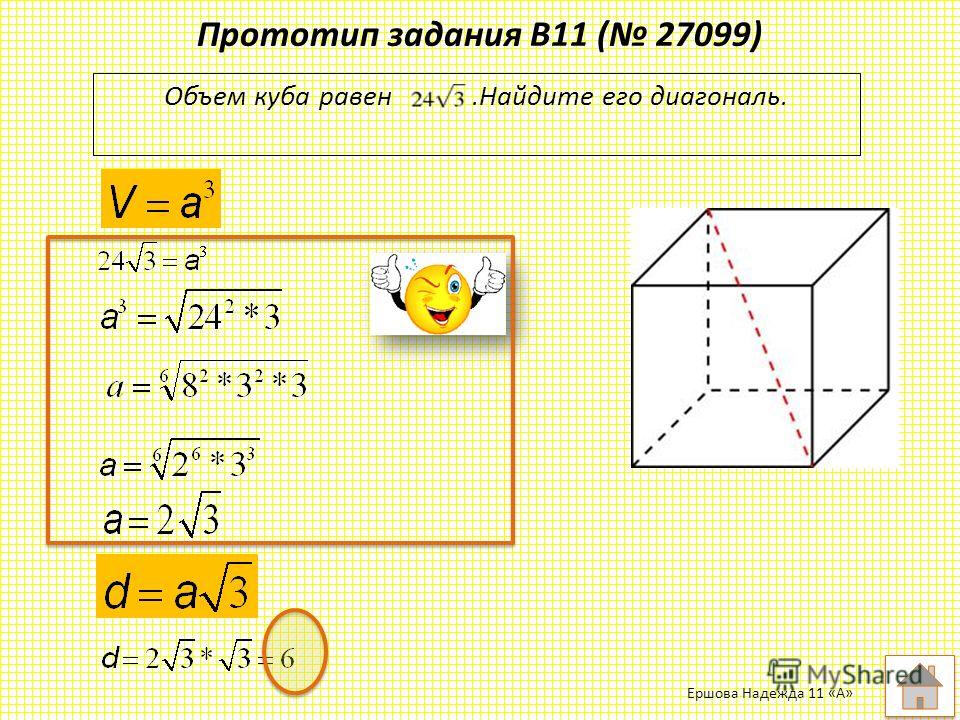 Известно практически каждому, что площадь квадрата находится умножением длин двух его сторон. Грани куба — квадраты, следовательно, площадь его поверхности равна сумме площадей этих квадратов. У куба шесть граней, поэтому формула площади куба будет выглядеть так: S=6*х 2 . Где х — длина ребра куба .
Известно практически каждому, что площадь квадрата находится умножением длин двух его сторон. Грани куба — квадраты, следовательно, площадь его поверхности равна сумме площадей этих квадратов. У куба шесть граней, поэтому формула площади куба будет выглядеть так: S=6*х 2 . Где х — длина ребра куба .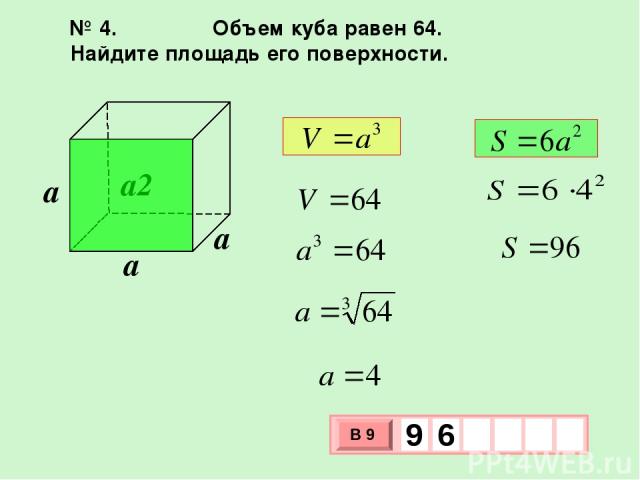 Здесь достаточно базовых знаний. Полученный результат подставляется в уже известную нам формулу площади поверхности куба: S=6*х 2 .
Здесь достаточно базовых знаний. Полученный результат подставляется в уже известную нам формулу площади поверхности куба: S=6*х 2 .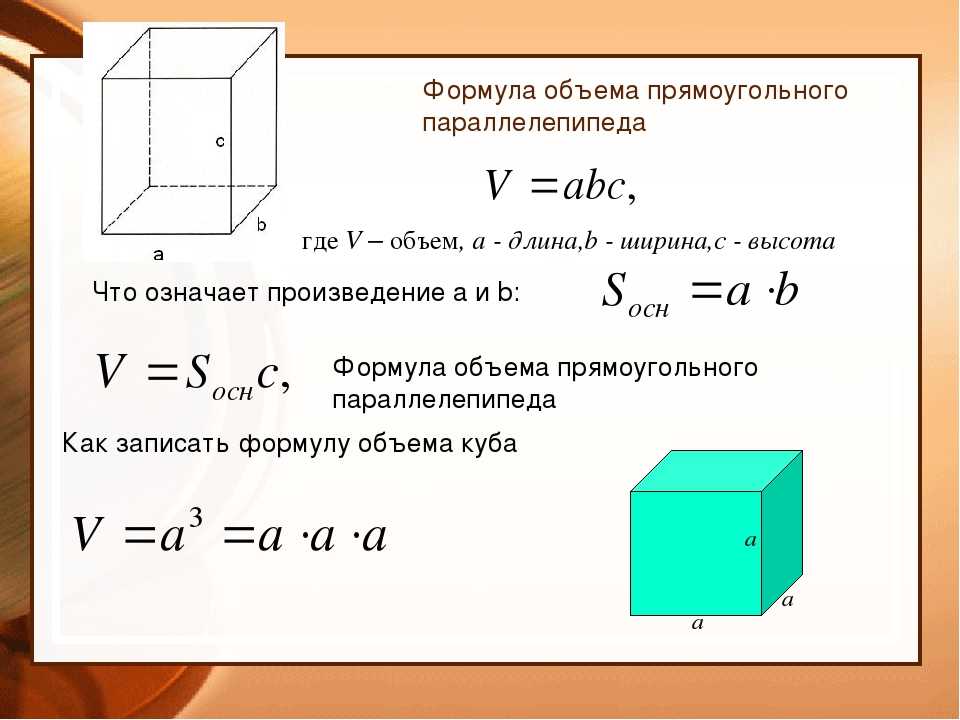 Поскольку его поверхность состоит из квадратов, все его края будут иметь одинаковую длину. Поэтому, исходя из размеров высоты, его длина и ширина будут составлять 2 см.
Поскольку его поверхность состоит из квадратов, все его края будут иметь одинаковую длину. Поэтому, исходя из размеров высоты, его длина и ширина будут составлять 2 см.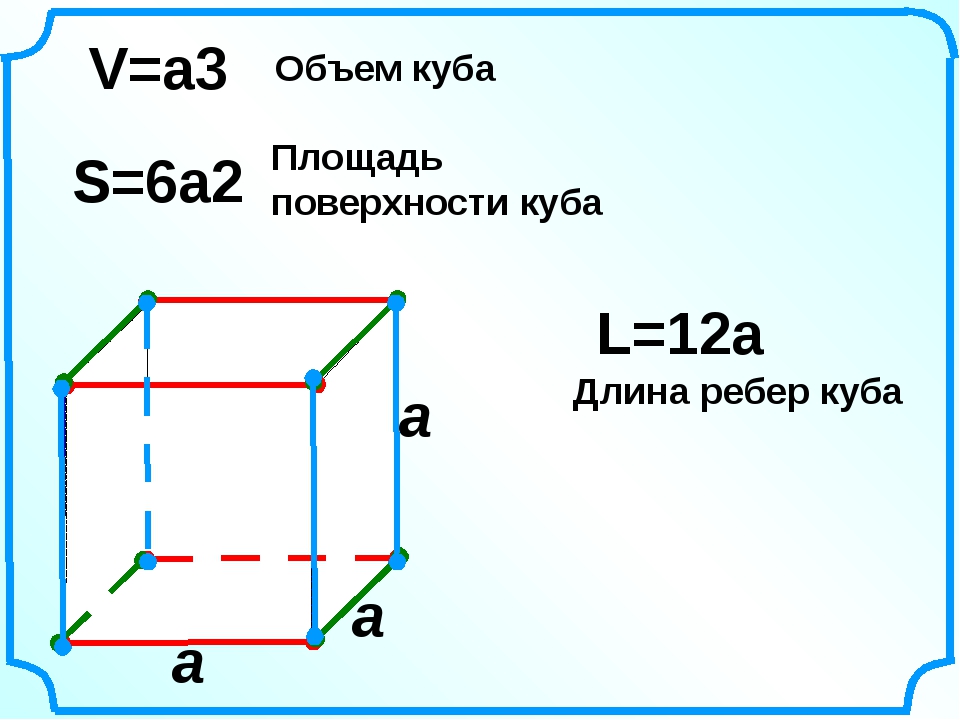
 д.
д.