Объем окружности формула: Объем шара — формула и расчет онлайн

Формула определения окружности по диаметру. Как найти длину окружности: через диаметр и радиус

Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.

Вычислить радиус

Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.

Рассчитать диаметр

Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.

Узнать длину окружности

Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика.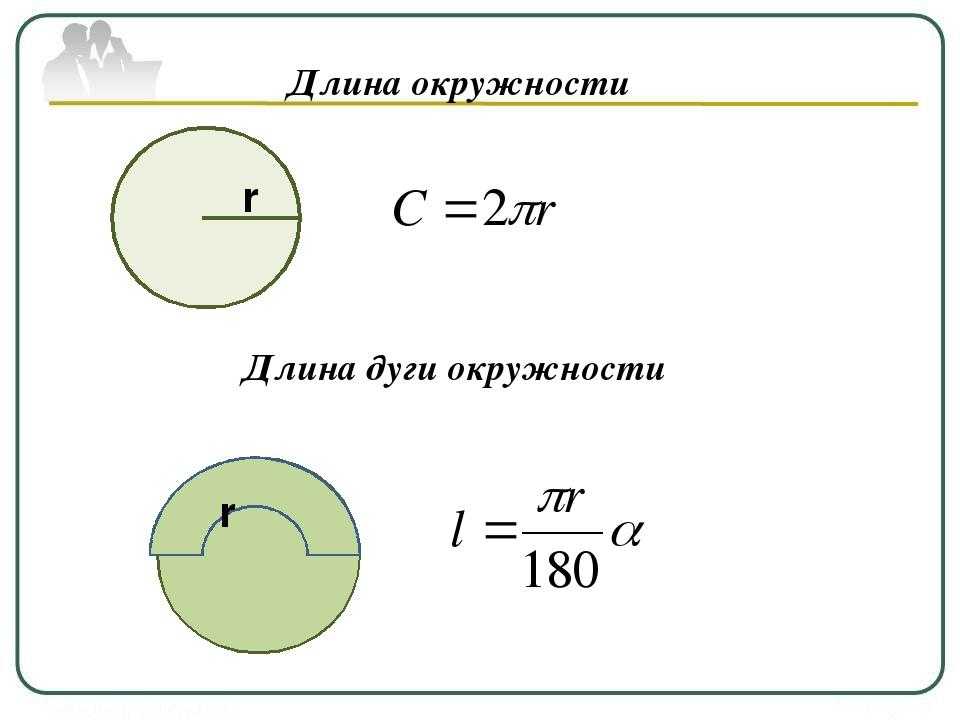 Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.

Вычислить площадь круга

Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.

Рассчитать площадь шара

Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.

Вычислить объем шара

Для вычисления объема шара используют формулу V=4/3(Pr 3). Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.

Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты

, устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.

Характеристики фигуры

Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.

В пределах окружности имеются точки Х такие , что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.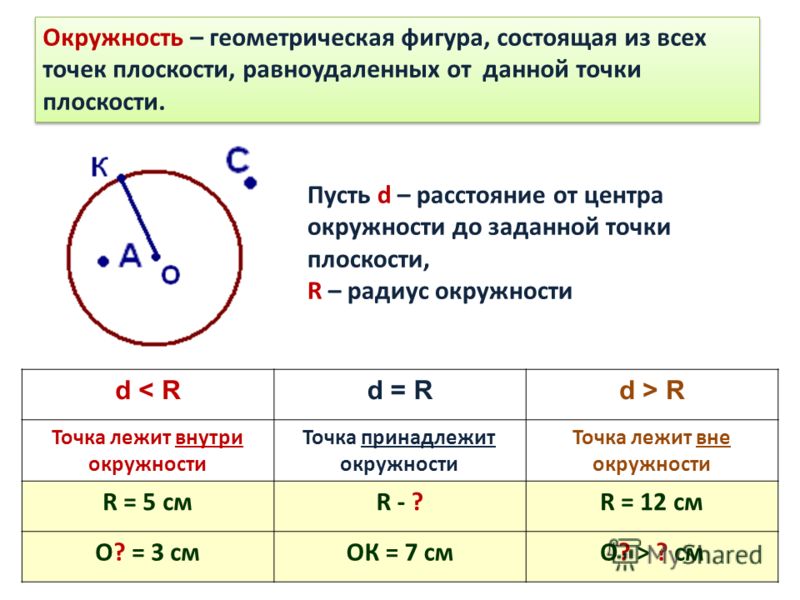

Основные термины окружности

Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками , проходящее через центр фигуры.

Основные формулы для вычислений

Параметры используются в формулах вычислений величин окружности:

Диаметр в формулах вычисления

В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.

Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него.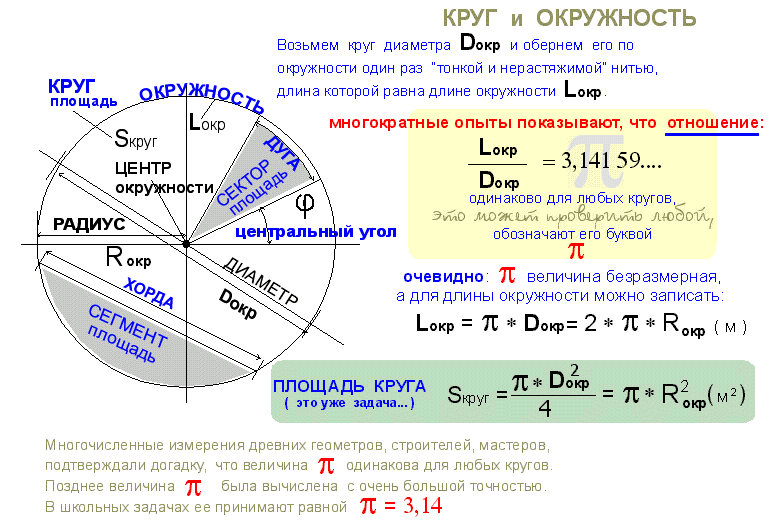 В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.

Расчёты по радиусу

Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.

Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?

Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.

Подручные способы вычисления

Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:

• При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
• Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
• Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.

Круглые предметы в истории человеческой жизни

Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.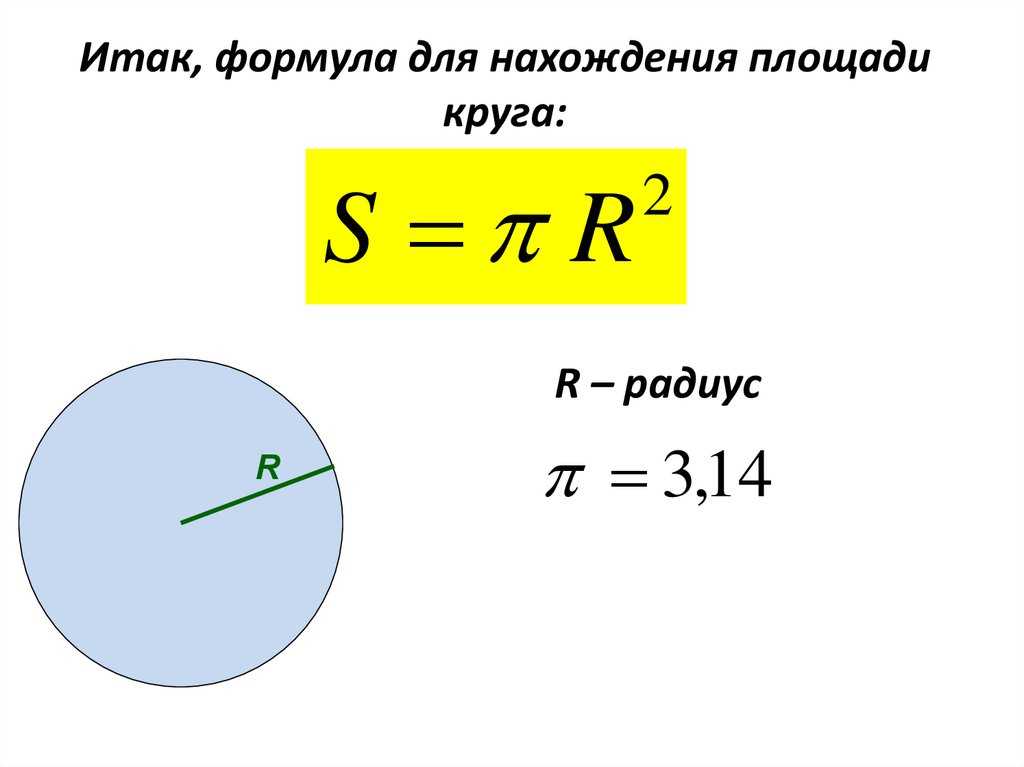

Форму колеса имеет гончарный круг , большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.

Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.

Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .

Определение длины окружности

Произвести расчёт окружности можно по следующей формуле:

L = π D = 2 π r

r — радиус окружности

D — диаметр окружности

L — длина окружности

π — 3.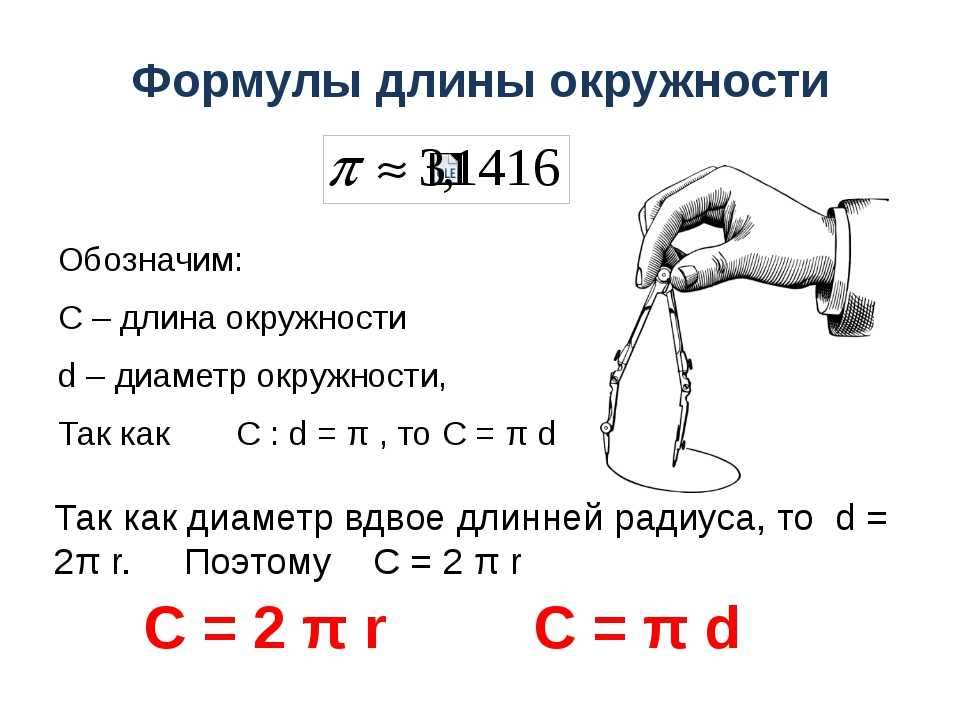 14

Задача:

Вычислить длину окружности , имеющей радиус 10 сантиметров.

Решение:

Формула для вычисления дины окружности имеет вид:

L = π D = 2

π r

где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.

Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:

L = 2 × 3,14 × 10 = 62,8 сантиметра

Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.

С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.

По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).

Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.

Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.

Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам.

Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.

Инструкция

Сначала надо исходные данные к задаче. Дело в том, что ее условии не может быть явно сказано, какова радиуса окружности . Вместо этого в задаче может быть дана длина диаметра окружности . Диаметр окружности — отрезок, который объединяет между собой две противоположные точки окружности , проходя через ее центр. Проанализировав определения окружности , можно сказать, что длина диаметра удвоенной длине радиуса.

Теперь можно принять радиус окружности равным R. Тогда для длины окружности необходимо воспользоваться формулой:
L = 2πR = πD, где L — длина окружности , D — диаметр окружности , который всегда в 2 раза радиуса.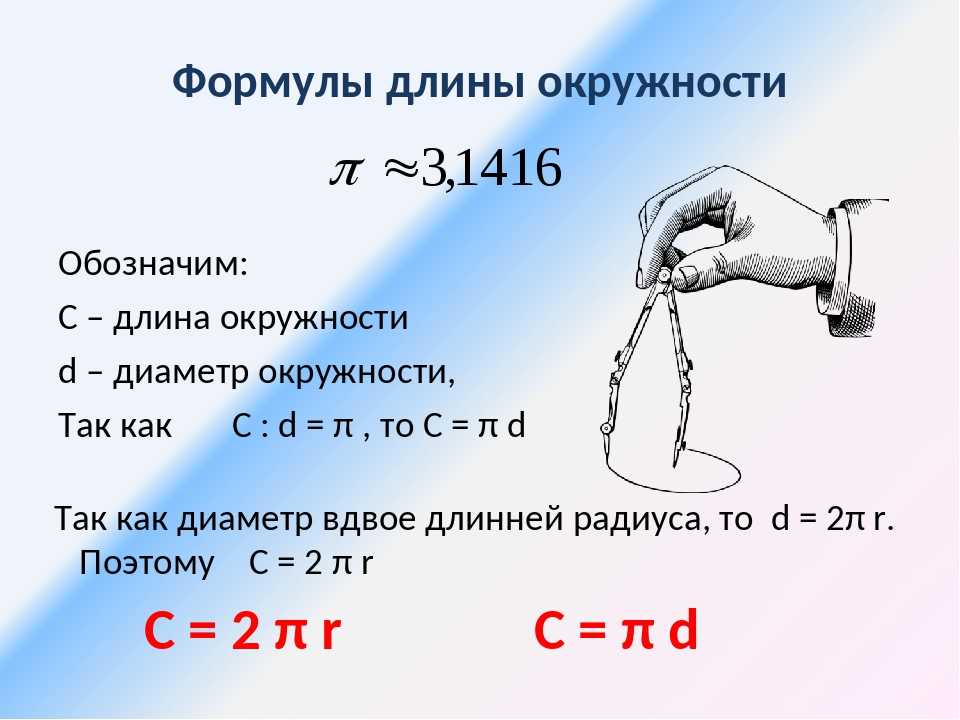

Обратите внимание

Окружность можно вписать в многоугольник, либо описать вокруг него. При этом, если окружность вписана, то она в точках касания со сторонами многоугольника будет делить их пополам. Чтобы узнать радиус вписанной окружности, нужно поделить площадь многоугольника на половину его периметра:
R = S/p.
Если окружность описана вокруг треугольника, то ее радиус находится по следующей формуле:
R = a*b*c/4S, где a, b, c — это стороны данного треугольника, S — площадь треугольника, вокруг которого описана окружность.
Если требуется описать окружность вокруг четырехугольника, то это можно будет сделать при соблюдении двух условий:

Четырехугольник должен быть выпуклым.
В сумме противоположные углы четырехугольника должны составлять 180°

Полезный совет

Помимо традиционного штангенциркуля, для начертания окружности можно применять и трафареты. В современных трафаретах включены окружность разных диаметров. Данные трафареты можно приобрести в любом магазине канцтоваров.

Источники:

• Как найти длину окружности?

Окружность — замкнутая кривая линия, все точки которой находятся на равном расстоянии от одной точки. Эта точка — центр окружности, а отрезок между точкой на кривой и ее центром называется радиусом окружности.

Инструкция

Если через центр окружности провести прямую линию, то ее отрезок между двумя точками пересечения этой прямой с окружностью называется диаметром данной окружности. Половина диаметра, от центра до точки пересечения диаметра с окружность — это радиус

окружности. Если окружность разрезать в произвольной точке, выпрямить и измерить, то полученная величина является длиной данной окружности.

Начертите несколько окружностей разным раствором циркуля. Визуальное сравнение позволяет сделать вывод, что больший диаметр очерчивает больший круг, ограниченный окружностью с большей длиной. Следовательно, между диаметром окружности и ее длиной существует прямо пропорциональная зависимость.

По физическому смыслу параметр «длина окружности» соответствует , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.

При увеличении числа сторон периметр вписанного многоугольника будет все больше приближаться к L. Р= b*n=2n*R*Sin (π/n)=n*D*Sin (π/n). Зависимость между длиной окружности L и ее диаметром D постоянна. Отношение L/D=n*Sin (π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «число пи» и выраженной бесконечной десятичной дробью. Для расчетов без применения вычислительной техники принимается значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для окружности разделите ее длину на число π=3,14.

И в чем ее отличие от круга. Возьмите ручку или цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, — это окружность. А вот синее содержимое внутри нее — и есть круг.

Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.

Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.

Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.

Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:

К примеру, радиус — 7 см. Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.

Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить Формула L = 2 Пи * R, где 2 — это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом

Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:

Ответ: диаметр равен 21,98 метрам.

Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:

D = 2 * (S / Пи) * (1 / 2)

S — в данном случае Допустим, в задаче она равна 30 кв. м. Получаем:

D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414

При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.

Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:

R = S / p (S — площадь заданного треугольника, а p — периметр, разделенный на 2).

Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.

Нередко находить диаметр окружности приходится и в быту. К примеру, при определении что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.

Объем шара: онлайн калькулятор, формулы, примеры решений

Фигура {$ main.figures[data. figure] $}

Рассчитываем {$ main.types[data.type] $}

Введите 1 величину

Сторона A

Диагональ фигуры (D)

Диагональ грани (d)

Введите 1 величину

Радиус (r)

Диаметр (d)

Введите 3 величины

Сторона A

Сторона B

Сторона C

Диагональ фигуры (d)

Введите 2 величины (радиус и диаметр основания приняты за одну величину)

Высота (h)

Образующая конуса (s)

Радиус (r)

Диаметр (d)

Введите H и 1 величину

Высота (h)

Радиус (r)

Диаметр (d)

Введите 3 величины

Количество сторон (n)

Высота (h)

Сторона a

Количество сторон (n)

Введите 2 величины

Сторона основания (a)

Высота (h)

Длина бокового ребра (s)

Угол (α)

Между стороной и плоскостью основания

{$ main.angles[data.angle] $}

Результат расчёта

• type == ‘volume'»>Объём: {$ result.v|number:4 $}
• Площать: {$ result.s|number:4 $}
• Площать: {$ result.s $}

Шар — это геометрическое тело вращения, образованное путем вращения круга или полукруга вокруг его диаметра. Также шар — это пространство, ограниченное сферической поверхностью. Существует множество реальных сферических объектов и связанных с ними задач, для решения которых требуется определить объем шара.

Шар и сфера

Круг — самая древняя геометрическая фигура, и античные ученые придавали ей сакральное значение. Круг — это символ нескончаемого времени и пространства, символ Вселенной и бытия. По мнению Пифагора, круг — прекраснейшая из фигур. В трехмерном пространстве окружность превращается в сферу, такую же идеальную, космическую и прекрасную, как и круг.

Сфера по-древнегречески означает «мяч». Сфера представляет собой поверхность, образованную бесконечным множеством точек, равноудаленных от центра фигуры. Пространство, ограниченное сферой, и есть шар. Шар — идеальная геометрическая фигура, форму которой принимают многие реальные объекты. К примеру, в реальной жизни форму шара имеют пушечные ядра, подшипники или мячи, в природе — капли воды, кроны деревьев или ягоды, в космосе — звезды, метеоры или планеты.

Объем шара

Определение объема сферической фигуры — сложная задача, ведь такое геометрическое тело нельзя разбить на кубы или треугольные призмы, формулы объемов которых уже известны. Современная наука позволяет вычислить объем шара при помощи определенного интеграла, однако каким образом была выведена формула объема в Древней Греции, когда об интегралах еще никто не слышал? Архимед вычислил объем шара при помощи конуса и цилиндра, так как формулы объемов этих фигур были уже определены древнегреческим философом и математиком Демокритом.

Архимед представил половину шара при помощи одинаковых конуса и цилиндра, при этом радиус каждой фигуры был равен ее высоте R = h.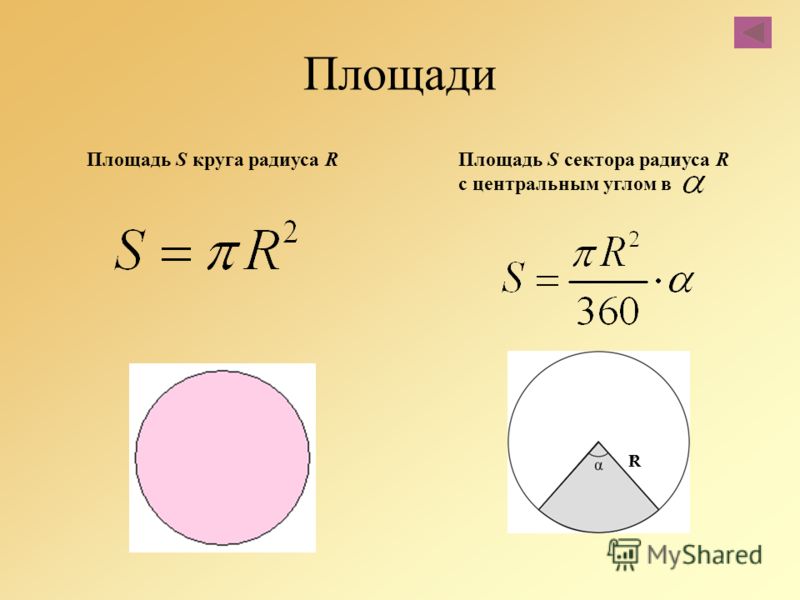 Античный ученый представил конус и цилиндр разбитыми на бесконечное количество маленьких цилиндров. Архимед понял, что если из объема цилиндра Vc вычесть объем конуса Vk, он получит объем одной полусферы Vsh:

0,5 Vsh = Vc − Vk

Объем конуса вычисляется по простой формуле:

Vk = 1/3 × So × h,

но зная, что So в данном случае — это площадь круга, а h = R, то формула трансформируется в:

Vk = 1/3 × pi × R × R² = 1/3 pi × R³

Объем цилиндра вычисляется по формуле:

Vc = pi × R² × h,

но считая, что высота цилиндра равна его радиусу, мы получаем:

Vc = pi × R³.

Используя эти формулы, Архимед получил:

0,5 Vsh = pi × R³ — 1/3 pi × R³ или Vsh = 4/3 pi × R³

Современное определение формулы объема шара выводится из интеграла от площади сферической поверхности, однако результат остается все тем же

Vsh = 4/3 pi × R³

Расчет объема шара может понадобиться как в реальной жизни, так и при решении абстрактных задач. Для вычисления объема шара при помощи онлайн-калькулятора вам понадобится узнать всего один параметр на выбор: диаметр или радиус сферы. Рассмотрим пару примеров.

Примеры из жизни

Пушечные ядра

Допустим, вы хотите узнать, сколько чугуна необходимо для отливки пушечного ядра шестифутового калибра. Вы знаете, что диаметр такого ядра составляет 9,6 сантиметров. Введите это число в ячейку калькулятора «Диаметр», и вы получите ответ в виде

V = 463,24

Таким образом, для выплавки пушечного ядра заданного калибра вам понадобится 463 кубических сантиметров или 0,463 литра чугуна.

Воздушные шары

Пусть вам любопытно, сколько воздуха необходимо для накачки воздушного шара идеальной сферической формы. Вы знаете, что радиус выбранного шарика составляет 10 см. Вбейте это значение в ячейку калькулятора «Радиус» и вы получите результат

V = 4188,7

Это означает, что для накачки одного такого шара вам понадобится 4188 кубических сантиметров или 4,18 литров воздуха.

Заключение

Необходимость определения объема шара может возникнуть в самых разных ситуациях: от абстрактных школьных задач до научных изысканий и производственных вопросов. Для решения вопросов любой сложности используйте наш онлайн-калькулятор, который мгновенно представит вам точный результат и необходимые математические выкладки.

Как посчитать периметр круга зная диаметр. Как найти и чему будет равна длина окружности

Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.

Вычислить радиус

Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.

Рассчитать диаметр

Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.

Узнать длину окружности

Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.

Вычислить площадь круга

Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.

Рассчитать площадь шара

Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.

Вычислить объем шара

Для вычисления объема шара используют формулу V=4/3(Pr 3). Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.

Окружностью называют кривую линию, которая ограничивает собой круг. В геометрии фигуры плоские, поэтому определение относится к двухмерному изображению. Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.

У окружности есть несколько характеристик, на основе которых производят расчеты, связанные с этой геометрической фигурой. В их число входит: диаметр, радиус, площадь и длина окружности. Эти характеристики взаимосвязаны, то есть для их вычисления достаточно информации хотя бы об одной из составляющих. Например, зная только радиус геометрической фигуры по формуле можно найти длину окружности, диаметр, и ее площадь.

• Радиус окружности – это отрезок внутри окружности, соединённый с ее центром.
• Диаметр – это отрезок внутри окружности, соединяющий ее точки и проходящий через центр. По сути, диаметр – это два радиуса. Именно так выглядит формула для его вычисления: D=2r.
• Есть еще одна составляющая окружности – хорда. Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр. Так вот ту хорду, которая через него проходит, тоже называют диаметром.

Как узнать длину окружности? Сейчас выясним.

Длина окружности: формула

Для обозначения этой характеристики выбрана латинская буква p. Еще Архимед доказал, что отношение длины окружности к ее диаметру является одним и тем же числом для всех окружностей: это число π, которое приблизительно равно 3,14159. Формула для вычисления π выглядит так: π = p/d. Согласно этой формуле, величина p равна πd, то есть длина окружности: p= πd. Поскольку d (диаметр) равен двум радиусам, то эту же формулу длины окружности можно записать как p=2πr.Рассмотрим применение формулы на примере простых задач:

Задача 1

У основания царь-колокола диаметр равен 6,6 метров. Какова длина окружности основания колокола?

1. Итак, формула для вычисления окружности — p= πd
2. Подставляем имеющееся значение в формулу: p=3,14*6,6= 20,724

Ответ: длина окружности основания колокола 20,7 метра.

Задача 2

Искусственный спутник Земли вращается на расстоянии 320 км от планеты. Радиус Земли – 6370 км. Какова длина круговой орбиты спутника?

1. 1.Вычислим радиус круговой орбиты спутника Земли: 6370+320=6690 (км)
2. 2.Вычислим длину круговой орбиты спутника по формуле: P=2πr
3. 3.P=2*3,14*6690=42013,2

Ответ: длина круговой орбиты спутника Земли 42013,2 км.

Способы измерения длины окружности

Вычисление длины окружности на практике используется не часто. Причиной тому приблизительное значение числа π. В быту для поиска длины круга используют специальный прибор – курвиметр. На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.

Как найти длину окружности? Нужно просто держать в голове незамысловатые формуля для вычислений.

Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.

Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .

Определение длины окружности

Произвести расчёт окружности можно по следующей формуле:

L = π D = 2 π r

r — радиус окружности

D — диаметр окружности

L — длина окружности

π — 3.14

Задача:

Вычислить длину окружности , имеющей радиус 10 сантиметров.

Решение:

Формула для вычисления дины окружности имеет вид:

L = π D = 2 π r

где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.

Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:

L = 2 × 3,14 × 10 = 62,8 сантиметра

Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.

С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.

По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).

Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.

Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.

Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.

§ 117. Длина окружности и площадь круга.

1. Длина окружности. Окружностью называется замкнутая плоская кривая линия, все точки которой находятся на равном расстоянии от одной точки (О), называемой центром окружности (рис. 27).

Окружность вычерчивается с помощью циркуля. Для этого острую ножку циркуля ставят в центр, а другую (с карандашом) вращают вокруг первой до тех пор, пока конец карандаша не вычертит полной окружности. Расстояние от центра до любой точки окружности называется её радиусом. Из определения следует, что все радиусы одной окружности равны между собой.

Отрезок прямой линии (АВ), соединяющий две любые точки окружности и проходящий через её центр, называется диаметром . Все диаметры одной окружности равны между собой; диаметр равен двум радиусам.

Как найти длину окружности? Практически в некоторых случаях длину окружности можно найти путём непосредственного измерения. Это можно сделать, например, при измерении окружности сравнительно небольших предметов (ведро, стакан и т. п.). Для этого можно воспользоваться рулеткой, тесьмой или шнуром.

В математике применяется приём косвенного определения длины окружности. Он состоит в вычислении по готовой формуле, которую мы сейчас выведем.

Если мы возьмём несколько больших и малых круглых предметов (монета, стакан, ведро, бочка и т. д.) и измерим у каждого из них длину окружности и длину диаметра, то получим для каждого предмета два числа (одно, измеряющее длину окружности, и другое — длину диаметра). Естественно, что для малых предметов эти числа будут небольшими, а для крупных — большими.

Однако если мы в каждом из этих случаев возьмём отношение полученных двух чисел (длины окружности и диаметра), то при тщательном выполнении измерения найдём почти одно и то же число. Обозначим длину окружности буквой С , длину диаметра буквой D , тогда отношение их будет иметь вид С: D . Фактические измерения всегда сопровождаются неизбежными неточностями. Но, выполнив указанный опыт и произведя необходимые вычисления, мы получим для отношения С: D примерно следующие числа: 3,13; 3,14; 3,15. Эти числа очень мало отличаются одно от другого.

В математике путём теоретических соображений установлено, что искомое отношение С: D никогда не меняется и оно равно бесконечной непериодической дроби, приближённое значение которой с точностью до десятитысячных долей равно 3,1416 . Это значит, что всякая окружность длиннее своего диаметра в одно и то же число раз. Это число принято обозначать греческой буквой π (пи). Тогда отношение длины окружности к диаметру запишется так: С: D = π . Мы будем ограничивать это число только сотыми долями, т. е. брать π = 3,14.

Напишем формулу для определения длины окружности.

Так как С: D = π , то

C = πD

т. е. длина окружности равна произведению числа π на диаметр.

Задача 1. Найти длину окружности (С ) круглой комнаты, если диаметр её D = 5,5 м.

Принимая во внимание изложенное выше, мы должны для решения этой задачи увеличить диаметр в 3,14 раза:

5,5 3,14 = 17,27 {м).

Задача 2. Найти радиус колеса, у которого длина окружности 125,6 см.

Эта задача обратна предыдущей. Найдём диаметр колеса:

125,6: 3,14 = 40 (см).

Найдём теперь радиус колеса:

40: 2 = 20 (см).

2. Площадь круга. Чтобы определить площадь круга, можно было бы начертить на бумаге круг данного радиуса, покрыть его прозрачной клетчатой бумагой и потом сосчитать клетки, находящиеся внутри окружности (рис.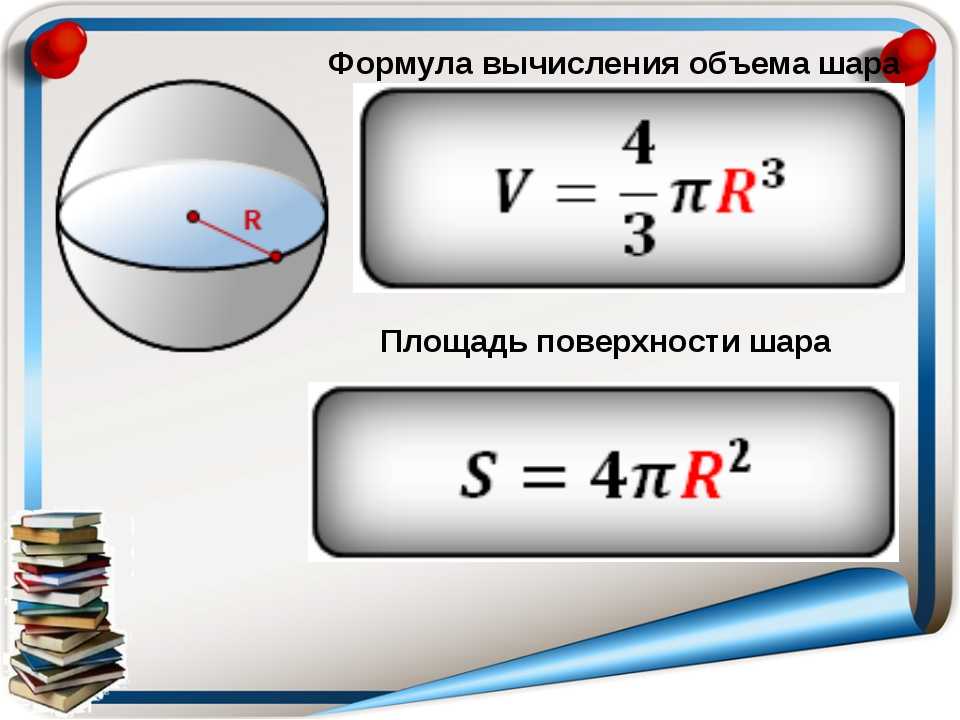 28).

Но такой способ неудобен по многим причинам. Во-первых, вблизи контура круга получается ряд неполных клеток, о величине которых судить трудно. Во-вторых, нельзя покрыть листом бумаги большой предмет (круглую клумбу, бассейн, фонтан и др.). В-третьих, подсчитав клетки, мы всё-таки не получаем никакого правила, позволяющего нам решать другую подобную задачу. В силу этого поступим иначе. Сравним круг с какой-нибудь знакомой нам фигурой и сделаем это следующим образом: вырежем круг из бумаги, разрежем его сначала по диаметру пополам, затем каждую половину разрежем ещё пополам, каждую четверть — ещё пополам и т. д., пока не разрежем круг, например, на 32 части, имеющие форму зубцов (рис. 29).

Затем сложим их так, как показано на рисунке 30, т. е. сначала расположим 16 зубцов в виде пилы, а затем в образовавшиеся отверстия вложим 15 зубцов и, наконец, последний оставшийся зубец разрежем по радиусу пополам и приложим одну часть слева, другую — справа. Тогда получится фигура, напоминающая прямоугольник.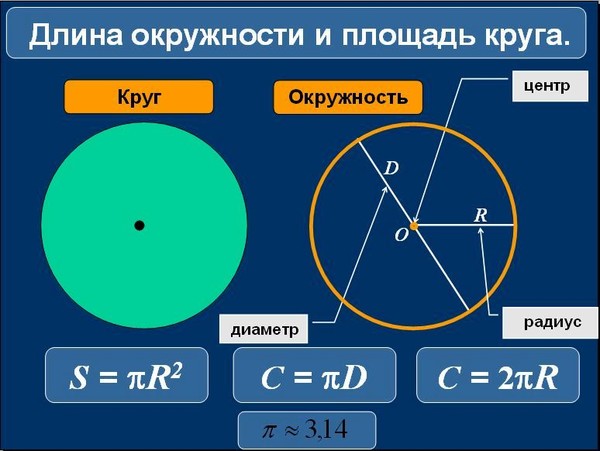

Длина этой фигуры (основание) равна приблизительно длине полуокружности, а высота — приблизительно радиусу. Тогда площадь такой фигуры можно найти путём умножения чисел, выражающих длину полуокружности и длину радиуса. Если обозначим площадь круга буквой S , длину окружности буквой С , радиус буквой r , то можем записать формулу для определения площади круга:

которая читается так: площадь круга равна длине полуокружности, умноженной на радиус.

Задача. Найти площадь круга, радиус которого равен 4 см. Найдём сначала длину окружности, потом длину полуокружности, а затем умножим её на радиус.

1) Длина окружности С = π D = 3,14 8 = 25,12 (см).

2) Длина половины окружности C / 2 = 25,12: 2= 12,56 (см).

3) Площадь круга S = C / 2 r = 12,56 4 = 50,24 (кв. см).

§ 118. Поверхность и объём цилиндра.

Задача 1. Найти полную поверхность цилиндра, у которого диаметр основания 20,6 см и высота 30,5 см.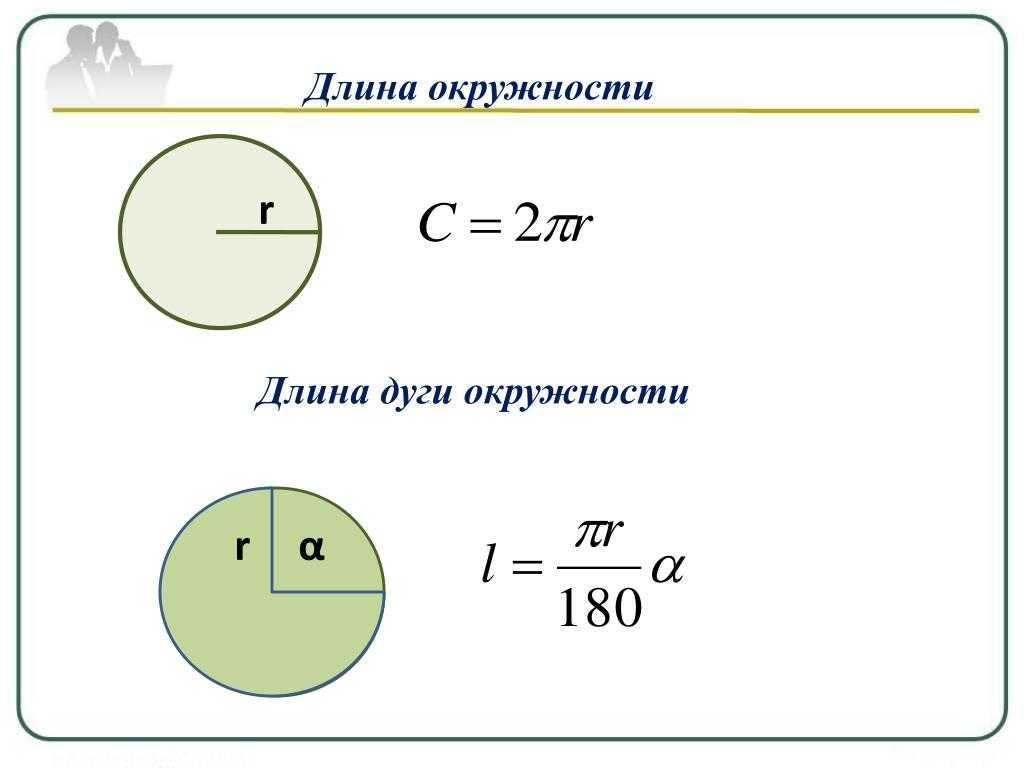

Форму цилиндра (рис. 31) имеют: ведро, стакан (не гранёный), кастрюля и множество других предметов.

Полная поверхность цилиндра (как и полная поверхность прямоугольного параллелепипеда) состоит из боковой поверхности и площадей двух оснований (рис. 32).

Чтобы наглядно представить себе, о чём идёт речь, необходимо аккуратно сделать модель цилиндра из бумаги. Если мы от этой модели отнимем два основания, т. е. два круга, а боковую поверхность разрежем вдоль и развернём, то будет совершенно ясно, как нужно вычислять полную поверхность цилиндра. Боковая поверхность развернётся в прямоугольник, основание которого равно длине окружности. Поэтому решение задачи будет иметь вид:

1) Длина окружности: 20,6 3,14 = 64,684 (см).

2) Площадь боковой поверхности: 64,684 30,5= 1972,862(кв.см).

3) Площадь одного основания: 32,342 10,3 = 333,1226 (кв.см).

4) Полная поверхность цилиндра:

1972,862 + 333,1226 + 333,1226 = 2639,1072 (кв. см) ≈ 2639 (кв.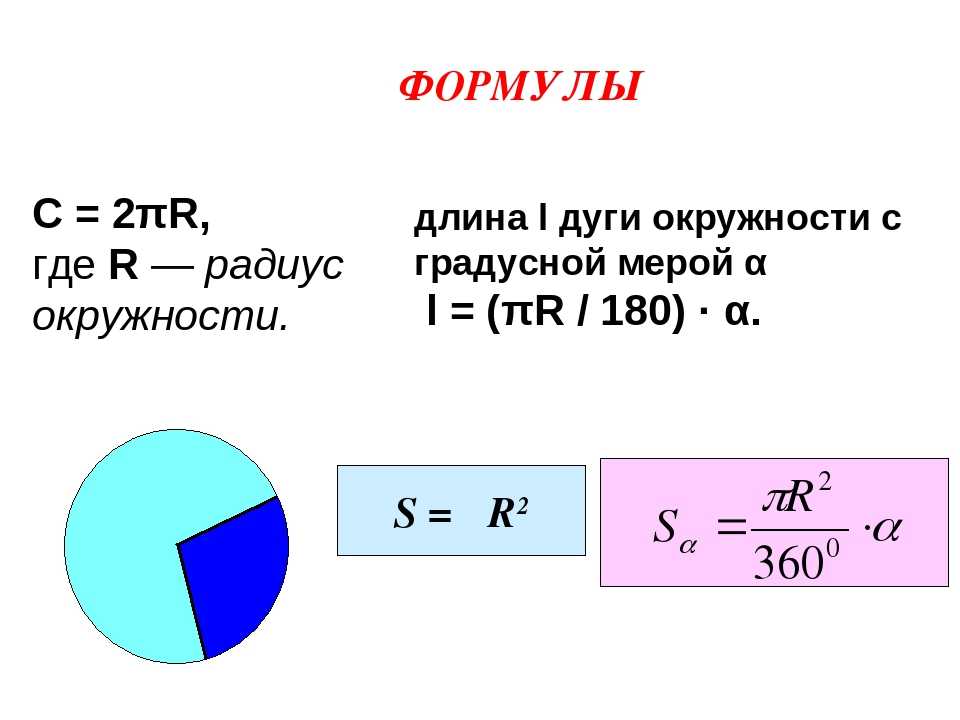 см).

Задача 2. Найти объём железной бочки, имеющей форму цилиндра с размерами: диаметр основания 60 см и высота 110 см.

Чтобы вычислить объём цилиндра, нужно припомнить, как мы вычисляли объём прямоугольного параллелепипеда (полезно прочитать § 61).

Единицей измерения объёма у нас будет кубический сантиметр. Сначала надо узнать, сколько кубических сантиметров можно расположить на площади основания, а затем найденное число умножить на высоту.

Чтобы узнать, сколько кубических сантиметров можно уложить на площади основания, надо вычислить площадь основания цилиндра. Так как основанием служит круг, то нужно найти площадь круга. Затем для определения объёма умножить её на высоту. Решение задачи имеет вид:

1) Длина окружности: 60 3,14 = 188,4 (см).

2) Площадь круга: 94,2 30 = 2826 (кв. см).

3) Объём цилиндра: 2826 110 = 310 860 (куб. см).

Ответ. Объём бочки 310,86 куб. дм.

Если обозначим объём цилиндра буквой V , площадь основания S , высоту цилиндра H , то можно написать формулу для определения объёма цилиндра:

V = S H

которая читается так: объём цилиндра равен площади основания, умноженной на высоту.

§ 119. Таблицы для вычисления длины окружности по диаметру.

При решении различных производственных задач часто приходится вычислять длину окружности. Представим себе рабочего, который изготовляет круглые детали по указанным ему диаметрам. Он должен всякий раз, зная диаметр, вычислить длину окружности. Чтобы сэкономить время и застраховать себя от ошибок, он обращается к готовым таблицам, в которых указаны диаметры и соответствующие им длины окружностей.

Приведём небольшую часть таких таблиц и расскажем, как ими пользоваться.

Пусть известно, что диаметр окружности равен 5 м. Ищем в таблице в вертикальном столбце под буквой D число 5. Это длина диаметра. Рядом с этим числом (вправо, в столбце под названием «Длина окружности») увидим число 15,708 (м). Совершенно так же найдём, что если D = 10 см, то длина окружности равна 31,416 см.

По этим же таблицам можно производить и обратные вычисления. Если известна длина окружности, то можно найти в таблице соответствующий ей диаметр. Пусть длина окружности равна приблизительно 34,56 см. Найдём в таблице число, наиболее близкое к данному. Таковым будет 34,558 (разница 0,002). Соответствующий такой длине окружности диаметр равен приблизительно 11 см.

Таблицы, о которых здесь сказано, имеются в различных справочниках. В частности, их можно найти в книжке «Четырёхзначные математические таблицы» В. М. Брадиса. и в задачнике по арифметике С. А. Пономарёва и Н. И. Сырнева.

В какой бы сфере экономики человек ни трудился, вольно или невольно он пользуется математическими знаниями, накопленными за многие столетия. С устройствами и механизмами, содержащими окружности, мы сталкиваемся ежедневно. Круглую форму имеет колесо, пицца, многие овощи и фрукты в разрезе образуют круг, а также тарелки, чашки, да и многое другое. Однако, правильно рассчитывать длину окружности умеет не каждый.

Чтобы вычислить длину окружности, необходимо вначале вспомнить, что такое окружность. Это множество всех точек плоскости, равноудаленных от данной. А круг – это геометрическое место точек плоскости, находящееся внутри окружности. Из вышесказанного следует, что периметр круга и длина окружности – это одно и то же.

Способы нахождения длины окружности

Помимо математического способа нахождения периметра круга, есть и практические.

• Взять веревку или шнур и обернуть один раз вокруг.
• Затем веревку измерить, полученное число и будет длиной окружности.
• Прокатить круглый предмет один раз и посчитать длину пути. Если предмет очень небольшой, можно несколько раз обмотать его бечевкой, затем размотать нить, измерить и поделить на число витков.
• Найти требуемую величину по формуле:

L = 2πr = πD ,

где L – искомая длина;

π – константа, приблизительно равна 3,14 r – радиус окружности, расстояние от ее центра до любой точки;

D – диаметр, он равен двум радиусам.

Применение формулы, чтобы найти длину окружности

• Пример 1. Беговая дорожка проходит вокруг окружности радиусом 47,8 метров. Найти длину данной беговой дорожки, приняв π = 3,14.

L = 2πr =2*3,14*47,8 ≈ 300(м)

Ответ: 300 метров

• Пример 2. Колесо велосипеда, обернувшись 10 раз, проехало 18,85 метра. Найти радиус колеса.

18,85: 10 =1,885 (м) – это периметр колеса.

1,885: π = 1,885: 3,1416 ≈ 0,6(м) – искомый диаметр

Ответ: диаметр колеса 0,6 метра

Удивительное число π

Несмотря на кажущуюся простоту формулы, почему-то многим трудно ее запомнить. Видимо, это происходит из-за того, что в формуле есть иррациональное число π, которое не присутствует в формулах площади других фигур, например, квадрата, треугольника или ромба. Нужно просто запомнить, что это константа, то есть постоянная, означающая отношение длины окружности к диаметру. Около 4 тысяч лет назад люди заметили, что отношение периметра круга к его радиусу (или диаметру) одинаково для любых окружностей.

Древние греки приближали число π дробью 22/7. Долгое время π высчитывали как среднее между длинами вписанных и описанных многоугольников в окружность. В третьем столетии нашей эры китайский математик провёл вычисление для 3072-угольника и получил приближённое значение π = 3,1416. Необходимо помнить, что π всегда постоянно для любой окружности. Его обозначение греческой буквой π появилось в 18 веке. Это первая буква греческих слов περιφέρεια — окружность и περίμετρος — периметр. В восемнадцатом веке было доказано, что эта величина иррациональна, то есть ее нельзя представить в виде m/n, где m – целое, а n – натуральное число.

Формулы объема — вывод, примеры

Формула объема – это математическое выражение, используемое для нахождения общего пространства (вакуума), занимаемого любым трехмерным объектом. Давайте подробно разберемся с формулами объема различных трехмерных форм.

Что такое формула объема?

Формула, используемая для расчета общей кубической емкости, которую может вместить объект, является формулой его объема. Единица объема трехмерной формы выражается в единицах  ³  или кубических единицах.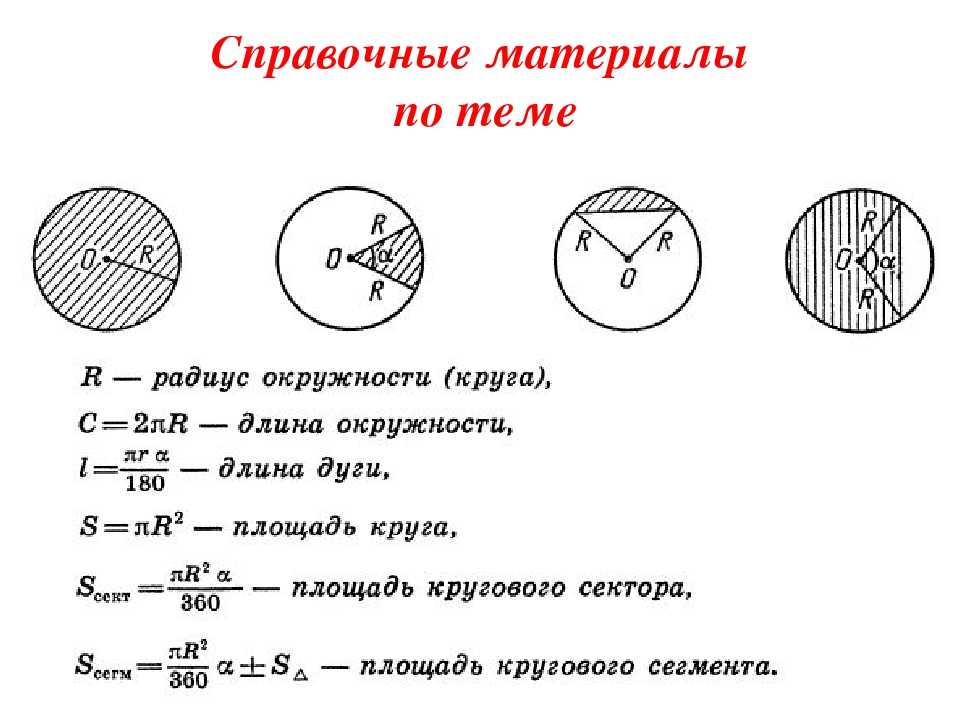 Посмотрите на приведенную ниже диаграмму формул объема, на которой показаны формулы объема соответствующих трехмерных фигур.

Давайте подробно узнаем об общих формулах объема различных форм.

Формулы объема трехмерных фигур

Теперь мы знаем, что формула объема используется для расчета объема трехмерного объекта. В этом разделе мы узнаем о формулах объема с соответствующими размерами различных трехмерных фигур.

Формула объема куба

Формула объема куба зависит от трех сторон куба, где все три стороны равны по размеру. Объем куба – это количество, занимаемое кубом. Общая формула объема куба имеет вид:

• Объем куба = a × a × a = a ³  кубических единиц, , где «a» — длина стороны куба.
• Объем формулы куба с использованием диагонали может быть задан как V = (√3×d ³ )/9, где d – длина диагонали куба.

Формула объема прямоугольного параллелепипеда

Чтобы рассчитать объем пространства, заключенного в прямоугольный параллелепипед, мы используем формулу объема прямоугольного параллелепипеда. Общая формула объема прямоугольного параллелепипеда математически выражается как:

• Объем прямоугольного параллелепипеда = площадь основания × высота в кубических единицах
• Площадь основания прямоугольного параллелепипеда = l × b квадратных единиц
• Следовательно, объем прямоугольного параллелепипеда, V = l × b × h = lbh единицы ³ ,  где «l», «b» и «h» представляют длину, ширину и высоту параллелепипеда.

Формула объема конуса

Чтобы рассчитать объем пространства, занимаемого конусом трехмерной формы с круглым основанием радиусом r и высотой h, мы используем формулу объема конуса. Общая формула объема конуса выражается как:

Объем конуса, В = (1/3)πr ² ч кубических единиц.

Здесь

• ‘r’ — радиус основания (окружности) конуса
• ‘h’ — высота конуса
• π — константа со значением 22/7 (или) 3,142.

Формула объема цилиндра

Формула объема цилиндра используется для определения количества пространства (вместимости), занимаемого внутри него. Мы знаем, что основанием правильного кругового цилиндра является окружность, а площадь окружности радиуса «r» равна πr ² . Таким образом, формула объема цилиндра:

Объем цилиндра = πr ² ч кубических единиц

Здесь

• ‘r’ – радиус основания (окружности) цилиндра
• ‘h’ — высота цилиндра
• π — это константа, значение которой равно 22/7 (или) 3,142.

Таким образом, объем цилиндра прямо пропорционален его высоте и квадрату радиуса. то есть объем цилиндра становится четырехкратным, если радиус цилиндра удваивается.

Объемная формула сферы

Мяч является прекрасным примером, который напоминает форму сферы. Это трехмерный твердый объект с круглой структурой. Количество воздуха, находящегося в шаре, называется объемом шара или шара. Формула объема сферы задается следующим образом:

Объем сферы = (2/3)πr ² ч
Если диаметр сферы = 2r
Следовательно, объем сферы равен (2/3)πr ² h = (2/3)πr ² (2r) = (4/3)πr ³  кубических единиц

Объем сферы равен (4/3)πr ³  кубических единиц

Здесь

• ‘r’ – радиус сферы
• ‘h’ — высота сферы
• π — это константа, значение которой равно 3,142 или 22/7.

Формула объема полушария

Полушарие является половиной сферы, мы можем легко вывести формулу объема полушария, используя формулу объема сферы. Теперь, учитывая, что радиус сферы равен r единиц, а объем сферы равен (4/3)πr ³ .

Таким образом, объем полушария может быть задан как: V = ½ (4/3)πr ³

Объем полушария = (2/3)πr ³ кубических единиц

3

‘r’ — радиус полушария

π — это константа, значение которой равно 3,142 или 22/7.

Формула объема призмы

Формула объема призмы определяется произведением площади основания и высоты призмы. Это математически выражается как:

Объем призмы V = B × h единиц ³ .

Здесь

• «B» — базовая площадь в квадратных единицах
• «h» — высота призмы в единицах.

Существует семь типов призм в зависимости от формы основания призмы. Формула объема призм зависит от различных оснований призм. Ознакомьтесь с объемом призмы, чтобы понять концепцию формул объема различных призм.

Формула объема пирамиды

Объем пирамиды составляет одну треть объема призмы (т. е. их основания и высоты равны). Таким образом,

Объем пирамиды (V) = (1/3) (Bh) единиц ³ , где

• B = площадь основания пирамиды в квадратных единицах
• h = Высота пирамиды (высота) в единицах

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.

Заказать бесплатный пробный урок

Примеры формулы объема

Пример 1: Цилиндрический резервуар   имеет радиус 3 единицы и высоту 8 единиц. Используя формулу объема, найдите объем цилиндра, найдите его площадь поверхности.

Решение:

Дано: r = 3 единицы, h = 8 единиц
При подстановке значений в формулу объема цилиндра имеем
Объем цилиндра = πr ² ч
V = π(3) ² (8)
V = π × 9 × 8 90 101 V = 72 π 90 101 Подставляя значение π = 3,14
V = 72 × 3,14 = 226,08 единиц ³
Объем цилиндра равен 226,08 единиц ³

Пример 2: Учитывая, что радиус конуса равен 9 единицам, а высота равна 4 единицам. Используя формулу объема, определите объем конуса.

Решение:

Дано: радиус = 4 единицы и высота = 9ед.
Формула объема конуса = (1/3)πr ² ч.
=1/3 × 3,14 × 4 ²  × 9
=1/3 × 452,16 90 101 =150,72 ед. ³
∴Объем конуса будет 150,72 ед. ³

7 дюймов, а высота 5 дюймов.

Решение: Дана длина прямоугольного параллелепипеда = 9дюймов, ширина прямоугольного параллелепипеда = 7 дюймов, а высота прямоугольного параллелепипеда = 5 дюймов.
Формула объема прямоугольного параллелепипеда = l × b × h 90 101 Подставив значения l, b и h в формулу объема, получим
V = 9 × 7 × 5
= 315
= 315 дюймов ³
∴Объем прямоугольного параллелепипеда будет 315 дюймов ²

Часто задаваемые вопросы по формулам объема

Что такое формула объема для прямоугольного параллелепипеда?

Формула объема прямоугольного параллелепипеда: l × b × h кубических единиц. Здесь «l», «b» и «h» обозначают длину, ширину и высоту прямоугольного параллелепипеда.

Какая связь между формулой объема сферы и полушария?

Формула объема полушария составляет половину формулы объема сферы. Это дается как:
Объем полусферы = ½ (формула объема сферы) = ½ (4/3)πr ³  = (2/3)πr ³  кубических единиц , где «r» – радиус полушария/сферы.

Какова формула объема конуса?

Формула объема конуса математически выражается как V = (1/3)πr ² ч куб. ед. Здесь «r» — радиус основания конуса, а «h» — высота конуса.

Какая связь между формулами объема призмы и пирамиды?

Формула объема пирамиды составляет 1/3 формулы объема призмы. Это дается как:
Объем пирамиды = 1/3 (формула объема призмы) = 1/3 (Bh) кубических единиц, где ‘B’ – площадь основания пирамиды/призмы, выраженная в единицах ²  и ‘h’ высота пирамиды/призмы, выраженная в единицах.

Формула диаметра сферы с использованием объема

LearnPracticeDownload

Объем формулы сферы можно найти через диаметр. Диаметр сферы — это самая длинная линия, проходящая внутри сферы и проходящая через центр сферы. Сфера — это трехмерная фигура, идеально симметричная и круглая по форме. Некоторыми примерами сфер являются шар, глобус и т. Д. Объем сферы — это количество пространства внутри нее (или) емкость сферы, которую она может удерживать. В этой статье мы выведем формулу диаметра сферы, используя объем.

1.	Как найти объем сферы с диаметром?
2.	Каков диаметр сферы в формуле с использованием объема?
3.	Как рассчитать диаметр сферы, используя объем?
4.	Часто задаваемые вопросы о формуле диаметра сферы с использованием объема

Как найти объем сферы с диаметром?

Мы знаем, что объем V сферы радиуса r рассчитывается по формуле V = (4/3) π r ³ . Это формула объема сферы через радиус. Мы знаем, что диаметр шара в два раза больше радиуса. т. е. диаметр, d = 2r. Отсюда получаем r = d/2. Подставив это в формулу объема,

V = (4/3) π (d/2) ³ = (4/3) π (d ³ /8) = (πd ³ )/6.

Таким образом, объем сферы в пересчете на диаметр (d) равен V = (πd ³ )/6.

Что такое диаметр сферы Формула с использованием объема?

В предыдущем разделе мы уже изучили формулу нахождения объема (V) сферы по ее диаметру (d). Мы можем просто решить эту формулу для диаметра (d), чтобы найти формулу диаметра сферы, используя ее объем. Объем сферы по диаметру равен
. V = (πd ³ )/6
⇒ 6V = πd ³ (умножить обе части на 6)
⇒ 6V/π = d ³ (разделить обе части на π)
⇒ (6V/π) ^(1/3) = d (увеличение мощности с обеих сторон на 1/3)

Таким образом, формула для диаметра сферы с использованием ее объема: d = (6V/ π) ^(1/3) .

Примечание: Здесь π — константа, приблизительно равная 22/7 (или) 3,14159…

Как рассчитать диаметр сферы, используя объем?

Рассмотрим сферу радиуса r, диаметра d и объема V. Мы можем рассчитать диаметр сферы, используя ее объем, тремя способами:

1. Подставим значение V в формулу объема сферы в терминах радиуса V = (4/3) π r ³ , решите его относительно r. Затем используйте d = 2r.
2. Подставьте значение V в формулу объема сферы через диаметр, V = (πd ³ )/6, решите ее для d.
3. Непосредственно подставьте значение V в формулу диаметра сферы, используя объем, d = (6V/π) ^(1/3) .

 

Решенные примеры формулы диаметра сферы с использованием объема

1. Пример 1: Объем сферического шара равен 36π кубических единиц. Найдите его диаметр.

   Решение:

   Объем данного сферического шара V = 36π кубических единиц.

   Метод 1

   Подставив это в формулу диаметра, используя объем,

   d = (6V/π) ^(1/3) = (6(36π) /π) ^(1/3) = (216) ^(1/3) = 6 единиц.

   Метод 2

   Использование формулы объема сферы,
   V = (4/3) π r ³
   ⇒ 36π = (4/3) π r ³
   ⇒ 36π × (3/4) × (1/π) = г ³
   ⇒ 27 = р ³
   ⇒ r = 3

   Итак, радиус сферы равен r = 3. Отсюда ее диаметр = 2(3) = 6 единиц.

   Ответ: Диаметр данного сферического шара = 6 единиц.

2. Пример 2: Объем сферы равен 28π см ³ . Найдите диаметр шара, используя объем.

   Решение

   Объем данной сферы V = 28π кубических единиц.

   Подставив это в формулу диаметра сферы, используя объем,

   d = (6V/π) ^(1/3) = (6(28π) /π) ^(1/3) = (168) ^(1/3) = (8) ^(1/3) × (21) ^(1/3) = 2 \(\sqrt[3]{21}\).

   Ответ: Диаметр данной сферы = 2 \(\sqrt[3]{21}\) см.

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по формуле диаметра сферы с использованием объема

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о формуле диаметра сферы с использованием объема

Как рассчитать объем сферы с диаметром?

Объем сферы (V) относительно ее радиуса (r) равен V = (4/3) π r ³ . Если d — его диаметр, то d = 2r. Отсюда получаем r = (d/2). Подставляя это в формулу объема, объем сферы в единицах диаметра равен V = (πd ³ )/6.

Как найти диаметр сферы по объему? 9(1/3), где d — диаметр сферы, а V — ее объем. В качестве альтернативы мы можем подставить значение V в формулу объема V = (4/3) π r

³ , решить ее для r и удвоить, чтобы найти диаметр.

Какая связь между диаметром и объемом сферы?

Связь между диаметром сферы и ее объемом можно изучить по формуле V = (πd ³ )/6, где d — диаметр, а V — объем сферы.

Какая формула используется для расчета радиуса и диаметра сферы с использованием объема?

Радиус и диаметр сферы можно рассчитать, зная объем. Формулы, которые можно использовать для определения радиуса и диаметра, приведены ниже:

• Формула для радиуса r сферы с использованием объема, V = (4/3) π r ³ .
• Формула для диаметра d сферы с использованием объема, V = (πd ³ )/6.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочий лист по объему

Рабочие листы по математике и визуальный учебный план

Определение объема и площади поверхности сферы | Преалгебра |

Результаты обучения

• Найдите объем и площадь поверхности сферы

Сфера имеет форму баскетбольного мяча, похожую на трехмерный круг. Как и в случае с кругом, размер сферы определяется ее радиусом, то есть расстоянием от центра сферы до любой точки на ее поверхности. Ниже приведены формулы объема и площади поверхности шара.

Показать, откуда берутся эти формулы, как мы это делали для прямоугольного тела, выходит за рамки этого курса. Мы аппроксимируем

π\pi π

с

3.143.143.14

.

Объем и площадь поверхности сферы

Для сферы радиусом

r:r\text{:}r:

пример

Сфера имеет радиус

666

дюймов. Найдите его 1. объем и 2. площадь поверхности.

Решение

Шаг 1 одинаков как для 1, так и для 2, поэтому мы покажем его только один раз.

Шаг 1. Прочтите проблему. Нарисуйте фигуру и подпишите ее данными данными.

1.
Шаг 2. Определите , что вы ищете.	объем сферы
Шаг 3. Имя. 9{3}V≈34​(3,14)63 V≈904,32 кубических дюймаV\ок. 904,32\text{кубических дюймов}V≈904,32 кубических дюймов
Шаг 6. Проверка: Дважды проверьте свои математические расчеты на калькуляторе.
Шаг 7. Ответьте на вопрос.	Объем примерно 904,32904,32904,32 кубических дюйма.

» data-label=»»>

2.
Шаг 2. Определите , что вы ищете. 9{2}S≈4(3,14)62 S≈452,16S\приблизительно 452,16S≈452,16
Шаг 6. Проверка: Дважды проверьте свои математические расчеты на калькуляторе
Шаг 7. Ответьте на вопрос.	Площадь поверхности составляет приблизительно 452,16452,16452,16 квадратных дюйма.

попробуй

пример

Земной шар имеет форму сферы радиусом

141414

см. Найдите его 1. объем и 2. площадь поверхности. Округлите ответ до сотых.

Показать решение

Решение

Шаг 1. Прочтите задачу. Нарисуйте фигуру с полученной информацией и подпишите ее.

1.
Шаг 2. Определите , что вы ищете.	объем сферы 9{3}V≈34​(3.14)143
Шаг 5. Решить.	В ≈ 11 488,21 В\приблизительно 11 488,21 В ≈ 11 488,21
Шаг 6. Проверка: Мы оставляем вам возможность проверить свои расчеты.
Шаг 7. Ответьте на вопрос.	Объем примерно 11 488,2111 488,2111 488,21 кубических дюйма.

2.	9{2}S≈4(3.14)142
Шаг 5. Решить.	С≈2461,76С\приблизительно 2461,76С≈2461,76
Шаг 6. Проверка: Мы оставляем вам возможность проверить свои расчеты. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт