Объем комнаты и площадь пола
Вот такая вот интересная задачка:
Объем комнаты 75 метров кубических, высота комнаты 3 метра. Найдите площадь пола.
Решение задачи тупо:
75 : 3 = 25 (метров квадратных)
Если объем комнаты разделить на её высоту, то получится площадь пола. Если в вашей задаче написано «объем комнаты 75 метров квадратных…», то значит эту задачу составляло туловище, которое ни фига не понимает в единицах измерения объемов. Объем не может измеряться в метрах квадратных, нормальные люди в них измеряют площадь.
А теперь бла-бла-бла на заданную тему.
Ничего сложного в этой задаче нет, просто вместо обычного прямоугольного параллелепипеда здесь нам рассказывают о комнате. В переводе на язык математики и применительно к параллелепипеду эта задача будет звучать так:
Объем прямоугольного параллелепипеда равен 75 кубических метров, его высота равна 3 метра. Найдите площадь основания этого прямоугольного параллелепипеда.
В чём маленький подвох, который многих может сбить с толку? Дело в том, что комнату мы привыкли видеть изнутри.
| Высота комнаты и площадь пола |
Эта комната изображена на стадии ремонта. После ремонта можете обставить её мебелью по своему вкусу. Кстати, большинство людей вспоминают про геометрию именно после начала ремонта — площади, периметры, объемы… Так вот, математики нам показывают прямоугольные параллелепипеды всегда снаружи.
| Прямоугольный параллелепипед с обозначениями |
Если в математике мы привыкли видеть любой объем снаружи, то попадая внутрь реального объема очень легко растеряться.
Теперь разберемся с названиями. То, что в комнате называется «объем комнаты», в математике называется просто «объем».
Еще один интересный момент. Комната может иметь любую форму с вертикальными стенами. Пол в комнате может быть квадратным, прямоугольным, треугольным, шестиугольным, круглым, бесформенным… В любом случае, его площадь будет равна 25 квадратных метров. Ведь любая двухмерная геометрическая фигура может иметь площадь в 25 метров в квадрате. При умножении этой площади на высоту в 3 метра мы всегда будем получать объем в 75 метров кубических.
Является ли подобная задача реальной? Волне. В отдельных бюрократических документах можно встреть объем комнаты. Например, при установке газового оборудования требования могут предъявляться не к площади комнаты, а к её объему. Исходя из высоты комнаты, которая может быть разной в разных зданиях, определяют требуемую площадь пола для соблюдения строительных норм.
P.S. Кстати, на сайте «Русский текст» вы можете найти редкие и уникальные тексты, статьи из старых газет, интересные публикации на русском языке. Любознательность ещё никому не навредила. Конечно, если любознательностью попользоваться с умом. Если вы прочтете какую-нибудь старую, давно забытую, но интересную статью о науке — вы станете умнее, чем были до этого.
Найти объем усеченного конуса онлайн
Пример решили: 13177 раз Сегодня решили: 0 раз
Введите высоту и радиусы оснований
Высота H Радиус R1 Радиус R2
Вычисление объема усеченного конуса
Скачать решение в PDF
Порекомендуйте наш сервис друзьям
Вконтакте
Одноклассники
Google+
Усеченный конус образуется путем отсечения плоскостью, параллельной основанию, части конуса. 3 $$
3 $$
Попробуйте другие сервисы
Найти объем параллелепипеда
Найти объем куба
Найти объем шара
Найти объем цилиндра
Найти объем усеченной пирамиды
Как найти объем, используя площадь и высоту?
Измерение — это часть математики, которая занимается изучением различных геометрических фигур, их площадей и объемов. Проще говоря, измерение — это все об измерении. Измерение различных размеров тела и расчет площади, площади поверхности и объема изучаются при измерении.
Объем
Объем определяется как трехмерное пространство, замкнутое или ограниченное объектом. Нахождение объема объекта может помочь нам определить количество, необходимое для заполнения объекта, например, количество воды, необходимое для заполнения бутылки, бассейна или резервуара для воды.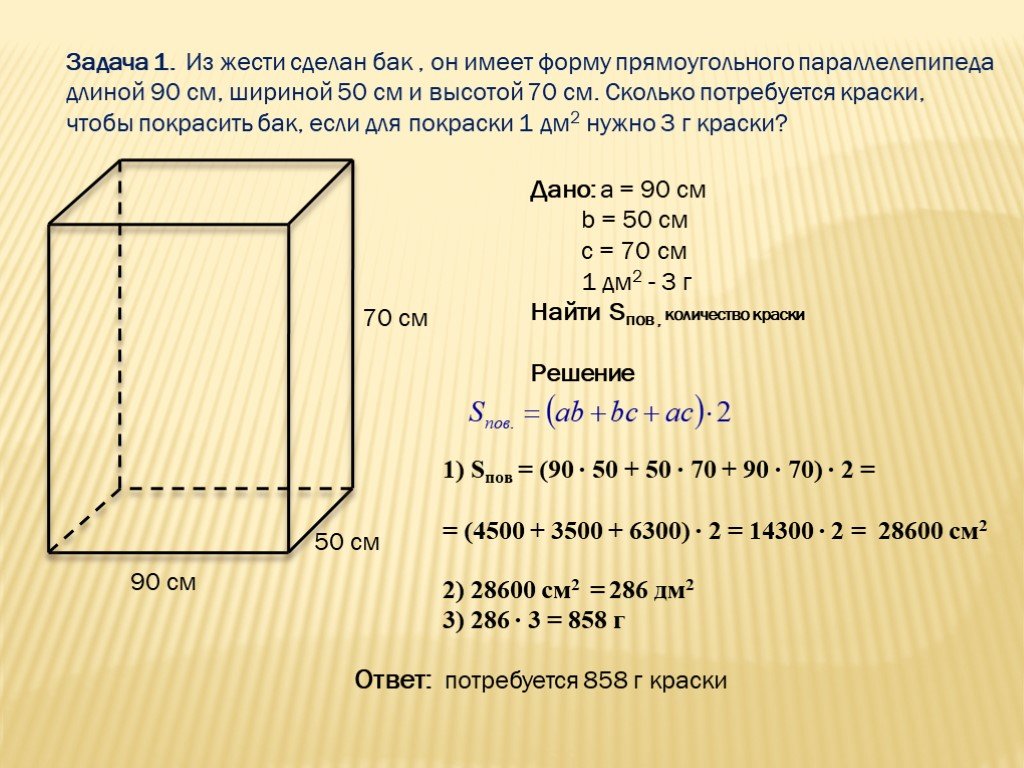 Объем объекта оценивается в кубических единицах, таких как кубические сантиметры, кубический дюйм, кубический фут, кубический метр и т. д.
Объем объекта оценивается в кубических единицах, таких как кубические сантиметры, кубический дюйм, кубический фут, кубический метр и т. д.
Объем большинства объектов можно легко рассчитать, зная площадь основания и высоту, даже сложных. Сложные объекты можно разделить на более простые фигуры, и, таким образом, сложив объемы этих более простых фигур, можно суммировать, чтобы получить объем всего объекта.
Как найти объем, используя площадь и высоту?
Чтобы найти объем данного объекта, это можно сделать следующими способами:
- Найти площадь основания
- Умножить площадь основания на соответствующую высоту.
Вычисление объема некоторых знакомых фигур,
Куб
Куб — это трехмерный объект, имеющий шесть конгруэнтных квадратных граней. Размеры всех шести квадратных граней куба одинаковы. Кубу редко также приписывают правильный шестигранник или квадратную призму.
Площадь основания куба = сторона × сторона
Высота куба = сторона
Объем куба = площадь основания × высота = сторона 3
Прямоугольник
Прямоугольник — это трехмерная твердотельная фигура, имеющая шесть граней, восемь вершин и 12 ребер.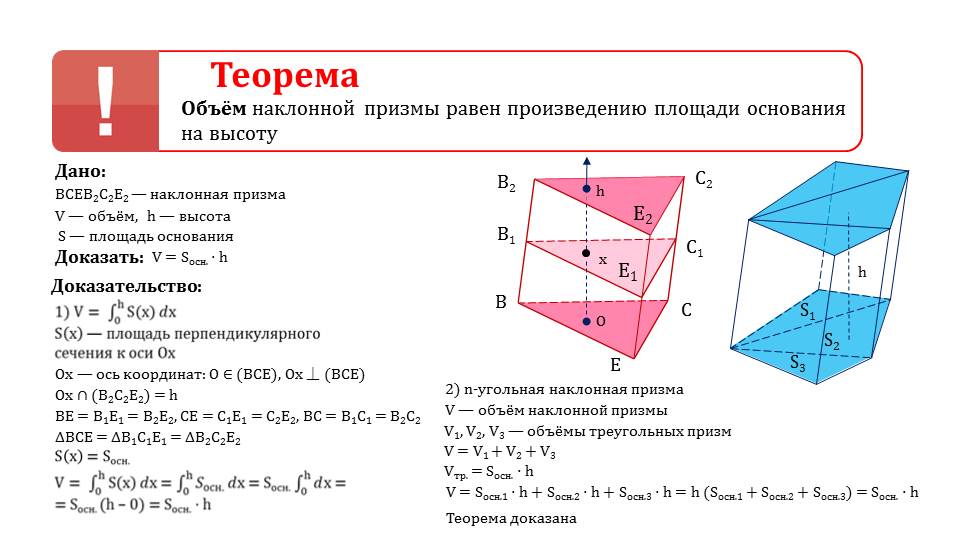 Это одна из распространенных форм вокруг нас, которая имеет три измерения: длину, ширину и высоту.
Это одна из распространенных форм вокруг нас, которая имеет три измерения: длину, ширину и высоту.
Площадь основания параллелепипеда = Длина × Ширина
Высота параллелепипеда = Глубина
Объем параллелепипеда = площадь основания × высота = Длина × Ширина × Глубина
Цилиндр
Цилиндр — это трехмерная объемная фигура в геометрии, которая имеет два параллельных круглых основания, ограниченных криволинейной поверхностью на точном расстоянии от центра. Свечи, батарейки — реальные примеры цилиндров.
Площадь основания цилиндра = 3,14 × R 2
Высота цилиндра = длина
Объем цилиндра = площадь основания x высота = 3,14 × R 2 × длина
4 Образец ПроблемыВопрос 1: Площадь основания куба 25 см 2 , а высота 5 см. Найдите объем.
Решение:
Том = базовая площадь × высота
= 25 × 5
= 125 см 3
Вопрос 2: Основная площадь AS 10 CM 2 2
Вопрос 2: Основная площадь AS 10 CM 2 29002 .
, а высота 50см. Найдите объем.
Решение:
Объем = площадь основания × высота
= 10 x 50
= 500 см 3
Вопрос 3: Площадь основания цилиндра 30 см 2 , а его длина 10 см. Найдите его объем.
Решение:
Том = базовая площадь × Высота
= 30 × 10
= 300 см 2
Урок видео: Volumes of Cylims
. Видео. , мы будем речь о том, как найти объем цилиндра. Сначала мы рассмотрим призмы и как вычислить объем призмы. А потом мы объясним, как цилиндр представляет собой круглую призму. Наконец, мы рассмотрим несколько примеры цилиндров и как вычислить их объемы.
Прежде чем мы поговорим о цилиндрах тогда давайте подумаем о призмах.
Призма представляет собой трехмерную фигуру с постоянное сечение. Вот, например, куб. Я отметил в разрезе с этим синим полосатым кусочком здесь. И если бы я разрезал эту призму на в любой точке этого прямоугольного параллелепипеда, в любой точке здесь, скажем, здесь, как это, и посмотрите на срез, который я получаю, у меня все равно был бы точно такой же крест раздел.
Вот еще один пример призмы. призма в виде звезды. То сечение, которое является звездой форма одинакова по всей длине призмы. А вот и круглая призма. Эта круглая форма одинакова для всех пути по длине призмы. На самом деле, эта круглая призма специальное название цилиндра.
Теперь, прежде чем мы зайдем слишком далеко насчет объемов, давайте поговорим о кубе, каждая сторона которого имеет длину в одну единицу. Площадь поперечного сечения этого куб будет одна единица на одну единицу, что составляет одну единицу в квадрате.
Теперь мы можем вычислить объем по умножив площадь поперечного сечения на длину или, в данном случае, на высоту призма. Итак, это будет один раз один, который равен единице. И поскольку это объем, это единицы в кубе.
Теперь, если мы возьмем наш единичный куб куб и сложить его поверх другого такого же, у нас будет две кубические единицы. Теперь треть составляет три кубических единицы. И четвертый делает четыре кубических единицы и так далее. Но что, если мы начнем с двух этих кубических единиц рядом друг с другом? Теперь каждый раз, когда мы добавляем дополнительный слой, мы добавляем еще две кубические единицы. Итак, три слоя дают нам шесть кубических единицы. И четыре слоя дают нам восемь кубических единиц. Итак, общая идея заключается в том, что для объем, вы берете площадь поперечного сечения, которая у нас была здесь, и умножаете ее на количество слоев, или длина, или высота этой призмы.
Теперь, как мы уже говорили, цилиндр просто призма с круглым поперечным сечением. Итак, еще раз, чтобы отработать громкость, мы просто вычисляем площадь поперечного сечения и умножаем ее на высоту. Чем он выше, тем больше объем. Теперь, помните, чтобы отработать площадь круга, это 𝜋 умноженное на квадрат радиуса. Итак, если мы назовем наш радиус 𝑟, площадь равна 𝜋 умножить на 𝑟 в квадрате. И если я позволю высоте моей цилиндр, или длина моего цилиндра, быть ℎ, потому что объем равен площадь поперечного сечения, умноженная на высоту, мы можем сказать, что объем равен 𝜋𝑟 в квадрате раз ℎ. И это результат того, что мы будем использовать в наших примерах в оставшейся части этого видео.
Например, найти объем цилиндр округлен до ближайшей десятой. И круг на конце наш цилиндр имеет радиус 4,2 фута.
И у цилиндра есть высота 6,5 футов. Итак, разметим 𝑟, радиус равен 4,2, а высота ℎ равна 6,5. Итак, наш подход будет что объем равен произведению площади поперечного сечения на высоту. А так как поперечное сечение площадь — это круг, площадь будет 𝜋 умножить на квадрат радиуса. Итак, это 𝜋 умножить на 4,2. в квадрате. Теперь важно помнить что в квадрате возводится только 4,2, а не 𝜋. Итак, это будет 𝜋 раз 17,64, что дает нам площадь 55,41769.441 и так далее квадратных футов.
Но чтобы отработать объем, помните, нам также нужно умножать на высоту. Итак, добавим это к нашему разработка. И 55,41769441 умножить на 6,5 дает нас 360,2150137, так далее, так далее, так далее кубических футов. Но вопрос задал нам округлить ответ до десятых. Итак, я собираюсь покрыть все вверх после десятого, а затем просто украдкой взгляните на следующую цифру, чтобы увидеть нужно ли мне округлить это до или нет.
Ну, следующая цифра — это всего лишь один. А если было пять и выше, тогда мы округлим два до трех. Но это не так; это всего лишь один. Итак, мы собираемся сохранить его как два. Итак, наш ответ на ближайший десятый — 360,2 кубических фута.Теперь посмотрим на аналогичный пример. Но на этот раз нам дали диаметр цилиндра, а не радиус.
Запомните, радиус половина диаметра. Итак, чтобы вычислить радиус, просто нужно разделить 14 на два или умножить на половину. И это дает нам семь дюймы. И формула нашего объема 𝑉 равно 𝜋𝑟 в квадрате ℎ. И так, подставив в числа для радиуса семь дюймов и высоты 13 дюймов, мы получили 𝜋 умножить на семь в квадрате на 13. Опять же, важно помните, что в квадрате только семерка, а не 𝜋.
Итак, это 𝜋 умножить на 49.раз 13. И когда мы вкладываем это в наш калькулятор и округляем до десятых, получаем 2001,2 кубических дюйма. В этом примере мы попросили найти объем цилиндра с радиусом четыре сантиметра и высота 14 сантиметров. Нам также говорят, что у нас есть чтобы оставить ответ в терминах 𝜋.
Теперь есть пара вещи здесь. Во-первых, нам не дали диаграмма. Во-вторых, мы должны оставить нашу ответьте в терминах 𝜋, так что это не вопрос простого ввода числа в калькулятор и округления. Теперь вам не нужна схема, но очень часто рисование диаграммы помогает вам организовать свои мысли о вопрос. Так что я бы порекомендовал на самом деле делаем быстрый набросок. Итак, наш цилиндр. У него высота 14 сантиметров и радиусом четыре сантиметра.
Далее мы можем записать формула объема. Объем цилиндра 𝜋 умножить на квадрат радиуса на его высоту. И мы можем заменить в числа, которые нам дали, поэтому 𝜋 равно четырем в квадрате, умноженным на 14, то есть 𝜋 умножить на 16 умножить на 14. И 16 умножить на 14 будет 224. Итак, наш ответ 224 умножить 𝜋. Теперь, из вопроса, оба из наши измерения были даны в сантиметрах. Итак, объем будет в кубических сантиметров. Так что у нас это. Это наш ответ. 224 𝜋 кубических сантиметра. Итак, когда вопрос говорит оставьте свой ответ в терминах 𝜋, это значит выразить его как кратное 𝜋.
Теперь мы можем сделать вещи немного сложнее, превратив эти вещи в слово или историю проблемы. Таким образом, вместо того, чтобы просто явно говоря, что у нас есть цилиндр и говоря вам, что радиус и высота и просто делая этот расчет, вы должны понять значение различные переменные из контекста вопроса.
Итак, давайте взглянем на некоторые примеры такие.
Учитывая, что примерно 7,5 галлонов воды может заполнить один кубический фут, примерно сколько целых галлонов воды находился бы в цилиндрическом резервуаре для воды диаметром 20 футов и высотой 12 футов, если он был полный?
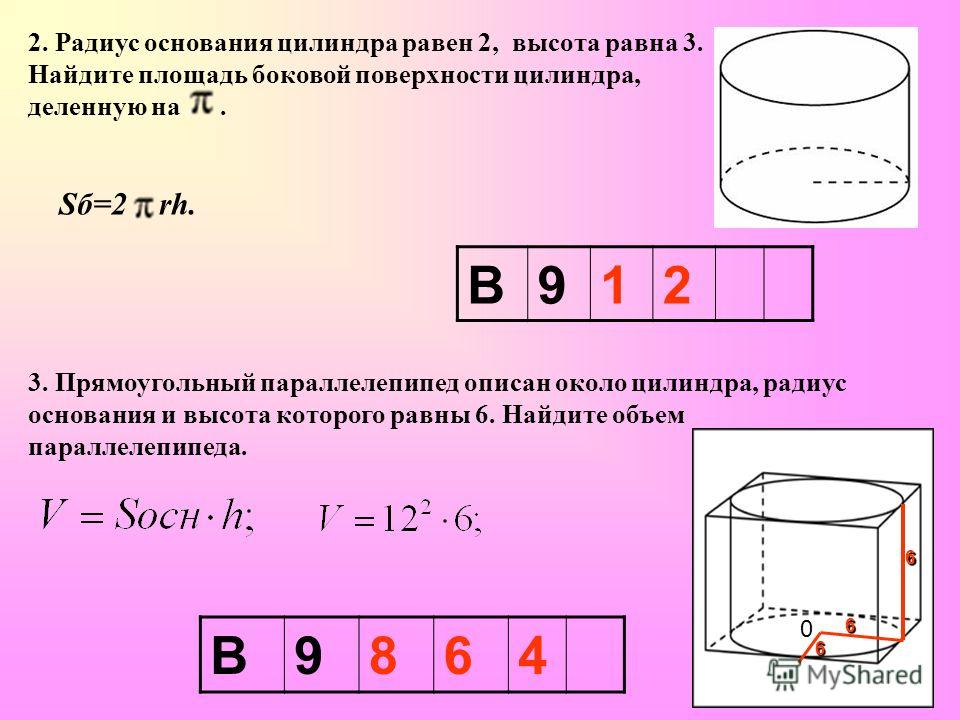
Ладно, сначала немного поработаем диаграмма. Здесь у нас есть цилиндрический полностью заполненный водой резервуар глубиной или высотой 12 футов и диаметром 20 ноги. Итак, во-первых, мы можем записать что объем равен 𝜋, умноженному на квадрат радиуса, умноженный на высоту. Теперь мы можем подставить числа что мы знаем. ну радиус это половина диаметра, поэтому половина 20 равна 10. Итак, квадрат радиуса равен быть 10 в квадрате. И важно помнить что это просто 10 в квадрате, а не 𝜋.
И высота 12, так что у нас есть надо умножить этот ответ на 12.
Итак, это вычисление 𝜋 умножить на 10 в квадрате, что равно 100, умножить на 12, значит 𝜋 умножить на 1200, или 1200𝜋 куб. ноги. Сейчас, на данный момент, я собираюсь оставьте мой ответ с точки зрения 𝜋 для максимальной точности. Если бы я начал округлять до нескольких десятичных разрядов, я бы учитывал эти ошибки округления в своих вычислениях и мой окончательный ответ может быть совершенно неправильным. Теперь мы проработали объем бака в кубических футах, но вопрос говорит, сколько целых галлонов воды будет в цилиндрическом резервуаре для воды.
Теперь каждый кубический фут содержит 7,5 галлонов воды. Итак, если есть 1200𝜋 куб. футов, будет в 7,5 раз больше галлонов воды. Итак, расчет нам нужен сделать, чтобы вычислить, что количество галлонов равно 7,5 умножить на 1200𝜋, что я могу сделать на своем калькулятор.
Теперь можно округлить вправо в конце вопроса. И вопрос сказал о том, как много целых галлонов, поэтому мне нужно округлить до ближайшего целого галлона. Итак, глядя на наш номер здесь, это будет 28274. Итак, мы можем написать наш ответ красиво и аккуратно в конце, 28274 галлона воды.
Что имеет больший объем, а куб, ребра которого имеют длину четыре сантиметра, или цилиндр радиусом три сантиметров и высотой восемь сантиметров?
Итак, что мы должны здесь сделать вычислить объем куба, а также вычислить объем цилиндр, а затем сравните два. Итак, сначала куб, нарисуем эскиз, четыре сантиметра на четыре сантиметра на четыре сантиметра. И объем просто будет четыре раза четыре раза четыре. А так как единицы длины были сантиметров, наш объем будет в кубических сантиметрах.
И четыре раза четыре раза четыре равно 64. Итак, объем куба 64 кубических сантиметра.
Теперь краткий набросок цилиндр. И используйте формулу объема равно 𝜋, умноженному на квадрат радиуса, умноженный на высоту. Теперь давайте вспомним, что квадрат относится только к трем. Это не относится к 𝜋. Итак, у нас есть 𝜋 умножить на три в квадрате умножить на восемь. А три в квадрате девять. Итак, девять умножить на восемь — это 72. Итак, у нас есть 𝜋 умножить на 72. Теперь он не запрашивает уровень. точности в вопросе. Но я округлил до двух десятичных знаков, чтобы дать мне 226,19кубических сантиметров.
Итак, снова замеры были в сантиметрах, объем в кубических сантиметрах, а два числа то, что мы должны сравнить, выражено в одних и тех же единицах, кубических сантиметрах. Теперь мы можем сравнить их.

 , а высота 50см. Найдите объем.
, а высота 50см. Найдите объем.  Призма представляет собой трехмерную фигуру с
постоянное сечение. Вот, например, куб. Я отметил в разрезе
с этим синим полосатым кусочком здесь. И если бы я разрезал эту призму на
в любой точке этого прямоугольного параллелепипеда, в любой точке здесь, скажем, здесь, как
это, и посмотрите на срез, который я получаю, у меня все равно был бы точно такой же крест
раздел.
Призма представляет собой трехмерную фигуру с
постоянное сечение. Вот, например, куб. Я отметил в разрезе
с этим синим полосатым кусочком здесь. И если бы я разрезал эту призму на
в любой точке этого прямоугольного параллелепипеда, в любой точке здесь, скажем, здесь, как
это, и посмотрите на срез, который я получаю, у меня все равно был бы точно такой же крест
раздел. Теперь мы можем вычислить объем по
умножив площадь поперечного сечения на длину или, в данном случае, на высоту
призма. Итак, это будет один раз один, который
равен единице. И поскольку это объем, это единицы
в кубе.
Теперь мы можем вычислить объем по
умножив площадь поперечного сечения на длину или, в данном случае, на высоту
призма. Итак, это будет один раз один, который
равен единице. И поскольку это объем, это единицы
в кубе.




 И высота 12, так что у нас есть
надо умножить этот ответ на 12.
И высота 12, так что у нас есть
надо умножить этот ответ на 12. Теперь можно округлить вправо
в конце вопроса. И вопрос сказал о том, как
много целых галлонов, поэтому мне нужно округлить до ближайшего целого галлона. Итак, глядя на наш номер здесь,
это будет 28274. Итак, мы можем написать наш ответ
красиво и аккуратно в конце, 28274 галлона воды.
Теперь можно округлить вправо
в конце вопроса. И вопрос сказал о том, как
много целых галлонов, поэтому мне нужно округлить до ближайшего целого галлона. Итак, глядя на наш номер здесь,
это будет 28274. Итак, мы можем написать наш ответ
красиво и аккуратно в конце, 28274 галлона воды.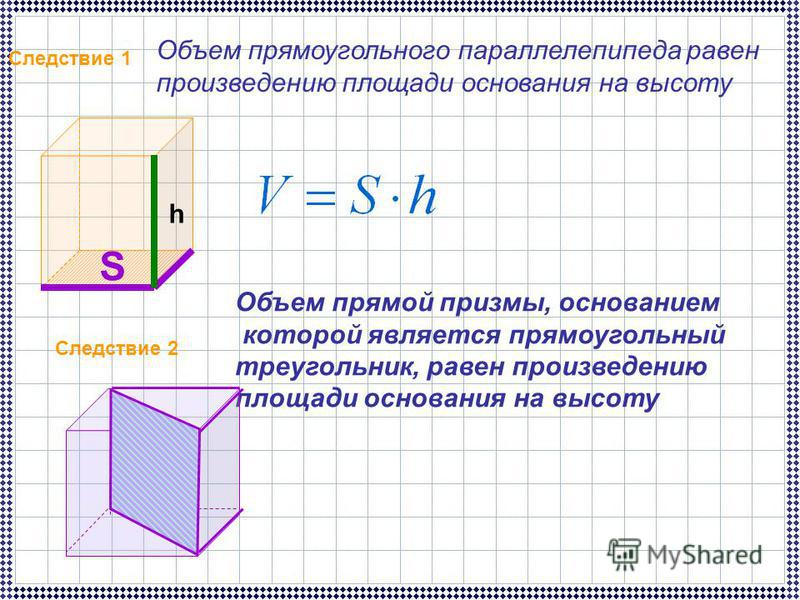 И четыре раза четыре раза четыре
равно 64. Итак, объем куба
64 кубических сантиметра.
И четыре раза четыре раза четыре
равно 64. Итак, объем куба
64 кубических сантиметра.