Экспонента | это… Что такое Экспонента?
У этого термина существуют и другие значения, см. Экспонента (значения).
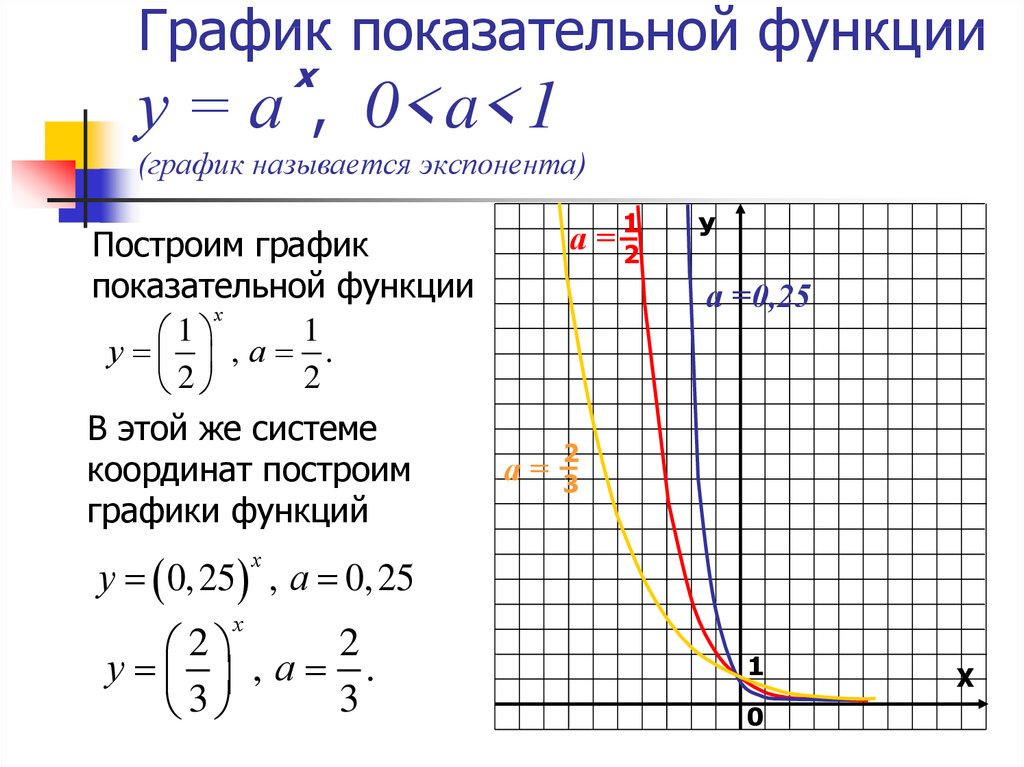
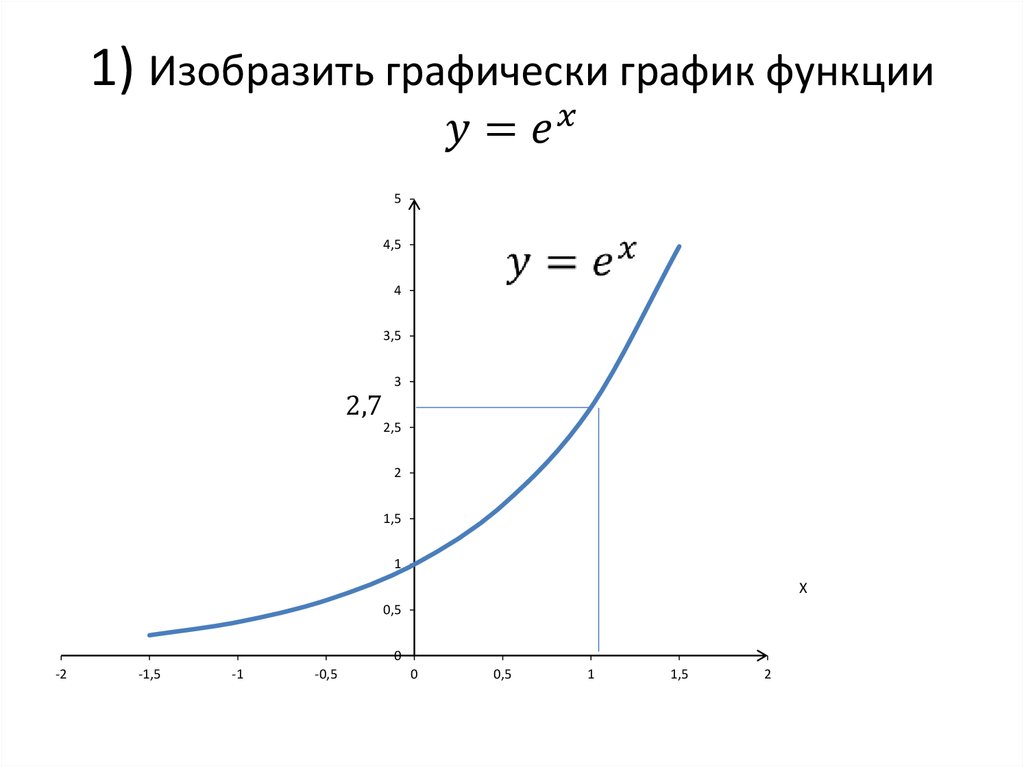
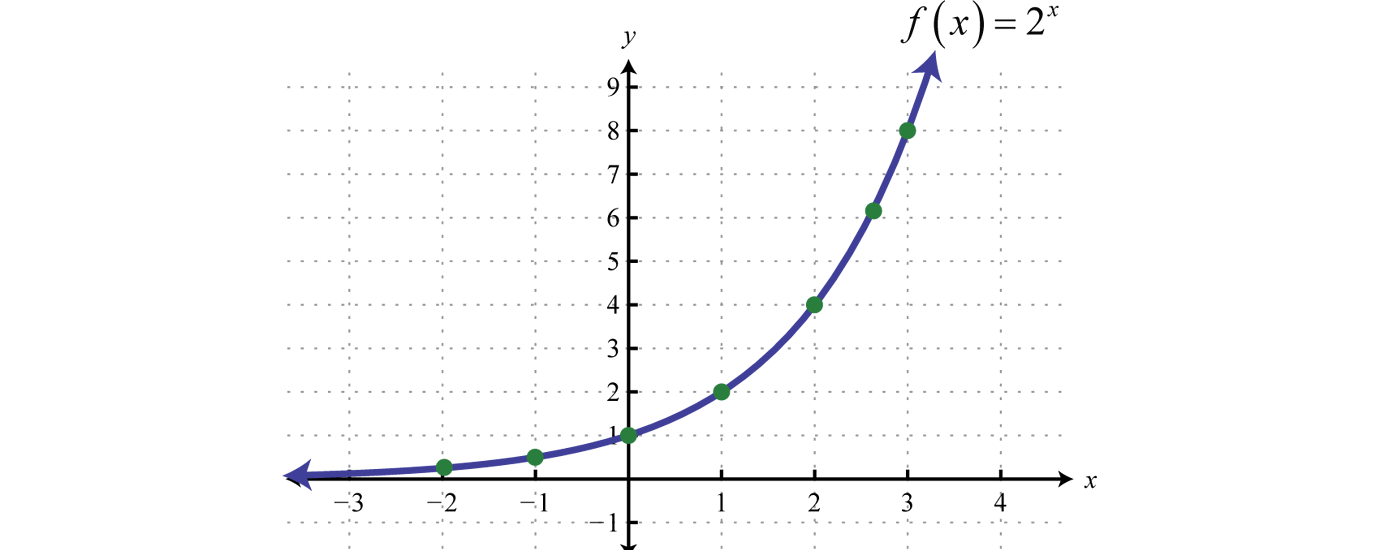
График экспоненты.
Касательная в нуле у функции наклонена на
Рядом для примера показаны (точками) и (пунктиром)
Экспонента — показательная функция , где e — основание натуральных логарифмов ().
Содержание
|
Определение
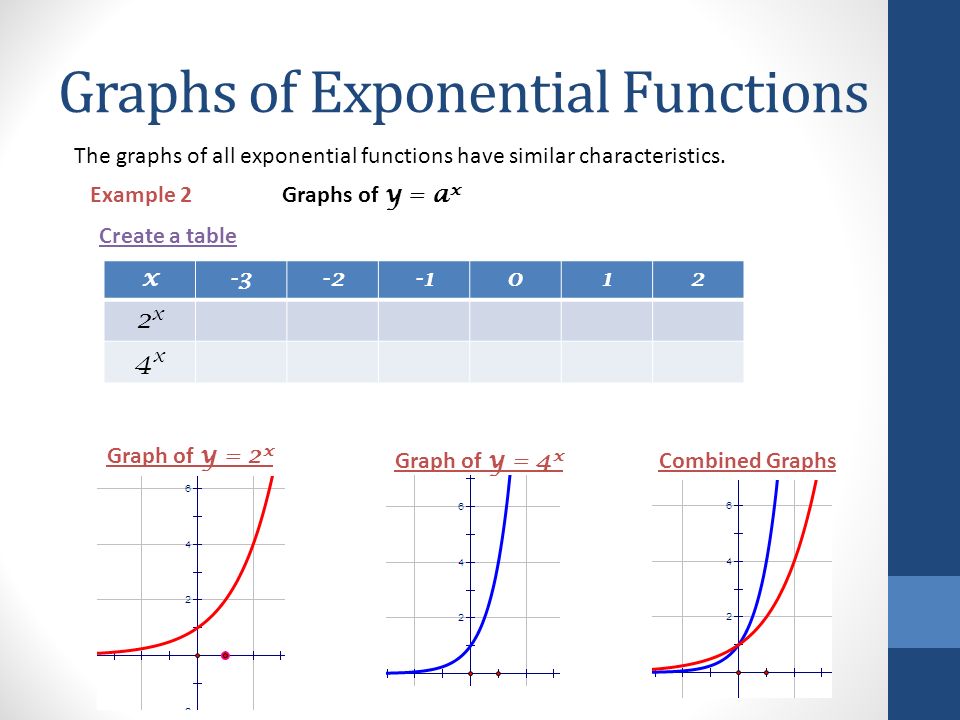
Экспоненциальная функция может быть определена различными эквивалентными способами. Например, через ряд Тейлора:
или через предел:
Здесь x — любое комплексное число.
Свойства
- , в частности
- Экспонента является единственным решением дифференциального уравнения с начальными данными .
 Кроме того через экспоненту выражаются общие решения однородных дифференциальных уравнений.
Кроме того через экспоненту выражаются общие решения однородных дифференциальных уравнений.
- Экспонента является единственным решением дифференциального уравнения с начальными данными .
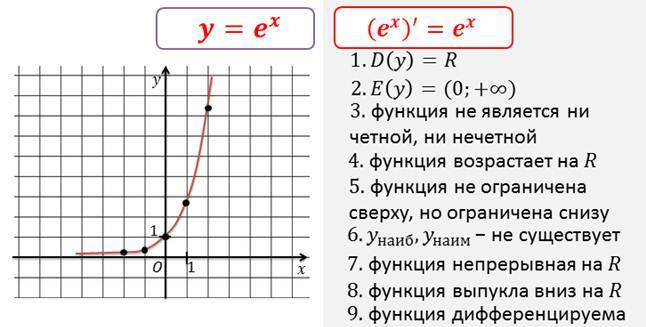
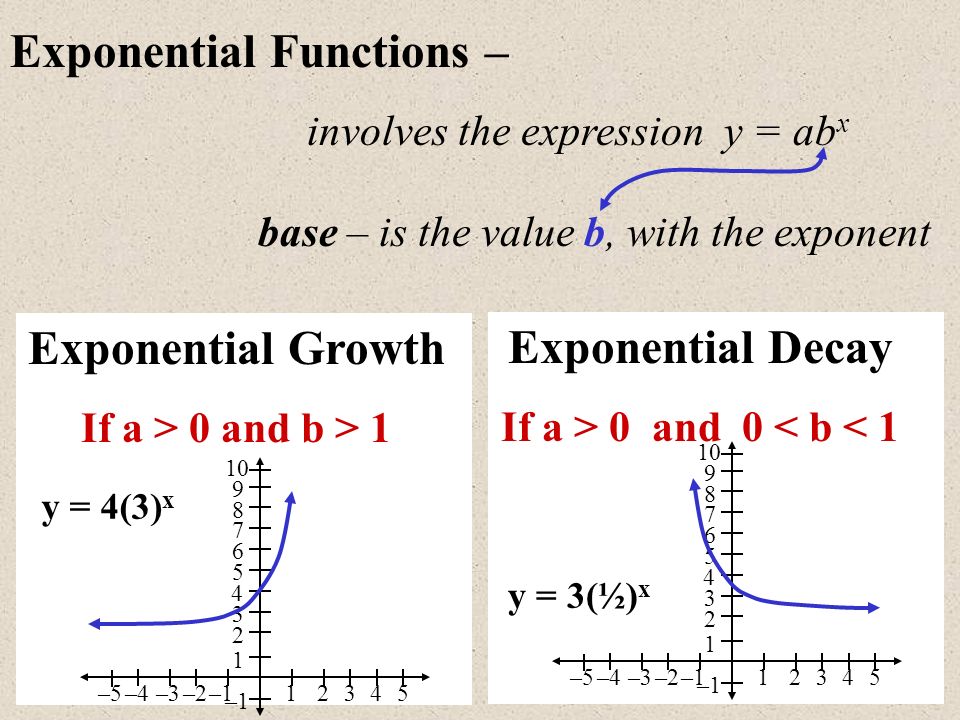
- Экспонента определена на всей вещественной оси. Она всюду возрастает и строго больше нуля.
- Экспонента является выпуклой функцией.
- Обратная функция к ней — натуральный логарифм .
- Фурье-образ экспоненты не существует
- однако преобразование Лапласа существует
- Производная в нуле равна 1, поэтому касательная к экспоненте в этой точке проходит под углом 45°.
- Основное функциональное свойство экспоненты, как и всякой показательной функции:
- .
- Непрерывная функция с таким свойством либо тождественно равна 0, либо имеет вид , где c — некоторая константа.
- где sinh и cosh — гиперболические синус и косинус.
Комплексная экспонента
График экспоненты в комплексной плоскости.
Легенда
Комплексная экспонента — математическая функция, задаваемая соотношением , где есть комплексное число.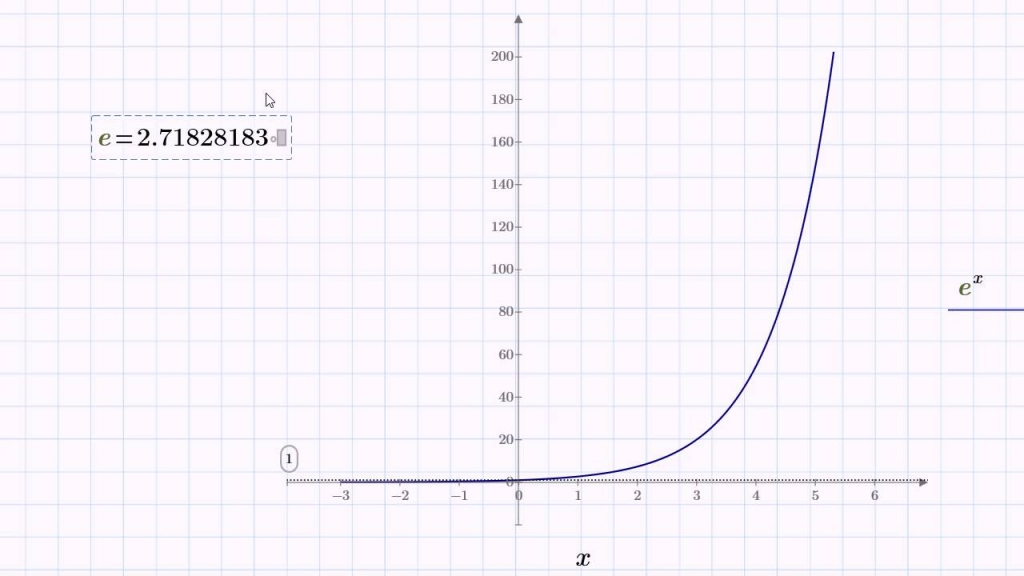 Комплексная экспонента определяется как аналитическое продолжение экспоненты вещественного переменного :
Комплексная экспонента определяется как аналитическое продолжение экспоненты вещественного переменного :
Определим формальное выражение
.
Определенное таким образом выражение на вещественной оси будет совпадать с классической вещественной экспонентой. Для полной корректности построения необходимо доказать аналитичность функции , то есть показать, что разлагается в некоторый сходящийся к данной функции ряд. Покажем это:
Сходимость данного ряда легко доказывается:
.
Ряд всюду сходится абсолютно, то есть вообще всюду сходится, таким образом, сумма этого ряда в каждой конкретной точке будет определять значение аналитической функции . Согласно теореме единственности, полученное продолжение будет единственно, следовательно, на комплексной плоскости функция всюду определена и аналитична.
Свойства
- Комплексная экспонента — целая голоморфная функция на всей комплексной плоскости. Ни в одной точке она не обращается в нуль.
- — периодическая функция с основным периодом 2πi: .

- Алгебраически, экспонента от комплексного аргумента может быть определена следующим образом:
- (формула Эйлера)
- В частности, имеет место (тождество Эйлера),
Вариации и обобщения
Аналогично экспонента определяется для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.
Матричная экспонента
Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:
Определённый таким образом ряд сходится для любого оператора с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы Следовательно, экспонента от матрицы всегда определена и сама является матрицей.
С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение с начальным условием имеет своим решением
Обратная функция
Обратной функцией к экспоненциальной функции является натуральный логарифм.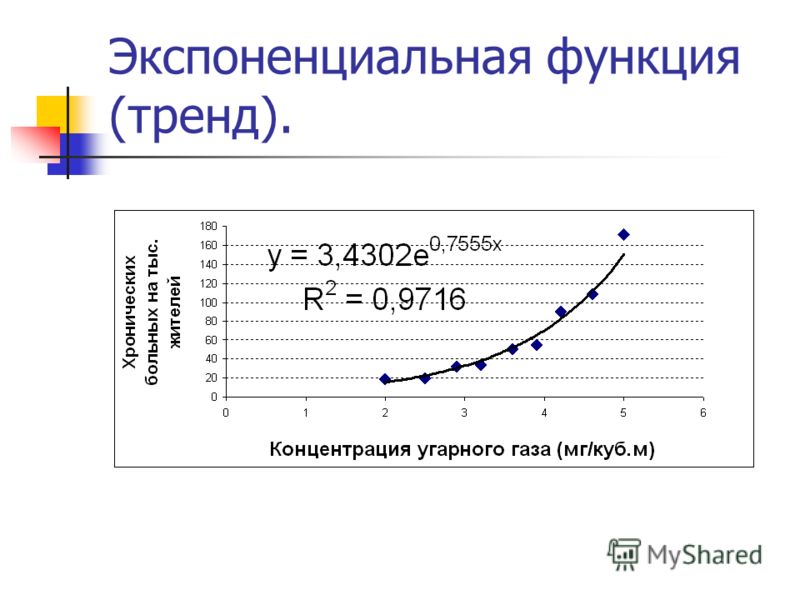 Обозначается :
Обозначается :
См. также
- Показательная функция
- Список интегралов от экспоненциальных функций
Литература
- Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. — Издание 5-е, исправленное. — М.: Наука, 1987. — 688 с.
- Хапланов М. Г. Теория функции комплексного переменного (краткий курс). — Издание 2-е, исправленное. — М.: Просвещение, 1965. — 209 с.
Экспонента | это… Что такое Экспонента?
У этого термина существуют и другие значения, см. Экспонента (значения).
График экспоненты.
Касательная в нуле у функции наклонена на
Рядом для примера показаны (точками) и (пунктиром)
Экспонента — показательная функция , где e — основание натуральных логарифмов ().
Содержание
|
Определение
Экспоненциальная функция может быть определена различными эквивалентными способами. Например, через ряд Тейлора:
или через предел:
Здесь x — любое комплексное число.
Свойства
- , в частности
- Экспонента является единственным решением дифференциального уравнения с начальными данными . Кроме того через экспоненту выражаются общие решения однородных дифференциальных уравнений.
- Экспонента определена на всей вещественной оси. Она всюду возрастает и строго больше нуля.
- Экспонента является выпуклой функцией.
- Обратная функция к ней — натуральный логарифм .
- Фурье-образ экспоненты не существует
- однако преобразование Лапласа существует
- Производная в нуле равна 1, поэтому касательная к экспоненте в этой точке проходит под углом 45°.

- Основное функциональное свойство экспоненты, как и всякой показательной функции:
- .
- Непрерывная функция с таким свойством либо тождественно равна 0, либо имеет вид , где c — некоторая константа.
- где sinh и cosh — гиперболические синус и косинус.
Комплексная экспонента
График экспоненты в комплексной плоскости.
Легенда
Комплексная экспонента — математическая функция, задаваемая соотношением , где есть комплексное число. Комплексная экспонента определяется как аналитическое продолжение экспоненты вещественного переменного :
Определим формальное выражение
.
Определенное таким образом выражение на вещественной оси будет совпадать с классической вещественной экспонентой. Для полной корректности построения необходимо доказать аналитичность функции , то есть показать, что разлагается в некоторый сходящийся к данной функции ряд. Покажем это:
Сходимость данного ряда легко доказывается:
.
Ряд всюду сходится абсолютно, то есть вообще всюду сходится, таким образом, сумма этого ряда в каждой конкретной точке будет определять значение аналитической функции . Согласно теореме единственности, полученное продолжение будет единственно, следовательно, на комплексной плоскости функция всюду определена и аналитична.
Свойства
- Комплексная экспонента — целая голоморфная функция на всей комплексной плоскости. Ни в одной точке она не обращается в нуль.
- — периодическая функция с основным периодом 2πi: . В силу периодичности комплексная экспонента бесконечнолистна. В качестве её области однолистности можно выбрать любую горизонтальную полосу высотой .
- Алгебраически, экспонента от комплексного аргумента может быть определена следующим образом:
- (формула Эйлера)
- В частности, имеет место (тождество Эйлера),
Вариации и обобщения
Аналогично экспонента определяется для элемента произвольной ассоциативной алгебры.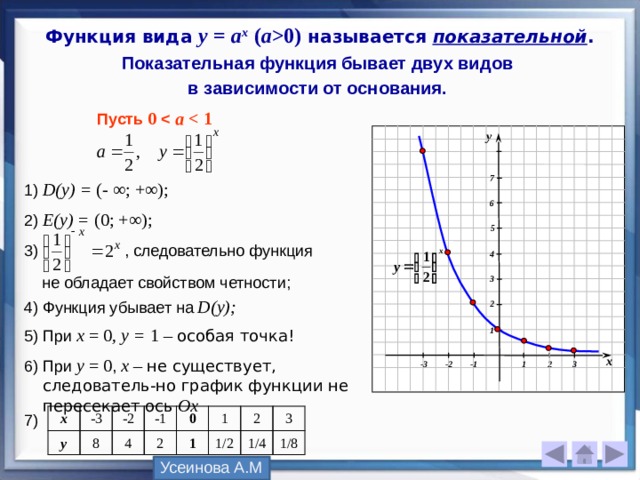 В конкретном случае требуется также доказательство того, что указанные пределы существуют.
В конкретном случае требуется также доказательство того, что указанные пределы существуют.
Матричная экспонента
Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:
Определённый таким образом ряд сходится для любого оператора с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы Следовательно, экспонента от матрицы всегда определена и сама является матрицей.
С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение с начальным условием имеет своим решением
Обратная функция
Обратной функцией к экспоненциальной функции является натуральный логарифм. Обозначается :
См. также
- Показательная функция
- Список интегралов от экспоненциальных функций
Литература
- Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного.

- Хапланов М. Г. Теория функции комплексного переменного (краткий курс). — Издание 2-е, исправленное. — М.: Просвещение, 1965. — 209 с.
: зачем мне участвовать?
| Главная
Распечатать страницу | Войти | Регистрация
| Экспонент конференции: зачем мне участвовать? |
Делиться |
|
более Последние новости
20.12.20222023 Конференц-звонок NASW-TX для подачи предложений открыт до 8 февраля!
20.12.2022Предупреждение о защите интересов – свидетельствовать на собрании TSBSWE 06.01.2023
более Календарь
03.03.2023
День социальной защиты в Капитолии
12.10.2023 » 14.10.2023
Регистрация спонсоров и участников конференции 2023
Что такое Консультативный совет экспонентов и почему он важен Сегодняшняя картина событий?
Когда конференции переходят на виртуальные мероприятия, что происходит со спонсорами и экспонентами? Они по-прежнему являются важной частью экосистемы мероприятия, но теперь их роль в новом формате неясна. Многие из наших клиентов имеют давние отношения со спонсорами и экспонентами, которые знают мероприятие так же хорошо, как и люди, его планирующие.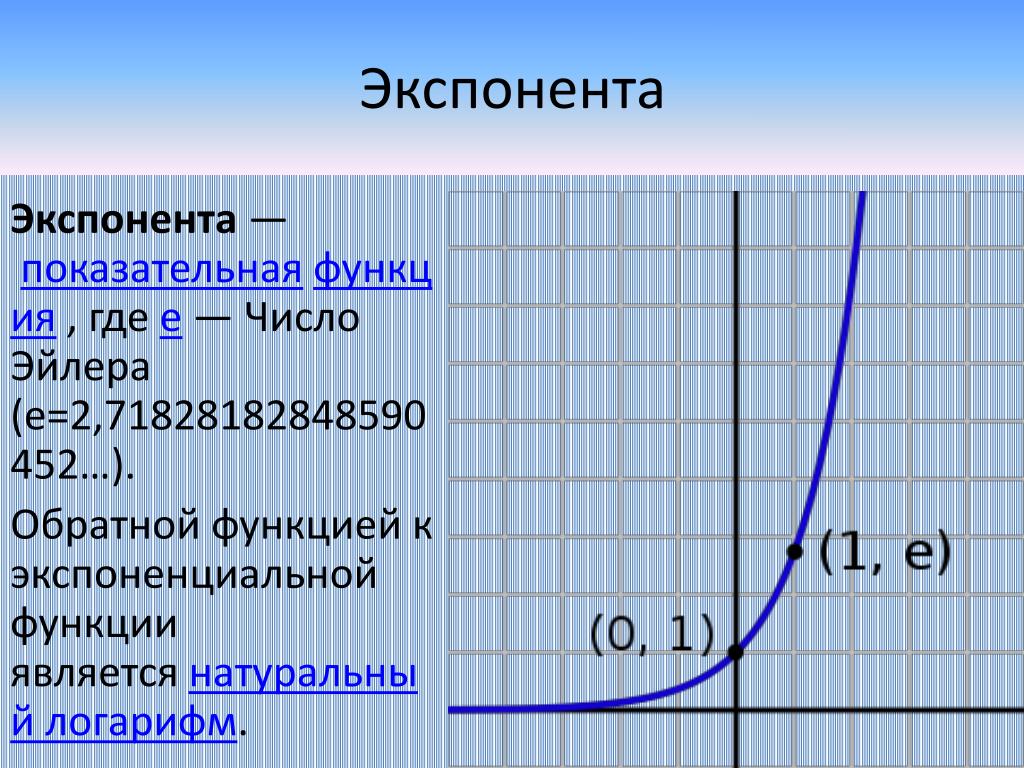
Должны ли вы обратиться к этим ключевым партнерам, чтобы узнать их мнение о том, как они должны участвовать в этом году, а также во время возвращения к физическим мероприятиям? Мы так думаем.
Необходимость постоянного диалога и двустороннего общения с экспонентами и спонсорами имеет решающее значение, особенно в связи с тем, что многие компании серьезно пересматривают свои спонсорские и выставочные планы.
Так как же создать среду, способствующую интерактивному общению и расширению возможностей для совместной работы и продвижения вперед?
Форма Консультативного совета экспонентов . За последние 25 с лишним лет я создал и возглавил множество консультативных советов экспонентов для наших клиентов, и сегодня они важнее, чем когда-либо.
Что такое Консультативный совет экспонентов (EAB)? Консультативный совет экспонентов представляет группу экспонентов и спонсоров, от малых до крупных компаний, которые собираются для обсуждения мероприятия.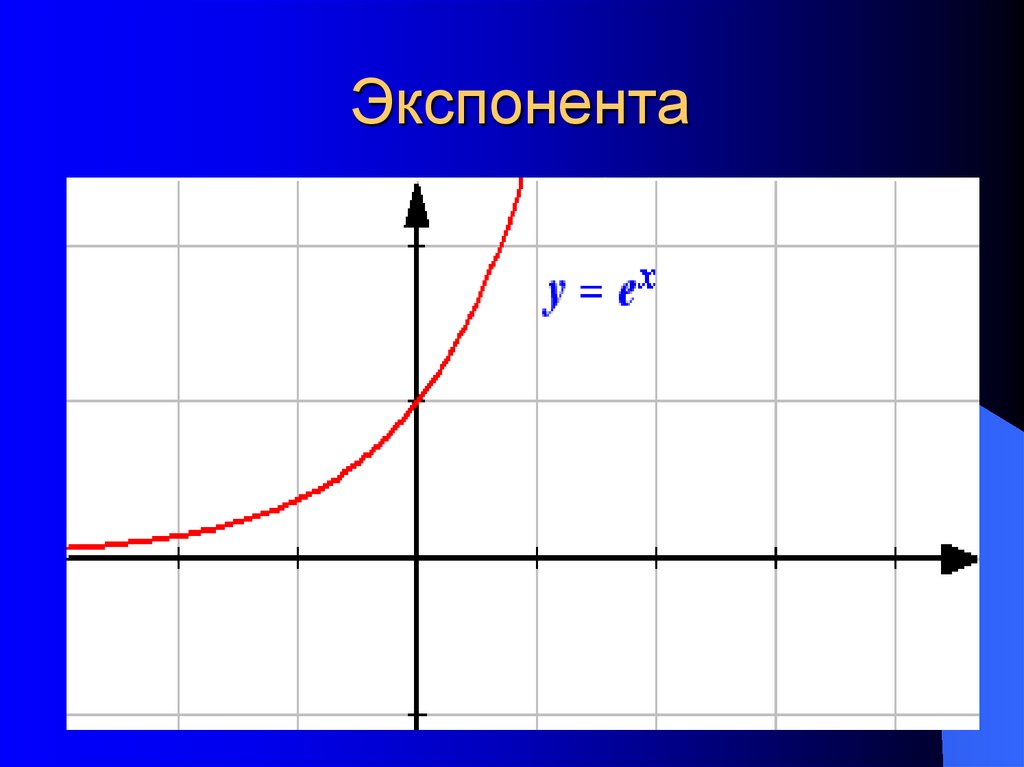 Группа обычно состоит из 25-50 участников при личном проведении встречи. Учитывая наш нынешний виртуальный мир, мы предлагаем провести серию встреч с 10 или около того экспонентами одновременно, чтобы каждый мог быть услышан.
Группа обычно состоит из 25-50 участников при личном проведении встречи. Учитывая наш нынешний виртуальный мир, мы предлагаем провести серию встреч с 10 или около того экспонентами одновременно, чтобы каждый мог быть услышан.
Какова цель Консультативного совета экспонентов? Формируя Консультативный совет экспонентов, вы создаете безопасное и здоровое место для сотрудничества спонсоров и экспонентов. Вы можете извлечь пользу из их опыта, мыслей и опасений, чтобы обсудить, что прошло хорошо, а что нет. Вы можете использовать их коллективный опыт и креативность, чтобы улучшить и сделать мероприятие более успешным в ближайшие годы. Это способ согласовать потребности и желания экспонентов с вашими потребностями как организатора мероприятия.
Как выбрать участников EAB? Вместе с вашим партнером по продажам и обслуживанию экспонентов составьте список приглашенных. Ищите участников из спонсирующих и экспонирующих компаний, которые сотрудничают и не стесняются делиться своими мыслями и идеями. Выберите экспонентов и спонсоров всех размеров и всех вертикалей (если применимо), чтобы получить самую широкую перспективу.
Выберите экспонентов и спонсоров всех размеров и всех вертикалей (если применимо), чтобы получить самую широкую перспективу.
Почему так важен Консультативный совет экспонентов? Сейчас как никогда важно, чтобы спонсоры и экспоненты чувствовали поддержку и были услышаны. Таким образом, включая спонсоров и экспонентов в процесс планирования мероприятия, они активно участвуют в формировании будущего мероприятия и в большей степени владеют им. Они также получают выгоду от участия — участие в EAB помогает им лучше планировать, составлять бюджет и использовать возможности, которые предлагает шоу.
Каков формат заседания Консультативного совета экспонентов? Открытые форумы обязательны. Каждому члену группы должна быть предоставлена возможность открыто обсудить свои опасения, тревоги и надежды по поводу конференции. Это поможет вам разработать формат шоу, пространство и спонсорские пакеты, которые наилучшим образом отражают все интересы для следующего мероприятия.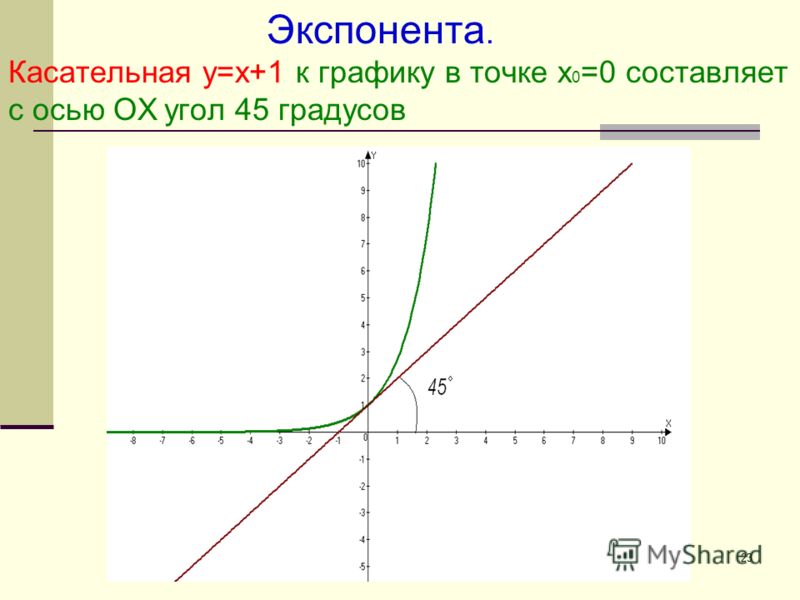 Мы советуем не отправлять опросы заранее, чтобы обеспечить плавный, неуправляемый разговор. Ваша команда может провести повторные звонки после заседания совета директоров, чтобы задать более подробные вопросы или обсудить предложенные планы.
Мы советуем не отправлять опросы заранее, чтобы обеспечить плавный, неуправляемый разговор. Ваша команда может провести повторные звонки после заседания совета директоров, чтобы задать более подробные вопросы или обсудить предложенные планы.
Как часто я должен проводить заседания Консультативного совета экспонентов? Целесообразно несколько встреч в год — они позволяют вам в течение года связываться со спонсорами, чтобы понять их текущее мнение. Это особенно важно, если они являются круглогодичными спонсорами.
Каковы преимущества EAB? Формирование группы, представленной вашими спонсорами и экспонентами, поможет подготовить ваше мероприятие ко всем результатам. Вместе вы можете создать гибкие взаимовыгодные пакеты. Они помогают установить стратегию ценообразования, обеспечивая понимание того, что они ценят, и ценность возможностей. Спонсоры и экспоненты чувствуют себя причастными к тому, как организовано мероприятие, и становятся послами мероприятия.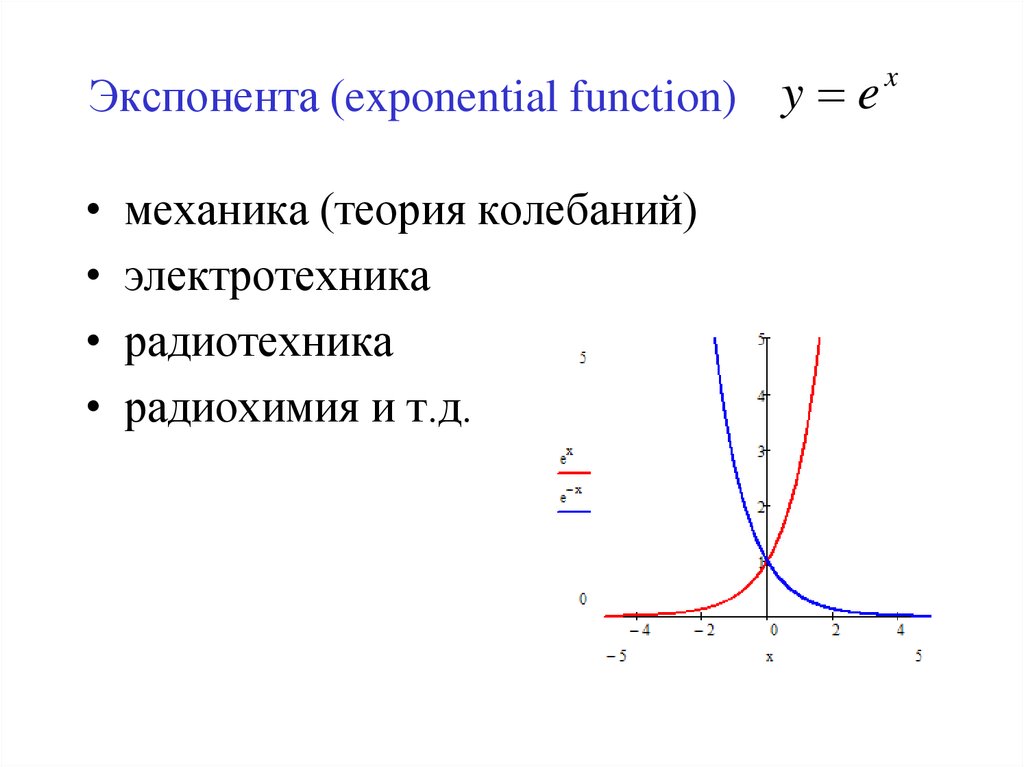

 Кроме того через экспоненту выражаются общие решения однородных дифференциальных уравнений.
Кроме того через экспоненту выражаются общие решения однородных дифференциальных уравнений.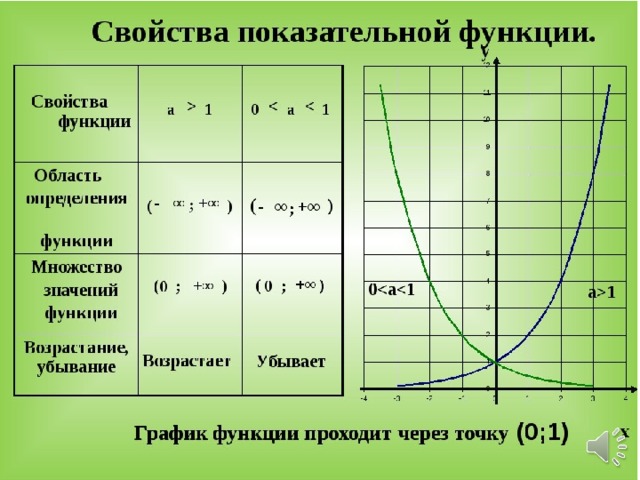
 1 Свойства
1 Свойства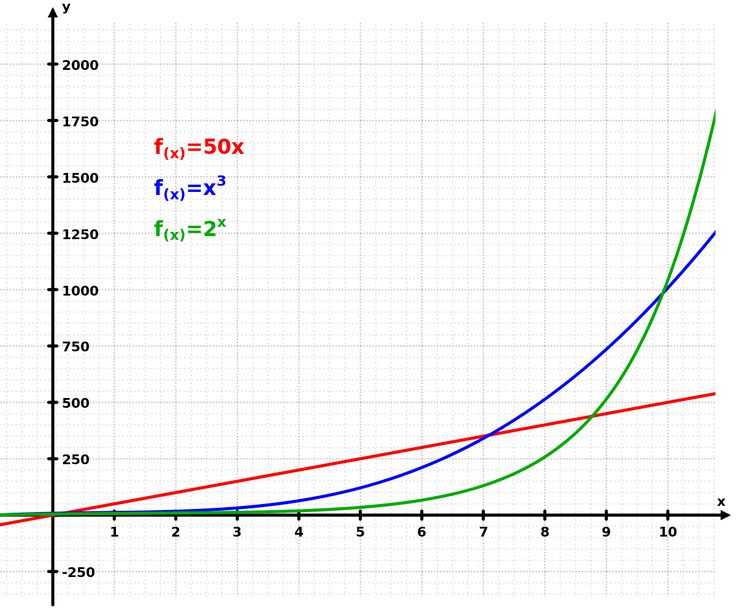

 Благодаря Early Bird Advertising ваше имя уже здесь.
Благодаря Early Bird Advertising ваше имя уже здесь.