Объем сферы через диаметр формула: Объем шара — формула и расчет онлайн

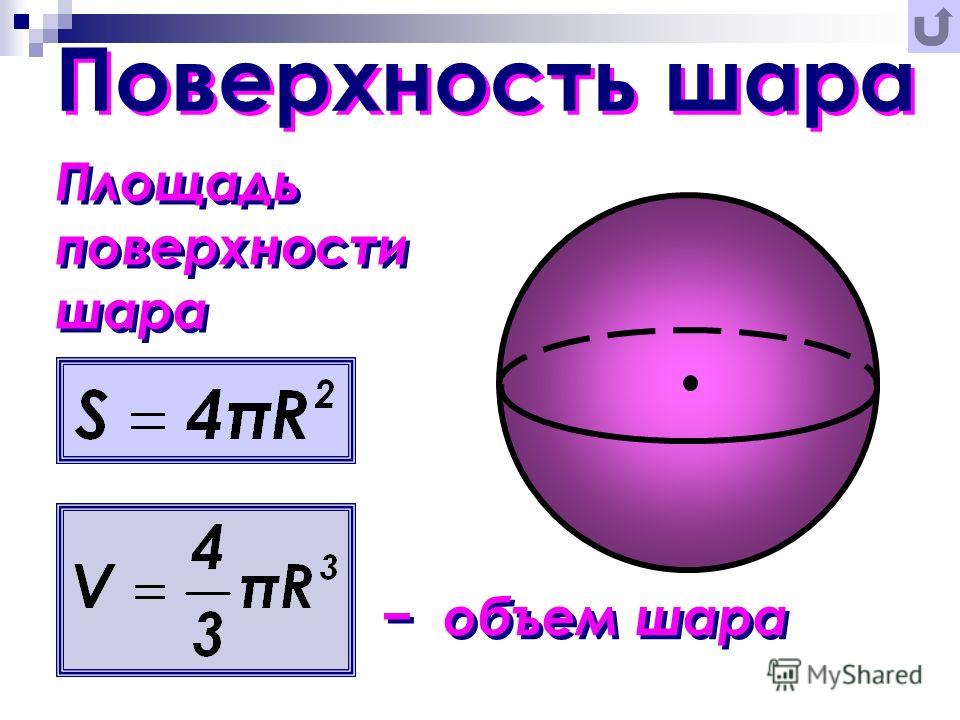
Диаметр шара: онлайн-калькуляторы и формулы

Шар, рассматриваемый в трёхмерном пространстве, представляет собой объёмную геометрическую фигуру. Любое правильное шаровидное тело состоит из совокупности точек эвклидова (3-хмерного) пространства, которые находятся на расстоянии от одной из них не далее заданного. Точка, относительно которой ведётся отсчёт и вокруг которой сосредоточены важные для этого пространственного тела отношения, получила название центра шара.

Его поверхность, являющаяся своего рода оболочкой, ограничивающей объём пространственного тела и представляющая совокупность равноудалённых от центра точек, названа сферой. Расстояние между центром и любой точкой сферы – это радиус шара. Образуется шар, в геометрии входящий в группу тел вращения, полным оборотом половины плоского круга вокруг своего диаметра, одновременно выступающего и диаметром шара.

Этот отрезок, называемый осью вращения, соединяет противолежащие точки на поверхности фигуры, называемые полюсами. Одновременно диаметр проходит через центральную точку шара.

• Диаметр шара через плошадь поверхности шара
• Диаметр шара через обьём шара

Способ вычисления диаметра шара при известном значении объёма фигуры

Диаметр шара, представляющий собой удвоенный радиус фигуры, может быть выведен из стандартной формулы, связывающей его с площадью поверхности: S = 4πR² или S = πD². Отсюда выводим диаметр:

D = √(S ⁄ π)

где S — площадь поверхности шара

Площадь (S):

мм²см²дм²м²

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Значение площади поверхности (сферы) конкретного шара S = 314.Тогда, принимая в качестве константы с точностью до сотых π = 3,14, вычисляем диаметр: D = √(314 ⁄ 3,14) = √100 = 10.

Способ нахождения диаметра шара при заданном значении его объёма

Объём шара связан с радиусом фигуры формулой V = 4 ⁄ 3 * πR³. Радиус представляет собой половину диаметра шара, то есть R = D ⁄ 2. Подставляя в формулу выраженный через диаметр радиус и выполняя преобразование для выделения диаметра, получаем следующее выражение: V = 4 ⁄ 3 * π(D ⁄ 2)³, V = 4 ⁄ 3* πD³ ⁄ 8, отсюда

D = ³√(6V / π)

где V — объём шара

Обьём (V):

мм³см³дм³м³

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Для примера примем значение объёма шара равным 11,304. Здесь, беря константу π с точностью до сотых (π = 3,14), получаем: D = ³√(6 * 11,304 / 3,14) или, выполняя вычисление D=6.

В природе этот пространственный объект имеет множество реальных аналогов, поэтому его свойства и параметры важны при решении массы научных задач в биологии, астрономии, физике. Ряд распространённых инженерных, строительных задач также проводится с использованием геометрических вычислений, связанных с шарообразными конструкциями. Нахождение диаметра шара – одна из них, и она может быть выполнена несколькими различными способами. Описание двух вариантов вычислений здесь и представлено.

основные формулы и пример их использования

В геометрии шар определяется как некое тело, представляющее собой совокупность всех точек пространства, которые располагаются от центра на расстоянии, не более заданного, называемого радиусом шара. Поверхность шара именуется сферой, а сам он образуется путем вращения полукруга около его диаметра, остающегося неподвижным.

С этим геометрическим телом очень часто сталкиваются инженеры-конструкторы и архитекторы, которым часто приходится вычислять объем шара . Скажем, в конструкции передней подвески подавляющего большинства современных автомобилей используются так называемые шаровые опоры, в которых, как нетрудно догадаться из самого названия, одними из основных элементов являются именно шары. С их помощью происходит соединение ступиц управляемых колес и рычагов. От того, насколько правильно будет вычислен их объем, во многом зависит не только долговечность этих узлов и правильность их работы, но и безопасность движения.

В технике широчайшее распространение получили такие детали, как шариковые подшипники, с помощью которых происходит крепление осей в неподвижных частях различных узлов и агрегатов и обеспечивается их вращение. Следует заметить, что при их расчете конструкторам требуется

найти объем шара (а точнее – шаров, помещаемых в обойму) с высокой степенью точности. Что касается изготовления металлических шариков для подшипников, то они производятся из металлической проволоки при помощи сложного технологического процесса, включающего в себя стадии формовки, закалки, грубой шлифовки, чистовой притирки и очистки. Кстати говоря, те шарики, которые входят в конструкцию всех шариковых ручек, изготавливаются по точно такой же технологии.

Достаточно часто шары используются и в архитектуре, причем там они чаще всего являются декоративными элементами зданий и других сооружений. В большинстве случаев они изготавливаются из гранита, что зачастую требует больших затрат ручного труда. Конечно, соблюдать столь высокую точность изготовления этих шаров, как тех, которые применяются в различных агрегатах и механизмах, не требуется.

Без шаров немыслима такая интересная и популярная игра, как бильярд. Для их производства используются различные материалы (кость, камень, металл, пластмассы) и используются различные технологические процессы. Одним из основных требований, предъявляемых к бильярдным шарам, является их высокая прочность и способность выдерживать высокие механические нагрузки (прежде всего, ударные). Кроме того, их поверхность должна представлять собой точную сферу для того, чтобы обеспечивалось плавное и ровное качение по поверхности бильярдных столов.

Наконец, без таких геометрических тел, как шары, не обходится ни одна новогодняя или рождественская елка. Изготавливаются эти украшения в большинстве случаев из стекла методом выдувания, и при их производстве наибольшее внимание уделяется не точности размеров, а эстетичности изделий.

Технологический процесс при этом практически полностью автоматизирован и вручную елочные шары только упаковываются.

Шар это геометрическое тело, образованное в результате вращения полукруга на оси своего диаметра.

Вычислить объем шара

Объем шара можно вычислить по формуле:

R – радиус шара

V – объем шара

Найти объем шара радиусом сантиметров.

Для того чтобы вычислить объем шара формула используется следующая:

где – искомый объем шара, – , – радиус.

Таким образом, при радиусе сантиметров объем шара равен:

V

3,14 × 103

= 4186,7

кубических сантиметров.

В геометрии шар определяется как некое тело, представляющее собой совокупность всех точек пространства, которые располагаются от центра на расстоянии, не более заданного, называемого радиусом шара.

Поверхность шара именуется сферой, а сам он образуется путем вращения полукруга около его диаметра, остающегося неподвижным.

С этим геометрическим телом очень часто сталкиваются инженеры-конструкторы и архитекторы, которым часто приходится вычислять объем шара . Скажем, в конструкции передней подвески подавляющего большинства современных автомобилей используются так называемые шаровые опоры, в которых, как нетрудно догадаться из самого названия, одними из основных элементов являются именно шары.

С их помощью происходит соединение ступиц управляемых колес и рычагов. От того, насколько правильно будет вычислен их объем, во многом зависит не только долговечность этих узлов и правильность их работы, но и безопасность движения.

В технике широчайшее распространение получили такие детали, как шариковые подшипники, с помощью которых происходит крепление осей в неподвижных частях различных узлов и агрегатов и обеспечивается их вращение.

Следует заметить, что при их расчете конструкторам требуется найти объем шара (а точнее – шаров, помещаемых в обойму) с высокой степенью точности. Что касается изготовления металлических шариков для подшипников, то они производятся из металлической проволоки при помощи сложного технологического процесса, включающего в себя стадии формовки, закалки, грубой шлифовки, чистовой притирки и очистки.

Кстати говоря, те шарики, которые входят в конструкцию всех шариковых ручек, изготавливаются по точно такой же технологии.

Достаточно часто шары используются и в архитектуре, причем там они чаще всего являются декоративными элементами зданий и других сооружений.

В большинстве случаев они изготавливаются из гранита, что зачастую требует больших затрат ручного труда. Конечно, соблюдать столь высокую точность изготовления этих шаров, как тех, которые применяются в различных агрегатах и механизмах, не требуется.

Без шаров немыслима такая интересная и популярная игра, как бильярд. Для их производства используются различные материалы (кость, камень, металл, пластмассы) и используются различные технологические процессы.

Одним из основных требований, предъявляемых к бильярдным шарам, является их высокая прочность и способность выдерживать высокие механические нагрузки (прежде всего, ударные). Кроме того, их поверхность должна представлять собой точную сферу для того, чтобы обеспечивалось плавное и ровное качение по поверхности бильярдных столов.

Наконец, без таких геометрических тел, как шары, не обходится ни одна новогодняя или рождественская елка. Изготавливаются эти украшения в большинстве случаев из стекла методом выдувания, и при их производстве наибольшее внимание уделяется не точности размеров, а эстетичности изделий.

Технологический процесс при этом практически полностью автоматизирован и вручную елочные шары только упаковываются.

Сфера — одно из простейших геометрических тел, в котором все точки ее поверхности находятся на одном и том же расстоянии от центра изображения. Расстояние от центра сферы до любой точки на ее поверхности называется радиусом.

Объем мяча

Диаметр шара называется удвоенным радиусом.

Как найти объем шара вокруг его радиуса

Если мы знаем радиус сферы, мы можем легко вычислить ее величину. Для этого умножьте куб на радиус и четверное число Pi, после чего результат будет разделен на три. Формула для определения объема шара по его радиусу выглядит следующим образом: .
Для тех, кто забыл, мы помним, что число Pi является фиксированным значением и равно 3.14.

Как найти объем сферы на диаметр

Если диаметр сферы известен из условий задачи, ее объем вычисляется по следующей формуле: , то есть.

число Pi следует умножить на диаметр диаметра, то полученный результат делится на 6.

Как определить массу шара

Масса тела — это физическая величина, указывающая степень ее инертности. Масса физического тела зависит от объема занимаемого пространства и плотности материала, из которого он собирается. Объем тела правильной формы (скажем, бить ) нетрудно рассчитать, и если материал, из которого он изготовлен, также известен, навалом это разрешено быть очень примитивным.

инструкции

первый Укажите сумму бить .

Как рассчитать объем шара

Для этого достаточно знать один из ваших параметров — радиус, диаметр, поверхность и т. Д. Скажите, знаете ли вы диаметр бить (d), его объем (V) разрешается определять, как одна шестая часть продукта с диаметром поднимается в кубе с числом Pi: V = π * d? / 6. Через радиус бить (r) объем выражается как одна треть произведения числа Pi, который в четыре раза увеличивается с радиусом, помещенным в куб: V = 4 * π * r? / 3.

второй подсчитывать навалом бить (m), умножьте его объем с великолепной плотностью вещества (p): m = p * V.

Если это материал бить не однородный, то мы должны взять среднюю плотность. В этой формуле мы заменяем объем бить через его известные параметры, допускается принимать по известному диаметру бить формула m = p * π * d? / 6 и для главного радиуса m = p * 4 * π * r? / 3.

третий Используйте для расчетов, например, типичный калькулятор программного обеспечения, который входит в базовую операционную систему Windows, любую сильную версию, используемую сегодня.

Самый простой способ начать — нажатием win + r, чтобы открыть типичный диалог для запуска программы, затем введите команду calc и нажмите кнопку OK. 3.

ПРОЕКТИРОВАНИЕ ВОДЫ И САНИТАЦИИ

E-mail: [email protected]

Время работы: Пн-Пт с 9-00 до 18-00 (без обеда)

Вычисление объема сферы через радиус или диаметр

Сфера — это геометрическое тело, представляющее собой совокупность всех точек пространства, расположенных от центра на некотором расстоянии.

Как рассчитать объем шара

Основной математической характеристикой шара является его радиус.

Количество шара — это количественная характеристика этого числа во Вселенной.

Формула расчета объема шара:

V = 4/3 * π * r 3

V = 1/6 * π * d 3

r — радиус сферы;
d — диаметр сферы.

См. Также статью о всех геометрических фигурах (линейный 1D, плоский 2D и 3D 3D).

Эта страница является самым простым веб-калькулятором для расчета объема шара по радиусу или диаметру.

Многие тела, которые мы встречаем в жизни или о которых слышали, имеют шарообразную форму, например футбольный мяч, падающая капля воды во время дождя или наша планета. В связи с этим является актуальным рассмотрение вопроса, как находить объем шара.

Фигура шар в геометрии

Перед тем как ответить на вопрос, шара, рассмотрим подробнее это тело. Некоторые люди путают его со сферой. Внешне они действительно похожи, однако шар — это заполненный внутри объект, сфера же представляет собой лишь внешнюю оболочку шара бесконечно малой толщины.

С точки зрения геометрии шар можно представить совокупностью точек, причем те из них, которые лежат на его поверхности (они образуют сферу), находятся на одинаковом расстоянии от центра фигуры. Это расстояние называют радиусом. По сути, радиус — это единственный параметр, с помощью которого можно описать любые свойства шара, такие как площадь его поверхности или объем.

На рисунке ниже приведен пример шара.

Если внимательно посмотреть на этот идеальный круглый объект, то можно догадаться, как его получить из обычного круга. Для этого достаточно вращать эту плоскую фигуру вокруг оси, совпадающей с его диаметром.

Одним из известных древних литературных источников, в котором достаточно подробно рассматриваются свойства этой объемной фигуры, является труд греческого философа Евклида — «Элементы».

Площадь поверхности и объем

Рассматривая вопрос, как находить объем шара, помимо этой величины, следует привести формулу для его площади, поскольку оба выражения можно связать друг с другом, как будет показано ниже.

Итак, чтобы вычислить объем шара, следует применить одну из следующих двух формул:

• V = 4/3 *pi * R3;
• V = 67/16 * R3.

Здесь R — радиус фигуры. Первая из приведенных формул является точной, однако, чтобы воспользоваться этим преимуществом, необходимо использовать соответствующее число знаков после запятой для числа pi. Второе выражение дает вполне хороший результат, отличаясь от первого всего на 0,03 %. Для ряда практических задач этой точности более чем достаточно.

Равна этой величине для сферы, то есть выражается формулой S = 4 * pi * R2. Если отсюда выразить радиус, а затем подставить его в первую формулу для объема, тогда получим: R = √ (S / (4 * pi)) = > V = S / 3 * √ (S / (4 * pi)).

Таким образом, мы рассмотрели вопросы, как найти объем шара через радиус и через площадь его поверхности. Эти выражения можно с успехом применять на практике. Далее в статье приведем пример их использования.

Задача с каплей дождя

Вода, когда находится в невесомости, приобретает форму шарообразной капли. Связано это с наличием сил поверхностного натяжения, которые стремятся минимизировать площадь поверхности. Шар, в свою очередь, обладает наименьшим ее значением среди всех геометрических фигур с одинаковой массой.

Во время дождя падающая капля воды находится в невесомости, поэтому ее формой является шар (здесь пренебрегаем силой сопротивления воздуха). Необходимо определить объем, площадь поверхности и радиус этой капли, если известно, что ее масса составляет 0,05 грамма.

Объем определить просто, для этого следует поделить известную массу на плотность H 2 O (ρ = 1 г/см 3). Тогда V = 0,05 / 1 = 0,05 см 3 .

Зная, как найти объем шара, следует выразить из формулы радиус и подставить полученное значение, имеем: R = ∛ (3 * V / (4 * pi)) = ∛ (3 * 0,05 / (4 * 3,1416)) = 0,2285 см.

Теперь значение радиуса подставляем в выражение для площади поверхности фигуры, получаем: S = 4 * 3,1416 * 0,22852 = 0,6561 см 2 .

Таким образом, зная, как находить объем шара, мы получили ответы на все вопросы задачи: R = 2,285 мм, S = 0,6561 см 2 и V = 0,05 см 3 .

Калькулятор объема сферы

Введение в калькулятор объема сферы

Объем сферы определяется ее формулой, в которой в основном рассматривается ее радиус (расстояние от середины сферы до любых точек на ее поверхности). Радиус в объеме сферы можно описать как множество всех точек, расположенных на расстоянии «r» от центра точки. Он абсолютно симметричен и не имеет ни ребер, ни вершин.

Формула для нахождения площади поверхности сферы приведена ниже: 92$$

Где,

• r – радиус площади поверхности сферы.
• π значение числа пи равно 3,14 или 3,14159. Это отношение длины окружности любого круга к диаметру круга.

Для расчета объема сферы этот калькулятор объема сферы выполняет формулу, требуя только значение радиуса. И вся формула решается этим онлайн-инструментом. Этот объемный сферический калькулятор упрощает вычисления и экономит время на выполнение ваших заданий или длительные вычисления по математике.

Что такое объем сферы?

Сфера — это множество точек в пространстве, расположенных на заданном расстоянии r от центра.

Объем — это пространство, занимаемое любым трехмерным телом. Объем измеряется в кубических единицах, таких как дюйм³, фут³, см³, м³ и т. д. Перед расчетом объема убедитесь, что все измерения должны быть в одних и тех же единицах.

Калькулятор объема конуса также можно найти на нашем портале.

Что такое Калькулятор объема сферы? 93$$

Преобразовав приведенную выше формулу, вы можете найти радиус:

$$r\;=\;\sqrt[3]{\frac{3v}{4π}}$$

, где v объем шара.

Поскольку все эти формулы разделены, может потребоваться время для их компиляции и поиска правильного ответа. Этот калькулятор площади поверхности сферы составляет эту формулу и дает ответ, решая уравнение с заданными значениями в формуле. Это передовая технология, которая использует фактическое значение числа пи и дает ответ.

Как пользоваться калькулятором объема сферы?

Калькулятор объема сферы прост и удобен в использовании. Просто выполните следующие шаги, чтобы рассчитать объем и окружность сферы.

Сначала вы должны ввести значение радиуса, затем есть кнопка с вкладкой вниз, где вы должны ввести единицу измерения радиуса. Вы увидите три варианта:

• Шаг №1: Введите значение радиуса.
• Шаг #2: Выберите значение радиуса в сантиметрах, метрах или миллиметрах.
• Шаг №3: Нажмите кнопку «РАССЧИТАТЬ».

После того, как вы нажмете кнопку «РАССЧИТАТЬ», калькулятор объема сферы немедленно рассчитает объем сферы и окружность.

Калькулятор разницы между длиной окружности сферы и вычислением объема сферы

Длина окружности сферы или сферы в 6,2832 раза больше радиуса. Окружность круга или сферы в 3,1416 раз больше диаметра.

Итак, между ними есть разница, и обе работают с разной функциональностью. Таким образом, чтобы ваша работа узнать из формулы, чтобы найти окружность сферы, которая является:

$$C\;=\;2πr$$

или

Используйте онлайн-калькулятор окружности для расчета окружности.

Что нужно помнить

• Площадь поверхности сферы = 4πr ²
• Объем сферы = 4/3 πr ³
• Вам нужно знать только радиус, чтобы рассчитать как объем, так и площадь сферы.
• Ответы на вопросы о площади поверхности всегда должны быть в квадратных единицах
• Ответы на задачи с объемом всегда должны быть в кубических единицах

Мы надеемся, что наш калькулятор объема сфер вам удался. Так что оставайтесь с нами, чтобы использовать лучшие онлайн-инструменты.

Внешние ресурсы:

• Как рассчитать объем сферы?
• Объем сферы в пересчете на диаметр.
• Формула объема сферы, примеры и приложения.
• Объем сферы с диаметром.

Объем сферы – определение, формула, вывод, примеры

Объем сферы – введение

Вы когда-нибудь задумывались: «Я могу нарисовать круг, но не могу нарисовать сферу? Почему?» Это связано с тем, что круг является двухмерной фигурой и не имеет объема, тогда как сфера представляет собой трехмерную форму без краев и вершин. Это означает, что его точки лежат в пространстве. Следовательно, вы не можете его нарисовать. По этой причине мы всегда находим объем сферы, чтобы рассчитать занимаемое ею пространство.

Прокрутите вперед, чтобы узнать о формуле объема сферы, выводе формулы объема сферы, некоторых решенных примерах, фактах и ​​многом другом.

Родственные игры

Каков объем шара?

Хотите знать, как мы можем найти объем сферы? Подождите, мы доберемся до этого, но сначала поймите, что означает объем сферы. Объем сферы является мерой трехмерного пространства, занимаемого сферой. Это зависит от радиуса сферы, который составляет половину диаметра (самая длинная линия внутри сферы, проходящая через центр сферы). 93)$

Интересные факты о сферах

Как насчет некоторых забавных и интересных фактов о сфере? Давайте взглянем!

1. Сфера симметричная и круглая. У него нет граней, углов или ребер.
2. Шары, шарики и даже Земля имеют форму сфер.
3. Полусфера — это точная половина сферы.
4. Все точки поверхности сферы находятся на одинаковом расстоянии «r» от центра.
5. Сфера появляется в природе, когда поверхность хочет быть как можно меньше. Например, если надуть воздушный шар, он естественным образом образует шар!

Заключение

Итак, как прошел урок? Мы надеемся, что вы получили четкое представление об объеме сфер.