Как исследовать функцию на ограниченность: 10.25. Исследуйте функцию на ограниченность:

ограниченность, существование наибольшего и наименьшего значений, существование промежуточных значений.

Определение. Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).

При этом не требуется непрерывность функции на концах отрезка или интервала, необходима только односторонняя непрерывность на концах отрезка или интервала.

Свойства функций, непрерывных на отрезке.

Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897)- немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке [a, b] выполняется условие –M  f(x)  M.

Доказательство этого свойства основано на том, что функция, непрерывная в точке х₀, ограничена в некоторой ее окрестности, а если разбивать отрезок [a, b] на бесконечное количество отрезков, которые “стягиваются” к точке х₀, то образуется некоторая окрестность точки х₀

.

Свойство 2: Функция, непрерывная на отрезке [a, b], принимает на нем наибольшее и наименьшее значения.

Т.е. существуют такие значения х₁ и х₂, что f(x₁) = m, f(x₂) = M, причем

m  f(x)  M

Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например – f(x) = sinx).

Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.

Свойство 3: (Вторая теорема Больцано – Коши). Функция, непрерывная на отрезке [a, b], принимает на этом отрезке все значения между двумя произвольными величинами.

Свойство 4: Если функция f(x) непрерывна в точке х = х₀, то существует некоторая окрестность точки х₀, в которой функция сохраняет знак.

Свойство 5: (Первая теорема Больцано (1781-1848) – Коши). Если функция f(x)- непрерывная на отрезке [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f(x) = 0.

Т.е. если sign(f(a))  sign(f(b)), то  х₀: f(x₀) = 0.

Определение. Функция f(x) называется равномерно непрерывной на отрезке [a, b], если для любого >0 существует >0 такое, что для любых точек х₁[a,b] и x₂[a,b] таких, что

х₂ – х₁< 

верно неравенство f(x₂) – f(x₁) < 

Отличие равномерной непрерывности от “обычной” в том, что для любого  существует свое , не зависящее от х, а при “обычной” непрерывности  зависит от  и х.

Свойство 6: Теорема Кантора (Кантор Георг (1845-1918)- немецкий математик). Функция, непрерывная на отрезке, равномерно непрерывна на нем.

(Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.)

Пример.

Функция непрерывна на интервале (0, а), но не является на нем равномерно непрерывной, т.к. существует такое число >0 такое, что существуют значения х₁ и х₂ такие, чтоf(x₁) – f(x₂)>,  — любое число при условии, что х₁ и х₂ близки к нулю.

Свойство 7: Если функция f(x) определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция х = g(y) тоже однозначна, монотонна и непрерывна.

Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.

в точке х = -1 функция непрерывна в точке х = 1 точка разрыва 1 – го рода

у

3

2

-4 -1 0 1 х

Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.

в точке х = 0 функция непрерывна в точке х = 1 точка разрыва 1 – го рода

у

2

1

- -/2 0 1 x

Ограниченные множества. Супремум и инфимум | матан #002

 

Определение. Множество $X\subset\mathbb{R}$ называется ограниченным сверху, если существует число $b$ такое, что $$\forall\,x\in X\ \to\ x\le b.$$ При этом говорят, что число $b$ ограничивает множество $X$ сверху.

 

Определение. Множество $X\subset\mathbb{R}$ называется ограниченным снизу, если существует число $a$ такое, что $$\forall\,x\in X\ \to\ x\ge a.$$ При этом говорят, что число $a$ ограничивает множество $X$ снизу

.

 

Определение. Множество $X\subset\mathbb{R}$ называется ограниченным, если оно ограничено и сверху и снизу.

 

Определение. Множество $X\subset\mathbb{R}$ называется неограниченным сверху, если оно не является ограниченным сверху.

 

Определение. Множество $X\subset\mathbb{R}$ называется неограниченным снизу, если оно не является ограниченным снизу.

 

Определение. Множество $X\subset\mathbb{R}$ называется неограниченным, если оно не является ограниченным.

 

Определение. Верхней гранью непустого множества $X\subset\mathbb{R}$ называется число $b$, удовлетворяющее условиям:

• $\forall\,x\in X\ \to\ x\le b$;
• $\forall\,b'<b\ \to\ \exists\,x\in X:\ x > b’$ 
  ($\forall\,\varepsilon>0\ \to\ \exists\,x\in X:\ x > b — \varepsilon$).
  \>

 

Определение. Нижней гранью непустого множества $X\subset\mathbb{R}$ называется число $a$, удовлетворяющее условиям:

• $\forall\,x\in X\ \to\ x\ge a$;
• $\forall\,a’> a\ \to\ \exists\,x\in X:\ x < a’$ 
  ($\forall\,\varepsilon>0\ \to\ \exists\,x\in X:\ x < a + \varepsilon$).

 

Верхняя и нижняя грани множества $X$ обозначаются символами $\sup X$, $\inf X$ соответственно.

 

Теорема (единственности). Числовое множество не может иметь больше одной верхней грани.

Доказательство. Допуская противное, предположим, что каждое из чисел $b$ и $b’$ ($b\ne b’$) является верхней гранью множества $X$. Пусть, для определённости, $b’ < b$. Но тогда $b’$ не является верхней гранью множества $X$.

Получили противоречие.Теорема доказана.

 

Замечание. Заметим, что в условиях теоремы не предполагается существование верхней грани. Теорема утверждает, что если верхняя грань существует, то она единственна. Значительно более глубокой является теорема о существовании верхней грани.

 

Теорема (о существовании верхней грани). Всякое непустое ограниченное сверху числовое множество имеет верхнюю грань.

Доказательство. Пусть $A$ — непустое ограниченное сверху множество. Рассмотрим непустое множество $B$, элементами которого являются все числа $b$, ограничивающие множество $A$ сверху. Тогда $$ \forall\,a\in A,\ \forall\,b\in B \ \to \ a\le b. $$ Из аксиомы непрерывности следует, что для некоторого $c\in\mathbb{R}$ $$ \forall\,a\in A,\ \forall\,b\in B \ \to \ a\le c\le b. $$ Покажем, что $\exists\,\sup A = c$.

Первое условие из определения верхней грани выполнено для $c$ в силу того, что $$ \forall\,a\in A\ \to \ a\le c.$$ Покажем, что выполняется и второе.

Пусть $c'<c$. Тогда $c’\not\in B$, так как $$\forall\,b\in B \ \to \ c\le b.$$ Следовательно, $c’$ не ограничивает множество $A$ сверху, то есть $$\exists\,x\in A:\ x > c’,$$так что второе условие также выполнено.

Следовательно, $c=\sup A$, и теорема доказана.

 

Определение. Расширенным множеством действительных чисел $\overline{\mathbb{R}}$} называется множество $$ \overline{\mathbb{R}} = \mathbb{R}\cup\{-\infty\}\cup\{+\infty\}. $$ То есть элементами множества $\overline{\mathbb{R}}$ являются все действительные числа и еще два символа: ${-\infty}$, ${+\infty}$.

 

В множестве $\overline{\mathbb{R}}$ не введены сложение и умножение, но имеется отношение порядка. Для двух элементов $a,b\in\overline{\mathbb{R}}$ в случае $a,b\in\mathbb{R}$ отношение порядка то же, что в $\mathbb{R}$. В других же случаях оно определено так: $$\forall\,a\in\mathbb{R}\ \to \ {-\infty}<a,\quad a<{+\infty};\qquad{-\infty}<{+\infty}.$$

 

Рассматривая множество $X\subset\mathbb{R}$ как подмножество расширенного множества действительных чисел ($X\subset\overline{\mathbb{R}}$), можно обобщить понятие $\sup X$. Это обобщающее определение будет отличаться от приведенных выше лишь тем, что в качестве $b$ можно брать не только число, но и элемент ${+\infty}$.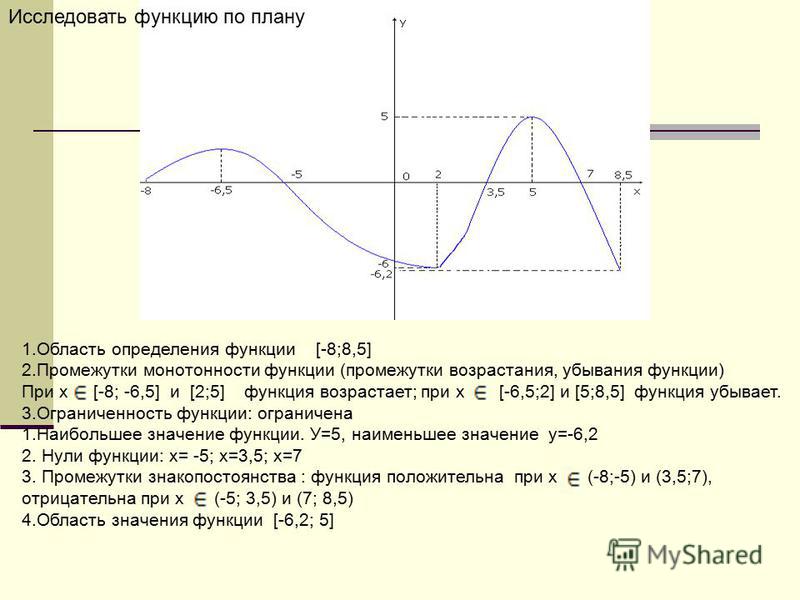

Тогда получим, что для непустого неограниченного сверху числовогомножества $X$ $$\sup X = +\infty.$$ 

Учитывая предыдущую теорему, получаем, что всякое непустое числовое множество имеет в расширенном множестве действительных чисел $\overline{\mathbb{R}}$ верхнюю грань.

 

Замечание. Все изложенные выше утверждения очевидным образом переносятся на понятие нижней грани.

pr.probability — Статистический тест на ограниченность ожидания

$\newcommand{\al}{\alpha} \newcommand{\de}{\дельта} \newcommand{\De}{\Дельта} \newcommand{\ep}{\эпсилон} \ новая команда {\ ga} {\ gamma} \newcommand{\Ga}{\Гамма} \newcommand{\la}{\лямбда} \newcommand{\Si}{\Sigma} \ новая команда {\ thh} {\ тета} \newcommand{\R}{\mathbb{R}} \newcommand{\E}{\operatorname{\mathsf E}} \newcommand{\PP}{\operatorname{\mathsf P}} \newcommand{\EE}{\mathcal E} \newcommand{\F}{\mathcal F} \newcommand{\I}{\mathcal I} \ новая команда {\ х} {\ mathbf х} \newcommand{\размер}{\текст{размер}} \newcommand{\pow}{\text{сила}} \newcommand{\st}{\text{глупый}}$

Интуитивно кажется ясным, что не может существовать «действительно хорошего» теста на конечность среднего, по той причине, что распределения с бесконечным средним значением или без него могут быть в определенном смысле близки к распределениям с конечным средним — и такие распределения было бы практически невозможно отличить друг от друга.

Сделаем строгое заявление по этому поводу. Пусть $\F$ и $\I$ обозначают множества всех вероятностных распределений $P$ (скажем, на $\R$) с конечными средними и с бесконечными/отсутствующими средними соответственно; таким образом, $\F\cup\I$ — это множество всех вероятностных распределений $P$ на $\R$. Скажем, нулевая гипотеза $H_0$ о неизвестном распределении $P$ состоит в том, что $P\in\F$ (то есть имеет конечное среднее значение), а альтернативная гипотеза $H_1$ состоит в том, что $P\in\I$ (что есть бесконечное/незначительное). 9{\otimes n}\de$, не отвергать нулевую гипотезу $H_0$, пока верна альтернативная гипотеза.

Всегда существует «глупый» тест $\de_\st$ такой, что $\de_\st(\x)=\al$ для всех выборок $\x$ (который полностью игнорирует «данные» $\x$ наблюдается), так что $\pow_P(\de_\st)=\al$ для всех $P$, откуда выполняется (1). Таким образом, для любого заданного $\al\in(0,1)$ всегда можно получить критерий уровня значимости $\al$, мощность которого равна $\al$ для всех распределений $P$; поскольку $\al$ обычно невелико, этот уровень мощности, конечно, довольно низок; то есть обычно вероятность ошибки II рода $1-\pow_P(\de_\st)=1-\al$ очень велика для «глупого» теста. J_j:=\begin{случаи} Q&\text{ если}j\in J, \\ P&\text{ если }j\notin J. \end{случаи} \end{уравнение*} Таким образом, (2) доказано. 9{-\al}\ell(x)$, где $F$ — кумулятивная функция распределения, а $\ell$ — медленно меняющаяся функция, $\al$ называется хвостовым индексом. Это должно иметь значение в вашей ситуации, так как среднее значение распределения будет конечным для $\al>1$ и бесконечным для $\al<1$. Google, например. «оценка индекса хвоста» или «оценка индекса хвоста в небольших выборках». Этот поток литературы, по-видимому, основан на статье Б. Хилла, где, согласно реферату, «не требуется принимать какую-либо глобальную форму для функции распределения, а просто форму поведения в хвост, где желательно сделать вывод».

Страница не найдена | CUHK Математика

1. Домашний
2. Страница не найдена

×

Сообщение об ошибке

Запрашиваемая вами страница не существует. Для вашего удобства был выполнен поиск по запросу курс ИЛИ конструктор ИЛИ 2021 ИЛИ math3050a ИЛИ учебник ИЛИ 209 ИЛИ pdf .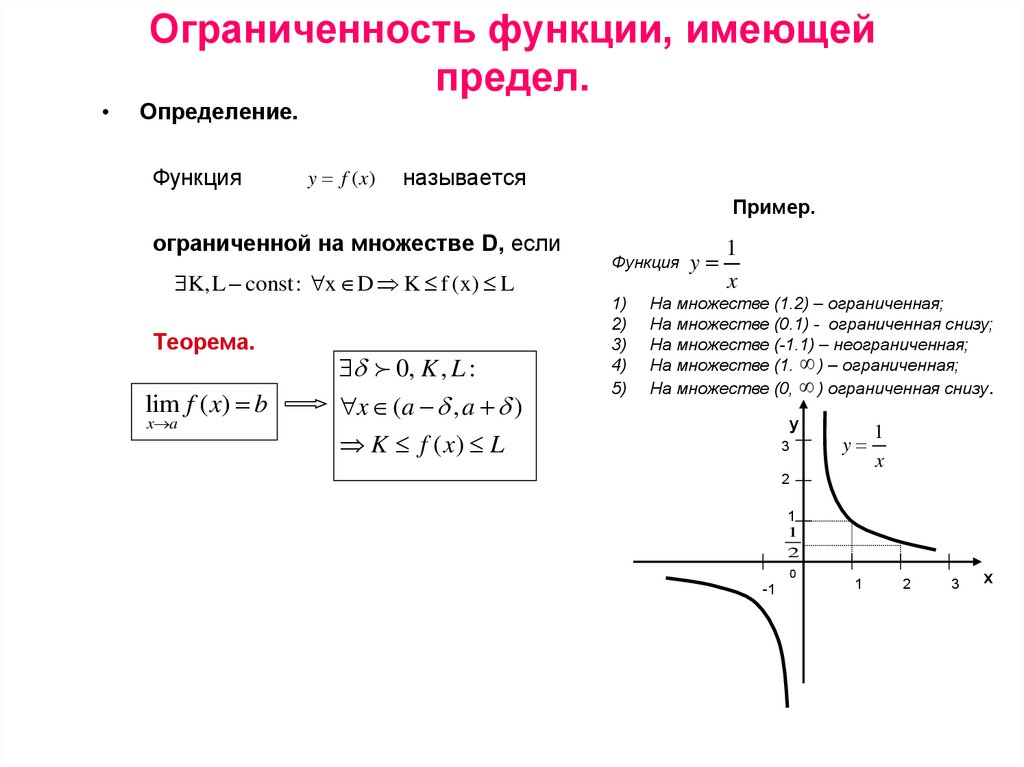

1. MATh3070A — Алгебраические структуры — 2016/17

   https://www.math.cuhk.edu.hk/course/1617/math3070a
   Курс Название: Алгебраические структуры Преподаватель: Доктор … 9Курс 0013 , включая конспекты лекций, промежуточные тесты, домашние задания и задания Tutorial , входит в объем выпускного экзамена. … лектор ЧАНЬ, Пин Шун Офис: LSB 209 Электронная почта: Преподавание …

2. SAYT1114 — Теория чисел и криптография — 2016/17

   https://www.math.cuhk.edu.hk/course/1617/sayt1114
   Курс Имя:  Теория чисел и криптография Преподаватель:  … Сигнал ливня действует в полдень, во второй половине дня tutorial сеансы также будут отменены. В ситуации, когда… Преподаватель ЧАНЬ, Пин Шун Офис: LSB 209 Электронная почта: Курс …

3. Проф.

   Джун ЗОУ https://www.math.cuhk.edu.hk/people/academic-staff/zou
   … SIAM J. Нумер. Анальный. 60 (2022), 751-780. (файл PDF ) (с Ят Тин Чоу и Фукун Хан) Метод прямой выборки… преобразования Радона. SIAM J. Imaging Sci. 14 ( 2021 ), 1004-1038. (файл PDF ) (с Ят Тин Чоу и Фукун Хан) А …

4. MATh3050A — Математический анализ I — 2017/18

   https://www.math.cuhk.edu.hk/course/1718/math3050a
   Курс Название: Математический анализ I Преподаватель: Проф. Чи Вай ЛЕУН Курс Год: 2017/18 Срок: 1       …

5. MATh2010B – Университетская математика – 2016/17

   https://www.math.cuhk.edu.hk/course/1617/math2010b
   Курс Имя: Университет Преподаватель математики: Доктор … весь семестр: Место проведения Ср. Общий … лектор ЧАНЬ, Пин-Шун Офис: LSB 209 Электронная почта: Время работы: по предварительной записи. …

6. MATh2010H — Университетская математика — 2019/20

   https://www.math.cuhk.edu.hk/course/1920/math2010h
   Курс Имя: Университет Преподаватель математики: Доктор Чанхао ЧЕН Курс Год: 2019/20 Срок: 2 …

7. Аспиранты-исследователи 2022-2023 Тестирование Страница

   https://www.math.cuhk.edu.hk/research-graduate-students-2022-2023-testing-page
   (по состоянию на 2021 /22 2-й срок) Мистер. … Г-н Ки Фунг ЧАН аспирант ( 2021 ) Офис: AB1 505 Тел.: 3943 4298 Электронная почта: … г-н Хайю ЧЕН Аспирант ( 2021 ) Офис: AB1 614 Тел.: 3943 4109 Электронная почта: …

8. UGED1533 — Математика в изобразительном искусстве — 2016/17

   https://www.math.cuhk.edu.hk/course/1617/uged1533
   Курс Название: Математика в изобразительном искусстве Преподаватель: Доктор Пинг Шун ЧАН Курс Год: 2016/17 Срок: 1 .

   No related posts.