Область допустимых значений
 Область допустимых значений алгебраического выражения (сокращенно ОДЗ) — это множество значений переменной, при которых это выражение определено.
Область допустимых значений алгебраического выражения (сокращенно ОДЗ) — это множество значений переменной, при которых это выражение определено.
В школьном курсе алгебры есть всего пять элементарных функций, которые имеют ограниченную область определения. Вот они:
1.  ОДЗ:
ОДЗ: 
Выражение, стоящее под знаком корня четной кратности, должно быть больше или равно нулю.
2.
 ОДЗ:
ОДЗ: 
Выражение, стоящее в знаменателе дроби, не может быть равно нулю.
3.  ОДЗ:
ОДЗ: 
Выражение, стоящее под знаком логарифма, должно быть строго больше нуля; выражение, стоящее в основании логарифма должно быть строго больше нуля и отлично от единицы.
4.  ,
,  ОДЗ:
ОДЗ: 
5. Есть две функции, которые содержат «скрытую» дробь:
 и
и 
6.  ОДЗ:
ОДЗ: 
Степень корня — натуральное число, отличное от 1.
Таким образом, функции  и
и  имеют разную область определения.
имеют разную область определения.
Если выражение содержит одну или несколько функций, которые определены на ограниченном множестве значений аргумента, то для того, чтобы найти ОДЗ выражения, нужно учесть все ограничения, которые накладываются этими функциями.
Чтобы найти область допустимых значений выражения, нужно исследовать, присутствуют ли в выражении функции, которые я перечислила выше. И по мере обнаружения этих функций, записывать задаваемые ими ограничения, двигаясь «снаружи» «внутрь».
Поясню на примере:
Найти область определения функции:

Чтобы найти область определения функции, нужно найти область допустимых значений выражения, которое стоит в правой части уравнения функции
Я специально выбрала «страшную», на первый взгляд, функцию, чтобы показать вам, на какие простые операции разбивается процесс нахождения области допустимых значений.
«Просканируем» выражение, стоящее в правой части равенства:

1. Мы видим дробь:

Знаменатель дроби не равен нулю. Записываем:

2. Мы видим в знаменателе логарифм:

Выражение, стоящее под знаком логарифма должно быть строго больше нуля; выражение, стоящее в основании логарифма должно быть строго больше нуля и отлично от единицы.
Записываем:



3.Мы видим квадратный корень:

Выражение, стоящее под знаком корня четной кратности, должно быть больше или равно нулю.
Записываем:

Теперь запишем все ограничения в систему неравенств:

Решение этой системы неравенств посмотрите в ВИДЕУРОКЕ:
И.В. Фельдман, репетитор по математике
Понятие функции является одним из основных в математике. Оно вводится следующим образом.
Пусть заданы два множества \(X\) и \(Y\). Если каждому элементу \(x\) из множества \(X\) поставлен в соответствие элемент \(y=f(x)\) множества \(Y\), то говорят, что на множестве \(X\) задана функция \(f\). При этом элемент \(x\) называется независимой переменной, а элемент \(y\) − зависимой переменной. В случае, когда \(x\ и \ y\) являются действительными числами, функцию \(y=f(x)\) можно представить в виде графика в декартовой системе координат \(Oxy\).
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции, то есть по оси абсцисс откладываются значения переменной \(x\), а по оси ординат откладываются значения переменной \(y\).
Область определения функции
Чтобы по графику функции \(y=f(x)\) найти ее область определения, нужно, двигаясь слева направо вдоль оси ОХ, записать все промежутки значений \(x\), на которых существует график функции.
Пример 1. Найти область определения функции: \(y=\sqrt{4x-x^3}\).
Решение: Поскольку квадратный корень можно извлекать только из неотрицательных чисел, то область определения данной функции задается неравенством \(4x-x^3\ge0 \Leftrightarrow x^3-4x\le0 \Rightarrow x(x-2)(x+2)\le0\).
Решая это неравенство с помощью метода интервалов, получим: \(x\in (-\infty; -] \cup [0;2]\).

Ответ: \(x\in (-\infty; -] \cup [0;2]\).
Множество значений функции \(E(y)\) – это множество всех значений, которые может принимать зависимая переменная \(y\).
Чтобы по графику функции \(y=f(x)\) найти ее множество значений, нужно, двигаясь снизу вверх вдоль оси OY, записать все промежутки значений \(y\), на которых существует график функции.
Пример 2. Найти множество значений функции: \(y = x^2 + 6x + 8\).
Решение: Поскольку \(y=x^2+6x+8=x^2+6x+9-1=(x+3)^2-1\ge-1\) и для каждого числа \(y\ge-1\) существуют решения уравнения \(x^2 + 6x + 8 = y\), определяемые формулой \(x_{1,2}=-3\pm \sqrt{y+1}\), то множеством значений функции \( y = x^2 + 6x + 8\) будет множество \([-1;+\infty)\).
Ответ: \(y\in [-1;+\infty)\).
Обратная функция
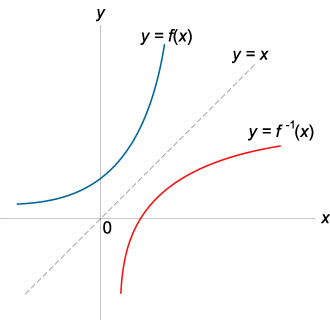
Пусть задана функция \(y=f(x)\). Чтобы найти обратную для нее функцию, надо из уравнения \(y=f(x)\) выразить переменную \(x\) через \(y\) и затем поменять переменные местами. Обратную функцию часто обозначают в виде \(y=f^{−1}(x)\). Исходная и обратная функции симметричны относительно прямой \(y=x\).
Чтобы для данной функции \(y = f(x)\) найти обратную, надо:
- В соотношении \(y = f(x)\) заменить \(x\) на \(y\), а \(y\) на \(x\): \(x = f(y)\).
- В полученном выражении \(x=f(y)\) выразить \(y\) через \( x\).
Например, \(y=3x-8: x=3y-8 \Rightarrow 3y=x+8 \Rightarrow y=\frac{x+8}3\).
Свойства взаимно обратных функций
Тождества. Пусть \(f\) и \(g\) – взаимно обратные функции. Это означает, что равенства \(y = f(x)\) и \(x = g(y)\) равносильны. Подставим одно из этих равенств в другое. Получим два тождества: \(f(g(y)) = y\) и \(g(f(x)) = x\).
Область определения. Пусть \(f\) и \(g\) – взаимно обратные функции. Область определения функции \(f\) совпадает с областью значений функции \(g\), и наоборот, область значений функции \(f\) совпадает с областью определения функции \(g\).
Монотонность. Если одна из взаимно обратных функций возрастает, то и другая возрастает. Аналогичное верно и для убывающих функций.
Графики. Графики взаимно обратных функций, построенные в одной и той же системе координат, симметричны друг другу относительно прямой \(y = x\).
Функция-это модель. Определим X, как множество значений независимой переменной // независимая -значит любая.
Функция это правило, с помощью которого по каждому значению независимой переменной из множества X можно найти единственное значение зависимой переменной. // т.е. для каждого х есть один у.
Из определения следует, что существует два понятия- независимая переменная (которую обозначаем х и она может принимать любые значения) и зависимая переменная (которую обозначаем y или f(х) и она высчитывается из функции, когда мы подставляем х).
НАПРИМЕР у=5+х
1. Независимая -это х, значит берем любое значение, пусть х=3
2. а теперь вычисляем у, значит у=5+х=5+3=8. (у зависима от х, потому что какой х подставим, такой у и получим)
Говорят, что переменная y функционально зависит от переменной x и обозначается это следующим образом: y = f (x).
НАПРИМЕР.
1.у=1/х. (наз.гипербола)
2. у=х^2. (наз. парабола)
3.у=3х+7. (наз. прямая)
4. у= √ х. (наз. ветвь параболы)
Независимая переменная (кот. мы обозначаем х) имеет название аргумент функции.
Область определения функции
Множество всех значений, которые принимает аргумент функции, называется областью определения функции и обозначается D (f) или D (y).
Рассмотрим D (у) для 1.,2.,3.,4.
1. D (у)= ( ∞; 0) и (0;+∞) //всё множество действительных чисел, кроме нуля.
2. D (у)= ( ∞; +∞)//всё мн-во действит.чисел
3. D (у)= ( ∞; +∞)//всё мн-во действит.чисел
4. D (у)= [0; +∞)// мн-во неотрицат.чисел
Зависимая переменная (кот. мы обозначаем у ) имеет название значение функции.
Область значения функции
Множество всех значений, которые может принять зависимая переменная, называется областью значения функции и обозначается E (f) или E (y).
Рассмотрим Е (у) для 1.,2.,3.,4.
1. Е (у)= ( ∞; 0) и (0;+∞) //всё множество действительных чисел, кроме нуля.
2. Е (у)= [0; +∞)// мн-во неотрицат.чисел
3. Е (у)=( ∞; +∞)//всё мн-во действит.чисел
4. Е (у)= [0; +∞)// мн-во неотрицат.чисел
Рассмотрим примеры подробнее
1) Постановка задачи. Найти функции у= 4х/(3+х)
Решение.
1. Найдем D (у)//т.е. какие значения может принимать х. для этого найдем ОДЗ(область допустимых значений дроби)
3+х≠0
х≠-3
значит D (у) данной функции ( ∞; 3) и (3;+∞)// всё множество действительных чисел, кроме 3.
2. Найдем Е (у)//т.е. какие значения может принимать у, при всех возможных х
решаем уравнение вида 4х/(3+х)=А, где А є Е (у)
(3+х)А=4х
3А=4х-хА
3А=х(4-А)
х=3А/(4-А)
значит Е (у) данной функции ( ∞; 4) и (4;+∞)// всё множество действительных чисел, кроме 4.
2) Постановка задачи. Найти D (у)и Е (у) функции, изображенной на графике
Область определения(значения х) смотрим по оси х- это промежуток [ 4; 7],
Областью значения(значения у) смотрим по оси у- это промежуток [ 4; 4].
Нужна помощь в учебе?
Предыдущая тема: Графический способ решения уравнений: алгоритм и примеры графиков
Следующая тема:   Свойства функции: разбираем на примере
Все неприличные комментарии будут удаляться.
Область определения функции | Онлайн калькулятор
Данный калькулятор позволит найти область определения функции онлайн.
Область определения функции y=f(x) – это множество всех значений аргумента x, на котором задана функция. Другими словами, это все x, для которых могут существовать значения y. На графике областью определения функции является промежуток, на котором есть график функции.
Область определения функции f(x), как правило, обозначается как D(f). Принадлежность к определенному множеству обозначается символом ∈, а X – область определения функции. Таким образом, формула x∈X означает, что множество всех значений x принадлежит к области определения функции f(x).
Приведем примеры определения основных элементарных функций. Областью определения постоянной функции y=f(x)=C является множество всех действительных чисел. Когда речь идет о степенной функции y=f(x)=xa, область определения зависит от показателя степени данной функции. При нахождении области определения функции y=f(x)= √(n&x) (корень n-ой степени) следует обращать внимание на четность или нечетность n.
Областью определения логарифмической функции являются все положительные действительные числа, и она не зависит от основания логарифма. Областью определения показательной функции, также как и у постоянной функции, является множество всех действительных чисел.
Областью определения сложных функций y=f1(f2(x)) является пересечение двух множеств: x∈D(f2) и множества всех x, для которых f2(x) ∈ D(f1). Следовательно, для того чтобы найти область определения сложной функции, необходимо решить систему неравенства.
Преимуществом онлайн калькулятора является то, что Вам нет необходимости знать и понимать, как находить область определения функции. Чтобы получить ответ, укажите функцию, для которой Вы хотите найти область определения. Основные примеры ввода функций и переменных для данного калькулятора указаны ниже.
Примеры функций: sqrt(16-ln(x^2))/sin(x)) или (5x^7+4x^6-3)/((3+2x-x^2)x^4)
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | cos((5pi)/12) | |
| 3 | Найти точное значение | arctan(-1) | |
| 4 | Найти точное значение | sin(75) | |
| 5 | Найти точное значение | arcsin(-1) | |
| 6 | Найти точное значение | sin(60 град. ) | |
| 7 | Найти точное значение | sin(pi/3) | |
| 8 | Найти точное значение | arctan(- квадратный корень 3) | |
| 9 | Найти точное значение | cos(pi/3) | |
| 10 | Найти точное значение | sin(0) | |
| 11 | Найти точное значение | cos(pi/12) | |
| 12 | Найти точное значение | sin(30 град. ) | |
| 13 | Найти точное значение | cos(60 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | sin((2pi)/3) | |
| 16 | Найти точное значение | arcsin(1) | |
| 17 | Найти точное значение | sin(pi/2) | |
| 18 | График | f(x)=x^2 | |
| 19 | Найти точное значение | sin(45 град. ) | |
| 20 | Найти точное значение | sin(15) | |
| 21 | Упростить | квадратный корень x^2 | |
| 22 | Найти точное значение | arccos(-1) | |
| 23 | Найти точное значение | tan(60 град. ) | |
| 24 | Найти точное значение | cos(45 град. ) | |
| 25 | Вычислить | логарифм по основанию 2 от 8 | |
| 26 | Упростить | квадратный корень x^3 | |
| 27 | Найти точное значение | arcsin(-1/2) | |
| 28 | Найти точное значение | cos(45) | |
| 29 | Найти точное значение | tan(30 град. ) | |
| 30 | Найти точное значение | tan(30) | |
| 31 | Найти точное значение | arcsin(1) | |
| 32 | Найти точное значение | arctan( квадратный корень 3) | |
| 33 | Найти точное значение | sin(45) | |
| 34 | Найти точное значение | cos(0) | |
| 35 | Найти точное значение | tan(45 град. ) | |
| 36 | Найти точное значение | arctan(0) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | График | y=x^2 | |
| 39 | Вычислить | натуральный логарифм 1 | |
| 40 | Вычислить | логарифм по основанию 3 от 81 | |
| 41 | Найти точное значение | cos(15) | |
| 42 | Вычислить | логарифм по основанию 5 от 125 | |
| 43 | Упростить | кубический корень из квадратного корня 64x^6 | |
| 44 | Вычислить | логарифм по основанию 3 от 81 | |
| 45 | Вычислить | логарифм по основанию 2 от 8 | |
| 46 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 47 | Найти точное значение | cos(75) | |
| 48 | Найти точное значение | sin((3pi)/4) | |
| 49 | Упростить | (1/( квадратный корень x+h)-1/( квадратный корень x))/h | |
| 50 | Упростить | кубический корень x^3 | |
| 51 | Найти точное значение | sin((5pi)/12) | |
| 52 | Найти точное значение | arcsin(-1/2) | |
| 53 | Найти точное значение | sin(30) | |
| 54 | Найти точное значение | sin(105) | |
| 55 | Найти точное значение | tan((3pi)/4) | |
| 56 | Упростить | квадратный корень s квадратный корень s^7 | |
| 57 | Упростить | корень четвертой степени x^4y^2z^2 | |
| 58 | Найти точное значение | sin(60) | |
| 59 | Найти точное значение | arccos(-( квадратный корень 2)/2) | |
| 60 | Найти точное значение | tan(0) | |
| 61 | Найти точное значение | sin((3pi)/2) | |
| 62 | Вычислить | логарифм по основанию 4 от 64 | |
| 63 | Упростить | корень шестой степени 64a^6b^7 | |
| 64 | Вычислить | квадратный корень 2 | |
| 65 | Найти точное значение | arccos(1) | |
| 66 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 67 | График | f(x)=2^x | |
| 68 | Найти точное значение | sin((3pi)/4) | |
| 69 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 70 | Вычислить | логарифм по основанию 5 от 25 | |
| 71 | Найти точное значение | tan(pi/2) | |
| 72 | Найти точное значение | cos((7pi)/12) | |
| 73 | Упростить | 1/( кубический корень от x^4) | |
| 74 | Найти точное значение | sin((5pi)/6) | |
| 75 | Преобразовать из градусов в радианы | 150 | |
| 76 | Найти точное значение | tan(pi/2) | |
| 77 | Множитель | x^3-8 | |
| 78 | Упростить | корень пятой степени 1/(x^3) | |
| 79 | Упростить | корень пятой степени 1/(x^3) | |
| 80 | Найти точное значение | sin(135) | |
| 81 | Преобразовать из градусов в радианы | 30 | |
| 82 | Преобразовать из градусов в радианы | 60 | |
| 83 | Найти точное значение | sin(120) | |
| 84 | Найти точное значение | tan((2pi)/3) | |
| 85 | Вычислить | -2^2 | |
| 86 | Найти точное значение | tan(15) | |
| 87 | Найти точное значение | tan((7pi)/6) | |
| 88 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 89 | Найти точное значение | sin(pi/2) | |
| 90 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 91 | Упростить | кубический корень 8x^7y^9z^3 | |
| 92 | Упростить | arccos(( квадратный корень 3)/2) | |
| 93 | Упростить | i^2 | |
| 94 | Вычислить | кубический корень 24 кубический корень 18 | |
| 95 | Упростить | квадратный корень 4x^2 | |
| 96 | Найти точное значение | sin((3pi)/4) | |
| 97 | Найти точное значение | tan((7pi)/6) | |
| 98 | Найти точное значение | tan((3pi)/4) | |
| 99 | Найти точное значение | arccos(-1/2) | |
| 100 | Упростить | корень четвертой степени x^4 |
3.1.1 Функция, область определения функции
Видеоурок: Функция. Область определения и область значений функции
Лекция: Функция, область определения функции
Функция — это некая модель, которая описывает зависимость независимой величины «х» от «у». «х» — это произвольная величина, которая еще называется аргументом, переменной, которая влияет на значение функции «у».
Функция обозначается следующим образом: y = f(x).
Значения, которые может принимать аргумент для конкретной функции, называются областью определения функции (D(f)).
То есть на конкретном промежутке функция может существовать. Значения, которые может принимать функция для конкретной области определения, называются областью значения функции (E(f)). То есть, иными слова, D(f) — это значение аргумента, а E(f) — значение функции.
Графиком любой функции называется множество точек на координатной плоскости, которые соответствуют функциональной зависимости.
Обратите внимание, функцией и графиком функции называется только та зависимость, в которой одному значению аргумента соответствует единственное значение функции.
Область определения функции зависит от знаний свойств функций.
Например, областью значения выражения, стоящего под знаком корня, не может быть отрицательным, а значение выражения, которое стоит в знаменателе, не может равняться нулю.
Рассмотрим область определения функции на конкретных примерах:
1. Функция:

Данная функция называется гиперболой.
Данная функция существует при всех «х», кроме х = 0, значит, D(f) = (-∞; 0) и (0; ∞).
2. Функция:

Данная функция называется параболой.
Данная функция существует при всех «х», значит, D(f) = (-∞; ∞).
3. Функция:

Данная функция называется линейной.
Данная функция существует при всех «х», значит, D(f) = (-∞; ∞).
4. Функция

Данная функция имеет вид ветви параболы.
Данная функция существует при неотрицательных «х», значит, D(f) = [0; ∞).
Тестирование онлайн
Понятие функции
Зависимость одной переменной от другой называется функциональной зависимостью. Зависимость переменной y от переменной x называется функцией, если каждому значению x соответствует единственное значение y.
Обозначение:
Переменную x называют независимой переменной или аргументом, а переменную y — зависимой. Говорят, что y является функцией от x. Значение y, соответствующее заданному значению x, называют значением функции.
Все значения, которые принимает x, образуют область определения функции; все значения, которые принимает y, образуют множество значений функции.
Обозначения:
D(f) — значения аргумента. E(f) — значения функции. Если функция задана формулой, то считают, что область определения состоит из всех значений переменной, при которых эта формула имеет смысл.
Графиком функции называется множество всех точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции. Если некоторому значению x=x0 соответствуют несколько значений (а не одно) y, то такое соответствие не является функцией. Для того чтобы множество точек координатной плоскости являлось графиком некоторой функции, необходимо и достаточно, чтобы любая прямая параллельная оси Оу, пересекалась с графиком не более чем в одной точке.
Способы задания функции
1) Функция может быть задана аналитически в виде формулы. Например,
2) Функция может быть задана таблицей из множества пар (x; y).
3) Функция может быть задана графически. Пары значений (x; y) изображаются на координатной плоскости.
Монотонность функции
Функция f(x) называется возрастающей на данном числовом промежутке, если большему значению аргумента соответствует большее значение функции. Представьте, что некоторая точка движется по графику слева направо. Тогда точка будет как бы «взбираться» вверх по графику.
Функция f(x) называется убывающей на данном числовом промежутке, если большему значению аргумента соответствует меньшее значение функции. Представьте, что некоторая точка движется по графику слева направо. Тогда точка будет как бы «скатываться» вниз по графику.
Функция, только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке.
Нули функции и промежутки знакопостоянства
Значения х, при которых y=0, называется нулями функции. Это абсциссы точек пересечения графика функции с осью Ох.
Такие промежутки значений x, на которых значения функции y либо только положительные, либо только отрицательные, называются промежутками знакопостоянства функции.
Четные и нечетные функции
Четная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0), то есть если точка a принадлежит области определения, то точка -a также принадлежит области определения.
2) Для любого значения x, принадлежащего области определения , выполняется равенство f(-x)=f(x)
3) График четной функции симметричен относительно оси Оу.
Нечетная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0).
2) для любого значения x, принадлежащего области определения , выполняется равенство f(-x)=-f(x)
3) График нечетной функции симметричен относительно начала координат (0; 0).
Не всякая функция является четной или нечетной. Функции общего вида не являются ни четными, ни нечетными.
Периодические функции
Функция f называется периодической, если существует такое число , что при любом x из области определения выполняется равенство f(x)=f(x-T)=f(x+T). T — это период функции.
Всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривают наименьший положительный период.
Значения периодической функции через промежуток, равный периоду, повторяются. Это используют при построении графиков.
90000 function — Scope and Return values in Python 90001 Stack Overflow 90002 90003 Products 90004 90003 Customers 90004 90003 Use cases 90004 90009 90010 90003 Stack Overflow Public questions and answers 90004 90003 Teams Private questions and answers for your team 90004 90003 Enterprise Private self-hosted questions and answers for your enterprise 90004 90003 Jobs Programming and related technical career opportunities 90004 90003 Talent Hire technical talent 90004 90003 Advertising Reach developers worldwide 90004 90009 .90000 15 Scoping Rules of R 90001 90002 A Diversion on Binding Values to Symbol 90003 90004 Watch a video of this section 90005 90004 How does R know which value to assign to which symbol? When I type 90005 90004 how does R know what value to assign to the symbol 90009 lm 90010? Why does not it give it the value of 90009 lm 90010 that is in the 90009 stats 90010 package? 90005 90004 When R tries to bind a value to a symbol, it searches through a series of 90009 environments 90010 to find the appropriate value.When you are working on the command line and need to retrieve the value of an R object, the order in which things occur is roughly 90005 90020 90021 Search the global environment (i.e. your workspace) for a symbol name matching the one requested. 90022 90021 Search the namespaces of each of the packages on the search list 90022 90025 90004 The search list can be found by using the 90009 search () 90010 function. 90005 90004 The 90031 global environment 90032 or the user’s workspace is always the first element of the search list and the 90009 base 90010 package is always the last.For better or for worse, the order of the packages on the search list matters, particularly if there are multiple objects with the same name in different packages. 90005 90004 Users can configure which packages get loaded on startup so if you are writing a function (or a package), you can not assume that there will be a set list of packages available in a given order. When a user loads a package with 90009 library () 90010 the namespace of that package gets put in position 2 of the search list (by default) and everything else gets shifted down the list.90005 90004 Note that R has separate namespaces for functions and non-functions so it’s possible to have an object named 90009 c 90010 and a function named 90009 c () 90010. 90005 90002 Scoping Rules 90003 90004 The scoping rules for R are the main feature that make it different from the original S language (in case you care about that). This may seem like an esoteric aspect of R, but it’s one of its more interesting and useful features. 90005 90004 The scoping rules of a language determine how a value is associated with a 90031 free variable 90032 in a function.R uses 90031 lexical scoping 90032 or 90031 static scoping 90032. An alternative to lexical scoping is 90031 dynamic scoping 90032 which is implemented by some languages. Lexical scoping turns out to be particularly useful for simplifying statistical computations 90005 90004 Related to the scoping rules is how R uses the 90031 search list 90032 to bind a value to a symbol 90005 90004 Consider the following function. 90005 90004 This function has 2 formal arguments 90009 x 90010 and 90009 y 90010.In the body of the function there is another symbol 90009 z 90010. In this case 90009 z 90010 is called a 90031 free variable 90032. 90005 90004 The scoping rules of a language determine how values are assigned to free variables. Free variables are not formal arguments and are not local variables (assigned insided the function body). 90005 90004 Lexical scoping in R means that 90005 90082 90004 90031 the values of free variables are searched for in the environment in which the function was defined 90032.90005 90087 90004 Okay then, what is an environment? 90005 90004 An 90031 environment 90032 is a collection of (symbol, value) pairs, i.e. 90009 x 90010 is a symbol and 90009 3.14 90010 might be its value. Every environment has a parent environment and it is possible for an environment to have multiple «children». The only environment without a parent is the 90031 empty environment 90032. 90005 90004 A function, together with an environment, makes up what is called a 90031 closure 90032 or 90031 function closure 90032.Most of the time we do not need to think too much about a function and its associated environment (making up the closure), but occasionally, this setup can be very useful. The function closure model can be used to create functions that «carry around» data with them. 90005 90004 How do we associate a value to a free variable? There is a search process that occurs that goes as follows: 90005 90108 90021 If the value of a symbol is not found in the environment in which a function was defined, then the search is continued in the 90031 parent environment 90032.90022 90021 The search continues down the sequence of parent environments until we hit the 90031 top-level environment 90032; this usually the global environment (workspace) or the namespace of a package. 90022 90021 After the top-level environment, the search continues down the search list until we hit the 90031 empty environment 90032. 90022 90121 90004 If a value for a given symbol can not be found once the empty environment is arrived at, then an error is thrown. 90005 90004 One implication of this search process is that it can be affected by the number of packages you have attached to the search list.The more packages you have attached, the more symbols R has to sort through in order to assign a value. That said, you’d have to have a pretty large number of packages attached in order to notice a real difference in performance. 90005 90002 Lexical Scoping: Why Does It Matter? 90003 90004 Watch a video of this section 90005 90004 Typically, a function is defined in the global environment, so that the values of free variables are just found in the user’s workspace. This behavior is logical for most people and is usually the «right thing» to do.However, in R you can have functions defined 90031 inside other functions 90032 (languages like C do not let you do this). Now things get interesting-in this case the environment in which a function is defined is the body of another function! 90005 90004 Here is an example of a function that returns another function as its return value. Remember, in R functions are treated like any other object and so this is perfectly valid. 90005 90004 The 90009 make.power () 90010 function is a kind of «constructor function» that can be used to construct other functions.90005 90004 Let’s take a look at the 90009 cube () 90010 function’s code. 90005 90004 Notice that 90009 cube () 90010 has a free variable 90009 n 90010. What is the value of 90009 n 90010 here? Well, its value is taken from the environment where the function was defined. When I defined the 90009 cube () 90010 function it was when I called 90009 make.power (3) 90010, so the value of 90009 n 90010 at that time was 3. 90005 90004 We can explore the environment of a function to see what objects are there and their values.90005 90004 We can also take a look at the 90009 square () 90010 function. 90005 90002 Lexical vs. Dynamic Scoping 90003 90004 We can use the following example to demonstrate the difference between lexical and dynamic scoping rules. 90005 90004 What is the value of the following expression? 90005 90004 With lexical scoping the value of 90009 y 90010 in the function 90009 g 90010 is looked up in the environment in which the function was defined, in this case the global environment, so the value of 90009 y 90010 is 10.With dynamic scoping, the value of 90009 y 90010 is looked up in the environment from which the function was 90031 called 90032 (sometimes referred to as the 90031 calling environment 90032). In R the calling environment is known as the 90031 parent frame 90032. In this case, the value of 90009 y 90010 would be 2. 90005 90004 When a function is 90031 defined 90032 in the global environment and is subsequently 90031 called 90032 from the global environment, then the defining environment and the calling environment are the same.This can sometimes give the appearance of dynamic scoping. 90005 90004 Consider this example. 90005 90004 Here, 90009 y 90010 is defined in the global environment, which also happens to be where the function 90009 g () 90010 is defined. 90005 90004 There are numerous other languages that support lexical scoping, including 90005 90108 90021 Scheme 90022 90021 Perl 90022 90021 Python 90022 90021 Common Lisp (all languages converge to Lisp, right?) 90022 90121 90004 Lexical scoping in R has consequences beyond how free variables are looked up.In particular, it’s the reason that all objects must be stored in memory in R. This is because all functions must carry a pointer to their respective defining environments, which could be 90031 anywhere 90032. In the S language (R’s close cousin), free variables are always looked up in the global workspace, so everything can be stored on the disk because the «defining environment» of all functions is the same. 90005 90002 Application: Optimization 90003 90004 Watch a video of this section 90005 90004 90223 NOTE 90224: This section requires some knowledge of statistical inference and modeling.If you do not have such knowledge, feel free to skip this section. 90005 90004 Why is any of this information about lexical scoping useful? 90005 90004 Optimization routines in R like 90009 optim () 90010, 90009 nlm () 90010, and 90009 optimize () 90010 require you to pass a function whose argument is a vector of parameters (e.g. a log-likelihood, or a cost function). However, an objective function that needs to be minimized might depend on a host of other things besides its parameters (like data).When writing software which does optimization, it may also be desirable to allow the user to hold certain parameters fixed. The scoping rules of R allow you to abstract away much of the complexity involved in these kinds of problems. 90005 90004 Here is an example of a «constructor» function that creates a negative log-likelihood function that can be minimized to find maximum likelihood estimates in a statistical model. 90005 90004 90223 Note 90224: Optimization functions in R 90031 minimize 90032 functions, so you need to use the negative log-likelihood.90005 90004 Now we can generate some data and then construct our negative log-likelihood. 90005 90004 Now that we have our 90009 nLL () 90010 function, we can try to minimize it with 90009 optim () 90010 to estimate the parameters. 90005 90004 You can see that the algorithm converged and obtained an estimate of 90009 mu 90010 and 90009 sigma 90010. 90005 90004 We can also try to estimate one parameter while holding another parameter fixed. Here we fix 90009 sigma 90010 to be equal to 2.90005 90004 Because we now have a one-dimensional problem, we can use the simpler 90009 optimize () 90010 function rather than 90009 optim () 90010. 90005 90004 We can also try to estimate 90009 sigma 90010 while holding 90009 mu 90010 fixed at 1. 90005 90002 Plotting the Likelihood 90003 90004 Another nice feature that you can take advantage of is plotting the negative log-likelihood to see how peaked or flat it is. 90005 90004 Here is the function when 90009 mu 90010 is fixed.90005 90004 90005 90004 Here is the function when 90009 sigma 90010 is fixed. 90005 90004 90005 90002 Summary 90003 90108 90021 Objective functions can be «built» which contain all of the necessary data for evaluating the function 90022 90021 No need to carry around long argument lists — useful for interactive and exploratory work. 90022 90021 Code can be simplified and cleaned up 90022 90021 Reference: Robert Gentleman and Ross Ihaka (2000). «Lexical Scope and Statistical Computing,» 90031 JCGS 90032, 9, 491-508.90022 90121 .90000 What’s the difference of name scope and a variable scope in tensorflow? 90001 Stack Overflow 90002 90003 Products 90004 90003 Customers 90004 90003 Use cases 90004 90009 90010 90003 Stack Overflow Public questions and answers 90004 90003 Teams Private questions and answers for your team 90004 90003 Enterprise Private self-hosted questions and answers for your enterprise 90004 90003 Jobs Programming and related technical career opportunities 90004 90003 Talent Hire technical talent 90004 90003 Advertising Reach developers worldwide 90004 90009 90024 Loading … 90025 90002 90003 90004 90003 Log in 90004 90009.90000 function — Return the enclosing scope variables in Python 90001 Stack Overflow 90002 90003 Products 90004 90003 Customers 90004 90003 Use cases 90004 90009 90010 90003 Stack Overflow Public questions and answers 90004 90003 Teams Private questions and answers for your team 90004 90003 Enterprise Private self-hosted questions and answers for your enterprise 90004 90003 Jobs Programming and related technical career opportunities 90004 90003 Talent Hire technical talent 90004 90003 Advertising Reach developers worldwide 90004 90009 .