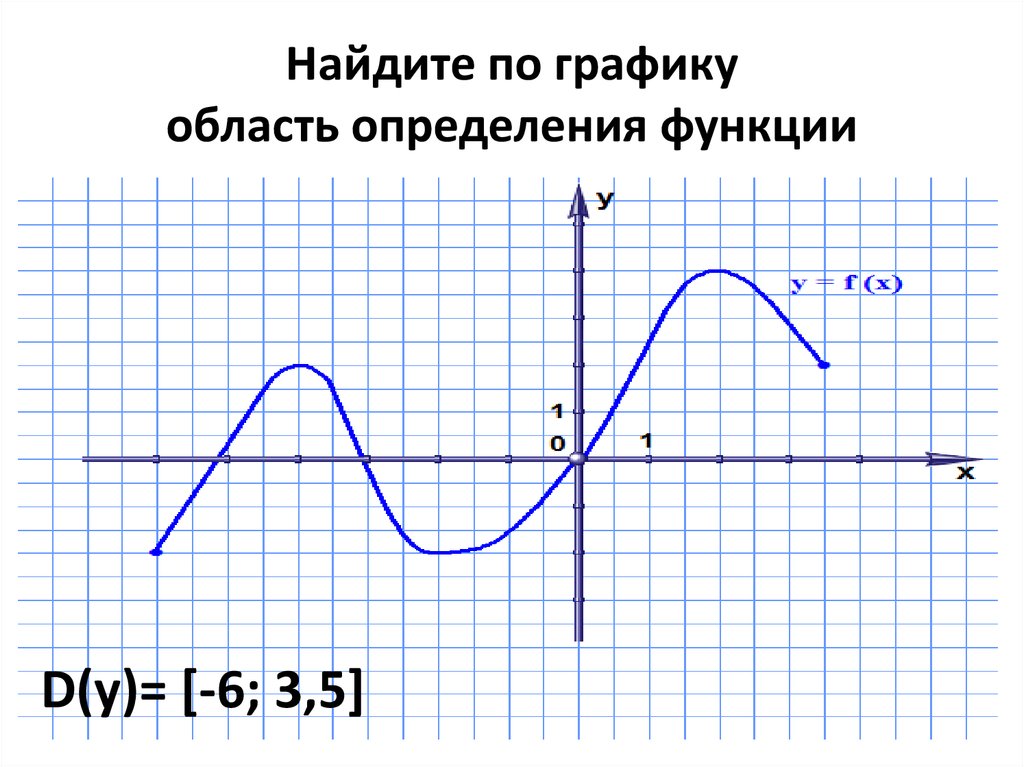
Исследование графика функции. Минимум и максимум
На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:
- область определения функции;
- область значений функции;
- нули функции;
- промежутки возрастания и убывания;
- точки максимума и минимума;
- наибольшее и наименьшее значение функции на отрезке.
Уточним терминологию:
Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось .
Ось ординат — вертикальная ось, или ось .
Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается .
Другими словами, мы сами выбираем , подставляем в формулу функции и получаем .
Область определения функции — множество тех (и только тех) значений аргумента , при которых функция существует.
Обозначается: или .
На нашем рисунке область определения функции — это отрезок . Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.
Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок — от самого нижнего до самого верхнего значения .
Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки и .
Значения функции положительны там, где . На нашем рисунке это промежутки и .
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от до .
Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества можно взять отрезок , интервал , объединение промежутков или всю числовую прямую.
Функция возрастает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Иными словами, чем больше , тем больше , то есть график идет вправо и вверх.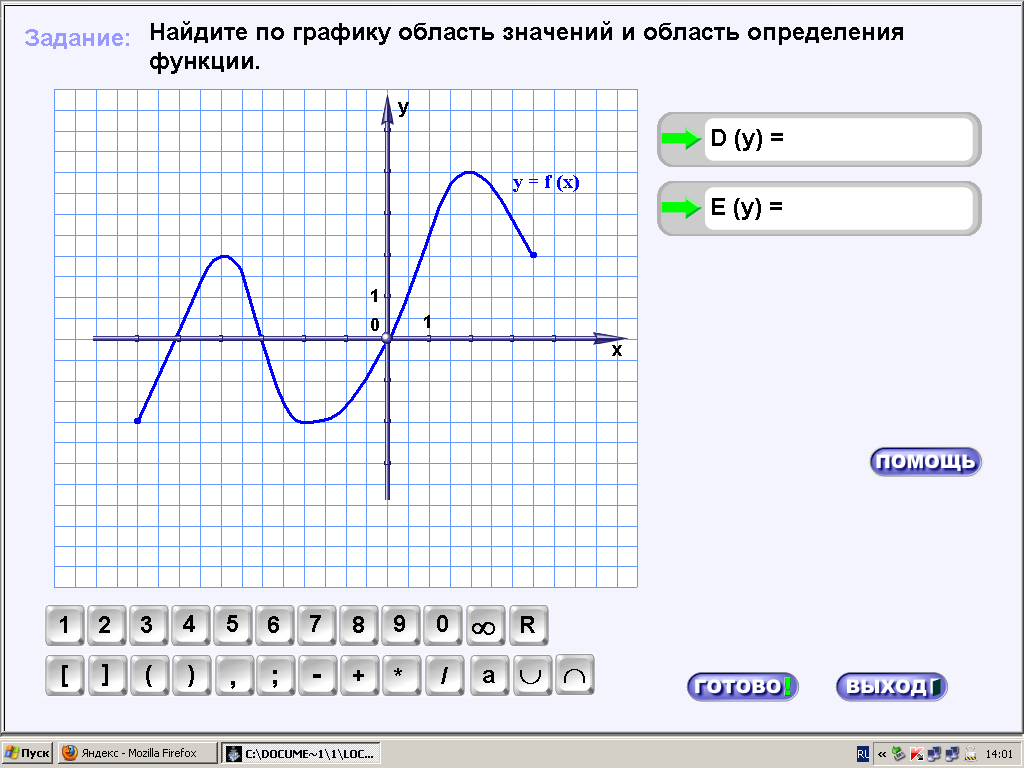
Функция убывает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Для убывающей функции большему значению соответствует меньшее значение . График идет вправо и вниз.
На нашем рисунке функция возрастает на промежутке и убывает на промежутках и .
Определим, что такое точки максимума и минимума функции.
Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.
На нашем рисунке — точка максимума.
Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».
На нашем рисунке — точка минимума.
Точка — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и на нашем графике не может быть точкой минимума.
Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это и .
А что делать, если нужно найти, например, минимум функции на отрезке ? В данном случае ответ: . Потому что минимум функции — это ее значение в точке минимума.
Аналогично, максимум нашей функции равен . Он достигается в точке .
Можно сказать, что экстремумы функции равны и .
Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.
В нашем случае наименьшее значение функции на отрезке равно и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно .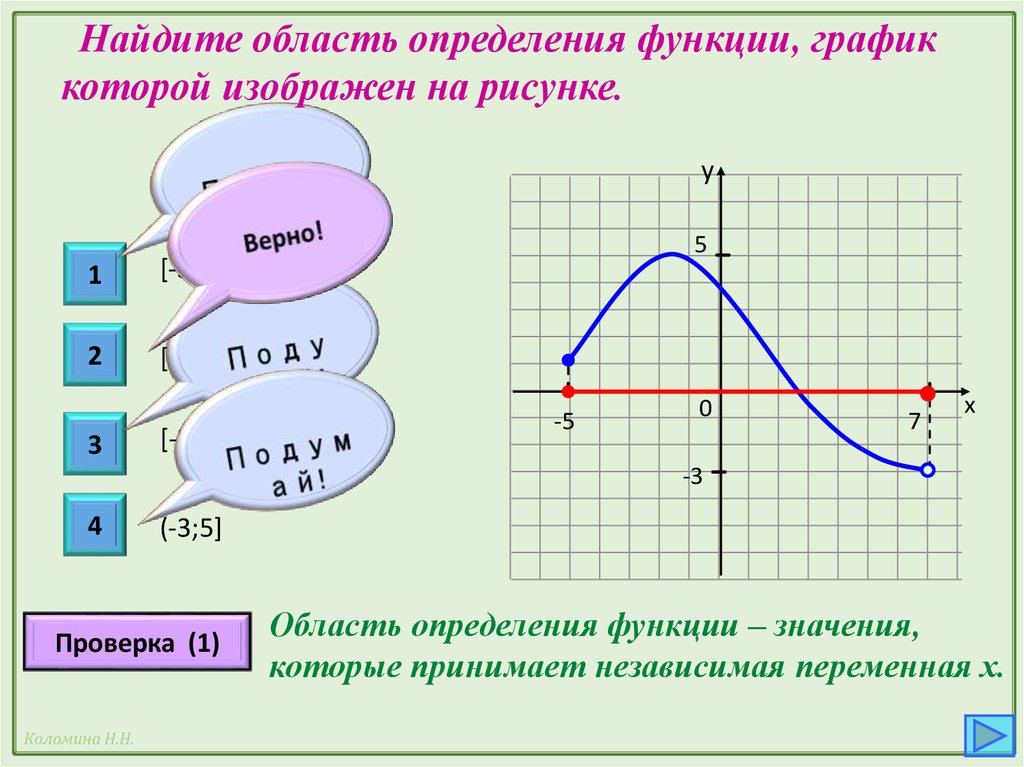
Оно достигается в левом конце отрезка.
В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.
Функция. Область значения функции. Область определения функции.
Функции играют фундаментальную роль во всех областях математики, а также в других науках и инженерии. Более абстрактные области математики, такие, как теория множеств, рассматривают очень общие типы функций, которые не могут быть определены конкретным правилом и не регулируются какими-либо знакомыми принципами. Характерным свойством функции является то, что она связывает ровно одно значение из множества x одному значению из y.
Математическое понятие функции выражает зависимость между двумя величинами, одна из которых независимая переменная x, аргумент функции или ее «входящее значение», а другая зависимая переменная — y «выходящее значение».
Функцией, заданной на множестве \(D\), называется закон, по которому каждому значению \(x\) из множества \(D\) ставится в соответствии одно определенное значение y.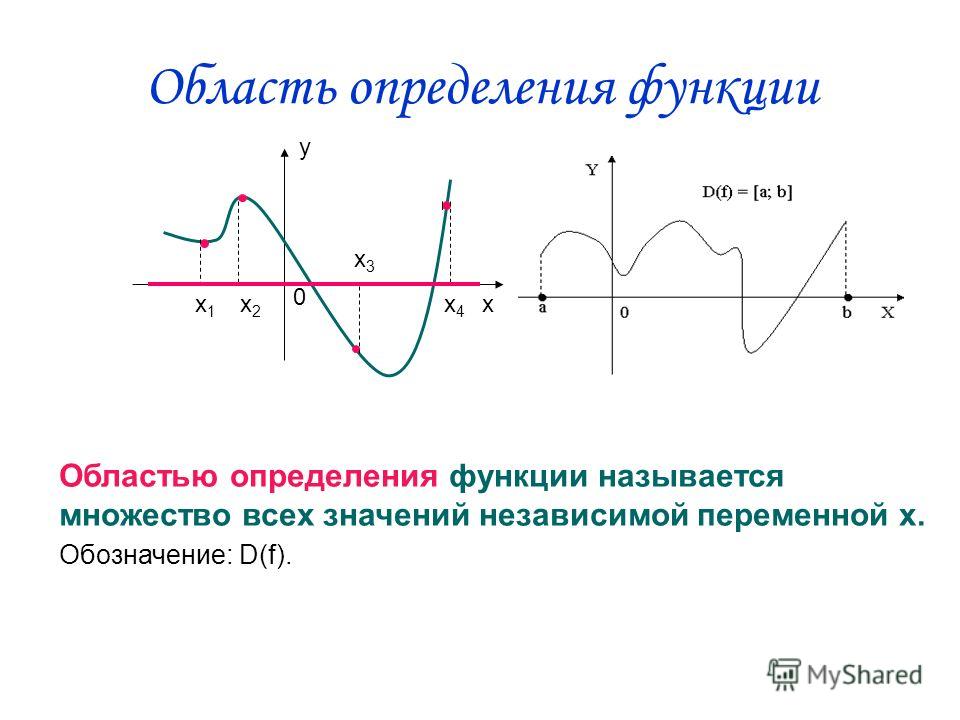
Будем обозначать функцию какой-нибудь буквой, например f, а ее значение в точке x будем обозначать \(f(x)\), произносится “эф от икс”, \(y\) является функцией от \(x\) и это записывают как равенство \(y=f(x)\). Мы можем обозначать функцию и другими буквами, например \(t,r,n.\)
Областью определения функции f называется множество всех допустимых значений переменной x от функции f. Функция может быть определена только для тех значений, при которых выражение f(x) имеет смысл.
Областью значений функции f называют множество значений, которые может принимать функция f.
Задать функцию — это значит описать какую-то конкретную зависимость так, чтобы каждый мог разобраться, о чем идет речь.
Чтобы задать функцию, нужно:
- записать формулу, которая задает функцию;
- нарисовать график функции;
- составить таблицу значений функции
Аргумент функции — это независимая переменная, от значений которой зависят значения функции.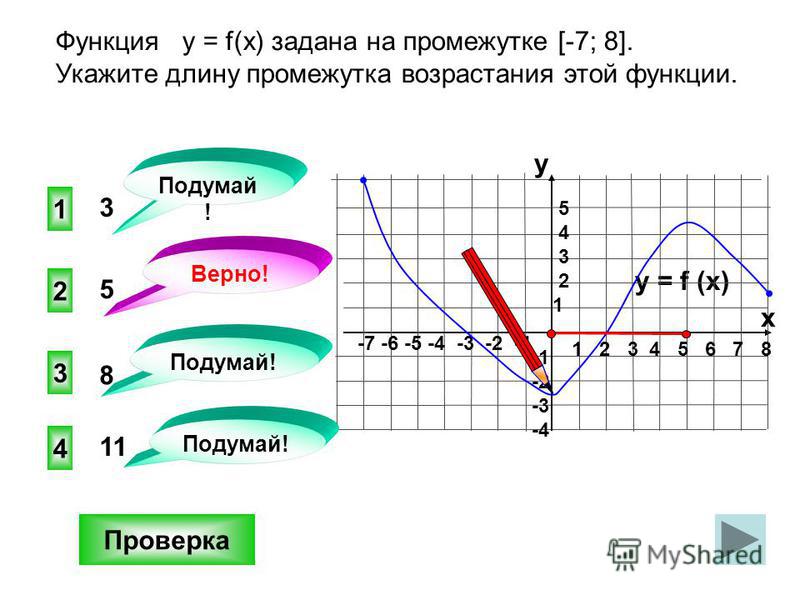
На рисунке нарисованы таблица значений и график функции \(y=-2x:\)
Задача 1. Нарисовать график функции \(2x+3.\)
Решение. Составим табдицу значений функции:
Перенесем на оси координат значения:
Есть много способов дать функцию: по формуле, по графику, по алгоритму, который вычисляет ее, по описанию ее свойств. Иногда функция описывается через ее связь с другими функциями, например, обратная функция. В прикладных дисциплинах функции часто определяются таблицами значений или формулой. Не все типы описания могут быть даны для каждой возможной функции, и необходимо провести четкое различие между самой функцией и несколькими способами ее представления или визуализации.
Функции в алгебре обычно выражаются в терминах алгебраических операций. Функции, изучаемые в анализе, такие как экспоненциальная функция, могут иметь дополнительные свойства, возникающие из непрерывности пространства, но в самом общем случае не могут быть определены одной формулой. Аналитические функции в комплексном анализе могут быть определены довольно конкретно через их разложения рядов. С другой стороны, в лямбда-исчислении функция является примитивным понятием, а не определяется в терминах теории множеств.
Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
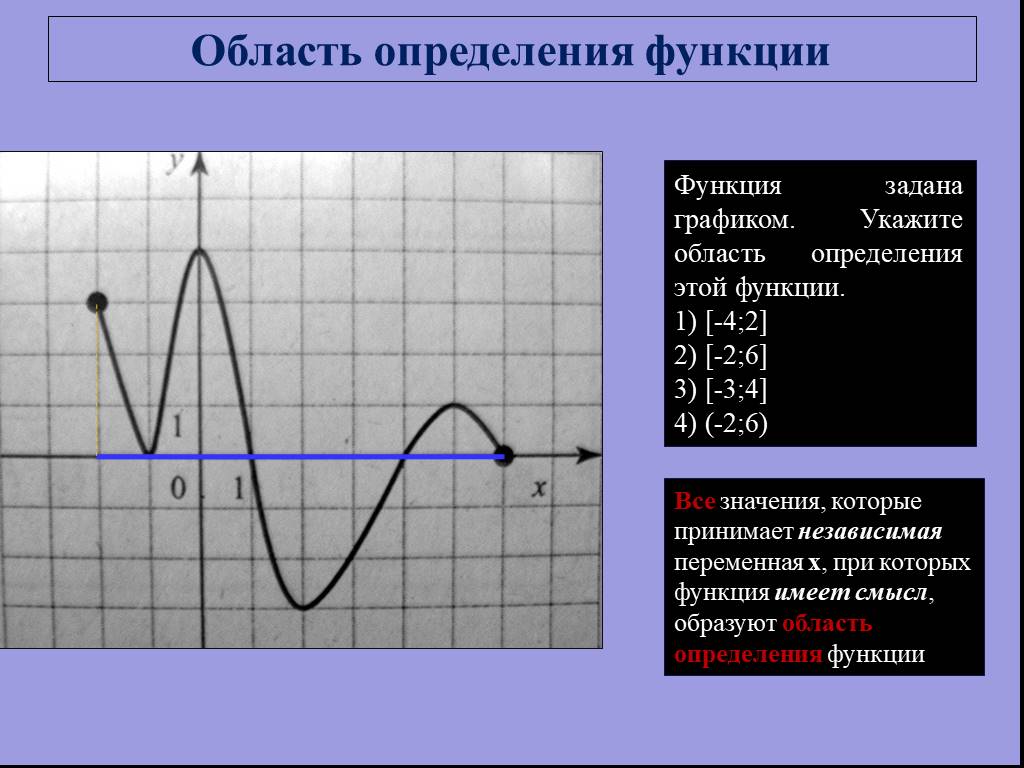
Найти домен и диапазон по графикам | Колледж Алгебра |
Другой способ определить область и диапазон функций — использовать графики.
Поскольку домен относится к набору возможных входных значений, домен графика состоит из всех входных значений, показанных на оси x . Диапазон представляет собой набор возможных выходных значений, которые показаны на оси и . Имейте в виду, что если график выходит за пределы той части графика, которую мы видим, домен и диапазон могут быть больше, чем видимые значения. См. рис. 6.
9Рис. 6 ,\infty\right)[−5,∞)
. Вертикальный экстент графика — это все значения диапазона
555
и ниже, поэтому диапазон равен
(−∞,5]\left(\mathrm{-\infty },5\right](−∞,5 ]
. Обратите внимание, что домен и диапазон всегда записываются от меньших значений к большим или слева направо для домена и от нижней части графика к верхней части графика для диапазона.Пример 6. Поиск домена и диапазона на графике
Найдите область определения и область значений функции
fff
, график которой показан на рис.
7.
рис. домен
fff
составляет
(−3,1]\left(-3,1\right](−3,1]
.
Рисунок 8
Протяженность графика по вертикали от 0 до –4, поэтому диапазон равен
[−4,0]\влево[-4,0\вправо][−4,0]
.
Пример 7. Определение области и диапазона по графику добычи нефти
Найдите область определения и диапазон функции
fff
, график которой показан на рисунке 9.
Рисунок 9. (кредит: модификация работы Управления энергетической информации США) горизонтальная ось — это «годы», которые мы представляем с помощью переменной
ttt
для времени.
Выходное количество — «тысячи баррелей нефти в день», которое мы представляем с помощью переменной
bbb
для баррелей. Граф может продолжаться влево и вправо за пределами того, что просматривается, но на основе видимой части графа мы можем определить домен как
1973≤t≤20081973\le t\le 20081973≤t≤t≤2008
и диапазон приблизительно равен
180≤b≤2010180\le b\le 2010180≤b≤2010
.
В интервальных обозначениях домен равен [1973, 2008], а диапазон равен примерно [180, 2010]. Для домена и диапазона мы аппроксимируем наименьшее и наибольшее значения, поскольку они не попадают точно на линии сетки.
Попробуйте 6
Учитывая график на рисунке 10, определите домен и диапазон, используя обозначение интервала.
Рисунок 10
Решение
Вопросы и ответы
Могут ли домен и диапазон функции совпадать?
Да.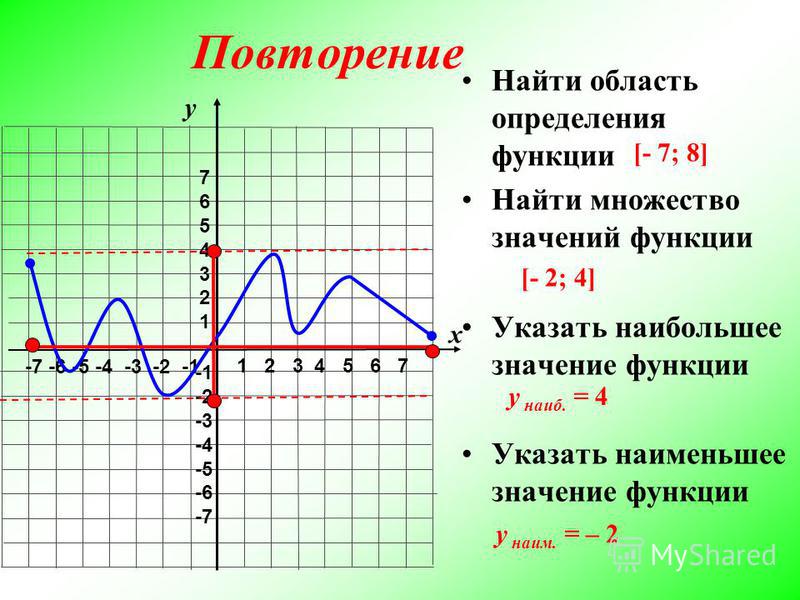
Например, область определения и диапазон функции кубического корня — это множество всех действительных чисел.
Лицензии и атрибуты
Лицензионный контент CC, совместно используемый ранее
- Precalculus. Автор : Джей Абрамсон и др. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/precalculus/pages/1-introduction-to-functions. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно по адресу: http://cnx.org/contents/[email protected]
Все права защищены.
Автор : Mathispower4u. Лицензия : Все права защищены . Условия лицензии : Стандартная лицензия YouTubeДомен и диапазон
Горячая математика домен из
функция
ф
(
Икс
)
это набор всех значений, для которых определена функция, и диапазон функции – это множество всех значений, которые
ф
берет.
(В начальной школе вы, вероятно, называли домен замещающим набором, а диапазон — набором решений. Их также можно было назвать входом и выходом функции.)
Пример 1:
Рассмотрим функцию, показанную на схеме.
Здесь домен представляет собой набор { А , Б , С , Е } . Д не находится в домене, так как функция не определена для Д .
Ассортимент — это набор { 1 , 3 , 4 } . 2 не входит в диапазон, так как в домене нет буквы, которая сопоставляется с 2 .
Вы также можете говорить о домене
связь
, где один элемент в домене может быть сопоставлен более чем с одним элементом в диапазоне.
Пример 2:
Рассмотрим отношение { ( 0 , 7 ) , ( 0 , 8 ) , ( 1 , 7 ) , ( 1 , 8 ) , ( 1 , 9) , ( 2 , 10 ) } .
Здесь отношение задано как набор упорядоченных пар. Домен представляет собой набор
Икс
-координаты,
{
0
,
1
,
2
}
, а диапазон — это набор
у
-координаты,
{
7
,
8
,
9,
10
}
.
Обратите внимание, что элементы домена
1
а также
2
связаны с более чем одним элементом диапазона, так что это нет функция.
Но чаще, и особенно при работе с графиками на координатной плоскости, мы имеем дело с функциями, где каждый элемент области связан с одним элементом диапазона. (См. Проверка вертикальной линии .)
Пример 3:
Область определения функции
ф ( Икс ) знак равно 1 Икс
все действительные числа, кроме нуля (поскольку при Икс знак равно 0 , функция не определена: деление на ноль запрещено!).
Диапазон также включает все действительные числа, кроме нуля. Вы можете видеть, что на кривой есть некоторая точка для каждого
у
-значение кроме
у
знак равно
0
.
Домены также можно указать явно, если есть значения, для которых функция может быть определена, но которые мы по каким-то причинам не хотим рассматривать.
Пример 4:
Следующие обозначения показывают, что область определения функции ограничена интервалом ( − 1 , 1 ) .
ф ( Икс ) знак равно Икс 2 , − 1 < Икс < 1
График этой функции такой, как показано. Обратите внимание на незакрашенные кружки, которые показывают, что функция не определена в
Икс
знак равно
−
1
а также
Икс
знак равно
1
.
у
-значения варьируются от
0
вплоть до
1
(включая
0
, но не включая
1
).