Область определения функции онлайн как найти: Область определения функции онлайн

Сложные функции.

Определение. Пусть даны функции . Функция вида называется сложной (композицией) функции на функцию .

Чтобы найти значение сложной функции , сначала необходимо по независимой переменной вычислить значение , а затем по найденному значению найти значение . При этом функцию называют внутренней функцией композиции, а функцию – внешней функцией композиции.

Правила построения графиков функций.

Пусть задан график функции . Справедливы правила:

1. График функции есть график функции , сдвинутый (при влево, при вправо) на единиц параллельно оси .

2. График функции есть график функции , сдвинутый (при вверх, при вниз) на единиц параллельно оси .

3. есть график функции , растянутый (при ) в раз и сжатый (при ) вдоль оси .

При график функции – зеркальное отображение графика функции от оси .

4. — график функции , сжатый в k раз при вдоль оси . При график функции — зеркальное отображение графика функции от оси .

Примеры.

I/Найти область определения функции .

1. .

Решение.

Функция представляет собой сумму функций. Область определения исходной функции состоит из всех значений , которые одновременно принадлежат области определения функций и .

Область определения подкоренного выражения неотрицательна, а логарифмической функции – положительные числа,

то решим систему неравенств:

Отметим на числовом луче точки и .

Следовательно, область определения исходной функции: .

2.

.

Решение.

Функция представляет собой сумму функций. Область определения исходной функции состоит из всех значений , которые одновременно принадлежат области определения функций и .

Область определения логарифмической функции – множество положительных чисел, а значение подкоренного выражения неотрицательное, то область определения заданной функции определяется как совокупность значений , при которых одновременно выполняются неравенства и . Решим систему неравенств:

Т. к. функция положительная на промежутке , то решим систему неравенств:

Следовательно, область определения исходной функции промежуток:

.

3. .

Решение.

Oбласть определения исходной функции – отрезок , поэтому справедливо неравенство: , решим двойное неравенство: .

Перейдём к решению системы неравенств:

Следовательно, областью определения функции является

объединение промежутков .

4. .

Решение.

Функция представляет собой сумму функций; область определения исходной функции состоит из всех значений , которые одновременно принадлежат области определения функций: , и .

Область определения логарифмической функции – множество положительных чисел, а значение подкоренного выражения неотрицательное, областью определения функции является интервал , то область определения заданной функции определяется как совокупность значений х, при которых одновременно выполняются неравенства: и .

Решим систему уравнений:

Областью определения функции является объединение промежутков: . Заметим, что области определения функций и совпадают.

Для функции область определения — . Объединяя области определения всех трёх функций, получим — область определения данной функции.

II.Построить графики функций:

1.

Решение.

Проводим построение графика следующим образом:

1. Изобразим график функции .

2.Изобразим график функции , который получается сжатием графика функции вдоль оси .

3.Начертим график функции , который является зеркальным отображением графика относительно оси .

4.Построим график функции , который получается растяжением в 3 раза вдоль оси графика функции .

2. .

Решение.

— модуль (абсолютная величина) числа а определяется следующим:

Первоначально находим нули подмодульных выражений: и .

Это числа поэтому всю числовую ось разбиваем на промежутки . На каждом из них по определению раскрываем модули .

При имеем т. к. ; ,

т. к. , то при исходная функция примет вид:

Затем при т. к. т. к. , то при исходная функция примет вид:

При имеем , т. к. т. к. .

При исходная функция примет вид .

Для построения графика функцию запишем в кусочно – заданном виде

Теперь построим график этой функции.

3.

Решение.

Исследуемая функция представлена в кусочно – заданном виде. Построим сначала график функции . Для этого построим график функции . Он получается путём параллельного переноса графика функции вправо на одну единицу вдоль оси График функции получим путём сдвига на две единицы вверх вдоль оси графика функции .

Теперь построим график функции Его получаем путём сдвига вдоль оси вверх на четыре единицы параболы. График функции получен построением зеркального отображения относительно оси графика функции . Сдвигая на 2 единицы вверх по оси график функции , получаем график функции .

Заметим, что значение функции . Тогда значение функции На графике это отмечено точкой. А теперь, после проведённых рассуждений построим график исходной функции.

III. Записать функцию как функцию:

1. аргумента , полагая ;

2. аргумента , полагая ;

3. найти композиции , указать внутренние и внешние функции и схемы вычисления сложных функций.

1.

Решение.

1. Полагая , — независимая переменная. Функция будет иметь вид . Тогда

Эта функция вычисляется по следующей схеме:

2. Полагая . считаем зависимой переменной . Функция будет иметь вид . Тогда

Эта функция вычисляется по следующей схеме

2.

Решение.

1. Пусть . В данной функции переменная — зависимая переменная, — независимая переменная. Функция будет иметь вид . Тогда .

Эта функция вычисляется по следующей схеме

.

2. Полагая ( считаем зависимой переменной от переменной ). Функция будет иметь вид . Тогда .

Эта функция вычисляется по следующей схеме

IY. Найти общий вид функции , если она удовлетворяет условию:

1) .

Решение.

Область определения функции .

Найдём Далее, . Найдём функцию , и, наконец, найдём общий вид функции .

Тесты по теме «Функция» онлайн

• Производная элементарных функций

  18.04.2020 11949 0

  Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Производная». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. Планируется, что на выполнение этого теста Вы потратите не более 5 минут.

• Графики функций, 9 класс (задание 11, ОГЭ)

  07.

  05.2020 8724 0

  Тестовая работа по теме «Графики функций». Задания в формате ОГЭ (задание № 11), где предлагается установить соответствие между графиками функций и формулами, которые их задают

• Что такое функция

  15.11.2020 2198

  Тест для проверки знаний по теме «Что такое функция», алгебра 7 класс.  

• Тест по заданию №11 (ОГЭ-2020) по теме: Функции и их графики: линейная, квадратичная, y=k/x.

  06.02.2020 1463

  0

  Тест состоит из основных прототипов задания №11 ОГЭ по математике. Тема: функции и их графики: линейная, квадратичная, обратная пропорциональность. В каждом задании ответом является последовательность из трёх цифр.

• Обработка числовой информации в электронных таблицах

  08.02.2022 1519 0

  Тест по теме «Обработка числовой информации в электронных таблицах» можно использовать в качестве теста в девятых классах по УМК Л.Л.Босовой

• тест по теме: Линейная функция, 7 класс- АЛГЕБРА

  05.04.2020 7643

  тест по теме: Линейная функция, 7 класс- АЛГЕБРА Данный тест предназачен для закрепления темы: Линейная функция. n

  31.10.2020 391 0

  Данный тест будет полезным  учителю для осуществления быстрого контроля на уроке, а также ребятам, которые желают проверить свои знания по данной теме.

• ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЁ ГРАФИК

  21.04.2020 4752 0

  Тест содержит 6 вопросов по теме «Линейная функция и её график»

• Преобразование графиков функции

  29.04.2020 1659 0

  Тест по теме «Преобразование графиков функции» предназначен для учащихся ГБПОУ КК ТИТ.                  

• Функция. Способы заданий функций

  25.03.2020 3174

  Тестовые задания по алгебре 7 класс по теме «Функция. Способы задания функции»

• Контрольная работа по математике на тему «Функции». Вариант 2.

  19.08.2022 23 0

  С помощью данного теста вы сможете узнать свою подготовку по теме Графики

• Функции, их свойства и графики

  24.03.2020 835 0

  Тест предназначен для проверки знаний по степенной, показательной и логарифмической функции, их свойствам и графикам

• Степенная функция

  07. 04.2020 578 0

  Тест предназначен для проверки знаний по темам Степенная функция, ее свойства и графики, преобразование степенных функций, взаимно обратные степенные функции

• Функция 8 класс

  25.02.2021 587 0

  Данный тест предназначен для обучающихся 8 класса. Цель теста — проверка знаний по теме Функция.

• Первообразная. Таблица первообразных

  29.03.2021 4554 0

  Тест предназначен на проверку знаний и умений учащихся по теме «Первообразная. Таблица первообразных.

• Производная и ее применение

  25.12.2019 7974 0

  Данный тест создан для проверки знаний по темам «Функция», «Производная»

• Домашнее задание по теме «Стандартные процедуры и функции для работы с символьными и строковыми величинами».

  19.05.2020 20 0

  Этот тест предназначен для закрепления дома знаний по теме «Стандартные процедуры и функции для работы с символьными и строковыми величинами».

• Показательная функция (11 класс)

  26. 09.2018 1690 0

  В тесте рассматриваются вопросы по теме: «Показательная функция»

• Самостоятельная № 1 функции и их графики

  11.09.2020 331 0

  Самостоятельная работа. Раздел: Функции и их графики. Область определения. Четность. Нечетность

• Функции и их свойства

  03.12.2020 1017 0

  Тест предназначен для поверки умения исследовать свойства функции, заданной в графическом и аналитическом виде. 

• Простейшие тригонометрические уравнения

  21. 10.2022 41 0

  Тест предназначен для проверки знаний при решении простейших тригонометрических уравнений.

• Функции. Графическая интерпретация.

  05.04.2020 57 0

  Тест предназначен для студентов ГБПОУ КК ТИТ                                                                                                     

• Исследование функции

  06.04.2020 229 0

  Тест предназначен для студентов 1 курса ГБПОУ КК ТИТ                                                                                       

• Построение графиков функций, заданных различными способами

  08. 04.2020 196 0

  Тест предназначен для учащихся ГБПОУ КК ТИТ по теме «Построение графиков функций заданных различными способами»

• Функция. Определение. Способы задания

  09.04.2020 2163 0

  Тест по темам «Функциональная зависимость. Способы задания функции»

• Непрерывные и непериодические функции

  20.04.2020 133 0

  Тест по теме «Непрерывные и непериодические функции» предназначен для учащихся ГБПОУ КК ТИТ.      

• Тест по модулю 4

  20. 08.2020 49 0

  Привет, ребята! Пришло время показать свои знания на практике. 

• Контрольная работа по теме «Простейшие функции»

  14.10.2020 157 0

  Контрольная работа предназначена для обучающихся восьмого класса и направлена на контроль знаний и умений по теме «Простейшие функции». 

• Математика.. Функция. Способы задания функции

  16.03.2021 472 0

  Тест создан  для  учащихся   7 классов   для   проверки   знаний   по   теме   «Функция»…

• Функция y=ax2

  02. 04.2018 794 0

  В тесте рассматриваются вопросы по теме: «Квадратичная функция»

• Функции в Паскале. Типы данных. Линейные программы.

  20.03.2020 696 0

  Задание предназначено для учащихся 8 классов, изучающих информатику с использованием УМК Л.Л. Босовой, А.Ю. Босовой (нужно знать §3.4).

• Условные программы

  23.03.2020 387 0

  Задание предназначено для учащихся 8 классов, изучающих информатику с использованием УМК Л.Л. Босовой, А.Ю. Босовой.

• Сложная функция (композиция)

  12. 04.2020 305 0

  Тест предназначен для студентов ГБПОУ КК «Тихорецкого индустриального техникума»                                   

• Тест по математике

  15.04.2020 8 0

  Данный тест содержит 10 вопросов по дисциплине математика по теме «свойства функции» . Содержит задания на выбор одного правильного ответа, задания множественного выбора, задания на установление соответствия, задания на установление последовательности, задания открытой формы

• Исследование свойств обратных тригонометрических функций

  28.04.2020 26 0

  Тест по теме «Исследование свойств обратных тригонометрических функций»  предназначен для учащихся ГБПОУ КК ТИТ

• Что означает в математике запись y=f(x)

  07. 05.2020 169 0

  Тест создан к учебнику «Алгебра 7 класс» под редакцией А.Г.Мордковича по теме «Что означает в математике записьy= f(x).

• Нахождение наибольшего и наименьшего значения функции

  17.09.2020 16 0

  Тест состоит из 15 вопросов, раскрывающий содержание темы : «Нахождение наибольшего и наименьшего значения функции»

• Исследование функции

  09.11.2020 569 0

  Тест на умение применять знания производной, некоторых элементарных функций, для исследования функций.   умение находить «ключевые» точки графика функции

• СОР № 2 — 10 кл ЕМН, 2 четверть, Алгоритмизация и программирование

  08.12.2020 162 0

  Проверочная работа по информатике для учащихся 10 классов естественно-математического направления общеобразовательных школ.

• Математика 10 класс

  11.12.2020 21 0

  Тест по математике 10 класс-функции. Тест направлен на повторение основных видов функций.

• Функция. Свойства функции

  26. 02.2021 405 0

  Данный тест предназначен для студентов 1 курса и может быть полезен для старшеклассников. В тесте предложены задания по теме «Функция и её свойства». Задания в тесте расчитаны на знание области определения функции, четности и нечетности функции, умение читать свойства функции по графикам

• Функция и ее исследование

  19.03.2021 5 0

  Тест предназначен для  проверки усвоенных знаний по теме «Функция»

• Графики функций

  21.03.2021 23 0

  Тест предназначен для закрепления изученного материала и его повторения.

• Функции, алгебра 7 класс

  12.11.2021 185 0

  Тест по алгебре для 7 класса по теме «Функции», предложен как тест для закрепления знаний по теме Функции. Содержит как основные понятия, так и примеры в которых нужно найти решение.

• Показательная функция

  06.04.2022 1 0

  Тест на тему «Показательная функция»                                                                                                                     .

• Функции Excel

  25. 05.2022 174 0

  В данном тесте представлены вопросы по изученной теме, связанной с функциями Microsoft Office Excel. 

• Контрольная работа по математике на тему: «Функции». Вариант 1

  19.08.2022 11 0

  С помощью данного теста вы сможете узнать свою подготовку по теме Функции

Как найти область определения и область значений функции — Криста Кинг Математика

Каковы домен и диапазон функции?

Мы часто определяем функцию уравнением, в котором переменные ???x??? и ???г??? представляют собой действительные числа, а где «???y???» (только переменная ???y???) сама по себе находится на одной стороне уравнения, и выражение, которое не содержит никакой другой переменной, кроме ???x??? находится на другой стороне. 2???.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Думайте о домене функции как о всех действительных числах, которые вы можете подставить вместо ???x??? не вызывая неопределенности функции. На что следует обратить внимание, так это на значения ???x??? что приведет к тому, что знаменатель дроби будет равен ???0??? и значения, которые заставили бы отрицательное число под знаком квадратного корня.

Диапазон функции — это действительные числа, которые будут получены для ???y??? от подстановки реальных номеров в домен для ???x???. Другими словами, областью значений являются все ???x???-значения или входные данные функции, а диапазоном являются все ???y???-значения или выходные данные функции.

Есть несколько часто используемых функций, которые имеют доменные ограничения:

В ???y=\frac{1}{x}???, ???x??? не может равняться ???0???

В ???y=\sqrt{x}???, ???x??? должен быть неотрицательным (либо положительным, либо ???0???)

Как найти область определения и диапазон функции

Пройти курс

Хотите узнать больше об Алгебре 1? У меня есть пошаговый курс для этого.

🙂

Учить больше

Нахождение области определения и области значений рациональной функции

Пример

Опишите область определения и область значений функции.

???f(x)=x+\frac{2}{x}???

В этой функции ???x??? не может быть равен ???0???, потому что это значение приводит к тому, что знаменатель дроби равен ???0???. Потому что установка ???x??? равно ???0??? это единственный способ сделать функцию неопределенной, домен функции — все ???x\neq 0???.

Давайте рассмотрим другой пример, где функция определяется набором координатных точек.

Другими словами, домен — это все значения x или входные данные функции, а диапазон — все значения y или выходные данные функции.

Пример

Что такое домен и диапазон набора.

???(-2,4)???, ???(1, 3)???, ???(2,5)???, ???(4,3)???

Домен состоит из всех значений ???x??? и помните, что координаты ???(x,y)???.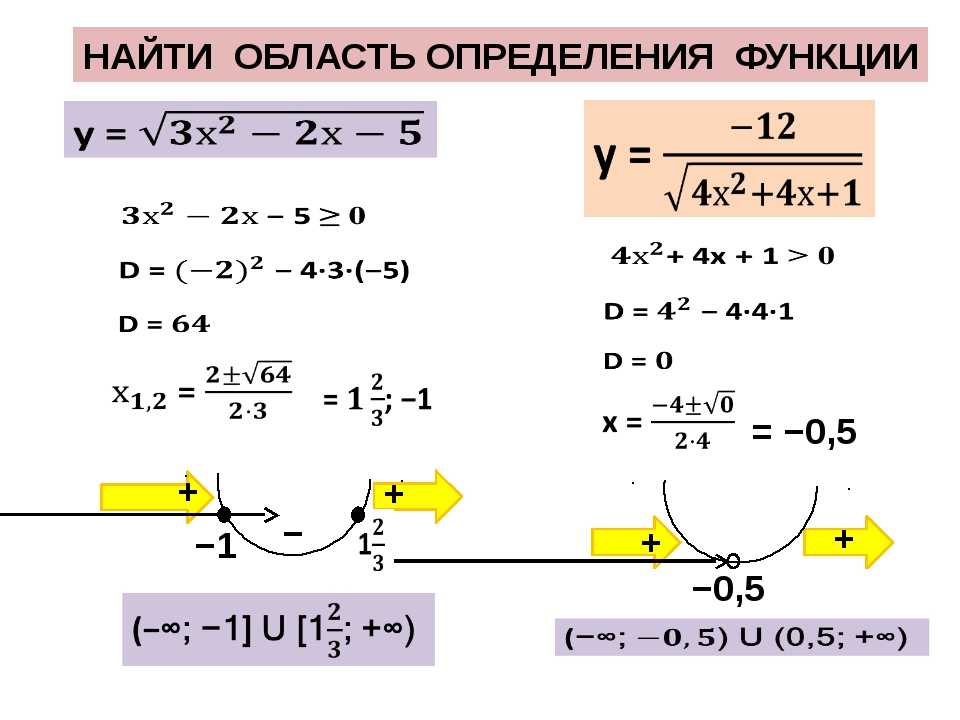 Поэтому домен

Домен: ???-2,\1,\2,\4???

Диапазон всех ???y???-значений.

Диапазон: ???4,\ 3,\ 5,\ 3???

За исключением того, что нам не нужно перечислять числа, которые повторяются более одного раза, и мы хотим расположить числа в порядке возрастания, поэтому мы можем задать диапазон как

Диапазон: ???3,\ 4,\ 5???

Давайте попробуем другой пример домена и диапазона.

Пример

Каковы домен и диапазон функции?

???f(x)=\frac{6}{x}???

В этом примере у нас есть ???x??? в знаменателе, что означает, что мы делим на ???x???. Нужно помнить, что мы не можем делить на ???0???, а ???x??? может быть любым числом, кроме ???0???. Таким образом, домен состоит из всех действительных чисел, кроме ???0???.

Домен: ???(-\infty,0)\cup(0,\infty)???

Так как ???x\neq0???, то будет асимптота при ???x=0???. Если мы подумаем о выводах ???6/x???, вы поймете, что не может быть вывода ???0???. Однако выходом может быть любое другое число. Таким образом, диапазон состоит из всех действительных чисел, кроме ???0???.

Диапазон: ???(-\infty,0)\cup(0,\infty)???

Получить доступ к полному курсу Алгебра 1

Начать

Изучайте математикуКриста Кинг 28 апреля 2021 г. математика, учитесь онлайн, онлайн-курс, онлайн-математика, алгебра, алгебра 1, алгебра i, домен и диапазон, домен и диапазон функции, домен, диапазон, домен функции, диапазон функции, нахождение домена и диапазона

0 лайков

Домен композиции | Колледж Алгебра

Результаты обучения

• Найдите область определения составной функции.
• Разложить составную функцию.

Как мы обсуждали ранее, домен составной функции , такой как [latex]f\circ g[/latex], зависит от домена [latex]g[/latex] и домена [latex]f [/латекс]. Важно знать, когда мы можем применять составную функцию, а когда нет, то есть знать область определения такой функции, как [latex]f\circ g[/latex]. Предположим, что мы знаем области определения функций [latex]f[/latex] и [latex]g[/latex] по отдельности. Если мы напишем составную функцию для ввода [латекс]x[/латекс] как [латекс]f\left(g\left(x\right)\right)[/латекс], мы сразу увидим, что [латекс] x[/latex] должен быть членом домена [latex]g[/latex] для того, чтобы выражение имело смысл, потому что в противном случае мы не сможем завершить вычисление внутренней функции. Однако мы также видим, что [latex]g\left(x\right)[/latex] должен быть членом домена [latex]f[/latex], иначе вычисление второй функции в [latex]f\left (g\left(x\right)\right)[/latex] не может быть завершено, и выражение по-прежнему не определено. Таким образом, домен [latex]f\circ g[/latex] состоит только из тех входных данных в домене [latex]g[/latex], которые производят выходные данные из [latex]g[/latex], принадлежащие домену [ латекс]ф[/латекс]. Обратите внимание, что домен [latex]f[/latex], составленный из [latex]g[/latex], представляет собой набор всех [latex]x[/latex], таких что [latex]x[/latex] находится в домене из [latex]g[/latex] и [latex]g\left(x\right)[/latex] находится в домене [latex]f[/latex].

Общее примечание. Область определения составной функции

Область определения составной функции [latex]f\left(g\left(x\right)\right)[/latex] — это набор этих входных данных [latex] x[/latex] в домене [latex]g[/latex], для которого [latex]g\left(x\right)[/latex] находится в домене [latex]f[/latex].

Как сделать: Для данной функциональной композиции [латекс]f\left(g\left(x\right)\right)[/latex] определите ее область определения.

1. Найдите домен [latex]g[/latex].
2. Найдите домен [latex]f[/latex].
3. Найдите те входные данные, [latex]x[/latex], в домене [latex]g[/latex], для которых [latex]g(x)[/latex] находится в домене [latex]f[/ латекс]. То есть исключить из домена [latex]g[/latex] те входные данные, [latex]x[/latex], для которых [latex]g(x)[/latex] не входит в домен [latex]. ж[/латекс]. Полученный набор является доменом [latex]f\circ g[/latex].

Пример. Нахождение области определения составной функции

Нахождение области определения

[латекс]\влево(f\circ g\right)\left(x\right)\text{ где}f\left(x\ справа)=\dfrac{5}{x — 1}\text{ и}g\left(x\right)=\dfrac{4}{3x — 2}[/latex]

Показать решение

Пример: нахождение области определения составной функции, включающей радикалы

Найдите область определения

[латекс]\лево(f\circ g\right)\left(x\right)\text{ где}f\left( x\right)=\sqrt{x+2}\text{ и }g\left(x\right)=\sqrt{3-x}[/latex]

Показать решение

Попробуйте

Найдите домен

[latex]\left(f\circ g\right)\left(x\right)\text{где}f\left(x\right)=\dfrac{1 }{x — 2}\text{ и }g\left(x\right)=\sqrt{x+4}[/latex]

Показать решение

Попробуйте

Мы можем использовать графики, чтобы визуализировать домен, который является результатом композиции двух функций.