Как найти область определения функции sin
Статьи › Находится › Как находится область определения функции заданной формулой
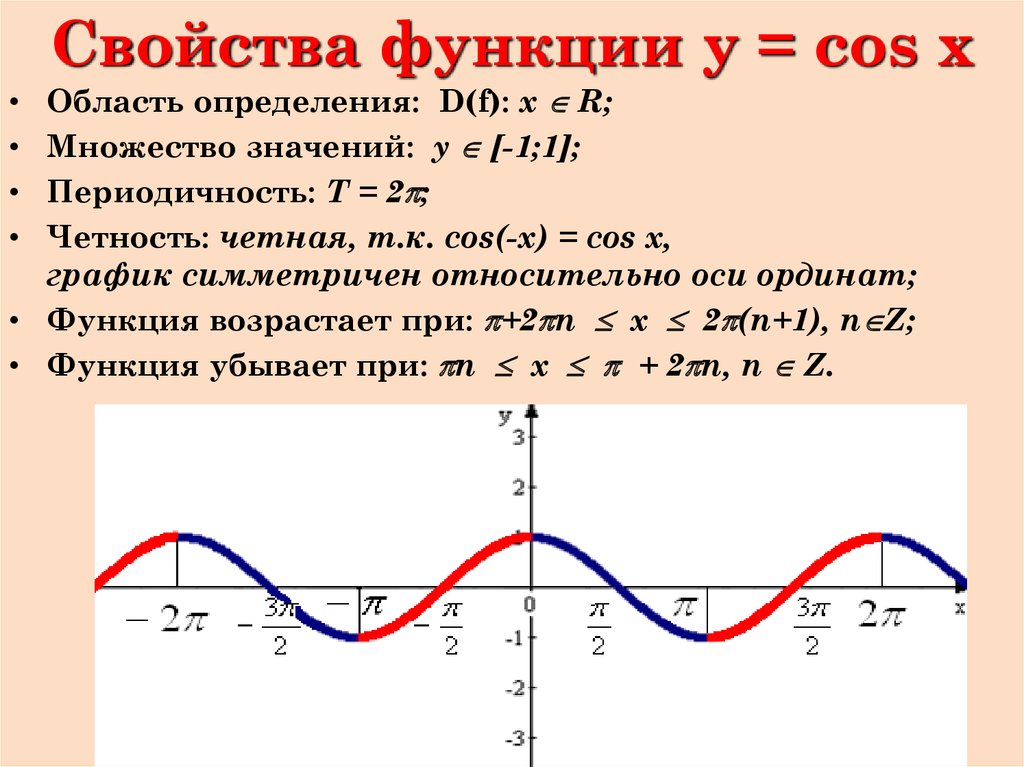
Итак, Областью определения функций y = sin x и y = cos x является множество R всех действительных чисел.
- Как найти область значения функции по формуле
- Как найти область определения функции y sin2x
- Как найти множество значений функции y sinx
- Как найти область определения логарифмической функции
- Как понять область значения функции
- Что такое область определения функции
- Как найти область определения функции y cos2x
- Как найти область определения функции с двумя переменными
- Что является областью определения функции y COSX
- Чему равен основной период функции y sinx
- Как определить четность функции y sinx
- Как найти область определения и множество значений
- Как найти область определения выражения
- Что такое LG
- Чему равна область значений функции
- Как найти область определения квадратичной функции
- Как найти область определения функции гиперболы
- Как найти область определения функции y 4x 8
- Как найти область определения функции y x 3
- Как найти область определения функции y 3x 2
- Какие значения принимает sinx
- Как найти область определения функции тангенса
- Как определить множество значений функции
- Что является графиком логарифмической функции
- Как решать логарифмические уравнения
- Когда логарифмическая функция является убывающей
- Как найти множество значений функции
- Как определить область значения линейной функции
- Что такое область значения функции 9 класс
Как найти область значения функции по формуле
Для того чтобы найти область значений на данном отрезке, необходимо: Найти вершину параболы по формуле: x = -b / (2 * a), подставить ее в формулу и найти y.
Это значение y будет минимальным/максимальным в зависимости от того, куда направлены ветви параболы.
Как найти область определения функции y sin2x
Y = sin 2x. Синус — тригонометрическая функция, непрерывная, значит, область определения функции — любое число. Функция независимо от своего аргумента принимает значения, находящиеся в промежутке от -1 до 1.
Как найти множество значений функции y sinx
Чтобы найти множество значений функции y = sin x, нужно выяснить, какие значения может принимать y при различных значениях x, т. е. установить, для каких значений y есть такие значения x, при которых sin x = y. Известно, что уравнение sin x = a имеет корни, если |a| ≤ 1, и не имеет корней, если |a| > 1.
Как найти область определения логарифмической функции
Зададим аргумент в log(x) большим 0, чтобы узнать, где определено данное выражение. Область определения ― это все значения x, при которых выражение определено.
Как понять область значения функции
Множество всех значений, которые принимает аргумент функции, называется областью определения функции: D(f) т.
е. смотрим по x. Множество всех значений, которые может принять зависимая переменная, называется областью значения функции: E(f) т.
Что такое область определения функции
Область определения — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.
Как найти область определения функции y cos2x
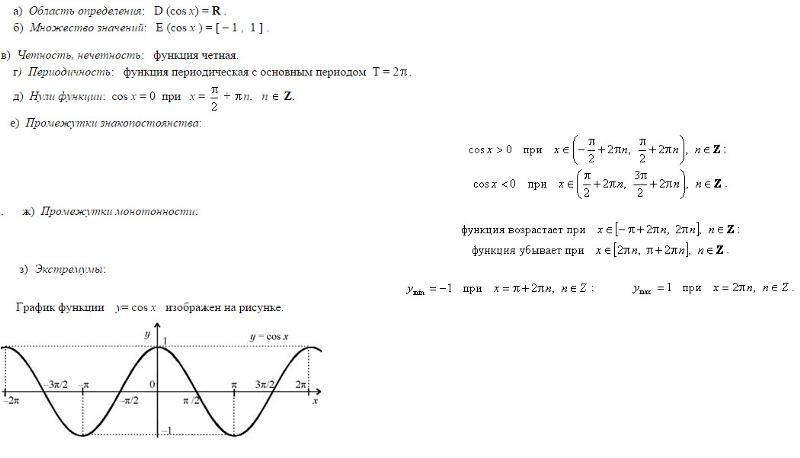
Ответы: Функция у = cos2x определена всюду (–∞; +∞), её областью значений является множество [0; 1].
Как найти область определения функции с двумя переменными
Областью определения функции двух переменных называется множество всех пар, для которых существует значение. Графически область определения представляет собой всю плоскость либо её часть. Так, областью определения функции является вся координатная плоскость — по той причине, что для любой точки существует значение.
Что является областью определения функции y COSX
Функция y = cosx определена на всей числовой прямой, и множеством её значений является отрезок − 1; 1.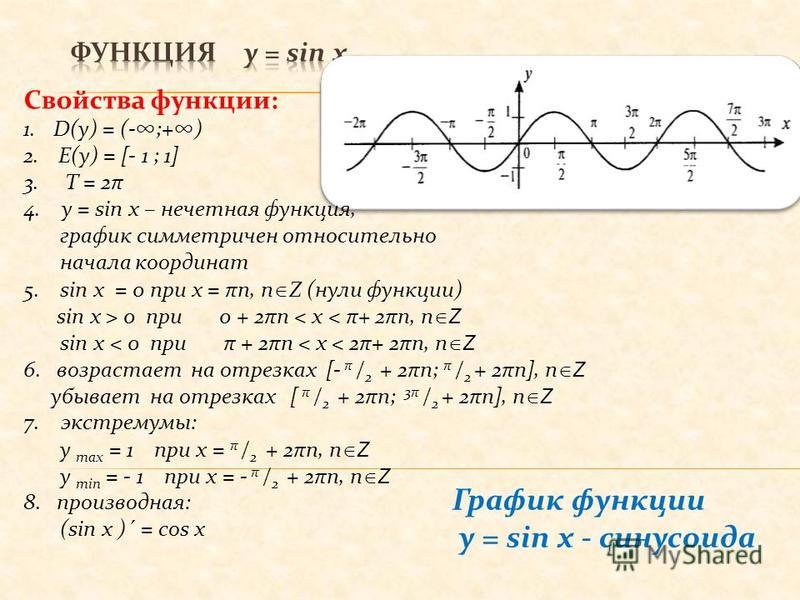
Поэтому её график не выходит за границы полосы между прямыми y = − 1 и y = 1.
Чему равен основной период функции y sinx
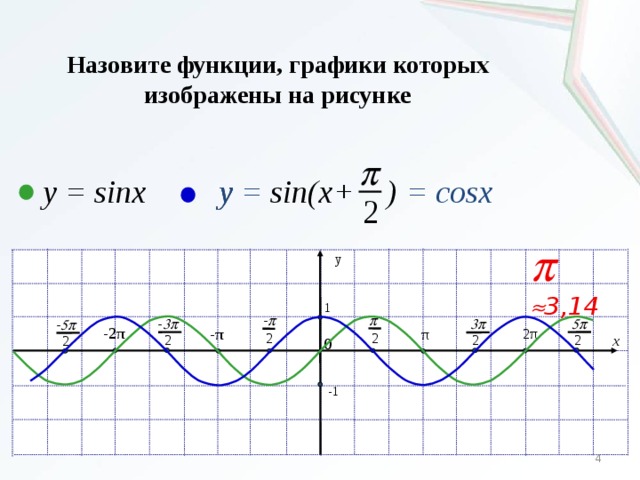
Значит, мы можем сказать, что функции y=sin x, y=cos x — периодические функции, с периодом 2π.
Как определить четность функции y sinx
Синус функция —ограниченная. Для того, чтобы определить чётность функции синус проверим следующие определения: функция чётная, f(−x)=f(x) и функцию нечётная, f(−x)=−f(x). Период функций y=sin x, y=cos xравен 2π, период функций tgx, ctgx равен π. чётной или нечётной?
Как найти область определения и множество значений
Значение y, соответствующее заданному значению x, называют значением функции. Все значения, которые принимает x, образуют область определения функции; все значения, которые принимает y, образуют множество значений функции.
Как найти область определения выражения
Областью определения выражения с одной переменной называется множество значений переменной, при которых это выражение имеет смысл.
Можно вычислить числовое значение алгебраического выражения при любом значении переменной из его области определения.
Что такое область определения и область значений функции
Ответы1. Областью определения функции являются все значения Х, на которых существует функция. Иными словами, те Х, которые можно подставить в уравнение функции и получить в результате Y. Область значения функции определяется значениями, которое принимает Y на всей своей области определения.
Что такое LG
LG (Lucky-Goldstar) — южнокорейская группа компаний, см. также: LG Electronics — южнокорейская компания по производству бытовой техники и электроники; LG Display — южнокорейская компания по производству жидкокристаллических дисплеев.
Чему равна область значений функции
Область значений (или множество значений) функции — множество, состоящее из всех значений, которые принимает функция.
Как найти область определения квадратичной функции
Графиком квадратичной функции является парабола, вершина которой находится в точке (− b 2 a; − b 2 − 4 a c 4 a).
Область определения функции — вся числовая прямая: D (f) = R = (− ∞; ∞). Область значений функции зависит от знака коэффициента.
Как найти область определения функции гиперболы
Область определения — любое число, кроме нуля. Область значения — любое число, кроме нуля. Функция не имеет наибольших или наименьших значений.
Как найти область определения функции y 4x 8
Так как в формуле функции y = 4x — 8 нет ни деления, ни корня, значит допустимы любые значения переменной х. Ответ: D(f) = (-∞; +∞).
Как найти область определения функции y x 3
Область определения функции.
Так как выражение x 3 является степенью с натуральным показателем, то оно имеет смысл для любого действительного числа x, значит, областью определения функции y = x 3 являются все действительные числа: D = R.
Как найти область определения функции y 3x 2
Ответ: D = (-∞;∞).
Какие значения принимает sinx
1) Функция у = sin х определена для всех значений х, так что областью ее определения является совокупность всех действительных чисел.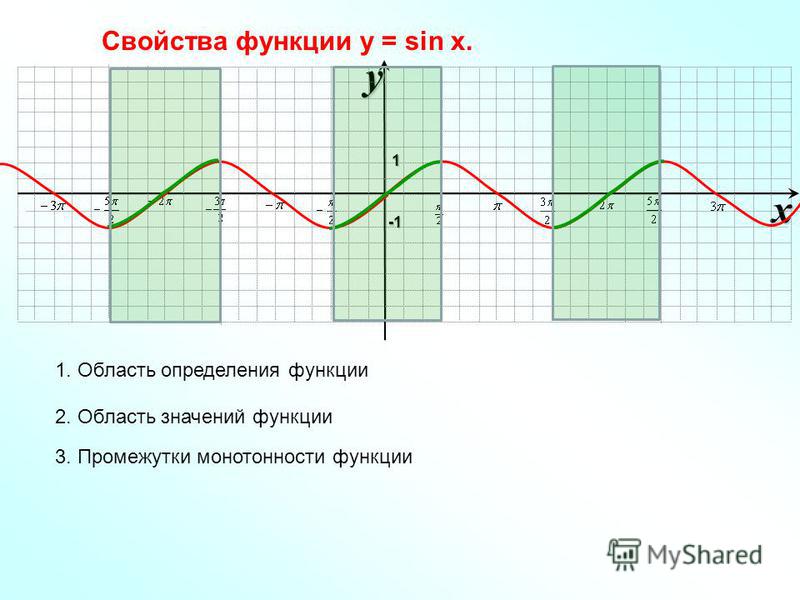
2) Функция у = sin х ограничена. Все значения, которые она принимает, заключены в интервале от —1 до 1, включая эти два числа.
Как найти область определения функции тангенса
Область определения функции y = tgx — множество ℝ действительных чисел, кроме x = π 2 + π n, n ∈ ℤ. Множество значений функции y = tgx — все действительные числа.
Как определить множество значений функции
Множество чисел, пробегаемое функцией у, когда х принимает все возможные значения (т. е. при всех значениях), называется множеством значений функции, или областью значений функции, или областью изменения функции и обозначается через E(f).
Что является графиком логарифмической функции
График логарифмической функции называют логарифмической кривой.
Как решать логарифмические уравнения
Алгоритм решения логарифмического уравнения:
- Написать ОДЗ.
- Упростить выражения слева и справа от знака равенства, используя свойства логарифмов, если это возможно.
- Если основания логарифмов одинаковые, избавиться от логарифмов.
- Решить уравнение и сравнить с ОДЗ, выписать в ответ корни.
Когда логарифмическая функция является убывающей
Область определения: множество всех положительных чисел, т. е. промежуток (0; +). Монотонность: если а > 1, то логарифмическая функция строго возрастает; если 0 < а < 1, то она строго убывает.
Как найти множество значений функции
Найти критические точки функции f(x) и выбрать те из них, которые принадлежат данному отрезку; вычислить значения функции на концах отрезка и в выбранных критических точках; среди найденных значений выбрать наименьшее и наибольшее значения; Множество значений функции заключить между этими значениями.
Как определить область значения линейной функции
Линейной функцией называется функция y = kx + b, где k и b — некоторые числа.Линейная функция:
- Область определения функции — множество R всех действительных чисел.
- Корни — единственный корень x = 0.
- Промежутки постоянного знака зависят от знака параметра k:
Что такое область значения функции 9 класс
Областью определения функции \(y = f(x)\) называют множество всех значений \(x\), для которых функция имеет смысл. Множество всех значений функции \(y = f(x)\), x ∈ X, называют областью значений функции.
Объяснение урока: Область определения и область значений тригонометрических функций
В этом объяснении мы узнаем, как определить область определения и область значений тригонометрической функции.
Начнем с определения области определения и диапазона функции.
Теорема: область определения и область значений функции
Область определения функции 𝑓(𝑥) — это множество всех возможных значений 𝑥, таких что функция 𝑓(𝑥) определено.
Диапазон функции 𝑓(𝑥) — это множество всех возможных значений функции 𝑓(𝑥)
может принимать, когда 𝑥 — любое число из области определения функции.
В частности, мы можем найти область определения и область значений функции по ее графику. Для данного графика функции его областью определения является часть горизонтальная ось, на которой существует график, а ее диапазон — это часть вертикальной оси, на которой существует график.
Одной из важных характеристик графика тригонометрической функции является то, что структура графика повторяется бесконечно. Когда поведение функции 𝑓(𝑥) повторяется на интервале длины 𝐿, то говорят, что 𝑓(𝑥) является периодическим с периодом 𝐿. Другими словами, периодическая функция с периодом 𝐿 должен удовлетворить 𝑓(𝑥)=𝑓(𝑥+𝐿), для любого 𝑥 в домене.
Чтобы изучить область определения и область значений периодической функции, нам сначала нужно понять область определения и область значений функции на интервале
длины 𝐿, например [0,𝐿]. Мы можем выбрать любой интервал длины 𝐿, но
в большинстве случаев будет удобно рассматривать интервал [0,𝐿].
Так как функция периодическая с периодом
𝐿, функция будет повторять то же поведение за пределами этого интервала. Следовательно, область значений периодической функции будет
такой же, как его диапазон на [0, 𝐿]. Кроме того, если функция определена для всех значений в
[0,𝐿], функция будет определена и для любых значений вне этого интервала в силу своей периодичности. В этом
случае область определения периодической функции — это все действительные числа, обозначаемые ℝ или
]−∞,∞[.
В нашем первом примере мы определим область определения и область значений периодической функции по заданному графику.
Пример 1. Определение области определения и области значений функции по графику
Рассмотрим следующий график функции 𝑓(𝜃).
- Каков домен 𝑓(𝜃)?
- Каков диапазон 𝑓(𝜃)?
Ответ
Прежде чем ответить на вопросы об области определения и области значений 𝑓(𝜃), отметим, что график функции
повторяется бесконечно.
Это означает, что функция 𝑓(𝜃) является периодической функцией. Мы можем видеть, что
функция имеет локальный минимум при 𝜃=0 и возвращается в то же место при 𝜃=2𝜋. Оттуда,
функция повторяет одни и те же значения. Это означает, что период этой функции равен 2𝜋.
Часть 1
В этой части нам нужно определить область определения периодической функции по заданному графику. Мы отметили, что период 𝑓(𝜃) равно 2𝜋. Напомним, что если периодическая функция задана на интервале длины равен периоду, функция определена для всех действительных чисел. Из данного графика видно, что 𝑓(𝜃) определяется для всех значений в интервале [0,2𝜋], длина которого равна периоду 2𝜋.
Следовательно, областью определения 𝑓(𝜃) являются все действительные числа, или ]−∞,∞[.
Часть 2
В этой части нам нужно определить диапазон периодической функции по заданному графику. Мы отметили, что период
𝑓(𝜃) равно 2𝜋. Напомним, что если область значений периодической функции совпадает со областью значений
функции на интервале, длина которого равна периоду, функция определена для всех действительных чисел.
Из приведенного графика мы видим, что
минимальное значение функции 𝑓(𝜃) на интервале [0,2𝜋] равно
−4, а его максимальное значение на этом интервале равно 6. Поскольку 𝑓(𝜃) принимает все значения между своими
максимум и минимум, диапазон 𝑓(𝜃) на этом интервале равен [−4,6].
Следовательно, диапазон 𝑓(𝜃) равен [−4,6].
В предыдущем примере мы рассмотрели область определения и область значений периодической функции из заданного графика. Мы можем использовать тот же метод, чтобы найти область и область значений функций синуса и косинуса. Напомним, что угол 2𝜋 радианы измеряют полный оборот на единичной окружности. Это означает, что значения тригонометрических отношений, синуса и косинуса, на единичной окружности останутся прежними, если мы добавим 2𝜋 радиан на любой угол. Это означает, что для любого угла 𝜃 радианы, sinsincoscos𝜃=(𝜃+2𝜋),𝜃=(𝜃+2𝜋).
Это говорит нам о том, что функции синуса и косинуса являются периодическими с периодом
2𝜋 радианы. Следовательно, мы можем найти область определения и диапазон синуса и
функции косинуса, рассматривая график этих функций на интервале длины 2𝜋.
Рассмотрим графики
грех𝜃 и cos𝜃.
Оба приведенных выше графика находятся на интервале [−3𝜋,3𝜋], но нам нужен только график на интервале длины 2𝜋. Итак, мы можем рассмотреть этот граф на интервале [0,2𝜋], чтобы найти домен и диапазон этих функции. Поскольку обе функции определены всюду в интервале [0,2𝜋], мы знаем, что области определения обоих синусов и функции косинуса — все действительные числа.
Также можно отметить, что минимальное значение обеих функций на интервале [0,2𝜋] равно −1, а максимальное значение равно 1. Поскольку обе функции принимают все значения между максимальным и минимальным, диапазон функций синуса и косинуса на этом интервале и, следовательно, над их областями есть [−1,1].
Мы суммируем эти результаты следующим образом.
Определение: Область определения и диапазон функций синуса и косинуса
Область определения функций sin𝜃 и cos𝜃 — это все действительные числа, ]−∞,∞[ или ℝ.
Диапазон функций sin𝜃 и cos𝜃 равен [−1,1].
Выше мы определили домен и диапазон sin𝜃 и cos𝜃 с помощью графика и периодичность этих тригонометрических функций. В нашем следующем примере мы будем использовать тот же метод для определения домена и диапазона периодическая функция.
Пример 2. Определение области определения и диапазона периодической функции по ее графику
На следующем графике показана функция 𝑓(𝜃). Предположим, что функция имеет период 2𝜋.
- Каков домен 𝑓(𝜃)?
- Каков диапазон 𝑓(𝜃)?
Ответ
Мы знаем, что все характеристики периодической функции содержатся в графике функции на интервале, длина которого равна период. Эта функция имеет период 2𝜋; следовательно, нам нужно рассматривать только его график на интервале длины 2𝜋. В этом примере функция 𝑓(𝜃) изображается на интервале длиной больше 2𝜋, так что это должно предоставить достаточную информацию для определения домена и диапазона 𝑓(𝜃).
Часть 1
Область определения функции — это набор всех возможных входных значений.
Из приведенного графика видно, что функция корректно определена при любых значениях
из 𝜃. Таким образом, областью определения 𝑓(𝜃) являются все действительные числа, или
]−∞,∞[.
Часть 2
Диапазон функции представляет собой набор всех возможных значений функции. Из данного графика мы видим, что эта функция колеблется между −7 и 3, принимая все значения между ними. График никогда не опускается ниже -7 или выше 3 по вертикальной оси. Следовательно, диапазон 𝑓(𝜃) равен [−7,3].
Когда нам даны алгебраические выражения тригонометрических функций, мы можем использовать функциональные преобразования, чтобы найти диапазон функции с помощью графические функции 𝑎𝜃+𝑏sin или 𝑎𝜃+𝑏cos для некоторых констант 𝑎 и 𝑏. Будем рассматривать только образ функций типа 𝑎𝜃+𝑏sin, так как образ последних будет идентичным.
Начнем с функции sin𝑥, которая имеет диапазон [−1,1]. Умножение функции на положительное
постоянная 𝑎 приводит к вертикальному расширению (растяжению или сжатию) на масштабный коэффициент 𝑎, который изменяет
диапазон функции от [−1,1] до [−𝑎,𝑎].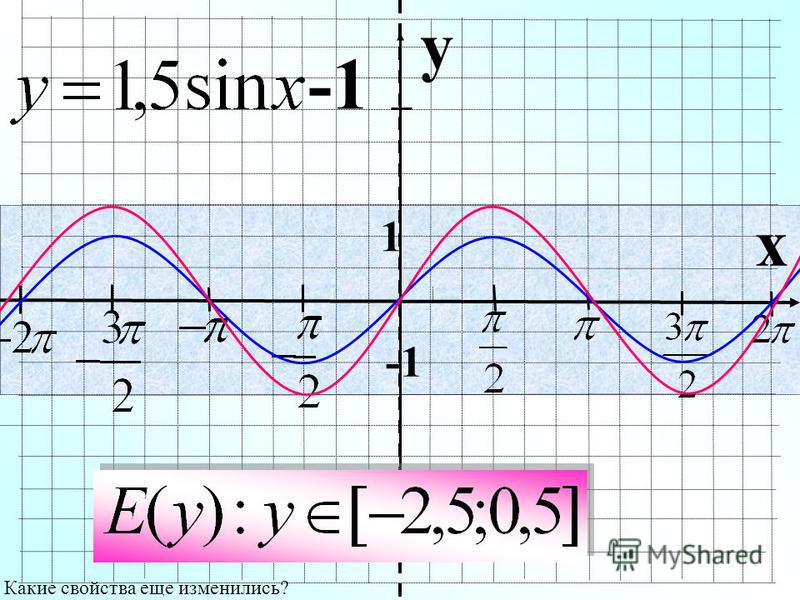
Далее, мы знаем, что добавление 𝑏 к функции приводит к сдвигу по вертикали (вверх, если 𝑏>0, и вниз, если 𝑏0) на 𝑏 единиц. Поскольку диапазон 𝑎𝑥sin равен [−|𝑎|,|𝑎|], сдвиг по вертикали на 𝑏 единиц изменил бы этот диапазон на [−|𝑎|+𝑏,|𝑎|+𝑏].
Например, давайте рассмотрим диапазон 2𝑥+1sin, используя следующую диаграмму.
На диаграмме сплошной синий график представляет функцию sin𝑥, которая имеет диапазон
[−1,1]. Умножение sin𝑥 на 2 изменяет диапазон от [−1,1] до [−2,2]. Двусторонние синие стрелки на диаграмме указывают на то, что исходный график растянут по вертикали в 2 раза, чтобы получить график
2𝑥sin, что дает штриховую кривую.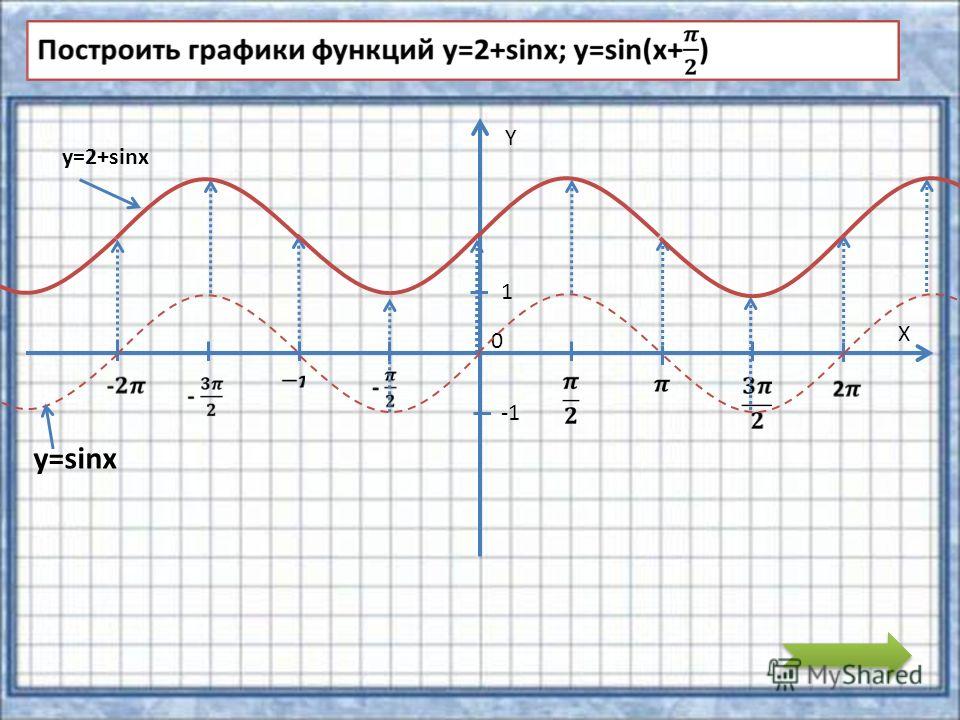
Как мы отмечали ранее, мы можем видеть, что диапазон 2𝑥sin равен
[−2,2]. Добавление 1 к 2𝑥sin сдвигает диапазон вверх на 1, что приводит к новому диапазону
[−1,3]. Вертикальные красные стрелки показывают, что график 2𝑥sin сдвинут вверх, чтобы получить
график 2𝑥+1sin. Мы можем заметить, что диапазон этого красного графика равен [−1,3], как и ожидалось.
В следующем примере мы определим диапазон функции синуса из ее алгебраического выражения.
Пример 3. Нахождение диапазона заданной синусоидальной функции
Найдите диапазон функции 𝑓(𝜃)=87𝜃sin.
Ответ
Напомним, что синусоидальная функция sin𝜃 является периодической и ее график колеблется между −1 и 1. Это говорит нам о том, что диапазон sin𝜃 равен [−1,1]. Мы можем использовать эту информацию определить диапазон заданной функции.
Диапазон — это набор всех возможных значений функции, поэтому мы ищем все возможные значения выражения 87𝜃,𝜃.sinwhereisanyrealnumber
Поскольку 𝜃 может принимать любое значение, умножение 𝜃 на 7 не меняет набор значений, которые могут получиться
от этого выражения.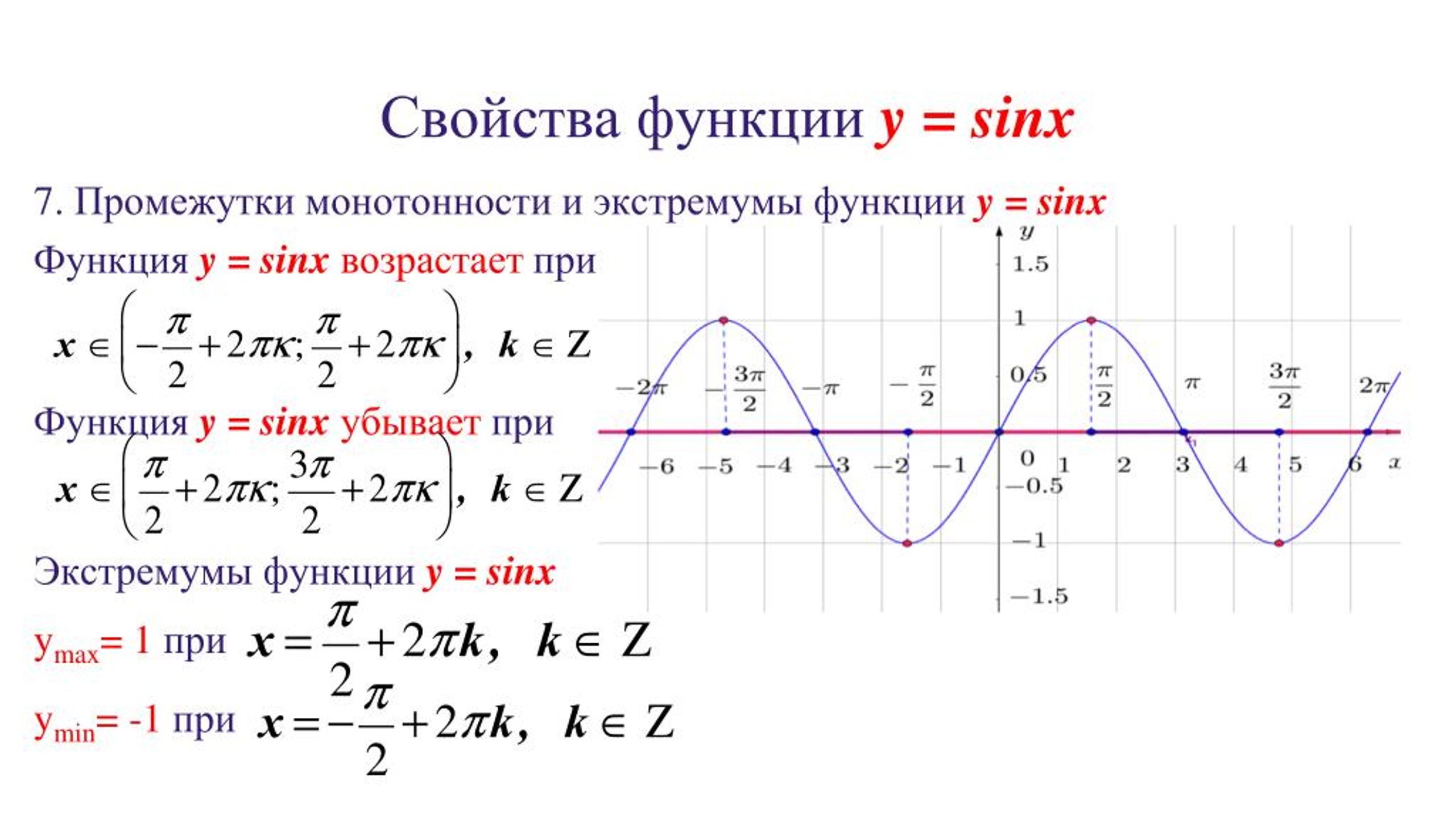
Поскольку sin𝜃 может принимать любые значения из [−1,1], мы знаем, что
sin7𝜃 также ограничен тем же диапазоном.
Умножение 8 на выражение sin7𝜃 растягивает график функции по вертикали в 8 раз. Это преобразование изменяет диапазон от [−1,1] до [−8,8].
Следовательно, диапазон 𝑓(𝜃)=87𝜃sin равен [−8,8].
В нашем следующем примере мы определим домен и диапазон функции косинуса, используя тот же метод.
Пример 4. Нахождение области определения и области значений тригонометрических функций
Рассмотрим функцию 𝑓(𝑥)=4(7𝑥+𝜋)+5cos.
- Какой домен у 𝑓(𝑥)?
- Каков диапазон 𝑓(𝑥)?
Ответ
Часть 1
Найдем домен 𝑓(𝑥). Область определения функции — это набор всех возможных входных значений. Мы знаем это
область определения функции cos𝜃 — все действительные числа. Это говорит нам об отсутствии ограничений на входные значения косинуса. В функции 𝑓(𝑥) выражение 7𝑥+𝜋 находится внутри функции косинуса.
Поскольку эта функция
корректно определен для любого действительного числа, область определения 𝑓(𝑥) — это все действительные числа, или
]−∞,∞[.
Часть 2
Рассмотрим диапазон 𝑓(𝑥). Диапазон — это набор всех возможных значений функции, поэтому нам нужно определить множество всех возможных значений выражения 4(7𝑥+𝜋)+5,𝑥.cosforanyrealnumber
Мы знаем, что диапазон 7𝑥+𝜋 — это все действительные числа, поэтому это выражение может принимать любое значение. Обозначая 𝜃=7𝑥+𝜋, нам нужно найти множество возможных значений выражения 4𝜃+5,𝜃.cosforanyrealnumber
Давайте подумаем над преобразованиями функций, чтобы получить диапазон этого выражения. Мы знаем, что cos𝜃 имеет диапазон [−1,1]. Умножение функции на 4 приводит к растяжению этого диапазона по вертикали в 4 раза, что приводит к диапазону [−4,4]. Добавление 5 к этому выражению сдвигает функцию вверх на 5, что дает нам диапазон [1,9].
В качестве альтернативы, мы можем найти это алгебраически, выполнив следующие вычисления:
−1≤𝜃≤1−4≤4𝜃≤41≤4𝜃+5≤9.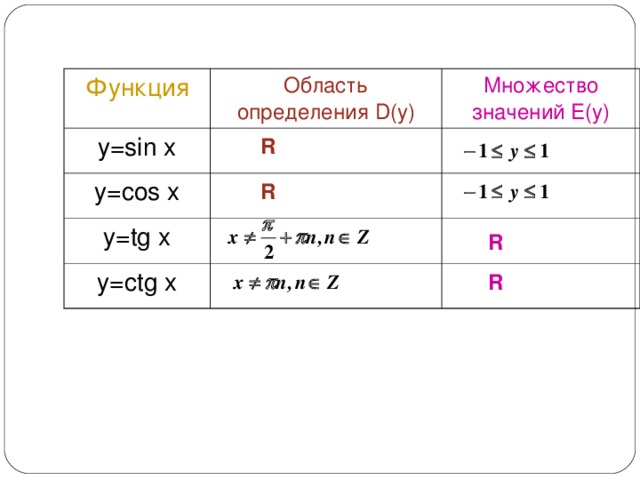
coscoscos
Это также приводит к диапазону [1,9].
Диапазон 𝑓(𝑥) равен [1,9].
В нашем следующем примере мы идентифицируем неизвестную константу в тригонометрической функции, когда нам задан диапазон функции.
Пример 5. Нахождение области значений тригонометрической функции по ее правилу
Область значений функции 𝑓(𝜃)=𝑎3𝜃cos равна −54,54. Найдите значение 𝑎, где 𝑎>0.
Ответ
Напомним, что диапазон cos𝜃 равен [−1,1], а область значений cos𝜃 все действительные числа. Поскольку и 3𝜃, и 𝜃 имеют одинаковый диапазон, cos3𝜃 имеет тот же диапазон, что и cos𝜃. Это говорит нам о том, что множество всех возможных исходов, то есть диапазон cos3𝜃 равно [−1,1].
Умножение функции на положительную константу 𝑎 приводит к вертикальному расширению на коэффициент 𝑎. Поскольку диапазон cos3𝜃 равно [−1,1], применение вертикального расширения к этому диапазону делает диапазон 𝑎3𝜃cos быть [−𝑎,𝑎].
Мы показали, что диапазон 𝑓(𝜃)=𝑎3𝜃cos равен [−𝑎,𝑎].
Мы
учитывая, что диапазон этой функции составляет −54,54. Это ведет к
𝑎=54.
До сих пор мы рассматривали примеры, касающиеся области определения и ряда функций, включающих синусы и косинусы. Обратим внимание на касательная функция. Напомним, что функция тангенса определяется как отношение функций синуса и косинуса тансинкос𝜃=𝜃𝜃.
Это означает, что функция тангенса будет иметь ограничения домена, когда функция косинуса равна нулю. Рассмотрим график tan𝜃 на интервале [−3𝜋,3𝜋] радиан.
Из графика видно, что функция тангенса повторяется
𝜋 радианы. Следовательно, период касательной функции равен
𝜋 радиан, что отличается от периода функций синуса и косинуса. Это означает, что мы можем найти домен и
диапазон касательной функции, исследуя ее график на интервале [0, 𝜋]. На этом интервале мы видим
что касательная функция не определена при 𝜃=𝜋2. Поскольку эта функция имеет период 𝜋, это
означает, что касательная функция не определена в каждом 𝜋, начиная с точки 𝜋2, как мы можем
см.
на графике. Другими словами, tan𝜃 не определен, когда
𝜃=𝜋2+𝑛𝜋,𝑛∈ℤ.
Чтобы найти диапазон tan𝜃, мы также можем рассмотреть его график на интервале [0,𝜋]. Мы видим, что график функции на этом интервале идет вверх до положительной бесконечности и вниз до отрицательной бесконечности. Это значит, что диапазон tan𝜃 — это набор всех действительных чисел.
Мы суммируем эти результаты следующим образом.
Определение: область определения и диапазон касательной функции 𝜃=𝜋2+𝑛𝜋,𝑛∈ℤ.
Домен tan𝜃, в градусах, представляет собой все действительные числа за исключением 𝜃=90+180𝑛,𝑛∈ℤ.∘∘
Диапазон tan𝜃 — это все действительные числа, обозначаемые либо ]−∞,∞[ либо ℝ.
В нашем последнем примере мы идентифицируем входные значения, в которых функция тангенса не определена.
Пример 6. Поиск значений, в которых тангенс не определен
Найдите значения 𝜃 в радианах, чтобы функция
𝑓(𝜃)=(3𝜃)загар не определен.
Ответ
Напомним, что область определения касательной функции tan𝜃, в радианы, исключая значения вида 𝜃=𝜋2+𝑛𝜋,𝑛∈ℤ.
Данная функция 𝑓(𝜃)=(3𝜃)tan включает в себя функцию тангенса, поэтому нам нужно найти значения 𝜃 такие, что эта функция не определена, когда вход 3𝜃 касательной дает одно из эти значения. Другими словами, 𝑓(𝜃) не определено, когда 3𝜃=𝜋2+𝑛𝜋,𝑛∈ℤ.
Разделив обе части приведенного выше уравнения на 3, мы получим, что функция 𝑓(𝜃)=(3𝜃)tan не определена. когда 𝜃 равно 𝜋6+𝑛𝜋3,𝑛∈ℤ.
Давайте закончим повторением нескольких важных моментов объяснения.
Ключевые моменты
- Если функция 𝑓(𝑥) является периодической с периодом 𝐿, то мы можем найти область определения и область значений эту функцию, рассматривая график этой функции на интервале [0,𝐿].
- Областью определения функций sin𝜃 и cos𝜃 являются все действительные числа, обозначаемые либо
]−∞,∞[ или ℝ.
Диапазон функций sin𝜃 и cos𝜃 равен [−1,1]. - Для любых констант 𝑎 и 𝑏 диапазон функции 𝑎𝑥+𝑏sin или 𝑎𝑥+𝑏cos равно [−|𝑎|+𝑏,|𝑎|+𝑏].
- Домен tan𝜃, в радианах, полностью реален числа, кроме 𝜃=𝜋2+𝑛𝜋,𝑛∈ℤ. Область загара в градусах реальна числа, кроме 𝜃=90+180𝑛,𝑛∈ℤ.∘∘ Диапазон tan𝜃 — это все действительные числа, обозначаемые либо ]−∞,∞[ или ℝ.
Область определения и диапазон тригонометрических функций и их графиков
на
Область определения функции определяется как конкретные заданные значения, которые независимая переменная, содержащаяся в функции, может принять в работу. Диапазон существует как результирующие значения, которые зависимая переменная может содержать значение «x» изменений по всему домену.
Для функций косинуса и синуса, диапазон и область значений
Для функций области значений косинуса и синуса ограничений нет.
Таким образом, их домен приводит к виду x ∈ R.
Важно отметить, что, тем не менее, диапазон для y = cos (x) и y = sin (x) находится между диапазоном (-1 & 1) . Следовательно, изменения, обнаруженные в этих функциях в отношении растяжений и сдвигов, приведут к влиянию на диапазон тригонометрических функций, но не на область определения тригонометрических функций.
Домен и диапазон синусоидальной функции
y = f(x)= Sin(x)
Диапазон: Значение лежит в пределах -1 ≤ y ≤ 1 Значения
Период: 2π = 360º
Синусоидальная функция является нечетной функцией
График SIN (x) Функция:
Домен и диапазон косин
y = f (x x = f (x x = f (x x = f (x x = f (x x = f (x x = f (x x = f (x x = f (x. ) = cos(x)
Диапазон: значение лежит в пределах -1 ≤ y ≤ 1
Domain: Defined for all the x real values
Period: 2π
Cosine is an even function
The Graph of cos(x) function:
Из приведенного выше графика видно, что диапазон остается прежним, а график сокращается
Домен и диапазон для функций касательной
Обратите внимание, что функция y = tan (x) состоит из вертикальных асимптот при .