Область значения это х или у: «Что такое область определения функции. и как ее находить?» — Яндекс Кью

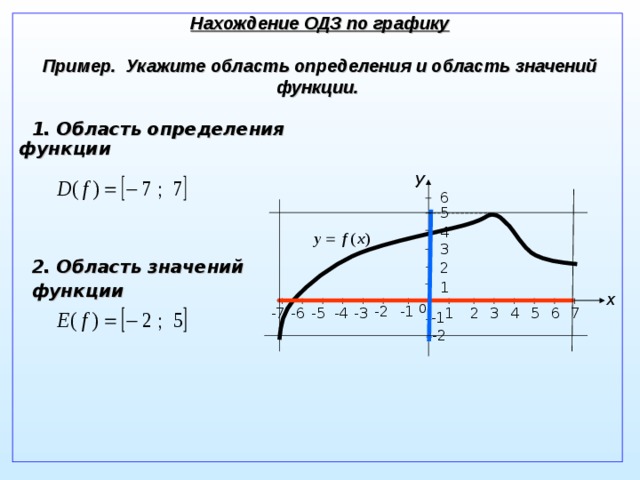
«Что такое область определения функции. и как ее находить?» — Яндекс Кью

Популярное

Сообщества

Точные науки

Анонимный вопрос

2 ноября 2018  ·

80,2 K

Ответить2Уточнить

Ольга Окунькова

Образование

195

Учитель математики в средней школе И ВУЗе. Не учу жизни, учу решать задачи. Готовлю к ОГЭ…  · 10 авг 2019

Функции, в школьном курсе математики, рассматривают в двумерной системе координат (чаще всего это x и у). Функций очень много. Но в школе проходят стандартные (можно сказать типовые). Область определения это те значения, которые функция может принимать.
Линейная функция определена везде. Возьмём гиперболу, точнее частный ее случай. y=1/x, но мы знаем, что на 0 делить нельзя, появляется ограничение х не равен 0.

Т.е. при х=0 функции не существует. На графике это выглядит как разрыв функции в этом месте.

25,9 K

Комментировать ответ…Комментировать…

Александр Воронов

1,0 K

Обожаю точные науки и испытываю огромный интерес к творчеству. При таком сочетании…  · 3 нояб 2018

Область определения — это все значения, которые может принимать аргумент функции.

Пример: y = 5 * x;

Здесь «x» может быть любым числом.

Пример: 1 / x — 5;

А здесь «x» не может быть равен 5, но может быть любым другим числом, ведь результата деления на 0 не приняли.

17,4 K

Комментировать ответ…Комментировать…

Первый

Валерий Смогунов

149

20 сент 2020

Отвечает

Валерий Смогунов

Есть уравнение, например, y=x+5; Область определения функции — это множество чисел Х, которые можно подставить в это уравнение. Всевозможные значения Y называются областью значений функции. Скорее всего так) Удачи! Читать далее

Комментировать ответ…Комментировать…

Виталий Новиков

-4

16 июн 2021

Ольга, почему вы решили, что y=1/x — функция? Где описание того, какое нагромождение всяких знаков типа «x»,»y» «=», «+» и т.д. представляет собой некое допустимое выражение, которое можно было бы назвать функцией? Ведь не кажется ли вам, что прежде чем искать область определения или значения чего либо, нужно дать определение этому «чему либо»? В каком учебнике… Читать далее

Комментировать ответ…Комментировать…

Vladimir

Технологии

6,4 K

Компьютеры и автомобили. YouTube: https://www.youtube.com/c/Коленвальщик/ Яндекс.Дзен: h…  · 4 нояб 2018  · youtube.com/c/Коленвальщик/

Есть уравнение, например, y=x+5;

Область определения функции — это множество чисел Х, которые можно подставить в это уравнение. 2

домен и диапазон

Горячая математика

домен из функция ф ( Икс ) это набор всех значений, для которых определена функция, и диапазон функции – это множество всех значений, которые ф берет.

(В начальной школе вы, вероятно, называли домен замещающим набором, а диапазон — набором решений. Их также можно было назвать входом и выходом функции.)

Пример 1:

Рассмотрим функцию, показанную на схеме.

Здесь домен представляет собой набор { А , Б , С , Е } . Д не находится в домене, так как функция не определена для Д .

Ассортимент — это набор { 1 , 3 , 4 } . 2 не входит в диапазон, так как в домене нет буквы, которая сопоставляется с 2 .

Вы также можете говорить о домене связь , где один элемент в домене может быть сопоставлен более чем с одним элементом в диапазоне.

Пример 2:

Рассмотрим отношение { ( 0 , 7 ) , ( 0 , 8 ) , ( 1 , 7 ) , ( 1 , 8 ) , ( 1 , 9) , ( 2 , 10 ) } .

Здесь отношение задано как набор упорядоченных пар. Домен представляет собой набор Икс -координаты, { 0 , 1 , 2 } , а диапазон — это набор у -координаты, { 7 , 8 , 9, 10 } . Обратите внимание, что элементы домена 1 и 2 связаны с более чем одним элементом диапазона, так что это нет функция.

Но чаще, и особенно при работе с графиками на координатной плоскости, мы имеем дело с функциями, где каждый элемент области связан с одним элементом диапазона. (См. Проверка вертикальной линии .)

Пример 3:

Область определения функции

ф ( Икс ) «=» 1 Икс

все действительные числа, кроме нуля (поскольку при Икс «=» 0 , функция не определена: деление на ноль запрещено!).

Диапазон также включает все действительные числа, кроме нуля. Вы можете видеть, что на кривой есть некоторая точка для каждого у -значение кроме у «=» 0 .

Домены также можно указать явно, если есть значения, для которых функция может быть определена, но которые мы по каким-то причинам не хотим рассматривать.

Пример 4:

Следующие обозначения показывают, что область определения функции ограничена интервалом ( − 1 , 1 ) .

ф ( Икс ) «=» Икс 2 , − 1 < Икс < 1

График этой функции такой, как показано. Обратите внимание на незакрашенные кружки, которые показывают, что функция не определена в Икс «=» − 1 и Икс «=» 1 . у -значения варьируются от 0 вплоть до 1 (включая 0 , но не включая 1 ). Таким образом, область действия функции

0 ≤ у < 1 .

Домен и диапазон

Домен и диапазон функции — это все возможные значения независимой переменной x, для которой определено y. Диапазон функции — это все возможные значения зависимой переменной y. Другими словами, домен — это набор значений, которые мы можем вставить в функцию, которая даст реальное значение y; диапазон — это набор значений, которые функция принимает в результате подстановки значения x в область определения функции.

С математической точки зрения, если задана функция f(x), значения, которые f(x) может принимать, составляют диапазон функции, а все возможные значения x составляют область. Рассмотрим функцию f(x) = x ² .

Пример:

f(x) = x ²

Нет значений x, которые приведут к тому, что функция будет неопределенной, и независимо от того, какое реальное значение x мы подставим, результат всегда будет реальным y -ценить. Таким образом, областью определения f(x) = x ² являются все значения x. Затем, глядя на график или тестируя несколько значений x, мы видим, что любое значение x, которое мы подставляем, приведет к положительному значению y. Таким образом, диапазон f(x) = x ² — все положительные значения y.

Обратите внимание, что в приведенных выше примерах мы описали домен и диапазон с помощью слов. Хотя это возможно для всех функций, для более краткого выражения доменов и диапазонов были разработаны различные нотации. Это значительно упрощает одновременное выражение доменов и диапазонов нескольких функций, особенно по мере усложнения функций. Двумя из этих обозначений являются интервальное обозначение и обозначение множества.

Обозначение интервала

При использовании записи интервалов домен и диапазон записываются как интервалы значений. В таблице ниже показаны основные символы, используемые в записи интервалов, и их значение:

Имя	Символ	Значение
Скобки	( )	Конечные точки не включены (эксклюзивно)
Кронштейны	[ ]	Конечные точки включены (включительно)
Союз	∪	«или» — используется для объединения двух или более наборов

При указании области в интервальной записи необходимо иметь в виду следующее:

• Сначала пишется наименьший член в интервале, затем запятая, а затем наибольший член.
• Первый член — это левая конечная точка, а второй — правая конечная точка.
• Конечные точки записываются либо в круглые, либо в квадратные скобки, в зависимости от того, включена конечная точка или нет.

Давайте рассмотрим тот же пример, что и выше, f(x) = x

2 , чтобы увидеть, как используется обозначение интервала. Напомним, что область определения f(x) = x ² состоит из всех действительных чисел. Другими словами, любое значение от отрицательной бесконечности до положительной бесконечности даст реальный результат. Таким образом, мы можем записать домен как:

(-∞, ∞)

Мы использовали круглые скобки, а не квадратные скобки вокруг каждой конечной точки, потому что конечные точки являются отрицательной и положительной бесконечностью, которые по определению не имеют границ. Напомним, что диапазон f(x) = x ² — все положительные значения y, включая 0. Таким образом, диапазон может быть записан в виде интервала:

[0, ∞)

Символ объединения используется, когда у нас есть функция, область определения или диапазон которой не могут быть описаны только с одним интервалом.

Символ объединения можно прочитать как «или», и он используется в различных областях математики. В контексте обозначения интервала это просто означает объединение двух заданных интервалов. Например, рассмотрим функцию:

Это то же самое, что и наша функция выше, за исключением того, что она не определена на интервале (0, 1). Таким образом, областью определения функции являются все значения x, кроме значений в интервале (0, 1), которые мы можем указать в записи интервала с помощью символа объединения следующим образом:

(-∞, 0] ∪ [1, ∞)

Обратите внимание, что можно также использовать несколько символов объединения для объединения большего количества интервалов таким же образом.

Нотация набора

При использовании нотации набора, также называемой нотацией построителя набора, мы используем символы неравенства для описания домена и диапазона как набора значений. Как и в обозначении интервалов, в обозначении наборов используется ряд символов, наиболее распространенные из которых показаны в таблице ниже:

Имя	Символ	Значение
Скобы	{ }	«набор» — указывает на набор
Вертикальная перекладина	|	«такой, что» — за символом следует ограничение
«Элемент»	∈	Указывает, что элемент является членом некоторого набора
Двойной удар R	ℝ	Набор всех действительных чисел
Союз	∪	«или» — используется для объединения двух или более наборов

Стандартные символы неравенства, такие как , ≥ и т.