Функция log, ее свойства и график (продолжение) 11 класс онлайн-подготовка на Ростелеком Лицей
1. Логарифм, определение, основные факты
Логарифмическая функция базируется на понятии логарифма и свойства показательной функции , где (основание степени а больше нуля и не равно единице).
Определение:
Логарифмом числа b по основанию а называется такой показатель степени, в которую нужно возвести основание а, чтобы получить число b.
Примеры:
Напомним основное правило: чтобы получить число, стоящее под логарифмом, необходимо основание логарифма возвести в степень – значение логарифма:
Напомним важные особенности и свойства показательной функции.
Рассмотрим первый случай, когда основание степени больше единицы: :
Рис. 1. График показательной функции, основание степени больше единицы
Такая функция монотонно возрастает на всей своей области определения.
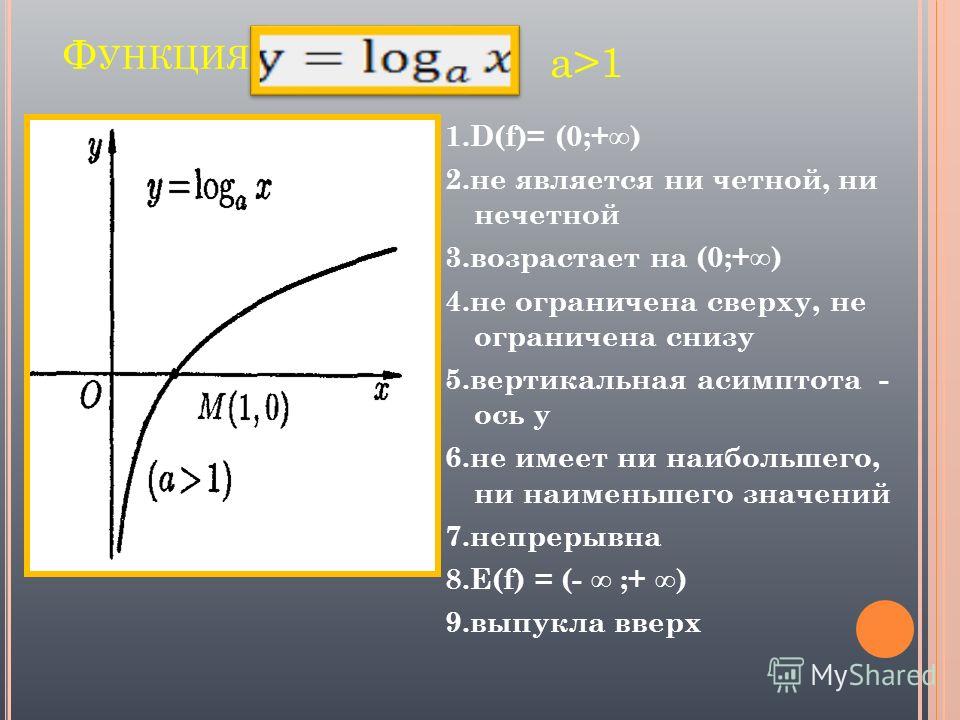
Рассмотрим второй случай, когда основание степени меньше единицы :
Рис. 2. График показательной функции, основание степени меньше единицы
Такая функция монотонно убывает на всей своей области определения.
В любом случае, показательная функция монотонна, принимает все положительные значения и, в силу своей монотонности, каждое положительное значение достигает при единственном значении аргумента. То есть, каждое конкретное значение функция достигает при единственном значении аргумента , корнем уравнения и есть логарифм:
По сути, мы получили обратную функцию. Прямая функция – это когда у нас есть независимая переменная х (аргумент), зависимая переменная у (функция), мы задали значение аргумента и по нему получаем значение функции. Обратная функция: пусть независимой переменной будет у, ведь мы уже оговорили, что каждому положительному значению у соответствует единственное значение х, определение функции соблюдается. Тогда х становится зависимой переменной.
Вывод:
Для монотонной прямой функции существует обратная функция . Суть функциональной зависимости не изменится, если мы введем переобозначение:
Получаем:
Но нам привычнее обозначать независимую переменную за х, а зависимую – за у:
Таким образом, мы получили логарифмическую функцию.
2. Свойства показательной функции
Используем общее правило получения обратной функции для конкретной показательной функции .
Заданная функция монотонно возрастает (согласно свойствам показательной функции), значит, существует обратная ей функция. Напоминаем, что для ее получения необходимо выполнить два действия:
Выразить х через у:
Поменять местами х и у:
3. Логарифмическая функция как обратная к показательной
Итак, получили функцию, обратную заданной: . Как известно, графики прямой и обратной функции симметричны относительно прямой у=х.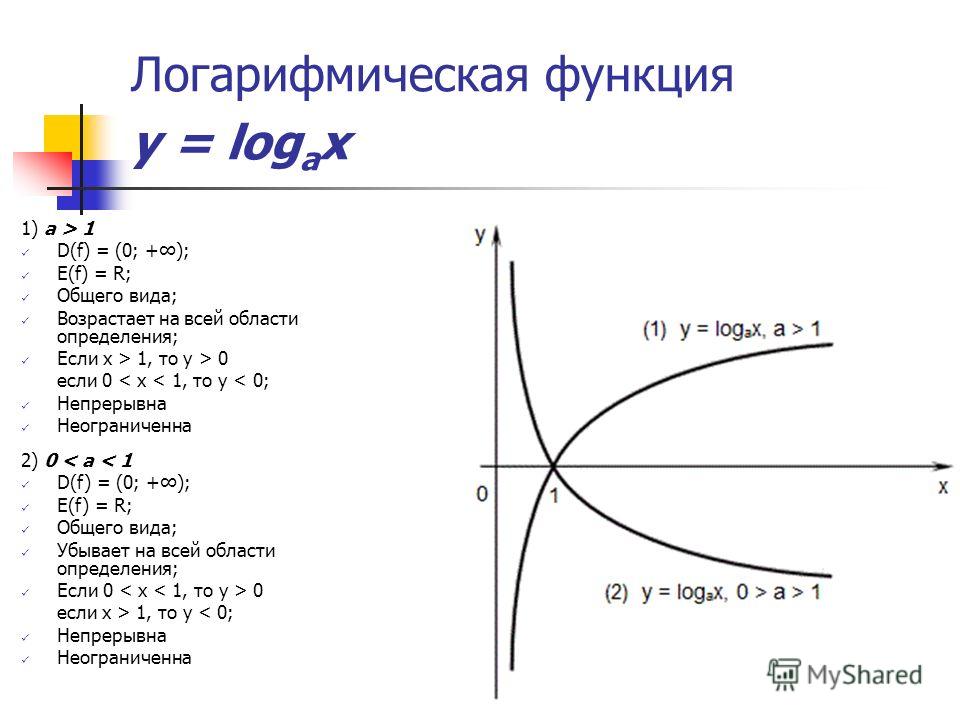 проиллюстрируем:
проиллюстрируем:
Рис. 3. Графики функций и
4. Примеры нахождения обратной функции
Данная задача решается аналогично и справедлива для любого основания степени.
Решим задачу при
Заданная функция монотонно убывает, значит, существует обратная ей функция. Получим ее:
Выразить х через у:
Поменять местами х и у:
Итак, получили функцию, обратную заданной: . Как известно, графики прямой и обратной функции симметричны относительно прямой у=х. проиллюстрируем:
Рис. 4. Графики функций и
Заметим, что мы получили логарифмические функции как обратные к показательным.
У прямой и обратной функций есть много общего, но есть и отличия. Рассмотрим это подробнее на примере функций и .
Рис. 5. Графики функций (слева) и (справа)
5. Связь прямой и обратной функции
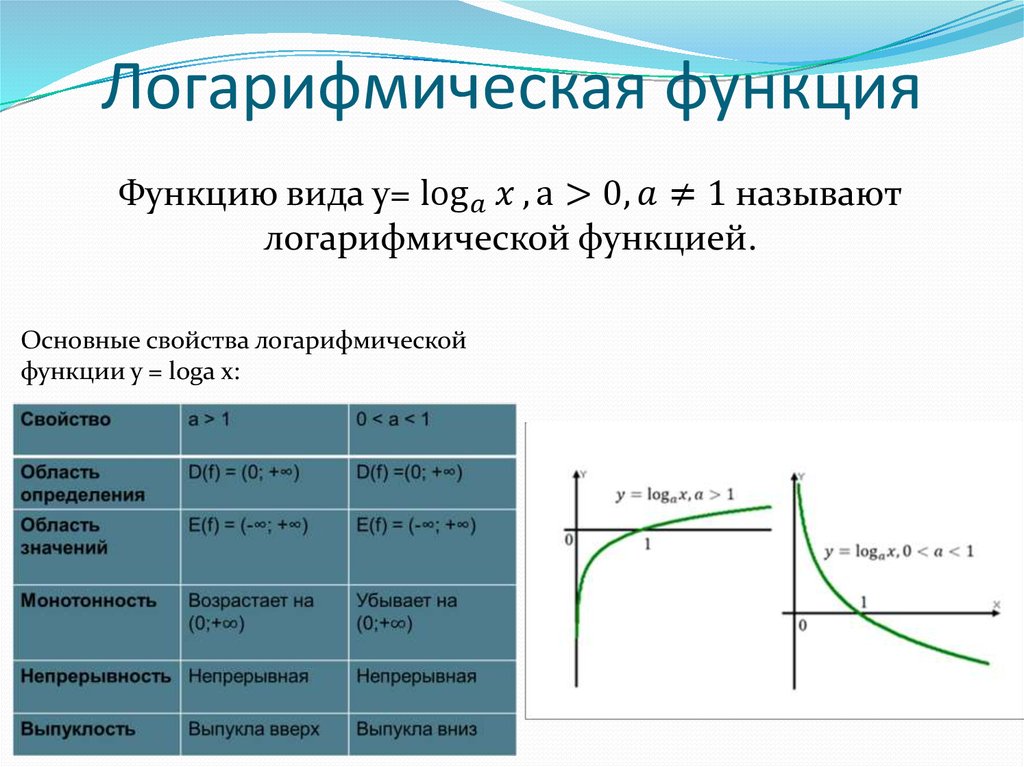
Свойства прямой (показательной) функции:
Область определения: ;
Область значений: ;
Функция возрастает;
Выпукла вниз.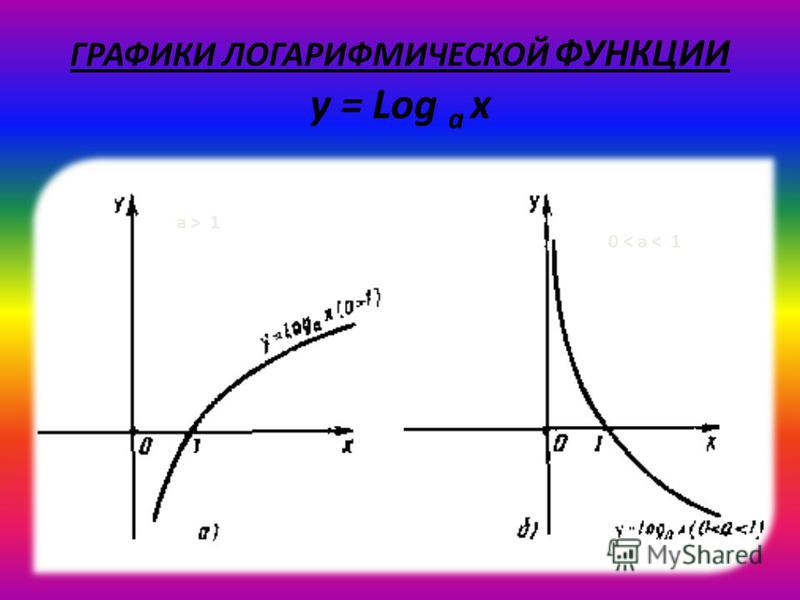
Свойства обратной (логарифмической) функции:
Область определения: ;
Область значений: ;
Функция возрастает;
Выпукла вверх.
Обратим внимание, что область определения и область значений прямой и обратной функции меняются местами. Кроме того, если прямая функция возрастает, то и обратная возрастает. И, наконец, если прямая функция выпукла вниз, то обратная – вверх.
Таким образом, мы подтвердили связь прямой и обратной функции.
Итак, мы изучили логарифмическую функцию и ее связь с показательной функцией. На следующем уроке мы продолжим рассматривать логарифмическую функцию и научимся решать типовые задачи.
Список литературы
- Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
- Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.
 : Просвещение.
: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Edu.glavsprav.ru (Источник).
- Nado5.ru (Источник).
- Uztest.ru (Источник).
Домашнее задание
1. Алгебра и начала анализа, 10–11 класс (А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын) 1990, № 504, 505, 507;
2. Укажите область определения функции, обратной к заданной, не записывая ее:
а) ; б) ; в) ; г)
3. Укажите область значений функции, прямой относительно заданной, не записывая ее:
а) ; б) ; в) ; г) ;
Натуральный логарифм — frwiki.wiki
Натуральный логарифм или натуральный логарифм , или гиперболический логарифм к XX — го века, преобразованная, как и другие логарифмические функции , сумм продуктов. Использование таких функций позволяет упростить вычисления, включающие многочисленные умножения, деления и возвышения до рациональных степеней. Его часто обозначают ln () .
Его часто обозначают ln () .
Говорят, что натуральный или натуральный логарифм имеет основание e, потому что ln (e) = 1 .
Натуральный логарифм числа x также можно определить как степень, в которую мы должны возвести e, чтобы получить x . Поэтому естественная функция логарифма является обратной биекцией из экспоненциальной функции . Это также первообразная, определенная на строго положительных действительных числах и обращающаяся в нуль в точке 1 обратной функции
Эта функция была отмечена l. или в начале XVIII — го века и в первой половине XIX — го века, а затем войти. или войти в конце XVIII — го века, а затем войти дифференцировать журнал функции (логарифм любого основания, или более конкретно логарифма ) или Logh ( «гиперболический логарифм»), до навязывают обозначения , рекомендованные AFNOR 1961 и стандарты ISO 80000-2: обозначение ln .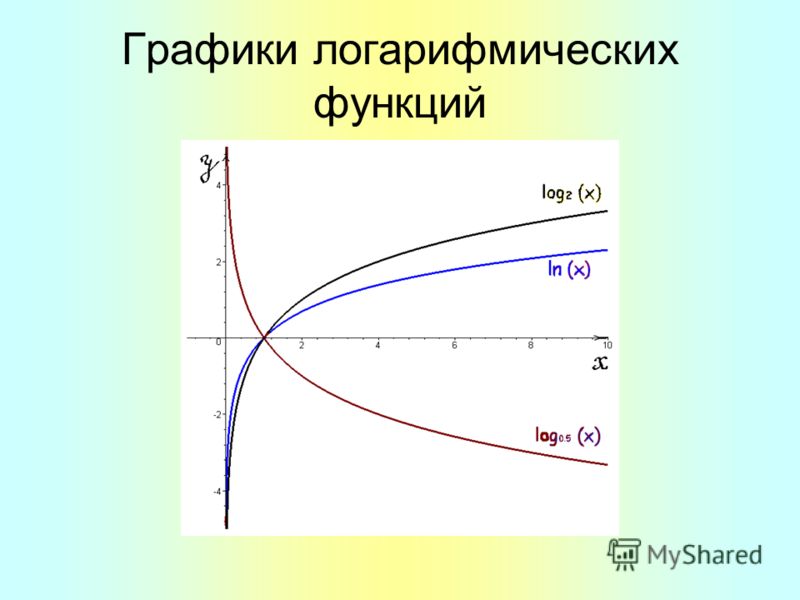 Однако с относительным успехом: логарифмическая нотация до сих пор используется в нескольких разделах математики, особенно в теории чисел, а также в нескольких языках программирования, таких как C , C ++ , SAS , R , MATLAB , Mathematica , Fortran. , и BASIC .
Однако с относительным успехом: логарифмическая нотация до сих пор используется в нескольких разделах математики, особенно в теории чисел, а также в нескольких языках программирования, таких как C , C ++ , SAS , R , MATLAB , Mathematica , Fortran. , и BASIC .
Резюме
- 1 История
- 2 Функция натурального логарифма как первообразная обратной функции
- 3 Исследование функции
- 4 Функция натурального логарифма как функция логарифма
- 5 Функция натурального логарифма как обратная экспоненциальной функции
- 6 Серийная разработка
- 7 Дополнительные свойства
- 7.1 Изучение пределов
- 7.2 Логарифмическая производная
- 7.3 Примитив
- 8 Функция натурального логарифма как функция комплексной переменной
- 9 Примечания и ссылки
- 10 См.
 Также
Также- 10.1 Статьи по теме
- 10.2 Внешние ссылки
Исторический
Таблица натуральных логарифмов от 0,01 до 100 с пятью десятичными знаками.
Этот логарифм называется неперианским в честь шотландского математика Джона Напьера, который установил первые логарифмические таблицы (которые на самом деле не являются таблицами натуральных логарифмов). Как правило , мы датировать происхождение натуральных логарифмов в 1647 году, когда Грегори Сент-Винсент работает на квадратуре на гиперболы и показывает , что полученная функция проверяет свойство аддитивности функций логарифмов . Сен-Винсент, однако, не видит никакой связи с логарифмами Напьера, и его ученик Альфонс Антуан де Сараса объяснит это в 1649 году . Натуральный логарифм сначала был назван «гиперболическим логарифмом» по отношению к площади под гиперболой, которую он представляет. Название «натуральный логарифм», данное Пьетро Менголи в 1659 году, было использовано в 1668 году в примечании Николая Меркатора к серии, носящей его имя.
Функция натурального логарифма как функция логарифма
Натуральный логарифм удовлетворяет тому же функциональному уравнению, что и любая функция логарифма , а именно: для всех действительных x и y строго положительных,
Действительно, при фиксированном y > 0 функция x ↦ ln ( xy ) (определенная на ] 0, + ∞ [ ) имеет ту же производную, что и натуральный логарифм, поэтому отличается от действительной константы k : ln ( xy ) = ln ( x ) + k , где k = ln ( y ), поскольку ln (1 y ) = ln (1) + k = k . {r}) = r \ ln (a).}
{r}) = r \ ln (a).}
Тот факт, что все функции логарифма пропорциональны друг другу, позволяет получить для любого строго положительного действительного числа a базовый логарифм a как функцию натурального логарифма:
Функция натурального логарифма как обратная экспоненциальной функции
Исследование натурального логарифма функции показал , что это взаимно однозначное соответствие с ] 0, + ∞ [ в ℝ. Его обратная биекция из ℝ в ] 0, + ∞ [ совпадает с экспоненциальной функцией , поскольку она является собственной производной и переводит значение 1 в 0. Это дает возможное определение экспоненциальной функции из логарифма. И наоборот, мы могли бы определить логарифм как взаимную биекцию экспоненты, а затем проверить его характеристику выше .
Демонстрация
Пусть f :] 0, + ∞ [→ ℝ и g : ℝ →] 0, + ∞ [ две взаимные биекции, взаимные. Конечно, мы имеем: f (1) = 0 тогда и только тогда, когда g (0) = 1 . Покажем, благодаря теореме о производной обратной биекции , что f является первообразной x ↦1/Икстогда и только тогда, когда g — его собственная производная.
Конечно, мы имеем: f (1) = 0 тогда и только тогда, когда g (0) = 1 . Покажем, благодаря теореме о производной обратной биекции , что f является первообразной x ↦1/Икстогда и только тогда, когда g — его собственная производная.
Если f дифференцируема и если для любого действительного
И наоборот, если г дифференцируема и если для любого действительного у , г ‘ ( у ) = г ( у ) , то F дифференцируема и
Другими словами :
что можно резюмировать в:
и позволяет решать уравнения, в которых неизвестное появляется в виде экспоненты.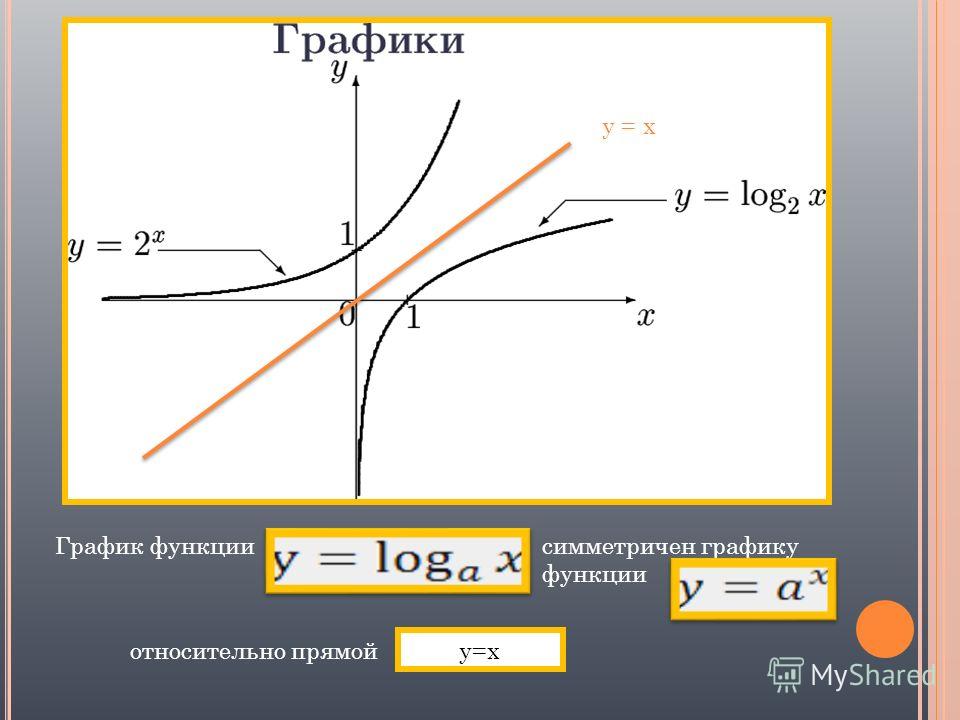 {3}} {3} } — \ cdots \\ & = x \ left ({\ frac {1} {1}} — x \ left ({\ frac {1} {2}} — x \ left ({\ frac {1} {3 }} — x \ left ({\ frac {1} {4}} — x \ left ({\ frac {1} {5}} — \ cdots \ right) \ right) \ right) \ right) \ right) . \ end {выровнено}}}
{3}} {3} } — \ cdots \\ & = x \ left ({\ frac {1} {1}} — x \ left ({\ frac {1} {2}} — x \ left ({\ frac {1} {3 }} — x \ left ({\ frac {1} {4}} — x \ left ({\ frac {1} {5}} — \ cdots \ right) \ right) \ right) \ right) \ right) . \ end {выровнено}}}
(См. Также Гипергеометрическая функция # Особые случаи .)
Согласно формуле Тейлора с интегралом остатка или теореме Абеля о радиальной сходимости , это разложение все еще верно для x = 1 . Таким образом, мы получаем сумму переменного гармонического ряда .
С другой стороны, заметим, что Леонард Эйлер смело применил это разложение к x = –1 . Не беспокоясь о сходимости, он показывает, что гармонический ряд является натуральным логарифмом1/1 — 1, то есть бесконечности. Сегодня мы формализуем это замечание Эйлера следующим образом: «Гармонический ряд, усеченный по N , близок к логарифму N, когда N велико» .
Чтобы получить лучшую скорость сходимости , из этого можно вывести:
- ∀Икс∈]-1,1[пер(1+Икс1-Икс)знак равно2Икс(11+13Икс2+15Икс4+17Икс6+19Икс8+⋯)знак равно2Икс(11+Икс2(13+Икс2(15+Икс2(17+Икс2(19+⋯))))),{\ Displaystyle {\ begin {align} \ forall x \ in \ left] -1,1 \ right [\ quad \ ln \ left ({\ frac {1 + x} {1-x}} \ right) & = 2x \ left ({\ frac {1} {1}} + {\ frac {1} {3}} x ^ {2} + {\ frac {1} {5}} x ^ {4} + {\ frac {1} {7}} x ^ {6} + {\ frac {1} {9}} x ^ {8} + \ cdots \ right) \\ & = 2x \ left ({\ frac {1} {1 }} + x ^ {2} \ left ({\ frac {1} {3}} + x ^ {2} \ left ({\ frac {1} {5}} + x ^ {2} \ left ({ \ frac {1} {7}} + x ^ {2} \ left ({\ frac {1} {9}} + \ cdots \ right) \ right) \ right) \ right) \ right), \ end { выровнено}}}
который переписан:
- ∀у∈]0,+∞[пер(у)знак равно2∑kзнак равно0∞12k+1(у-1у+1)2k+1.
 {x} \ ln {(t)} \ \ mathrm {d} t = x \ ln {(x)} — x + 1}.
{x} \ ln {(t)} \ \ mathrm {d} t = x \ ln {(x)} — x + 1}.
Следовательно, согласно основной теореме анализа примитивы являются функциями вида пер{\ displaystyle \ ln}
- Икс↦Икспер(Икс)-Икс+k,k∈р{\ displaystyle x \ mapsto x \ ln {(x)} — x + k, \ quad k \ in \ mathbb {R}},
простейший из них — функция . Икс↦Икспер(Икс)-Икс{\ displaystyle x \ mapsto x \ ln {(x)} — x}
Функция натурального логарифма как функция комплексной переменной
Вопрос о том, можно ли продлить натуральный логарифм (то есть , чтобы установить его на более широком множестве , что ] 0, + ∞ [ ) возникла во второй половине XVII — го века с серийным развития функций. Проблема в том, что не существует однозначной непрерывной функции на ℂ *, обладающей алгебраическим свойством функций логарифмирования и совпадающей на ] 0, + ∞ [ с действительной функцией натурального логарифма.
Однако мы можем определить логарифм отрицательного числа, положив для любого строго положительного вещественного a ln (- a ) = ln ( a ) + iπ , но определенная таким образом функция не обладает алгебраическими свойствами функции логарифма real natural . {2}}}}для более строго положительной реальной.
{2}}}}для более строго положительной реальной.
Примечания и ссылки
- ↑ См., Например, (la) Леонард Эйлер , « Наблюдения за вариациями около серий в конечностях » , Commentarii academiae scientificarum Petropolitanae , vol. 9,, стр. 160–188 ; также в Opera Omnia , Series Prima, Opera Mathematica, Volumen Quartum Decimum, Teubner, 1925.
- ↑ См., Например, Огюстен Коши , Упражнения по анализу и математической физике , т. 3, стр. 379, читайте онлайн в Google Книгах .
- ↑ См.
 , Например, Адриан-Мари Лежандр , Очерк теории чисел , Париж, Дюпра, год VI (1797 или 1798).
, Например, Адриан-Мари Лежандр , Очерк теории чисел , Париж, Дюпра, год VI (1797 или 1798). - ↑ Смотрите, например (из) Эдмунд Ландау , Handbuch дер Lehre фон дер дер Verteilung Primzahlen , Берлин, 1909 ( 2 е изд. Челси, Нью — Йорк, 1953).
- ↑ См. Учебники во Франции до 1972 года. Или, например: Николай Пискунов , Математический анализ, 5- е изд., 1972. Издания «Мир» , Москва III.10 с. 91 .
- ↑ Например, см. ( In ) LBW Jolley, Summing of Series , 2 e (revised) edition, Dover Publications , New York, 1961, читать онлайн .

- ↑ NF X 02-1 01 по числовым таблицам Дж. Лаборда, стр. VI, 1976.
- ↑ ISO 80000-2: 2009 , Международная организация по стандартизации .
- ↑ Например, см. Эту заметку (в) Г. Х. Харди и Э. М. Райт , Введение в теорию чисел ( 1- е изд. 1938 г.) [ Retail Editions ]( 6- е изд., Oxford, 2008, 1.7) « log x — это, конечно,« непьеровский »логарифм x по основанию e. «Общие» логарифмы не представляют математического интереса. »
- ↑ А. Дахан-Далмедико и Дж.
 Пайффер , История математики: дороги и лабиринты ,[ подробности изданий ], стр. 214.
Пайффер , История математики: дороги и лабиринты ,[ подробности изданий ], стр. 214. - ↑ Жан-Пьер Ле Гофф, «Из так называемого метода исчерпания — Грегуар де Сен-Винсент», в «Математическая демонстрация в истории» , IREM de Besançon.
- ↑ Симона Тромплер, « История логарифмов » , ULB ,, стр. 11.
- ↑ (la) Mengoli, Geometriae speciosae Elementa. Ссылки и ссылки, собранные (в) Джеффом Миллером « Самые ранние известные применения некоторых математических слов — натуральный логарифм » .
 (La) Леонард Эйлер, Introductio in analysin infinitorum , том 1, Bousquet, Lausanne, 1748, пример 1, стр. 228 ; также в Opera Omnia , Series Prima, Opera Mathematica, vol. 8, Teubner, 1922.
(La) Леонард Эйлер, Introductio in analysin infinitorum , том 1, Bousquet, Lausanne, 1748, пример 1, стр. 228 ; также в Opera Omnia , Series Prima, Opera Mathematica, vol. 8, Teubner, 1922.
Смотрите также
Статьи по Теме
- Пример применения теоремы Гельфонда-Шнайдера : ln (3) / ln (2) трансцендентно
- Натуральный логарифм 2 (дюйм)
- Двоичный логарифм
- Дискретный логарифм
- Интегральный логарифм
- W-функция Ламберта
внешние ссылки
«Моделирование как эпистемологический вопрос для введения свойств экспонент в классы», конференция Жана Домбреса : части 1 , 2 и 3
Обычные математические функции | |
|---|---|
| Рациональная алгебраическая функция |
|
| Иррациональная алгебраическая функция |
|
| Трансцендентная функция |
|
Число е | |
|---|---|
| Приложения |
|
| Определения |
|
| Люди |
|
<img src=»https://fr. wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
ЛОГАРИФМЫ И ИХ ОБРАТНЫЕ
ЛОГАРИФМЫ И ИХ ОБРАТНЫЕ Если логарифмическая функция является однозначной,
его обратные выходы. Обратная логарифмическая функция
показательная функция. Когда вы рисуете оба логарифмических
функция и обратная ей, а также график линии y = x,
вы заметите, что графики логарифмической функции и
экспоненциальные функции являются зеркальными отображениями друг друга с
относительно прямой y = x. Если бы вы свернули график вдоль
линию y = x и поднесите бумагу к свету, вы заметите
что два графика накладываются друг на друга. Другая
можно сказать, что логарифмическая функция и ее обратная
симметричны относительно прямой y = x.
Проработайте следующие примеры.
Пример 1: Найдите обратное значение .
- Отзывов: Напомним, что состав
функции с ее обратной вернет вас туда, где вы
начал.
 Например, предположим, что правило f(x) принимает 3 и
свяжите его с 10; тогда правило примет 10 и
связать его обратно с 3. Другой способ заявить об этом . Общий способ заявить это для любого x в области ф ( х ).
Например, предположим, что правило f(x) принимает 3 и
свяжите его с 10; тогда правило примет 10 и
связать его обратно с 3. Другой способ заявить об этом . Общий способ заявить это для любого x в области ф ( х ). - Решение: Что касается этой проблемы,
Основание равно 10, показатель степени равен х, и задачу можно преобразовать. экспоненциальной функции, которую можно упростить до
Напомним, что область определения f(x) равна диапазону , а диапазон f(x) равен области определения . Домен f (x) и диапазон это также . В терминах графиков этих функций это означает, что весь график f(x) будет располагаться правее вертикальной линии x = — 1, а весь график функции будет располагаться над линией г = — 1.
Давайте проверим наш ответ, найдя точки на обоих графиках. В исходном графике. Это означает, что точка (99, 2) находится на графике функции f(x). Если мы сможем показать, что точка (2, 99) находится на обратной стороне, мы покажем, что наш ответ верен, по крайней мере, для этих двух точек.
 указывает на то, что точка (2, 99) расположена на графике обратной функции. Мы правильно вычислили обратную логарифмическую функцию f(x). Это не «чистое» доказательство вашей правоты; Однако,
работает на начальном уровне.
указывает на то, что точка (2, 99) расположена на графике обратной функции. Мы правильно вычислили обратную логарифмическую функцию f(x). Это не «чистое» доказательство вашей правоты; Однако,
работает на начальном уровне.
Пример 2: Найдите обратную функцию .
- Решение: Используя тот факт, что
и основание e, мы можем определить обратную функцию
- Шаг 1:
- Мы можем преобразовать это уравнение в показательное уравнение с основанием e. Сначала изолируйте член Ln, вычитая 3 из
каждая сторона.
можно написать
- Шаг 2:
- Преобразуйте приведенное выше уравнение в показательное уравнение с основанием e:
- Шаг 3:
- Когда вы добавляете 7 к обеим сторонам мы, срок изолирован..
- Шаг 4:
- Обратите внимание, что область определения f(x) — это набор всех действительных чисел больше 7, а диапазон
также множество всех действительных чисел больше 7.

- Шаг 5:
- Вы можете проверить свой ответ, построив график обеих функций и определив, симметричны ли они прямой y = x. Вы также можете рассчитать баллы. Предположим, что (8, 3) — точка на
график исходной функции, то если мы сможем показать
; т. е. точка (3, 8) расположена на графике функции , то, скорее всего, мы правильно вычислили обратную
Отличная работа.
Если вы хотите рассмотреть другой пример,
нажмите Пример.
Если вы хотите решить несколько задач и проверить решения, нажмите
в ответе ниже.
Задача 1: Найдите обратную функцию, если она существует
Если он не существует, указывается ограниченный домен, на котором он будет существовать.
Ответ
Задача 2: Найдите обратную функцию, если она существует
Если он не существует, указывается ограниченный домен, на котором он будет существовать.
Ответ
Задача 3: Найдите обратную функцию, если она существует
Если он не существует, указывается ограниченный домен, на котором он будет существовать.
Ответ
Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.
Связаться с нами
Математика Медикс, ООО. — П.О. Box 12395 — Эль-Пасо, Техас 79913 — США
пользователей онлайн за последний час
| 9 | Оценить | квадратный корень из 12 | ||
| 10 | Оценить | квадратный корень из 20 | ||
| 11 | Оценить | квадратный корень из 50 | 94 | |
| 18 | Оценить | квадратный корень из 45 | ||
| 19 | Оценить | квадратный корень из 32 | ||
| 20 | Оценить | квадратный корень из 18 | 92 |
образование — как увидеть логарифм как обратную экспоненциальную функцию?
Спросил
Изменено 6 лет назад
Просмотрено 11 тысяч раз
$\begingroup$
Я видел здесь, в math. stackexchange, некоторые доказательства того, как функции log и exp связаны друг с другом, но я хочу понять это интуитивно.
stackexchange, некоторые доказательства того, как функции log и exp связаны друг с другом, но я хочу понять это интуитивно.
Проще говоря, как бы вы объяснили связь между этими двумя функциями?
- функции
- образование
- показательная функция
$\endgroup$
8
$\begingroup$
Вы хотите понять, что экспонента и логарифм обратны друг другу:
(i)$ f(x) = y$, если мы хотим найти обратную, мы выражаем $x$ через $y$. покажу графически.. (Это в равной степени применимо и для других показателей) 9y=x\iff \log_ax=y\;,\;\;x>0$$
Прописью: логарифмом по основанию $\;a\;$ положительного числа $\;x\;$ является показатель степени, до которой нужно возвести основание, чтобы получить $\;x\;$ .
Таким образом, например, $\;\log_381=4\;$, так как основание $\;3\;$ нужно возвести в четвертую степень, чтобы получить $\;81\;$. {\,y_{\,0}}$$
это желаемое обращение $(2)$. 9y=x$ и попросил нас найти $y$. Никто не мог этого сделать. Затем она сказала: «Определите эту вещь, называемую логарифмом, такую, что $\operatorname{log}_{base}(\mathrm{answer})=\mathrm{expponent}$», и дала нам мнемонику « b ase a ». nswer e xponent», чтобы запомнить его. Я до сих пор время от времени использую «bax».
{\,y_{\,0}}$$
это желаемое обращение $(2)$. 9y=x$ и попросил нас найти $y$. Никто не мог этого сделать. Затем она сказала: «Определите эту вещь, называемую логарифмом, такую, что $\operatorname{log}_{base}(\mathrm{answer})=\mathrm{expponent}$», и дала нам мнемонику « b ase a ». nswer e xponent», чтобы запомнить его. Я до сих пор время от времени использую «bax».
Все остальные свойства возникли из «ну, оказывается, когда вы определяете журнал таким образом, вы получаете такие-то и такие-то свойства», такие как правила умножения, на проверку которых мы затем потратили следующие несколько занятий.
$\endgroup$
$\begingroup$
Неспециалисту может быть полезно знать, что логарифмы использовались в качестве инструмента для умножения еще тогда, когда корабли плыли по небесной навигации. Сумма логарифмов двух чисел есть логарифм их произведения. Обширные таблицы журналов были опубликованы и использовались наизусть. Это стало хорошей дополнительной темой для математики в 6-м классе в 1958 году. Наш учитель не дал намёка на связь с интегралами, но преподавал связь с показателями степени.
Обширные таблицы журналов были опубликованы и использовались наизусть. Это стало хорошей дополнительной темой для математики в 6-м классе в 1958 году. Наш учитель не дал намёка на связь с интегралами, но преподавал связь с показателями степени.
В качестве физической корреляции логарифмическая линейка использует графики одной оси экспоненциальной функции для преобразования умножения в сложение длин, графическую таблицу журнала.
$\endgroup$
$\begingroup$
Можно указать на их противоположные алгебраические свойства.
Для логарифмов у вас есть правило произведения:
$$ \log(a b) = \log(a) + \log(b) $$
Таким образом, логарифм произведения есть сумма логарифмов его множителей .
9x$ легко видеть, что эти свойства подразумевают обратное функциональное отношение, так как два правила дают нам$$ \log(\exp(x)) = x \log(e) = x $$
(по крайней мере это должно быть ясно, когда $x$ является целым числом, но это также работает с рациональными числами.

 : Просвещение.
: Просвещение. Также
Также {x} \ ln {(t)} \ \ mathrm {d} t = x \ ln {(x)} — x + 1}.
{x} \ ln {(t)} \ \ mathrm {d} t = x \ ln {(x)} — x + 1}.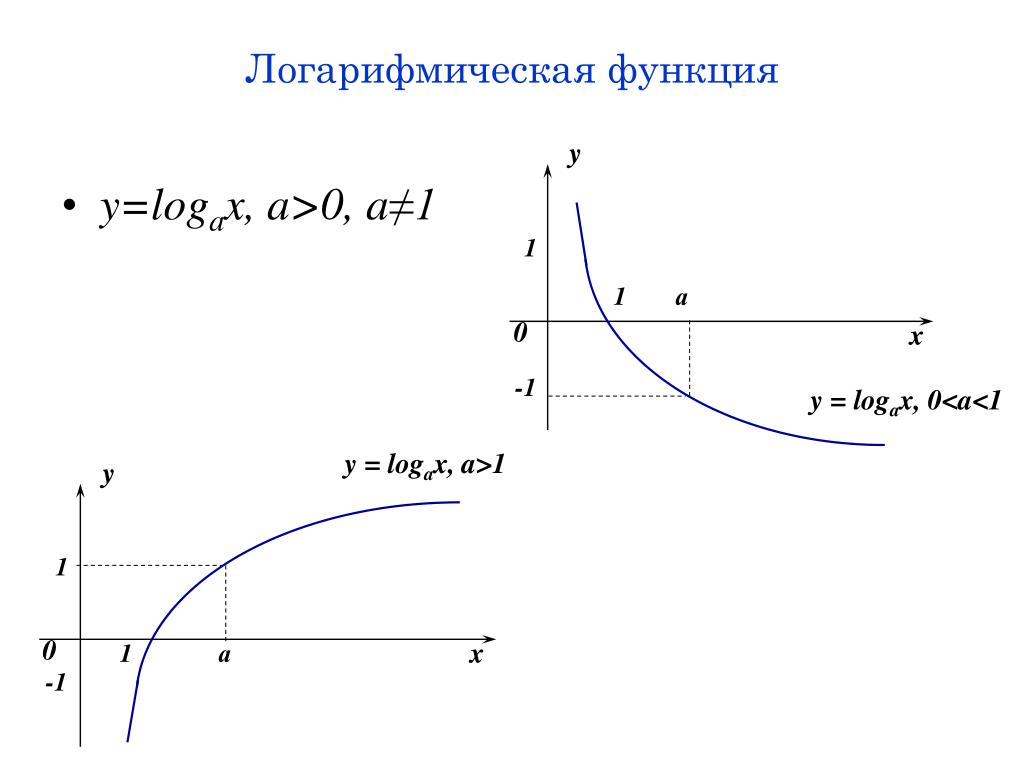 , Например, Адриан-Мари Лежандр , Очерк теории чисел , Париж, Дюпра, год VI (1797 или 1798).
, Например, Адриан-Мари Лежандр , Очерк теории чисел , Париж, Дюпра, год VI (1797 или 1798).
 Пайффер , История математики: дороги и лабиринты ,[ подробности изданий ], стр. 214.
Пайффер , История математики: дороги и лабиринты ,[ подробности изданий ], стр. 214. (La) Леонард Эйлер, Introductio in analysin infinitorum , том 1, Bousquet, Lausanne, 1748, пример 1, стр. 228 ; также в Opera Omnia , Series Prima, Opera Mathematica, vol. 8, Teubner, 1922.
(La) Леонард Эйлер, Introductio in analysin infinitorum , том 1, Bousquet, Lausanne, 1748, пример 1, стр. 228 ; также в Opera Omnia , Series Prima, Opera Mathematica, vol. 8, Teubner, 1922.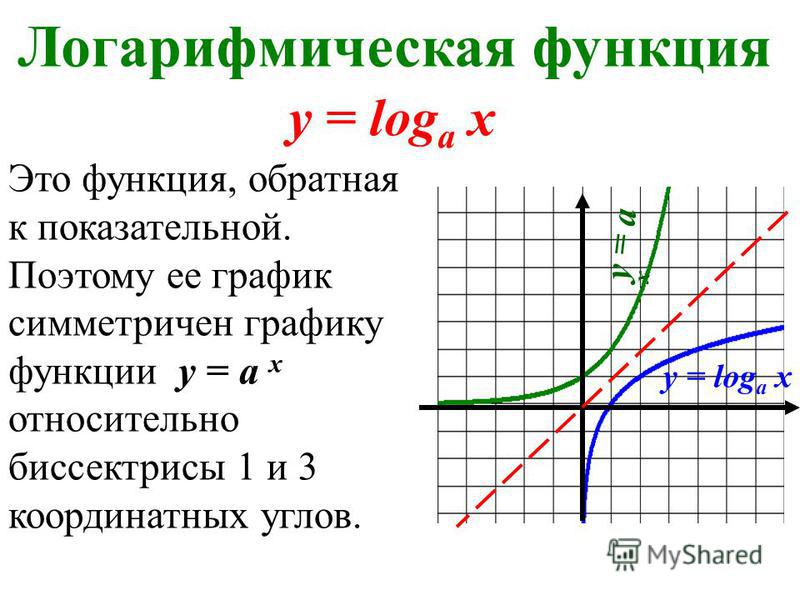 Например, предположим, что правило f(x) принимает 3 и
свяжите его с 10; тогда правило примет 10 и
связать его обратно с 3. Другой способ заявить об этом . Общий способ заявить это для любого x в области ф ( х ).
Например, предположим, что правило f(x) принимает 3 и
свяжите его с 10; тогда правило примет 10 и
связать его обратно с 3. Другой способ заявить об этом . Общий способ заявить это для любого x в области ф ( х ). 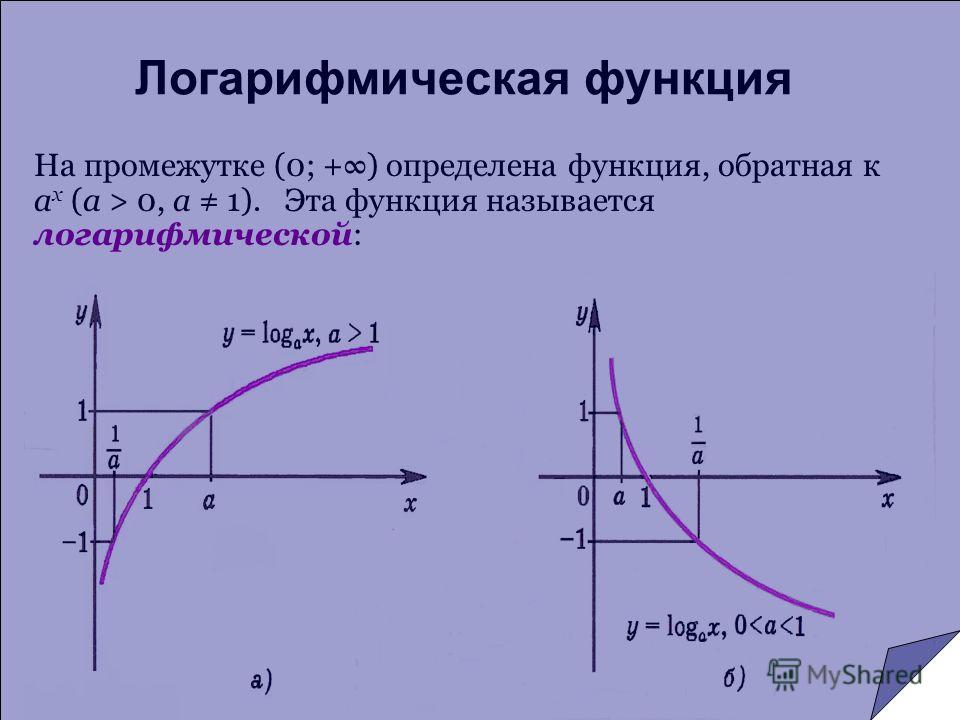 указывает на то, что точка (2, 99) расположена на графике обратной функции. Мы правильно вычислили обратную логарифмическую функцию f(x). Это не «чистое» доказательство вашей правоты; Однако,
работает на начальном уровне.
указывает на то, что точка (2, 99) расположена на графике обратной функции. Мы правильно вычислили обратную логарифмическую функцию f(x). Это не «чистое» доказательство вашей правоты; Однако,
работает на начальном уровне.