x=\frac{-\left(-800\cos(120)-1600\right)±\sqrt{1440000-4\left(4\cos(120)+5\right)\times \left(\frac{320000}{3}\right)}}{2\left(4\cos(120)+5\right)}
Возведите -1600-800\cos(120) в квадрат.
x=\frac{-\left(-800\cos(120)-1600\right)±\sqrt{1440000-12\times \left(\frac{320000}{3}\right)}}{2\left(4\cos(120)+5\right)}
Умножьте -4 на 5+4\cos(120).
x=\frac{-\left(-800\cos(120)-1600\right)±\sqrt{1440000-1280000}}{2\left(4\cos(120)+5\right)}
Умножьте -12 на \frac{320000}{3}.
x=\frac{-\left(-800\cos(120)-1600\right)±\sqrt{160000}}{2\left(4\cos(120)+5\right)}
Прибавьте 1440000 к -1280000.
x=\frac{-\left(-800\cos(120)-1600\right)±400}{2\left(4\cos(120)+5\right)}
Извлеките квадратный корень из 160000.
x=\frac{1200±400}{2\left(4\cos(120)+5\right)}
Число, противоположное -1600-800\cos(120), равно 1200.
x=\frac{1200±400}{6}
Умножьте 2 на 5+4\cos(120).
x=\frac{1600}{6}
Решите уравнение x=\frac{1200±400}{6} при условии, что ± — плюс.
Извлеките квадратный корень из обеих частей уравнения.
x-200=\frac{200}{3} x-200=-\frac{200}{3}
Упростите.
x=\frac{800}{3} x=\frac{400}{3}
Прибавьте 200 к обеим частям уравнения.
35B/Тригонометрическая и показательная формы
Если вещественную x и мнимую y части комплексного числа выразить через модуль r = | z | и аргумент (x = rcos φ, y = rsin φ), то всякое комплексное число z, кроме нуля, можно записать в тригонометрической форме
z = r(cos φ + isin φ).
Сложение, вычитание, умножение и деление комплексных чисел.
Определение 1. Суммой двух комплексных чисел c1=(a1;b1), c2=(a2;b2) называют комплексное число c=c1+c2=(a1+a2;b1+b2).
Определение 2. Разностью двух комплексных чисел c1=(a1;b1), c2=(a2;b2) называют комплексное число c=c1+(-c2)=(a1-a2;b1-b2).
Определение 3.
Произведением комплексного числа
c=(a;b) на действительное число , называют
комплексное число c=( a; b).
Определение 4. Произведением двух комплексных чисел c1=(a1;b1), c2=(a2;b2) называют комплексное число c=(a1*a2-b1*b2;a1*b2+a2*b1).
Возведение в степень.
Из операции умножения комплексных чисел следует, что
В общем случае получим:,
где n – целое положительное число.
Это выражение называется формулой Муавра.
36в
Извлечение корня есть действие, обратное возведению в степень. Поэтому (см. предыдущий параграф) модуль корня (целой степени) из комплексного числа получается извлечением корня той же степени из модуля подкоренного числа, а аргумент – делением аргумента на показатель корня:
(В)
Корень n-й степени из всякого комплексного
числа имеет
n различных значений. Все они Все они
имеют одинаковые модули
;
аргументы же получаются из аргумента
одного из них последовательным
прибавлением угла (1/n)*360°.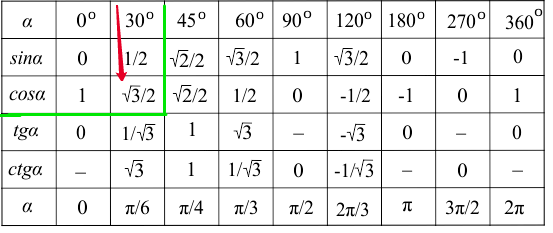 Действительно,
пусть φ0 есть
аргумент подкоренного числа. Тогда φ0
+ 360°; φ0 +2•360°
и т. д. также являются его аргументами.
Формула (В) показывает, что за аргумент
корня можно принять не только ,
но также 360°, 360°
и т. д. Соответствующие значения корня
не все различны между собой: аргумент 360,
т. е.
+360°,
дает то же комплексное число, что и
аргумент
;
аргумент 360°
=
360°+360°
дает то же комплексное число, что и
аргумент
360°,
и т.д. Различных значений корня будет
ровно n. См. примеры.
Пример 1. Извлечь
квадратный корень из числа – 9i. Модуль
этого числа есть 9. Значит, модуль корня
равен Аргумент
подкоренного числа можно принять равным
— 90°, — 90°+360°, — 90°+2•360° и т. д.
В первом
случае получаем:
Действительно,
пусть φ0 есть
аргумент подкоренного числа. Тогда φ0
+ 360°; φ0 +2•360°
и т. д. также являются его аргументами.
Формула (В) показывает, что за аргумент
корня можно принять не только ,
но также 360°, 360°
и т. д. Соответствующие значения корня
не все различны между собой: аргумент 360,
т. е.
+360°,
дает то же комплексное число, что и
аргумент
;
аргумент 360°
=
360°+360°
дает то же комплексное число, что и
аргумент
360°,
и т.д. Различных значений корня будет
ровно n. См. примеры.
Пример 1. Извлечь
квадратный корень из числа – 9i. Модуль
этого числа есть 9. Значит, модуль корня
равен Аргумент
подкоренного числа можно принять равным
— 90°, — 90°+360°, — 90°+2•360° и т. д.
В первом
случае получаем:
(1)
Во втором случае
(2)
В третьем случае
т. e. то же, что в первом. Беря φ = — 90°
+ 3 • 360°, — 90° + 4 • 360° или φ = — 90° — 360°; — 90°
— 2•360° и т. д., мы будем поочередно получать
значения (1) и (2). Пример 2. Извлечь
квадратный корень из числа 16. Аргумент
этого числа есть 360°k (k – целое число).
Аргумент корня будет 360 k : 2 = 180k. Если k
есть нуль или четное число, то аргумент
корня равен нулю или кратен 360°. Тогда
161/2= 4 (cos 0° +isin 0°) = 4. Если же k –
нечетное число, то аргумент будет 180°
или отличаться от 180° на кратное 360°.
Тогда 161/2 = 4 (соs 180° + isin180°) = —
4.
Пример 3. Извлечь кубический корень
из 1. Модуль корня равен Аргумент
подкоренного числа есть 360k (k –любое
целое число). Аргумент корня будет 120°k.
Полагая k = 0,1,2, находим три значения
аргумента корня: 0°, 120°, 240°. Соответствующие
значения корня будут*:
z1
= cos 0° + isin 0° = 1,
z2
= cos 120° + isin 120° = z3
= cos 240° + isin 240° =
Н
а
фиг. 17 эти значения изображены точками
A1, A2,
A3.
Треугольник
A1A2A3
– равносторонний. Он вписан в окружность
радиуса 1.
Пример 4. Извлечь корень
шестой степени из -1. Аргумент подкоренного
числа -1 есть 180° + 360°k. Аргумент корня
равен 30° + 60°k.
Пример 2. Извлечь
квадратный корень из числа 16. Аргумент
этого числа есть 360°k (k – целое число).
Аргумент корня будет 360 k : 2 = 180k. Если k
есть нуль или четное число, то аргумент
корня равен нулю или кратен 360°. Тогда
161/2= 4 (cos 0° +isin 0°) = 4. Если же k –
нечетное число, то аргумент будет 180°
или отличаться от 180° на кратное 360°.
Тогда 161/2 = 4 (соs 180° + isin180°) = —
4.
Пример 3. Извлечь кубический корень
из 1. Модуль корня равен Аргумент
подкоренного числа есть 360k (k –любое
целое число). Аргумент корня будет 120°k.
Полагая k = 0,1,2, находим три значения
аргумента корня: 0°, 120°, 240°. Соответствующие
значения корня будут*:
z1
= cos 0° + isin 0° = 1,
z2
= cos 120° + isin 120° = z3
= cos 240° + isin 240° =
Н
а
фиг. 17 эти значения изображены точками
A1, A2,
A3.
Треугольник
A1A2A3
– равносторонний. Он вписан в окружность
радиуса 1.
Пример 4. Извлечь корень
шестой степени из -1. Аргумент подкоренного
числа -1 есть 180° + 360°k. Аргумент корня
равен 30° + 60°k.
Из формулы (В) следует, что n корней
из какого-либо комплексного числа и n
корней из сопряженного числа попарно
сопряжены.
Пример 5. Корни четвертой
степени из числа 16(cos120° + isin120°) = — 8 +
будут:
z1 =
2(cos 30° + isin 30°) = +
i;
z2 = 2(cos 120°
+ isin 120°) = -1 +
i;
z3
= 2(cos 210° + isin 210°) = _
— i;
z4 = 2(cos
300° + isin 300°) = 1 —
i,
а
корни той же степени из числа 16 (cos120° —
isin120°) = -8 —
будут: =
2(cos 30° — isin 30°) =
—
i; =
2(cos 120° — isin 120°) = -1 —
i; =
2(cos 210° — isin 210°) = —
+
i; =
2(cos 300° — isin 300°) = 1 +
i.
Числа
z1 и
,
z2 и
и
т. д. попарно сопряжены. *Эти
результаты полезно проверить. Помножив
число само на себя по правилу § 38, найдем
Помножив
число само на себя по правилу § 38, найдем
Корни n-й степени из единицы — комплексные корни многочлена . Другими словами, это комплексные числа, n-я степень которых равна 1.
Представим комплексную единицу в тригонометрическом виде:
Тогда по формуле Муавра, получим:
Здесь uk — корни из единицы.
Корни из единицы могут также быть представлены в показательной форме:
Из этих формул вытекает, что корней из единицы всегда ровно n, и все они различны.
Cos 120 градусов — Найдите значение Cos 120 градусов
LearnPracticeDownload
Значение cos 120 градусов равно -0,5 . Cos 120 градусов в радианах записывается как cos (120° × π/180°), т. е. cos (2π/3) или cos (2,094395.
- Cos 120°: -0,5
- Cos 120° в дробях: -(1/2)
- Cos (-120 градусов): -0,5
- Cos 120° в радианах: cos (2π/3) или cos (2,0943951 . . .)
Каково значение Cos 120 градусов?
Значение cos 120 градусов в десятичной системе равно -0,5. Cos 120 градусов также можно выразить с помощью эквивалента данного угла (120 градусов) в радианах (2,09439 . . .)
Мы знаем, используя преобразование градусов в радианы, что θ в радианах = θ в градусах × (pi/180° )
⇒ 120 градусов = 120° × (π/180°) рад = 2π/3 или 2,0943 . . .
∴ cos 120° = cos(2,0943) = -(1/2) или -0,5
Объяснение:
Для cos 120 градусов угол 120° лежит между 90° и 180° (второй квадрант). Поскольку функция косинуса во втором квадранте отрицательна, значение cos 120° = -(1/2) или -0,5
Поскольку функция косинуса является периодической функцией, мы можем представить cos 120° как cos 120 градусов = cos(120° + n × 360°), n ∈ Z.
⇒ cos 120° = cos 480° = cos 840° и так далее.
Примечание: Поскольку косинус является четной функцией, значение cos(-120°) = cos(120°).
Методы определения значения косинуса 120 градусов
Функция косинуса отрицательна во 2-м квадранте. Значение cos 120° указано как -0,5. Мы можем найти значение cos 120 градусов по:
- Используя единичный круг
- Использование тригонометрических функций
Cos 120 градусов с использованием единичной окружности
Чтобы найти значение cos 120 градусов с помощью единичной окружности:
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол 120° с положительной осью x.
- Косвенный угол 120 градусов равен координате x (-0,5) точки пересечения (-0,5, 0,866) единичной окружности и r.
Следовательно, значение cos 120° = x = -0,5
Cos 120° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить cos 120 градусов как:
- ± √(1-sin²(120 °))
- ± 1/√(1 + tan²(120°))
- ± кроватка 120°/√(1 + кроватка²(120°))
- ±√(косек²(120°) — 1)/косек 120°
- 1/сек 120°
Примечание.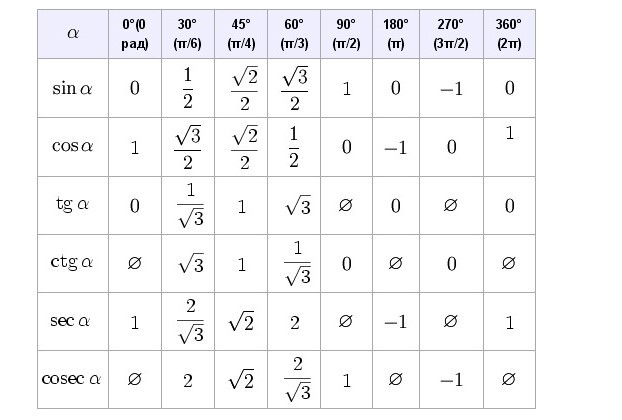 Поскольку 120° лежит во 2-м квадранте, окончательное значение cos 120° будет отрицательным.
Поскольку 120° лежит во 2-м квадранте, окончательное значение cos 120° будет отрицательным.
Мы можем использовать тригонометрические тождества для представления cos 120° как
- -cos(180° — 120°) = -cos 60°
- -cos(180° + 120°) = -cos 300°
- sin(90° + 120°) = sin 210°
- sin(90° — 120°) = sin(-30°)
☛ Также проверьте:
- cos 210 градусов
- потому что 90 градусов
- потому что 225 градусов
- потому что 540 градусов
- потому что 58 градусов
- потому что 1170 градусов
Примеры использования Cos 120 градусов
Пример 1: Используя значение cos 120°, решите: (1-sin²(120°)).
Решение:
Мы знаем, (1-sin²(120°)) = (cos²(120°)) = 0,25
⇒ (1-sin²(120°)) = 0,25Пример 2. Найдите значение 2 cos(120°)/3 sin(-30°).

Решение:
Используя тригонометрические тождества, мы знаем, что cos(120°) = sin(90° — 120°) = sin(-30°).
⇒ cos(120°) = sin(-30°)
⇒ Значение 2 cos(120°)/3 sin(-30°) = 2/3Пример 3: Найдите значение (cos² 60° — sin² 60°). [Подсказка: используйте cos 120° = -0,5]
Решение:
Используя формулу cos 2a,
(cos² 60° — sin² 60°) = cos(2 × 60°) = cos 120°
∵ cos 120° = -0,5
⇒ (cos² 60° — sin² 60°) = -0,5
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о Cos 120 Degrees
Что такое Cos 120 Degrees?
Cos 120 градусов — значение тригонометрической функции косинуса для угла, равного 120 градусам. Значение cos 120° равно -(1/2) или -0,5
Значение cos 120° равно -(1/2) или -0,5
Каково значение Cos 120 градусов в пересчете на Tan 120°?
Мы знаем, что используя тригонометрические тождества, мы можем записать cos 120° как -1/√(1 + tan²(120°)). Здесь значение тангенса 120° равно -1,732050.
Каково значение Cos 120° в пересчете на Cosec 120°?
Поскольку функцию косинуса можно представить с помощью функции косеканса, мы можем записать cos 120° как -[√(cosec²(120°) — 1)/cosec 120°]. Значение cosec 120° равно 1,15470.
Как найти косинус 120° с точки зрения других тригонометрических функций?
Используя формулу тригонометрии, значение cos 120° может быть выражено через другие тригонометрические функции следующим образом:
- ± √(1-sin²(120°))
- ± 1/√(1 + tan²(120°))
- ± кроватка 120°/√(1 + кроватка²(120°))
- ± √(косек²(120°) — 1)/косек 120°
- 1/сек 120°
☛ Также проверьте: тригонометрическую таблицу
Как найти значение Cos 120 градусов?
Значение cos 120 градусов можно рассчитать, построив угол 120° с осью x и затем найдя координаты соответствующей точки (-0,5, 0,866) на единичной окружности. Значение cos 120° равно координате x (-0,5). ∴ cos 120° = -0,5.
Значение cos 120° равно координате x (-0,5). ∴ cos 120° = -0,5.
Скачать БЕСПЛАТНЫЕ учебные материалы
Тригонометрия
Рабочие листы по математике и
наглядная программа
Значение Cos 120 градусов и других тригонометрических углов
Cos 120 градусов может быть равно минусу (-0,5). Cos — одна из функций тригонометрии, которая имеет дело с отношениями между углами и сторонами прямоугольного треугольника. Короче говоря, мы можем сказать, что измерение треугольника (в частности, прямоугольного треугольника) — это тригонометрия.
Теперь возникает вопрос, что такое прямоугольный треугольник? Мы знаем, что треугольник — это замкнутая фигура с тремя сторонами и тремя углами. Прямоугольным треугольником называется треугольник, у которого один из внутренних углов равен 90 градусов, а два других угла меньше 90 градусов. Некоторыми из важных функций тригонометрии являются Sin, Cos и Tan. Использование этих функций находит применение в области астрономии, инженерии, архитектурного проектирования и физики.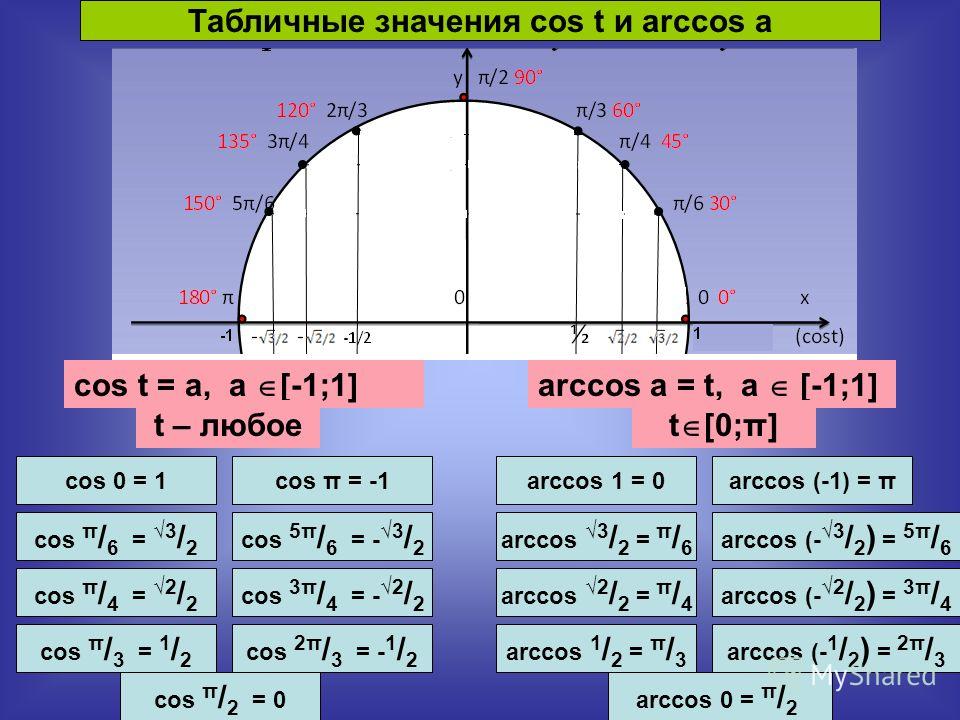
Возьмем прямоугольный треугольник, выделим один из углов как () и назовем три стороны следующим образом:
Гипотенуза: Самая длинная сторона треугольника, противоположная 90 градусам.
Перпендикуляр (Противоположный): это сторона, противоположная неизвестному углу и перпендикулярная основанию (то есть угол между основанием и перпендикуляром составляет 90 градусов).
Основание (примыкающее): сторона, на которую опирается треугольник, а также содержит оба угла (90 градусов и неизвестный угол) Тригонометрия. Любая другая важная формула тригонометрии выводится с помощью этих соотношений.
Ниже приведены важные отношения, называемые Sin, Cos и Tan. Sin и cos являются фундаментальными или базовыми отношениями, тогда как Tan, sec, cot и sec являются производными функциями. Ниже приведены отношения Sin, Cos и Tan.
функция синуса (sin)
\[sin\theta =\frac{opposite}{гипотенуза}\]
функция косинуса (cos)
\costa2 {adjacent}{гипотенуза}\]функция тангенса (тангенс)
Первый квадрант: все углы от 0⁰ до 90⁰ лежат в первом квадранте. Значение всех функций (Sin, Tan, Cos) в этом квадранте положительно. Показано как A (представляет все) на второй диаграмме, приведенной ниже.
Второй квадрант: Все углы между 90⁰ и 180⁰ лежат во втором квадранте.
 Значение только Sin положительно в этом квадранте. Показано как S (представляет Sin) на второй диаграмме, приведенной ниже.
Значение только Sin положительно в этом квадранте. Показано как S (представляет Sin) на второй диаграмме, приведенной ниже.Третий квадрант: Все углы между 180⁰ и 270⁰ лежат в третьем квадранте. В этом квадранте значение положительно только Tan. Обозначается буквой T (представляет Тан) на второй диаграмме, приведенной ниже.
Четвертый квадрант: Все углы между 270⁰ и 360⁰ лежат в четвертом квадранте. Значение только Cos является положительным в этом квадранте. Обозначается как C (представляет Cos) на второй диаграмме, приведенной ниже.
Отца тригонометрии зовут Гиппарх, так как ему приписывают составление первой тригонометрической таблицы.
 Гиппарх использовал эти тригонометрические таблицы для решения задач тригонометрии и сферической тригонометрии.
Гиппарх использовал эти тригонометрические таблицы для решения задач тригонометрии и сферической тригонометрии.Как мы все знаем, тригонометрические отношения — это в основном отношения между сторонами прямоугольного треугольника. Эти отношения выражаются в терминах тригонометрических функций как B и C, которые являются сторонами треугольника.
Функция синуса, также называемая sin, определяется как отношение стороны, противоположной углу, к гипотенузе. \[cos\theta =\frac{Adjacent}{Hypoteneuse}\]
Функция косинуса, также называемая cos, определяется как отношение прилежащей стороны к гипотенузе.
\[cos\theta =\frac{Adjacent}{Hypoteneuse}\]
Функция тангенса, также называемая тангенсом, определяется как отношение противоположного катета к корректирующему катету треугольника.
 \[Tan\theta =\frac{sin\theta }{cos\theta}\]
\[Tan\theta =\frac{sin\theta }{cos\theta}\]Это три основных тригонометрических отношения, которые чрезвычайно важны при изучении тригонометрии, и в этой статье в основном рассматриваются cos и значение курса 120.
Гипотенуза в прямоугольном треугольнике известна как сторона, противоположная до угла 90°. Это самая длинная сторона треугольника.
Прилегающая сторона — это сторона, примыкающая к его углу.
Противоположная сторона называется стороной, противоположной прилежащему углу.
Основными терминами для смежных и противоположных являются перпендикуляр и основание, которые в основном используются на практике.
- Автор Vaibhav_Raj_Asthana
- Последнее изменение 19-07-2022
- Автор Вайбхав_Радж_Астхана
- Последнее изменение 19-07-2022
\[Tan\theta =\frac{sin\theta }{cos\theta }\]
Квадрант и правило приведения
Как указано выше, углы, отличные от угла 90 градусов в прямоугольном треугольнике являются острыми (т. е. менее 90 градусов). Чтобы найти значение функций для углов более 90 градусов, мы следуем набору правил, известных как правила приведения. Возьмем четыре оси, чтобы разделить 360 градусов на четыре квадранта. Углы всегда измеряются против часовой стрелки от положительной оси x. Данная диаграмма показывает 30 градусов от положительной оси x. Изображение будет загружено в ближайшее времяИзображение будет загружено в ближайшее времяИзображение будет загружено в ближайшее время.
е. менее 90 градусов). Чтобы найти значение функций для углов более 90 градусов, мы следуем набору правил, известных как правила приведения. Возьмем четыре оси, чтобы разделить 360 градусов на четыре квадранта. Углы всегда измеряются против часовой стрелки от положительной оси x. Данная диаграмма показывает 30 градусов от положительной оси x. Изображение будет загружено в ближайшее времяИзображение будет загружено в ближайшее времяИзображение будет загружено в ближайшее время.
Имеется четыре квадранта, как показано на рисунке ниже. Каждый квадрант содержит диапазон углов:
(Изображение скоро будет загружено)
Начиная с четвертого квадранта, мы можем сказать, что квадрант следует ряду CAST, где C означает Cos, A означает все, S означает Sin, а T означает Tan.
Родственные углы
Значения sin, cos и tan некоторых углов равны значениям sin, cos и tan других углов.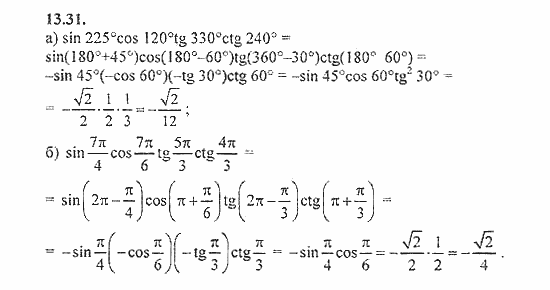 Возьмем пример cos(-30⁰). Поскольку 30 градусов лежат в первом квадранте, мы можем сказать, что cos(-30⁰) равен cos(30⁰), потому что все углы в первом квадранте положительны. Точно так же cos(390⁰) также равно cos(30⁰). На приведенных ниже диаграммах показаны заштрихованные углы sin, cos и tan, имеющие одинаковую величину.
Возьмем пример cos(-30⁰). Поскольку 30 градусов лежат в первом квадранте, мы можем сказать, что cos(-30⁰) равен cos(30⁰), потому что все углы в первом квадранте положительны. Точно так же cos(390⁰) также равно cos(30⁰). На приведенных ниже диаграммах показаны заштрихованные углы sin, cos и tan, имеющие одинаковую величину.
Рис. 1: sin 30⁰ = 0,5
Рис. 2: sin 150⁰ = 0,5
Рис. 3: sin 210⁰ = -0,5
Рис. 4: sin 330⁰ = -0,5
эти углы называются смежными углами. Изображение, приведенное ниже, показывает значение всех углов cos.
(Изображение скоро будет загружено)
Cos 120
Значение Cos 120⁰ равно — ½. Это сумма, обратная значению косинуса 60⁰ или косинуса 60⁰. Косинус — одна из основных тригонометрических функций. Он выражается как отношение основания прямоугольного треугольника к его гипотенузе.
Как найти значение Cos 120?
Углы прямоугольного треугольника выражаются кратными или дольными числами 180⁰ или π в радианах.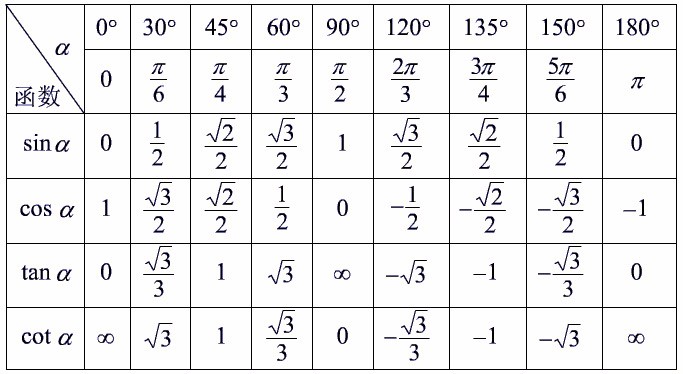 Следовательно, чтобы найти значение cos 120⁰, нам придется выразить 120⁰ через 180⁰ или 90⁰.
Следовательно, чтобы найти значение cos 120⁰, нам придется выразить 120⁰ через 180⁰ или 90⁰.
Случай 1:
Выразим 120⁰ как (180 — 60)⁰
cos 120⁰ = cos (180 — 60)⁰
Так как, cos (180⁰ — x) = — cos x.
Следовательно, cos (180 — 60)⁰ = — cos 60⁰
=> cos 120⁰ = -½
Случай 2:
Выразим 120⁰ как (90 + 30)⁰
cos 120⁰ = cos (90 + 30)⁰
Так как, cos (90⁰ + x) = — sin x.
Следовательно, cos (90 + 30)⁰ = -sin 30⁰
=> cos 120⁰= — ½
Решенные примеры
Вопрос 1. Найдите точное значение cos (- 390⁰).
Решение: Мы знаем, что cos(-x) = cos(x)
поэтому , cos (- 390⁰) = cos (390⁰).
Поскольку угол 390⁰ больше угла 360⁰,
находим угол t такой, что
t = 390 — (360) = 30⁰
Итак,
Cos (390⁰) = Cos ( 30⁰)
Мы знаем, что значение Cos 30⁰ равно \[\sqrt{\frac{3}{2}}\]
Значение cos 120 — это минус половина, которую можно записать как -1/2 или -0,5. Изучение косинуса или косинуса относится к тригонометрии — разделу математики, который занимается изучением конкретных функций углов и их применением в вычислениях. Тригонометрия — это раздел математики, который в основном занимается отношениями между сторонами и углами треугольников. Тригонометрия была впервые открыта в эллинистический период, то есть в третьем веке до нашей эры. Тригонометрия считается чрезвычайно важным исследованием, поскольку ее можно применять как для изучения геометрии, так и для астрономических исследований. Греки в основном углублялись в концепцию расчета хорд, в то время как опытные математики в Индии углублялись в изучение тригонометрических отношений, которые также известны как тригонометрические функции, такие как синус. Тригонометрия является чрезвычайно важным исследованием, поскольку она применяется к различным дисциплинам, таким как обслуживание, небесная механика, навигация и так далее.
Изучение косинуса или косинуса относится к тригонометрии — разделу математики, который занимается изучением конкретных функций углов и их применением в вычислениях. Тригонометрия — это раздел математики, который в основном занимается отношениями между сторонами и углами треугольников. Тригонометрия была впервые открыта в эллинистический период, то есть в третьем веке до нашей эры. Тригонометрия считается чрезвычайно важным исследованием, поскольку ее можно применять как для изучения геометрии, так и для астрономических исследований. Греки в основном углублялись в концепцию расчета хорд, в то время как опытные математики в Индии углублялись в изучение тригонометрических отношений, которые также известны как тригонометрические функции, такие как синус. Тригонометрия является чрезвычайно важным исследованием, поскольку она применяется к различным дисциплинам, таким как обслуживание, небесная механика, навигация и так далее.
Cos 120 Градус: Как найти значение cos 120?
Cos 120 ° обычно используется как в тригонометрии, так и в исчислении в старших классах. Связь между различными сторонами и углами треугольника называется тригонометрией. Тригонометрия используется в ряде задач, таких как машиностроение, авиастроение, строительство зданий и т. д. Синус, косинус и тангенс — это три основных тригонометрических отношения, которые используются для вычисления тригонометрических сумм. Cos является одной из 6 тригонометрических функций и широко используется как в математике, так и в физике.
Связь между различными сторонами и углами треугольника называется тригонометрией. Тригонометрия используется в ряде задач, таких как машиностроение, авиастроение, строительство зданий и т. д. Синус, косинус и тангенс — это три основных тригонометрических отношения, которые используются для вычисления тригонометрических сумм. Cos является одной из 6 тригонометрических функций и широко используется как в математике, так и в физике.
Общая концепция тригонометрии основана на прямоугольном треугольнике. Значение cos 120° равно -1/2 или -0,5, поскольку оно находится во 2-м квадранте, где косинус отрицательный. Формула косинуса: cos x = (прилежащая сторона) / (гипотенуза). Здесь прилежащая сторона примыкает к углу x, а гипотенуза — самая длинная сторона треугольника. Студенты могут найти подробное объяснение ниже.
Cos 120
° : Значение Чтобы найти значение cos 120 ° , учащиеся должны нарисовать прямоугольный треугольник (см. изображение ниже) и могут использовать любую из двух формул, например,
cos (180° – θ) = – cos
или
cos (90° + θ) = – грехθ.
Учащиеся уже должны знать, что cos θ = \(\frac{основание}{гипотенуза}\) = \(\frac{b}{h}\)
Учащимся важно уметь определять перпендикуляр, гипотенузу и основание треугольника. При проверке будут указаны значения a, b, h, и на их основе вы сможете рассчитать cos θ.
Так как нам уже известны значения тригонометрических углов для sin, cos и tan от 0 до 90. Воспользуемся формулой, чтобы найти значение cos 120.
| Degrees | 0 ° | 30 ° | 45 ° | 60 ° | 90 ° |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| tan | 0 | 1/√3 | 1 | √3 | ∞ |
Используя cos (180° – θ) = – cosθ
1.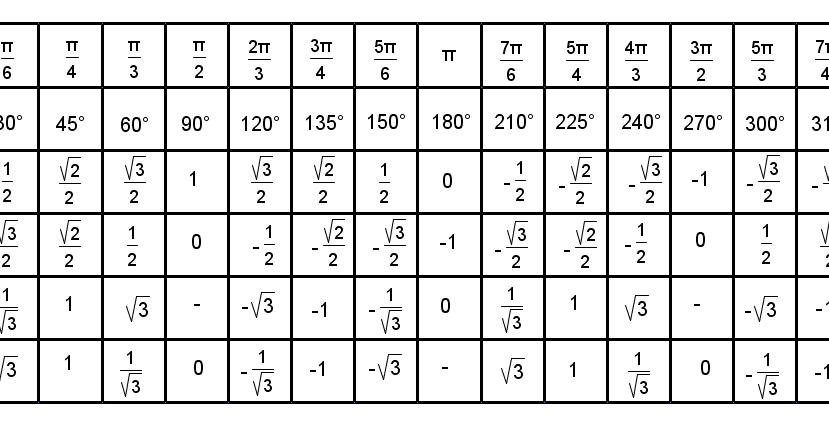 cos 120° = cos (180° – 60°) = -cos 60 = -1/2.
cos 120° = cos (180° – 60°) = -cos 60 = -1/2.
Используя cos (90° + θ) = – sinθ
1. cos (90° + 30°) = – sin30° = -1/2.
Тригонометрическая таблица: Cos 120
Теперь, когда вы знаете значение косинуса 120°, позвольте нам предоставить вам полную тригонометрическую таблицу:
| Angles | 0 ° | 30 ° or π/6 | 45 ° or π/4 | 60 ° or π/3 | 90 ° or π/2 | 120 ° or 2π/3 | 180 ° or π | 270 ° or 3π/2 | 360 ° или 2π |
| Sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | √3/2 | 0 | −1 | 0 |
| Cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1/2 | −1 | 0 | 1 |
| Tan | 0 | 1/ √3 | 1 | √3 | Не определено | -√3 | 0 | Not Defined | 0 |
| Cot | Not Defined | √3 | 1 | 1/√3 | 0 | -1/√3 | Not Defined | 0 | Not Defined |
| Cosec | Not Defined | 2 | √2 | 2/√3 | 1 | 2/√3 | Not Defined | −1 | Not Defined |
| Sec | 1 | 2/√3 | √2 | 2 | Not Defined | -2 | −1 | Not Defined | 1 |
Practice 12th CBSE Exam Questions
Учитесь у Embibe
Студенты могут бесплатно получить доступ к следующим учебным материалам только на Embibe для подготовки к экзамену:
Тригонометрические тождества
Вот некоторые личности, на основе которых задаются вопросы:
а) sin (90° – A) = cos A
b) cos (90° – A) = sin A
c) tan (90° – A) = cot A
d) cot (90° – A) = tan A
e) с (90° – A) = cosec A
f) cosec (90° – A) = с A
Примеры вопросов
i) Оценить cos 48° – sin 42°.
ii) Найти cosec 31° – sec 59°.
iii) Вычислите cos 38°, cos 52° – sin 38°, sin 52° = 0.
iv) Вычислите sin 60°, cos 30° + sin 30°, cos 60°.
v) 2 тангенс 2 45° + cos 2 30° – sin 2 60°.
vi) Выразите отношения cos A, tan A и sec A через sin A.
Часто задаваемые вопросы
Часто задаваемые вопросы, связанные с cos 120, перечислены ниже:
Q.1. Как найти cos 120 без калькулятора?
Ответ. Вы можете использовать обе следующие формулы
i) cos (180° – θ) = – cosθ
или
ii) cos (90° + θ) = – sinθ
Q.2. Что такое cos 120 в радианах?
Ответ. В радианах значение cos 120 равно 2π/3, т.е. равно -1/2.
Q.3. Как вы оцениваете cos 120?
Ответ.

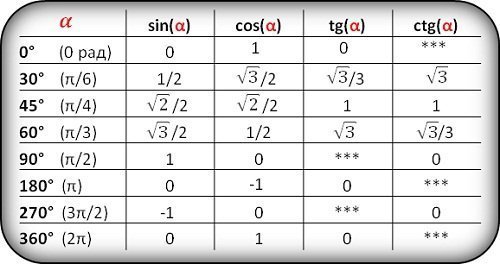
 Значение только Sin положительно в этом квадранте. Показано как S (представляет Sin) на второй диаграмме, приведенной ниже.
Значение только Sin положительно в этом квадранте. Показано как S (представляет Sin) на второй диаграмме, приведенной ниже. Гиппарх использовал эти тригонометрические таблицы для решения задач тригонометрии и сферической тригонометрии.
Гиппарх использовал эти тригонометрические таблицы для решения задач тригонометрии и сферической тригонометрии.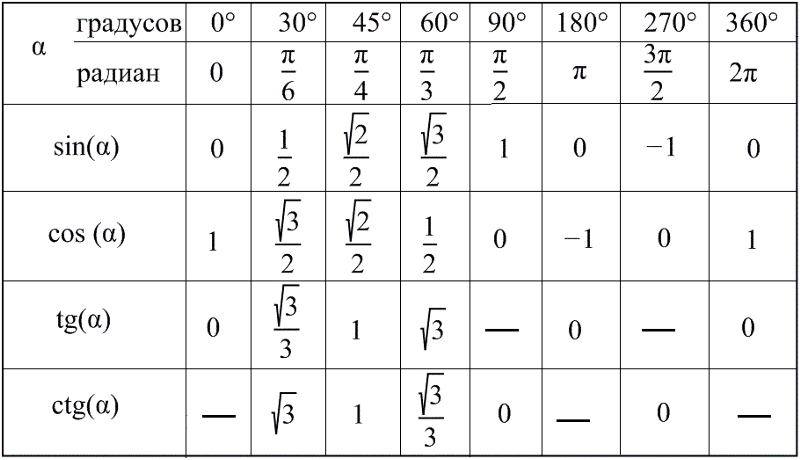 \[Tan\theta =\frac{sin\theta }{cos\theta}\]
\[Tan\theta =\frac{sin\theta }{cos\theta}\]