Калькулятор уравнений с модулем: Решение уравнения с модулем онлайн · Как пользоваться Контрольная Работа РУ

Содержание

Графический способ решения уравнений с модулем

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Тема урока

Графический способ
решения уравнений с модулем
Тема урока

2. Задай функцию формулой

3. Задай функцию формулой

4. Задай функцию формулой

5. Задай функцию формулой

6. Задай функцию формулой

7. Задай функцию формулой

8. Задай функцию формулой

9.

Задай функцию формулой

10. Задай функцию формулой

Выполнила ученица 10 «А»
Засыпалова Анна

17. Правило построения графика функции y=f(|x|). :

1. Построим график функции y=f(x), для х≥0
2. Достроим левую часть графика, симметричную
построенной правой части относительно оси
ординат

18. 1.Построить график функции y=|x|

1.Построить график функции
Построение:
1).
х
у
0
0
2
2
Строим график функции
y=x, х ≥0
2)Симметрично
отображаем
построенную часть
графика относительно
оси оу.
.
y=|x|
Y
y=|x|
X

20. 2. Построить график функции Y=|x|²-4|x|+3

2. Построить график функции
+3
1)Строим
Y=|x|²-4|x|
Построение.
y=x²-4x+3,
х≥0
Y
Y=|x|²-4|x|+3
а)Хверш= -в/2а=-4/2=2
Уверш=2²-4·2+3=-1
(2;-1)-вершина параболы
б)Нули функции (точки пересечения с ох)
x²-4x+3=0
х1=1
х2=3
(1;0) (3;0) — точки пересечения графика с осью ох
в)Если х=0, то у=3
(0;3)
2).

Симметрично отображаем построенную часть
графика относительно оси оу
X

21. 3. Построить график функции у = sin|x|

Y
•X

22. 4. Построить график функции y=cos|x|

Y
X

23. 5. Построить график функции y= cos|x|+2

5. Построить график функции y= cos|x|
+2
Y
X

24. 6. Построить график функции у=3|х|+2

Построение.
1)Cтроим график функции
у=3х+2, х≥0
х
у
0
2
Y
1
5
X
2).Симметрично
отобразим построенную
часть графика
относительно оси ох.
Y
у=3|х|+2
X
Выполнила: Кузьмина Валерия
ученица 10 «а» класса

27. Правило Построения графика функции y=|f(x)|

1.Построить график y=f(x)
2.Сохранить без изменения части графика
y=f(x), расположенные выше оси OX.
3.Отобразить симметрично оси OX части
графика y=f(x), расположенные ниже
оси OX.
y
2
-1
0
x

30. 2) Построить график функции Y=|X²-4x+3|. Построение.

y
0
1
3
x

31. 3) Построить график функции y=|cosx| Построение.

3) Построить график функции y=|
cosx|
Построение.
y
1
0
-1
x

32. 4)Построить график функции y=|sinx|-4 Построение.

y
1
0
-1
-4
x

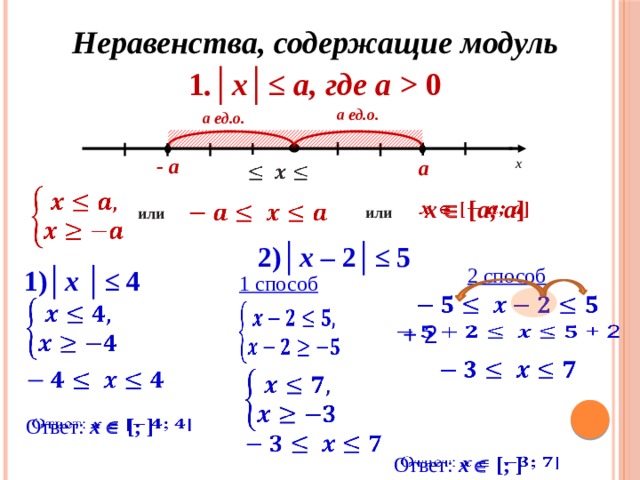
33. Решение уравнений, содержащих модуль

Решение
уравнений,
содержащих
Способы решения уравнений,
содержащих модуль
Использование
определения модуля
Графический способ
Метод введения
новой переменной

35. Графический способ

|х-2|=
у
х
1. у =|х-2|
2. у =
0
1 2
4
х
Ответ: 1; 4.
х

36. Задания командам

Реши уравнение графическим способом
а) |x-1|=2;
б) x2 = |x|;
в)sin|x| = — х2;
г) |x-1|= |x|-1;
д) 3|x|=4 — х2 (МФТИ, 2000г)
е)|x2-3x|=2x-4 (МГУ, 2000г)
№/
Команда
1
команда
2
команда
1
2
3
4
5
6
Устная
работа
итог
Слово «модуль» произошло от латинского слова «modulus», что в переводе
означает «мера».

Это многозначное слово(омоним), которое имеет множество
значений и применяется не только в математике, но и в архитектуре, физике,
технике, программировании и других точных науках.
В архитектуре — это исходная единица измерения, устанавливаемая для данного
архитектурного сооружения и служащая для выражения кратных соотношений его
составных элементов.
В технике — это термин, применяемый в различных областях техники, не имеющий
универсального значения и служащий для обозначения различных коэффициентов
и величин, например модуль зацепления, модуль упругости и .т.п.
Модуль объемного сжатия( в физике)-отношение нормального напряжения в
материале к относительному удлинению.

44. Модуль числа

Абсолютная величина или модуль,
обозначается |x|, |x-1| , |a|

45. Знак модуля

Считают, что термин предложил
использовать
Котс, ученик Ньютона. Лейбниц тоже
использовал
эту функцию, которую называл модулем и
обозначал: mol x.

Общепринятое обозначение
абсолютной величины введено в 1841
году Вейерштрассом.
Для комплексных чисел это понятие ввели
Коши и Арган в начале XIX века.
Математики шутят.
Трехмерная кубическая линейка
Калькулятор для умных

English Русский Правила

Модуль Вычислительная гидродинамика для моделирования течений жидкости и газа

Ламинарный режим течения

Моделируйте стационарное или переходное ламинарное течение, включая ползущее течение, с помощью решения уравнений Навье-Стокса.

Инструменты модуля позволяют анализировать течение жидкостей и газов как с постоянными, так и с переменными свойствами. Можно учесть зависимость вязкости и плотности среды от температуры, локального состава смеси, электрического поля, а также от любой другой полевой переменной. В общем случае, плотность, вязкость и источниковые члены уравнения сохранения импульса могут быть описаны произвольными функциями от любой зависимой переменной или её производной.

Для моделирования течения неньютоновских жидкостей можно использовать готовые реологические модели вязкости, например

степенную модель, модели Карро, Бингама, Гершеля-Балкли или Кассона.

Кроме того, можно моделировать ламинарное течение в подвижных системах, например в запорной арматуре или в аппаратах с вращающейся крыльчаткой.

Турбулентный режим течения

В модуле «Вычислительная гидродинамика» представлен обширный набор моделей турбулентной вязкости на основе осреднённых по Рейнольдсу уравнений Навье-Стокса (RANS-модели). С их помощью можно моделировать стационарные и переходные турбулентные течения в широком диапазоне параметров. Кроме того, можно изменять или дополнять модельные уравнения непосредственно в пользовательском интерфейсе программы, например, чтобы использовать в расчёте модель турбулентности, не представленную в модуле.

RANS-модели турбулентности

Двухпараметрические модели

k-ε-модель
Реалистичная k-ε-модель
k-ω-модель
SST-модель
Низкорейнольдсовая k-ε-модель

С дополнительными уравнениями переноса

Модель Спаларта-Аллмареса
Модель v2-f

Алгебраические модели

Алгебраическая Y+
Модель L-VEL

Описание пристеночной области

Пристеночные функции

Устойчивые модели с ограниченной точностью, которые можно использовать на грубых сетках.

Низкорейнольдсовое описание

Расчёт поля течения во всей пристеночной области. Высокая точность, но требуется подробная сетка.

Автоматический выбор модели пристеночной области

Комбинация устойчивости моделей с пристеночными функциями и точности низкорейнольдсовых моделей, в зависимости от размера элементов сетки.

Метод крупных вихрей

В рамках метода крупных вихрей (LES) крупные трёхмерные нестационарные турбулентные структуры разрешаются непосредственно на сетке, а мелкомасштабные турбулентные вихри описываются с помощью приближённых подсеточных моделей. При использовании погланслойных сеточных элементов этот метод позволяет с высокой точностью рассчитать нестационарное поле течения, а также потоки и силы на границах. В модуле реализованы вариационная многомасштабная модель на основе оценки невязки (RBVM), вариационная многомасштабная модель на основе оценки невязки с вязкостью (RBVMWV) и вариационная многомасштабная версия модели Смагоринского.

Многофазные потоки и течения со свободной поверхностью

Для численного анализа раздельных течений со свободной поверхностью, а также моделирования многофазных систем, содержащих отдельные пузырьки газа или капли жидкости, используются методы расчёта межфазной границы. При решении подобных задач с помощью методов функции уровня и фазового поля можно точно определить положение границы раздела фаз с учётом поверхностного натяжения, в том числе при изменении топологии межфазной границы.

В случае, когда пузырьки, капли или частицы малы в масштабе расчётной области, а количество их велико, целесообразно перейти к использованию дисперсных моделей многофазных потоков. В рамках этих моделей рассчитываются значения массовой или объёмной доли фаз, а также учитывается влияние дисперсной фазы на перенос импульса в осреднённом потоке. В модуле представлены следующие модели: пузырькового течения, многофазной смеси, Эйлера-Эйлера и переноса фазы в многофазной смеси.

Гидродинамика пористых сред

В модуле «Вычислительная гидродинамика» представлено три варианта математического описания гидродинамических процессов в пористых средах, что существенно упрощает процедуру построения расчётных моделей.

Модель, основанная на законе Дарси, является надежным инструментом моделирования течений в пористых структурах, применение которого не требует больших вычислительных ресурсов. Эта модель применима как к однофазным, так и к многофазным потокам. Уравнения Бринкмана представляют собой более общую форму закона Дарси. Эта модель более требовательна к вычислительным ресурсам, но при этом она позволяет учесть инерционные эффекты и диссипацию кинетической энергии в результате вязкого трения. Как правило, уравнения Бринкмана используются для описания процессов в структурах с высокой пористостью.

Для сквозного моделирования течения в области пористой среды и в свободном объёме при ламинарном и турбулентном режимах течения можно использовать комбинированную модель

Free and Porous Media Flow. В рамках этой модели для описания течения в пористой области используются уравнения Бринкмана, а для течения в свободном объёме — уравнения Навье-Стокса.

Более подробные сведения о специальных инструментах моделирования гидродинамики пористых сред представлены на страницах описания модулей «Течения в пористых средах» и «Течения в грунтах».

Течение при высоких числах Маха

Моделируйте околозвуковое и сверхзвуковое течение сжимаемых сред при ламинарном и турбулентном режимах. Модель ламинарного течения обычно применима для описания систем низкого давления. В неё включены уравнения сохранения импульса, массы и энергии идеальных газов. Для турбулентного режима течения при высоких числах Маха доступны две модели турбулентной вязкости — k-ε-модель и модель Спаларта-Аллмареса.

В обоих случаях в процессе решения этих моделей можно использовать алгоритм адаптивного построения расчётной сетки. Алгоритм сгущает сетку в областях с очень высокими градиентами скорости и давления и таким образом позволяет определить положение скачков уплотнения.

Течение в ротационных аппаратах

Ротационные аппараты, например миксеры и турбонасосы, имеют широкое промышленное применение. В модуле «Вычислительная гидродинамика» представлены интерфейсы, в которых для моделирования ротационных аппаратов используются уравнения гидродинамики, сформулированные во вращающихся системах координат. Доступны модели как ламинарных, так и турбулентных течений. С помощью этих интерфейсов можно решать задачи либо в полностью нестационарной постановке, либо в приближении «замороженного» ротора. Метод «замороженного» ротора позволяет оценить средние скорости, изменение давления, степень перемешивания, средние температуры, концентрации и другие параметры без привлечения значительных вычислительных ресурсов.

В целом, с помощью инструментов модуля можно решать гидродинамические задачи в любых подвижных системах координат, а не только во вращающихся. Например, можно моделировать режимы открытия и закрытия клапанов и задвижек. Подвижные системы координат можно использовать для моделирования процессов в системах, в которых одна конструкция скользит вдоль другой, а в зазоре между ними движется жидкость. Такие задачи легко настраиваются и решаются с помощью подвижных сеток.

Тонкие жидкие плёнки

Для описания течений в тонких областях, например в тонких масляных плёнках между подвижными деталями механизмов (задачи трибологии), в модуль «Вычислительная гидродинамика» включены интерфейсы Thin Film Flow.

Реализованные в них математические формулировки обычно используются для моделирования смазки, решения задач эластогидродинамики или учёта вязких потерь в слое между подвижными деталями, например в моделях МЭМС-устройств.

Уравнения мелкой воды

Уравнения мелкой воды позволяют моделировать движение жидкости со свободной поверхностью в случае, когда глубина слоя жидкости намного меньше характерного масштаба в продольном направлении. Уравнения мелкой воды, которые получаются в результате осреднения уравнений Навье-Стокса по глубине, в качестве зависимых переменных содержат толщину слоя и плотность потока импульса жидкости. Эти уравнения можно использовать для моделирования таких явлений как, например, цунами или наводнение.

Мультифизические модели явлений реального мира

Моделирование нескольких физических явлений в COMSOL Multiphysics^® не сложнее решения простой задачи.

Неизотермическое ламинарное течение

Учёт сил плавучести и зависимости свойств жидкости от температуры; условия непрерывности температуры и теплового потока на границе «твёрдое тело — жидкость».

Неизотермическое турбулентное течение

Низкорейнольдсовое описание или тепловые пристеночные функции для расчёта сопряженного теплообмена на границе «твёрдое тело — жидкость» на основе RANS и LES моделей.

FSI: односторонняя связь

Взаимодействие твёрдых деформируемых тел и потока жидкости с учётом силового воздействия со стороны жидкости при условии пренебрежимо малых деформаций, не оказывающих влияния на структуру течения.

FSI: двусторонняя связь

Взаимодействие твёрдых деформируемых тел и потока жидкости с учётом силового воздействия со стороны жидкости и влияния больших деформаций на структуру течения.

Химически-реагирующие потоки

Моделирование переноса массы компонентов смеси и химических реакций в слабых и концентрированных смесях на основе закона Фика или осреднённой модели диффузии.

Расширенные модели реагирующих потоков

Полная система уравнений диффузии Стефана-Максвелла для ламинарных потоков.

Миксеры

Многофазные потоки и течения со свободной поверхностью в ротационных аппаратах; библиотека деталей, содержащая геометрические модели импеллеров и сосудов.

Трассировка частиц

⁴

Модель многофазной среды Эйлера-Лагранжа, в рамках которой твёрдые частицы или жидкие капли описываются как дискретные объекты.

Течение в трубопроводах и CFD

⁵

Модели неизотермического течения в трубах и каналах, соединённых с 2D/3D жидкими доменами, при ламинарном и турбулентном режимах.

Требуется модуль «Механика конструкций», или «MEMS», или «Динамика многотельных систем»
Требуется модуль «Химические реакции», или «Электрохимические аккумуляторы», или «Топливные ячейки и электролизёры»
Требуется модуль «Миксер»
Требуется модуль «Трассировка частиц»
Требуется модуль «Течения в трубопроводах»

Общие функции, адаптированные для решения задач CFD

Для моделирования гидродинамических процессов в модуле «Вычислительная гидродинамика» представлены специальные функции, которые бесшовно интегрируются с инструментами платформы COMSOL Multiphysics^® и обеспечивают унифицированный рабочий процесс построения расчётных моделей.

Гидродинамические интерфейсы

В модуле «Вычислительная гидродинамика» содержится множество гидродинамических интерфейсов, специально разработанных для моделирования различных режимов течений: ламинарных и турбулентных, однофазных и многофазных, сжимаемых и несжимаемых, при низких и высоких числах Маха, в тонких пленках и на мелководье. Каждый гидродинамический интерфейс представляет собой совокупность систем уравнений, граничных и начальных условий, настроек расчётной сетки и решателей для стационарного и динамического анализа, а также набор предварительно настроенных графиков и выходных данных.

Материалы

В состав модуля «Вычислительная гидродинамика» включён справочник свойств наиболее распространённых газов и жидкостей. Подключение дополнительного модуля «Химические реакции» или «Термодинамика жидкостей и газов» позволит рассчитывать термодинамические свойства и свойства переноса газов и жидкостей (например коэффициент вязкости, плотность, коэффициенты диффузии и теплопроводности, теплоты образования и фазовых переходов) на основе самых общих термодинамических соотношений.

Дискретизация

В гидродинамических интерфейсах для дискретизации дифференциальных уравнений двумерной, двумерной осесимметричной и трёхмерной расчётной модели используются методы Галёркина/наименьших квадратов и Петрова-Галёркина. Базисные функции подобраны так, чтобы стабилизировать в уравнениях переноса гиперболические члены и члены, содержащие давление. Методы расчёта с учётом разрывов параметров сокращают паразитные осцилляции решения. Кроме того, для обеспечения сохранения импульса, массы и энергии на внутренних и внешних границах применяются разрывные методы Галёркина.

Обработка и визуализация результатов

При использовании гидродинамических интерфейсов автоматически создаётся ряд стандартных графиков для анализа полей скорости и давления. Для визуализации течения можно построить линии тока. Поверхностные и объёмные графики позволяют отобразить скалярные поля, например давление и модуль скорости. Также имеется обширный список производных значений и переменных (например, коэффициент сопротивления), которые можно легко вывести на график или в таблицу.

Геометрия

Создавайте домены для области течения на основе геометрических моделей, импортированных из CAD. Используйте специальные инструменты для автоматического или ручного удаления не влияющих на структуру течения геометрических элементов. Импортируйте, исправляйте и упрощайте геометрические модели самых популярных CAD-форматов с помощью модуля «CAD-импорт и CAD-операции». Создавайте комплексные геометрические модели, используя встроенные геометрические операции.

Генерация сетки

В автоматическом режиме построения расчётной сетки, учитываются граничные условия, заданные в настройках гидродинамических интерфейсов. На твёрдых стенках автоматически создаются призматические элементы, необходимые для расчёта градиентов скорости в области пограничного слоя.

Решатели

Уравнения гидродинамики обычно сильно нелинейны. Для решения уравнений расчётной модели используется автоматически настраиваемый метод Ньютона с подходящим алгоритмом релаксации. При решении крупномасштабных задач для ускорения сходимости линейных итераций метода Ньютона применяются новейшие алгебраические или геометрические многосеточные методы, специально разработанные для решения уравнений переноса.

Для максимально точного расчёта полей скорости и давления в нестационарных задачах в комбинации с нелинейными решателями используются методы дискретизации по времени с автоматическим выбором временного шага и определением порядка полиномов.

Приложения для моделирования

С помощью cреды разработки приложений, входящей в состав COMSOL Multiphysics^®, можно создавать пользовательские интерфейсы для любых расчётных моделей. Этот инструмент позволяет создавать специализированные приложения с возможностью контроля входных данных и результатов расчёта. Приложения можно использовать в самых разных целях: для автоматизации сложных и повторяющихся действий, создания и обновления отчетов, создания удобных интерфейсов для пользователей, повышения доступности моделей в организации, повышения конкурентоспособности.

Библиотека Sympy: символьные вычисления в Python

Что такое SymPy? Это библиотека символьной математики языка Python. Она является реальной альтернативой таким математическим пакетам как Mathematica или Maple и обладает очень простым и легко расширяемым кодом. SymPy написана исключительно на языке Python и не требует никаких сторонних библиотек.

Документацию и исходный код этой библиотеки можно найти на ее официальной странице.

Первые шаги с SymPy

Используем SymPy как обычный калькулятор

В библиотеке SymPy есть три встроенных численных типа данных: Real, Rational и Integer. С Real и Integer все понятно, а класс Rational представляет рациональное число как пару чисел: числитель и знаменатель рациональной дроби. Таким образом, Rational(1, 2) представляет собой 1/2, а, например, Rational(5, 2) — соответственно 5/2.

import sympy as sym
a = sym.Rational(1, 2) # дает 1/2
a * 2 # дает 1

Библиотека SymPy использует библиотеку mpmath, что позволяет производить вычисления с произвольной точностью. Таким образом, ряд констант (например, пи, e), которые в данной библиотеке рассматриваются как символы, могут быть вычислены с любой точностью.

sym.pi**2 # результат pi**2
sym.pi.evalf() # результат 3.14159265358979
(sym.pi + sym.exp(1)).evalf() # результат 5.85987448204884

Как можно заметить, функция evalf() дает на выходе число с плавающей точкой.

В SymPy есть также класс, представляющий такое понятие в математике, как бесконечность. Он обозначается следующим образом: oo.

sym.oo > 99999 # результат True
sym.oo + 1 # результат oo

Символы

В отличие от ряда других систем компьютерной алгебры, в SymPy можно в явном виде задавать символьные переменные. Это происходит следующим образом:

x = sym.Symbol('x')
y = sym.Symbol('y')

После их задания, с ними можно производить различные манипуляции.

x + y + x - y # результат 2*x
(x + y) ** 2 # результат (x + y)**2

С символами можно производить преобразования с использованием некоторых операторов языка Python. А именно, арифметических (+, -`, ``*, **) и логических (&, |, ~) .

Библиотека SymPy позволяет задавать форму вывода результатов на экран. Обычно мы используем формат такого вида:

sym.init_printing(use_unicode=False, wrap_line=True)

Алгебраические преобразования

SymPy способна на сложные алгебраические преобразования. Здесь мы рассмотрим наиболее востребованные из них, а именно раскрытие скобок и упрощение выражений.

Раскрытие скобок

Чтобы раскрыть скобки в алгебраических выражениях, используйте следующий синтаксис:

sym. expand((x + y) ** 3)

?³+3?²?+3??²+?³

3 * x * y ** 2 + 3 * y * x ** 2 + x ** 3 + y ** 3

?³+3?²?+3??²+?³

При помощи ключевого слова можно добавить поддержку работы с комплексными переменными, а также раскрытие скобок в тригонометрических функциях.

sym.expand(x + y, complex=True)#результат re(?)+re(?)+?im(?)+?im(?)
sym.expand(sym.cos(x + y), trig=True)
# результат −sin(?)sin(?)+cos(?)cos(?)

Упрощение выражений

Если вы хотите привести выражение к более простому виду (возможно, сократить какие-то члены), то используйте функцию simplify.

sym.simplify((x + x * y) / x) # результат y + 1

Также надо сказать, что для определенных видов математических функций существуют альтернативные, более конкретные функции для упрощения выражений. Так, для упрощения степенных функций есть функция powsimp, для тригонометрических —trigsimp, а для логарифмических — logcombine, radsimp.

Вычисления

Вычисления пределов

Для вычисления пределов в SymPy предусмотрен очень простой синтаксис, а именно limit(function, variable, point). Например, если вы хотите вычислить предел функции f(x), где x -> 0, то надо написать limit(f(x), x, 0).

sym. limit(sym.sin(x) / x, x, 0) # результат 1

Также можно вычислять пределы, которые стремятся к бесконечности.

sym.limit(x, x, sym.oo) # результат oo
sym.limit(1 / x, x, sym.oo) # результат 0
sym.limit(x ** x, x, 0) # результат 1

Дифференцирование

Для дифференцирования выражений в SymPy есть функция diff(func, var). Ниже даны примеры ее работы.

sym.diff(sym.sin(x), x) # результат cos(?)
sym.diff(sym.sin(2 * x), x) # результат 2cos(2?)
sym.diff(sym.tan(x), x)

tan²(?)+1

Проверим результат последней функции при помощи определения производной через предел.

sym.limit((sym.tan(x + y) - sym.tan(x)) / y, y, 0)

tan²(?)+1 Результат тот же.

Также при помощи этой же функции могут быть вычислены производные более высоких порядков. Синтаксис функции будет следующим: diff(func, var, n). Ниже приведено несколько примеров.

sym.diff(sym.sin(2 * x), x, 1) # результат 2cos(2?)
sym.diff(sym.sin(2 * x), x, 2) # результат −4sin(2?)
sym.diff(sym.sin(2 * x), x, 3) # результат −8cos(2?)

Разложение в ряд

Для разложения выражения в ряд Тейлора используется следующий синтаксис: series(expr, var).

sym.series(sym.cos(x), x)

1−?²/2+?⁴/24+?(?⁶)

sym.series(1/sym.cos(x), x)

1+?²/2+5?⁴/24+?(?⁶)

Интегрирование

В SymPy реализована поддержка определенных и неопределенных интегралов при помощи функции integrate(). Интегрировать можно элементарные, трансцендентные и специальные функции. Интегрирование осуществляется с помощью расширенного алгоритма Риша-Нормана. Также используются различные эвристики и шаблоны. Вот примеры интегрирования элементарных функций:

sym. integrate(sym.sin(x), x) # результат −cos(?)
sym.integrate(sym.log(x), x) # результат ?log(?)−?

Также несложно посчитать интеграл и от специальных функций. Возьмем, например, функцию Гаусса:

sym.integrate(sym.exp(-x ** 2) * sym.erf(x), x)

Результат вычисления можете посмотреть сами. Вот примеры вычисления определенных интегралов.

sym.integrate(x**3, (x, -1, 1)) # результат 0
sym.integrate(sym.sin(x), (x, 0, sym.pi / 2)) # результат 1
sym.integrate(sym.cos(x), (x, -sym.pi / 2, sym.pi / 2)) 
# результат 2

Также можно вычислять определенные интегралы с бесконечными пределами интегрирования (несобственные интегралы).

sym.integrate(sym.exp(-x), (x, 0, sym.oo)) # результат 1

Решение уравнений

При помощи SymPy можно решать алгебраические уравнения с одной или несколькими переменными. Для этого используется функция solveset().

sym.solveset(x ** 4 - 1, x) # результат {−1,1,−?,?}

Как можно заметить, первое выражение функции solveset() приравнивается к 0 и решается относительно х. Также возможно решать некоторые уравнения с трансцендентными функциями.

sym. solveset(sym.exp(x) + 1, x) # результат {?(2??+?)|?∈ℤ}

Системы линейных уравнений

SymPy способна решать широкий класс полиномиальных уравнений. Также при помощи данной библиотеки можно решать и системы уравнений. При этом переменные, относительно которых должна быть разрешена система, передаются в виде кортежа во втором аргументе функции solve(), которая используется для таких задач.

solution = sym.solve((x + 5 * y - 2, -3 * x + 6 * y - 15), (x, y))
solution[x], solution[y] # результат (-3, 1)

Факторизация

Другим мощным методом исследования полиномиальных уравнений является факторизация многочленов (то есть представление многочлена в виде произведения многочленов меньших степеней). Для этого в SymPy предусмотрена функция factor(), которая способна производить факторизацию очень широкого класса полиномов.

f = x ** 4 - 3 * x ** 2 + 1
sym.factor(f)

(?²−?−1)(?²+?−1)

sym.factor(f, modulus=5)

(?−2)²(?+2)²

Булевы уравнения

Также в SymPy реализована возможность решения булевых уравнений, что по сути означает проверку булевого выражения на истинность. Для этого используется функция satisfiable().

sym. satisfiable(x & y) # результат {x: True, y: True}

Данный результат говорит нам о том, что выражение (x & y) будет истинным тогда и только тогда, когда x и y истинны. Если выражение не может быть истинным ни при каких значениях переменных, то функция вернет результат False.

sym.satisfiable(x & ~x) # результат False

Линейная алгебра

Матрицы

Матрицы в SymPy создаются как экземпляры класса Matrix:

sym.Matrix([[1, 0], [0, 1]])

[10] [01]

В отличие от NumPy, мы можем использовать в матрицах символьные переменные:

x, y = sym. symbols('x, y')
A = sym.Matrix([[1, x], [y, 1]])
A

[1 ?] [? 1]

И производить с ними разные манипуляции:

A**2

[??+1 2?] [2? ??+1]

Дифференциальные уравнения

При помощи библиотеки SymPy можно решать некоторые обыкновенные дифференциальные уравнения. Для этого используется функция dsolve(). Для начала нам надо задать неопределенную функцию. Это можно сделать, передав параметр cls=Function в функцию symbols().

f, g = sym.symbols('f g', cls=sym.Function)

Теперь f и g заданы как неопределенные функции. мы можем в этом убедиться, просто вызвав f(x).

f(x) # результат ?(?)
f(x).diff(x, x) + f(x)

?(?)+?²/??²?(?)

Теперь решим следующее дифференциальное уравнение:

sym.dsolve(f(x).diff(x, x) + f(x), f(x))
# результат ?(?)=?1sin(?)+?2cos(?)

Чтобы улучшить решаемость и помочь этой функции в поиске решения, можно передавать в нее определенные ключевые аргументы. Например, если мы видим, что это уравнение с разделяемыми переменными, то мы можем передать в функцию аргумент hint='separable'.

sym. dsolve(sym.sin(x) * sym.cos(f(x)) + sym.cos(x) * sym.sin(f(x)) * f(x).diff(x), f(x), hint='separable') 
# результат [Eq(f(x), -acos(C1/cos(x)) + 2*pi), Eq(f(x), 
#            acos(C1/cos(x)))]

Английский для программистов

Наш телеграм канал с тестами по английскому языку для программистов. Английский это часть карьеры программиста. Поэтому полезно заняться им уже сейчас

Скачать

Расчетные модули > Прочие расчетные модули > Калькулятор свойств общего сечения

Нужно больше? Задайте нам вопрос

Обзор

Этот модуль определяет свойства сечений для составных сечений с прямоугольниками, полыми кругами, сплошными кругами, стандартными стальными профилями AISC и обычными многогранными сплошными формами. Нажмите здесь, чтобы посмотреть видео:

Секции AISC можно вызывать из файлов базы данных и включать в сборную секцию. Все разделы 13-го издания Руководства по стальным конструкциям AISC доступны и могут быть переориентированы по мере необходимости.

Расчетные значения свойств сечения включают: площадь, моменты инерции, положение центра тяжести, крайние расстояния волокон, модули сечения и радиус вращения.

Основное использование

• Прежде чем начать ввод данных, убедитесь, что вы настроили систему координат X-Y для единообразной ссылки на расположение всех компонентов.

•Для каждой прямоугольной формы введите высоту, ширину и центр области, измеренные от базы.

• Полые круглые сечения вводятся путем указания внешнего радиуса и толщины. Сплошные круглые сечения вводятся путем указания внешнего радиуса и установки нулевой толщины.

•Для сечений AISC можно использовать поля ввода Xcg и Ycg, чтобы определить положение центра тяжести сечения по отношению к системе отсчета. Модуль знает расположение центроидов элементов AISC по отношению к их собственным экстремальным положениям волокон. Однако вам необходимо ввести положение центра тяжести элемента по отношению к другим элементам в застроенной секции. Будьте осторожны, так как это может быть сложно при вводе каналов, углов и тройников, которые поворачиваются.

• Уникальная функция позволяет пользователю указать, что секции AISC можно поворачивать с шагом в один градус, стальные угловые секции также можно зеркально отображать вокруг их оси Y, а всю сборную секцию можно поворачивать на любой желаемый угол.

Допущения и ограничения

Модуль работает на простой процедуре расчета:

• Рассчитать момент инерции каждой формы,

• Рассчитать 9 нейтральных осей группы, формы и формы0003

• Рассчитайте момент инерции группы, используя уравнения I + A*D2.

Более сложный анализ, такой как полярный момент инерции, пластические модули и константы потери устойчивости, в настоящее время выходит за рамки модуля, но постоянная разработка добавит эти элементы в будущих обновлениях.

Прокатный профиль/таблица

На этой вкладке можно указать до 10 профилей из базы данных AISC Edition для использования в сборном элементе.

Квадратные кнопки в верхней части вкладки используются для представления секций компонентов, составляющих вашу сборную форму. Когда для конкретной кнопки указана секция, под соответствующей кнопкой будет показан маленький зеленый треугольник, обращенный вверх. Нажмите любую кнопку, чтобы добавить раздел или вид и изменить раздел, который уже был назначен этой кнопке.

Примечание. Важно понимать, что пронумерованные кнопки на различных вкладках НЕ ОТНОСЯТСЯ к различным составным формам. Вместо этого каждый экземпляр этого модуля создает только ОДНУ составную форму, а общая составная форма состоит из комбинации ВСЕХ секций, которые в настоящее время существуют на ЛЮБЫХ кнопках на вкладке «Свернутое сечение/Таблица», вкладке «Прямоугольная и круглая» и вкладка «Общие фигуры».

Чтобы вставить раздел AISC, вы можете:

• Введите имя раздела и нажмите [Tab]. Модуль выполнит поиск в базе данных и извлечет информацию.

• Используйте кнопку [Обзор стальных профилей] для отображения базы данных металлоконструкций, в которой вы можете перемещаться и выбирать нужный профиль.

Угол поворота: против часовой стрелки

Если вам нужно повернуть секцию, нажмите одну из четырех кнопок углового поворота.

Повернуть секцию на 180 градусов вокруг собственной оси y-y

Этот флажок будет отображаться только для секций с одним углом. Он предлагает возможность зеркального отражения секции с одним углом, если это необходимо.

Xcg и Ycg

Введите положение центральной оси сечения, измеренное от исходной точки (начало предполагаемой декартовой системы координат X-Y).

Свойства сечения

Эти значения будут заполнены после того, как вы сделаете свой выбор из базы данных AISC. ОДНАКО вы можете изменить эти значения самостоятельно. Особое значение для несимметричных сечений имеет правильный ввод «Xbar» и «Ybar». Это расстояние от нижнего левого края сечения, измеренное вверх и вправо, до положения центральной оси сечения.

База данных Стальной секции

Нажмите кнопку [Обзор стальных секций], чтобы отобразить окно базы данных AISC:

Прямоугольная и циркулярная

Эта вкладка позволяет указать простые прямоугольные и циркулярные сварные сварки. .

Не используется / Прямоугольная / Круглая

Выберите форму, которую вы хотите использовать для этого элемента.

Прямоугольный ввод данных

При выборе прямоугольной формы ввод данных состоит из высоты и ширины.

Круговой ввод данных

Когда выбрана круглая форма, ввод данных состоит из внешнего радиуса и толщины стенки (не внутреннего радиуса). Чтобы смоделировать твердое круглое сечение, введите соответствующий Внешний радиус и установите Толщину стенки на ноль.

Xcg и Ycg

Введите положение центральной оси сечения, измеренное от исходной точки (начало предполагаемой X-Y декартовой системы координат).

Общие формы

На этой вкладке можно выбрать одну из распространенных многоугольных фигур. При каждом выборе справочный чертеж и подсказки для ввода данных будут меняться.

Квадратные кнопки в верхней части вкладки используются для представления разделов компонентов, составляющих вашу сборную форму. Когда для конкретной кнопки указана секция, под соответствующей кнопкой будет показан маленький зеленый треугольник, обращенный вверх. Нажмите любую кнопку, чтобы добавить раздел или вид и изменить раздел, который уже был назначен этой кнопке.

Xcg и Ycg

Угол поворота: против часовой стрелки

Для этих фигур можно поворачивать секцию с шагом в один градус. Положительные углы представляют вращение против часовой стрелки.

Расчеты

Подробная таблица свойств

В этой таблице представлены все элементы компонентов, добавленные вами в раздел. Он сообщает об их индивидуальном местоположении, свойствах и максимальном расстоянии от центра тяжести для каждого из четырех ребер.

Примечание. Эта таблица прокручивается вправо. Просто используйте полосу прокрутки в нижней части таблицы.

Общая площадь

Общая площадь всех определенных форм, включая площадь любых секций AISC, которые были включены в застроенную форму.

Инерция: Ixx и Iyy

Общий момент инерции составного сечения определяется путем применения следующего уравнения ко всем определенным формам:

Ixx = Iox + (A * dy2) и Iyy = Ioy + (A * dx2)

, где d = расстояние от центра тяжести фигуры. к общему К.Г. составного сечения, измеренного в направлении, указанном нижним индексом.

Модуль сечения: Sxx и Syy

Эти значения являются рассчитанными модулями сечения составного сечения. Значения определяются путем деления Ixx или Iyy на крайние расстояния волокон выше, ниже, справа и слева от центра тяжести секции.

Радиус вращения

Радиус вращения составного сечения определяется с помощью типичного уравнения: rxx = (Ixx/A)½ и ryy = (Iyy/A)½.

Максимальное расстояние от ЦТ

Для каждой секции в построенной форме в этих столбцах указано расстояние от крайних волокон этой секции до ЦТ. составного сечения.

Sketch

Генератор файлов модулей – PlantPredict

Этот алгоритм используется для создания файла модуля с использованием основных входных данных таблицы данных и допущений по умолчанию. В его основе лежит модель эквивалентной схемы с одним диодом для фотоэлектрических модулей (как определено на принципиальных схемах ниже для модулей с рекомбинацией и без нее; путь рекомбинационного тока показан пунктирной линией).

Уравнение, управляющее этой эквивалентной цепью, получено с использованием закона тока Кирхгофа, который гласит, что ток должен в сумме равняться нулю в любом соединении цепи:

Результирующие основные уравнения:

и все остальные переменные определены ниже в разделе «Входы». Конкретное применение модели с одним диодом основано на процессе и наборе предположений, разработанных Андре Мермудом. Все необходимые входные данные могут быть получены из спецификации стандартного модуля от любого производителя.

Расчет сопротивления шунта и сопротивления шунта в темноте.

Сопротивление шунта по умолчанию рассчитывается в соответствии со следующим уравнением, квантованным (округленным) до размера шага, зависящего от того, в каком диапазоне находится исходное расчетное значение.

…где K — «множитель сопротивления шунта», множитель для конкретной технологии (по умолчанию 5,0 для модулей c-Si и 3,0 для модулей CdTe). В таблице ниже указано квантование (интервал округления) для каждого диапазона необработанных значений сопротивления шунта.

Rsh,темн. Сопротивление рассчитывается путем умножения Rsh на константу и квантуется аналогично сопротивлению шунта.

, где Kdark — множитель темнового шунта. В таблице ниже указано квантование (интервал округления) для каждого диапазона необработанных значений.

2. Рассчитайте параметр рекомбинации , если тип модели «1-диод с рекомбинацией» (в противном случае пропустите).

При создании модуля с рекомбинацией необходимо оценить параметр рекомбинации, который выводится из максимального параметра рекомбинации. Чтобы найти максимальный параметр рекомбинации, последовательное сопротивление устанавливается равным (приблизительно) нулю. Затем алгоритм увеличивает параметр рекомбинации, начиная с нуля, и решает систему уравнений на каждой итерации.

Система уравнений определяется с помощью управляющего уравнения «1-диод с рекомбинацией», приведенного выше, при 3 различных условиях: (I = I _sc , V = 0), (I = 0, V = V _oc ), и (I = I _тр , V = V _тр ). Алгоритм нелинейного решения методом наименьших квадратов Левенберга-Марквада используется для решения системы уравнений и вычисления следующих неизвестных: I _ph (световой ток), γ и I ₀ . Исходные догадки для решения системы уравнений таковы:

Итеративный цикл завершается, когда выполняется условие I ₀ /I _ph < 1 x 10 ^-12 . Значение параметра рекомбинации (di ² /μτ) от предыдущей итерации до достижения этого предела принимается за максимальный параметр рекомбинации . Окончательное значение параметра рекомбинации рассчитывается с использованием простого соотношения:

3. Рассчитайте максимальное последовательное сопротивление.

Следующим шагом является расчет максимального теоретического последовательного сопротивления, которое служит верхним пределом для расчета фактического последовательного сопротивления. Алгоритм перебирает постепенно увеличивающиеся значения R _s , начиная с (почти) нуля. На каждой итерации решается система уравнений для определения оптимальных значений неизвестных аналогично шагу 2. Следует использовать соответствующее определяющее уравнение («модель с 1 диодом» или «модель с 1 диодом с рекомбинацией»). Кроме того, для варианта использования нерекомбинационной «модели с 1 диодом» единственными неизвестными, вычисляемыми из системы уравнений, являются I ₀ и γ. Световой ток рассчитывается по следующей формуле:

, где Rs,i — это значение последовательного сопротивления i ^th итерации. Итеративный цикл завершается, когда либо решение не может быть найдено, либо соотношение I ₀ / I _ph < 1 x 10 ^-12 . Это соотношение является несколько условно, но эмпирически определенным пределом. Значение R _s в предыдущей итерации до достижения этого предела равно R _с, _макс.

4. Рассчитайте последовательное сопротивление и окончательные параметры одиночного диода.

Модель с 1 диодом (без рекомбинации)

Для варианта использования «Модель с 1 диодом» определите значение последовательного сопротивления, которое обеспечит относительную эффективность 97% при 200 Вт/м ² и 25⁰C. Алгоритм делает это, перебирая значения R _s между 20% и 95% R _{s. max} (определено на предыдущем шаге). На каждой итерации система уравнений решается аналогично предыдущим шагам с использованием управляющего уравнения «модели с 1 диодом» и тех же трех условий. Решение системы уравнений используется для расчета линейной зависимости γ (µ _γ ) (см. отдельную документацию по расчету µ _γ). Затем рассчитывается относительная эффективность при 200 Вт/м ² (см. отдельную документацию по алгоритму EIR).

В конце каждой итерации записывается ошибка между рассчитанным значением EIR при 200 Вт/м ² и желаемым значением 0,97. Ошибка, рассчитанная на текущей итерации, сравнивается с предыдущей итерацией. Если знак ошибки меняется (т.е. ошибка с положительного на отрицательный), то в качестве оптимального выбирается значение R _s из предыдущей итерации.

Значения I ₀ , γ и µ _γ, рассчитанные на итерации, соответствующей оптимальному R _s значение являются окончательными параметрами одиночного диода.

1-диодная модель с рекомбинацией

В случае рекомбинации последовательное сопротивление рассчитывается по простой зависимости:

Значения для I ₀ и γ путем решения соответствующей системы уравнений с окончательным значением последовательного сопротивления и используются в качестве входных данных для расчета μ _γ .

Этот алгоритм вычисляет линейную температурную зависимость коэффициента идеальности диода. Как правило, это достигается путем определения значения, которое приводит к температурному коэффициенту максимальной мощности, максимально близкому к входным данным из таблицы данных.

Определите направление, в котором должна увеличиваться мю-гамма .

Линейная зависимость гаммы от температуры увеличивается один раз в положительном и отрицательном направлениях, создавая набор из трех значений:

Для каждого из этих значений γ настраивается по температуре на 45⁰C, в дополнение к регулировке температуры всех других входных параметров одиночного диода (см. раздел документации алгоритма, озаглавленный «Температурная коррекция модели с одним диодом»).

Рассчитайте Pmp при STC, затем для каждого из трех значений мю-гаммы рассчитайте Pmp при 45⁰C и рассчитайте mu_Pmp , используя следующее уравнение:

Если ошибка между вычисленными mu_Pmp и mu_Pmp из входных данных таблицы уменьшается для mu_gamma + приращение , то mu_gamma следует увеличивать в положительном направлении для достижения оптимального значения.

Итеративное приращение к оптимальному значению , которое генерирует близко к введенному значению mu_Pmp .

Увеличивайте mu_gamma в направлении, определенном на шаге 1, выполняя вычисления, аналогичные шагу 1, и проверяя ошибку между calculate_mu_Pmp и mu_Pmp на каждой итерации. Оптимальное значение mu_Pmp , которое предшествует ошибке между вычисляемым_mu_Pmp и mu_Pmp начинают увеличиваться.

Эффективная характеристика освещенности (EIR) модуля — это его относительная эффективность в различных нестандартных условиях. Это иногда называют «реакцией модуля при слабом освещении». Следующий алгоритм описывает, как рассчитать относительную эффективность при одном условии (температура/излучение без STC). Этот процесс можно повторить при различных условиях, чтобы получить кривую EIR.

Рассчитайте точку максимальной мощности при стандартных условиях испытаний (STC).

Точка максимальной мощности рассчитывается с использованием параметров одного диода в STC.

Температура и освещенность регулируют все соответствующие параметры одного диода до T_actual и G_actual .

См. раздел документации по алгоритму, озаглавленный «Температурная коррекция модели с одним диодом».

Рассчитайте точку максимальной мощности по параметрам одного диода с поправкой на температуру/освещенность.

Используя параметры одного диода с поправкой на температуру, рассчитайте точку максимальной мощности, как в шаге 1.

Рассчитайте относительную эффективность.

, где EIRi – относительная эффективность при заданной освещенности в десятичной форме, Pmp,i – точка максимальной мощности при данной освещенности, а Pmax,norm – нормированная максимальная (идеальная) точка мощности при заданной излучение, как описано следующим уравнением:

, где Pmp, 1000 — точка максимальной мощности при 1000 Вт/м ² и i — заданная освещенность.

Этот алгоритм находит оптимальное значение последовательного сопротивления (с постоянными всеми остальными параметрами одиночного диода), которое создает рассчитанную моделью эффективную освещенность (EIR), близкую к некоторому целевому (заданному пользователем) EIR. Таким образом, алгоритм «настраивает» последовательное сопротивление модуля на требуемый EIR.

Определите направление, в котором должно увеличиваться последовательное сопротивление.

Начиная с Rs,max/2 последовательное сопротивление увеличивается один раз в положительном и отрицательном направлениях. Относительные КПД при 800, 600, 400 и 200 Вт/м ² рассчитаны для каждого из трех последовательных сопротивлений: Rs,max /2 – приращение, Rs,max /2, Rs,max /2 + приращение (см. «Создание файла модуля: Расчет эффективной освещенности (EIR)»). Ошибка между каждым из трех сгенерированных EIR и целевым EIR рассчитывается с использованием взвешенной среднеквадратичной ошибки:

где, например,

Если добавление приращения к рупий,макс. /2 уменьшило ошибку, то алгоритм будет увеличивать приращение в положительном направлении (и наоборот).

Итеративно найдите оптимальное значение последовательного сопротивления, при котором EIR будет наиболее близким к целевому EIR.

Затем алгоритм увеличивает рупий в направлении, определенном на шаге 1, вычисляя ошибку EIR в конце каждой итерации с использованием уравнения на шаге 1. Он делает это до тех пор, пока ошибка EIR снова не начнет увеличиваться, рупий достигает рупий, макс. (в случае, если приращение положительное), или рупий, достигает 0,05 рупий, макс. (в случае, если приращение отрицательное). Используя это окончательное значение Rs , пересчитываются следующие параметры одного диода: I ₀ , γ и μ _{γ .}

Параметр ввода «Ключевые точки ВАХ» предоставляет альтернативу параметрам «базового листа данных» в качестве входных данных для алгоритма генерации файла модуля. Это этап предварительной обработки для генератора файлов основного модуля. Этот формат ввода смоделирован на основе стандарта испытаний IEC-61853-1, определенного Международной электротехнической комиссией (IEC) как: «Требования к оценке производительности фотоэлектрического модуля с точки зрения номинальной мощности (ватт) в диапазоне освещенности и температуры…a вторая цель — предоставить полный набор параметров характеристики модуля при различных значениях освещенности и температуры». См. «Входы» ниже для получения дополнительной информации.

*Важное примечание: Эти входные данные предназначены для нескольких условий температуры/излучения (, ). Каждый набор входных данных представлен строкой в пользовательском интерфейсе ключевых точек ВАХ. Минимальный требуемый ввод — это данные в STC.

Алгоритм ключевых точек IV

Единственная необходимая строка ввода предназначена для условий STC. Приведенные значения максимальной мощности, напряжения при максимальной мощности, тока при максимальной мощности, тока короткого замыкания и напряжения холостого хода считаются окончательными «Электрическими характеристиками при STC» модуля.

Если данные представлены при нескольких температурах, температурные коэффициенты будут рассчитаны для P mp , V oc и I sc . Это делается путем выполнения линейной регрессии, где значения x представляют собой температуру, а значения y представляют собой соответствующие электрические характеристики при каждой температуре (и G = 1000 Вт/м ² ). Результирующие температурные коэффициенты рассчитываются в единицах [%] путем деления наклона линейной аппроксимации на соответствующую электрическую характеристику при STC.

Для каждой температуры, если предоставлены данные при нескольких значениях освещенности, относительная эффективность при каждом освещении рассчитывается для каждого из них, как описано в шаге 4 документации «Расчет эффективного отклика на облучение (EIR)».

Параметр ввода «Полные кривые ВАХ» предоставляет другие альтернативные параметры «базового листа данных» в качестве входных данных для алгоритма генерации файла модуля. Это этап предварительной обработки для генератора файлов основного модуля.

*Важное примечание: ВАХ предназначены для получения нескольких условий температуры/освещенности (, ). Минимальный требуемый ввод — это данные в STC.

Алгоритм полных ВАХ

Для каждой кривой ВАХ (при уникальном наборе условий температуры и освещенности):

Ток короткого замыкания извлекается путем получения значения тока, при котором напряжение равно нулю. Если кривая IV не включает точку на пересечении I, берется ближайшая точка и выполняется интерполяция к оси I с использованием наклона кривой IV, ближайшей к оси I.

Напряжение холостого хода извлекается путем получения значения напряжения, при котором ток равен нулю. Если кривая ВАХ не включает точку на пересечении V, берется ближайшая точка и выполняется интерполяция к оси V с использованием наклона кривой ВАХ, ближайшей к оси V.

Точка максимальной мощности определяется путем перемножения каждого набора значений тока и напряжения вместе и взятия максимума из полученного списка. Ток при максимальной мощности и напряжение при максимальной мощности соответствуют точке максимальной мощности.

После извлечения параметра для каждой предоставленной кривой ВАХ полученные данные обрабатываются, как описано в документации «Ключевые точки ВАХ», для расчета температурных коэффициентов и относительной эффективности.

Калькулятор модуля | Расчетный модуль

✖Диаметр делительной окружности зубчатого колеса представляет собой воображаемую окружность, концентрическую к зубчатому колесу, вдоль которой измеряется шаг зубьев.ⓘ Диаметр делительной окружности [d _{Citch Circle}]

Alnangstromarpentastronomical Unitattometomate of LengthBarleyCornbylion Light Aurbohr RadiusCable (международный) кабельный (UK) Кабель (US) Calibercentimeterchaincabit (Greek) кубит (на длинный) выявление (uk) decameter -artair -artartear -artair -artair suniar -artear -artair suniar -artear -artair suniar -artair srinear -stariemeter -artair suniar -artartearedear -stareear -artaryearedeameterChiT RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK )ПарсекОкуньПетаметрПикаПикометрПланк ДлинаТочкаПолюсКварталТростникТростник (Длинный)РодРоман АктусВеревкаРусский АрчинПротяженность (Ткань)Солнце РадиусТераметрТвипВара КастелланаВара КонукераВара Де ТареаЯрдЙоктометрЙо ттаметрZeptometerZettameter

+10%

-10%

✖Количество зубьев на колесе – это количество зубьев на колесе. ⓘ Количество зубьев на колесе [T]

0 9002 +10%

-10%

✖Модуль — это единица измерения размера, указывающая, насколько велика или мала шестеренка.ⓘ Модуль [м]

907:10

AlnAngstromArpentAstronomical UnitAttometerAU of LengthBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedReed (Long)RodRoman ActusRopeRussian ArchinSpan ( Ткань)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter

⎘ Копировать

👎

Формула

Перезагрузить

👍

Модульное решение

ШАГ 0: Сводка предварительных расчетов

ШАГ 1: Преобразование входных данных в базовые единицы

Диаметр делительной окружности: 0,11 метра —> 0,11 метра Преобразование не требуется
Количество зубьев на колесе: 12 — > Преобразование не требуется

ШАГ 2: Вычисление формулы

ШАГ 3: Преобразование результата в единицу измерения

0,00916666666666667 Метр —>9,16666666666667 Миллиметр (проверьте преобразование здесь)33 0,009166666666666667 < 10+ калькуляторов зубчатых передач

Формула модуля

Модуль = диаметр делительной окружности/количество зубьев на колесе.
m = d _{делительная окружность} /T

Что такое нормальный модуль в шестерне?

Нормальный модуль (КШ) Модификации цилиндрических зубчатых колес изготавливаются на зуборезных или шлифовальных станках, даже если они имеют разные углы наклона винтовой линии. Имеют значение межосевого расстояния, отличное от такового у прямозубой шестерни, хотя имеют тот же размер модуля и такое же количество зубьев шестерни.

Что такое пример модуля?

Когда длина забора составляет шесть футов, каждая длина в шесть футов является примером модуля. Когда машина состоит из нескольких частей, которые могут стоять отдельно и собираться вместе, каждая часть является примером модуля.

Как рассчитать модуль?

Калькулятор модуля использует модуль = диаметр делительной окружности/количество зубьев на колесе для расчета модуля. Модуль — это единица измерения, указывающая, насколько велика или мала шестерня. Это отношение эталонного диаметра шестерни к количеству зубьев. Модуль обозначен символом м .

Как рассчитать модуль с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для модуля, введите диаметр делительной окружности (d _{делительной окружности} ) и количество зубьев на колесе (T) и нажмите кнопку расчета. Вот как можно объяснить расчет модуля с заданными входными значениями -> 9,166667 = 0,11/12 .

Часто задаваемые вопросы

Что такое модуль?

Модуль — это единица размера, указывающая, насколько велика или мала шестерня. Это отношение эталонного диаметра шестерни к количеству зубьев и представляется как м = d _{делительной окружности} / T или модуль = диаметр делительной окружности / количество зубьев на колесе . Диаметр делительной окружности зубчатого колеса представляет собой воображаемую окружность, концентрическую по отношению к зубчатому колесу, вдоль которой измеряется шаг зубьев, а количество зубьев на колесе — это количество зубьев на колесе.