Обратная и обратимая функция: Обратная функция — урок. Алгебра, 10 класс.

Обратная функция

1. Рассмотрим две функции, и , графики которых изображены, соответственно, на рисунках 1 и 2. Функция обладает следующим свойством: каждое свое значение функция принимает только при одном значении аргумента. То есть, если , то уравнение имеет единственное решение . В геометрической интерпретации это означает, что параллельная оси абсцисс прямая пересекает график функции  ровно в одной точке.

Определение 1. Если функция каждое свое значение принимает только при одном значении аргумента, то эта функция называется обратимой. Иначе можно сказать, что разным значениям аргумента соответствуют разные значения функции .

Функция таким свойством не обладает. Например, отмеченное на рисунке 2 значение функции принимается при разных значениях аргумента, и , то есть и . Другими словами, уравнение имеет при данном значении два корня.

Прямая, параллельная оси абсцисс, может пересечь график этой функции  более чем в одной точке.

Свойство функции принимать каждое свое значение только при одном значении аргумента, то есть быть обратимой, позволяет определить новую функцию. А именно функцию, которая ставит в соответствие значению то единственное значение , при котором . То есть ставит числу в соответствие единственный корень уравнения . Назовем эту функцию обратной к функции и обозначим буквой . Таким образом, .

Отметим, что в отличие от функции , для функции задать таким же способом обратную функцию не удастся, поскольку уравнение может иметь несколько корней. Дадим определение обратной фукции.

Определение 2. Пусть задана обратимая функция . Функция , определенная на множестве , и ставящая в соответствие числу число ), такое, что , называется обратной к функции .

2. Найдем обратную функцию к функции . Область определения функции , отрезок , обозначим буквой , то есть . Множество значений функции составляет отрезок , обозначенный буквой , то есть

Функция числу из промежутка ставит в соответствие корень квадратный из этого числа, например, . Функция является обратимой, поскольку разным значениям ее аргумента соответствуют разные значения функции.

Обратная функция определена на промежутке и произвольному числу ставит в соответствие число , которое определяется условием , то есть равенством (рис.4). Выражаем из этого равенства , возведя обе части равенства в квадрат, . Таким образом, функция произвольному числу ставит в соответствие число , равное . Значит, для каждого имеем , то есть .

Независимой переменной, то есть аргументом обратной функции , является переменная , а зависимой — переменная . То есть, в сравнении с функцией , переменные поменялись ролями. Если теперь переменные обозначить традиционным образом, а именно, буквой х — аргумент функции , а зависимую переменную – буквой , то функция примет вид . Таким образом, мы нашли, что квадратичная функция , заданная на отрезке , является обратной к функции .. Множество значений обратной функции — отрезок .

График обратной функции мы можем изобразить в той же системе координат, что и график . Для этого отрезок , составляющий область определения функции нужно отложить на оси ординат, поскольку на этой оси располагаются значения аргумента функции. Точки графика функции имеют координаты , при этом (рис.5).

На рисунке 5 показано, что области определения и множества значений функций «меняются местами»: и .

Обратная функция

Урок 3. Алгебра 10 класс

На этом уроке мы познакомимся с понятиями прямой и обратной функции, обратимой функции. Научимся находить обратные функции. Рассмотрим свойства обратных функций.

Конспект урока «Обратная функция»

Вопросы занятия:

·     познакомиться с понятиями прямой и обратной функции;

·     познакомиться с понятием обратимой функции;

·     научиться находить обратные функции;

·     рассмотреть свойство обратных функций.

Материал урока

Прежде чем приступить к изучению новой темы, давайте вспомним, что же такое функция и какие основные понятия с ней связаны.

Определение.

Если даны числовое множество X и правило f, которое позволяет поставить в соответствие каждому элементу x из множества X определенное число y, то говорят, что задана функция y=f(x) с областью определения X.

Область определения обозначается D(f).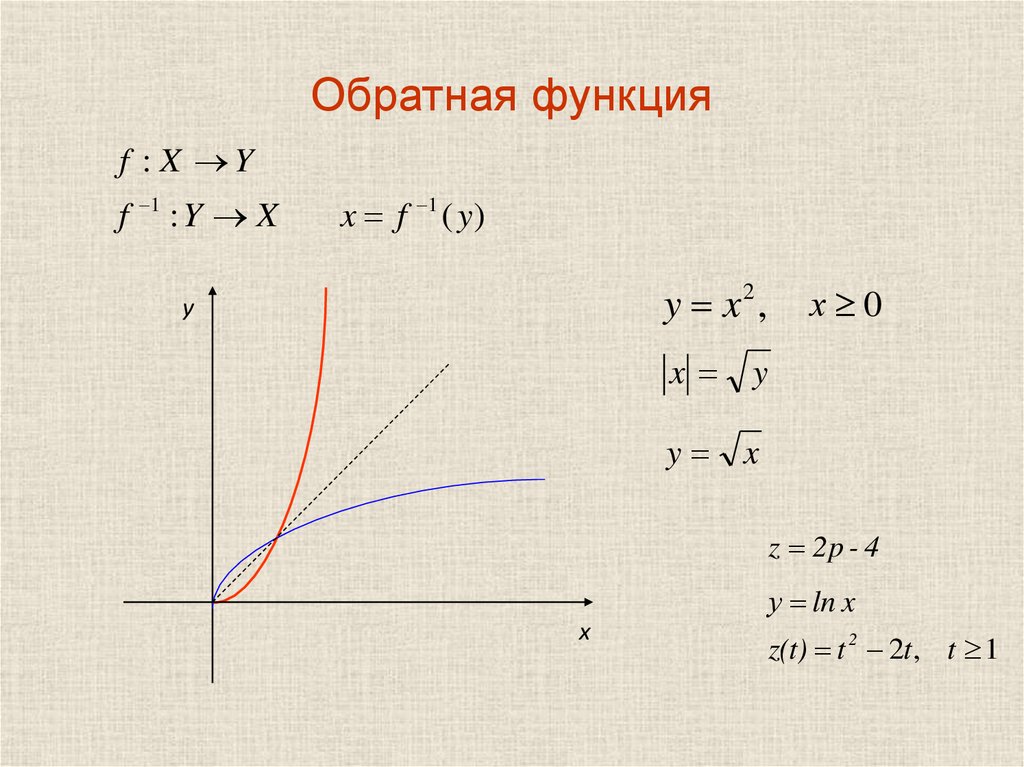

x – независимая переменная или аргумент.

y – зависимая переменная.

Множество всех значений y=f(x), где x принадлежит множеству X называют областью значений функции и обозначают E(f).

Рассмотрим задачу.

Задача.

Рассмотрим ещё одну задачу.

Задача.

Давайте назовём первую задачу прямой, тогда вторая задача будет обратной к первой.

Давайте рассмотрим с вами ещё одну задачу.

Задача.

 

Назовём функцию v(t) обратимой функцией, а t(v) – обратной функцией.

Определение.

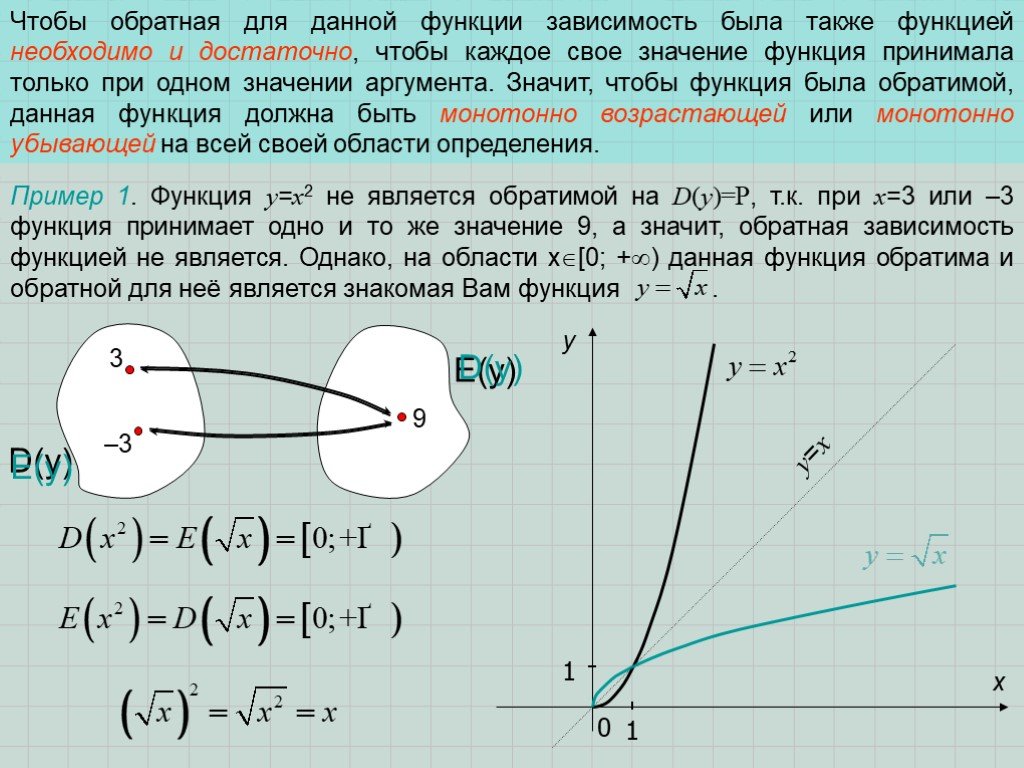
Если функция y=f(x) принимает каждое своё значение у только при одном значении x, то эту функцию называют обратимой.

Приведём примеры обратимых функций:

 

Рассмотрим функцию y=x².

Определение.

Пусть y = f(x) – обратимая функция. Тогда каждому y из множества значений функции соответствует одно определённое число

x из области определения, такое, что f(x) = y. Это соответствие определяет функцию x от y, которую обозначим x = g(y). Поменяем местами x и y: y = g(x). Функцию y = g(x) называют обратной к функции y = f(x). Обозначают f^-1(x).

Давайте разберём это определение на примере.

Пример.

Область определения исходной функции равна области значений обратной функции и наоборот, область значений исходной функции равна области определения обратной функции.

Сформулируем основные свойства обратных функций.

Решим несколько примеров.

Пример.

Пример.

Предыдущий урок 2 Свойства числовых функций

Следующий урок 4 Числовая окружность

Получите полный комплект видеоуроков, тестов и презентаций Алгебра 10 класс

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Обратные отношения и как их найти

Является ли обратная функция? Поиск обратных областей Ограниченные домены Работающие примеры Доказательство обратных

Purplemath

Объяснение обратных функций в вашем учебнике, вероятно, состоит из двух частей. В первой части было много фигурных скобок и списков точек; во второй части много функций « y =» или » f ( x )=» , для которых вы должны найти обратные функции, если это возможно.

Первая часть (с набором баллов) появится в вашем домашнем задании и, возможно, в тесте; вторая часть (с уравнениями) обязательно появится в вашем тесте, и вы даже можете использовать ее на последующих занятиях.

Содержание продолжается ниже

MathHelp.com

Обратные отношения

Что является обратным отношением?

Обратное отношение имеет все те же точки, что и исходное отношение, за исключением того, что x и y поменялись местами. Чтобы найти («создать»?) обратное для данного отношения, это все, что вам нужно сделать: вы поменяете местами x и y .

Например, предположим, что ваши отношения состоят из следующих пунктов:

{ (1, 0), (−3, 5), (0, 4) }

Тогда обратное отношение задается этим набором точек:

{ (0, 1), (5, −3), (4, 0) }

(Обратите внимание, что порядок точек не имеет значения; вы можете переставить точки так, чтобы x были «по порядку» или нет. Это ваш выбор. )

Ваш учебник начался с отношений, но быстро перешел к функциям. Имейте в виду разницу между этими двумя. Отношение — это просто соединение информации; функция — это правильное отношение. В частности, функция проходит Тест Вертикальной Линии, который подтверждает, что никто не x -значение соответствует более чем одному y -значение; ни одна вертикальная линия не будет пересекать график функции более одного раза. (С другой стороны, с отношением все ставки сняты.)

Когда вас начинают с функции, которая является отношением с хорошим поведением, тогда возникает вопрос: «Является ли обратное тоже функцией? Обратное также хорошо себя ведет?»

Используя набор точек сверху, отношение, с которого мы начали, выше, графики, подобные этому:

Вы знаете, что это функция (и вы можете быстро проверить с помощью теста вертикальной линии): нет двух различных точки, которые имеют одинаковые x -значение. Обратный график представлен синими точками ниже:

Поскольку синие точки (точки инверсии) не имеют двух точек с общим значением x , эта обратная функция также является функцией.

---

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в поиске обратной зависимости, состоящей из наборов точек. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку и выберите «Найти обратное отношение», чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)

Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.

(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)

Как найти обратное на графике?

Ваш учебник, вероятно, подробно рассказывал о том, как инверсия является «отражением в линии

y = x ». Он пытался сказать, что вы можете взять свою функцию, нарисовать линию y = x (которая представляет собой диагональную линию из левого нижнего угла в правый верхний), поместить на эту линию двустороннее зеркало, и вы могли бы «увидеть» обратное отражение в зеркале. На практике это свойство «отражения» может помочь вам нарисовать обратное:

Нарисуйте точки и линию отражения:

Отразите точки поперек линии:

На этом последнем рисунке вы можете видеть, что существует определенная графическая связь между точками функции и точками обратной функции. Вы можете использовать это отношение, если вам дан случайный график и вам предлагается построить график обратного.

---

Предположим, вам дан этот график:

Обратите внимание, что я НЕ сказал вам, что это за функция!

Теперь нарисуйте линию отражения:

(Неплохо было бы использовать для этого линейку, будьте аккуратны!).

Теперь взгляните на график и проведите диагонали от известных точек на графике к их «отражениям» по другую сторону линии:

Обратите внимание, что точки на самом деле НА линии y = x не двигаются; то есть там, где функция пересекает диагональ, обратная функция тоже пересекает диагональ.

Теперь нарисуйте несколько точек графика:

. ..и соедините точки:

Даже не зная правила или формулы исходной функции (синяя линия), вы можете нарисовать обратную (фиолетовая линия) .

---

URL: https://www.purplemath.com/modules/invrsfcn.htm

.

Теория чисел

Java

Структуры данных

Предварительное исчисление

Исчисление

Две функции являются обратными друг другу, если они «отменяют друг друга» в следующем смысле: если выходные данные одной используются в качестве входных данных для другой , они оставляют исходный ввод без изменений. 9{-1}$ обозначают обратную обратимую функцию $f$.

Обычный источник путаницы для студентов проистекает из того, насколько это обозначение похоже на возведение в степень.

Однако, если мы хотим применить к чему-то степень $-1$, это что-то должно быть значением . Буква $f$ обозначает функцию, а не значение!

С другой стороны, $f(x)$ является значением — это выход функции $f$ при входе $x$. {- 1}(х)$. 9{-1}(х)$.

Поскольку каждая точка $(x,y)$ на графике обратимой функции дает точку $(y,x)$ на графике обратной функции и наоборот, а областью определения функции является множество допустимых входов $x$, а область значений — это множество доступных выходов $y$ — сразу получаем, что область определения обратимой функции — это область значений ее обратной, а область значений такой функции — это область обратного ему.

Тест горизонтальной линии 92$ (показан синим цветом ниже) и его отражение относительно линии $y=x$ (показано красным цветом ниже).

Обратите внимание, красная кривая не проходит тест на вертикальную линию! То есть существует вертикальная линия, пересекающая красную кривую более одного раза [например, линия, проходящая через $(4,2)$ и $(4,-2)$].

Эквивалентно, существует по крайней мере один $x$ (например, $x=4$), связанный с более чем одним значением $y$ (например, как $2$, так и $-2$). Следовательно, красная кривая не представляет собой функцию.