Однородные диффуры: Однородные дифференциальные уравнения: определение, примеры

Содержание

Лекция Однородные дифференциальные уравнения первого порядка

Скачать с Depositfiles

Лекция 2

Однородные дифференциальные уравнения первого порядка

Определение: Функция называется однородной функцией n-го измерения относительно переменных х и у, если при любом справедливо тождество

Примеры: — однородная функция первого измерения

— второго измерения

— нулевого измерения.

Определение. Дифференциальное уравнение первого порядка

(1)

называется однородным относительно х и у, если функция есть однородная функция нулевого измерения относительно х и у , т.е.

Решение однородного уравнения:

По условию: .

Полагая здесь , получим: , и уравнение (1) запишем так:

(1’)

Заметим, что перед делением на х следует проверить наличие частного решения .

Сделаем подстановку ; ; .

;

Подставляя сюда после интегрирования , получим общий интеграл уравнения (1).

Пример. Найти общий интеграл дифф. уравнения .

Решение. Замена: ; ;

;

— общий интеграл

Замечание: Уравнение вида будет однородным тогда и только тогда, когда и будут однородными функциями одного и того же измерения.

Пример. Найти общий интеграл уравнения: — однородное уравнение. Заметим, что оно допускает частное решение .

Если , то делаем замену ; ; , ;

; ; . – общий интеграл.

Определение:

Линейным ДУ первого порядка называется уравнение, линейное относительно неизвестной функции и ее производной:

(1)

где и — непрерывные функции или константы.

Решение уравнения (1) будем искать решение в виде произведения двух функций

(2)

Тогда

Тогда уравнение (1) можно записать в виде:

, или

(3)

Выберем так, чтобы выполнялось равенство:

(кроме ) (4)

Тогда

Полагаем здесь (нам нужно любое решение уравнения (4))

Окончательно получим общее решение в виде

Постоянную С можно найти из начальных условий: .

Пример: Решить задачу Коши

; ;

Уравнение Бернулли

Уравнения вида

(1)

где и – непрерывные функции (или константы), и , называется уравнениями Бернулли. Заметим, что они допускают нулевое решение . Если, то они приводятся к линейным уравнениям заменой

(2)

Поделим обе части уравнения (1) на , получим

(3)

(4)

-линейное д.у. Найдем его общее решение, сделаем в нем обратную замену и получим общее решение уравнения (1).

Пример. Найти общее решение уравнения

(5)

Уравнение имеет нулевое решение . Найдем другие решения.

; ; ;

— линейное д.у.

Практика

1. Уравнения с разделяющимися переменными.

1); 2); ;

3); 4) ; ;

2. Однородные

1); ; ;

2); 3);

4); 5);

6) ;

3. Линейные первого порядка

1) ; 2);

3); 4).

4. Уравнения Бернулли

1); 2).

Скачать с Depositfiles

Краткий курс высшей математики

Шнейдер В. Е. и др. Краткий курс высшей математики. Учеб. пособие для втузов. М., «Высш. школа», 1972. 640 с.

Данное учебное пособие предназначено для студентов вечерних факультетов втузов и заводов-втузов. Оно в основном охватывает весь материал, предусмотренный обязательной программой. Достаточное количество решенных примеров и задач способствует лучшему усвоению теоретического материала.

ПРЕДИСЛОВИЕ
ГЛАВА I. МЕТОД КООРДИНАТ. ПОНЯТИЕ ФУНКЦИИ
§ 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. КООРДИНАТЫ ТОЧКИ НА ПРЯМОЙ
2. Геометрическое изображение действительных чисел. Координаты точки на прямой
3. Абсолютная величина действительного числа
4. Расстояние между двумя точками на прямой
§ 2. КООРДИНАТЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
2. Расстояние между двумя точками на плоскости
3. Деление отрезка в данном отношении
4. Координаты точки в пространстве
5. Расстояние между двумя точками в пространстве
§ 3. УГОЛ МЕЖДУ ДВУМЯ ОСЯМИ. ПОЛЯРНЫЕ КООРДИНАТЫ
2. Полярные координаты
3. Зависимость между декартовыми и полярными координатами
§ 4. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ
2. Понятие функции
3. График функции
4. Способы задания функций
5. Основные элементарные функции и их графики
6.

Сложные функции. Элементарные функции
7. Целые и дробно-рациональные функции
8. Функции четные и нечетные. Периодические функции
§ 5. УРАВНЕНИЕ ЛИНИИ
2. Нахождение уравнения линии по ее геометрическим свойствам

§ 6 ПРЕОБРАЗОВАНИЕ КООРДИНАТ
2. Поворот осей координат
ГЛАВА II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
§ 1. ПРЯМАЯ
2. Уравнение прямой с угловым коэффициентом
3. Уравнение прямой, параллельной оси ординат
4. Общее уравнение прямой и его частные случаи
5. Точка пересечения прямых. Построение прямой по ее уравнению
6. Вычисление угла между двумя прямыми. Условия параллельности и перпендикулярности двух прямых
7. Уравнение прямой, проходящей через данную точку в заданном направлении
8. Пучок прямых
9. Уравнение прямой, проходящей через две данные точки
10. Расстояние от точки до прямой
§ 2. КРИВЫЕ ВТОРОГО ПОРЯДКА
2. Окружность
3. Эллипс
4. Гипербола
5. Парабола
6. Окружность, эллипс, гипербола и парабола как конические сечения
7.

Упрощение уравнения кривой второго порядка. График квадратного трехчлена
8. Уравнение равносторонней гиперболы, асимптоты которой приняты за оси координат
9. График дробно-линейной функции
10. Преобразование уравнения кривой второго порядка, не содержащего члена с произведением координат
ГЛАВА III. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЫ
§ 1. ЭЛЕМЕНТЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ
2. Определитель третьего порядка
3. Понятие об определителях высших порядков
§ 2. СИСТЕМЫ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ
2. Однородная система двух уравнений первой степени с тремя неизвестными
3. Система трех уравнений первой степени с тремя неизвестными
4. Однородная система трех уравнений первой степени с тремя неизвестными
§ 3. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
2. Линейные операции над векторами
4. Проекция вектора на ось и составляются вектора по оси
5. Разложение вектора на составляющие по осям координат
6. Направляющие косинусы вектора
7. Условие коллинеарности двух векторов
8.

Скалярное произведение
9. Выражение скалярного произведения через проекции перемножаемых векторов
10. Косинус угла между двумя векторами
11. Векторное произведение
12. Выражение векторного произведения через проекции перемножаемых векторов
13. Смешанное произведение трех векторов
14. Геометрический смысл смешанного произведения
15. Условие компланарности трех векторов
§ 4. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
2. Равенство матриц. Действия над матрицами
3. Обратная матрица
4. Матричная запись и матричное решение системы уравнений первой степени
§ 5. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ
2. Преобразование координат
3. Приведение квадратичной формы к каноническому виду
4. Упрощение общего уравнения кривой второго порядка
ГЛАВА IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
§ 1. ПЛОСКОСТЬ
2. Нормальный вектор плоскости. Уравнение плоскости, проходящей через данную точку
3. Общее уравнение плоскости и его частные случаи
4. Построение плоскости по ее уравнению
5.

Угол между плоскостями. Условия параллельности и перпендикулярности двух плоскостей
6. Точка пересечения трех плоскостей
§ 2. ПРЯМАЯ В ПРОСТРАНСТВЕ
2. Общие уравнения прямой
3. Векторное уравнение прямой. Параметрические уравнения прямой
4. Канонические уравнения прямой
5. Уравнения прямой, проходящей через две точки
6. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых
§ 3. Прямая и плоскость в пространстве
2. Точка пересечения прямой с плоскостью
3. Расстояние от точки до плоскости
4. Пучок плоскостей
§ 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
2. Цилиндрические поверхности
3. Конические поверхности
4. Поверхность вращения
6. Гиперболоиды

7. Параболоиды
ГЛАВА V. ТЕОРИЯ ПРЕДЕЛОВ
§ 1. ПРЕДЕЛ ФУНКЦИИ
2. Предел функции при х -> -оо
3. Предел функции при х->х0
4. Бесконечно малые функции. Ограниченные функции
5. Бесконечно большие функции и их связь с бесконечно малыми функциями
6.

Основные теоремы о пределах
7. Предел функции при x -> 0
8. Последовательность. Число e
9. Натуральные логарифмы
10. Сравнение бесконечно малых функций
§ 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ
2. Операции над непрерывными функциями. Непрерывность элементарных функций
3. Свойства функций, непрерывных на сегменте
4. Понятие об обратной функции
5. Обратные тригонометрические функции
6. Показательная и логарифмическая функции
7. Понятие о гиперболических функциях
ГЛАВА VI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
1. Приращение аргумента и приращение функции

2. Определение непрерывности функции с помощью понятии приращения аргумента и приращения функции
3. Задачи, приводящие к понятию производной
4. Определение производной и ее механический смысл
5. Дифференцируемость функции
6. Геометрический смысл производной
7. Производные некоторых основных элементарных функций
8. Основные правила дифференцирования
9. Производная обратной функции
10.

Производные обратных тригонометрических функций
11. Производная сложной функции
§ 12. Производные гиперболических функций
13. Производная степенной функции с любым показателем
14. Сводная таблица формул дифференцирования
15. Неявные функции и их дифференцирование
16. Уравнения касательной а нормали к кривой
17. Графическое дифференцирование
§ 2. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
1. Нахождение производных высших порядков

2. Механический смысл второй производной
§ 3. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
2. Производная как отношение дифференциалов
3. Дифференциал суммы, произведения и частного функций
4. Дифференциал сложной функции. Инвариантность формы дифференциала
5. Применение дифференциала к приближенным вычислениям
6. Дифференциалы высших порядков
§ 4. ФУНКЦИИ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ, И ИХ ДИФФЕРЕНЦИРОВАНИЕ
2. Дифференцирование функций, заданных параметрически
§ 5. ВЕКТОРНАЯ ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
2. Векторная функция скалярного аргумента и ее производная
3.

Уравнения касательной прямой и нормальной плоскости к пространственной кривой
4. Механический смысл первой и второй производных векторной функции скалярного аргумента
§ 6. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
2. Теорема Ролля
3. Теорема Лагранжа
4. Правило Лопиталя
§ 7. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ
2. Максимум и минимум функции
3. Достаточный признак существования экстремума, основанный на знаке второй производной
4. Отыскание наибольшего и наименьшего значений функции
5. Применение теории максимума и минимума к решению задач
6. Выпуклость и вогнутость графика функции. Точки перегиба
7. Асимптоты графика функции
8. Общая схема исследования функции и построение ее графика
§ 8. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
2. Уточнение найденных значений корней методом хорд и касательных
§ 9. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА
ГЛАВА VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА
2.

Геометрический смысл неопределенного интеграла
3. Таблица основных интегралов
4. Основные свойства неопределенного интеграла
§ 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ

2. Интегрирование методом замены переменной
3. Интегрирование по частям
§ 3. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
2. Рациональные дроби. Выделение правильной рациональной дроби
3. Интегрирование простейших рациональных дробей
4. Разложение правильной рациональной дроби на простейшие дроби
5. Метод неопределенных коэффициентов
6. Интегрирование рациональных дробей
§ 4. Интегрирование тригонометрических функций
2. Рациональные функции двух переменных
3. Интегралы вида
§ 5. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ
2. Интеграл вида
3. Интегралы видов
4. Интегралы вида
§ 6. ОБЩИЕ ЗАМЕЧАНИЯ О МЕТОДАХ ИНТЕГРИРОВАНИЯ. ИНТЕГРАЛЫ, НЕ БЕРУЩИЕСЯ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
2. Понятие об интегралах, не берущихся в элементарных функциях
ГЛАВА VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1.

ЗАДАЧИ, ПРИВОДЯЩИЕ К ОПРЕДЕЛЕННОМУ ИНТЕГРАЛУ
2. Задача о работе переменной силы
§ 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2. Свойства определенного интеграла
3. Производная интеграла по переменной верхней границе
4. Формула Ньютона—Лейбница
5. Замена переменной в определенном интеграле
6. Интегрирование по частям в определенном интеграле
§ 3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
2. Вычисление площади в полярных координатах
3. Вычисление объема тела по известным поперечным сечениям
4. Объем тела вращения
5. Длина дуги кривой
6. Дифференциал дуги
7. Площадь поверхности вращения
8. Общие замечания о решении задач методом интегральных сумм
§ 4. КРИВИЗНА ПЛОСКОЙ КРИВОЙ
2. Вычисление кривизны
3. Радиус кривизны. Круг кривизны. Центр кривизны
4. Эволюта и эвольвента
§ 5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
2. Интегралы от разрывных функций
3. Признаки сходимости несобственных интегралов
§ 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
2.

Метод трапеций
3. Метод параболических трапеций (метод Симпсона)
ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
2. График функции двух переменных
3. Функции трех и большего числа переменных
§ 2. Предел функции нескольких переменных. Непрерывность функции. Точки разрыва
2. Непрерывность функции нескольких переменных
3. Понятие области
4. Точки разрыва
5. Свойства функций, непрерывных в ограниченной замкнутой области
§ 3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ
2. Геометрический смысл частных производных функции двух переменных
3. Частные производные высших порядков
§ 4. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
2. Полный дифференциал функции
3. Приложение полного дифференциала к приближенным вычислениям
§ 5. Дифференцирование сложных и неявных функций
2. Инвариантность формы полного дифференциала
3. Дифференцирование неявных функций
§ 6. СКАЛЯРНОЕ ПОЛЕ
2. Производная по направлению
3.

Градиент
4. Касательная плоскость а нормаль к поверхности
5. Геометрический смысл полного дифференциала функции двух переменных
§ 7. ЭКСТРЕМУМ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ
2. Наибольшее и наименьшее значения функции двух переменных
ГЛАВА X. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
§ 1. ДВОЙНОЙ ИНТЕГРАЛ
2. Двойной интеграл. Теорема существования
3. Свойства двойного интеграла
4. Вычисление двойного интеграла в декартовых координатах
5. Вычисление двойного интеграла в полярных координатах
6. Приложения двойного интеграла
§ 2. ТРОЙНОЙ ИНТЕГРАЛ
2. Тройной интеграл и его свойства
3. Вычисление тройного интеграла в декартовых координатах
4. Вычисление тройного интеграла в цилиндрических координатах
5. Приложения тройного интеграла
§ 3. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
2. Задача о работе. Криволинейный интеграл
3. Вычисление криволинейного интеграла
4. Формула Остроградского — Грина
5. Независимость криволинейного интеграла от пути интегрирования
6.

Отыскание первообразной по полному дифференциалу
7. Криволинейный интеграл по длине дуги
ГЛАВА XI. РЯДЫ
§ 1. ЧИСЛОВЫЕ РЯДЫ
2. Геометрическая прогрессия
3. Простейшие свойства числовых рядов
4. Необходимый признак сходимости ряда
5. Достаточные признаки сходимости знакоположительных рядов
6. Знакопеременные ряды
7. Остаток ряда и его оценка
§ 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
2. Правильно сходящиеся функциональные ряды и их свойства
§ 3. СТЕПЕННЫЕ РЯДЫ
2. Свойства степенных рядов
3. Ряды по степеням разности х-а
4. Разложение функций в степенные ряды. Ряд Тейлора
5. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена
§ 4. ПРИЛОЖЕНИЕ РЯДОВ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
2. Приближенное вычисление интегралов
§ 5. ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ. СТЕПЕННЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
2. Числовые ряды с комплексными членами
3. Степенные ряды в комплексной области
§ 6. РЯДЫ ФУРЬЕ
2. Ряд Фурье
3.

Сходимость ряда Фурье
4. Ряды Фурье для четных и нечетных функций
5. Разложение в ряд Фурье функций с периодом 2l
ГЛАВА XII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§ 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
2. Дифференциальные уравнения первого порядка
3. Уравнения с разделяющимися переменными
4. Однородные уравнения
5. Линейные уравнения
6. Уравнение в полных дифференциалах
7. Особые решения
8. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера
§ 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
2. Простейшие уравнения второго порядка, допускающие понижение порядка
3. Понятие о дифференциальных уравнениях высших порядков
§ 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
2. Линейные однородные дифференциальные уравнения второго порядка
3. Линейные неоднородные дифференциальные уравнения второго порядка
4. Метод вариации произвольных постоянных
§ 4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
2.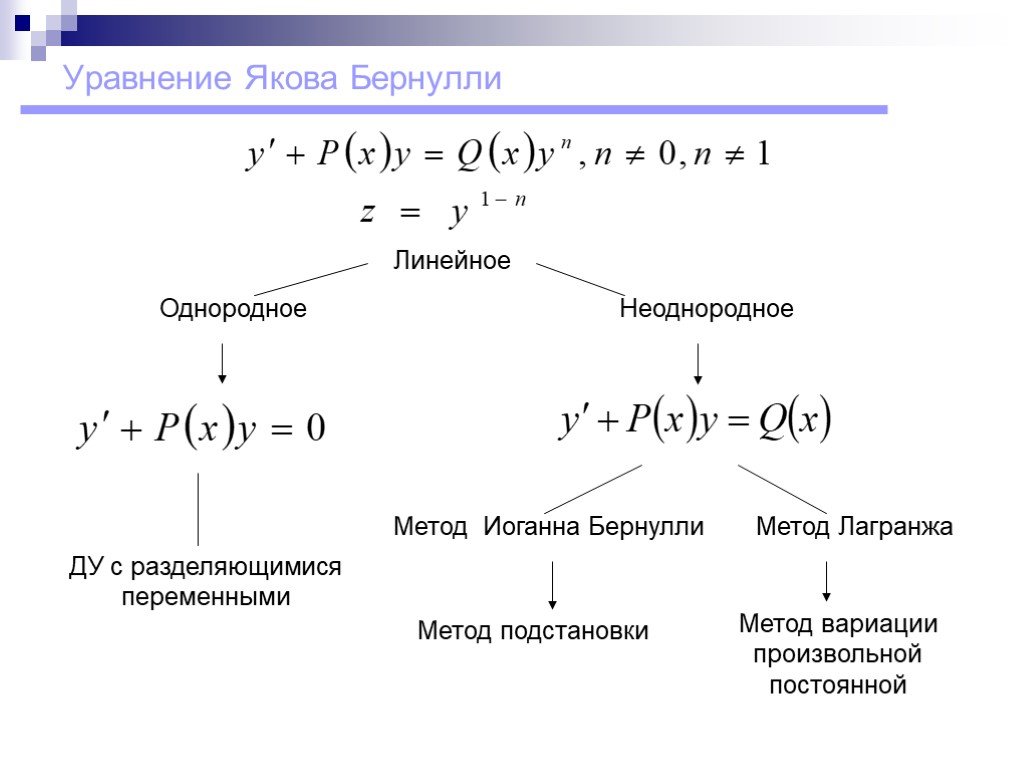

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
3. Приложение линейных дифференциальных уравнений второго порядка к изучению механических и электрических колебаний
§ 5. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
2. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами
§ 6. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ РЯДОВ
§ 7. ПОНЯТИЕ О СИСТЕМАХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
2. Системы линейных дифференциальных уравнений с постоянными коэффициентами
ПРИЛОЖЕНИЕ 1. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА
ПРИЛОЖЕНИЕ 2. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

Влияние рассеивателя из диоксида титана на угловую однородность цвета в белых светодиодах с конформным люминофорным покрытием

Влияние рассеивателя из диоксида титана на угловую однородность цвета в белых светодиодах с конформным покрытием люминофора

Ли, Кванг-Чол
Ким, Санг-Мук
Луна, Чон-Ха

Аннотация

Белые светоизлучающие диоды (СИД) резко развились и постепенно вытеснили традиционный источник света в качестве твердотельного освещения в течение последнего десятилетия. Этого сейчас достаточно для применения подсветки по производительности, но по-прежнему недостаточно по цветопередаче. В частности, большинство белых светодиодов с преобразованием люминофора имеют плохую угловую однородность цвета. В этом исследовании мы использовали особый метод конформного покрытия люминофором в процессе упаковки, чтобы уменьшить дисперсию коррелированной цветовой температуры (CCT) между упаковками и пространственной CCT в упаковке. Кроме того, чтобы уменьшить пространственную дисперсию CCT без значительного снижения светоотдачи, мы применили порошок TiO2 субмикрометрового масштаба в качестве рассеивателя в слое люминофора или в герметизирующем слое белого светодиода со слоем конформного покрытия люминофора и исследовали влияние рассеивателя из диоксида титана на угловые однородность цвета и оптические характеристики. Независимо от содержания диффузора пространственная дисперсия CCT и светоотдача уменьшались с увеличением содержания диффузора. Тем не менее, среди условий достижения равноценной однородности цвета светоотдача в случае 0,1 мас. % рассеивателя, вмешанного в слой герметизации, была на 20 % выше, чем в случае 5 мас. % диффузора, вмешанного в слой люминофора. Эти явления возникают из-за различий в потерях светорассеяния, вызванных в 10 раз большим объемом диффузора, смешанным в слое люминофора, чем в герметизирующем слое.

Публикация:: Десятая международная конференция по твердотельному освещению
Дата публикации:: август 2010 г.
DOI:: 10.1117/12.861108
Биб-код:: 2010SPIE.7784E..10L «/>

Artnovion Acoustics — PRO AUDIO & STUDIO

Дата вступления в силу: 22 мая 2018 г.

Artnovion Lda («нас», «мы» или «наш») управляет веб-сайтом («Сервис»).

Эта страница информирует вас о нашей политике в отношении сбора, использования и раскрытия персональных данных при использовании вами нашего Сервиса, а также о вариантах выбора, связанных с этими данными.

Мы используем ваши данные для предоставления и улучшения Сервиса. Используя Сервис, вы соглашаетесь на сбор и использование информации в соответствии с этой политикой. Если иное не определено в настоящей Политике конфиденциальности, термины, используемые в настоящей Политике конфиденциальности, имеют те же значения, что и в наших Условиях.

Определения

Сервис: означает веб-сайт, управляемый Artnovion Lda
Персональные данные: Персональные данные означают данные о живом человеке, которого можно идентифицировать по этим данным (или по тем и другим сведениям, которые либо находятся в нашем распоряжении, либо могут оказаться в нашем распоряжении).
Данные об использовании: Данные об использовании — это данные, собираемые автоматически либо при использовании Сервиса, либо из самой инфраструктуры Сервиса (например, продолжительность посещения страницы).
Файлы cookie: Файлы cookie — это небольшие фрагменты данных, хранящиеся на вашем устройстве (компьютере или мобильном устройстве).
Контроллер данных: Контроллер данных означает физическое или юридическое лицо, которое (самостоятельно, совместно или совместно с другими людьми) определяет цели и способ обработки любой личной информации.
В целях настоящей Политики конфиденциальности мы являемся контролером ваших личных данных.
Обработчики данных (или поставщики услуг): Обработчик данных (или Поставщик услуг) означает любое физическое или юридическое лицо, которое обрабатывает данные от имени Контроллера данных.
Мы можем использовать услуги различных поставщиков услуг для более эффективной обработки ваших данных.
Субъект данных (или пользователь): Субъект данных — любое живое физическое лицо, использующее наш Сервис и являющееся субъектом Персональных данных.

Сбор и использование информации

Мы собираем несколько различных типов информации для различных целей, чтобы предоставлять вам и улучшать наш Сервис.

Типы собираемых данных

Персональные данные

При использовании нашего Сервиса мы можем попросить вас предоставить нам определенную личную информацию, которая может быть использована для связи или идентификации вас («Личные данные»). Личная информация может включать, но не ограничивается:

Адрес электронной почты
Имя и фамилия
Номер телефона
Адрес, штат, провинция, почтовый индекс, город
Файлы cookie и данные об использовании

Мы можем использовать ваши Персональные данные для связи с вами с информационными бюллетенями, маркетинговыми или рекламными материалами и другой информацией, которая может вас заинтересовать. Вы можете отказаться от получения каких-либо или всех этих сообщений от нас, перейдя по ссылке для отказа от подписки или инструкциям, приведенным в любом электронном письме, которое мы отправляем, или связавшись с нами.

Данные об использовании

Мы также можем собирать информацию, которую ваш браузер отправляет каждый раз, когда вы посещаете наш Сервис или когда вы получаете доступ к Сервису с мобильного устройства или через него («Данные об использовании»).

Эти данные об использовании могут включать в себя такую информацию, как адрес интернет-протокола вашего компьютера (например, IP-адрес), тип браузера, версия браузера, страницы нашего Сервиса, которые вы посещаете, время и дата вашего посещения, время, проведенное на этих страницах. , уникальные идентификаторы устройств и другие диагностические данные.

Когда вы получаете доступ к Сервису с мобильного устройства или через него, эти Данные об использовании могут включать такую информацию, как тип используемого вами мобильного устройства, уникальный идентификатор вашего мобильного устройства, IP-адрес вашего мобильного устройства, вашу мобильную операционную систему, тип мобильного интернет-браузера, который вы используете, уникальные идентификаторы устройств и другие диагностические данные.

Отслеживание данных файлов cookie

Мы используем файлы cookie и аналогичные технологии отслеживания для отслеживания активности в нашем Сервисе и хранения определенной информации.

Файлы cookie — это файлы с небольшим объемом данных, которые могут включать анонимный уникальный идентификатор. Файлы cookie отправляются в ваш браузер с веб-сайта и сохраняются на вашем устройстве. Также используются технологии отслеживания, такие как маяки, теги и сценарии для сбора и отслеживания информации, а также для улучшения и анализа нашего Сервиса.

Вы можете указать своему браузеру отказаться от всех файлов cookie или указать, когда файл cookie отправляется. Однако, если вы не принимаете файлы cookie, вы не сможете использовать некоторые части нашего Сервиса.

Примеры файлов cookie, которые мы используем:

Сеансовые файлы cookie. Мы используем сеансовые файлы cookie для работы нашего Сервиса.
Файлы cookie предпочтений. Мы используем файлы cookie предпочтений, чтобы запомнить ваши предпочтения и различные настройки.
Защитные файлы cookie. Мы используем файлы cookie безопасности в целях безопасности.

Использование данных

Artnovion Lda использует собранные данные для различных целей:

Для предоставления и поддержки нашего Сервиса
Чтобы уведомить вас об изменениях в нашем Сервисе
Чтобы позволить вам участвовать в интерактивных функциях нашего Сервиса, когда вы решите это сделать
Для обеспечения поддержки клиентов
Для сбора анализа или ценной информации, чтобы мы могли улучшить наш Сервис
Для мониторинга использования нашего Сервиса
Для обнаружения, предотвращения и устранения технических проблем
Для предоставления вам новостей, специальных предложений и общей информации о других товарах, услугах и событиях, которые мы предлагаем, которые аналогичны тем, которые вы уже приобрели или о которых спрашивали, если вы не решили не получать такую информацию

Правовая основа для обработки персональных данных в соответствии с Общим регламентом по защите данных (GDPR)

Если вы находитесь в Европейской экономической зоне (ЕЭЗ), правовая основа Artnovion Lda для сбора и использования личной информации, описанной в настоящей Политике конфиденциальности, зависит от Данные, которые мы собираем, и конкретный контекст, в котором мы их собираем.

Artnovion Lda может обрабатывать ваши Персональные данные, потому что:

Нам необходимо выполнить договор с вами
Вы дали нам на это разрешение
Обработка соответствует нашим законным интересам и не противоречит вашим правам
Для обработки платежей
Соблюдать закон

Хранение данных

Artnovion Lda будет хранить ваши Персональные данные только до тех пор, пока это необходимо для целей, изложенных в настоящей Политике конфиденциальности. Мы будем хранить и использовать ваши Персональные данные в объеме, необходимом для выполнения наших юридических обязательств (например, если мы обязаны хранить ваши данные в соответствии с действующим законодательством), разрешать споры и обеспечивать соблюдение наших юридических соглашений и политик.

Artnovion Lda также сохраняет данные об использовании для целей внутреннего анализа. Данные об использовании обычно хранятся в течение более короткого периода времени, за исключением случаев, когда эти данные используются для усиления безопасности или улучшения функциональности нашего Сервиса, или когда мы по закону обязаны хранить эти данные в течение более длительных периодов времени.

Передача данных

Ваша информация, включая Персональные данные, может передаваться и храниться на компьютерах, расположенных за пределами вашего штата, провинции, страны или другой государственной юрисдикции, где законы о защите данных могут отличаться от законов вашей юрисдикции.

Если вы находитесь за пределами Португалии и решили предоставить нам информацию, обратите внимание, что мы передаем данные, включая Персональные данные, в Португалию и обрабатываем их там.

Ваше согласие с настоящей Политикой конфиденциальности, за которым следует предоставление такой информации, означает ваше согласие на эту передачу.

Artnovion Lda предпримет все разумно необходимые шаги для обеспечения безопасного обращения с вашими данными в соответствии с настоящей Политикой конфиденциальности, и никакая передача ваших личных данных не будет осуществляться организации или стране, если не будут приняты надлежащие меры контроля, включая безопасность ваших данных и другой личной информации.

Раскрытие данных

Раскрытие информации для правоохранительных органов

При определенных обстоятельствах Artnovion Lda может быть обязано раскрыть ваши Персональные данные, если это требуется по закону или в ответ на действительные запросы государственных органов (например, суда или правительства). агентство).

Юридические требования

Artnovion Lda может раскрывать ваши Персональные данные, добросовестно полагая, что такое действие необходимо для:

Для выполнения юридических обязательств
Для защиты и защиты прав или собственности Artnovion Lda
Для предотвращения или расследования возможных правонарушений в связи с Сервисом
Для защиты личной безопасности пользователей Сервиса или общественности
Для защиты от юридической ответственности

Безопасность данных

Безопасность ваших данных важна для нас, но помните, что ни один метод передачи через Интернет или метод электронного хранения не является безопасным на 100%. Хотя мы стремимся использовать коммерчески приемлемые средства для защиты ваших Персональных данных, мы не можем гарантировать их абсолютную безопасность.

Ваши права на защиту данных в соответствии с Общим регламентом по защите данных (GDPR)

Если вы являетесь резидентом Европейской экономической зоны (ЕЭЗ), у вас есть определенные права на защиту данных. Artnovion Lda стремится предпринять разумные шаги, чтобы вы могли исправить, изменить, удалить или ограничить использование ваших Персональных данных.

Если вы хотите получить информацию о том, какие Персональные данные о вас хранятся у нас, и если вы хотите, чтобы они были удалены из наших систем, свяжитесь с нами.

При определенных обстоятельствах у вас есть следующие права на защиту данных:

Право на доступ, обновление или удаление имеющейся у нас информации о вас. Когда это возможно, вы можете получить доступ, обновить или запросить удаление ваших личных данных непосредственно в разделе настроек вашей учетной записи. Если вы не можете выполнить эти действия самостоятельно, свяжитесь с нами, чтобы помочь вам.
Право на исправление. Вы имеете право на исправление вашей информации, если эта информация неточна или неполна.
Право на возражение. Вы имеете право возражать против обработки нами ваших Персональных данных.
Право ограничения. Вы имеете право потребовать, чтобы мы ограничили обработку вашей личной информации.
Право на переносимость данных. Вы имеете право на получение копии имеющейся у нас информации о вас в структурированном, машиночитаемом и широко используемом формате.
Право на отзыв согласия. Вы также имеете право отозвать свое согласие в любое время, когда Artnovion Lda полагалась на ваше согласие на обработку вашей личной информации.

Обратите внимание, что мы можем попросить вас подтвердить свою личность, прежде чем отвечать на такие запросы.

Вы имеете право подать жалобу в орган по защите данных в отношении сбора и использования нами ваших личных данных. Для получения дополнительной информации обратитесь в местный орган по защите данных в Европейской экономической зоне (ЕЭЗ).

Поставщики услуг

Мы можем нанимать сторонние компании и частных лиц для содействия нашему Сервису («Поставщики услуг»), для предоставления Сервиса от нашего имени, для оказания услуг, связанных с Сервисом, или для оказания нам помощи в анализе того, как используется наш Сервис.

Эти третьи стороны имеют доступ к вашим Персональным данным только для выполнения этих задач от нашего имени и обязаны не раскрывать и не использовать их для каких-либо других целей.

Analytics

Мы можем использовать сторонних поставщиков услуг для мониторинга и анализа использования нашего Сервиса.

Google Analytics: Google Analytics — это служба веб-аналитики, предлагаемая Google, которая отслеживает и сообщает о трафике веб-сайта. Google использует собранные данные для отслеживания и мониторинга использования нашего Сервиса. Эти данные передаются другим службам Google. Google может использовать собранные данные для контекстуализации и персонализации рекламы своей собственной рекламной сети.
Для получения дополнительной информации о политике конфиденциальности Google посетите веб-страницу условий конфиденциальности Google: http://www.google.com/intl/en/policies/privacy/

Поведенческий ремаркетинг

Artnovion Lda использует услуги ремаркетинга для рекламы на сторонних веб-сайтах после того, как вы посетили наш Сервис. Мы и наши сторонние поставщики используем файлы cookie для информирования, оптимизации и показа рекламы на основе ваших прошлых посещений нашего Сервиса.

Google AdWords: Служба ремаркетинга Google AdWords предоставляется компанией Google Inc.
Вы можете отказаться от Google Analytics для медийной рекламы и настроить рекламу в контекстно-медийной сети Google, посетив страницу настроек рекламы Google: http://www. google.com/settings/ объявления
Google также рекомендует установить надстройку браузера для отказа от Google Analytics — https://tools.google.com/dlpage/gaoptout — для вашего веб-браузера. Надстройка браузера Google Analytics Opt-out предоставляет посетителям возможность запретить сбор и использование их данных службой Google Analytics.
Для получения дополнительной информации о политике конфиденциальности Google посетите веб-страницу условий конфиденциальности Google: http://www.google.com/intl/en/policies/privacy/
Твиттер: Услуга ремаркетинга в Твиттере предоставляется компанией Twitter Inc.
Вы можете отказаться от рекламы Твиттера на основе интересов, следуя их инструкциям: https://support.twitter.com/articles/20170405
Вы можете узнать больше о методах и политике конфиденциальности Твиттера, посетив страницу их Политики конфиденциальности: https://twitter.com/privacy
Фейсбук: Услуга ремаркетинга Facebook предоставляется компанией Facebook Inc.
Вы можете узнать больше о рекламе Facebook на основе интересов, посетив эту страницу: https://www.facebook.com/help/164968693837950
Чтобы отказаться от рекламы Facebook на основе интересов, следуйте этим инструкциям Facebook: https://www.facebook.com/help/568137493302217
Facebook придерживается принципов саморегулирования поведенческой онлайн-рекламы, установленных Альянсом цифровой рекламы. . Вы также можете отказаться от Facebook и других участвующих компаний через Альянс цифровой рекламы в США http://www.aboutads.info/choices/, Альянс цифровой рекламы Канады в Канаде http://youradchoices.ca/ или Европейский Альянс Интерактивной Цифровой Рекламы в Европе http://www.youronlinechoices.eu/, или откажитесь, используя настройки вашего мобильного устройства.
Для получения дополнительной информации о методах конфиденциальности Facebook, пожалуйста, посетите Политику данных Facebook: https://www.facebook.com/privacy/explanation

Платежи

Мы можем предоставлять платные продукты и/или услуги в рамках Сервиса. В этом случае мы используем сторонние сервисы для обработки платежей (например, платежные системы).

Мы не будем хранить или собирать данные вашей платежной карты. Эта информация предоставляется непосредственно нашим сторонним платежным системам, чье использование вашей личной информации регулируется их Политикой конфиденциальности. Эти платежные системы придерживаются стандартов, установленных PCI-DSS и управляемых Советом по стандартам безопасности PCI, который является совместным усилием таких брендов, как Visa, Mastercard, American Express и Discover. Требования PCI-DSS помогают обеспечить безопасную обработку платежной информации.

Ссылки на другие сайты

Наш Сервис может содержать ссылки на другие сайты, которыми мы не управляем. Если вы нажмете на стороннюю ссылку, вы будете перенаправлены на сайт этой третьей стороны. Мы настоятельно рекомендуем вам ознакомиться с Политикой конфиденциальности каждого сайта, который вы посещаете.

Мы не контролируем и не несем ответственности за содержание, политику конфиденциальности или практику любых сторонних сайтов или служб.

Конфиденциальность детей

Наша Служба не предназначена для лиц моложе 18 лет («Дети»).

Мы сознательно не собираем личную информацию от лиц моложе 18 лет. Если вы являетесь родителем или опекуном и знаете, что ваши Дети предоставили нам Персональные данные, свяжитесь с нами. Если нам станет известно, что мы собрали Личные данные детей без проверки согласия родителей, мы предпримем шаги для удаления этой информации с наших серверов.

Изменения в настоящей Политике конфиденциальности

Мы можем время от времени обновлять нашу Политику конфиденциальности. Мы сообщим вам о любых изменениях, опубликовав новую Политику конфиденциальности на этой странице.

Мы сообщим вам об этом по электронной почте и/или в виде заметного уведомления в нашем Сервисе до того, как изменение вступит в силу, и обновим «дату вступления в силу» в верхней части настоящей Политики конфиденциальности.

Рекомендуется периодически просматривать настоящую Политику конфиденциальности на предмет любых изменений.