Уравнение окружности по заданному центру и радиусу в различных формах
УчебаМатематикаГеометрия
Этот онлайн-калькулятор показывает уравнение окружности в стандартной, параметрической и общей формах, по заданному центру и радиусу окружности. Описание и формулы приведены под калькулятором
Уравнение окружности по заданному центру и радиусу в различных формах
Центр окружности
Радиус
Стандартное уравнение окружности
Общее уравнение окружности
Параметрическое уравнение окружности
Уравнение окружности
Уравнение окружности — это алгебраический способ описания всех точек, лежащих на некоторой окружности. То есть если координаты точки x и y обращают уравнение окружности в равенство — эта точка принадлежит данной окружности. Существуют разные формы записи уравнения окружности:
- общее уравнение окружности
- стандартное уравнение окружности1
- параметрическое уравнение окружности
- уравнение окружности в полярных координатах
Общее уравнение окружности
Общее уравнение окружности с центром и радиусом выглядит так:
,
где
В таком виде довольно сложно судить о свойствах заданной этим уравнением окружности, а именно, о координатах центра и радиусе.
Но эту форму достаточно легко привести к стандартной форме (ниже), которая гораздо нагляднее.
Стандартное уравнение окружности
Стандартное уравнение окружности с центром и радиусом выглядит так:
Переход от общей формы к стандартной заключается в применении метода выделения полного квадрата. Получив стандартную форму, можно легко узнать координаты центра и радиус. Подробнее можно посмотреть здесь — Метод выделения полного квадрата и здесь — Нахождение центра и радиуса окружности по общему уравнению окружности.
Параметрическое уравнение окружности
Параметрическое уравнение окружности с центром и радиусом выглядит так:
Уравнение называется «параметрическим», потому что и x и y зависят от «параметра» тета. Это переменная, которая может принимать любые значения (но конечно это должно быть одно и то же значение в обоих уравнениях). Для параметрического уравнения используется определение синуса и косинуса в прямоугольном треугольнике построенном на радиусе и перпендикуляров от точки на окружности до координатных осей.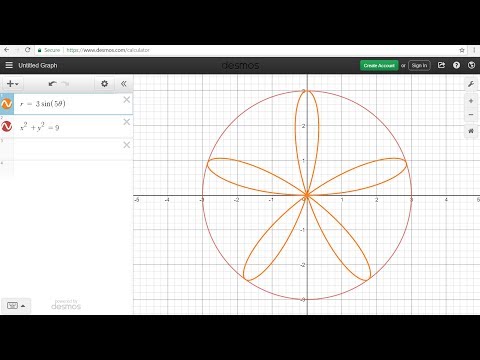
Уравнение окружности в полярных координатах
Для записи уравнения окружности в полярных координатах требуются полярные координаты центра окружности по отношению к началу координат. Если полярные координаты центра окружности — это , то полярные координаты точки окружности должны удовлетворять следующему уравнению:
,
где a — радиус окружности.
Так, во всяком случае, его называют в англоязычной литературе. Насчет русского термина я не уверен, по-моему эту форму рассматривают просто как еще один способ записи общего уравнения окружности, тем более что переход от общего уравнения к стандартному довольно простой. ↩
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Уравнение окружности, проходящей через три заданные точки
- • Нахождение центра и радиуса окружности по общему уравнению окружности
- • Треугольник. Описанная окружность
- • Треугольник. Вписанная окружность
- • Уравнение прямой по двум точкам
- • Раздел: Геометрия ( 97 калькуляторов )
#алгебра #Уравнение окружности Алгебра Геометрия Общее окружность Параметрическое Стандартное уравнение
PLANETCALC, Уравнение окружности по заданному центру и радиусу в различных формах
Timur2021-10-05 12:01:17
| 1 | Упростить | квадратный корень из s квадратный корень из s^7 | |
| 2 | Упростить | кубический корень из 8x^7y^9z^3 | |
| 3 | Упростить | arccos(( квадратный корень из 3)/2) | |
| 4 | Risolvere per ? | sin(x)=1/2 | |
| 5 | Упростить | квадратный корень из s квадратный корень из s^3 | |
| 6 | Risolvere per ? | cos(x)=1/2 | |
| 7 | Risolvere per x | sin(x)=-1/2 | |
| 8 | Преобразовать из градусов в радианы | 225 | |
| 9 | Risolvere per ? | cos(x)=( квадратный корень из 2)/2 | |
| 10 | Risolvere per x | cos(x)=( квадратный корень из 3)/2 | |
| 11 | Risolvere per x | sin(x)=( квадратный корень из 3)/2 | |
| 12 | График | g(x)=3/4* корень пятой степени из x | |
| 13 | Найти центр и радиус | x^2+y^2=9 | |
| 14 | Преобразовать из градусов в радианы | 120 град. 2+n-72)=1/(n+9) |
— eMathHelp
Этот калькулятор найдет либо уравнение окружности по заданным параметрам, либо центр, радиус, диаметр, окружность (периметр), площадь, эксцентриситет, линейный эксцентриситет, точки пересечения по осям x, точки пересечения с y, домен и диапазон введенных значений. круг. Кроме того, он будет отображать круг. Шаги доступны.
Связанные калькуляторы: Калькулятор параболы, Калькулятор эллипса, Калькулятор гиперболы, Калькулятор конического сечения
Тип:
из уравненияиз данных
Уравнение:
Если калькулятор что-то не рассчитал, или вы обнаружили ошибку, или у вас есть предложение/отзыв, пожалуйста, напишите его в комментариях ниже.
{2} = 9{2} = 9 \pi$$$.
Эксцентриситет и линейный эксцентриситет окружности равны $$$0$$$.
Х-пересечения можно найти, установив $$$y = 0$$$ в уравнении и решив $$$x$$$ (шаги см. в калькуляторе перехватов).
x-отрезки: $$$\left(-3, 0\right)$$$, $$$\left(3, 0\right)$$$
y-отрезки можно найти, установив $ $$x = 0$$$ в уравнении и решение для $$$y$$$: (шаги см. в калькуляторе перехватов).
y-отрезков: $$$\left(0, -3\right)$$$, $$$\left(0, 3\right)$$$ 9{2} — 9 = 0$$$А.
График: см. графический калькулятор.
Центр: $$$\влево(0, 0\вправо)$$$A.
Радиус: $$$3$$$A.
Диаметр: $$$6$$$A.
Окружность: $$$6 \pi\приблизительно 18,849555921538759$$$A.
Площадь: $$$9 \pi\ок. 28,274333882308139$$$A.
Эксцентриситет: $$$0$$$A.
Линейный эксцентриситет: $$$0$$$A.
точек пересечения: $$$\влево(-3, 0\вправо)$$$, $$$\влево(3, 0\вправо)$$$A.
y-отрезки: $$$\left(0, -3\right)$$$, $$$\left(0, 3\right)$$$A.
Домен: $$$\left[-3, 3\right]$$$A.
Диапазон: $$$\влево[-3, 3\вправо]$$$A.
Как нарисовать круг
Автор:
Малкольм МакКинси
Факт проверено
Пол Маццола0134 Построение круга
Построение круга требуются две вещи: координаты центральной точки и радиус круга. Окружность – это множество всех точек, находящихся на одинаковом расстоянии от данной точки, центра окружности. Радиус r – это расстояние от центральной точки до самой окружности.
На графике все эти точки на окружности могут быть определены и нанесены на график с использованием координат (x,y) .
Уравнения окружности
Два выражения показывают, как построить окружность: форма центр-радиус и стандартная форма . Where x and y are the coordinates for all the circle’s points, h and k represent the center point’s x and y values, with r as the radius of the окружность
Форма с центром и радиусом
Форма с центром и радиусом выглядит следующим образом:
Стандартное уравнение окружности
Стандартная, или общая, форма требует немного больше усилий, чем форма центр-радиус, для получения и построения графика. Уравнение стандартной формы выглядит следующим образом:
Стандартная форма уравнения окружностиВ общей форме D , E и F заданы значения, такие как целые числа, которые являются коэффициентами x и и значений.
Использование формы центр-радиус {use-crf}
Если вы не уверены, что предполагаемая формула является уравнением, необходимым для построения круга, вы можете проверить ее.
Он должен иметь четыре атрибута:
Члены x и y должны быть возведены в квадрат.
Все элементы в выражении должны быть положительными (что достигается возведением в квадрат значений в скобках).
Центральная точка задается как (h,k) , координаты x и y .
Значение для r , радиуса, должно быть задано и должно быть положительным числом (что имеет здравый смысл, у вас не может быть отрицательной меры радиуса). 9{2}r2, а число, квадратный корень из которого является фактическим радиусом.
Если повезет, квадратное значение r будет целым числом, но вы все равно можете найти квадратный корень из десятичных дробей с помощью калькулятора.
Какая форма центр-радиус?
Попробуйте эти семь уравнений, чтобы узнать, сможете ли вы распознать форму центра и радиуса. Какие из них являются уравнениями центра и радиуса, а какие просто уравнениями линий или кривых?
(x−2)2+(y−3)2=16{\left(x-2\right)}^{2}+{\left(y-3\right)}^{2} =16(x−2)2+(y−3)2=16 9{2}+-6x+3y=x2+-6x+3
Только уравнения 1, 3, 5 и 6 являются формами центр-радиус.
Второе уравнение изображает прямую линию; четвертое уравнение представляет собой известную форму пересечения наклона; последнее уравнение изображает параболу.Как начертить уравнение окружности
Окружность можно рассматривать как нарисованную линию, которая изгибается как в своих значениях x , так и y . Это может показаться очевидным, но рассмотрите это уравнение:
Здесь x только значение возводится в квадрат, что означает, что мы получим кривую, но только кривую, идущую вверх и вниз, а не замыкающуюся на себя. Мы получаем параболическую кривую, так что она проходит мимо вершины нашей сетки, два ее конца никогда не встречаются и не видны снова.
Введем второй показатель степени x, и мы получим более живые кривые, но они, опять же, не поворачиваются вспять.
Кривые могут извиваться вверх и вниз по оси Y по мере того, как линия перемещается по оси X, но линия на графике по-прежнему не возвращается на себя, как змея, кусающая себя за хвост.
Чтобы кривая отображалась в виде круга, необходимо изменить и , показатель степени x , и , показатель степени и . Как только вы возьмете в квадрат значения x и y , вы получите круг, возвращающийся к самому себе!
Часто форма центра-радиуса не содержит ссылок на такие единицы измерения, как мм, м, дюймы, футы или ярды. В этом случае просто используйте одиночные поля сетки при подсчете единиц радиуса.
Центр в исходной точке
Если центральной точкой является исходная точка (0, 0) графика, форма центра-радиуса будет сильно упрощенной:
Например, круг с радиусом 7 единицы и центр в (0, 0) выглядит следующим образом в виде формулы и графика:
Построение графика начала центра окружностиКак построить график окружности, используя стандартную форму
Если ваше уравнение окружности соответствует стандарту или общему форма , вы должны сначала завершить квадрат, а затем преобразовать его в форму центра и радиуса.
Предположим, у вас есть это уравнение:Перепишите уравнение так, чтобы все x-члены были в первых скобках, а y-члены — во вторых:
Вы выделили константу справа и добавили значения ?1{?}_{1}? 1 и ?2{?}_{2}?2 в обе стороны. Значения ?1{?}_{1}?1 и ?2{?}_{2}?2 – это числа, необходимые в каждой группе для завершения квадрата.
Возьмите коэффициент x и разделите на 2 . Приведите его в порядок. Это ваше новое значение для ?1{?}_{1}?1:
Повторите это для значения, которое нужно найти с y-terms:
Замените неизвестные значения ?1{?}_{1}?1 и ?2{?}_{2}?2 в уравнении новыми рассчитанными значениями:
Упрощение:
Теперь у вас есть форма центра-радиуса для графика. Вы можете подставить значения, чтобы найти этот круг с центральной точкой (-4, 3) и радиусом 5,385 единиц (квадратный корень из 29 ):
Изображение круга в стандартной формеout for
С практической точки зрения помните, что центральная точка, хотя и необходима, на самом деле не является частью круга.
Второе уравнение изображает прямую линию; четвертое уравнение представляет собой известную форму пересечения наклона; последнее уравнение изображает параболу.
Предположим, у вас есть это уравнение: