Как правильно вычислить диаметр по длине окружности
Статьи › Школа › Длина окружности как находится › Чему равна длина окружности диаметр которой равен 6 см
Если перед нами стоит задача найти диаметр по длине окружности D = C: π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14. Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.
- Сколько диаметров в данной окружности
- Как правильно определить диаметр трубы
- Как рассчитать диаметр по окружности
- Как вычислить длину окружности круга
- Как вычислить радиус окружности по длине
- Как рассчитать длину окружности
- Как найти диаметр окружности O
- Как узнать длину окружности по диаметру
- Как найти диаметр трубы по длине окружности
- Чему равен диаметр по отношению к окружности
- Как указать диаметр окружности
- Каким числом выражается отношение длины окружности к длине диаметра
- Что значит отношение длины окружности к диаметру
- Как найти длину всей окружности
- Как показать диаметр окружности
- Чему равна длине окружности
- Как начертить в окружности диаметр
Сколько диаметров в данной окружности
Диаметр — самая длинная хорда.
В окружности также можно провести бесконечное количество диаметров.
Как правильно определить диаметр трубы
Отмечаем точку касания концов шнурка, отрезаем фрагмент шнурка, распрямляем и прикладываем к линейке. Мы узнали длину окружности сечения трубы. Теперь по несложной школьной формуле узнаем диаметр: длину окружности делим на 3,14.
Как рассчитать диаметр по окружности
Онлайн калькулятор:
1. Каков диаметр (d) если длина окружности C? Формула d = C/π, где π ≈ 3.14. Пример
2. Каков диаметр окружности (d) если её радиус r? Формула d = 2⋅r. Пример
3. Каков диаметр окружности (d) если её площадь S? Формула d = √4S/π, где π ≈ 3.14. Пример
Как вычислить длину окружности круга
Мы имеем формулу для вычисления длины окружности, если известен диаметр: C = π ⋅ d. Если вспомним, что d = 2 r, то формула длины окружности будет выглядеть так: C = 2 π ⋅ r.
Как вычислить радиус окружности по длине
Умножьте число пи на два.
Разделите длину окружности на результат:
1. R — искомый радиус окружности.
2. P — длина окружности (периметр круга).
Как рассчитать длину окружности
Длина окружности равна произведению пи π и диаметра d. Так как диаметр d в 2 раз больше радиуса r, длину окружности можно вычислить, зная радиус, по формуле 2πr 2 π r.
Как найти диаметр окружности O
Общая формула.
Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.
Как узнать длину окружности по диаметру
Просто умножьте диаметр на число пи:
1. O — искомая длина окружности.
2. π (пи) — константа, равная 3,14.
3. d —диаметр окружности.
Как найти диаметр трубы по длине окружности
Измерьте окружность с помощью гибкой ленты и разделите внешнюю окружность на 3,1415. Здесь длина окружности примерно на 1/32″ (0,03″) меньше, чем 6″ = 5,97″.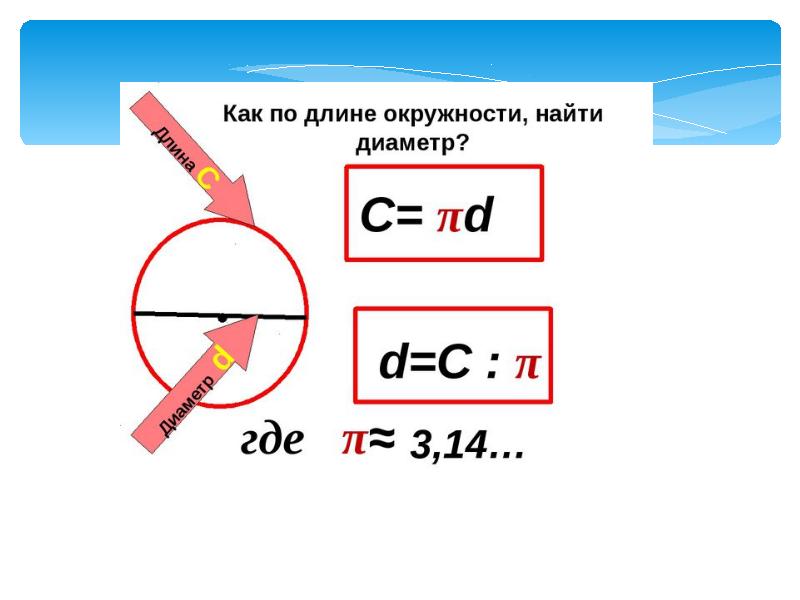
Итак, 5,97 ÷ 3,1415 = диаметр 1,900″ — номинальная труба 1 1/2″.
Чему равен диаметр по отношению к окружности
Формула для вычисления длины окружности: C=πd или C=2πr C = π d или C = 2 π r, где d — диаметр, а r — радиус.
Как указать диаметр окружности
Для обозначения окружностей пользуются специальным знаком диаметра. Он проставляется перед размерным числом. Если необходимо указать несколько диаметров из одного центра, то размерные линии располагают по диагонали через центр окружности (а). Также размерную линию диаметра можно показать с обрывом.
Каким числом выражается отношение длины окружности к длине диаметра
Отношение длины окружности к ее диаметру есть одно и то же число для всех окружностей. Это число принято обозначать греческой буквой π («пи»).
Что значит отношение длины окружности к диаметру
Для всех окружностей справедливо, что отношение длины окружности к её диаметру есть одно и то же число. Это число принято обозначать греческой буквой π («пи»).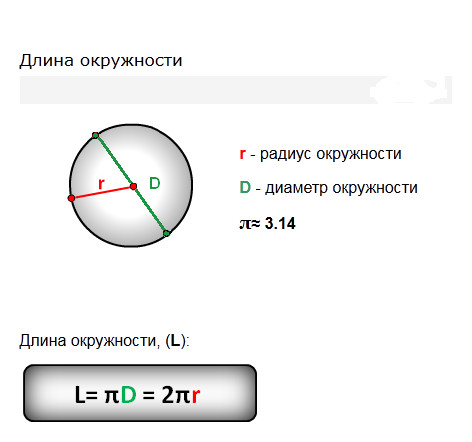
У этого числа за запятой бесконечное множество цифр, порядок которых не повторяется.
Как найти длину всей окружности
Для вычисления длины окружности необходимо число Пи умножить на два и умножить на длину его радиуса (2πR).
Как показать диаметр окружности
1. Если известен радиус: если вам известен радиус окружности, то, для того чтобы узнать диаметр, нужно его удвоить, то есть удваиваем радиус. 2. Если вам известна длина окружности, то, для того чтобы вычислить диаметр, следует разделить ее на π(пи).
Чему равна длине окружности
Длина окружности обозначается через \(C\), диаметр и радиус \(D = 2R\), значит, C = π ⋅ D, или C = 2 π ⋅ R.
Как начертить в окружности диаметр
Если соединить любую точку окружности с ее центром, то получится отрезок, который называется радиусом. Если соединить 2 точки окружности, проходящих через центр, получится отрезок, который называется диаметром.
Формула для измерения длины окружности
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Н. 11Муниципальное бюджетное образовательное учреждение «Березовская средняя школа»
Мамонова В.М. 11Муниципальное бюджетное образовательное учреждение «Березовская средняя школа»
Автор работы награжден дипломом победителя III степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Геометрия – одна из самых древних наук, она возникла очень давно, ещё до нашей эры. В переводе с греческого слово «геометрия» означает «землемерие».
Геометрия – наука о пространстве, точнее – наука о формах, размерах и границах тех частей пространства, которые в нем занимают вещественные тела; раздел математики, изучающий пространственные отношения и их обобщения.
В школе предмет «Геометрия» изучается с 7 класса и, по мнению многих учащихся, является одним из самых сложных школьных предметов.
Что же геометрия означает в нашей жизни? Кое – кто, возможно, считает, что различные замысловатые линии, фигуры, поверхности можно встретить только в книгах ученых математиков. Однако стоит посмотреть вокруг, и можно увидеть, что многие предметы имеют форму, похожую на уже знакомые геометрические фигуры. Оказывается их много. Просто это не всегда бросается в глаза.
Геометрия – древнейшая наука и первые расчеты производились более тысячи лет назад. Древние люди составляли на стенах пещер орнаменты из треугольников, ромбов, кругов. Со временем человек научился использовать свойства фигур в практической жизни.
Многие вещи, окружающие нас, напоминают окружность, например, обруч, кольцо, тарелка. Арбуз, глобус, мячи – похожи на шар. Предметов, имеющих форму цилиндра и конуса в окружающем нас мире очень много: трубы, кастрюли, бочки, стаканы, консервные банки.
В современной архитектуре смело используются самые разные геометрические формы. Многие жилые дома украшаются колоннами.
Геометрические фигуры различной формы можно увидеть в постройке соборов и конструкциях мостов.
По улице движутся автомобили, трамваи, автобусы, мотоциклы и велосипеды. Их колеса с геометрической точки зрения – круги. Сложную форму имеет корпус подводной лодки. Корпус космического спутника состоит из цилиндра.
Сложную форму имеют и детали машин – гайки, винты, зубчатые колеса.
В природе много замечательных геометрических форм. Необыкновенно красивы и разнообразны многоугольники, созданные природой. Кристаллы горного хрусталя напоминают отточенный карандаш. Кристалл соли имеет форму куба, кристаллы алмаза имеют форму правильного восьмигранника – октаэдра. Кто из нас не любовался в зимний солнечный день искристыми снежинками? Каждая снежинка – это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной. Снежинки – это одна из самых красивых геометрических фигур. Обычная горошина, капельки росы – имеют форму шара.
Многих животных природа наделила талантом строить себе дома в форме геометрических тел.
Из всего сказанного можно сделать вывод: геометрия нужна не только для того чтобы называть части строений или формы окружающего нас мира, с помощью геометрии можно решить многие задачи, ответить на многие вопросы.
Цель: вывести формулу длины окружности.
Задачи: изучить окружность, её элементы, показать связь между ними. Гипотеза: формулу длины окружности можно вывести практическим путем.
Методы исследования:
- Изучение литературы по данной теме.
- Практическая работа на измерение длины окружности.
- Анализ, сравнение, сопоставление.
Глава 1. Что такое окружность?
Окружность – замкнутая, плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
Круг – часть плоскости, ограниченная окружностью.
Радиус – отрезок прямой, соединяющий центр окружности с какой – либо её точкой, а также длина этого отрезка. Обычно обозначается R.
Диаметр – отрезок прямой, соединяющий пару наиболее удаленных друг от друга точек окружности, а также длина этого отрезка. Диаметр всегда проходит через центр окружности. Обычно обозначается d или Ø. Диаметр равен удвоенному радиусу окружности: d = 2R, R = d/2.
Отношение длины окружности к её диаметру одинаково для всех окружностей. Это отношение есть трансцендентное число, обозначаемое греческой буквой пи: …
Длина окружности: C = 2πR= πd
Радиус окружности: R = C/2π
Диаметр окружности: d = C/π
Площадь круга: S = πR2 = πd2/4
Радиус круга: R = (S/π), где — корень квадратный.
Диаметр круга: d = 2(S/π)
Круг Окружность
Исторические сведения
В древней Греции круг и окружность считались венцом совершенства.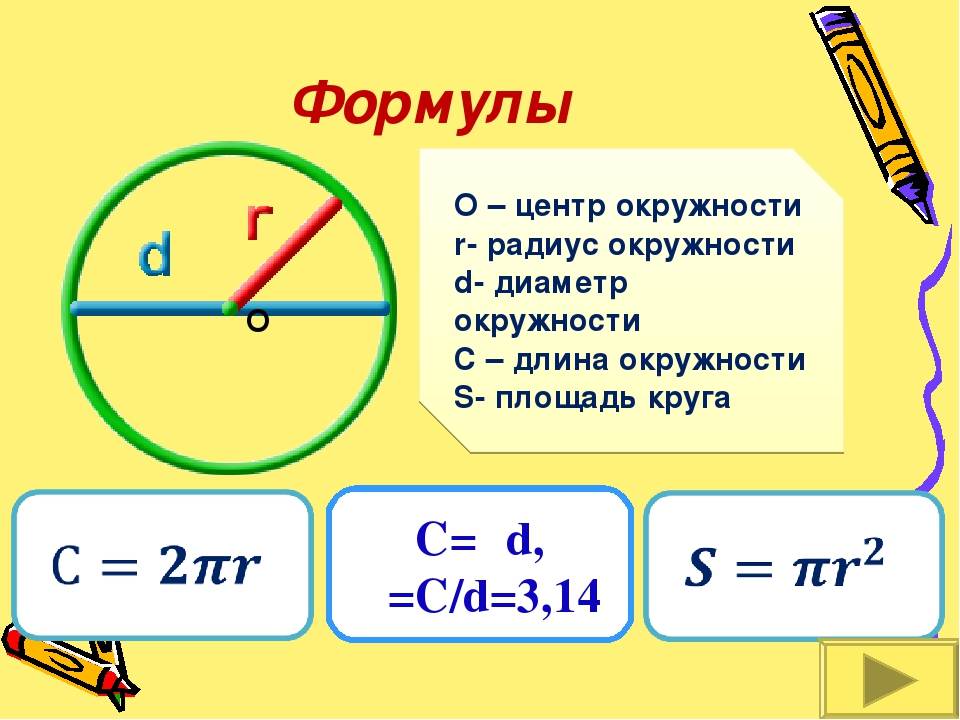
Действительно, в каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности сделало возможным возникновение колеса, поскольку ось и втулка колеса должны все время быть в соприкосновении. Но ещё до колеса люди использовали круглые бревна – катки для перевозки тяжестей. Рисунки на стенах египетских пирамид рассказывают нам, что именно так доставлялись огромные камни на строительство этих пирамид.
Глава 2. Вывод формулы длины окружности
Как же можно вывести формулу для вычисления длины окружности? Самое простое, что приходит на ум – это измерить с помощью нити длину предметов, имеющих форму круга или окружности. Так как у любой окружности и у круга имеется диаметр, то вполне возможно его измерить.
Итак, для измерений необходимы предметы цилиндрической формы, такие как: кружка, термос, кастрюля; и предметы, имеющие непосредственно форму круга, например циферблат часов и барометр бытовой.
Первый этап работы заключается в измерении с помощью нити длины окружности выбранных предметов. Затем нужно длину нити измерить с помощью линейки. На втором этапе подобным образом можно измерить диаметры данных предметов. Должна же существовать какая – то связь между длиной окружности и её диаметром.
Измерение длины окружности с помощью нити и линейки.
Измерение диаметра окружности с помощью нити и линейки.
В результате проведённых измерений были получены следующие результаты:
Кружка для чая: C = 22 см, d = 7 см.
Термос: C = 43 см, d = 13,7см.
Кастрюля: C = 64 см, d = 20,5см.
Циферблат часов: C = 70 см, d = 22,6 см.
Барометр бытовой: C = 47,4 см, d = 15,1 см.
Нетрудно увидеть, что длина окружности каждого предмета больше её диаметра в несколько раз. Что же получится, если посчитать, во сколько раз длина окружности больше диаметра в каждом случае? Для вычислений можно воспользоваться калькулятором.
C/d = 22 см / 7 см = 3,14285 3,14
C/d = 43 см / 13, 7 см = 3,13868 3,14
C/d = 64 см / 20,5 см = 3,13725
C/d = 71 см / 22,6 см = 3,14159 3,14
C/d = 47,4см / 15,1 см = 3,13907 3,14
Как видно из полученных вычислений, отношение длины окружности к диаметру, если округлить его до сотых долей, является одним и тем же числом C/d3,14. Таким образом, получается, что если длину окружности любого размера разделить на её диаметр, то это отношение всегда будет приближаться к числу 3,14.
Отношение длины окружности к её диаметру одинаково для всех окружностей.
Это есть известное число π 3,14. Т. е. C/d = π, отсюда следует, что C = πd.
d = 2r, где r – радиус окружности, тогда C = 2πr.
Заключение
В ходе исследовательской работы с помощью измерений и вычислений мы вывели формулу для вычисления длины окружности:
|
C = 2πr |
Определили, как с помощью эксперимента получить известное число
π = 3,14
Литература
- Геометрия.
7-9 классы: учебник для общеобразовательных учреждений / [Л.А. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. ]. – М. Просвещение, 2016г. – 384 с.:ил. - Красота математики М. Давыдов г. Н.Новгород 2007г.
- http://ru.wikipedia.org/wiki/. [Электронный ресурс].
7-9 классы: учебник для общеобразовательных учреждений / [Л.А. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. ]. – М. Просвещение, 2016г. – 384 с.:ил.Просмотров работы: 589
Окружность и биссектрисы – Процедуры компоновки металлов
ОКРУЖНОСТЬ И КАК НАЙТИ
Есть несколько способов найти длину окружности трубы и круглой трубы. Знание окружности является ключом к созданию точных шаблонов для использования с трубой. Чем точнее будут ваши цифры при разработке этих шаблонов, тем лучше они вам подойдут. Как и во всем, практика и опыт создания шаблонов также повысят точность.
Наиболее часто используемый метод для вычисления длины окружности — использование формулы Pi x диаметр. Круглая труба с наружным диаметром 6 дюймов имеет окружность 18,85 дюйма. 6 дюймов x Пи = 18,85 дюйма. Когда дело доходит до работы с трубой, вы должны знать, что труба измеряется номинально.
Это означает, что труба 6 дюймов не имеет наружный диаметр 6 дюймов. К счастью, все производители труб следуют стандарту, и существует бесчисленное количество таблиц и диаграмм, в которых перечислены все размеры труб и даже указаны окружности всех размеров! Пожалуйста, обратитесь к указателю, чтобы найти эти таблицы, диаграммы и другую информацию.
В следующих нескольких разделах мы начнем разрабатывать шаблоны для использования с трубой. Независимо от сложности шаблона, есть несколько ключевых понятий, которые используются со всеми из них, включая определение окружности. Мы подробно представим эти концепции только один раз, если вам нужна помощь, пожалуйста, вернитесь к предыдущим разделам.
Речь пойдет о делении окружности трубы на несколько равных частей, что поможет разработать шаблон. Мы будем называть эти строки строками элементов. Чем больше у вас линий элементов, тем точнее соответствие.
Как было сказано ранее, ремесленники придумали множество способов решения сложных проблем, и эта книга предлагает один из них.
Ниже у нас есть 4-х дюймовая труба. Обратившись к диаграмме, мы видим, что наружный диаметр этой трубы составляет 4,50 дюйма. Также на графике мы видим, что его общая длина окружности составляет 14,125 дюйма. Для этой книги мы разделим все окружности на 16 равных пространств, в которых будут элементы линий. На удобной диаграмме сзади также показано расстояние для деления окружности на 16 частей, а также на 12, 8, 6, 4 и 2. Помните, что чем больше у вас линий элементов, тем точнее будет ваш шаблон. Если бы у нас не было диаграммы, вам пришлось бы разделить общую окружность на количество необходимых пробелов. При этом потребуется некоторое округление, но вы должны знать, что отклонение на 1/16 дюйма 16 раз приведет к отклонению на полный 1 дюйм.
Если вы разделите 14,125 на 16, вы получите 0,883. Диаграмма в обратном состоянии .875. .875 или 7/8” гораздо легче работать с рулеткой, чем с .883. Разница примерно 1/132 на строку, это будет приемлемо.
Для начала мы нарисуем вид сбоку, который покажет высоту нашей секции трубы.
Далее нам нужно нарисовать нашу растяжку. Мы знаем, что длина окружности равна 14,125. Мы можем нарисовать вертикаль рядом с видом сбоку на трубу, а затем продолжить горизонтальные линии (показаны красным), которые являются верхней и нижней линиями на виде сбоку, чтобы установить общую высоту трубы и провести их до длины 14,125. ». Как только у нас есть высота и растяжка, мы готовы разместить линии элементов.
При работе с трубой и разработке шаблонов вам нужно будет освежить в памяти базовую геометрию и деление углов пополам. Для этой задачи мы будем использовать компас.
Ниже у нас есть угол CAB с вершиной в точке A.
Сначала мы можем провести дугу из вершины A, которая пересекает линию рядом с точками C и B. Затем от этих двух пересечений мы можем провести две дополнительные дуги вправо.
Из вершины A проведите линию, которая пересекается в точке D, где пересекаются дуги.
При использовании этого метода угол будет поровну разделен на два угла одинакового измерения.
Этот метод можно повторить и при необходимости снова разделить на 4 равные части.
Попробуем аналогичный метод на круге. Нарисованный круг имеет диаметр 3 дюйма, поэтому радиус 1 ½ дюйма.
Установив компас на радиус окружности 1 ½ дюйма, а затем проведя дугу из точки А, а затем В, они пересекаются в точках 1 и 2. Если затем провести линию из центра круга в каждую точку, вы только что разделили эту четверть круга на три равные части. См. ниже…
Если вы сделаете это снова между A, 1, 2 и B, вы можете разделить эту четверть круга на 6 равных частей.
Как мы кратко рассмотрели ранее, мы используем числа, чтобы помочь с определением мест соединения линий. Эти линии будут использоваться, когда мы соединяем две или более деталей вместе, чтобы сделать одну сборку. По мере того, как мы будем продолжать, вы будете лучше понимать, как работает эта система нумерации.
Как найти длину окружности трубы? – Обзоры Вики
Внешний диаметр от внешнего края до внешнего края поперек трубы.
Чтобы найти его, измерьте окружность трубы гибкой измерительной лентой. Разделите длину окружности на число пи , или примерно 3,14159.
Что такое окружность трубы? Окружность трубы — это расстояние вокруг трубы . Для того чтобы рассчитать длину окружности, необходимо знать диаметр трубы. Диаметр – это расстояние от одной стороны трубы до прямо противоположной стороны трубы. Вы также должны знать число Пи. Пи обычно оценивается как 3,14.
Какова длина окружности 20-дюймовой трубы? Окружность = 125,6 дюйма .
Дополнительно Какова окружность трубы диаметром 3/4 дюйма? Информация о размерах труб
| Стандартные размеры ниппелей и труб | ||
|---|---|---|
| Размер трубы | Внешний диаметр (Н.Д.) | Окружность | 3/4″ | 1,050″ | 3,299″ |
| 1″ | 1,315″ | 4,131″ |
| 1 1/4″ | 1,660″ | 5,215″ |
Какова длина окружности 3 дюймов? Если диаметр равен 3 дюймам, то длина окружности будет 3π .
Если вам не разрешено пользоваться калькуляторами, большинство преподавателей рекомендуют использовать 3,14 в качестве значения π и выполнять вычисления вручную.
Как найти длину окружности?
Какова длина окружности числа 4? Ответ: длина окружности радиусом 4 равна 8 π .
Какова длина окружности 6 круга? Найдите окружность. Диаметр круга 6 дюймов. Мы можем подставить эту информацию в нашу формулу и найти длину окружности. Наш ответ: 18,84 дюйма .
Какова длина окружности диаметром 7 см?
∴ , длина окружности примерно 43,98 см .
Также Какова длина окружности 36-дюймовой трубы? Ответ: длина окружности диаметром 36 дюймов равна 113 .
Какова длина окружности 18 трубы?
2 ответа. Ответ: 56,57 .
Каков диаметр трубы 8? Таблица размеров труб
| ТАБЛИЦА ТРУБ ТОЛЩИНА СТЕНКИ (дюймы) | ||
|---|---|---|
| Номинальный | Н. Д. Дюймы | 80-е и Э.Х. |
| 6 | 6,625 | .432 |
| 7 | 7,625 | .500 |
| 8 | 8,625 | .500 |
Какова длина окружности 1 меди трубка?
Номинальная стандартная медная труба «1 дюйм» имеет наружный диаметр 1,125″, что соответствует длине окружности 3,534″ . Номинальная стандартная медная труба «3/4 дюйма» имеет внешний диаметр 0,875″, что соответствует окружности 2,749″.
Какова длина окружности 16-дюймовой трубы?
16π≈ 50,27 в .
Какова длина окружности числа 6? Найдите окружность. Диаметр круга 6 дюймов. Мы можем подставить эту информацию в нашу формулу и найти длину окружности. Наш ответ: 18,84 дюйма .
Какова длина окружности 2,5 дюйма? Окружность и площади
| Размер в дюймах | Окружность в дюймах | Площадь в квадратных дюймах |
|---|---|---|
| 2 1/4 | 7,0 69 | 3,976 |
| 2 1/2 | 7,854 | 4,909 |
| 2 3/4 | 8,639 | 5,940 |
| 3 | 9,425 | 7,069 |
Что такое окружность на примере?
Окружность определяется как расстояние вокруг чего-либо круглого или закругленного, особенно расстояние вокруг края круга.