|
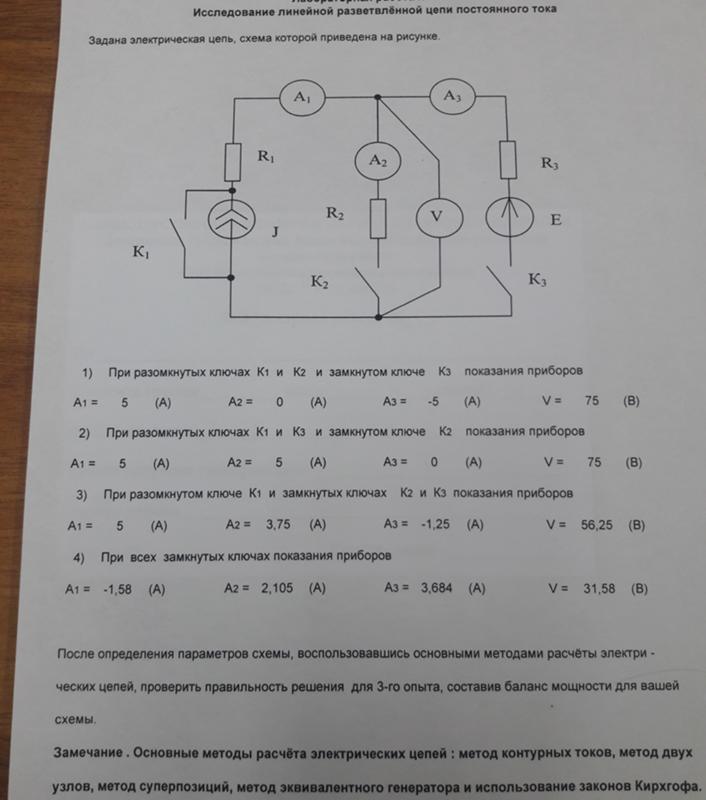
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Расчет электрических цепей постоянного тока, не содержащих источников ЭДС
Похожие презентации:
Расчет цепи постоянного тока
Электрические цепи постоянного тока
Электрические цепи постоянного тока
Электрическая цепь постоянного тока
Электрические цепи постоянного тока
Линейные электрические цепи.
Цепи постоянного тока
Электротехника и электроника. Электрические цепи постоянного тока. (Лекция 1)
Электрические цепи постоянного тока. Лекция 1
Электрические цепи постоянного тока
Расчет электрических цепей
постоянного тока, не содержащих
источников ЭДС
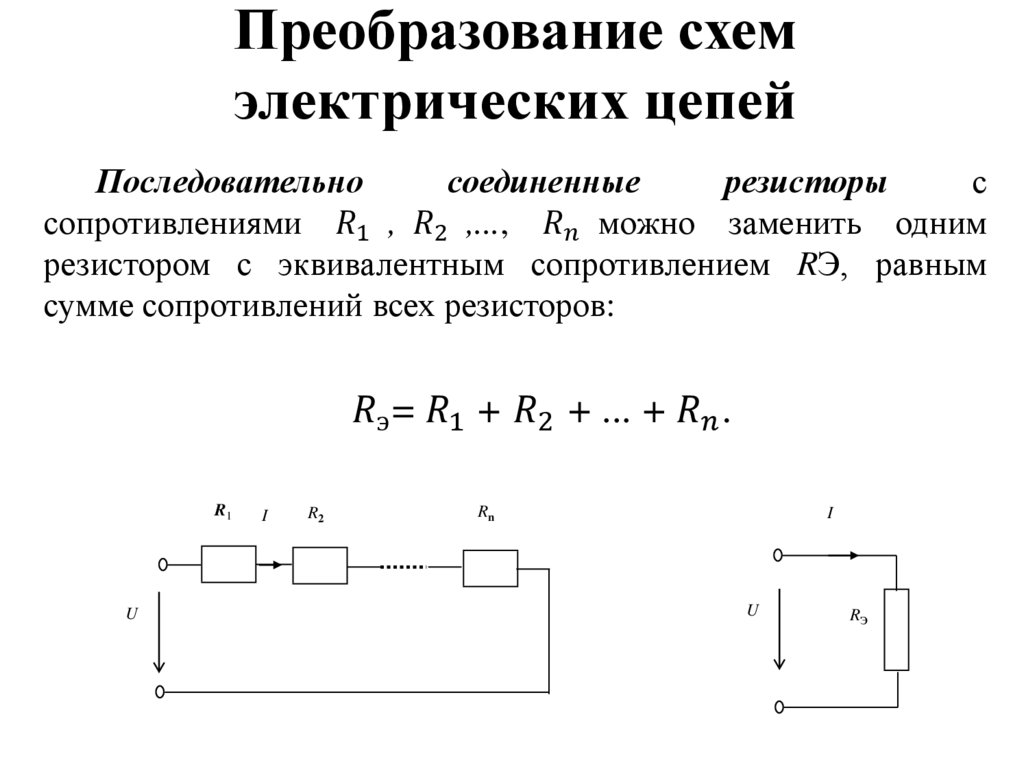
1.Последовательное соединение резисторов
Резистор – элемент цепи с заметным сопротивлением
R
I
R1
U1
R2
R3
U2
U3
U
I
Rобщ
I const
U U1 U 2 U 3 …
IR IR1 IR2 IR3 …
Rобщ R1 R2 R3 …
U
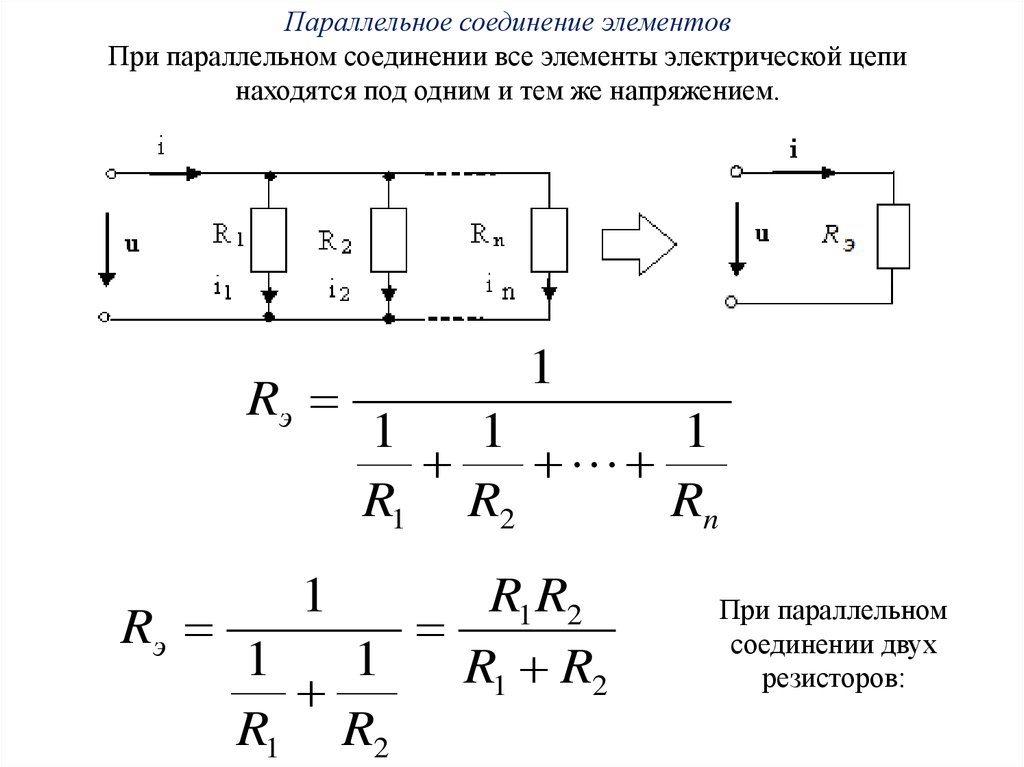
2. Параллельное соединение резисторов
I1
R1
I2
R2
I3
R3
I
U const
I I1 I 2 I 3 …
U
U U U
…
Rобщ R1 R2 R3
U
I
Rобщ
U
1
Rобщ
1
1
1
…
R1 R2 R3
3. Смешанное соединение резисторов
А) Метод последовательного упрощения цепи
R
A
B
R
R1
3R
R
R
R
A
B
R
3R
2.
 75R
75R4
3R
R
R 3R 3R
R 3R
4
R AB R R
R1
R
RAB
R
A
B
R
3R
4
Б) Метод поиска точек с одинаковыми потенциалами
Если две точки цепи имеют одинаковые потенциалы, то
1) Их можно соединять
2) Их можно разъединять
3) Резисторы, включенные между ними, можно исключить
Как узнать, что потенциалы точек одинаковы?
Точки имеют одинаковые потенциалы, если:
1) Они соединены проводником с нулевым сопротивлением
2) Они симметричны геометрически и по отношению к
точкам подключения
Задача
Определить сопротивление проволочного куба при подключении к двум
наиболее удаленным друг от друга вершинам. Сопротивление каждого ребра
куба равно R
B
F
C
A B
C D E
F G H
G
A
H
E
A
C
D
R E
3
R
6
F
G
H R
3
B
В) Общий метод расчета общего сопротивления
R2
R1 C
A
B
R5
R3
RAB — ?
R4
R1 R3
R2 R4
C D
R1 R3
R2 R4
C D
D
I
I
U
Приложим к концам цепи напряжение U
и рассчитаем ток I, протекающий через
цепь
По закону Ома
R
U
I
I1
A
R1 C
I5
I2
Найти: I, I1, I2, I3, I4, I5
B
R5
R3
I3
R2
Дано: U, R1, R2, R3, R4, R5
Необходима система из 6 неза-висимых
уравнений для токов
R4
D
I4
I
I
U
Закон сохранения заряда:
A : I I1 I 3
(1)
B : I I2 I4
C : I1 I 2 I 5
D : I3 I5 I 4
(2)
(3)
I1
A
R1 C R2 I 2
R5
R4
R3
I 3 D I 4
I5
Работа сил электрического поля над
зарядом не зависит от траектории
движения заряда
B
I
I
U
Работа сил электрического поля над
зарядом при премещении по замкнутому
контуру равна нулю
ADCB : I 3 R3 I 5 R5 I 2 R2 U (4)
ACBDA : I1R1 I 2 R2 I 4 R4 I3R3 0 (5)
Записанные уравнения объединим в систему:
I I1 I3 0
I I2 I4 0
I1 I 2 I5 0
I1R1 I5 R5 I 2 R2 U
I1R1 I 2 R2 I 4 R4 I3R3 0
Общее решение системы имеет вид
I U f ( R1, R2 , R3 , R4 , R5 )
По определению
R
U
I
1
f ( R1, R2 , R3 , R4 , R5 )
Расчет разветвлённых электрических
цепей постоянного тока, содержащих
источники ЭДС
1.
 Метод Кирхгофа
Метод КирхгофаСложная электрическая цепь постоянного тока содержит произвольным
образом соединенные источники тока и резисторы.
Задача расчета сложной цепи состоит в определении всех неизвестных
токов, текущих в цепи.
В методе Кирхгофа расчёт начинается с расстановки токов, текущих в
ветвях схемы. Направление тока в каждой ветви выбирается произвольно.
1
R1
A
I2
I4
I1
R2
3
R4
R3
I3
R5
I5
4
B
C
Общее число уравнений, составленных для расчёта цепи, равно числу
неизвестных токов.
2
1
R1
A
I2
I4
I1
R2
3
R4
R3
I3
R5
I5
C
4
B
В данной цепи для расчета токов I1, I2, I3, I4, I5 необходимо составить 5
независимых уравнений
Для составления уравнений используются 2 правила Кирхгофа
2
1
R1
A
I2
I4
I1
R2
3
R4
R3
I3
R5
I5
C
4
B
Первое правило Кирхгофа формулируется для узлов цепи.
 Узел — точка
Узел — точкацепи, в которой сходится не менее 3-х проводников.
Ветвь схемы – участок электрической цепи между соседними узлами.
Первое правило Кирхгофа:
В любом узле цепи сумма входящих токов равна сумме выходящих
токов.
2
1
R1
R2
A
I2
I4
I1
3
R4
R3
I3
R5
I5
C
4
B
Для узла А
I1 I 2 I3 I 4
или
I1 I 2 I3 I 4 0 (1)
Для узла В
I 4 I1 I5
или
I1 I 4 I5 0 (2)
Число независимых уравнений, составленных по первому правилу Кирхгофа,
на одно уравнение меньше числа узлов в цепи
Второе правило Кирхгофа формулируется для контуров, которые
можно выделить в рассматриваемой схеме. Контур – любая замкнутая
часть схемы.
2
1
3
R1
R2
A
I2
I4
I1
R4
R3
I3
R5
I5
C
4
B
Работа сил электрического поля при перемещении заряда по произвольному замкнутому контуру равна нулю. Запишем это равенство для
наружного контура рассматриваемой цепи:
R1
1
2
3
R2
I1
q
R5
I5
ЭП
ЭП
ЭП
ЭП
ЭП
ARЭП
A
A
A
A
A
2
R2
3
R5 0
1
qI1R1 q 1 q 2 qI 2 R2 q 3 qI 5 R5 0
I1R1 I 2 R2 I5 R5 1 2 3
I2
Второе правило Кирхгофа:
Для любого замкнутого контура цепи, при выбранном направлении обхода
контура, алгебраическая сумма напряжений на резисторах контура равна
алгебраической сумме ЭДС источников тока, встреченных при обходе
контура.
 Направление обхода контура выбирается произвольно.
Направление обхода контура выбирается произвольно.В сумму напряжений на резисторах слагаемые входят со знаком «+», если
направление тока текущего через резистор, совпадает с направлением
обхода, и со знаком «-», если направления противоположны.
В сумму ЭДС слагаемые входят со знаком «+», если направление ЭДС,
Источника совпадает с направлением обхода, и со знаком «-», если
направления противоположны
Число независимых
уравнений, которые можно
составить по второму правилу
Кирхгофа равно числу
простых контуров цепи
1
R1
1
R4
2
3
R2
R3
4
R5
2
3
2
1
R1
A
I2
I4
I1
R2
3
R4
R3
I3
R5
I5
C
4
B
BR1R2CB :
I1R1 I 2 R2 I5 R5 1 2 3
(3)
BAR2CB :
I 4 R4 I 2 R2 I5 R5 4 2 3
(4)
AR3CR2 A :
I3R3 I 2 R2 3 2
(5)
I1 I 2 I3 I 4 0
(1)
I1 I 4 I5 0
(2)
I1R1 I 2 R2 I5 R5 1 2 3
(3)
I 4 R4 I 2 R2 I5 R5 4 2 3 (4)
I3R3 I 2 R2 3 2
(5)
Для любой сколь угодно сложной цепи правила Кирхгофа позволяют
составить достаточное число независимых уравнений для нахождения всех
токов в цепи
3.
 Метод контурных токов
Метод контурных токовНедостаток метода Кирхгофа — в необходимости решения системы
уравнений, число которых равно числу неизвестных токов. Достаточно
простая схема, содержащая много ветвей, приводит к системе из большого
числа уравнений, что усложняет вычисления.
В методе контурных токов число уравнений сводится к числу простых
контуров, содержащихся в рассматриваемой схеме.
В качестве примера, применим метод контурных токов
для расчёта цепи, рассмотренной в методе Кирхгофа.
Полагаем, что в каждом
простом контуре течёт свой
«контурный ток». Направление «контурных токов» во
всех контурах одинаково: по
часовой или против часовой
стрелки.
1
R1
i1
1
R4
4
2
R2
R3
i3
R5
3
i2
2
3
Для нахождения «контурных токов», для каждого контура составляется
уравнение по второму правилу Кирхгофа.
Для конура №1:
Для контура №2
Для контура №3
R1i1 (i1 i3 ) R4 1 4
(1)
R2i2 (i2 i3 ) R3 2 3
(2)
R5i3 R4 (i3 i1 ) R3 (i3 i2 ) 4
(3)
Раскрывая скобки и приводя подобные получим систему уравнений для
нахождения «контурных токов»:
R1 R4 i1 R4i3 1 4
R2 R3 i2 R3i3 2 3
R4i1 R3i2 R3 R4 R5 i3 4
После решения системы возвращаемся к исходной схеме, и находим
неизвестные токи, текущие в ветвях схемы:
I1 i1; I 2 i2 ; I 3 i3 i2 ;
I 4 i3 i1;
I 5 i3
Полученное с отрицательным знаком значение тока свидетельствует о
противоположном предполагаемому направлении тока в данной ветви.
Сокращение числа уравнений на два, по сравнению с методом Кирхгофа,
делает применение метода контурных токов более предпочтительным.
English Русский Правила
Калькулятор предварительной зарядки| Sensata Technologies
Следующий калькулятор может помочь в разработке схемы предварительной зарядки для электромобиля. Он рассчитает сопротивление предварительного заряда, необходимое для достижения желаемого процента заряда емкости системы за желаемое время.
Представленные здесь результаты приведены только для справки. Пожалуйста, свяжитесь с отделом разработки приложений Sensata для ознакомления с результатами расчетов и помощи в выборе продукта.
Дополнительные технические сведения о предварительной зарядке см. в этом техническом документе. КАЛЬКУЛЯТОР И ЕГО РЕЗУЛЬТАТЫ ПРЕДОСТАВЛЯЮТСЯ «КАК ЕСТЬ», И НАСТОЯЩИМ SENSATA ОТКАЗЫВАЕТСЯ ОТ ВСЕХ ГАРАНТИЙ, ЯВНЫХ ИЛИ ПОДРАЗУМЕВАЕМЫХ, ПРЕДУСМОТРЕННЫХ ЗАКОНОМ ИЛИ ИНЫМ ОБРАЗОМ, ВКЛЮЧАЯ, ПОМИМО ПРОЧЕГО, ВСЕ ПОДРАЗУМЕВАЕМЫЕ ГАРАНТИИ ПРИГОДНОСТИ ДЛЯ ОПРЕДЕЛЕННОЙ ЦЕЛИ.
Перейти к определениям
ЧАСТЬ 1. Рассчитайте максимальное сопротивление предварительной зарядки, при котором система будет заряжаться до желаемого процента за желаемое время. Напряжение батареиНапряжение батареи Вб
Единица измерения напряжения батареи — Выберите -кВВ
Желаемое время предварительной зарядки (МАКС.)Требуемое время предварительной зарядки (МАКС.) Тмакс
Требуемое время предварительной зарядки (МАКС.) Единица измерения — Нет — смс
% Желаемая предварительная зарядка д %
5 тау = 99,326% по умолчанию.
Емкость системыЕмкость системы С
Единица измерения емкости системы — Нет -FmFuFnFpF
Требуемое количество постоянных времени н
МАКС. Сопротивление предварительной зарядки R1макс Ом
ЧАСТЬ 2. Рассчитайте энергию, мощность и пусковой ток, возникающие в результате использования выбранного значения сопротивления.
Рассчитайте энергию, мощность и пусковой ток, возникающие в результате использования выбранного значения сопротивления.Выбранное значение резистора R1 Ом
Использовать «МАКСИМАЛЬНОЕ сопротивление предварительной зарядки» выше?
Общее последовательное сопротивление в главной цепиПолное последовательное сопротивление в главной цепи R2
Полное последовательное сопротивление в блоке главной цепи — Нет -кОммОм
Постоянная времени т сек
Фактическое время предварительной зарядки Т сек
Пусковой ток цепи предварительной зарядки я(0) A
Энергия, рассеиваемая резистором предварительной зарядки Э(Т) J
Средняя мощность павг Вт
Пиковая мощность пп W
Дельта напряжения, оставшаяся после предварительной зарядки Вд(Т) V
Пусковой ток главного контактора после предварительной зарядки Я А
| Постоянная Эйлера | и | 2,71828 | Числовая константа. |
| Напряжение батареи | Вб | Напряжение системы/батареи (пост. ток). | |
| Прошедшее время | т | Прошло время с начала предварительной зарядки. | |
| Требуемое время предварительной зарядки (МАКС.) | Т_{макс.} | Максимально допустимое время для получения системой желаемого уровня заряда. | |
| % Желаемый предварительный заряд | д | Процент заряда емкости системы, необходимый перед замыканием главного контактора. | |
| Емкость системы | С | Емкость системы/нагрузки, которую необходимо предварительно зарядить. | |
| Требуемое количество постоянных времени | п | n=-ln|1-q| | Количество постоянных времени, необходимых для предварительного заряда емкости нагрузки до требуемого процента. |
| МАКС. сопротивление предварительной зарядке | R_{1,max} | R_{1,max} = \frac {T_{max}} {nC} | Максимальное сопротивление предварительной зарядки, при котором емкость нагрузки будет заряжаться до желаемого уровня за желаемое время. Фактическое используемое сопротивление предварительной зарядки может быть меньше, что приведет к более быстрой предварительной зарядке, но также и к более высокому рассеиванию мощности через резистор. Фактическое используемое сопротивление предварительной зарядки может быть меньше, что приведет к более быстрой предварительной зарядке, но также и к более высокому рассеиванию мощности через резистор. |
| Выбранное значение резистора | Р_1 | Выбранное значение резистора предварительной зарядки. Максимальное сопротивление, рассчитанное выше, можно использовать для этого, установив флажок, но также можно указать любое другое значение, например, для экспериментов с резисторами, которые легко доступны на рынке, или для более быстрой предварительной зарядки. | |
| Общее последовательное сопротивление в главной цепи | Р_2 | Суммарное сопротивление нагрузки(ей), проводников, контактных сопротивлений выключателей и разъемов и т.д. в главной цепи. Это можно определить следующим образом: Когда ваша система полностью собрана и подключена, положительный главный контактор (K_2) находится в разомкнутом состоянии, а главный отрицательный контактор (K_1) и контактор предварительной зарядки (K_3) находятся в замкнутом состоянии, используйте омметр. для измерения сопротивления на плюсовых силовых клеммах главного контактора (K_2). Это используется для определения пускового тока через главный контактор (K_2), когда он замкнут после выполнения предварительной зарядки. R_2 должно быть намного меньше, чем R_1, иначе схема предзаряда не понадобилась бы. для измерения сопротивления на плюсовых силовых клеммах главного контактора (K_2). Это используется для определения пускового тока через главный контактор (K_2), когда он замкнут после выполнения предварительной зарядки. R_2 должно быть намного меньше, чем R_1, иначе схема предзаряда не понадобилась бы. | |
| Постоянная времени | т | τ=R_1C | Постоянная времени для RC-цепи. Это время, необходимое для зарядки конденсатора до 63,2% SOC. Пятикратные константы — хорошее практическое правило для полной зарядки конденсатора. Меньшее значение может привести к сварке главного контактора. Это можно настроить, изменив ввод времени предварительной зарядки «T_{max}». |
| Фактическое время предварительной зарядки | Т | 9{\frac{-t}{R_1C}} Оставшееся падение напряжения на главном контакторе после предварительной зарядки. Это, наряду с последовательным сопротивлением в главной цепи, будет определять пусковой ток через главный контактор, когда он замкнут. | |
| Пусковой ток главного контактора после предварительной зарядки | И_м | I_m = \frac{V_d(T)}{R_2} | После завершения предварительной зарядки это пусковой ток, которому подвергается главный контактор, когда он замкнут. |
Представленные здесь результаты приведены только для справки. Пожалуйста, свяжитесь с отделом разработки приложений Sensata для ознакомления с результатами расчетов и помощи в выборе продукта.
Linear Circuits 1: Анализ постоянного тока
Об этом курсе
58 895 недавних просмотров
В этом курсе объясняется, как анализировать цепи с источниками постоянного тока или напряжения. Источник постоянного тока является постоянным. Цепи с резисторами, конденсаторами и катушками индуктивности рассматриваются как аналитически, так и экспериментально. Продемонстрированы некоторые практические приложения в датчиках.
Гибкие срокиГибкие сроки
Сброс сроков в соответствии с вашим графиком.
Совместно используемый сертификат
Получите сертификат по завершении
100% онлайн100% онлайн
Начните немедленно и учитесь по собственному графику.
Часов на выполнениеПрибл. 85 часов
Доступные языкиАнглийский
Субтитры: арабский, французский, португальский (европейский), итальянский, португальский (бразильский), вьетнамский, немецкий, русский, английский, испанский
Гибкие срокиГибкие сроки
Сброс сроков в соответствии с вашим графиком.
Совместно используемый сертификатСовместно используемый сертификат
Получите сертификат по завершении
100% онлайн100% онлайн
Начните немедленно и учитесь по собственному графику.
Часов на выполнениеПрибл. 85 часов
Доступные языкиАнглийский
Субтитры: арабский, французский, португальский (европейский), итальянский, португальский (бразильский), вьетнамский, немецкий, русский, английский, испанский
Инструкторы
Доктор Бонни Х.
 Ферри
ФерриПрофессор
Электрика и компьютерная инженерия
243 640 .
Школа электротехники и вычислительной техники
71 904 Учащиеся
6 Курсы
Доктор Мэри Энн Вайтнауэр
59,858 Учащиеся
1 Курс
Предлагает
Технологический институт Джорджии
передовая наука и техника.
Reviews
4.5
Filled StarFilled StarFilled StarFilled StarHalf Filled Star325 reviews
5 stars
69.
 78%
78%4 stars
19.78%
3 stars
7.04%
2 звезды
1.47%
1 звезда0002 от RR14 марта 2019 г.
Очень длинный набор вопросов.
Но полезно понимать концепции и иметь опыт решения многих задач с небольшими отклонениями.
Есть четкая идея решения цепей постоянного тока.
Filled StarFilled StarFilled StarFilled StarFilled Starот KMM 5 марта 2022 г.
Мне очень понравился этот курс. Я думаю, что это будет очень полезно для моего будущего кругового курса. Преподаватели курса отличные.
Заполненная звездаЗаполненная звездаЗаполненная звездаЗаполненная звездаЗаполненная звездаот RAA, 21 августа 2020 г.
Этот курс очень помогает мне понять оставшиеся предметы в области электротехники и электроники.
Filled StarFilled StarFilled StarFilled StarFilled Starby NS 1 марта 2020 г.
Это очень хороший и фундаментальный курс для ответвлений цепи.


 Графики функций е(ω
Графики функций е(ω
 Графики гармоник токов и полный ток в неразветвленной части цепи. По оси абсцисс ωt, рад. По оси ординат ток, А.
Графики гармоник токов и полный ток в неразветвленной части цепи. По оси абсцисс ωt, рад. По оси ординат ток, А.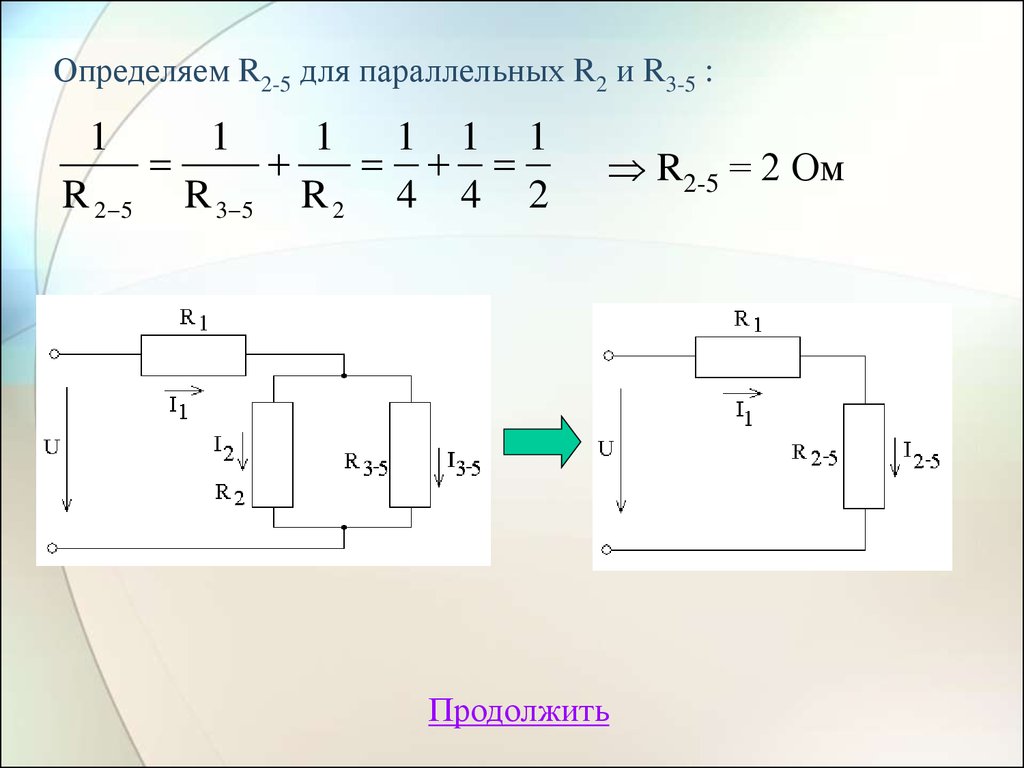 78%
78%