Окружности картинка: Картинка радиус окружности — 71 фото

alexxlab / / Разное

Окружность | matematicus.ru

Окружность — это геометрическая фигура, состоящая из всех точек плоскости, равноудаленных от некоторой точки этой же плоскости на заданное расстояние (рисунок 1).

Круг — часть плоскости, которая ограниченна окружностью (рисунок 1).

Другое понятие круга.

Круг — это часть плоскости, которая лежит внутри окружности, вместе с самой окружностью (рисунок 1).

Рисунок 1

Радиус r — это любой отрезок, соединяющий центр окружности и точку окружности. На рисунке 2 это отрезок OC.

Также радиус от лат. называли спицу в колесе.

Рисунок 2

Хорда — это отрезок AB, соединяющий две точки окружности (рисунок 2).
Диаметр — это хорда BE, проходящая через цент окружности (рисунок 2).
Если на окружности взять две точки, то они разобьют окружность на две части (рисунок 2).

Каждая из этих кривых называется дугой окружности, а точки A и D — концы этих дуг.

Дуга обозначается как ∪ AD (рисунок 2).

Длина дуги окружности  ∪AB (рисунок 3) находится по формуле:


Рисунок 3

Сектор круга — это часть плоскости, ограниченная двумя радиусами и его дугой (рисунок 3).

Площадь сектора, формула:

Сегмент круга — это часть плоскости, ограниченная хордой и дугой (рисунок 3).

Площадь сектора окружности, формула:

Касательной называется прямая a, имеющая с окружностью только одну общую точку A (рисунок 5).

Формула для расчета длины окружности через радиус:

L=2πr

Формула для расчета длины окружности через диаметр:

L=2πd

Формула для определения площади круга через радиус:

S=πR2

Формула для определения площади круга через диаметр:

Рисунок 4

Центральный угол — это угол с вершиной в центре окружности.

Вписанный угол — это угол, вершина которого лежит на окружности, а стороны пересекают окружность.

Формула для определения длины хорды ∪ AB через радиус и центральный угол ∠BOA:

AB=2rsin α/2

Формула для определения длины хорды через радиус и вписанный угол ∠CED:

CD=2rsinα

Свойства касательной к окружности

Одно из свойств касательной к окружности (рисунок 5) заключается в том, что касательная a к окружности перпендикулярна ее радиусу OA. Из этого вытекает аналогичное свойство, т.е. касательная , проходящая через точку касания с окружностью, перпендикулярна диаметру.

OA⊥a

Рисунок 5

Рисунок 6

CA, CB – касательные
A, B – точки касания
CA = CB
В соответствии с рисунком 6, получаем свойство

∠1 = ∠2; ∠3 = ∠4

Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Свойства секущей окружности

Секущая окружности — это прямая BE, имеющая с окружностью две общие точки (рисунок 7).

В соответствии с рисунком 7, получаем свойство

BA2=BF⋅BD

BA2=BE⋅BC

где AB — касательная

BE, BF — секущие

Из этого свойства вытекает следующее свойство, произведения отрезков секущих, проведенных из одной точки равны:

BF⋅BD=BE⋅BC

Рисунок 7

Свойства окружности

  1. Диаметр окружности равен сумме двух радиусов, то есть

d =r+r=2·r

  1. Через три точки, не лежащих на одной прямой, можно построить только единственную окружность.
  2. Если взять все замкнутые кривые с одинаковой длиной, то окружность имеет максимальную величину площади.

  3. Кратчайшее расстояние от центра окружности к секущей или хорде всегда меньше величины радиуса.

  4. Если две окружности соприкасаются внешне или внутренне в одной точке, то точка касания и центры этих окружностей лежат на одной прямой.

Свойства углов окружности

На рисунке 8
∪ CB — дуга окружности
∠COB — центральный угол
∠CAB — вписанный угол
Получаем следующее тождество:

∠CAB = ∠COB/2

при этом длина  дуги окружности ∪ CB должна быть меньше длины полуокружности.

Рисунок 8

Вписанные углы, опирающиеся на одну и ту же дугу, равны (рисунок 9).

Рисунок 9

Вписанный угол, опирающийся на полуокружность – прямой (рисунок 10).

Рисунок 10

Свойство хорд окружности

Рисунок 11

AB; CD – хорды

E — точка пересечения хорд

AE · EB = CE · ED

Если две хорды окружности пересекаются, то произведение отрезков одной хорды AB равно произведению отрезков другой хорды

CD

Рисунок 12

Если хорда AB равна хорде DC, то их дуги тоже равны, т. е.

AB=DC ⇒ ∪AB=∪DC

Рисунок 13

Если хорда AB параллельна хорде DC, то их дуги равны, т.е.

AB//DC ⇒ ∪AB=∪DC

Рисунок 14

Если радиус окружности OD перпендикулярен хорде AB, то он делит хорду пополам в точке их пересечения С, т.е.

OD⊥AB ⇒ ∪AC=∪BC

Рисунок 15

Сумма двух вписанных углов, опирающих на одну хорду и находящихся по разные стороны от нее, равна 180°, т.е.

α + β = 180°

Рисунок 16

Задача 1

Хорды AB и CD пересекаются в точке E. Найдите ED, если AE = 5, BE = 2, CE = 2,5.

Решение

По свойствам хорды имеем

АЕ·ЕВ=СЕ·ЕD
5·2=2,5·ЕD
10=2,5·ЕD

Отсюда

ED=4

Задача 2

Хорда AB стягивает дугу, равную 119°, а хорда AC – дугу, равную 43°. Найдите угол BAC.

Решение

∠ВАС равен половине дуги на которую опирается
Дуга равна 3600-1190-430=1980

Угол BAC равен:

$\angle{BAC}=\frac{198}{2}=96$

Урок 3. Окружность в перспективе. Как нарисовать кружку и вазу

В этом уроке мы разберемся, как изображать объекты, в основе которых лежат окружности: чайник, вазу, бокал, кувшин, колонну, маяк.

Содержание:

  • Принципы рисования эллипсов
  • Рисуем эллипсы
  • Рисуем кружку
  • Рисуем вазу
  • Тест на рисование эллипсов

Ненадолго вернемся к коробкам из прошлого урока. Только теперь рассмотрим кубическую форму. Обратите внимание, как квадраты плоскостей, уходящих вдаль, сплющиваются. Верхние и нижние грани превращаются в трапеции. И тем сильнее они сужаются по вертикальной оси, чем ближе находятся к уровню глаз (к линии горизонта).

То же самое происходит и с окружностями. Чем дальше от линии горизонта они находятся, тем больше они открываются (обратите внимание на верхние и нижние плоскости этих спилов). А на уровне глаз окружность сужается до линии. Мы видим лишь переднюю грань предмета.

Принципы рисования эллипсов:

Принцип 1. У эллипса есть две оси симметрии: большая и малая. Они перпендикулярны. Здесь будем работать с наиболее частым случаем – когда предмет расположен прямо, то есть вертикальная ось (малая) находится под углом в 90°, а горизонтальная (большая) – под углом в 180°.

Принцип 2. У эллипса 4 вершины (они лежат на пересечении с осями). Эти точки в наибольшей степени удалены от центра. Форма эллипса выглядит искаженной, если соседние с вершинами точки смещены на тот же уровень (на эллипсе справа показано красным цветом).

Принцип 3. Другая крайность – это заострение боков эллипсов. Они должны быть скругленными. В бока можно вписать окружности. И чем больше раскрыт эллипс, тем больше диаметр этой окружности относительно высоты эллипса (на примере ниже это сравнение показано бледно-голубым цветом).

Принцип 4. Центр эллипса смещен вдаль (вверх) относительно геометрического центра из-за перспективного искажения. То есть ближняя половина эллипса больше дальней. Однако обратите внимание, что это смещение очень незначительно. Разберем, почему. Начнем с квадратов, поскольку круг вписывается в эту форму. Ниже показаны кубы, справа их верхние квадратные грани в перспективе. Проведены оси красным. Сравните, насколько их ближние половины больше дальних. Разница очень небольшая. То же самое будет и для эллипсов, вписанных в них. Ошибочно преувеличивать в рисунках эту разницу между ближней и дальней половинками эллипсов.

Рисуем эллипсы

Шаг 1. Для начала проведем две перпендикулярных оси.

Шаг 2. Отметим границы произвольного эллипса симметрично по горизонтальной оси. А для вертикальной верхнюю половину (дальнюю) сделаем чуть-чуть меньше нижней. 

Шаг 3. Нарисуем по этим отметкам прямоугольник, в который будем вписывать эллипс.

Шаг 4. Наметим легкие дуги в местах пересечения осей и прямоугольника.

Шаг 5. Соединим легкими линиями эти дуги, стараясь изобразить эллипс более симметрично.

Шаг 6. По обозначенному пути проведем более четкую линию. Смягчим ластиком лишнее. 

Более правильно было бы при рисовании эллипса вписывать его в квадратную плоскость в перспективе, то есть в трапецию. Однако, во-первых, сложно точно построить такую трапецию, зная лишь вершины эллипса. А во-вторых, овал, вписанный в квадрат в перспективе, мало отличается от вписанного в прямоугольник по тем же самым вершинам.

Рисуем кружку

Шаг 1. Начинаем с общих пропорций предмета. Измеряем, сколько раз ширина кружки (ее верха) умещается в высоте. Можно пока не учитывать ручку, однако надо оставить для нее достаточно места на листе. Намечаем общие габариты. Находим середину предмета по ширине и проводим через нее вертикальную ось. Чтобы нарисовать ее ровно, удобно сделать 2-3 вспомогательные отметки по высоте предмета на том же расстоянии от ближнего края листа, что и первая отметка середины предмета.

Шаг 2. Найдем высоту верхнего эллипса. Для этого измерим, сколько раз она умещается в его ширине (которую мы нашли ранее). Отметим нижнюю границу эллипса от верхнего края кружки. Легкими линиями нарисуем прямоугольник по намеченным крайним точкам.

Шаг 3. Проведем горизонтальную ось и впишем эллипс в прямоугольник. Затем найдем ширину нижней части кружки, сравнив ее с шириной верха. Высоту нижнего эллипса мы найдем, измерив расстояние по вертикали от самой нижней отметки кружки до нижней отметки ее бока (до точки, через которую пройдет горизонтальная ось этого эллипса). Найденное расстояние – это половина искомой высоты. Удвоим его и отложим от самой нижней точки кружки. Здесь важно не запутаться: в данном случае ось надо провести через нижнюю точку бока кружки, а не через низ самой кружки. Иначе пропорции нарушатся. Зная высоту нижнего эллипса, проверим, соблюдается ли принцип их постепенного раскрытия по мере удаления от уровня глаз. Верхний эллипс расположен ближе к уровню наших глаз, чем нижний, поэтому должен быть уже. Найдем, сколько раз высота нижнего овала помещается в его ширине – около четырех раз. Для верхнего овала было соотношение примерно 5 к 1. Таким образом нижний овал шире, то есть раскрыт в большей степени. Принцип соблюдается.

Шаг 4. Рисуем стенки кружки, соединяя боковые вершины верхнего и нижнего эллипсов. Для большей объемности покажем толщину стенки. Нарисуем второй овал внутри верхнего. При этом учитываем, что из-за перспективного искажения толщина стенок выглядит не одинаковой. Передняя и дальняя стенки визуально сужаются сильнее боковых примерно в два раза. Отметим вершины внутреннего овала на некотором расстоянии от вершин первого овала. Делаем этот отступ чуть больше для боковых вершин. Ставим отметки симметрично относительно вертикальной и горизонтальной осей. Нарисуем новый эллипс через эти вершины. 

Шаг 5. Найдем расположение ручки и ее общие пропорции, а затем схематично наметим основные отрезки, формирующие ее контур. Их наклоны определяем методом визирования (а где-то — на глаз).

Шаг 6. Уточним контур ручки, сделаем его более плавным. По необходимости подправим очертания кружки. Смягчим немного ластиком линии построения. Выделим более сильным нажимом на карандаш контуры, расположенные ближе к нам. Кружка готова!

Рисуем вазу

В этом упражнении поработаем с воображением. Придумаем свою вазу и потренируемся рисовать эллипсы.

В прошлом задании для построения кружки было достаточно нарисовать два эллипса. Две ключевые окружности (верхняя и нижняя) определяли ее форму. Диаметр кружки равномерно уменьшался от верха к низу. А, например, форма вазы из рисунка ниже зависит от четырех окружностей (причем верхняя находится на уровне глаз, поэтому превратилась в линию).

Перейдем к рисованию. И помним важный принцип: чем дальше эллипс от уровня глаз, тем более он раскрыт.

Шаг 1. Проведем вертикальную ось. От нее симметрично отложим горизонтальные оси будущих эллипсов. Длину вертикальной и горизонтальных осей, а также количество эллипсов и расстояние между ними выбирайте сами.

Шаг 2. Обозначим боковые вершины эллипсов симметрично относительно вертикальной оси. Теперь перейдем к обозначению верхних и нижних вершин. И здесь пользуемся принципом постепенного раскрытия эллипсов по мере удаления от линии горизонта. Например, здесь мы рисовали вазу, расположенную в целом ниже уровня глаз. Для первого эллипса взяли высоту, примерно в пять раз меньше ширины. Измеряли это карандашом. Для последующих эллипсов постепенно увеличивали степень раскрытия. Так высота среднего эллипса укладывается в ширине примерно четыре раза, а для самого нижнего – примерно три раза. Чем ближе друг к другу эллипсы, тем ближе они по степени раскрытия. Чем дальше – тем больше разница. Намечая вершины, нижнюю половинку (ближнюю) делаем чуть-чуть больше верхней (дальней).

Шаг 3. Через вершины легкими линиями рисуем прямоугольники. А затем вписываем в них эллипсы.

Шаг 4. Теперь самое интересное: надо соединить боковые вершины эллипсов линиями. Вам решать, какими они будут, прямыми или округлыми, вогнутыми или выпуклыми. Можно сделать пару вариантов. Постарайтесь наиболее симметрично повторить форму внешнего контура для двух половинок вазы. Чтобы проверить симметрию, пробуйте перевернуть работу вверх ногами. Взглянув на предмет по-новому, проще увидеть расхождения.

Шаг 5. Так же, как мы делали для кружки, здесь можно показать толщину стенки. Нарисуем внутри верхнего эллипса еще один поменьше, предварительно наметив его вершины. Смягчим ластиком оси и дальние половинки эллипсов. Можно чуть высветлить те эллипсы, в которых изменение формы вазы более плавное.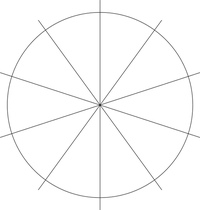 Рисунок готов!

Проверьте свои знания

Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.