Онлайн арктангенс числа: Арктангенс — калькулятор онлайн

Решение уравнений tgx=a. Понятие арктангенса числа

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Решение уравнений tgx=a. Понятие арктангенса числа.

Преподаватель математики СПб СВУ МО РФ
Лошак В.С.
АРКТАНГЕНС ЧИСЛА
m-ось тангенсов
tg
О
1
А
В
C
K
1
m
подобен ОВС
AК OC
AК BC
BC
OК
OК OC
OAК
AК sin
OК cos
OC 1
sin
BC
cos
BC tg
АРКТАНГЕНС ЧИСЛА
tg
1
О
В
равен ординате
Тангенс числа
точки пересечения оси тангенсов
и прямой, соединяющей точку,
на
изображающую число
единичной окружности, с началом
координат.
C
1
m
BC tg
m
0
tg

4. Уравнение tgx=a

a
tgx a, a R
1
arctga
0
1
m
x k , k Z.
x arctga k , k Z .

5. АРКТАНГЕНС ЧИСЛА

Определение. Арктангенсом числа a
называется такое число ; ,
2 2
тангенс которого равен a.
tg arctga a, a R
2
arctga
2
,

6. АРКТАНГЕНС ЧИСЛА

• Например
3
arctg
;
6
3
arctg 0 0;
arctg1 ;
4
т.к.
т.к.
т.к.
3
; tg
.
2 6 2
6
3
2
2
0
4
2
2
; tg 0 0.
; tg
4
1.
АРКТАНГЕНС ЧИСЛА
Основные формулы
tg arctga a, arctga ; , a R.
2 2
arctg a arctga
arctg tg , ;
2 2
1
cos arctga
2
1 a

8. АРКТАНГЕНС ЧИСЛА Основные формулы

1
а
arctga
1
arctg a arctga
0
-а
arctga
m

9. АРКТАНГЕНС ЧИСЛА Основные формулы

1
cos
2
1 tg
arctga ;
arctga
2 2
1
1
cos arctga
1 tg 2 (arctga)
1 a2

10.

АРКТАНГЕНС ЧИСЛА Основные формулы• Вычислите:
1
3
2arctg1 3arctg
2 3arctg
3
4
3
3 0
2
6 2 2
2 3
1
6 4
2. 6arctg 3 4 arcsin
3
4
2
3
3
3. 3arctg 2 arccos 3 2
6
6
3
2
1.
5
7
2
2
6
6

11. АРКТАНГЕНС ЧИСЛА Основные формулы

tg arctga a
• Например
5 5
4.
tg arctg 3 3
5. tg arctg
3 3
1
1
6. sin arctg
sin
3
6 2
1
1
1
7. cos arctg
26
2
5
1
25
1
5
5
26
5
25
26
26
26
1
cos arctga
1 a2

12. АРКТАНГЕНС ЧИСЛА Основные формулы

Вычислите:
2
5
7. cos 5 arctg 1 cos cos cos
4
2
4
4
1
1
1
3
8. ctg arctg
1
1
3 tg arctg
3
3
1
ctg
tg
1
1
2
tg
arctg
2
1
4
2
9. tg 2arctg
2
1
3
2 1 tg 2 arctg 1 1
4
2
tg 2
2tg
1 tg 2

13.

АРКТАНГЕНС ЧИСЛА Основные формулы• Вычислите:
10.
11.
arctg tg
7 7
arctg tg , ;
2 2
2
5
arctg tg arctg tg
7
7
2
2
2
arctg tg arctg tg
7
7
7

14. Уравнение tgx=a

a
tgx a, a R
1
arctga
0
1
arctga
m
x arctga k , k Z .

15. Уравнение tgx=a

• Пример 1.
3
tgx
3
3
x arctg
k
3
x k , k Z .
Пример 2.
tg 2 x 4
2 x arctg 4 k
1
k
x arctg 4 , k Z .
2
2
6
Ответ: k , k Z .
6
1
k
Ответ: 2 arctg 4 2 , k Z .

16. Уравнение tgx=a

• Пример 3.
tg 2 x 3;
4
2x
4
3
k ;
7
2 x k ;
12
Ответ:
3
ctg 2 x
4 3
2x
4
2x
arctg 3 k ;
3
4
k ;
7
k
x , k Z.
24
2
7
k
, k Z.
24
2

English     Русский Правила

Арксинус, арккосинус и арктангенс числа

Содержание статьи

1. Арксинус числа

2. Арккосинус числа

3. Арктангенс числа

4. Арккотангенс

Функции с приставкой arc — это функции, обратные тригонометрическим. Например, для функции $sinα$ обратной функцией является её арксинус, записывается как $arcsinα$, а для функции косинуса обратной будет функция арккосинус, записывается как $arccosα$. Проще говоря, обратные тригонометрическим функции с приставкой $arc$ являются множеством значений углов $α$, от которых берётся какая-либо обычная тригонометрическая функция, также иногда функции с приставкой $arc$ используют как меру длины дуги, ограничивающей угол $α$.

Рисунок 1. Единичная окружность. Автор24 — интернет-биржа студенческих работ

Рассмотрим теперь непосредственно определения для функций арксинус, арккосинус, арктангенс и арккотангенс по отдельности.

Арксинус числа

Определение 1

Арксинус числа $x$ — это множество значений углов, для которых $sinα = x$. Также определение арксинуса можно записать так: $arcsin(x) = α$.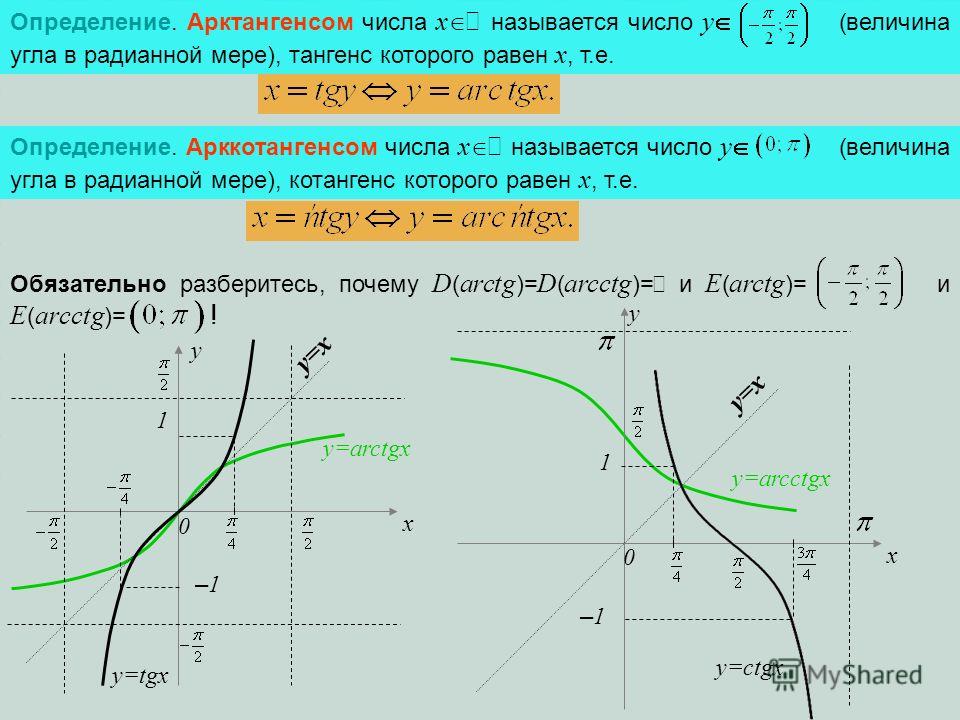

Рассмотрим рисунок 1, на котором изображена окружность с радиусом, равным единице. Как мы помним, $sinα$ — это отношение противолежащей стороны к гипотенузе, численно он равен длине стороны $AC$. Так как арксинус его обратная функция и есть не что иное как угол, от которого берётся синус, свойства арксинуса очень похожи на свойства синуса:

• Область определения функции арксинуса $D(y)= \ [-1;1\ ]$, для синуса $D(y)=\ [-\frac{π}{2};\frac{π}{2}\ ]$;
• Область значения для арксинуса $E = \ [-\frac{π}{2};\frac{π}{2}\ ]$, для синуса $E = \ [-1;1\ ]$
• Функции синуса и арксинуса обе возрастающие;
• Функции арксинуса и синуса обе нечётные, то есть: $arcsin(-x)= -arcsinx$;
• Функция $y=arcsin(x)$ равна нулю при $x=0$.

График арксинуса выглядит следующим образом:

Рисунок 2. График арксинуса. Автор24 — интернет-биржа студенческих работ

Арккосинус числа

Определение 2

Арккосинус числа $x$ — это множество значений углов, для которых $cosα = x$, то есть это значение угла.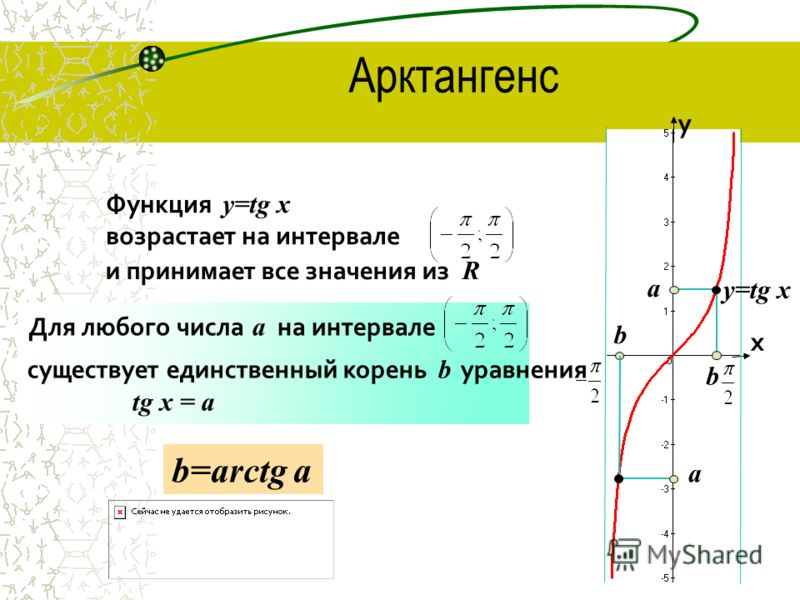

Свойства арккосинуса в сравнении с косинусом:

• Область определения функции арккосинуса $D(y)= \ [-1;1\ ]$, для косинуса $D(y)=\ [0; π\ ]$;
• Область значения для арккосинуса $E = \ [0; π\ ]$, для косинуса $E = \ [-1;1\ ]$;
• График функции арккосинуса симметричен относительно точки $(0; \frac{ π}{2})$, следовательно, он не является ни чётным, ни нечётным, в отличии от функции косинуса, которая является чётной;
• График функции арккосинуса $y= arccos(x)$ является убывающим, это происходит на всей его области определения, так же, как и c графиком косинуса.
• Функция $y=arccos(x)$ равна нулю при $x=1$.

Рисунок 3. График арккосинуса. Автор24 — интернет-биржа студенческих работ

Арктангенс числа

Определение 3

Арктангенс числа $x$ — это множество значений углов, для которых $tgα = x$.

Свойства арктангенса:

• $D(y)= \ [-\infty;1\ ]$;
• $E = \ [-\frac{π}{2};\frac{π}{2}\ ]$;
• Данная функция нечётная;
• Функция $y= arctgx$ возрастающая на всей области определения;
• Функция $y= arctgx$ равна нулю при $x=0$.

Рисунок 4. График арктангенса. Автор24 — интернет-биржа студенческих работ

Арккотангенс

Определение 4

Арккотангенс числа $x$ — это множество значений углов, для которых $ctgα = x$.

Свойства функции арккотангенса:

• $D(y)= \ [-\infty;1\ ]$;
• $E = \ [0; π\ ]$;
• Данная функция не является ни чётной, ни нечётной;
• Функция $y= arcсtgx$ убывает на всей области определения;

Рисунок 5. График арккотангенса. Автор24 — интернет-биржа студенческих работ

Пример 1

Найдите значение следующих выражений: $arcsin(\frac{1}{2}), arccos(-\frac{\sqrt{2}}{2}), arcctg(\frac{\sqrt{3}}{3}), arccos(-\frac{1}{2})$.

Решение:

$arcsin(\frac{1}{2}) = \frac{π}{6}$

$arccos(\frac{\sqrt{2}}{2}) = \frac{π}{4}$

$arcctg(\frac{\sqrt{3}}{3}) = \frac{π}{4}$

Здесь мы имеем арккосинус отрицательного числа $arccos(-\frac{-1}{2})$, для того чтобы его вычислить, необходимо прибегнуть к следующей формуле: $arccos(-α) = π – arccos(α)$

$arccos(-\frac{-1}{2}) = π – arccos(\frac{-1}{2}) = π – \frac{π}{3} = \frac{2π}{3}$

Сообщество экспертов Автор24

Автор этой статьи Дата последнего обновления статьи: 13.

02.2022

Шкала арктангенса. Это как логарифмическая шкала, но бесконечная

Это Words and Buttons Online  — коллекция интерактивных #учебников, #демонстраций и #викторин по #математике, #алгоритмам и #программированию.

И теперь, когда весь мир усвоил концепцию логарифмического масштаба и экспоненциального роста, пришло время узнать что-то еще лучшее.

Обычно мы не можем отображать такие числа, как 1, 1000 и 1 000 000, на одном и том же графике. Потому что, если мы хотим видеть 1 размером в один пиксель высотой, нам также придется поместить миллион пикселей на тот же экран. Технически мы можем это сделать, но сюжет станет слишком утомительным для прокрутки.

При экспоненциальном росте числа имеют тенденцию увеличиваться от 1 до миллиона значительно быстрее, но мы все же можем показать эти числа вместе, если поместим их в логарифмическую шкалу. Логарифм — это противоядие от экспоненциальной функции. Где y = a ^x , там x = log _a (y) .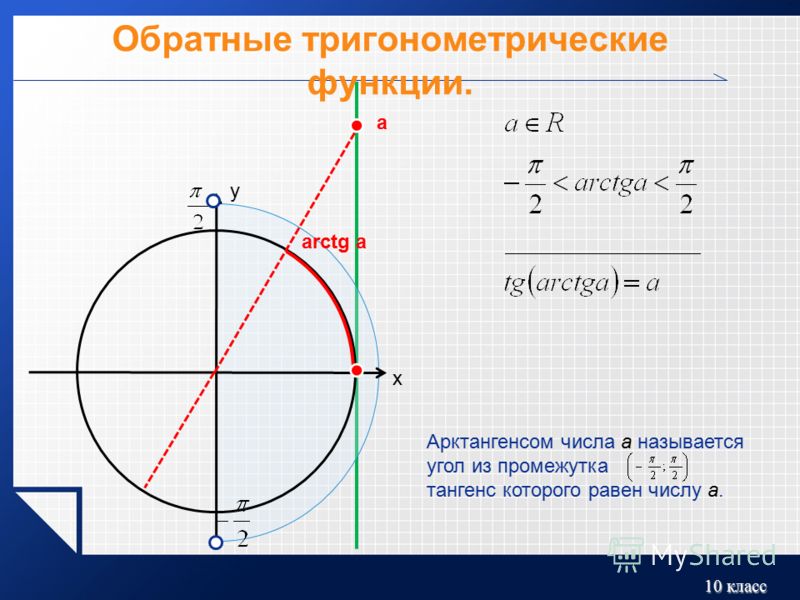

Десятичные логарифмы 1, 1000 и 1 000 000 (которые совпадают с 10 ⁰ , 10 ³ и 10 ⁶ ) равны только 0, 3 и 6. Мы можем показать их все на тот же сюжет легко.

Но что, если процесс не экспоненциальный? Что это, что-то другое, что-то совершенно неузнаваемое? Что, если числа, которые мы хотим увидеть, варьируются от 1 до 10 ^{1 000 000} ? Тогда это та же проблема с прокруткой.

Для чего-то другого, кроме экспоненциальной функции, нам нужна другая шкала. Давайте возьмем за основу эту шкалу арктангенса и посмотрим, хороша ли она.

Тангенс и арктангенс

Касательная функция непрерывна от -½Π до +½Π .

Она идет к -∞ , когда приближается к -½Π справа, и плавно растет к +∞ , когда приближается к +½Π .

Он ведет себя как y = x в 0 .

Конечно, это тоже периодично, но это не важно в данный момент.

Для наших целей он действует как транслятор из диапазона (-½Π, +½Π) в бесконечное пространство (-∞, +∞) действительных чисел.

Функция арктангенса обратна тангенсу. Он переводит любое действительное число из (-∞, +∞) обратно в диапазон (-½Π, +½Π) .

Используя арктангенс в качестве масштаба, мы можем отобразить любую функцию на экране. И не просто фрагмент, а вся функция.

Пример сюжета

Это функциональный плоттер, который может выполнять как линейную, так и арктангенциальную шкалу. Все кликабельно-перетаскиваемо, есть даже ярлык для масштаба на Shift+колесико мыши.

Не стесняйтесь попробовать свои собственные функции. Плоттер принимает строки кода JavaScript, каждая из которых оценивается как f(x) .

Шкала:
Линейная
Арктагенная

F(x) :
exp(x — 1) — 4 х*х*х — квт(2.)*х -exp(-x — 1) + 4

х : и : множитель:

Конечно, мы не можем обмануть математику. напр. этот график имеет только 409600 пикселей, что означает, что мы не можем отобразить на нем более 1,2 МБ информации. Информация, необходимая для отображения каждой точки графика функции от -∞ до ∞, безусловно, бесконечна. Так что нам приходится жить с ошибкой репрезентации. Тем не менее, шкала арктангенса позволяет вам выбрать, где и когда вы хотите, чтобы эта ошибка проявлялась.

Это делает его полезным инструментом для изучения функций, их пределов, систем уравнений и т. д.

П. С.

Код этой страницы, включая плоттер, доступен на GitHub.

ATan—Справка | ArcGIS for Desktop

Доступно с лицензией Spatial Analyst.

• Сводка
• Иллюстрация
• Использование
• Синтаксис
• Пример кода
• Среды
• Информация о лицензировании

Сводка

Вычисляет арктангенс ячеек растра.

Иллюстрация

OutRas = ATan(InRas)

Использование

• В математике все тригонометрические функции имеют определенный диапазон допустимых входных значений, называемый доменом. Выходные значения каждой функции также имеют определенный диапазон. Для этого инструмента

  Обратите внимание, что здесь -∞ и ∞ представляют наименьшее отрицательное и наибольшее положительное значение, поддерживаемое конкретным растровым форматом, соответственно.

• Входные значения для этого инструмента интерпретируются как безразмерные.

• Выходные значения всегда являются значениями с плавающей запятой, независимо от типа входных данных.

• Выходные значения этого инструмента в радианах. Если требуются градусы, результирующий растр необходимо умножить на коэффициент преобразования радиан в градусы, равный 180/pi, или примерно 57,296.

  Для дополнительной помощи доступны процедура и несколько примеров преобразования вывода в радианах в градусы.

• Дополнительные сведения о средах геообработки, применимых к этому инструменту, см. в разделах Среды анализа и Spatial Analyst.

Syntax

 ATan (in_raster_or_constant) 

Parameter	Explanation	Data Type
in_raster_or_constant	The input for which to calculate the inverse tangent values. Чтобы использовать число в качестве входных данных для этого параметра, размер и экстент ячейки должны быть сначала установлены в среде.	Растровый слой | Константа

Возвращаемое значение

Значения представляют собой арктангенс входных значений.

Имя	Объяснение	Тип данных
Out_1 растр	Растр

Пример кода

ATan, пример 1 (окно Python)

В этом примере вычисляется арктангенс значений входного растра Grid.

 импорт аркпи
из окружения импорта arcpy
импорт из arcpy.sa *
env.workspace = "C:/sapyexamples/данные"
outATan = ATan ("градусы")
outATan.save("C:/sapyexamples/output/outatan")
 

AТан, пример 2 (автономный скрипт)

В этом примере вычисляется арктангенс значений входного растра Grid и выводится растр TIFF.

 # Имя: ATan_Ex_02. 
No related posts.