Онлайн калькулятор координаты вектора: Онлайн калькулятор. Координаты вектора по двум точкам

Содержание

Смешанное произведение векторов. Онлайн калькулятор

Данный онлайн калькулятор вычисляет смешанное произведение векторов. Дается подробное решение. Для вычисления смешанного произведения векторов выберите способ представления векторов (по координатам или по двум точкам) введите данные в ячейки и нажимайте на кнопку «Вычислить.»

Очистить все ячейки?

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Смешанное произведение векторов (теория)

Смешанное произведение трех векторов это число, которое получается при скалярном произведении результата векторного произведения первых двух векторов на третьий вектор. Другими словами, если заданы три вектора a, b и c, то для получения смешанного произведения этих векторов, сначала векторно умножаются первые два вектора и полученный вектор [ab] скалярно умножается на вектор c.

Смешанное произведение трех векторов a, b и c обозначается так: abc или так (a,b,c). Тогда можно записать:

abc=([ab],c)

Прежде чем сформулировать теорему, представляющую геометрический смысл смешанного произведения, ознакомьтесь с понятиями правая тройка, левая тройка, правая система координат, левая система координат (определения 2, 2′ и 3 на странице векторное произведение векторов онлайн).

Для определенности, в дальнейшем мы будем рассматривать только правые системы координат.

Теорема 1. Смешанное произведение векторов ([ab],c) равно объему параллелипеда, построенного на приведенных к общему началу векторах a, b, c, взятому со знаком плюс, если тройка a, b, c правая, и со знаком минус, если тройка a, b, c левая. Если векторы a, b, c компланарны, то ([ab],c) равно нулю.

Следствие 1. Имеет место следующее равенство:

([ab],c)=(a,[bc]).

(1)

Для доказательства следствия заметим, что из переместительного свойства скалярного произведения имеем:

(a,[bc])= ([bc],a).

(2)

Следовательно нам достаточно доказать, что

([ab],c)=([bc],a)

(3)

Из выражения (3) видно, что левая и правая часть равны объему параллелипеда. Но и знаки правой и левой частей совпадают, так как тройки векторов abc и bca имеют одинаковую ориентацию.

Доказанное равенство (1) позволяет записать смешанное произведение трех векторов a, b, c просто в виде abc, не указывая, какие именно два вектора перемножаются векторно первые два или последние два.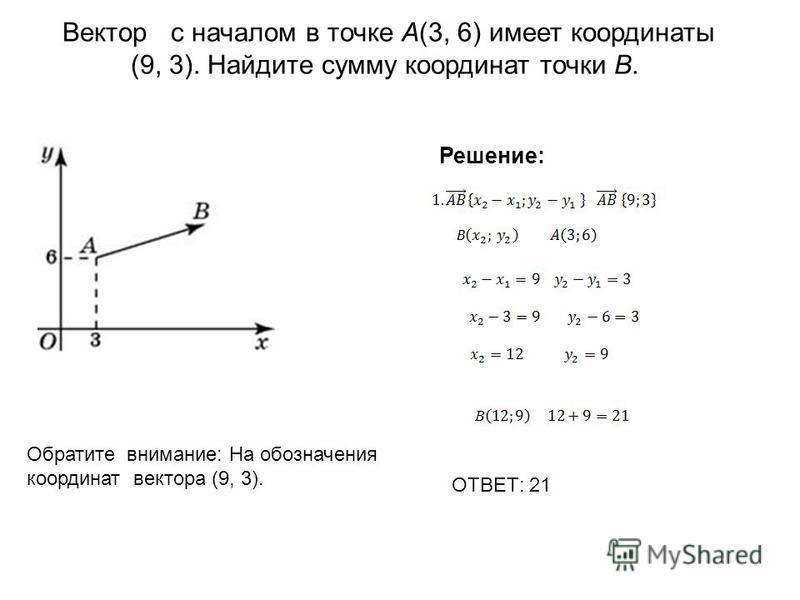

Следствие 2. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.

Доказательство вытекает из теоремы 1. Действительно, если векторы компланарны, то смешанное произведение этих векторов равно нулю. Обратное, если смешанное произведение равно нулю, то из теоремы 1 вытекает компланарность этих векторов (так как объем параллелипеда, построенного на приведенных к общему началу векторах равно нулю).

Следствие 3. Смешанное произведение трех векторов, два из которых совпадают, равно нулю.

Действительно. Если два вектора из трех совпадают, то они компланарны. Следовательно, смешанное произведение этих векторов равно нулю.

Смешанное произведение векторов в декартовых координатах

Теорема 2. Пусть три вектора a, b и c определены своими декартовыми прямоугольными координатами

a={x₁, y₁, z₁}, b={x₂, y₂, z₂}, c={x₃, y₃, z₃}.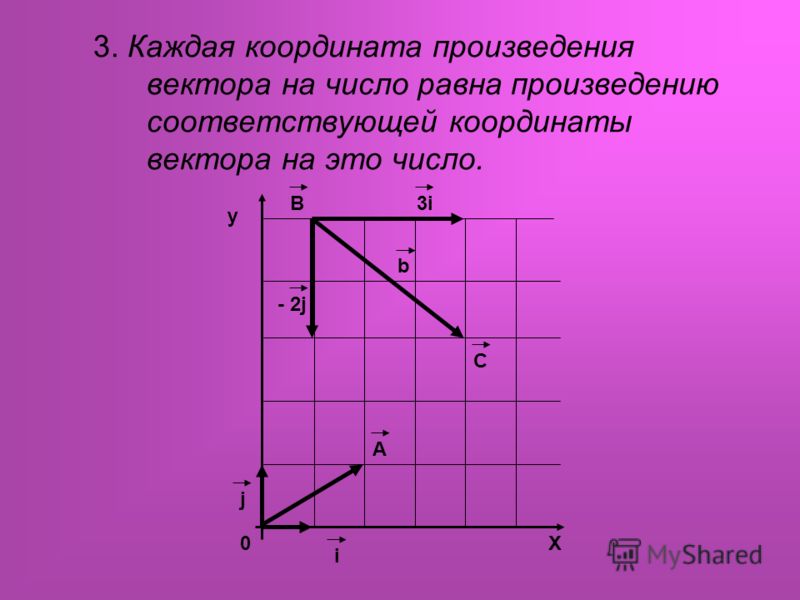

Тогда смешанное произведение abc равняется определителю, строки которого соответственно равны координатам перемножаемых векторов:

Доказательство. Смешанное произведение

abc равно скалярному произведению векторов [ab] и c. Векторное произведение векторов [ab] в декартовых координатах вычисляется формулой (подробнее смотрите на странице векторное произведение векторов онлайн):

[ab]={y₁z₂—y₂z₁, z₁x₂−z₂x₁, x₁y₂−x₂y₁}.

Тогда скалярное произведение векторов [ab] и c можно записать так:

abc=([ab],c)=x₃(y₁z₂—y₂z₁)+ y₃(z₁x₂−z₂x₁)+ z₃(x₁y₂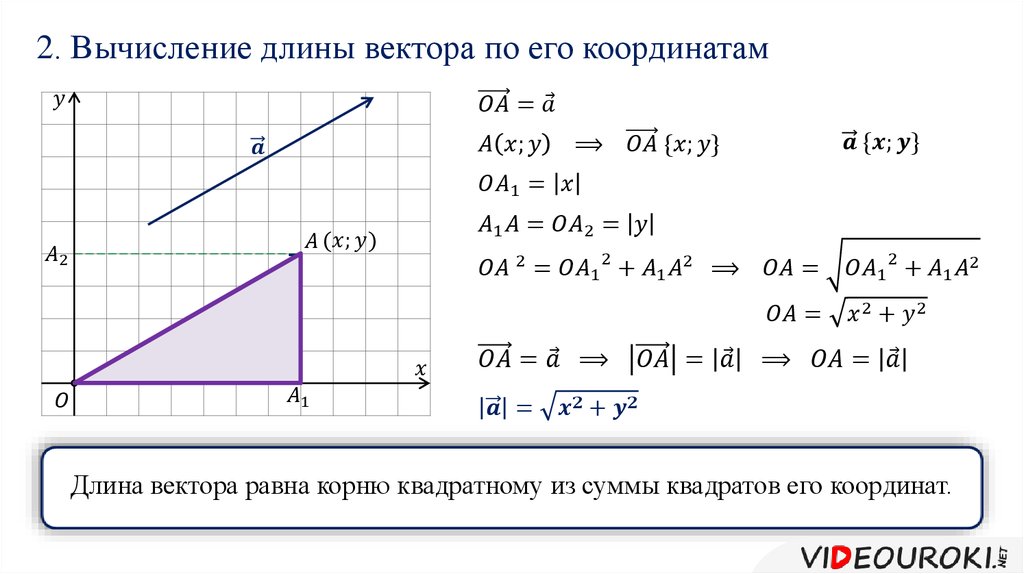 −x₂y₁).

(5)

Последнее выражение можно записать, используя определители второго порядка:

Формулы (6) и (4) эквивалентны, так как (6) является разложением определителя (4) по третьей строке.

Теорема доказана.

Следствие 3. Для компланарности трех векторов

a={x₁, y₁, z₁}, b={x₂, y₂, z₂}, c={x₃, y₃, z₃}.

необходимо и достаточно равенство нулю определителя, строки которой заполнены координатами этих векторов, т.е:

Для доказательства следствия достаточно рассмотреть формулу (4) и следствие 2.

Смешанное произведение векторов на примерах

Пример 1. Найти смешанное произведение векторов abс, где

Решение.

Для вычисления смешанного произведения векторов a, b, c составим матрицу, строки которой образуются векторами a, b, c:

Смешанное произведение векторов a, b, c равен определителю матрицы L. Вычислим определитель матрицы L, разложив определитель по строке 1:

Ответ.

Смешанное произведение векторов a, b, c равен :

abc=−58.

Пример 2. Найти смешанное произведение векторов abс, где

Начальная точка вектора a:

Конечная точка вектора a:

Вектор b:

Начальная точка вектора c:

Конечная точка вектора c:

Решение.

Переместим вектор a на начало координат. Для этого вычтем из соответствующих координат конечной точки

B координаты начальной точки A:

Переместим вектор c на начало координат. Для этого вычтем из соответствующих координат конечной точки F координаты начальной точки E:

Ответ.

Смешанное произведение векторов a, b, c равен :

abc=76.

Wolfram|Альфа-примеры: векторный анализ

Ого! Wolfram|Alpha не работает без JavaScript.

Пожалуйста, включите JavaScript. Если вы не знаете, как это сделать, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram|Alpha.

Примеры для

Векторный анализ — это изучение вычислений над векторными полями. Такие операторы, как дивергенция, градиент и завиток, можно использовать для анализа поведения скалярных и векторных многомерных функций. Wolfram|Alpha может вычислять эти операторы наряду с другими, такими как лапласиан, якобиан и гессиан. 92лапласианский калькулятор

Векторный анализ тождеств

Исследуйте тождества, включающие векторные функции и операторы, такие как div, grad и curl.

Рассчитайте альтернативные формы выражения векторного анализа:

Div (Grad F) Curl (Curl F) Grad (f. G)

GO Далее

Multivaible Calculus Web App

Связанные примеры

Деривавы

Интеграл

. Преобразования

Пределы

Матрицы

Векторы 92/п) с.р.т. r, t, and p

Pro
Web Apps
Mobile Apps
Products
Business
API & Developer Solutions

Resources & Tools
About
Contact
Connect

Язык Wolfram Language
Mathematica
Демонстрации Wolfram
Wolfram for Education
MathWorld

Калькулятор единичных векторов.

{2}}\ ) 9{2}}}\hat{k}\)

Однако онлайн-калькулятор единичного тангенциального вектора поможет вам найти тангенс-вектор векторной функции-значения в заданных точках.

Вывод формулы единичного вектора:

$ \hat {v} $ = единичный вектор с одной величиной и направлением
$ \vec {v} $ = вектор с любым направлением и величиной
$ \mid\vec {v} \mid$ = величина вектора $ \vec{v} $
x = вектор по оси x
y = вектор по оси y
z = вектор по оси z
$ \hat{i} $ = единичный вектор для оси x
$ \hat{j} $ = единичный вектор для оси y
$ \hat{k} $ = единичный вектор для оси z

Как найти единичный вектор?

Для мгновенных расчетов вам просто нужно добавить значения компонентов в калькулятор величины и направления, и он сделает все за считанные секунды. И даже вы можете выполнять вычисления вручную с помощью этих простых шагов:

Пример:

Найдите единичный вектор вектора u = (8, -3, 5) в том же направлении. 92)} $$
$$ |u| = \sqrt{(64 + 9 + 25)} $$
$$ |u| = \sqrt{(98)} $$
$$ |u| = 9,9 $$

В случае, если вас беспокоит величина какого-либо вектора, воспользуйтесь нашим удобным калькулятором единичных векторов для точного определения величины. Итак, величина вектора u равна 9,9. Теперь разделите каждую компоненту вектора на | у |.
а_2 = а_1 / | ты | = 8 / 9,9 = 0,8081

b_2 = b_1 / | ты | = -3 / 9,9 = -0,3031

c_2 = c_1 / | ты | = 5 / 9,9 = 0,5051

Теперь запишите все полученные значения в векторной форме как:
$$ u = (0,8081, -0,3031, 0,5051) $$

Наконец, возьмите сумму всех этих значений. Если величина равна 1, то результат правильный.

Однако онлайн-калькулятор производной по направлению определяет производную по направлению и градиент функции в заданной точке вектора.

Пример 1:

Вычислить единичный вектор вектора v = {3, 4} в двумерном пространстве.

Решение:

Заданные значения:

x = 3
y = 4

Величина вектора:

$$ \vec{v} = 5 $$
Калькулятор направления вектора находит направление, используя значения координат x и y. Таким образом, угол направления θ равен:
$$ θ = 53,1301 градус $$
Единичный вектор вычисляется путем деления каждой координаты вектора на величину.
Таким образом, единичный вектор:

$$ \vec{e} \) = (3/5, 4/5 $$
$$ \vec{e} \) = (0,6, 0,8) $$

Пример 2:

Найдите недостающую компоненту единичного вектора z в трехмерном пространстве, где x равно 0,9sinØ

Как работает калькулятор единичных векторов?

Онлайн-калькулятор единичного нормального вектора определяет единичный вектор в направлении введенных векторов, выполнив следующие шаги:

Ввод:

Сначала выберите метод и размеры вектора из раскрывающегося списка.
При выборе из списка размеров 2D или 3D калькулятор показывает разные диаграммы для обоих вариантов.

Затем подставьте все соответствующие значения в поля.
Нажмите кнопку «Вычислить единичный вектор».

Вывод:

Калькулятор вектора нормалей вычисляет модуль вектора, угловое направление и единичный вектор.

Часто задаваемые вопросы:

Есть ли у единичного вектора единицы измерения?

Нет, у единичного вектора нет ни единиц, ни размеров, у него есть только направления.

Что такое полярный вектор?

Вектор, который имеет либо точку приложения, либо начальную точку, определяется как полярный вектор. Скорость — лучший пример полярного вектора.

Какова величина нулевого вектора?

Нулевой вектор — это нулевой вектор с нулевыми величинами. Скорость стационарных объектов является примером нулевого вектора.

Когда два вектора равны?

Два вектора равны, если они представляют одинаковую величину и направление.

Всегда ли единичные векторы перпендикулярны?

Нет, единичные векторы не всегда перпендикулярны. Эти векторы всегда касательны и параллельны исходному вектору.

Заключение:

Онлайн-калькулятор единичных векторов вычисляет единичный вектор, величину и угол вектора из другого вектора.