Как исследовать на непрерывность функцию примеры: определение, классификация, алгоритм исследования функции на непрерывность, примеры

Ошибка

Перейти к основному содержанию

Вся размещенная на ресурсе информационная продукция предназначена для детей, достигших возраста шестнадцати лет (16+)

Извините, не удалось найти запрашиваемый Вами файл

Подробнее об этой ошибке

Перейти на… Перейти на…Новостной форумКомплексные числа (с приложениями к задачам электротехники)Лекционный материал по теме «Комплексные числа»Разбор типовых задач задач по теме «Комплексные числа»Примеры решения задач по теме «Комплексные числа»КОМПЛЕКСНЫЕ ЧИСЛАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийТеория функций комплексного переменного. Операционное исчислениеПрезентация по теме «Комплексные числа»Дополнительный материал к темеОсновы линейной алгебры с приложениями в других разделах математикиЛекционный материал по теме «Матрицы. Определители»Лекционный материал по теме «Системы линейных алгебраических уравнений (СЛАУ).

Применение СЛАУ в экономике»Лекционный материал по теме «Линейные операторы»Примеры решения по теме «Системы линейных алгебраических уравнений»ЛИНЕЙНАЯ АЛГЕБРАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийЛинейная алгебра для экономистовМатрицы. ОпределителиВекторная алгебра.Аналитическая геометрияЛекционный материал по теме «Векторная алгебра. Линейные операции над векторами»Лекционный материал по теме «Скалярное, векторное и смешанное произведения векторов»Примеры решения задач по теме «Векторная алгебра. Линейные операции над векторами»Примеры решения задач по теме «Скалярное, векторное и смешанное произведения векторов»ВЕКТОРНАЯ АЛГЕБРАВекторная алгебра и аналитическая геометрияПрезентация по теме «Векторная алгебра»Векторная алгебра.Аналитическая геометрияТеоретический материал по теме «Метод координат на плоскости и в пространстве»Лекционный материал по теме «Прямая на плоскости»Лекционный материал по теме «Кривые второго порядка»Лекционный материал по теме «Прямая в пространстве»Лекционный материал по теме «Плоскость в пространстве»Лекционный материал по теме «Поверхности второго порядка»Примеры решения задач по теме «Прямая на плоскости»Примеры решения задач по теме «Кривые второго порядка»Примеры решения задач по темам «Прямая и плоскость в пространстве»АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯВекторная алгебра и аналитическая геометрияСправочный материал «Прямая на плоскости»Справочный материал «Кривые второго порядка»Справочный материал «Прямая и плоскость в пространстве»Линейная алгебра для экономистовПрезентация по теме «Прямая на плоскости»Презентация по теме «Уравнения плоскости и прямой в пространстве»▶ Виртуальный тренажер «Прямая на плоскости» 👨‍🎓Введение в анализНачала анализаЛекционный материал по теме «Множества, функции, основные характеристики функций. Основные элементарные функции»Лекционный материал по теме «Предел функции, основные теоремы о пределах.Замечательные пределы. Бесконечно малые функции»Лекционный материал по теме «Непрерывность функции»Примеры решения задач по теме «Множества, функции, основные характеристики функций. Основные элементарные функции»Примеры решения задач по теме «Предел функции. Раскрытие математических неопределенностей»ВВЕДЕНИЕ В АНАЛИЗУпражнения для самостоятельного решения Тест «Введение в анализ»Презентация по теме «Введение в анализ»1. Понятие функцииПрименение функций в экономической теории и практикеПрименение пределов в экономических расчетахПриложение понятия непрерывности функций в экономике▶ Виртуальная справочная «Тригонометрические функции» 👨‍🎓Дифференциальное исчисление функций одной переменнойПриложения дифференциального исчисления функции одной переменнойЛекционный материал по теме «Дифференциальное исчисление функции одной переменной»Лекционный материал по теме «Основные теоремы дифференциального исчисления. Правила Лопиталя»Лекционный материал по теме «Формулы Тейлора и Маклорена»Лекционный материал по теме «Приложения дифференциального исчисления»Примеры решения задач по теме «Дифференциальное исчисление функций одной переменной»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙТест «Основные правила и формулы дифференцирования»Тест «Дифференциальное исчисление функций одной переменной»Основы дифференцирования. Часть 1Основы дифференцирования. Часть 2Основы дифференцирования. Часть 3Приложения производной Исследование функций, Примеры решения задачПрименение производных при решении экономических задачИнтегральное исчисление функции одной переменнойЛекционный материал по теме «Неопределенный интеграл»Лекционный материал по теме «Определенный интеграл»Практическое занятие 1. Непосредственное интегрирование (неопределённый интеграл)Практическое занятие 2. Интегрирование заменой переменной (неопределённый интеграл)Практическое занятие 3. Интегрирование по частям. Интегрирование выражений, содержащих квадратный многочлен (неопределённый интеграл)Практическое занятие 4. Интегрирование рациональных дробей (неопределенный интеграл)Практическое занятие 5. Определенный интегралПримеры решения задач по теме «Неопределенный интеграл»Примеры решения задач по теме «Определенный интеграл»ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙТест «Таблица основных неопределенных интегралов»Тест «Интегрирование функций одной переменной»1. Неопределенный интеграл. Основы интегрирования2. Интегрирование иррациональных выражений 3. Интегрирование тригонометрических выражений 4. Определенный интегралДифференциальное исчисление функций нескольких переменныхЛекционный материал по теме «Функции нескольких переменных»Примеры решения задач по теме «Функции нескольких переменных»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХТест «Дифференциальное исчисление функций нескольких переменных»1. Функции нескольких переменныхПрименение функций нескольких переменных в экономикеОбыкновенные дифференциальные уравненияОбыкновенные дифференциальные уравнения и их приложенияДифференциальные уравнения первого порядкаДифференциальные уравнения высших порядковСистемы дифференциальных уравнений и устойчивость их решенийЛекционный материал по теме «Дифференциальные уравнения 1-го порядка»Лекционный материал по теме «Дифференциальные уравнения высших порядков»Примеры решения задач по теме «Дифференциальные уравнения»ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯТест «Обыкновенные дифференциальные уравнения»1. Дифференциальные уравнения 1-го порядка2. Дифференциальные уравнения высших порядковСпециальные разделы высшей математикиСпециальные разделы высшей математики: практикум Кратные, криволинейные и поверхностные интегралы. Элементы теории поляПоверхностные интегралы. Векторный анализЛекционный материал по теме «Двойные интегралы»Примеры решения задач по теме «Двойные интегралы»КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ2. Двойные интегралыРядыЛекционный материал по теме «Числовые ряды»Лекционный материал по теме «Функциональные ряды»Примеры решения задач по теме «Ряды»1. Числовые ряды2. Функциональные ряды3. Разложение функций в степенные рядыТеория функций комплексного переменного. Операционное исчисление.Основы теории функций комплексного переменногоОперационное исчисление.Теория функций комплексного переменного. Операционное исчислениеТеория вероятностей Теория вероятностей (случайные события)Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы: практикумЛекционный материал по теме «Основные подходы к определению вероятности»Лекционный материал по теме «Алгебра событий. Основные теоремы о вероятности»Лекционный материал по теме «Дискретные случайные величины»Лекционный материал по теме «Непрерывные случайные величины»Лекционный материал по теме «Числовые характеристики случайных величин»Лекционный материал по теме «Моменты и другие характеристики распределений»Лекционный материал по теме «Нормальное распределение»Практическое занятие 1. КомбинаторикаПрактическое занятие 2. Действия над событиями. Вероятность событияПрактическое занятие 3. Теоремы умножения и сложения вероятностей событийПрактическое занятие 4. Формула полной вероятности Практическое занятие 5. Схема Бернулли. Локальная и интегральная теоремы ЛапласаПрактическое занятие 6. Дискретные случайные величины. Числовые характеристикиПрактическое занятие 7. Непрерывные случайные величины. Классические законы распределения НСВПримеры решения задач по теме «Комбинаторика»Примеры решения задач по теме «Классическое определение вероятности»Примеры решения задач по теме «Теоремы сложения и умножения»Примеры решения задач по теме «Формула полной вероятности. Формулы Байеса»Примеры решения задач по теме «Схема независимых испытаний Бернулли»Примеры решения задач по теме «Дискретные случайные величины»Примеры решения задач по теме «Основные числовые характеристики дискретных случайных величин»Примеры решения задач по теме «Непрерывные случайные величины»Примеры решения задач по теме «Основные числовые характеристики непрерывных случайных величин»Примеры решения задач по теме «Классические законы распределения дискретных случайных величин»Примеры решения задач по теме «Классические законы распределения непрерывных случайных величин»Таблица значений функции ЛапласаТЕОРИЯ ВЕРОЯТНОСТЕЙТест по разделу «Случайные события»Тест по теме «Числовые характеристики случайных величин»Тест по теме «Дискретные случайные величины»Тест по теме «Непрерывные случайные величины»Основные подходы к определению вероятностиАлгебра событий. Основные теоремы о вероятностиТеория вероятностей (Лыткина Е.М.,Чихачев А.С., 2013)Математическая статистикаОсновы математической статистикиМатематическая статистика: практикумПримеры решения задач по математической статистикиМАТЕМАТИЧЕСКАЯ СТАТИСТИКАТест по разделу «Математическая статистика». Тема «Статистическое распределение. Точечные и интервальные оценки параметров распределения»Тест по разделу «Математическая статистика». Тема «Статистические гипотезы. Корреляционный и регрессионный анализ»Вероятность, случайные процессы, математическая статистикаСтатистический метод и основы его примененияВероятностно-статистические методы на примере задач исследования работы железнодорожного транспорта Марковские процессы и СМО. Учебное пособиеЛекционный материал по теме «Марковский процесс с дискретным временем»Лекционный материал по теме «Марковский процесс с непрерывным временем»Лекционный материал по теме «Системы массового обслуживания»Примеры решения задач по теме «Марковские процессы»СЛУЧАЙНЫЕ ПРОЦЕССЫЛабораторные работы Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы. ПрактикумЛекция «Марковские процессы»Цепи МарковаСистемы массового обслуживания (СМО)СМОВыбор группы*Тест «Таблица основных неопределенных интегралов»*Тест «Интегрирование функций одной переменной»*Тест «Дифференциальное исчисление функций нескольких переменных»*Тест «Обыкновенные дифференциальные уравнения»*Тест по разделу «Случайные события»*Тест по теме «Дискретные случайные величины»*Тест по теме «Непрерывные случайные величины»*Тест по теме «Числовые характеристики случайных величин»*Тест «Введение в анализ»*Тест «Основные правила и формулы дифференцирования»*Тест «Дифференциальное исчисление функций одной переменной»*Экзаменационный тест «Таблица основных неопределенных интегралов»*Экзаменационный тест «Интегрирование функций одной переменной»*Экзаменационный тест «Дифференциальное исчисление функций нескольких переменных»*Экзаменационный тест «Обыкновенные дифференциальные уравнения»Контрольная работа. Дифференциальное исчисление функций нескольких переменныхКонтрольная работа. Неопределенный интеграл (методы интегрирования)Контрольная работа. Неопределенный интеграл (интегрирование рациональных дробей)Контрольная работа. Определенный интегралКонтрольная работа. Обыкновенные дифференциальные уравненияКонтрольная работа 1. Теория вероятностей (случайные события)Контрольная работа 2. Теория вероятностей (характеристики дискретной случайной величины)Контрольная работа 3. Теория вероятностей (характеристики непрерывной случайной величины)Контрольная работа 4. Теория вероятностей (классические законы распределения дискретной случайной величины)Контрольная работа 5. Теория вероятностей (классические законы распределения непрерывной случайной величины)Экзамен Математика (2 семестр). СОД.1,2,3-19-1 (И,З)ЭКЗАМЕН. Математика (3 семестр)_СОД.1,2,3-19 (з)

6.4. Исследование функции на непрерывность

В задании требуется найти все точки разрыва функции (если они есть), указать их тип и построить эскиз графика функции в окрестности каждой из этих точек. Кроме примеров данного раздела см. также примеры 3.1-3.7.

Пример 6.27. Исследовать на непрерывность функцию .

Решение. Заданная элементарная функция определена на множестве , таким образом, она заведомо непрерывна во всех точках этого множества, а ее точкой разрыва является .

Поскольку ; , то в точке заданная функция имеет разрыв 2-го рода (бесконечный разрыв). Эскиз графика в окрестности точки представлен на рис. 6.8.

П ример 6.28. Исследовать на непрерывность функцию .

Решение. Область определения заданной элементарной функции представляет собой множество , а значит, она непрерывна во всех точках этого множества и имеет точку разрыва . Выполняются равенства: , но при этом не существует, поэтому в точке заданная функция имеет разрыв 1-го рода, причем устранимый (эскиз графика в окрестности точки изображен на рис. 6.9).

З аметим, что если доопределить заданную функцию в точке , приняв , то соответствующая новая функция будет непрерывной всюду на числовой оси.

Пример 6.29. Исследовать на непрерывность .

Решение. Согласно определению модуля, получим если и если , поэтому заданную функцию можно записать так:

в точке же не определена.

При является непрерывной, т.к. – непрерывная функция, при также непрерывна.

Х арактер разрыва в точке установим, вычислив, соответствующий правый и левый пределы:

,

.

Оба они существуют (при этом различны), поэтому в точке имеет разрыв 1-го рода, не являющийся устранимым. Эскиз графика в окрестности точки разрыва изображен на рис. 6.10.

Пример 6.30. Исследовать на непрерывность .

Решение. Заданная элементарная функция определена на числовой прямой всюду, кроме точек, в которых ее знаменатель обращается в ноль, т.е. , , . Таким образом, точками разрыва заведомо являются …

Установим характер разрыва при . Поскольку при , то , т. е. — точка разрыва первого рода, причем устранимого.

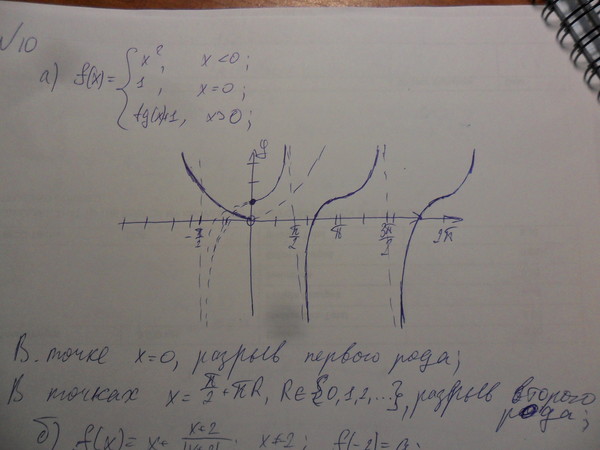
Установим характер разрыва при , … Поскольку , причем для , то

, .

Итак, имеет бесконечное множество точек разрыва 2-го рода , … и одну точку устранимого разрыва 1-го рода ; эскиз графика в окрестностях этих точек изображен на рис. 6.11

П ример 6.31. Исследовать на непрерывность

Решение. Функция определена на всей числовой прямой, причем она заведомо непрерывна в любой точке . Посмотрим, есть ли разрыв в точке .

,

.

Здесь учтено, что при , т.е. при . По условию задачи , поэтому можно записать, что и, следовательно, непрерывна в точке (а, значит, и на всей числовой оси).

Кроме примеров данного раздела см. также примеры 4.4, 4.6 – 4.9.

Пример 6.32. Найти первую и вторую производные функции .

Решение. Заметим, что данная функция является сложной, причем можно записать: . Далее, используя известное свойство логарифма, преобразуем функцию к виду , после чего, согласно правилу дифференцирования сложной функции, получим:

.

Следует заметить, что если не использовать вышеуказанное свойство логарифма, то выкладки будут несколько длиннее:

.

Вычислим вторую производную:

Пример 6.33. Найти производную функции, заданной параметрически: — константы.

Решение.

Пример 6.34. Найти производную функции, заданной неявно: .

Решение. Перепишем заданное соотношение в виде Далее приравняем нулю производную по левой части этого соотношения, вычисленную как производную сложной функции:

; ;

.

Из последнего уравнения выразим через и :

; ;

Исчисление I — Непрерывность (практические задачи)

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т. е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 2.9: Непрерывность

1. График \(f\left( x \right)\) приведен ниже. По этому графику определите, где функция является разрывной. Решение
2. График \(f\left( x \right)\) приведен ниже. По этому графику определите, где функция является разрывной. Решение

Для задач 3–7, использующих только свойства 1–9 из раздела «Предельные свойства», односторонние предельные свойства (при необходимости) и определение непрерывности определяют, является ли данная функция непрерывной или разрывной в указанных точках.

1. \(\displaystyle f\left( x \right) = \frac{{4x + 5}}{{92} — 3з — 10}}\)
   1. \(г = — 2\)
   2. \(г = 0\)
   3. \(г = 5\)
   Решение
2. \(g\left( x \right) = \left\{ {\begin{array}{rl}{2x}&{x < 6}\\{x - 1}&{x \ge 6}\end {массив}} \право. 2}} & {t < - 2} \\ {t + 6} & {t \ ge - 2}\end{массив}} \right.\) 9{2t}} = 0\) на \(\left[ {1,3} \right]\) Решение

3.2: Непрерывность в точке, проверка непрерывности, типы разрывов

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

1195

В предыдущей концепции непрерывность функции была представлена ​​интуитивно через образ использования карандаша для рисования графика на листе бумаги (на определенном интервале области) и никогда не отрывая карандаша от бумаги. Пока карандаш не отрывается от бумаги, график можно считать непрерывным на протяжении этого интервала рисования. Это, конечно, не строгое описание непрерывности, но учитывая эту аналогию, какие у вас могут быть ожидания в отношении арифметических операций над двумя функциями, обе из которых непрерывны на общем интервале? или существование минимумов и максимумов непрерывная функция ; или существование промежуточных значений между двумя значениями функции?

---

Свойства непрерывных функций

Предыдущая концепция определяла характеристики функции, непрерывной в точке и на интервале. Давайте исследуем. Имея две функции f(x) и g(x), непрерывные на замкнутом интервале [a,b], можно ли ожидать, что арифметические операции над этими двумя функциями также дадут функции, непрерывные на [a,b]?

Для заданных функций f(x)=x+3 и g(x)=−x+0,5 в замкнутом интервале [−1,1] определить, непрерывны ли f(x) и g(x) в интервале .

Функции f(x) и g(x) показаны на графике. Проверка графика каждой функции и ее уравнения показывает, что каждый из них определен на замкнутом интервале, а предел функции в каждой точке интервала равен значению функции в этой точке. Обе функции непрерывны на интервале.

Фонд CK-12 — CC BY-NC-SA

Используя те же функции и интервал, что и выше, определите, является ли h(x)=f(x)+g(x) непрерывным в интервале.

Сумма двух функций равна h(x)=3,5 и показана на рисунке. Суммарная функция, константа, определяется на замкнутом интервале, и предел функции в каждой точке интервала равен значению постоянной функции в каждой точке. Суммарная функция непрерывна на интервале.

CK-12 Foundation — CC BY-NC-SA

Продолжая использовать интервал и функции, указанные выше, определите, является ли h(x)=f(x)g(x) непрерывным в интервале.

Произведение двух функций равно h(x)=(x+3)(−x+0,5)=−x ² +2,5x−1,5 и показано на рисунке. Функция продукта, парабола, определяется на замкнутом интервале, и предел функции в каждой точке интервала равен значению функции продукта в каждой точке. Функция произведения непрерывна на интервале.

CK-12 Foundation — CC BY-NC-SA

Как насчет отношения двух непрерывных функций?

Учитывая функции f(x)=x+3 и g(x)=−x+0,5 в замкнутом интервале [−1,1], определить, ^f(x) / _g(x) непрерывен в интервале.

Частное двух функций равно

и показано на рисунке.

CK-12 Foundation — CC BY-NC-SA

В замкнутом интервале [−1,1] x=0,5 — единственное место, где функция h(x) не определена, и

р на замкнутом интервале.

Выводы, полученные в приведенных выше простых функциях, могут быть обобщены в следующих свойствах.

Если f(x) и g(x) непрерывны при любом действительном значении c на закрытом интервале [a,b], то следующие непрерывны также при любом действительном значении c на замкнутом интервале [a,b]:

Теорема о промежуточном значении и теорема об экстремальном значении (минимум-максимум) — два других свойства функции, непрерывной на замкнутом интервале.

Теорема о промежуточном значении и теорема об экстремальном значении. ).

Теорему о промежуточном значении можно использовать для анализа и аппроксимации нулей функций.

Используйте функцию промежуточного значения, чтобы показать, что существует по крайней мере один нуль функции f(x)=3x ⁴ −3x ³ −2x+1 в указанном интервале [1,2].

График этой функции, показанный ниже, имеет форму параболы и непрерывен на интервале.

CC BY-NC-SA

Чтобы применить теорему о промежуточном значении, нам нужно найти пару из x- значений, которые имеют функциональные значения с разными знаками. Несколько значений показаны в таблице ниже.

х	1.1	1,2	1,3
ф(х)	-0,80	-0,36	0,37

Мы видим, что знак значений функции меняется с отрицательного на положительный где-то между 1,2 и 1,3. Следовательно, по теореме о промежуточном значении в интервале (1.2, 1.3) существует некоторое значение c такое, что f(c)=0.

Экстремальное значение (теорема минимума-максимума) является следствием теоремы о промежуточном значении.

Теорема об экстремальных значениях (минимум-максимум) утверждает, что если функция f(x) непрерывна в замкнутом интервале I, то f(x) имеет как максимальное, так и минимальное значение в I.

---

Примеры

Пример 1

Ранее вас спросили о ваших ожиданиях относительно непрерывности функций, образованных арифметическими операциями над двумя непрерывными функциями. Вывод этого раздела состоит в том, что, за исключением отношения функций, арифметические операции над двумя функциями, непрерывными в точке или на интервале, дают новую функцию, непрерывную в точке или на интервале. С частным двух функций всегда нужно определить, где знаменатель равен 0; в этом месте фактор-функция не является непрерывной.

Пример 2

Рассмотрим f(x)=x ³ +1 и интервал I=[−2,2]. Определить минимальное и максимальное значения.

Поскольку функция непрерывна на отрезке I, эта функция имеет минимум и максимум на отрезке. График функции показывает, что при x=−2 функция имеет минимальное значение f(−2)=−7; а при x=2 максимальное значение f(2)=9.

CC BY-NC-SA

---

Обзор

Для № 1-5 объясните, как вы узнали, что функция имеет корень в заданном интервале. (Подсказка: используйте функцию промежуточного значения, чтобы показать, что в указанном интервале есть хотя бы один нуль функции.):

1. f(x)=x ³ +2x ² −x+1, в интервале [-3,-2].
2. f(x)=x ^.5 −x√3−1, в интервале [9,10].
3. f(x)=x2+x−2, в интервале [-3,0].
4. f(x)=4×2−1×2+3x+2, в интервале [-1,0].
5. f(x)=2x+3−4, в интервале [-3,0].
6. Верно или неверно: f(x)=sin(x)+cos(x) имеет корень на интервале [0,π].
7. Верно или неверно: по теореме о промежуточном значении f(x)=sin(x)+cos2(x) не имеет корня на отрезке [0,π], поскольку f(0)=f(π)=1.
8. Верно или неверно: f(x)=x2+1cos(x) имеет корень на интервале [0,π].
9. На каком интервале f(x)=x−sin(x)+1 гарантированно IVT имеет корень?

10. Найдите интервал, на котором f(x)=e ^x +x имеет корень.

11. Найдите интервалы, на которых f(x)=x ³ +5x ² −4x−20 имеет корень.

Для #12-15 используйте теорему об экстремальных значениях, чтобы определить, является ли данное утверждение истинным или ложным.

12. Теорема об экстремальном значении гарантирует, что функция |sin(x3)| ^0,5 имеет минимальное значение на интервале [-3, 3].
13. Теорема об экстремальном значении гарантирует, что функция (x−1) ³ имеет максимальное значение на интервале [1, 3].
14. Теорема об экстремальном значении гарантирует, что функция x ² +3x+2 имеет минимальное значение на интервале [-3, 0].
15. Теорема об экстремальном значении гарантирует, что функция ^4x / _{x ² +3x+2} имеет минимальное значение на интервале [-3, 0].

---

Обзор (ответы)

Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 2. 10.

---

Словарь

Срок	Определение
Непрерывный	Непрерывность для точки существует, когда левый и правый пределы соответствуют функции, вычисленной в этой точке. Чтобы функция была непрерывной, она должна быть непрерывной в каждой точке непрерывной области.
Непрерывная функция	Непрерывная функция — это функция без разрывов и пропусков. Он содержит бесконечное, неисчислимое количество значений.
прерывистая в точке	Функция разрывна в точке a, если функция не определена в точке x=a.
теорема об экстремальном значении	Теорема об экстремальных значениях утверждает, что в каждом интервале [a,b], где функция непрерывна, есть по крайней мере один максимум и один минимум. Другими словами, он должен иметь как минимум два крайних значения.
теорема о промежуточном значении	Теорема о промежуточном значении утверждает, что если f(x) непрерывна на некотором интервале [a,b] и n находится между f(a) и f(b), то существует некоторое c∈[a,b], такое что f (с)=n.
точек разрыва	Точки разрыва функции — это входные значения функции, где функция разрывна.

---

Дополнительные ресурсы

PLIX: Play, Learn, Interact, eXplore — свойства непрерывных функций

Видео: Непрерывность и теорема о промежуточном значении

Реальный мир: новые орбиты

---

Эта страница под заголовком 3.2: Непрерывность в точке, Проверка непрерывности, Типы разрывов распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 через исходный контент, отредактированный в соответствии со стилем и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.