Как вычислить площадь трапеции по четырем сторонам. Калькулятор периметра трапеции
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту:
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h . Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d 1 d 2 *sinα .
Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d 1 d 2 *sinα .
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα:
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2 .
Формула площади криволинейной трапеции
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение:
Постройте трапецию АМРС.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .
Задача №2:
Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.Решение: Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х 2 – а 2) = (b 2 – х 2) ↔ 6х 2 = b 2 + 5а 2 ↔ х = √(5а 2 + b 2)/6.
Таким образом, ОЕ = х = √(5а 2 + b 2)/6.
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Этот калькулятор рассчитал 2192 задачи на тему «Площадь трапеции»
ПЛОЩАДЬ ТРАПЕЦИИ
Выберете формулу вычисления площади трапеции, которую Вы планируете применить для решения поставленной перед Вами задачи:
Общая теория для вычисления площади трапеции.
Трапеция — это плоская фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, и четырех отрезков (сторон), соединяющих попарно эти четыре точки, у которой две противоположные стороны параллельны (лежат на параллельных прямых), а две другие не параллельны.
Точки называются вершинами трапеции и обозначаются заглавными латинскими буквами.
Отрезки называются сторонами трапеции и обозначаются парой заглавных латинских букв соответственно вершинам, которые отрезки соединяют.
Две параллельные стороны трапеции называются основаниями трапеции .
Две не параллельные стороны трапеции называются боковыми сторонами трапеции .
На рисунке №1 представлена трапеция ABCD с вершинами A,B ,C, D и сторонами AB, BC, CD, DA.
AB ǁ DC — основания трапеции ABCD.
AD, BC — боковые стороны трапеции ABCD.
Угол, образованный лучами AB и AD, называется углом при вершине A. Обозначается он как ÐA или ÐBAD, или ÐDAB.
Угол, образованный лучами BA и BC, называется углом при вершине B. Обозначается он как ÐB или ÐABC, или ÐCBA.
Угол, образованный лучами CB и CD, называется углом при вершине C. Обозначается он как ÐC или ÐDCB, или ÐBCD.
Угол, образованный лучами AD и CD, называется углом при вершине D. Обозначается он как ÐD или ÐADC, или ÐCDA.
Рисунок №2: Трапеция ABCD
На рисунке №2 отрезок MN, соединяющий середины боковых сторон, называется средней линией трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме. То есть,.
Рисунок №3: Равнобедренная трапеция ABCD
На Рисунке №3, AD=BC.
Трапеция называется равнобедренной (равнобокой) , если ее боковые стороны равны.
Рисунок №4: Прямоугольная трапеция ABCD
На Рисунке №4 угол D — прямой (равен 90 о).
Трапеция называется прямоугольной, если угол при боковой стороне прямой.
Площадью S плоской фигуры, к которым относится и трапеция, называется ограниченное замкнутое пространство на плоскости. Площадь плоской фигуры показывает величину этой фигуры.
Площадь обладает несколькими свойствами:
1. Она не может быть отрицательной.
Она не может быть отрицательной.
2. Если дана некоторая замкнутая область на плоскости, которая составлена из нескольких фигур, не пересекающихся друг с другом (то есть, фигуры не имеют общих внутренних точек, но вполне могут касаться друг друга), то площадь такой области равна сумме площадей составляющих ее фигур.
3. Если две фигуры равны, то и площади их равны.
4. Площадь квадрата, который построен на единичном отрезке, равна единице.
За единицу измерения площади принимают площадь квадрата, сторона которого равна единице измерения отрезков.
При решении задач часто используются следующие формулы вычисления площади трапеции:
1. Площадь трапеции равна полусумме ее оснований умноженной на высоту:
2. Площадь трапеции равна произведению ее средней линии на высоту:
3. При известных длинах оснований и боковых сторон трапеции её площадь можно вычислить по формуле:
4. Возможно вычислить площадь равнобедренной трапеции при известной длине радиуса вписанной в трапецию окружности и известном значении угла при основании по следующей формуле:
Пример 1: Вычислить площадь трапеции с основаниями a=7, b=3 и высотой h=15.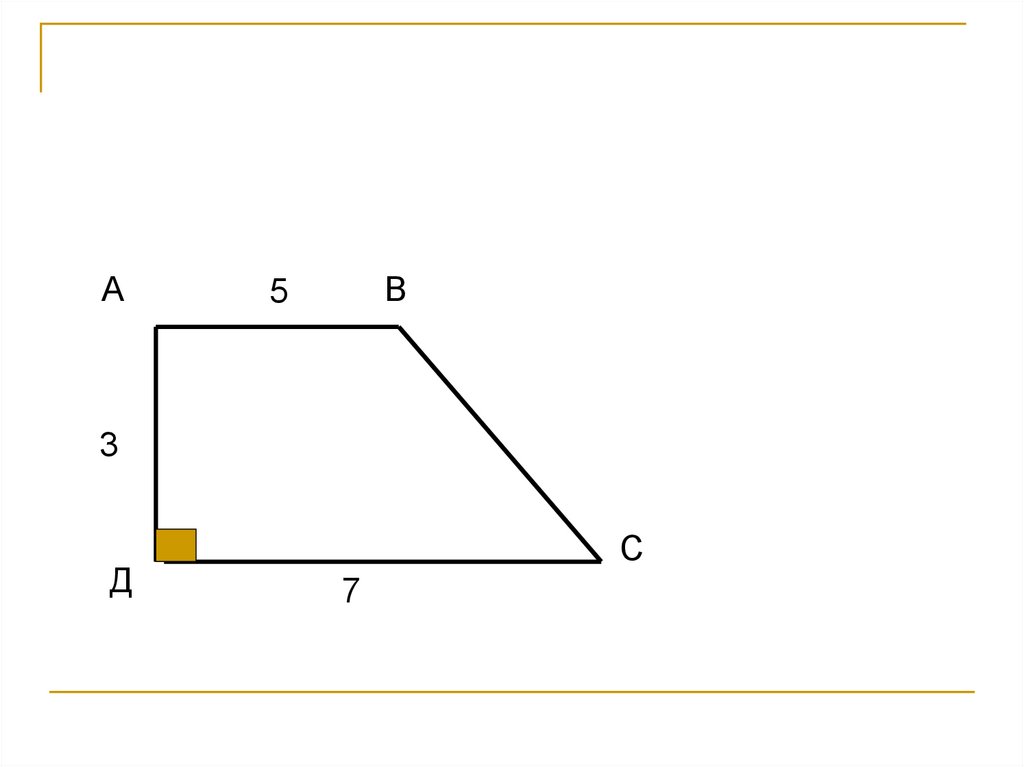
Решение:
Ответ:
Пример 2: Найти сторону основания трапеции с площадью S=35 см 2 , высотой h=7см и вторым основанием b = 2 см.
Решение:
Для нахождения стороны основания трапеции воспользуемся формулой вычисления площади:
Выразим из данной формулы сторону основания трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 3: Найти высоту трапеции с площадью S=17 см 2 и основаниями a=30 см, b = 4 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 4: Вычислить площадь трапеции с высотой h=24 и средней линией m=5.
Решение:
Для нахождения площади трапеции воспользуемся следующей формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 5: Найти высоту трапеции с площадью S = 48 см 2 и средней линией m=6 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы высоту трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 6: Найти среднюю линию трапеции с площадью S = 56 и высотой h=4.
Решение:
Для нахождения средней линии трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы среднюю линию трапеции:
Таким образом, имеем следующее.
И . Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.
Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции.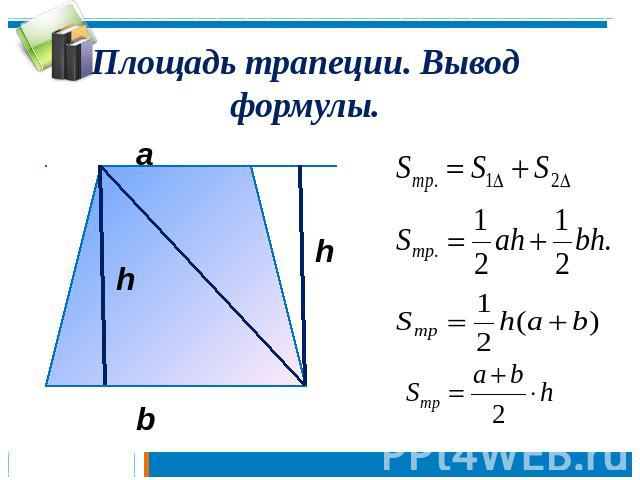 Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Как и у треугольников, у трапеция есть частные виды в виде равнобедренной (равнобокой) трапеции, у которой длина боковых сторон одинаковы и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.
Трапеции обладают некоторыми интересными свойствами:
- Средняя линия трапеции равна полусумме оснований и параллельна им.
- У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
- Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
- Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
- Если сумма углов, образованных сторонами трапеции у любого ее основания равна 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.

- Равнобедренную трапецию можно описать окружностью. И наоборот. Если в трапеция вписывается в окружность, значит она равнобедренная.
- Отрезок, проходящий через середины оснований равнобедренной трапеции будет перпендикулярен ее основаниям и представляет собой ось симетрии.
Как найти площадь трапеции .
Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается в виде выражения:
где S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота трапеции.
Понять и запомнить эту формулу можно следующим образом. Как следует из рисунка ниже трапецию с использованием средней линии можно преобразовать в прямоугольник, длина которого и будет равна полусумме оснований.
Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.
Есть еще одна простая формула для подсчета ее площади. Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.
В этом случае площадь трапеции может быть найдена по формуле:
S = ((a+b)/2)*√c 2 -((b-a) 2 +c 2 -d 2 /2(b-a)) 2
где S-площадь, a,b-основания, c,d-боковые стороны трапеции.
Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.
В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм.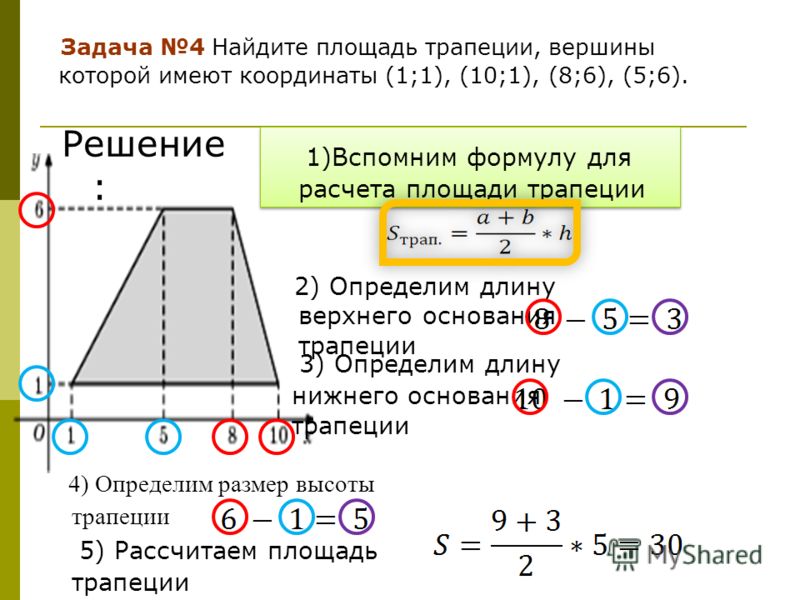 Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:
S = ½ * (a+b) * h
т.е. взять полусумму оснований, умноженную на высоту.
Также удастся вычислить площадь трапеции, если известно значение высоты и средней линии. Обозначим среднюю линию — m. Тогда
Решим задачу посложнее: известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь отыщется по формуле:
Тогда площадь отыщется по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sin α
где d с индексами 1 и 2 — диагонали. В данной формуле в расчете приводится синус угла.
При известных длинах оснований a и b и двух углах при нижнем основании площадь вычисляется так:
S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))
Площадь равнобедренной трапеции
Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.
Найти площадь равнобедренной трапеции можно несколькими способами.
- Через длины трех сторон. В этом случае длины боковых сторон будут совпадать, поэтому обозначены одной величиной — с, а и b — длины оснований:
- Если известна длина верхнего основания, боковой стороны и величина угла при нижнем основании, то площадь вычисляется так:
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — боковая сторона.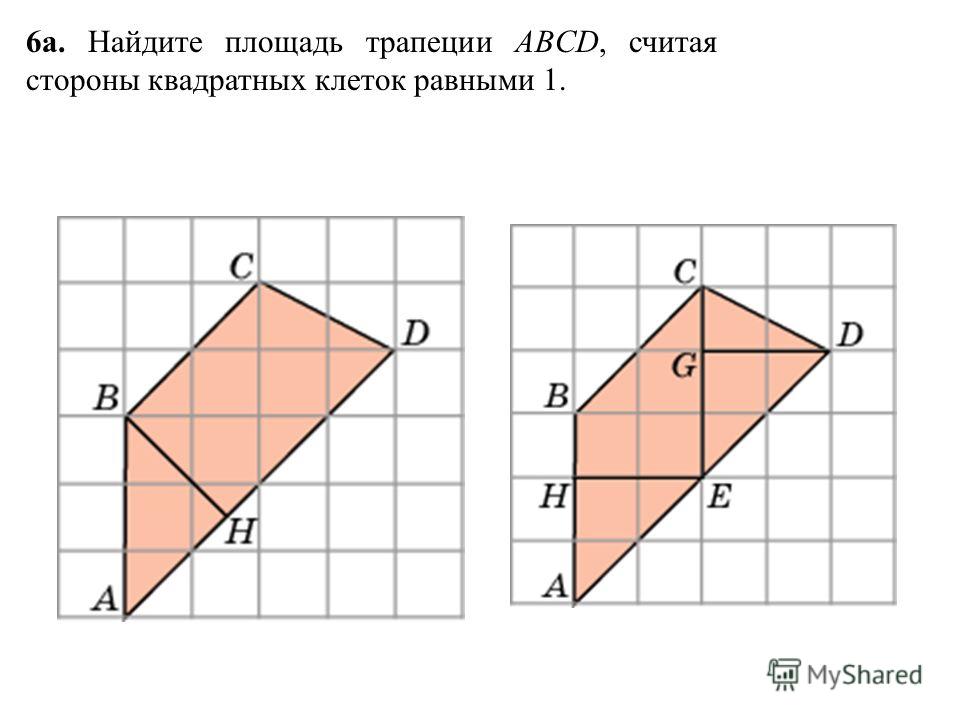
- Если вместо верхнего основания известна длина нижнего – b, площадь рассчитывается по формуле:
S = c * sin α * (b – c * cos α)
- Если когда известны два основания и угол при нижнем основании, площадь вычисляется через тангенс угла:
S = ½ * (b2 – a2) * tg α
- Также площадь рассчитывается через диагонали и угол между ними. В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
S = ½ * d2 * sin α
- Вычислим площадь трапеции, зная длину боковой стороны, средней линии и величину угла при нижнем основании.
Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:
S = m * c * sin α
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:
S = 4r2 / sin α
Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):
Зная основания и угол, площадь равнобедренной трапеции вычисляется так:
S = a * b / sin α
(эта и последующие формулы верны только для трапеций с вписанной окружностью).
Через основания и радиус окружности площадь ищется так:
Если известны только основания, то площадь считается по формуле:
Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям. В этом случае боковая сторона по длине совпадает с высотой трапеции.
Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.
Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.
- Если известны длины оснований и высота (или перпендикулярная боковая сторона), то площадь рассчитывается по формуле:
S = (a + b) * h / 2
В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:
S = (a + b) * c / 2
- Другой способ рассчитать площадь — перемножить длину средней линии на высоту:
или на длину боковой перпендикулярной стороны:
- Следующий способ вычисления — через половину произведения диагоналей и синус угла между ними:
S = ½ * d1 * d2 * sin α
Если диагонали перпендикулярны, то формула упрощается до:
S = ½ * d1 * d2
- Еще один способ вычисления — через полупериметр (сумма длин двух противоположных сторон) и радиус вписанной окружности.

Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
S = (2r + c) * r
- Если в трапецию вписана окружность, то площадь вычисляется так же:
где m — длина средней линии.
Площадь криволинейной трапеции
Криволинейная трапеция представляет из себя плоскую фигуру, ограниченную графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке , осью абсцисс и прямыми x = a, x = b. По сути, две ее стороны параллельны друг другу (основания), третья сторона перпендикулярна основаниям, а четвертая представляет из себя кривую, соответствующую графику функции.
Площадь криволинейной трапеции ищут через интеграл по формуле Ньютона-Лейбница:
Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают одинаковыми свойствами углов. Как у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов. А сумма углов, прилежащих к боковой стороне, — 180 градусам.
А сумма углов, прилежащих к боковой стороне, — 180 градусам.
Трапеция — это особый вид четырехугольника, у которого две противолежащие стороны параллельны друг другу, а две другие — нет. Трапецеидальную форму имеют различные реальные объекты, поэтому вам может понадобиться рассчитать периметр такой геометрической фигуры для решения повседневных или школьных задач.
Геометрия трапеции
Трапеция (от греч. «трапезион» — стол) — это фигура на плоскости, ограниченная четырьмя отрезками, два из которых параллельны, а два — нет. Параллельные отрезки носят название оснований трапеции, а непараллельные — боковых сторон фигуры. Боковые стороны и их углы наклона определяют вид трапеции, которая может быть разносторонней, равнобедренной или прямоугольной. Помимо оснований и боковых сторон, трапеция имеет еще два элемента:
- высота — расстояние между параллельными основаниями фигуры;
- средняя линия — отрезок, соединяющий середины боковых сторон.
Данная геометрическая фигура широко распространена в реальной жизни.
Трапеция в реальности
В повседневной жизни трапецеидальную форму принимают многие реальные предметы. Вы легко найдете трапеции в следующих сферах человеческой деятельности:
- дизайн интерьеров и декор — диваны, столешницы, стены, ковры, подвесные потолки;
- ландшафтный дизайн — границы газонов и искусственных водоемов, формы декоративных элементов;
- мода — форма одежды, обуви и аксессуаров;
- архитектура — окна, стены, основания зданий;
- производство — различные изделия и детали.
При столь широком использовании трапеций специалистам часто приходится вычислять периметр геометрической фигуры.
Периметр трапеции
Периметр фигуры — это числовая характеристика, которая рассчитывается как сумма длин всех сторон n-угольника. Трапеция — это четырехугольник и в общем случае все его стороны имеют разную длину, поэтому периметр рассчитывается по формуле:
P = a + b + c + d,
где a и c – основания фигуры, b и d – ее боковые стороны.
Несмотря на то, что при вычислении периметра трапеции нам нет нужды узнавать высоту, программный код калькулятора требует ввода этой переменной. Так как высота никак не влияет на вычисления, при использовании нашего онлайн-калькулятора вы можете ввести любое значение высоты, которое больше нуля. Рассмотрим пару примеров.
Примеры из реальной жизни
Платок
Допустим, у вас есть платок в форме трапеции, и вы хотите отделать его бахромой. Вам понадобится узнать периметр платка, чтобы не купить лишнего материала или не ходить в магазин два раза. Пусть ваш равнобедренный платок имеет следующие параметры: a = 120 см, b = 60 см, c = 100 см, d = 60 см. Вбиваем эти данные в онлайн-форму и получаем ответ в виде:
Таким образом, периметр платка составляет 340 см, и именно такой длины должна быть тесьма бахромы для его отделки.
Откосы
К примеру, вы решили сделать откосы для нестандартных металлопластиковых окон, которые имеют трапецеидальную форму. Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок. Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Следовательно, периметр трапециевидного окна составляет 390 см, и именно столько вам понадобится купить пластиковых панелей для формирования откосов.
Заключение
Трапеция — популярная в повседневности фигура, определение параметров которой может понадобиться в самых неожиданных ситуациях. Расчет периметров трапецией необходим многим профессионалам: от инженеров и архитекторов до дизайнеров и механиков. Наш каталог онлайн-калькуляторов позволит вам выполнить расчеты для любых геометрических фигур и тел.
Объем усеченной трапеции онлайн калькулятор. Формулы объема пирамиды полной и усеченной
- 22.09.2014
Принцип действия. При нажатии кнопки первой цифры кода SA1 триггер DD1.
 1 переключится и на входе D триггера DD1.2 появится напряжение высокого уровня. Поэтому при нажатии очередной кнопки кода SA2 триггер DD1.2 изменяет свое состояние и подготавливает к переключению следующий триггер. В случае дальнейшего правильного набора последним сработает триггер DD2.2, и …
1 переключится и на входе D триггера DD1.2 появится напряжение высокого уровня. Поэтому при нажатии очередной кнопки кода SA2 триггер DD1.2 изменяет свое состояние и подготавливает к переключению следующий триггер. В случае дальнейшего правильного набора последним сработает триггер DD2.2, и … - 03.10.2014
Предлагаемое устройство стабилизирует напряжение до 24В и током до 2А с защитой от замыкания. В случае неустойчивого запуска стабилизатора следует применить синхронизацию от автономного генератора импульсов рис. 2 . Схема стабилизатора показана на рис.1. На VT1 VT2 собран триггер Шмитта, который управляет мощным регулирующим транзистором VT3. Детали: VT3 снабжен теплоотводом …
- 20.09.2014
Усилитель (см. фото) выполнен по традиционной схеме с автосмещением на лампах: выходные – AL5, драйверы – 6Г7, кенотрон – AZ1. Схема одного из двух каналов стереоусилителя показана на рис.1. С регулятора громкости сигнал поступает на сетку лампы 6Г7, усиливается и с анода этой лампы через разделительный конденсатор C4 подается на …
- 15.
 11.2017
11.2017NE555 — универсальный таймер — устройство для формирования (генерации) одиночных и повторяющихся импульсов со стабильными временными характеристиками. Представляет собой асинхронный RS-триггер со специфическими порогами входов, точно заданными аналоговыми компараторами и встроенным делителем напряжения (прецизионный триггер Шмитта с RS-триггером). Применяется для построения различных генераторов, модуляторов, реле времени, пороговых устройств и прочих …
– это многогранник, который образуется основанием пирамиды и параллельным ему сечением. Можно сказать, что усеченная пирамида – это пирамиду со срезанной верхушкой. Эта фигура обладает множеством уникальных свойств:
- Боковые грани пирамиды являются трапециями;
- Боковые ребра правильной усеченной пирамиды одинаковой длины и наклонены к основанию под одинаковым углом;
- Основания являются подобными многоугольниками;
- В правильной усеченной пирамиде, грани представляют собой одинаковые равнобедренные трапеции, площадь которых равна.
 Также они наклонены к основанию под одним углом.
Также они наклонены к основанию под одним углом.
Формула площади боковой поверхности усеченной пирамиды представляет собой сумму площадей ее сторон:
Так как стороны усеченной пирамиды представляют собой трапеции, то для расчета параметров придется воспользоваться формулой площади трапеции . Для правильной усеченной пирамиды можно применить другую формулу расчета площади. Так как все ее стороны, грани, и углы при основании равны, то можно применить периметры основания и апофему, а также вывести площадь через угол при основании.
Если по условиям в правильной усеченной пирамиде даны апофема (высота боковой стороны) и длины сторон основания, то можно произвести расчет площади через полупроизведение суммы периметров оснований и апофемы:
Давайте рассмотрим пример расчета площади боковой поверхности усеченной пирамиды.
Дана правильная пятиугольная пирамида. Апофема l = 5 см, длина грани в большом основании равна a = 6 см, а грань в меньшем основании b = 4 см.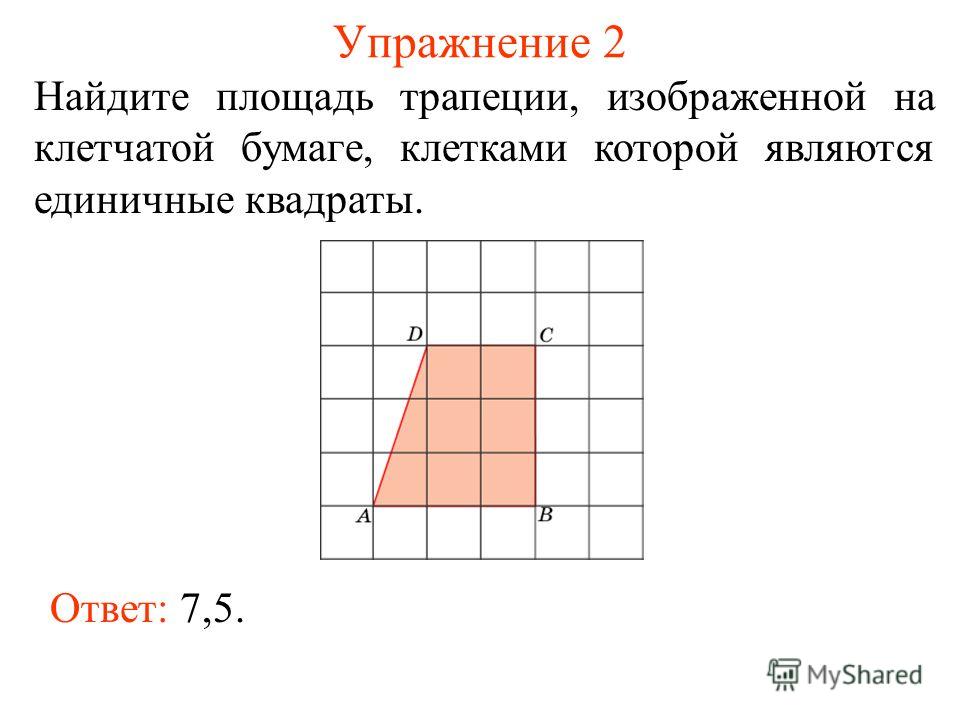 Рассчитайте площадь усеченной пирамиды.
Рассчитайте площадь усеченной пирамиды.
Для начала найдем периметры оснований. Так как нам дана пятиугольная пирамида, мы понимаем, что основания представляют собой пятиугольники. Значит, в основаниях лежит фигура с пятью одинаковыми сторонами. Найдем периметр большего основания:
Таким же образом находим периметр меньшего основания:
Теперь можем рассчитывать площадь правильной усеченной пирамиды. Подставляем данные в формулу:
Таким образом, мы рассчитали площадь правильной усеченной пирамиды через периметры и апофему.
Еще один способ расчета площади боковой поверхности правильной пирамиды, это формула через углы у основания и площадь этих самых оснований .
Давайте рассмотрим пример расчета. Помним, что данная формула применяется только для правильной усеченной пирамиды.
Пусть дана правильная четырехугольная пирамида. Грань нижнего основания a = 6 см, а грань верхнего b = 4 см. Двухгранный угол при основании β = 60°. Найдите площадь боковой поверхности правильной усеченной пирамиды.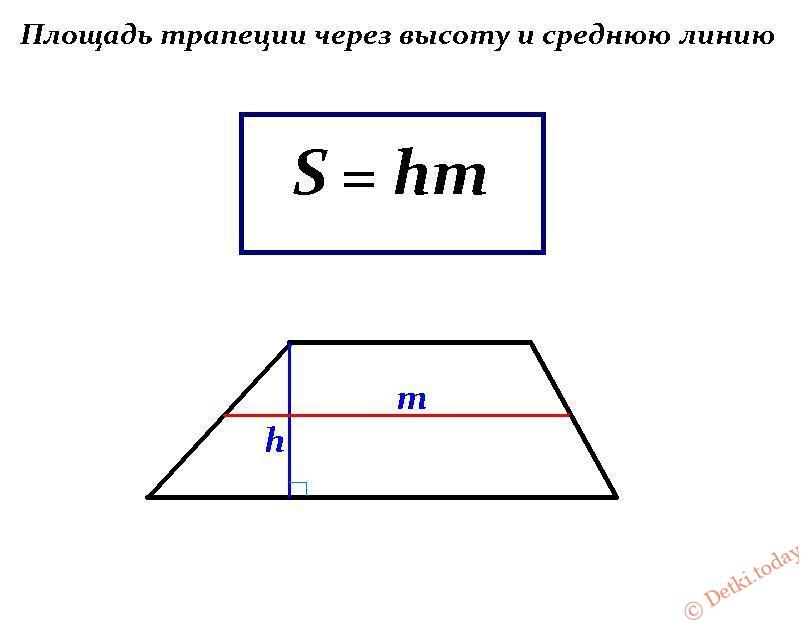
Для начала рассчитаем площадь оснований. Так как пирамида правильная, все грани оснований равны между собой. Учитывая, что в основании лежит четырехугольник, понимаем, что нужно будет рассчитать площадь квадрата . Она представляет собой произведение ширины на длину, но в квадрате эти значения совпадают. Найдем площадь большего основания:
Теперь используем найденные значения для расчета площади боковой поверхности.
Зная несколько несложных формул, мы легко рассчитали площадь боковой трапеции усеченной пирамиды через различные значения.
Умение вычислять объем пространственных фигур является важным при решение ряда практических задач по геометрии. Одной из распространенных фигур является пирамида. В данной статье рассмотрим пирамиды как полной, так и усеченной.
Пирамида как объемная фигура
Каждый знает о египетских пирамидах, поэтому хорошо представляет, о какой фигуре пойдет речь. Тем не менее египетские каменные сооружения являются лишь частным случаем огромного класса пирамид.
Рассматриваемый геометрический объект в общем случае представляет собой многоугольное основание, каждая вершина которого соединена с некоторой точкой в пространстве, не принадлежащей плоскости основания. Данное определение приводит к фигуре, состоящей из одного n-угольника и n треугольников.
Любая пирамида состоит из n+1 граней, 2*n ребер и n+1 вершины. Поскольку рассматриваемая фигура является совершенным полиэдром, то числа отмеченных элементов подчиняются равенству Эйлера:
2*n = (n+1) + (n+1) — 2.
Многоугольник, находящийся в основании, дает название пирамиды, например, треугольная, пятиугольная и так далее. Набор пирамид с разными основаниями приведен на фото ниже.
Точка, в которой n треугольников фигуры соединяются, называется вершиной пирамиды. Если из нее опустить на основание перпендикуляр и он пересечет его в геометрическом центре, тогда такая фигура будет называться прямой. Если это условие не выполняется, то имеет место наклонная пирамида.
Прямая фигура, основание которой образовано равносторонним (равноугольным) n-угольником, называется правильной.
Формула объема пирамиды
Для вычисления объема пирамиды воспользуемся интегральным исчислением. Для этого разобьем фигуру параллельными основанию секущими плоскостями на бесконечное число тонких слоев. Рисунок ниже показывает четырехугольную пирамиду высотой h и длиной стороны L, в которой четырехугольником отмечен тонкий слой сечения.
Площадь каждого такого слоя можно вычислить по формуле:
A(z) = A 0 *(h-z) 2 /h 2 .
Здесь A 0 — площадь основания, z — значение вертикальной координаты. Видно, что если z = 0, то формула дает значение A 0 .
Чтобы получить формулу объема пирамиды, следует вычислить интеграл по всей высоте фигуры, то есть:
V = ∫ h 0 (A(z)*dz).
Подставляя зависимость A(z) и вычисляя первообразную, приходим к выражению:
V = -A 0 *(h-z) 3 /(3*h 2)| h 0 = 1/3*A 0 *h.
Мы получили формулу объема пирамиды. Чтобы найти величину V, достаточно умножить высоту фигуры на площадь основания, а затем результат поделить на три.
Заметим, что полученное выражение справедливо для вычисления объема пирамиды произвольного типа. То есть она может быть наклонной, а ее основание представлять собой произвольный n-угольник.
и ее объем
Полученную в пункте выше общую формулу для объема можно уточнить в случае пирамиды с правильным основанием. Площадь такого основания вычисляется по следующей формуле:
A 0 = n/4*L 2 *ctg(pi/n).
Здесь L является длиной стороны правильного многоугольника с n вершинами. Символ pi — это число пи.
Подставляя выражение для A 0 в общую формулу, получаем объем правильной пирамиды:
V n = 1/3*n/4*L 2 *h*ctg(pi/n) = n/12*L 2 *h*ctg(pi/n).
Например, для треугольной пирамиды эта формула приводит к следующему выражению:
V 3 = 3/12*L 2 *h*ctg(60 o) = √3/12*L 2 *h.
Для правильной четырехугольной пирамиды формула объема приобретает вид:
V 4 = 4/12*L 2 *h*ctg(45 o) = 1/3*L 2 *h.
Определение объемов правильных пирамид требует знания стороны их основания и высоты фигуры.
Пирамида усеченная
Предположим, что мы взяли произвольную пирамиду и отсекли у нее часть боковой поверхности, содержащей вершину. Оставшаяся фигура называется усеченной пирамидой. Она состоит уже из двух n-угольных оснований и n трапеций, которые их соединяют. Если секущая плоскость была параллельна основанию фигуры, тогда образуется усеченная пирамида с параллельными подобными основаниями. То есть длины сторон одного из них можно получить, умножая длины другого на некоторый коэффициент k.
Рисунок выше демонстрирует усеченную правильную Видно, что верхнее основание ее так же, как и нижнее, образовано правильным шестиугольником.
Формула которую можно вывести, используя подобное приведенному интегральное исчисление, имеет вид:
V = 1/3*h*(A 0 + A 1 + √(A 0 *A 1)).
Где A 0 и A 1 — площади нижнего (большого) и верхнего (маленького) оснований соответственно. Переменной h обозначается высота усеченной пирамиды.
Объем пирамиды Хеопса
Любопытно решить задачу на определение объема, который заключает внутри себя самая большая египетская пирамида.
В 1984 году британские египтологи Марк Легнер (Mark Lehner) и Джон Гудман (Jon Goodman) установили точные размеры пирамиды Хеопса. Ее первоначальная высота равнялась 146,50 метра (в настоящее время около 137 метров). Средняя длина каждой из четырех сторон сооружения составила 230,363 метра. Основание пирамиды с высокой точностью является квадратным.
Воспользуемся приведенными цифрами для определения объема этого каменного гиганта. Поскольку пирамида является правильной четырехугольной, тогда для нее справедлива формула:
Подставляем цифры, получаем:
V 4 = 1/3*(230,363) 2 *146,5 ≈ 2591444 м 3 .
Объем пирамиды Хеопса равен практически 2,6 млн м 3 .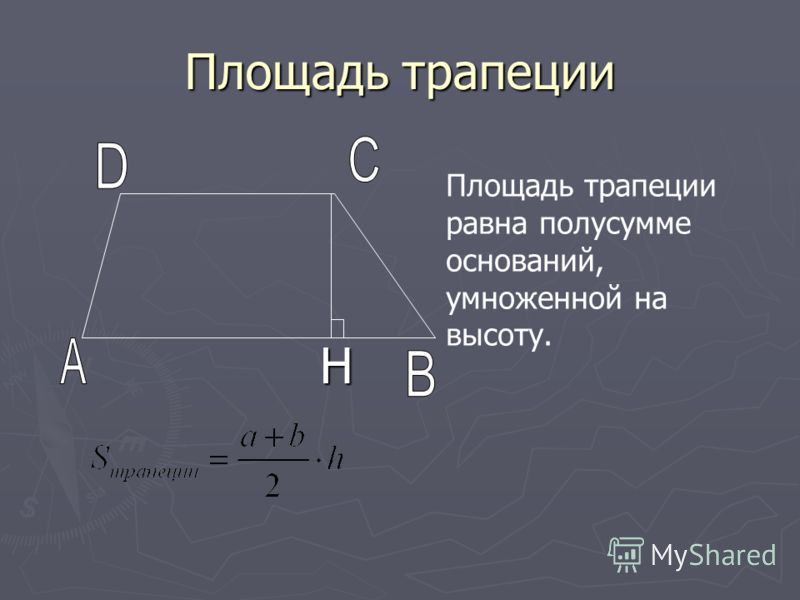 Для сравнения отметим, что олимпийский бассейн имеет объем 2,5 тыс. м 3 . То есть для заполнения всей пирамиды Хеопса понадобится больше 1000 таких бассейнов!
Для сравнения отметим, что олимпийский бассейн имеет объем 2,5 тыс. м 3 . То есть для заполнения всей пирамиды Хеопса понадобится больше 1000 таких бассейнов!
Пирамидой называется многогранник, одна из граней которого многоугольник (основание ), а все остальные грани – треугольники с общей вершиной (боковые грани ) (рис. 15). Пирамида называется правильной , если ее основанием является правильный многоугольник и вершина пирамиды проектируется в центр основания (рис. 16). Треугольная пирамида, у которой все ребра равны, называется тетраэдром .
Боковым ребром пирамиды называется сторона боковой грани, не принадлежащая основанию Высотой пирамиды называется расстояние от ее вершины до плоскости основания. Все боковые ребра правильной пирамиды равны между собой, все боковые грани – равные равнобедренные треугольники. Высота боковой грани правильной пирамиды, проведенная из вершины, называется апофемой .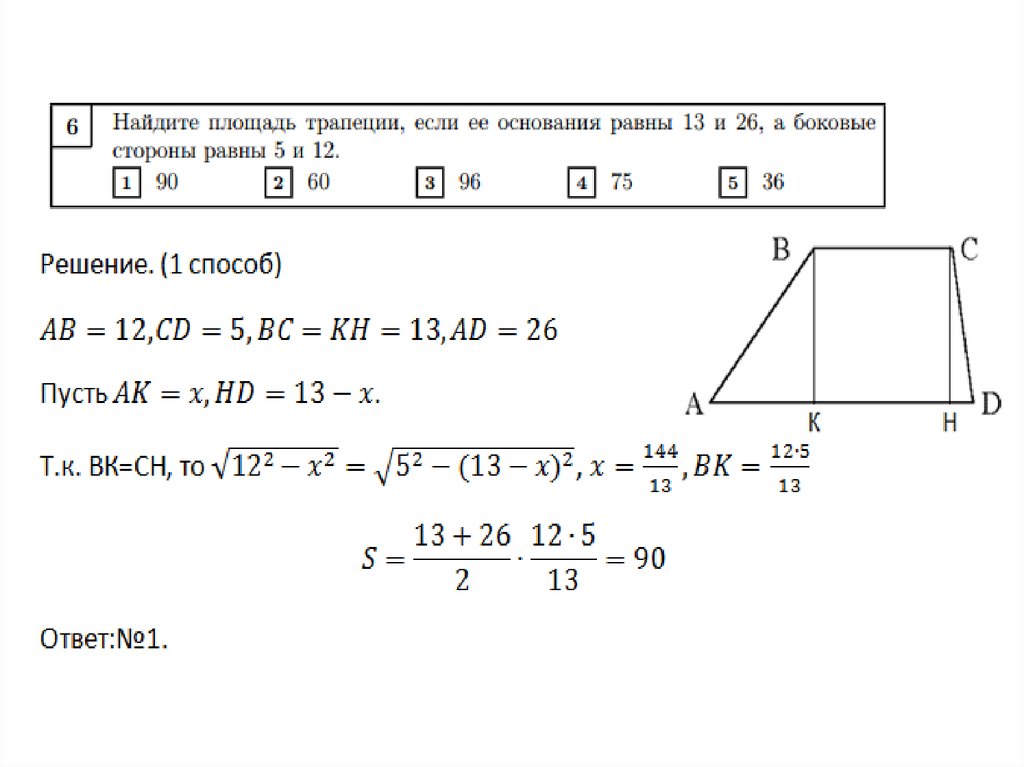 Диагональным сечением называется сечение пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.
Диагональным сечением называется сечение пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.
Площадью боковой поверхности пирамиды называется сумма площадей всех боковых граней. Площадью полной поверхности называется сумма площадей всех боковых граней и основания.
Теоремы
1. Если в пирамиде все боковые ребра равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности описанной около основания.
2. Если в пирамиде все боковые ребра имеют равные длины, то вершина пирамиды проектируется в центр окружности описанной около основания.
3. Если в пирамиде все грани равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности вписанной в основание.
Для вычисления объема произвольной пирамиды верна формула:
где V – объем;
S осн – площадь основания;
H – высота пирамиды.
Для правильной пирамиды верны формулы:
где p – периметр основания;
h а – апофема;
H – высота;
S полн
S бок
S осн – площадь основания;
V – объем правильной пирамиды.
Усеченной пирамидой называется часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды (рис. 17). Правильной усеченной пирамидой называется часть правильной пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды.
Основания усеченной пирамиды – подобные многоугольники. Боковые грани – трапеции. Высотой усеченной пирамиды называется расстояние между ее основаниями. Диагональю усеченной пирамиды называется отрезок, соединяющий ее вершины, не лежащие в одной грани. Диагональным сечением называется сечение усеченной пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.
Для усеченной пирамиды справедливы формулы:
(4)
где S 1 , S 2 – площади верхнего и нижнего оснований;
S полн – площадь полной поверхности;
S бок – площадь боковой поверхности;
H – высота;
V – объем усеченной пирамиды.
Для правильной усеченной пирамиды верна формула:
где p 1 , p 2 – периметры оснований;
h а – апофема правильной усеченной пирамиды.
Пример 1. В правильной треугольной пирамиде двугранный угол при основании равен 60º. Найти тангенс угла наклона бокового ребра к плоскости основания.
Решение. Сделаем рисунок (рис. 18).
Пирамида правильная, значит в основании равносторонний треугольник и все боковые грани равные равнобедренные треугольники. Двугранный угол при основании – это угол наклона боковой грани пирамиды к плоскости основания. Линейным углом будет угол a между двумя перпендикулярами: и т.е. Вершина пирамиды проектируется в центре треугольника (центр описанной окружности и вписанной окружности в треугольник АВС ). Угол наклона бокового ребра (например SB ) – это угол между самим ребром и его проекцией на плоскость основания.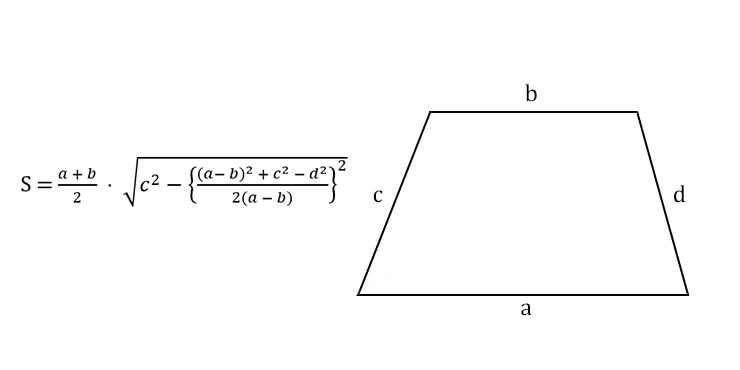 Для ребра SB этим углом будет угол SBD . Чтобы найти тангенс необходимо знать катеты SO и OB . Пусть длина отрезка BD равна 3а . Точкой О отрезок BD делится на части: и Из находим SO : Из находим:
Для ребра SB этим углом будет угол SBD . Чтобы найти тангенс необходимо знать катеты SO и OB . Пусть длина отрезка BD равна 3а . Точкой О отрезок BD делится на части: и Из находим SO : Из находим:
Ответ:
Пример 2. Найти объем правильной усеченной четырехугольной пирамиды, если диагонали ее оснований равны см и см, а высота 4 см.
Решение. Для нахождения объема усеченной пирамиды воспользуемся формулой (4). Чтобы найти площади оснований необходимо найти стороны квадратов-оснований, зная их диагонали. Стороны оснований равны соответственно 2 см и 8 см. Значит площади оснований и Подставив все данные в формулу, вычислим объем усеченной пирамиды:
Ответ: 112 см 3 .
Пример 3. Найти площадь боковой грани правильной треугольной усеченной пирамиды, стороны оснований которой равны 10 см и 4 см, а высота пирамиды 2 см.
Решение. Сделаем рисунок (рис.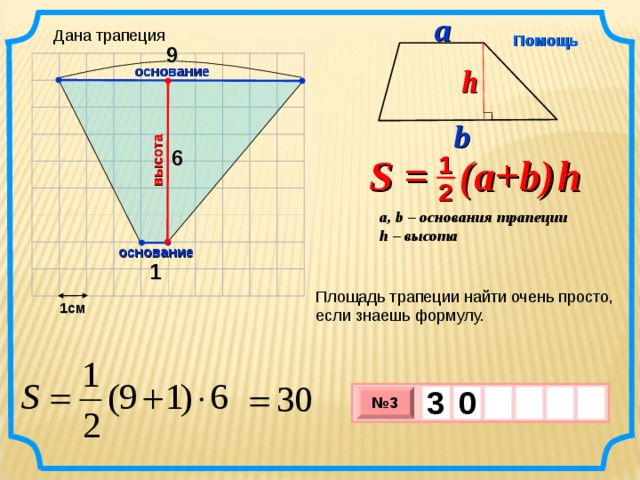 19).
19).
Боковая грань данной пирамиды является равнобокая трапеция. Для вычисления площади трапеции необходимо знать основания и высоту. Основания даны по условию, остается неизвестной только высота. Ее найдем из где А 1 Е перпендикуляр из точки А 1 на плоскость нижнего основания, A 1 D – перпендикуляр из А 1 на АС . А 1 Е = 2 см, так как это высота пирамиды. Для нахождения DE сделаем дополнительно рисунок, на котором изобразим вид сверху (рис. 20). Точка О – проекция центров верхнего и нижнего оснований. так как (см. рис. 20) и С другой стороны ОК – радиус вписанной в окружности и ОМ – радиус вписанной в окружности:
MK = DE .
По теореме Пифагора из
Площадь боковой грани:
Ответ:
Пример 4. В основании пирамиды лежит равнобокая трапеция, основания которой а и b (a > b ). Каждая боковая грань образует с плоскостью основания пирамиды угол равный j . Найти площадь полной поверхности пирамиды.
Найти площадь полной поверхности пирамиды.
Решение. Сделаем рисунок (рис. 21). Площадь полной поверхности пирамиды SABCD равна сумме площадей и площади трапеции ABCD .
Воспользуемся утверждением, что если все грани пирамиды равнонаклонены к плоскости основания, то вершина проектируется в центр вписанной в основание окружности. Точка О – проекция вершины S на основание пирамиды. Треугольник SOD является ортогональной проекцией треугольника CSD на плоскость основания. По теореме о площади ортогональной проекции плоской фигуры получим:
Аналогично и значит Таким образом задача свелась к нахождению площади трапеции АВСD . Изобразим трапецию ABCD отдельно (рис.22). Точка О – центр вписанной в трапецию окружности.
Так как в трапецию можно вписать окружность, то или Из по теореме Пифагора имеем
Трапеция формула площади: Все формулы площади трапеции — найти онлайн — ЭкоДом: Дом своими руками
Содержание
Все формулы площади равнобедренной трапеции
1. Формула площади равнобедренной трапеции через стороны и угол
Формула площади равнобедренной трапеции через стороны и угол
а — нижнее основание
b — верхнее основание
с — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S ):
Формула площади равнобедренной трапеции через стороны и угол, (S ):
2. Формулы площади равнобедренной трапеции если в нее вписана окружность
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α, β — углы трапеции
а — нижнее основание
b — верхнее основание
Формула площади равнобедренной трапеции через радиус вписанной окружности, (S ):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
R — радиус вписанной окружности
m — средняя линия
O — центр вписанной окружности
c — боковые стороны
а — нижнее основание
b — верхнее основание
Формула площади равнобедренной трапеции через радиус вписанной окружности, стороны и среднюю линию (S ):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α, β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
c — боковая сторона
m — средняя линия трапеции
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
a — нижнее основание
b — верхнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S ):
Площадь трапеции | Онлайн калькуляторы, расчеты и формулы на GELEOT.

RU
Трапеция – это четырехугольник, у которого две стороны параллельны друг другу. Высотой трапеции называют линию, перпендикулярную основаниями, для удобства ее часто проводят из тупого угла трапеции на большее основание. Средняя линия трапеции – это линия, которая параллельна основаниям, и разделяет боковые стороны ровно пополам. Среднюю линию трапеции можно найти средним арифметическим оснований – сложив их и разделив на два.
Площадь трапеции в самом простом виде – это произведение средней линии на высоту, или если раскрыть формулу средней линии, то произведение полусуммы оснований на высоту.
Доказательством этой формулы будет служить представление площади трапеции, как суммы площадей двух треугольников полученных при проведении диагонали.
Площади этих треугольников будут равны соответственно и (для того, чтобы нарисовать высоту во втором треугольнике, необходимо будет продлить основание b). Площадь трапеции будет равна сумме полученных выражений, где мы вынесем высоту за скобку, и получим искомую формулу:
Вывести формулу, для того чтобы вычислить площадь трапеции через стороны, можно с помощью метода подстановки.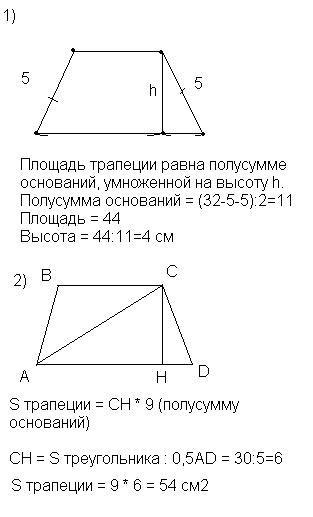
Проведя две высоты в трапеции, получаем по бокам прямоугольные треугольники с известными гипотенузами и неизвестными катетами x и y.
Таким образом x+y=d-b, y=d-b-x.
Одинаковый катет у обоих треугольников – высота, которую мы ищем. Через теорему Пифагора в прямоугольных треугольниках выражаем высоту и . Приравнивая, получаем a2-x2=c2-y2 или x2-y2=a2-c2.
x2-(d-b-x)2=a2-c2 — Подставляем вместо х полученное выше выражение d-b-y.
x2-d2+bd+dx-b2+bd-bx-x2+dx-bx=a2-c2 — Раскрываем скобки.
x2-d2+2bd+2dx-b2-2bx-x2=a2-c2 — Приводим подобные слагаемые.
2dx-2bx=a2-c2+d2+b2-2bd — Переносим все вправо, оставляя слева только y.
2x(d-b)=a2-c2+(d-b)2 — Выносим общие множители.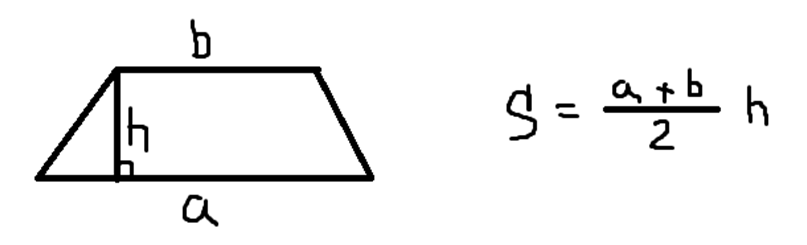
Подставляем обратно y в формулу высоты .
Формула площади трапеции через стороны будет выглядеть так:
Площадь трапеции через диагонали и угол между ними считается условным делением трапеции на четыре треугольника, точно также как и площадь любого произвольного четырехугольника.
Площадь равнобедренной трапеции можно найти еще одним способом, если даны угол при основании и радиус вписанной окружности. Дело в том, что центр вписанной окружности, откуда берет свое начало радиус, находится точно в центре трапеции, таким образом, приравнивая высоту и диаметр окружности (либо удвоенный радиус). Также одно из свойств трапеции, описанной вокруг окружности – это равенство суммы оснований и суммы боковых сторон, значит, мы сможем найти среднюю линию, зная боковые стороны. Проведя высоту, из прямоугольного треугольника получаем боковую сторону и среднюю линию
Тогда площадь трапеции равна
формулы площади, доказательства. Трапеция на занятиях с репетитоом по математике — Колпаков Александр Николаевич
Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
1) , где AD и BC основания, а BH-высота трапеции. Доказательство: проведем диагональ BD и выразим площади треугольников ABD и CDB через полупроизведение их оснований на высоту:
, где DP – внешняя высота в
Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:
Вынесем за скобку
Что и требовалось доказать.
Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то
2) Применение общей формулы площади четырехугольника.
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению .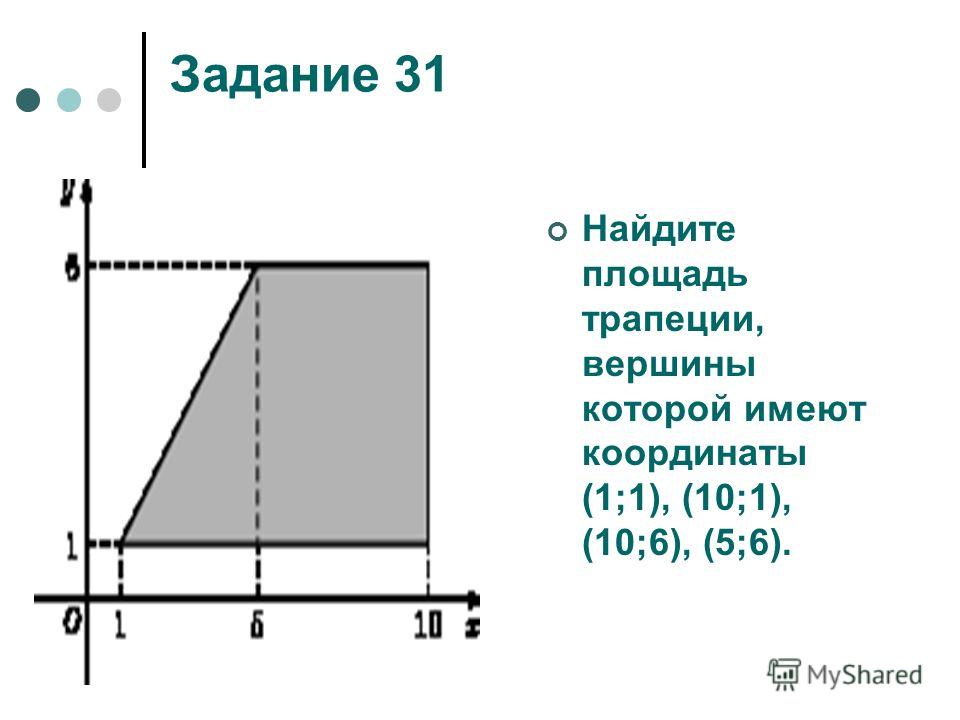 Отсюда
Отсюда
3) Метод сдвига диагонали
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции. С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
Спецприемы репетитора по математике.
Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать. Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Доказательство: проведем высоты SM и SN в треугольниках BCS и ADS и выразим сумму площадей этих треугольников:
Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:
Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.
В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции.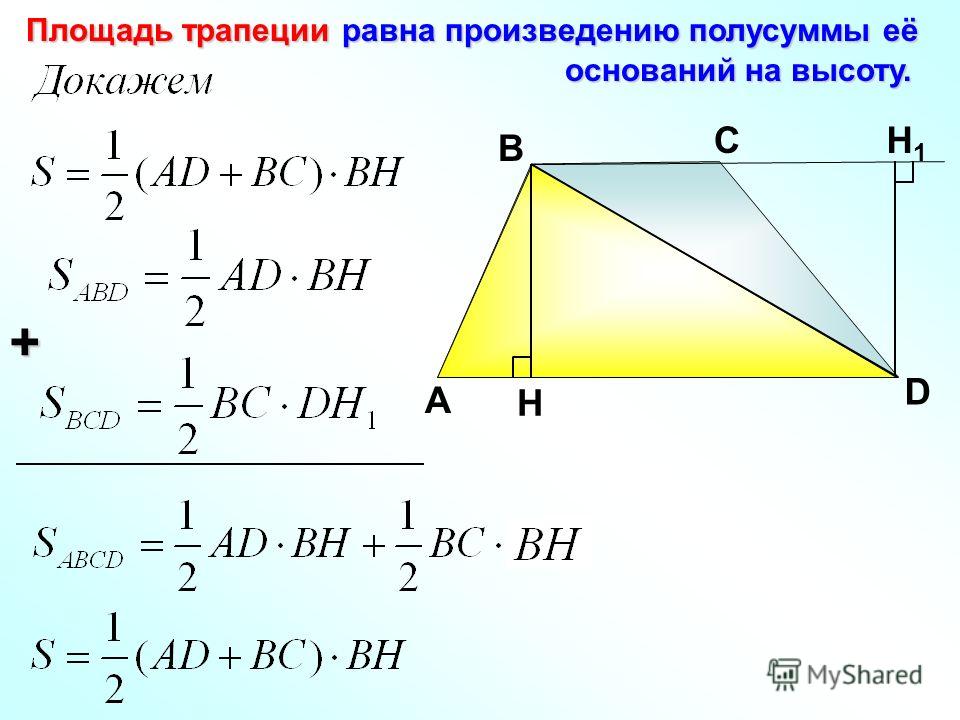 Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы :). Приходите на занятия!
Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы :). Приходите на занятия!
Задачи на площадь трапеции:
Замечание репетитора по математике: Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.
1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол . Найти площадь трапеции, если ее высота равна 6см.
Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см. Найдите расстояние до нее от середины противоположной боковой стороны.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).
Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.
Колпаков А.Н.
Репетитор по математике в Москве, подготовка к ЕГЭ в Строгино.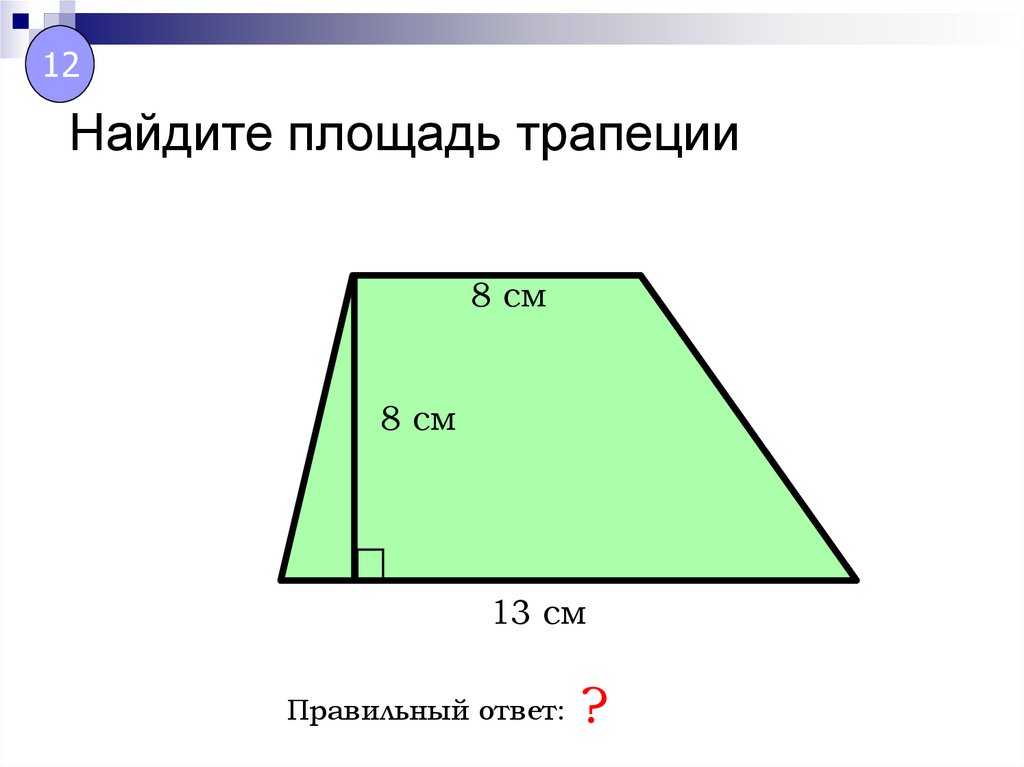
Как рассчитать площадь трапеции. Формула площади трапеции
Основные свойства трапеции
1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
AB + CD = BC + AD
2. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.
5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:
BC : AD = OC : AO = OB : DO
7. Диагонали трапеции d1 и d2 связаны со сторонами соотношением:
d12 + d22 = 2ab + c2 + d2
Формулы определения длин сторон трапеции:
1.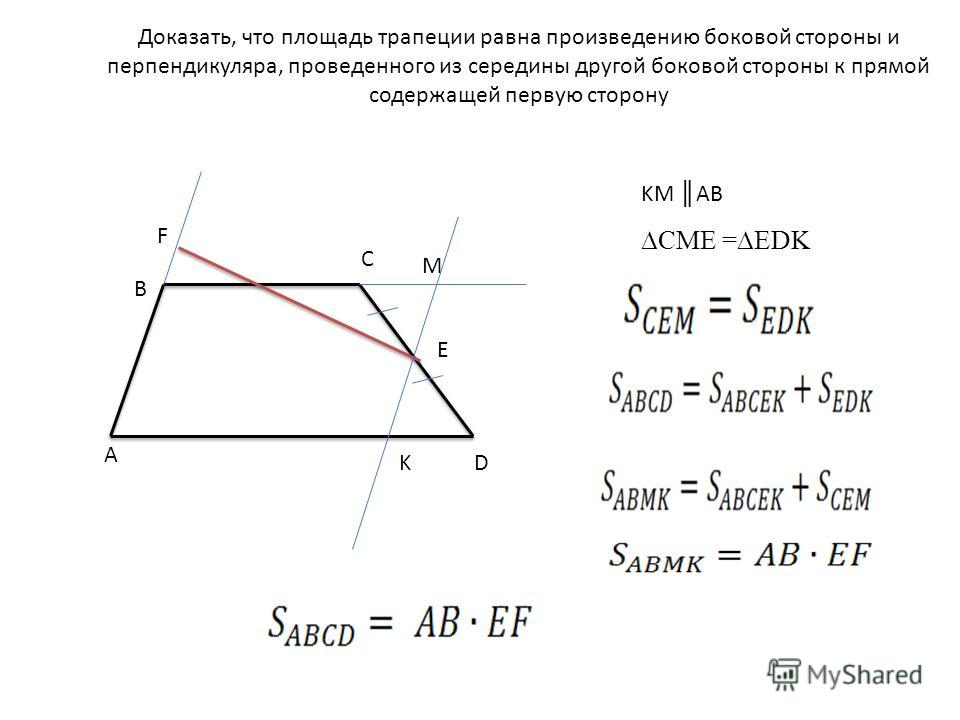 Формула длины оснований трапеции через среднюю линию и другую основу:
Формула длины оснований трапеции через среднюю линию и другую основу:
a = 2m – b
b = 2m – a
2. Формулы длины основ через высоту и углы при нижнем основании:
a = b + h · (ctg α + ctg β)
b = a – h · (ctg α + ctg β)
3. Формулы длины основ через боковые стороны и углы при нижнем основании:
a = b + c·cos α + d·cos β
b = a – c·cos α – d·cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
| с = | h | d = | h |
| sin α | sin β |
Как найти площадь трапеции через четыре стороны
Отнимите от большего основания меньшее.
Найдите квадрат полученного числа.
Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.
Поделите полученное число на удвоенную разность оснований.
Найдите квадрат результата и отнимите его от квадрата боковой стороны.
Найдите корень из полученного числа.
Умножьте результат на половину от суммы оснований.
- S – искомая площадь трапеции.
- a, b – основания трапеции.
- c, d – боковые стороны.
Средняя линия трапеции
Определение.
Средняя линия – отрезок, соединяющий середины боковых сторон трапеции.
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Через длины оснований и высоту
Чему равна площадь трапеции, если:
основание a =
основание b =
высота h =
Ответ: S =
0
ед.²
Округление ответа:
Чему равна площадь трапеции если известны основания a и b, а также высота h?
Формула
S = ½ ⋅ (a + b) ⋅ h
Пример
Если у трапеции основание a = 3 см, основание b = 6 см, а высота h = 4 см, то её площадь:
S = ½ ⋅ (3 + 6) ⋅ 4 = 36 / 2 = 18 см²
Площадь трапеции через перпендикулярные диагонали
{S= dfrac{1}{2} d_1 cdot d_2}
Формула для нахождения площади трапеции через перпендикулярные диагонали: {S=dfrac{1}{2}d_1 cdot d_2}, где d1, d2 — диагонали трапеции (перпендикулярные).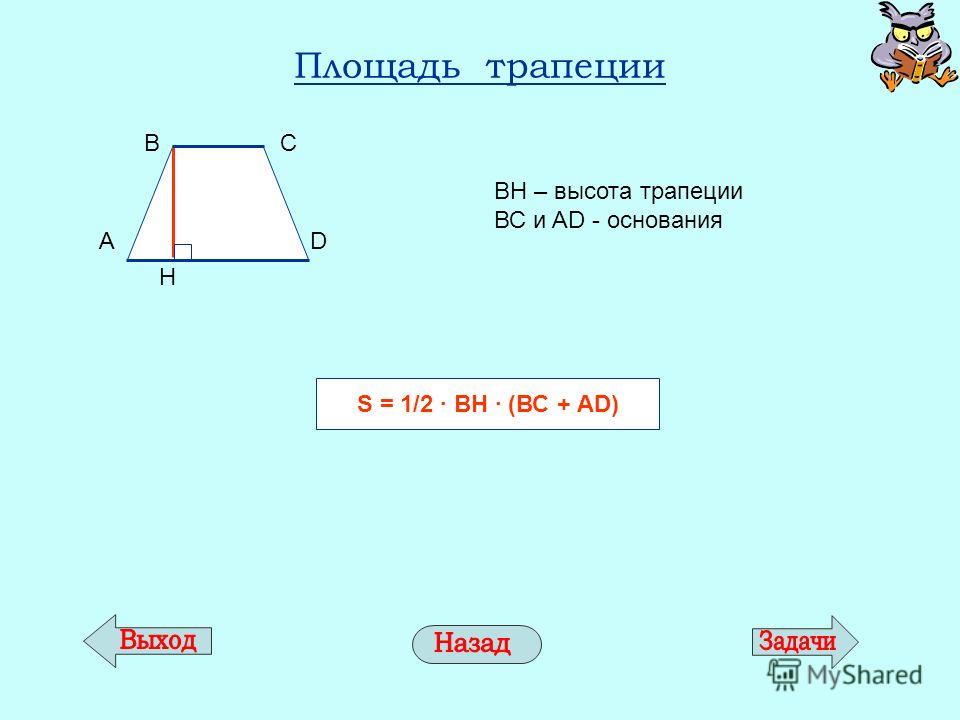
Как вычислить площадь равнобедренной трапеции через четыре стороны
Отнимите от большего основания трапеции меньшее и поделите результат на два.
Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.
Найдите корень из результата.
Умножьте полученное число на сумму оснований и поделите на два.
- S — искомая площадь трапеции.
- a, b — основания трапеции.
- c, d — боковые стороны (напомним, в равнобедренной трапеции они равны).
Таблица с формулами площади трапеции
В зависимости от известных исходных данных и вида трапеции, площадь трапеции можно вычислить по различным формулам.
Найти площадь равнобедренной трапеции, зная радиус вписанной окружности и угол
Радиус вписанной окружности r
Угол трапеции α
Сообщить об ошибке
Через среднюю линию, боковую сторону и угол при основании
Чему равна площадь трапеции, если:
средняя линия m =
сторона c =
угол α =
Ответ: S =
0
ед.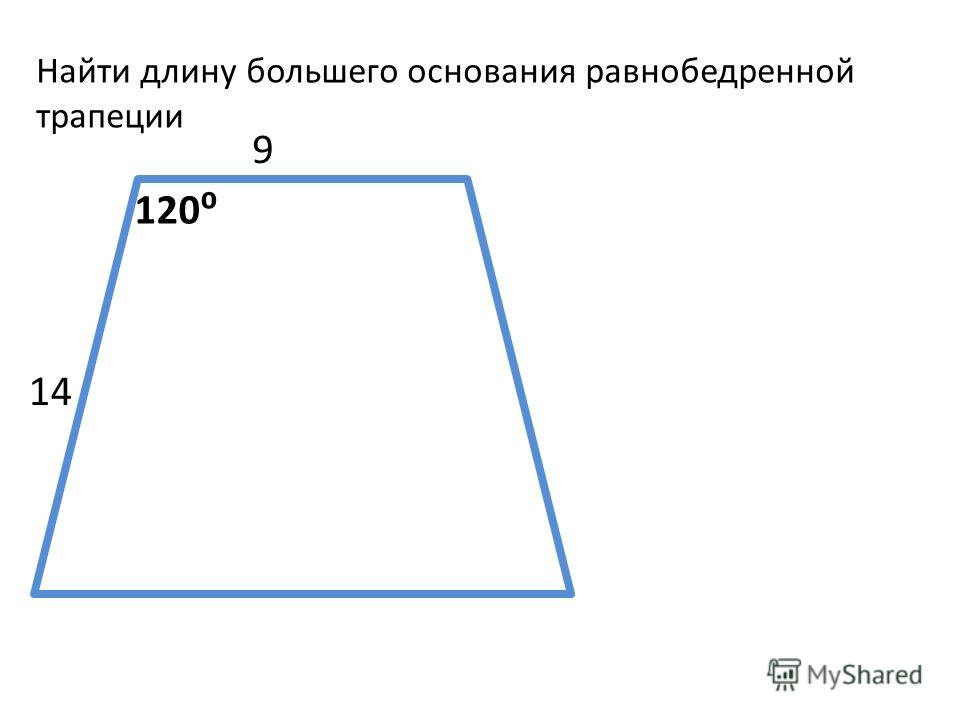 ²
²
Округление ответа:
Чему равна площадь равнобедренной трапеции если средняя линия m, боковая сторона с, a угол при основании α?
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Пусть a и b основания трапеции. доказать что отрезок, соединяющий середины её диагоналей равен 1/2 * | а – б|?
Возьмем трапецию ABCD
Определим точку М как середину диагонали АС, точку N как середину диагонали BD. Тогда средняя линия трапеции KF будет проходить через точки M и N.
Вспомним свойство средней линии трапеции: средняя линия трапеции является параллельной основаниям и равняется полусумме их длин.
Рассмотрим треугольник ACD:
MF = AD/2
Рассмотрим треугольник BCD
NF = BC/2
Выразим MN через отрезки MF и NF:
MN = MF-NF
Подставим в формулу значения отрезков MF и NF:
MN = AD/2-BC/2 = (AD-BC)/2
Площадь трапеции через основания и два угла
[ S = frac{1}{2} left( b^{2} – a^{2} right) frac{ sin(alpha) cdot sin(beta) }{sin(alpha + beta)} ]
- Параллельные стороны называются основаниями трапеции.

- Две другие стороны называются боковыми сторонами.
- Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
- Расстояние между основаниями называется высотой трапеции.
- Трапеция, у которой боковые стороны равны, называется равнобокой (или равнобедренной)
- Трапеция, один из углов которой прямой, называется прямоугольной.
- Средняя линия трапеции параллельна основаниям и равна их полусумме.
- Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
- У равнобокой трапеции углы при основании равны.
- У равнобокой трапеции диагонали равны.
- Если трапеция равнобокая, то около нее можно описать окружность.
- Если сумма оснований трапеции равна сумме боковых сторон, то в нее можно вписать окружность.

- В трапеции середины оснований, точка пересечения диагоналей и продолжения боковых сторон находятся на одной прямой.
Найти площадь трапеции, зная диагонали и угол между ними
Диагональ трапеции d1
Диагональ трапеции d2
Угол между диагоналями α
Источники
- https://ru.onlinemschool.com/math/formula/trapezium/
- https://Lifehacker.ru/kak-najti-ploshhad-trapecii/
- https://poschitat.online/ploshad-trapecii
- https://mnogoformul.ru/ploshhad-trapecii-formuly-i-kalkulyator-online
- https://doza.pro/art/math/geometry/area-trapezium
- https://geleot.ru/education/math/geometry/area/trapezoid
- https://yandex.ru/q/question/hw.math/kak_naiti_ploshchad_trapetsii_5a22794d/?answer_id=6adac048-9ff1-4e4b-8aae-c657d64364f1&w=answer&w_question_id=1327ad2e-f410-4eda-9d70-bc19c2d134e5&w_origin=grave_unauth
- https://calcsbox.com/post/formula-plosadi-trapecii. html
Площадь трапеции (формула) и как ее найти для любой трапеции на рисунке
Главная / ЧАстые ВОпросы
18 января 2021
- Что такое трапеция
- Что такое площадь
- Главная формула площади трапеции
- Доказательство теоремы о площади трапеции
- Как еще можно найти площадь (другие формулы)
- Формулы площади для равнобедренной трапеции
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo. ru. В этой статье мы расскажем, как посчитать площадь трапеции. Эту тему подробно изучают в школе в 8-м классе.
ru. В этой статье мы расскажем, как посчитать площадь трапеции. Эту тему подробно изучают в школе в 8-м классе.
Но в классической программе учителя дают далеко не все формулы, с помощью которых можно вычислить нужное значение. И ограничиваются, как правило, одной или двумя.
Мы же дадим максимально развернутый ответ на этот вопрос. Ведь трапеция – это весьма примечательная и сложная фигура в геометрии. А соответственно, и формулы для вычисления ее площади отличаются определенной сложностью и громоздкостью.
Тут нет банальных «перемножить длины сторон», как у площади прямоугольника. Все гораздо мудреней.
Что такое трапеция
Но для начала будет нелишним напомнить, что из себя представляет трапеция.
Трапеция – это геометрическая фигура, которая является четырехугольником, и у которой две противоположные стороны параллельны.
Последнее утверждение очень важное. ТОЛЬКО ДВЕ противоположные стороны параллельны у трапеции. Ведь если бы обе пары лежали на параллельных прямых, то это был бы уже параллелограмм.
Вот так выглядит трапеция:
А вот так параллелограмм:
Кстати, именно по этому принципу древний математик Евклид и разделил все четырехугольники на две большие категории.
Именно он впервые описал разные геометрические фигуры, в том числе трапеции и параллелограммы. И все свои соображения подробно изложил в книге «Начала», которая датируется 300 годом до нашей эры.
Что такое площадь
Раз уж мы решили вычислять эту величину, напомним, что она обозначает.
Площадь – это численное значение геометрической фигуры, нарисованной в двухмерном (плоском) пространстве. А проще говоря, это пространство, которое ограничено границами фигуры, и находится как бы внутри нее.
В нашем случае площадь трапеции – это область, закрашенная синим цветом:
Кстати, в древности вместо термина «площадь» говорили «квадратура». Считалось, что любую фигуру можно разбить на равные квадраты со стороной «один». Частично это понятие докатилось и до наших дней.
Ведь именно в «квадратных метрах» мы измеряем площадь комнаты/квартиры/дачи/офиса. И в «квадратных километрах» частенько озвучивают площадь какой-то территории. Например, когда в телевизионных новостях говорят о масштабах лесных пожаров или наводнений.
И в «квадратных километрах» частенько озвучивают площадь какой-то территории. Например, когда в телевизионных новостях говорят о масштабах лесных пожаров или наводнений.
Главная формула для вычисления площади трапеции
Та формула, которую изучают в школе, основана на вычислении площади трапеции по длине ее оснований и высоте.
Основания трапеции – это стороны, которые лежат на параллельных прямых. Другая пара сторон называется боковыми.
Высота – это отрезок, проведенный из вершины любого угла к противоположному основанию под углом 90 градусов.
То есть мы имеем вот такие исходные данные:
Здесь «a» и «b» являются основаниями трапеции, а «h» — высотой.
И тогда формула для вычисления площади трапеции выглядит вот так:
Например, если длины сторон и высота равны:
- a = 7 см
- b = 3 см
- h = 5 см
то площадь такой трапеции будет равна:
Опять же заметьте, если стороны и высота у трапеции обозначались в сантиметрах, то площадь будет измеряться в квадратных сантиметрах (то самое понятие «квадратуры», о котором мы писали выше).
То же самое – миллиметры/квадратные миллиметры, метры/квадратные метры, километры/квадратные километры и так далее.
Доказательство теоремы о площади трапеции
Любая формула в геометрии требует доказательства. И в нашем случае, формулы вычисления площади трапеции также доказывают во время уроков.
Возьмем для примера трапецию:
В ней AD и BC – основания, BH – высота. Нам надо доказать, что:
Доказательство строится на том, что если провести диагональ BD, то она разделит нашу трапецию на два треугольника. Это будут треугольники ABD и BCD.
И чтобы получить площадь нашей трапеции, нужно посчитать отдельно площади этих треугольников и сложить их.
А как вычислять площадь треугольника, мы уже знаем (или должны знать, согласно школьному курсу). Надо перемножить длину его основания и высоту и поделить на два.
У треугольника ABD высота – это BH. А у треугольника BCD в силу его выпуклости нам пришлось продлить зрительно основание BC, чтобы получить высоту Dh3.
И получается:
Но в случае с трапецией высоты равны, то есть BH = Dh3. И тогда формулу площади для второго треугольника можно заменить на:
И наконец, с учетом всего вышесказанного начинаем вычислять площадь нашей трапеции. Она равна:
Как часто говориться на уроках геометрии – что и требовалось доказать!
Извиняемся за столь подробное описание доказательства. Но, во-первых, это требуется в рамках школьной программы. А во-вторых, всегда ведь интересно докопаться до самой сути и понять, как и почему именно так что-то устроено.
Как еще можно найти площадь трапеции (другие формулы)
На этот раз мы уже не будем приводить подробные доказательства каждой из формул. Иначе это займет слишком много времени и места. Просто поверьте, все они правильные и по ним можно вычислить площадь трапеции.
По высоте и средней линии
Средняя линия – это та, которая делит боковые стороны трапеции на две равные части.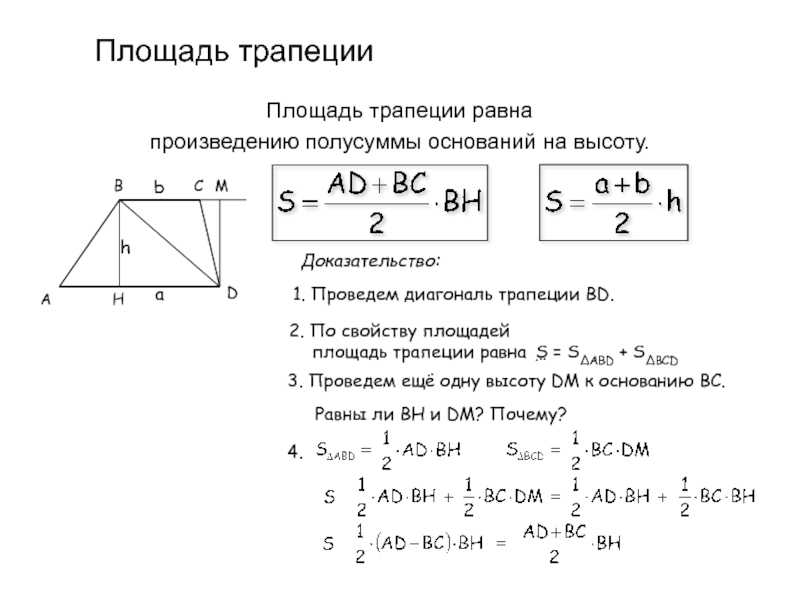 Формула площади выглядит совсем просто:
Формула площади выглядит совсем просто:
По четырем сторонам
Тут формула гораздо сложнее:
Площадь трапеции через диагонали
По основанию и углам при нем
Формулы площади для равнобедренной трапеции
Равнобедренная трапеция – та, у которой боковые стороны равны. А соответственно, они еще и соприкасаются с основаниями под одинаковыми углами.
Это частный случай, и для него верны все перечисленные формулы. Но с учетом равенства сторон и углов формулы заметно упрощаются.
По четырем сторонам
По малому основанию, боковой стороне и углу у большого основания
По большому основанию, углу при нем и боковой стороне
По основаниям и углам
Как видите, формулы громоздкие и весьма сложные сами по себе. Без калькулятора здесь точно не обойтись. С другой стороны, они крайне редко применяются. И служат скорее дополнительными средствами.
Вот и все, что мы хотели рассказать о том, как вычислять площадь трапеции.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo. ru
ru
Как найти площадь трапеции: формула, калькулятор онлайн
Информация
В нашей жизни такая отрасль, как строительство, является одной из важнейших. Это связанно с тем, что именно строительство позволяет нам жить в комфортных условиях, когда тепло, сухо и тихо. Однако, строительство также является невероятно ответственной сферой деятельности. Это целый процесс, состоящий из проектирования, расчетов, технических работ и многих других нюансов. Специалисты, осуществляющие все работы (механические и теоретические) в процессе строительства, несут большую ответственность за жизни тех людей, которые в дальнейшем будут эксплуатировать здание.
Поэтому они обязаны внимательно проводить расчеты различных значений показателей, одним и которых является формула площади трапеции. Данная формула является одной из многих формул, которые обязаны знать специалисты определенных отраслей. Также стоит учитывать существующее разнообразие трапеций: прямоугольные, равнобедренные и произвольные. Всю подобную информацию обязаны учитывать сотрудники многих отраслей и знать, как найти площадь трапеции.
Всю подобную информацию обязаны учитывать сотрудники многих отраслей и знать, как найти площадь трапеции.
Онлайн калькулятор расчёта площади трапеции
Мы разработали калькулятор, который существенно упрощает работу людям как в сфере строительства, так и в многих других сферах деятельности. Наш калькулятор поможет просчитать площадь прямоугольной трапеции в кротчайшие сроки и избегая вероятности допущения какой-либо ошибки при расчетах. Помимо прямоугольной трапеции, калькулятор может рассчитать площадь равнобедренной трапеции, также просто. Для этого Вам нужно просто ввести исходные данные, которые запрашивает калькулятор.
Наш калькулятор запрограммирован таким образом, что он не только рассчитывает площадь любого вида трапеции, и сообщает чему она ровна, в одно мгновение, но и демонстрирует формулы расчета, а также дает Вам возможность выбрать по какой формуле рассчитать площадь трапеции.
Наш калькулятор онлайн дает большое количество преимуществ:
- Возможность расчета площади трапеции через любую формулу;
- Сэкономить много времени, благодаря отсутствию необходимости самостоятельного расчета;
- Исключить допущение ошибок при расчетах, поскольку программа не попадает под влияние человеческого фактора.

Таким образом, калькулятор онлайн является эффективным инструментом как для строителя, так и любого другого человека, который столкнулся с необходимостью расчета какого-либо показателя.
Как найти площадь трапеции: формулы и примеры
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h.
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h. Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.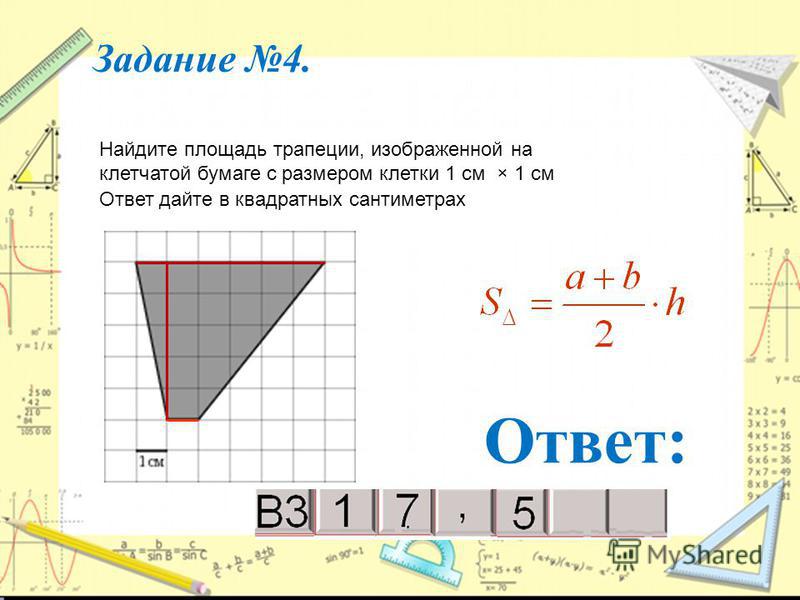
Рассмотрим еще один вариант: в трапеции проведены диагонали d1и d2, которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d1d2 *sinα.
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c2 – ( ( 1/2(b – a)) * ((b – a)2 + c2 – d2) )2.
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r2/sinα. Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 300: S = 8r2.
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d1 и d2, а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h2.
Формула площади криволинейной трапеции
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка [a; b] на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок [a; b]), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫baf(x)dx = F(x)│ba = F(b) – F(a). В этой формуле F – первообразная нашей функции на выбранном отрезке [a; b]. И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение: Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ2 = АР2 + РХ2). И высчитать его площадь: SAPX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см2.
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими.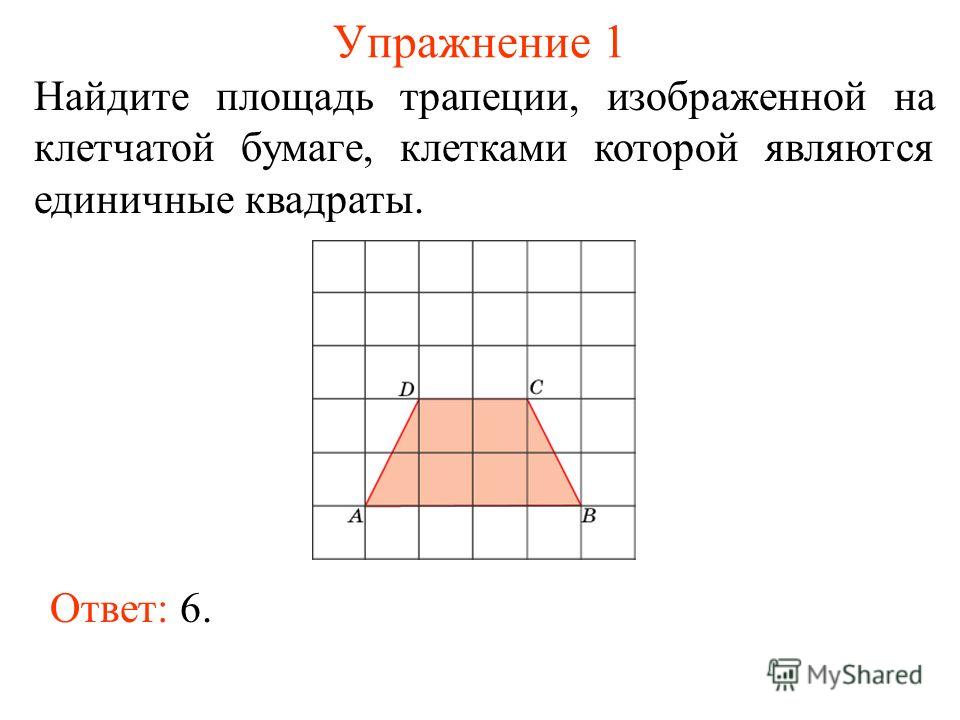 Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что SAMPC = SAPX = 54 см2.
Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Решение: Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
Введем еще одно обозначение – ОЕ = х. А также высоту h1 для треугольника ТМЕ и высоту h2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h1 = 1/5(b + х) * h2. Преобразуем и получим: h1/ h2 = 1/5 * ((b + х)/(х + а)).
Преобразуем и получим: h1/ h2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h1/ h2 = (х – а)/( b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х2 – а2) = (b2 – х2) ↔ 6х2 = b2 + 5а2 ↔ х = √(5а2 + b2)/6.
Таким образом, ОЕ = х = √(5а2 + b2)/6.
Также советуем посмотреть вам наше новое видео по теме нахождения площади фигур, в том числе и трапеции:
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.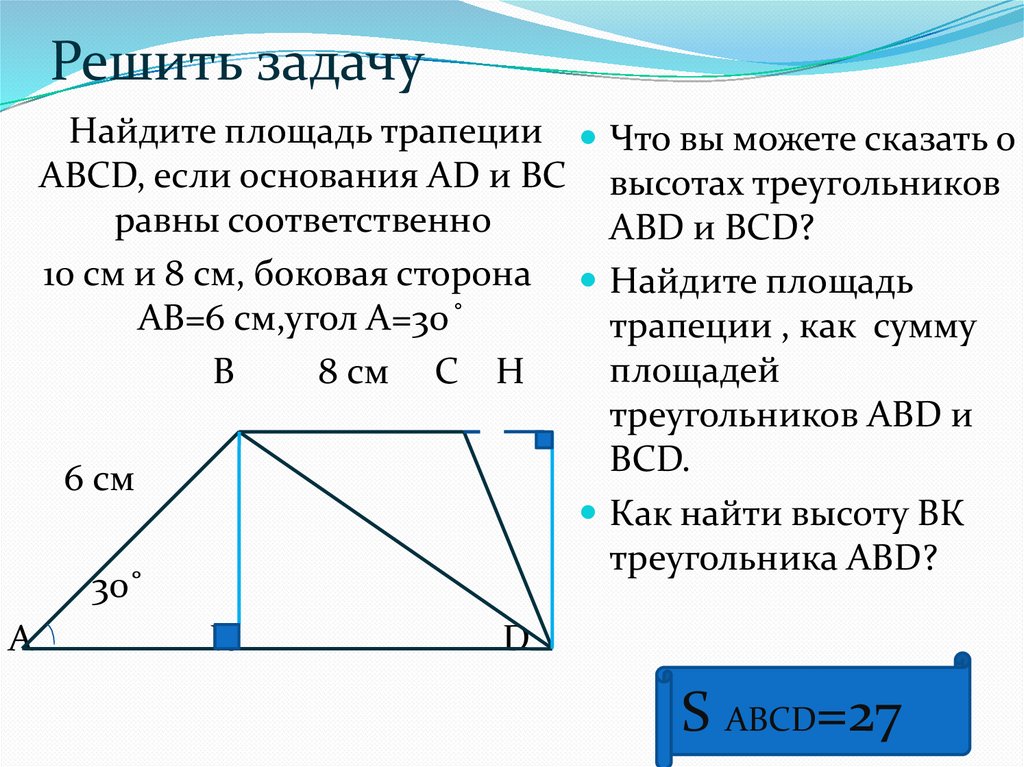
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Как найти площадь трапеции (формула и видео) // Tutors.com
Содержание
- Что такое трапеция?
- Как найти площадь трапеции
- Площадь трапеции, формула
Трапеция представляет собой четырехугольник с одной парой параллельных сторон. Итак, этот четырехсторонний многоугольник представляет собой плоскую фигуру и замкнутую фигуру. Он имеет четыре отрезка линии и четыре внутренних угла.Параллельные стороны — это две базы трапеции ; две другие стороны — его ноги.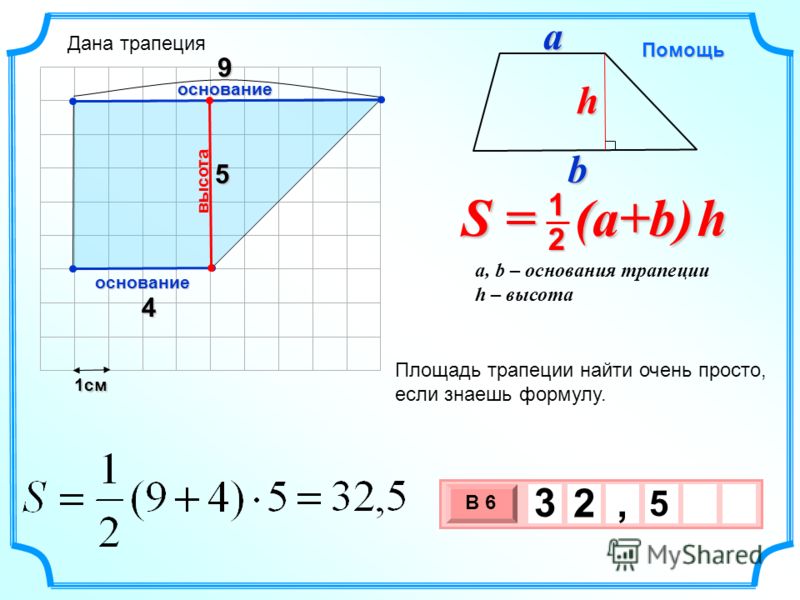
Обычно у трапеции более длинная параллельная сторона — основание , — горизонтально. Перпендикулярная линия от основания к другой параллельной стороне даст вам высоту трапеции или высоту .
Что такое средний по математике?
В математике среднее значение представляет собой сумму группы чисел, деленную на количество элементов в группе.
Итак, если у вас есть три человека, которые держат книги, вы можете найти среднее количество книг, которые они держат, вот так: Мартин держит 5 книг, Мак держит 3 книги, а Мария держит 4 книги. Вместе 12 книг держат 3 человека. Итак, 12 книг ÷ 3 человека = в среднем по 4 книги.
Чтобы найти площадь трапеции, вы найдете среднюю длину двух оснований.
Как найти площадь трапеции
Чтобы найти площадь любой трапеции, начните с обозначения ее основания и высоты.На нашей трапеции обозначьте более длинное основание a и более короткое основание b. Обозначьте линию, перпендикулярную двум основаниям, h для высоты или высоты трапеции.
Обратите внимание, мы не пометили ноги. Нам не нужно ничего знать о длине ног или углах вершин, чтобы найти площадь.
Площадь трапеции, формула
Формула площади трапеции — это среднее значение оснований, умноженное на высоту. В формуле длинное и короткое основание — это a и b, а высота — h:
Умножение на 12 аналогично делению на 2.Мы берем половину суммы длины двух оснований (их среднее значение), а затем умножаем ее на высоту или высоту, чтобы найти площадь в квадратных единицах.
Уравнение площади трапеции
Трапеция LMNO имеет параллельные основания LM и NO. Линейный сегмент LM имеет длину 7 см, а линейный сегмент NO — 13 см. Мы обозначим более длинную сторону NO как a, а короткую сторону LM как b. Высота h 5 см.
Сначала давайте подставим эти числа в нашу формулу:
площадь = 13 см + 7 см2 × 5 см
Далее складываем 13 плюс 7 и получаем:
площадь = 20 см2 × 5 см
Потом делим на два и получаем:
площадь = 10 см × 5 см
Наконец, умножаем и получаем ответ:
площадь = 50 см2
Площадь этой трапеции составляет 50 квадратных сантиметров.
Площадь трапеции Примеры
Теперь попробуйте! Другая трапеция имеет длинное основание a, 11 метров, и более короткое основание b, 7 метров. Его высота h составляет 9 метров. Какая площадь в квадратных метрах?
площадь = 11 см + 7 см2 × 9 см
Получили 81 квадратный метр? Ваш ответ для площади всегда выражается в квадратных единицах линейного измерения. Таким образом, трапеция, измеренная в футах, дает площадь в квадратных футах, сантиметры — в квадратных сантиметрах и так далее.
Помните, что умножение на 1/2 аналогично делению на 2, поэтому вы можете сложить длины оснований, а затем разделить их сумму на два, если вам так легче.
Из-за коммутативности умножения вы можете переставить эти три числа, 12, высоту h и длину основания a + b, в любом порядке, чтобы упростить вычисление.
Итак, с трапецией LMNO вы могли бы написать такую формулу, как:
площадь = 12 × 9 × (11 + 7)
Пример # 2
Вот вам еще один пример. Новая трапеция перевернута по сравнению с тем, как вы их обычно видите, но пусть это вас не остановит! Короткое основание b имеет длину 21 дюйм. Длинное основание a (на этот раз вверху рисунка) составляет 31 дюйм в длину. Высота h (независимо от того, с какой стороны вы смотрите на трапецию) составляет 5 дюймов.
Длинное основание a (на этот раз вверху рисунка) составляет 31 дюйм в длину. Высота h (независимо от того, с какой стороны вы смотрите на трапецию) составляет 5 дюймов.
площадь = 12 × 5 × (31 + 21)
ИЛИ
площадь = 12 × (31 + 21) × 5
ИЛИ
площадь = 31 + 212 × 5
Как бы вы ни использовали формулу, вы всегда получите один и тот же ответ: площадь = 130 дюйм2
Краткое содержание урока
В этом уроке и видео мы рассмотрели, что такое трапеция, изучили, как средние значения играют роль в геометрии, научились маркировать и использовать части трапеции для вычисления площади, а также узнали формулу для вычисления площади трапеции в квадратные единицы.
Следующий урок:
Формула Герона
Площадь трапеции — пояснения и примеры
Напомним, трапеция , также называемая трапецией , — это четырехугольник с одной парой параллельных сторон и другой парой непараллельных сторон. Подобно квадрату и прямоугольнику, трапеция также плоская. Следовательно, это 2D.
Подобно квадрату и прямоугольнику, трапеция также плоская. Следовательно, это 2D.
В трапеции параллельные стороны известны как основания, а пара непараллельных сторон известна как ноги.Расстояние по перпендикуляру между двумя параллельными сторонами трапеции называется высотой трапеции.
Проще говоря, основание и высота трапеции перпендикулярны друг другу.
Трапеции могут быть как правыми трапециями (два угла 90 градусов), так и равнобедренными трапециями (две стороны одинаковой длины). Но иметь один прямой угол невозможно, потому что у него есть пара параллельных сторон, которые ограничивают его, образуя два прямых угла одновременно.
Из этой статьи вы узнаете:
- Как найти площадь трапеции,
- Как получить формулу площади трапеции и,
- Как найти площадь трапеции с помощью трапеции формула площади.
Как найти площадь трапеции?
Площадь трапеции — это область, покрытая трапецией в двухмерной плоскости.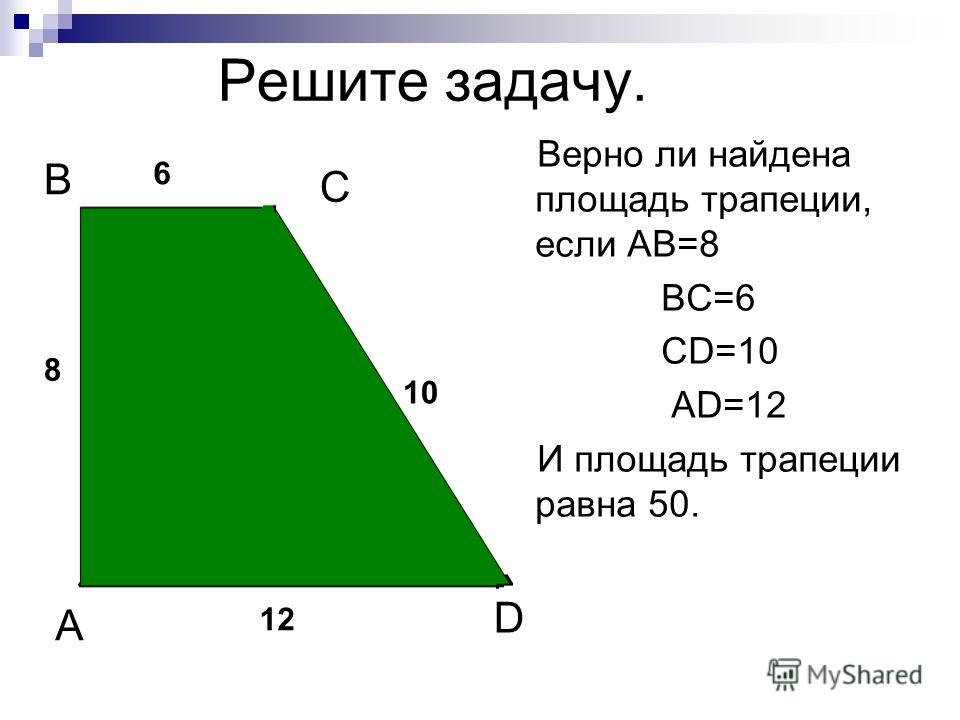 Это пространство, заключенное в 2D-геометрии.
Это пространство, заключенное в 2D-геометрии.
На рисунке выше трапеция состоит из двух треугольников и одного прямоугольника.Следовательно, мы можем вычислить площадь трапеции, взяв сумму площадей двух треугольников и одного прямоугольника.
Вывести формулу площади трапеции
Площадь трапеции ADEF = (½ x AB x FB ) + ( BC x FB ) + (½ x CD x EC )
= ( ¹ / ₂ × AB × h ) + ( BC × h ) + (¹ / ₂ × CD × h )
= ¹ / ₂ × h × ( AB + 2 BC + CD )
= ¹ / ₂ × h × ( FE + AD )
Но, FE = b 1 и AB = b 2
Следовательно, Площадь трапеция ADEF ,
= ¹ / ₂ × h × (b 1 + b 2 ) ……………….(Это формула площади трапеции)
Формула площади трапеции
Согласно формуле площади трапеции, площадь трапеции равна половине произведения высоты и суммы двух оснований.
Площадь = ½ x (сумма параллельных сторон) x (расстояние по перпендикуляру между параллельными сторонами).
Площадь = ½ h (b 1 + b 2 )
Где h — высота, а b 1, и b 2 — параллельные стороны трапеции.
Как определить площадь неправильной трапеции?
Неровная трапеция имеет непараллельные стороны неравной длины. Чтобы найти его площадь, вам нужно найти сумму оснований и умножить ее на половину высоты.
В вопросе иногда не хватает высоты, что можно найти с помощью теоремы Пифагора.
Как найти периметр трапеции?
Вы знаете, что периметр — это сумма всех длин внешнего края фигуры.Следовательно, периметр трапеции — это сумма длин всех 4 сторон.
Пример 1
Вычислите площадь трапеции, высота которой составляет 5 см, а основания — 14 см и 10 см.
Решение
Пусть b 1 = 14 см и b 2 = 10 см
Площадь трапеции = ½ h (b 1 + b 2 ) см 2
= ½ x 5 (14 + 10) см 2
= ½ x 5 x 24 см 2
= 60 см 2
Пример 2
Найдите площадь трапеции с высота 30 мм, а основания 60 мм и 40 мм.
Раствор
Площадь трапеции = ½ h (b 1 + b 2 ) кв. Единиц
= ½ x 30 x (60 + 40) мм 2
= ½ x 30 x 100 мм 2
= 1500 мм 2
Пример 3
Площадь трапеции составляет 322 квадратных дюйма. Если длины двух параллельных сторон трапеции составляют 19 дюймов и 27 дюймов, найдите высоту трапеции.
Раствор
Площадь трапеции = ½ часа (b 1 + b 2 ) кв.единицы измерения.
⇒ 322 квадратных дюйма = ½ x в x (19 + 27) кв. дюймов
⇒ 322 квадратных дюйма = ½ x h x 46 кв. дюймы
⇒ 322 = 23h
Разделите обе стороны на 23.
h = 14
Итак, высота трапеции составляет 14 дюймов.
Пример 4
При условии, что высота трапеции составляет 16 м, а длина одного основания — 25 м. Рассчитайте размер другого основания трапеции, если его площадь составляет 352 м 2 .
Решение
Пусть b 1 = 25 м
Площадь трапеции = ½ h (b 1 + b 2 ) кв. Единиц
⇒ 352 м 2 = ½ x 16 м x (25 m + b 2 ) квадратных единиц
⇒ 352 = 8 x (25 + b 2 )
⇒ 352 = 200 + 8b 2
Вычтите 200 с обеих сторон.
⇒ 152 = 8b 2
Разделите обе стороны на 8, чтобы получить;
b 2 = 19
Следовательно, длина другого основания трапеции составляет 19 м.
Пример 5
Рассчитайте площадь трапеции, показанной ниже.
Решение
Поскольку стороны (непараллельные стороны) трапеции равны, то высоту трапеции можно рассчитать следующим образом;
Чтобы получить основание двух треугольников, вычтите 15 см из 27 см и разделите на 2.
⇒ (27-15) / 2 см
⇒ 12/2 см = 6 см
12 2 = h 2 + 6 2 По теореме Пифагора высота (h) рассчитывается как;
144 = h 2 + 36.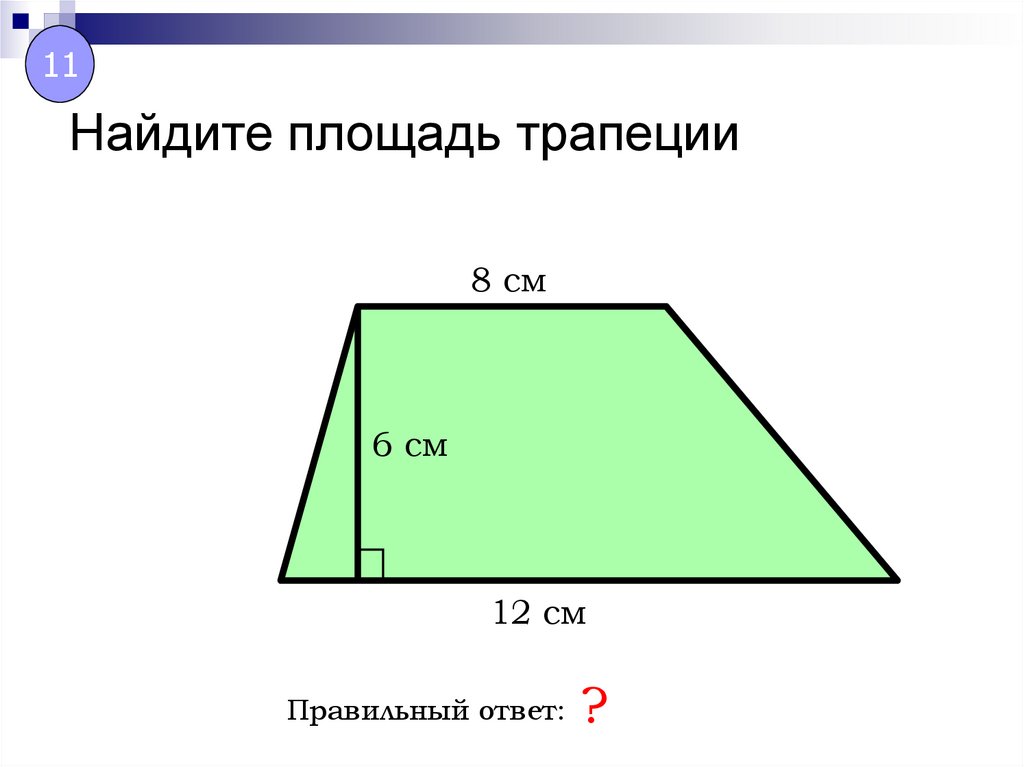
Вычтем 36 с обеих сторон.
h 2 = 108.
h = 10,39 см.
Следовательно, высота трапеции 10,39 см.
Теперь вычислите площадь трапеции.
Площадь трапеции = ½ ч (b 1 + b 2 ) кв. единицы измерения.
= ½ x 10,39 x (27 + 15) см 2 .
= ½ x 10,39 x 42 см 2 .
= 218,19 см 2 .
Пример 6
Одно основание трапеции на 10 м больше высоты.Если другое основание составляет 18 м, а площадь трапеции равна 480 м 2 , найдите высоту и основание трапеции.
Решение
Пусть высота = x
Другая база равна 10 м, чем высота = x + 10.
Площадь трапеции = ½ h (b 1 + b 2 ) Кв. единицы измерения.
Путем подстановки
480 = ½ * x * (x + 10 + 18)
480 = ½ * x * (x + 28)
Используйте свойство распределения, чтобы удалить круглые скобки.
480 = ½x 2 + 14x
Умножьте каждый член на 2.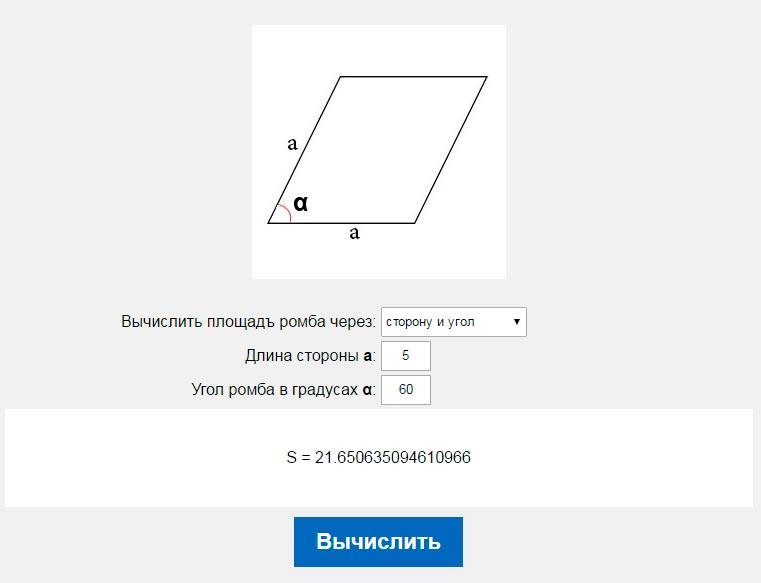
960 = x 2 + 28x
x 2 + 28x — 960 = 0
Решите квадратное уравнение, чтобы получить;
x = — 48 или x = 20
Подставьте положительное значение x в уравнение высоты и основания.
Высота: x = 20 м.
Другая база = x + 10 = 10 + 20 = 30 м.
Следовательно, другое основание и высота трапеции 30 и 20 м соответственно.
Практические задачи
- Найдите площадь трапеции, у которой есть параллельные основания длиной 9 единиц и 12 единиц, а высота равна 15 единицам.
- Для трапециевидной фигуры сумма параллельных оснований составляет 25 м, а высота — 10 м. Определите площадь этой фигуры.
- Рассмотрим трапецию площадью 112b квадратных футов, где b — более короткая базовая длина. Какова высота этой трапеции, если длины двух параллельных оснований таковы, что одно основание в два раза больше, чем другое основание?
Калькулятор площади трапеции
Если у вас когда-либо были проблемы с запоминанием формул в классе геометрии, эта область калькулятора трапеции обязательно вам поможет.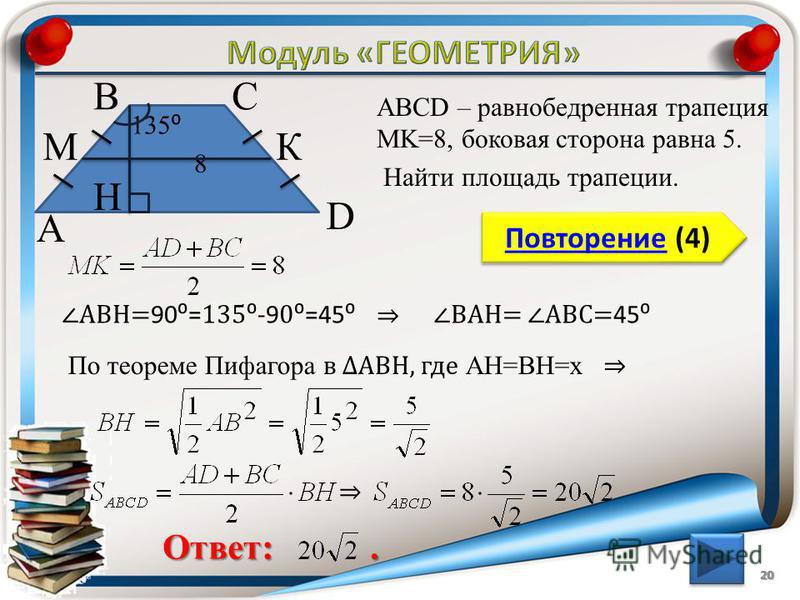 Всего за несколько простых шагов вы сможете найти площадь трапеции и определить все другие ее свойства, такие как длины сторон или внутренние углы. Итак, если вас беспокоят такие вопросы, как «как найти периметр трапеции», не смотрите дальше — просто продолжайте читать, чтобы узнать!
Всего за несколько простых шагов вы сможете найти площадь трапеции и определить все другие ее свойства, такие как длины сторон или внутренние углы. Итак, если вас беспокоят такие вопросы, как «как найти периметр трапеции», не смотрите дальше — просто продолжайте читать, чтобы узнать!
Вы также можете воспользоваться нашим калькулятором длины окружности, чтобы более подробно проанализировать геометрию круга.
Что такое трапеция?
Трапеция — это четырехсторонняя геометрическая форма, две стороны которой параллельны друг другу.Эти две стороны ( a и b на изображении выше) называются основаниями трапеции. Две другие стороны ( c и d ) называются ножками. h — высота трапеции.
Сумма всех внутренних углов трапеции дает 360 °. Кроме того, углы на одной стороне ножки называются смежными и всегда в сумме составляют 180 °:
α + β = 180 °
γ + δ = 180 °
Как найти площадь трапеции?
Площадь трапеции находится по следующей формуле:
A = (a + b) * h / 2
Вы можете заметить, что для трапеции с a = b (и, следовательно, c = d = h) формула упрощается до A = a * h , что в точности соответствует формуле для площади прямоугольника.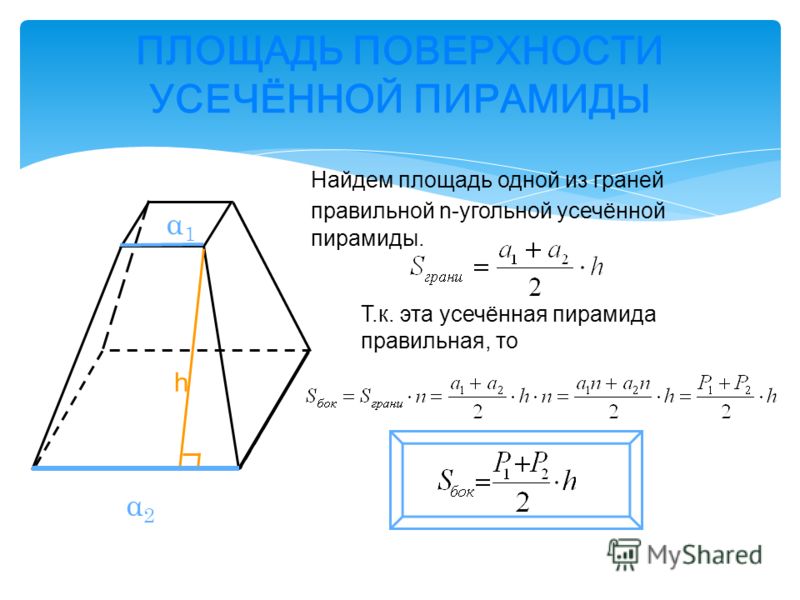
Как найти периметр трапеции?
Вы также можете использовать вычислитель площади трапеции, чтобы найти периметр этой геометрической формы. Просто сложите все стороны длины вместе:
P = a + b + c + d
Использование калькулятора площади трапеции: пример
Предположим, вы хотите вычислить площадь определенной трапеции. Все данные:
α = 30 °
γ = 125 °
h = 6 см
a = 4 см
P = 25 см
Рассчитайте оставшиеся внутренние углы.Поскольку
α + β = 180 °,β = 180 ° - 30 ° = 150 °.Аналогично, как
γ + δ = 180 °,δ = 180 ° - 125 ° = 55 °.Найдите длины сторон трапеции, используя формулу синуса угла:
sin 30 ° = ц / ч
sin 55 ° = д / ч
c = sin 30 ° * 6 = 12 см
d = sin 55 ° * 6 = 7,325 см
- Вычтите значения a, c и d из периметра трапеции, чтобы найти длину второго основания:
b = P - a - c - d = 25-4-12-7.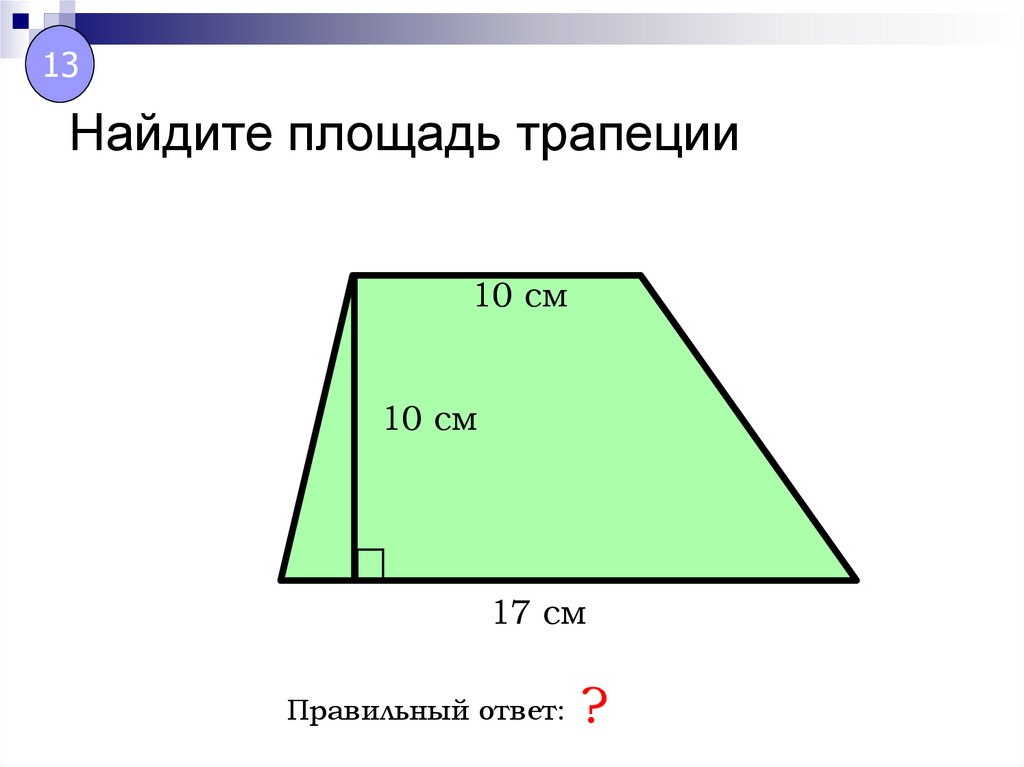 325 = 1,675 см
325 = 1,675 см
- Наконец, примените формулу площади трапеции:
A = (a + b) * h / 2 = (4 + 1,675) * 6/2 = 17,026 см²
Обязательно взгляните и на калькулятор шестиугольника!
Площадь трапеции. Определение, формула и калькулятор
Площадь трапеции. Определение, формула и калькулятор — Открытый справочник по математике
Количество квадратных единиц, необходимое для полного заполнения
трапеция.
Формула: Средняя ширина × высота
Попробуйте это Перетащите оранжевые точки, чтобы переместить трапецию и изменить ее размер. Как размер трапеции
изменяется, производится пересчет площади.
Формула площади
Площадь трапеции равна средней ширине, умноженной на высоту, или по формуле:
где
b1, b2 — длины каждого основания,
h — высота (высота)
Напомним, что основания — это две параллельные стороны трапеции.
Высота (или высота) трапеции — это
перпендикулярное расстояние
между двумя базами.
В приведенном выше апплете нажмите «заморозить размеры». Когда вы перетаскиваете любую вершину, вы увидите, что трапеция перерисовывается, сохраняя неизменными высоту и основания. Обратите внимание, как область в отображаемой формуле не меняется. Площадь зависит только от высоты и длины основания, поэтому, как видите, существует множество трапеций с заданным набором размеров, которые имеют одинаковую площадь.
Вывод формулы
См. Раздел «Как получить формулу площади трапеции».
Калькулятор
Используйте калькулятор выше, чтобы рассчитать высоту, базовую длину и площадь трапеции.
Введите любые три значения, и будет вычислено недостающее.
Например: введите высоту и две базовые длины и нажмите «Рассчитать». Площадь будет рассчитана.
Точно так же, если вы введете площадь и две длины основания, будет рассчитана высота, необходимая для получения этой площади.
Определение высоты по площади
Как найти высоту (высоту) трапеции, задайте две базы и площадь.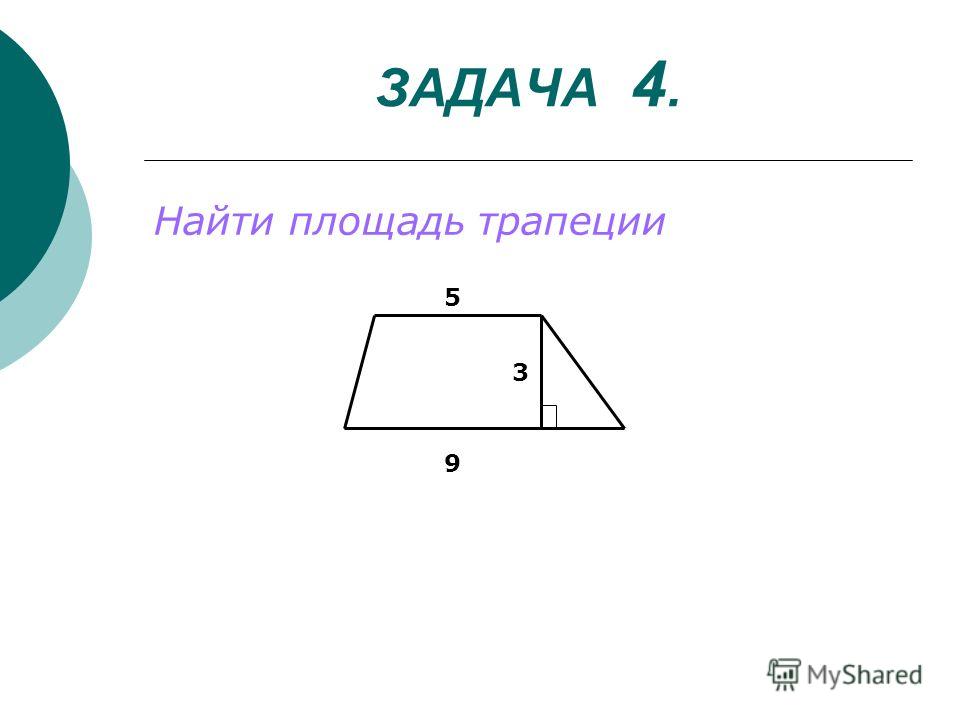 Приведенная выше основная формула площади имеет четыре переменные (площадь, два основания и высоту). Если мы знаем какие-то три, мы всегда сможем найти четвертый.
Приведенная выше основная формула площади имеет четыре переменные (площадь, два основания и высоту). Если мы знаем какие-то три, мы всегда сможем найти четвертый.
Так, например, если мы знаем площадь и две базы, мы можем найти высоту, просто изменив основную формулу:
Где a — площадь, а b1, b2 — две базы.
Поиск базы в районе
Как найти основание трапеции, укажите одно из оснований, высоту и площадь.
Приведенная выше основная формула площади имеет четыре переменные (площадь, два основания и высоту).Если мы знаем какие-то три, мы всегда сможем найти четвертый.
Так, например, если мы знаем площадь, одно основание и высоту, мы можем найти недостающее основание, просто изменив основную формулу:
Где a — это площадь, b — известная база, а h — высота (высота).
Если известно медианное значение
Напомним, что
медиана (м) трапеции
— отрезок прямой, соединяющий середины непараллельных сторон.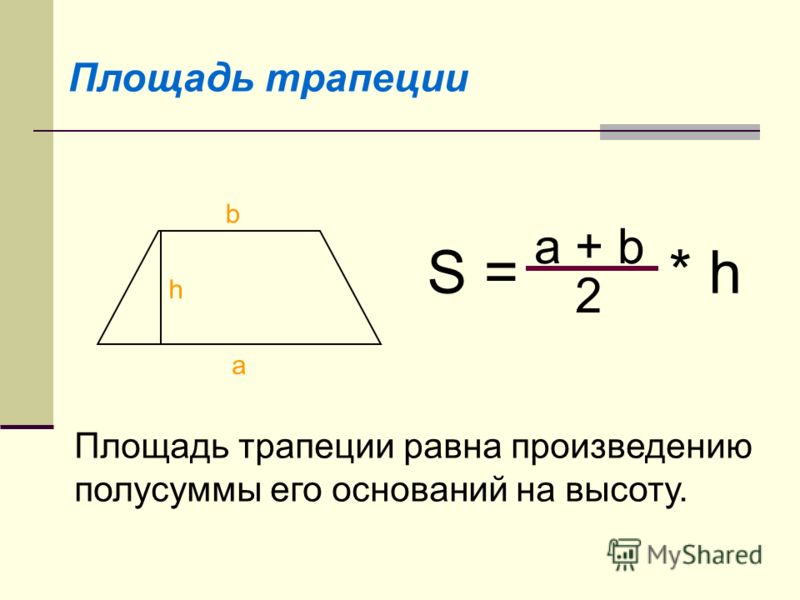 Напомним также, что длина медианы — это среднее значение двух параллельных сторон.См. Медиану трапеции
Напомним также, что длина медианы — это среднее значение двух параллельных сторон.См. Медиану трапеции
Где м, — это медиана, а х — высота (высота).
Площадь как сложная форма
Другой способ найти площадь трапеции — рассматривать ее как более простые формы, а затем добавлять или вычитать их площади, чтобы найти результат. Для
Например, трапецию можно рассматривать как меньший прямоугольник плюс два прямоугольных треугольника:
Дополнительные сведения об этой общей технике см. В разделе «Область неправильных многоугольников».
Координатная геометрия
В координатной геометрии, если вы знаете координаты четырех вершин,
вы можете рассчитать различные его свойства, в том числе площадь и периметр.Для получения дополнительной информации см. Площадь и периметр трапеции (Координатная геометрия).
Что стоит попробовать
- На рисунке выше нажмите «скрыть детали»
- Перетащите оранжевые точки на вершинах, чтобы образовалась трапеция произвольного размера.

- Рассчитайте площадь по формуле
- Теперь попробуйте оценить площадь трапеции, просто глядя на
квадратов внутри нее - Когда вы закончите, нажмите «Показать детали», чтобы увидеть, насколько близко вы подошли.
Другие полигоны
Общий
Типы многоугольника
Площадь различных типов полигонов
Периметр различных типов полигонов
Углы, связанные с многоугольниками
Именованные полигоны
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Площадь трапеции Калькулятор
- Цель использования
- требуется способность
- Комментарий / запрос
- потребности возможность смены левой и правой сторон
[1] 2021.03.31 02:55 Мужчина / До 20 лет / Другое / Немного /
- Цель использования
- найдите область трапеции с неизвестной высотой
[2] 2021/02/26 00:48 Женский / До 20 лет / Начальная школа / Младший старшеклассник / Не совсем /
- Цель использования
- Догоняй по математике работа
[3] 23. 02.2021 22:14 Женский / — / Старшая школа / Университет / Аспирант / Полезно /
02.2021 22:14 Женский / — / Старшая школа / Университет / Аспирант / Полезно /
- Цель использования
- Помощь со школой
[4] 2021.01.21 00:14 Мужчина / До 20 лет / Начальная школа / Неполный средний класс / Полезно /
- Цель использования
- Расчеты для инженерного проекта в работе
[5 ] 22.09.2020 04:12 Женщина / Уровень 20 лет / Инженер / Очень / 9002 1
- Цель использования
- Требуется поверхность крыши в саду
[6] 24.07.2020 19:57 Мужской / 20-летний уровень / Высшая школа / Университет / Аспирант / Очень /
- Цель использования
- помогите с домашним заданием
[7] 30.01.2020 10:10 Женский / До 20 лет / Начальная школа / Младший школьник / — /
- Цель использования
- Разработка плана этажа дома
- Комментарий / Запрос
- Было бы Было бы неплохо, если бы была включена формула для нахождения длин диагональных сторон трапеции
[8] 2019/11/28 02:47 Женщина / Уровень 20 / Домохозяйка / Очень /
- Цель использования
- Путать формулой 908 25
[9] 2018/12/03 10:50 Женщина / Моложе 20 лет / Начальная школа / Ученица неполной средней школы / Очень /
- Сообщение об ошибке
- Шеттейл размером 110 × 110 × 110 × 87 футов и высотой 18 футов.
 Сколько бумаги требуется для крышки бака.
Сколько бумаги требуется для крышки бака.
[10] 2018/06/24 01:51 Мужчина / уровень 50 лет / Пенсионеры A / Очень /
Обнаружение формул для площади — элементарная математика
Формулы площади
Студенты, у которых есть неформальное представление о том, что область — это «количество двумерного« материала », содержащегося внутри области, могут изобрести для себя большинство формул, которые их часто просят просто запомнить. Каждая формула, которую они изобретают заново, помогает им лучше понять (и запомнить) другие известные им формулы. (См. Также площадь поверхности.)
Площадь прямоугольников
Выбирая квадрат в качестве единицы площади, мы получаем интуитивное представление о площади прямоугольников.Если мы решим, что площадь этого квадрата равна 1, то прямоугольник, который в 7 раз длиннее, будет иметь площадь 7 × 1.
Прямоугольник, который вдвое превышает высоту, будет иметь удвоенную площадь, поэтому площадь составляет 2 × 7 единиц площади. Мы можем сосчитать два ряда по семь квадратов. Точно так же он имеет 3 ряда по 7 квадратов (или 7 столбцов по 3 квадрата), всего 7 × 3 квадратов, поэтому его площадь составляет 21 квадратную единицу.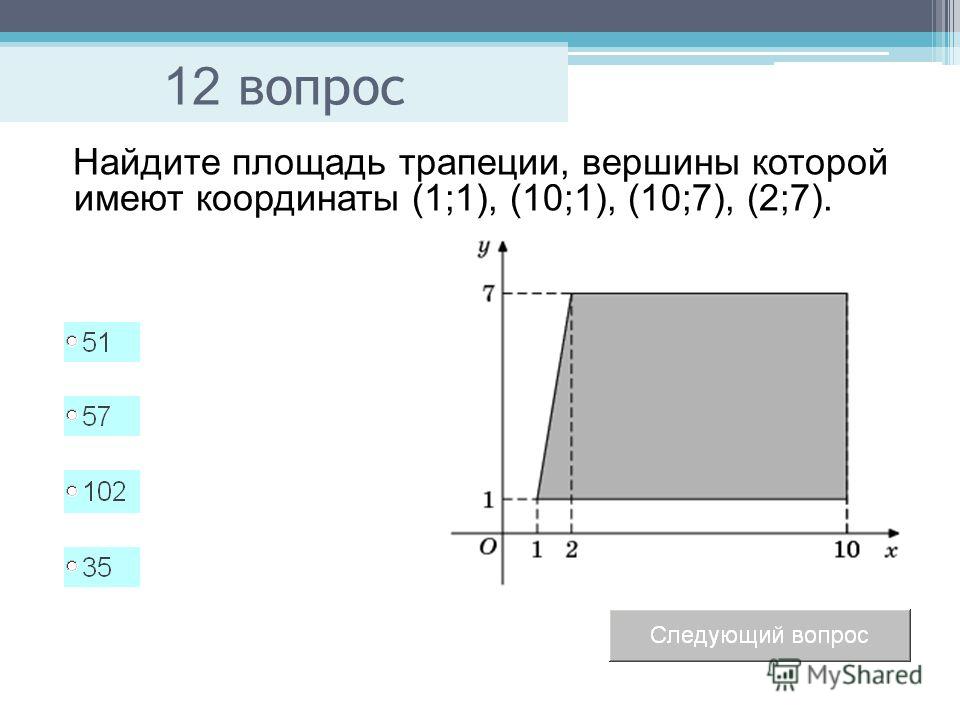
Количество квадратов в одном ряду — это длина прямоугольника. Количество строк — это высота прямоугольника.Таким образом, площадь равна длине × высоте.
Поскольку прямоугольник можно нарисовать под наклоном, «высота» определяется как «направление, перпендикулярное основанию», а «основание» определяется как, ну, с какой бы стороны вы ни выбрали его.
Это работает для подсчета чисел. Это работает даже для дробей. Показанный здесь синий прямоугольник измеряет половину единицы длины на пять с половиной единиц длины. Если мы выберем соответствующий квадрат в качестве единицы площади, мы увидим, что синий прямоугольник содержит пять половин площади и одну четверть единицы площади, или всего две и три четверти единицы площади.(Розовые части показывают завершение каждой квадратной единицы площади.)
Чтобы включить все числа , мы определяем площадь прямоугольника как основание × высота (где «основание» и «высота» означают длины , этих сторон, , измеренные в те же единицы ).
Площадь параллелограммов
Идея
Мы можем вычислить формулу площади параллелограмма, разрезав параллелограмм и переставив части, чтобы получился прямоугольник.Поскольку параллелограмм и прямоугольник состоят из одинаковых частей, они обязательно имеют одинаковую площадь. (См. Определение площади, чтобы узнать, почему эти области одинаковы.)
Мы видим, что они и имеют точно такую же длину основания (синий) и точно такую же высоту (зеленый). Поскольку основание × высота дает площадь прямоугольника, мы можем использовать те же измерения на параллелограмме, чтобы вычислить его площадь: основание × высота .(Как и раньше, «высота» измеряется перпендикулярно основанию, а «основание» — это та сторона, которую вы выбрали первой. См. Параллелограмм.)
На разрезе, показанном выше, легко увидеть, что базовая длина не изменилась. Фактически, перпендикулярный разрез можно делать где угодно по основанию.
Укрепление отверстий
Интуиция и доказательство
Это рассечение дает интуитивное понимание формулы площади параллелограмма, причина того, что он должен быть таким, какой есть.Но мы не сомневались, действительно ли рассечение «работает». То есть, когда мы разрезаем параллелограмм и переставляем его части, мы ожидаем, что получит , и результат определенно будет таким. Но внешность может быть обманчива. Что убеждает нас в том, что когда мы перемещаем этот треугольник, в результате получается прямоугольник? Что, если это больше похоже (хотя и менее преувеличено)? Если в результате не всегда получается идеальный прямоугольник, мы не можем использовать наши знания формулы площади прямоугольника, чтобы разработать формулу для параллелограмма.В старших классах учащиеся смогут доказать, что две части параллелограмма, если правильно собрать их, действительно образуют прямоугольник. В классах K-8 учащиеся по большей части должны полагаться на визуальный эксперимент и получать интуитивное ощущение.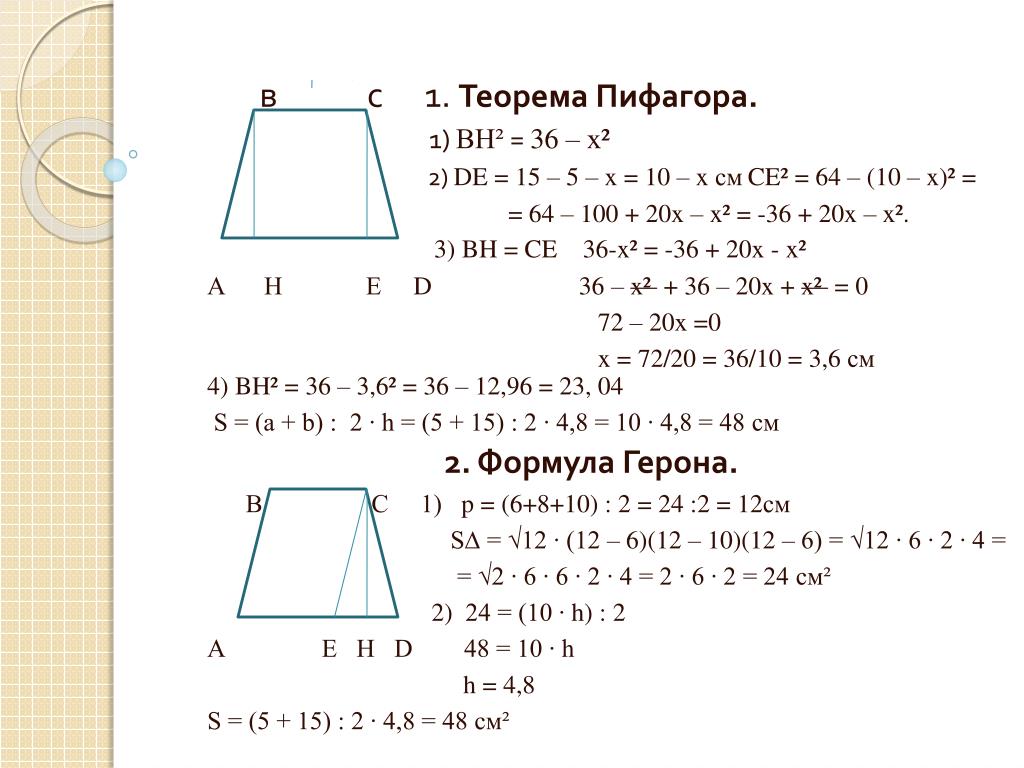 Узнайте больше о том, почему эти вскрытия работают.
Узнайте больше о том, почему эти вскрытия работают.
Что, если мы выберем короткую сторону в качестве основания?
Мы можем выбрать любую сторону в качестве основы; «Высота» определяется как измеряемая перпендикулярно стороне, которую мы выбираем в качестве основания. Если мы возьмем за основу короткую сторону (синюю), то рассечение, показанное выше, не будет таким убедительным.Резка на такой высоте и перестановка деталей оставляет беспорядок:
В этом конкретном примере мы можем спасти беспорядок, сделав еще один разрез, но что, если бы параллелограмм был еще длиннее и тоньше?
Оказывается, любой параллелограмм , независимо от его длины и тонкости, можно разрезать таким образом, чтобы части — возможно, многие из них — могли быть преобразованы в прямоугольник. Но нужно потрудиться, чтобы показать, что это всегда можно сделать. Нам нужна другая идея.
Немного другая идея рассечения в этом случае значительно упрощает жизнь. (Самостоятельно вы можете показать, что это работает и в исходном корпусе.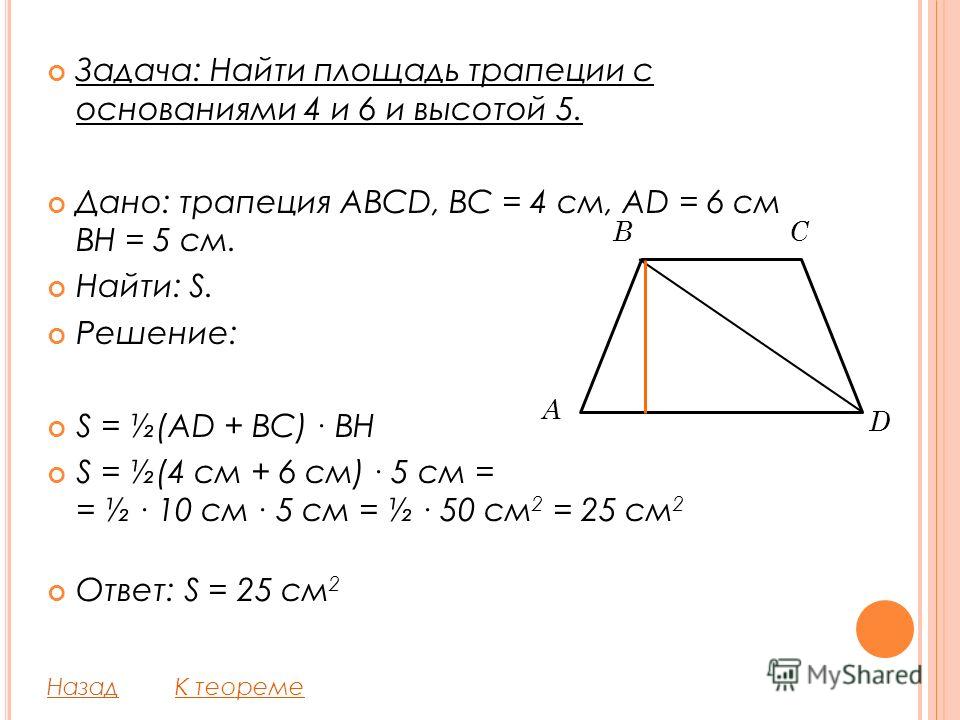 )
)
- Заключите параллелограмм в прямоугольник.
- Две части прямоугольника, которые находятся внутри параллелограмма , а не , являются конгруэнтными треугольниками.
- Сдвиньте один из этих треугольников по направлению к другому, пока они не встретятся, образуя прямоугольник. Поскольку общая площадь внешнего прямоугольника не изменилась (это тот же прямоугольник, что и раньше), а желтая область не изменилась (части просто перемещались), разница между ними — фиолетовыми областями — должна быть такой же.Как и раньше, мы также можем видеть, что размеры прямоугольной фиолетовой области являются основанием и высотой исходного параллелограмма.
Интуиция и доказательство, повтор: Опять же, рассечение дает существенное понимание, но требуется немного больше работы, чтобы убедиться, что два желтых треугольника, которые, безусловно, выглядят так, как будто они соединяются вместе, образуя прямоугольник, на самом деле точно подходят, а не просто почти .
Почему так важно быть осторожным?
Когда мы строим другие формулы площади (см. Ниже), мы захотим, чтобы использовал , как найти площадь параллелограмма, и поэтому мы хотим иметь возможность полагаться на найденное нами правило.Мы, , можем быть уверены, что перестановка частей не изменит площадь: то есть, в конце концов, то, как мы определяем область . Но мы также должны быть уверены, что детали подходят друг к другу, как мы заявляем, что это , иначе мы не можем полагаться на сделанные нами измерения. И мы должны быть уверены, что правило base × height не зависит от удачного выбора базы.
В большинстве учебных программ учащиеся не имеют достаточной систематической базы геометрических знаний до 8-го класса, чтобы убедительно доказать, что эти вскрытия работают.Но интуитивного понимания достаточно для объяснения и обоснования формул и хорошей основы для дальнейшего изучения геометрии.
Площадь треугольника
Знание того, как найти площадь параллелограмма, помогает нам найти площадь треугольника.
Рассечение треугольника
Мы можем разрезать треугольник на две части — одну из них треугольник, а одну трапецию — разрезав его параллельно основанию. Если мы разрежем высоту ровно пополам с этим срезом, две части сложатся вместе, образуя параллелограмм с тем же основанием , но с половиной высоты .
Итак, основание × на полувысоте дает площадь треугольника. На аналогичном разрезе видна полубаза × высота . Любой из них сокращается до bh .
Удвоение треугольника и уменьшение полученной площади вдвое
Другой способ мышления: две копии треугольника образуют параллелограмм с тем же основанием, и такой же высотой , что и треугольник.
Площадь параллелограмма составляет основание × высота , но это вдвое больше площади треугольника, поэтому площадь треугольника составляет от основания × высоты , как мы видели с методом рассечения.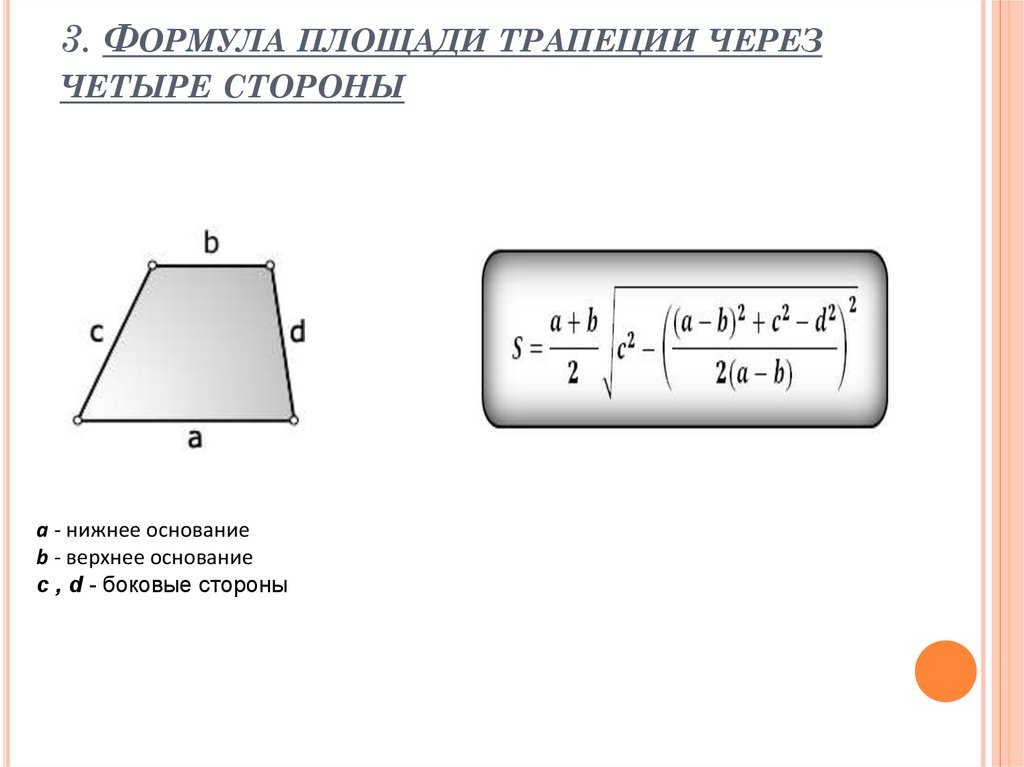
(Как всегда, выберите «основание» и измерьте высоту перпендикулярно этому основанию, от основания до противоположной вершины.)
Площадь трапеции
Удвоение трапеции и уменьшение полученной площади вдвое
Как и в случае с треугольником, две копии трапеции можно соединить вместе, чтобы получился параллелограмм.
Высота параллелограмма равна высоте трапеции, но его основание равно сумме двух оснований трапеции.Таким образом, площадь параллелограмма равна по высоте × ( base1 + base2 ). Но эта площадь составляет две трапеции , поэтому нам нужно разрезать ее пополам, чтобы получить площадь трапеции.
Рассечение трапеции
Мы также можем разрезать трапецию так же, как мы разрезали треугольник, с одним срезом, разрезающим ее высоту пополам. Две части соединяются вместе, образуя параллелограмм, основание которого является суммой двух оснований трапеции, но высота которого равна половине высоты трапеции.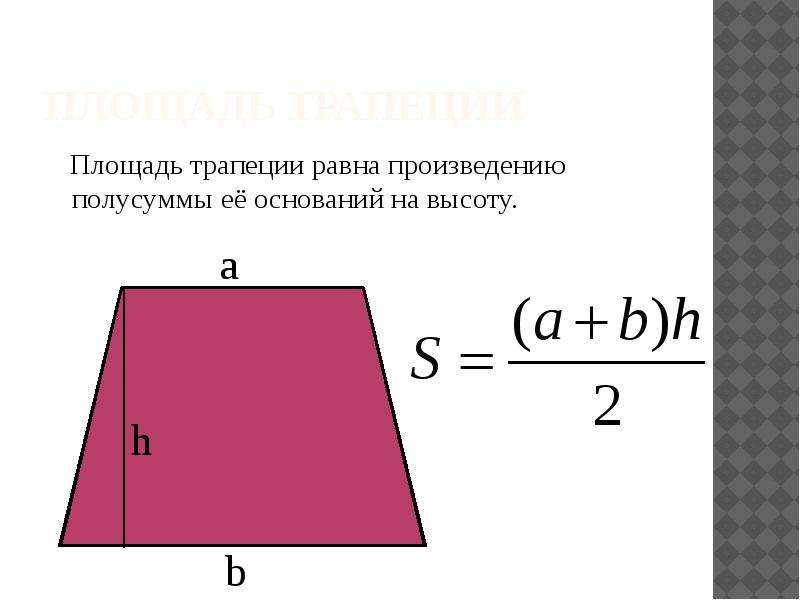
В случае трапеции основания не могут быть выбраны произвольно. Две параллельные стороны являются основаниями, а высота, как всегда, представляет собой перпендикулярное расстояние от одного основания до противоположного.
Площадь этого параллелограмма равна его высоте (полувысоте трапеции), умноженной на его основание (сумма оснований трапеции), поэтому его площадь равна полувысоте × ( основание1 + основание2 ). Поскольку параллелограмм состоит из того же материала, что и трапеция, это тоже площадь трапеции.
В любом случае площадь трапеции составляет × по высоте × ( base1 + base2 ) .
Площадь остальных четырехугольников
Площадь ромба
Площадь ромба может быть найдена путем разрезания и перестановки частей в форме параллелограмма. Это можно сделать несколькими способами:
- Разрежьте более короткую диагональ (a), чтобы получились два совпадающих треугольника.
 Переместите нижнюю половину треугольника рядом с верхней половиной, чтобы получился параллелограмм.Более короткая диагональ (a) становится основанием параллелограмма, а половина более длинной диагонали (b) становится высотой параллелограмма. Таким образом, площадь ромба равна a * b или произведению диагоналей, что является стандартной формулой для ромба.
Переместите нижнюю половину треугольника рядом с верхней половиной, чтобы получился параллелограмм.Более короткая диагональ (a) становится основанием параллелограмма, а половина более длинной диагонали (b) становится высотой параллелограмма. Таким образом, площадь ромба равна a * b или произведению диагоналей, что является стандартной формулой для ромба. - Другой аналогичный способ — разрезать ромб на четыре равных треугольника и переставить их в прямоугольник с более короткой диагональю в качестве основания и половиной длинной диагонали в качестве высоты.
- После разрезания ромба на два равных треугольника мы можем вычислить площадь одного из треугольников, которая равна * основанию (a) * высоте (b) = ab.Затем умножьте на два, так как их два: 2 * ab = ab.
Площадь кайта
Площадь воздушного змея может быть похожа на площадь ромба. Если разрезать более длинную диагональ, получатся два равных треугольника. Если мы переставим их, мы можем сформировать параллелограмм с более длинной диагональю (b) в качестве основания и половиной более короткой диагонали (a) в качестве высоты.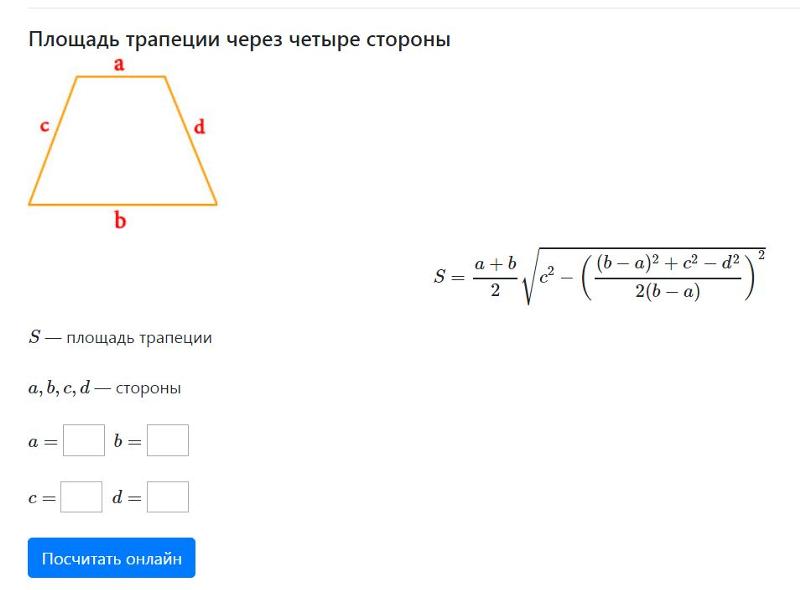 Итак, площадь становится b * a = ab. Более сложный подход требует немного алгебры. Разрежьте змей по более короткой диагонали, чтобы сформировать два треугольника с более короткой диагональю (a) в качестве основы.Таким образом, площадь первого треугольника — * волнистая, где волнистая — высота. Площадь второго треугольника равна a * (b — волнистый), где (b — волнистый) — оставшаяся часть большей диагонали. Таким образом, общая площадь становится (a * волнистая) + (a * (b — волнистая)). Вынося за скобки a, получаем a (волнистый + b — волнистый) = ab.
Итак, площадь становится b * a = ab. Более сложный подход требует немного алгебры. Разрежьте змей по более короткой диагонали, чтобы сформировать два треугольника с более короткой диагональю (a) в качестве основы.Таким образом, площадь первого треугольника — * волнистая, где волнистая — высота. Площадь второго треугольника равна a * (b — волнистый), где (b — волнистый) — оставшаяся часть большей диагонали. Таким образом, общая площадь становится (a * волнистая) + (a * (b — волнистая)). Вынося за скобки a, получаем a (волнистый + b — волнистый) = ab.
Ну что вы знаете. По сути, вам нужно только знать формулу для площади параллелограмма, а затем вывести формулу для других.
.
Быстро найти нужную формулу для расчета онлайн. Геометрия. Алгебра.
R — большая полуось
r — малая полуось
π ≈ 3.14
Формула площади эллипса, через полуоси:
Калькулятор, вычислить площадь элипса:
Рейтинг: 5 / 5
1. Формула площади равнобедренной трапеции через стороны и угол
а — нижнее основание
b — верхнее основание
с — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S ):
Формула площади равнобедренной трапеции через стороны и угол, (S ):
2. Формулы площади равнобедренной трапеции если в нее вписана окружность
Формулы площади равнобедренной трапеции если в нее вписана окружность
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α, β — углы трапеции
а — нижнее основание
b — верхнее основание
Формула площади равнобедренной трапеции через радиус вписанной окружности, (S ):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
R — радиус вписанной окружности
m — средняя линия
O — центр вписанной окружности
c — боковые стороны
а — нижнее основание
b — верхнее основание
Формула площади равнобедренной трапеции через радиус вписанной окружности, стороны и среднюю линию (S ):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
3.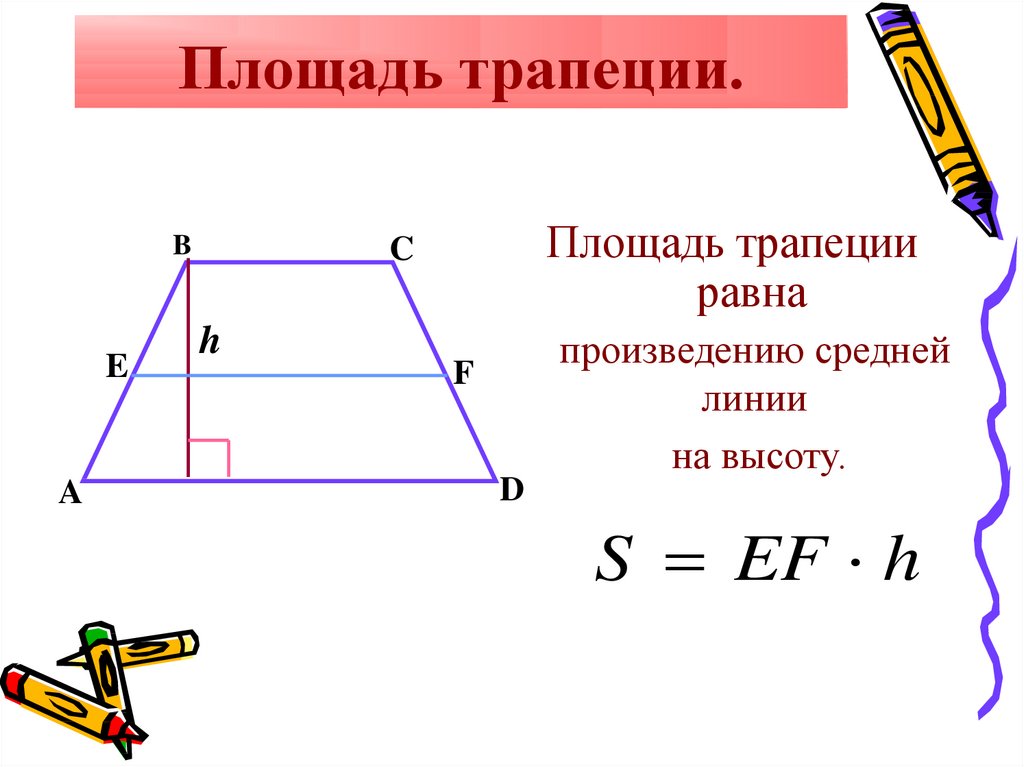 Формула площади равнобедренной трапеции через диагонали и угол между ними
Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α, β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
c — боковая сторона
m — средняя линия трапеции
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
a — нижнее основание
b — верхнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S ):
Рейтинг: 5 / 5
a, b, c — стороны треугольника
α, β, γ— противолежащие углы
Площадь треугольника через сторону и два угла (S):
Формулы для треугольника:
Сторона произвольного треугольника
Стороны равнобедренного треугольника
Стороны прямоугольного треугольника
Высота произвольного треугольника
Высота прямоугольного треугольника
Высота, медиана, биссектриса равнобедренного треугольника
Высота=медиана=биссектриса равностороннего треугольника
Биссектриса произвольного треугольника
Биссектриса прямоугольного треугольника
Медиана произвольного треугольника
Медиана прямоугольного треугольника
Все разделы по геометрии
Рейтинг: 0 / 5
Зная длины всех трех сторон
и используя формулу Герона можно найти площадь разностороннего треугольника
a, b, c — стороны треугольника
p — полупериметр, p=(a+b+c)/2
Формула (Герона) площади треугольника через полупериметр (S):
Калькулятор — вычислить, найти площадь треугольника:
a =
b =
c =
S=
Формулы для треугольника:
Сторона произвольного треугольника
Стороны равнобедренного треугольника
Стороны прямоугольного треугольника
Высота произвольного треугольника
Высота прямоугольного треугольника
Высота, медиана, биссектриса равнобедренного треугольника
Высота=медиана=биссектриса равностороннего треугольника
Биссектриса произвольного треугольника
Биссектриса прямоугольного треугольника
Медиана произвольного треугольника
Медиана прямоугольного треугольника
Все разделы по геометрии
Рейтинг: 5 / 5
Треугольник это плоская фигура, которая имеет три стороны и три угла. Сумма всех трех углов, равна 180 градусов.
Сумма всех трех углов, равна 180 градусов.
Высота треугольника это — опущенный перпендикуляр из вершины угла на противоположенную сторону или ее продолжение, которую в этом случае, называют основанием.
Что бы найти площадь треугольника,
для этого надо основание умножить на высоту и разделить на два
1. Площадь разностороннего треугольника
h — высота треугольника
a — основание
Формула площади треугольника (S):
Калькулятор для расчета площади треугольника
Высота, h =
Основание, a =
Количество знаков после запятой: 212461015
Площадь треугольника, S =
2. Площадь треугольника с тупым углом
h — высота треугольника
a — основание
Формула площади треугольника с тупым углом (S):
Формулы для треугольника:
Сторона произвольного треугольника
Стороны равнобедренного треугольника
Стороны прямоугольного треугольника
Высота произвольного треугольника
Высота прямоугольного треугольника
Высота, медиана, биссектриса равнобедренного треугольника
Высота=медиана=биссектриса равностороннего треугольника
Биссектриса произвольного треугольника
Биссектриса прямоугольного треугольника
Медиана произвольного треугольника
Медиана прямоугольного треугольника
Все разделы по геометрии
Рейтинг: 5 / 5
Зная у треугольника
две стороны и синус угла между ними, находим по формуле, его площадь
a, b, c — стороны треугольника
α, β, γ — углы
Формулы площади треугольника, через две стороны и угол между ними, (S):
Калькулятор — вычислить, найти площадь треугольника:
Формулы для треугольника:
Сторона произвольного треугольника
Стороны равнобедренного треугольника
Стороны прямоугольного треугольника
Высота произвольного треугольника
Высота прямоугольного треугольника
Высота, медиана, биссектриса равнобедренного треугольника
Высота=медиана=биссектриса равностороннего треугольника
Биссектриса произвольного треугольника
Биссектриса прямоугольного треугольника
Медиана произвольного треугольника
Медиана прямоугольного треугольника
Все разделы по геометрии
Рейтинг: 0 / 5
Прямоугольный треугольник, так же как и любой другой треугольник, имеет три стороны и три угла. Разница только в том, что один угол прямой, т. е. 90 градусов и два остальных, острых угла в сумме составляют, тоже 90 градусов.
Разница только в том, что один угол прямой, т. е. 90 градусов и два остальных, острых угла в сумме составляют, тоже 90 градусов.
Две стороны, которые формируют прямой угол, называют катетами, а третья сторона напротив прямого угла, называется — гипотенуза
1. Если известны только катеты
a, b — катеты треугольника
Формула площади треугольника через катеты ( S ) :
2. Если известны острый угол и гипотенуза или катет
c — гипотенуза
a, b — катеты
α, β — острые углы
Формулы площади прямоугольного треугольника через гипотенузу и угол ( S ) :
Формулы площади прямоугольного треугольника через катет и угол ( S ) :
Как известно, сумма острых углов в прямоугольном треугольнике равна 90 градусов, а если
то справедливы следующие тождества:
3. Если известны радиус вписанной окружности и гипотенуза
Если известны радиус вписанной окружности и гипотенуза
c — гипотенуза
c1, c2 — отрезки полученные делением гипотенузы, точкой касания окружности
r — радиус вписанной окружности
О — центр вписанной окружности
Формулы площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу ( S ) :
Рейтинг: 4 / 5
b — основание треугольника
a — равные стороны
h — высота
Формула площади треугольника через высоту h и основание b, (S):
Калькулятор — вычислить, найти площадь треугольника через высоту и основание:
b (основание) =
h (высота)=
S (площадь) =
Формула площади треугольника через, стороны a, b, (S):
Калькулятор — вычислить, найти площадь треугольника через равные стороны и основание:
a (сторона)=
b (основание)=
S (площадь)=
b — основание треугольника
a — равные стороны
h — высота
Формулы для треугольника:
Сторона произвольного треугольника
Стороны равнобедренного треугольника
Стороны прямоугольного треугольника
Высота произвольного треугольника
Высота прямоугольного треугольника
Высота, медиана, биссектриса равнобедренного треугольника
Высота=медиана=биссектриса равностороннего треугольника
Биссектриса произвольного треугольника
Биссектриса прямоугольного треугольника
Медиана произвольного треугольника
Медиана прямоугольного треугольника
Все разделы по геометрии
Рейтинг: 5 / 5
Если вы знаете сторону или высоту
вы можете найти площадь равностороннего треугольника
a — сторона треугольника
h — высота
Площадь треугольника через сторону a и высоту h, (S):
Площадь треугольника только через сторону a, (S):
Калькулятор для расчета площади равностороннего треугольника
Площадь треугольника только через высоту h, (S):
Калькулятор для расчета площади равностороннего треугольника
a — сторона треугольника
h — высота
Формулы для треугольника:
Сторона произвольного треугольника
Стороны равнобедренного треугольника
Стороны прямоугольного треугольника
Высота произвольного треугольника
Высота прямоугольного треугольника
Высота, медиана, биссектриса равнобедренного треугольника
Высота=медиана=биссектриса равностороннего треугольника
Биссектриса произвольного треугольника
Биссектриса прямоугольного треугольника
Медиана произвольного треугольника
Медиана прямоугольного треугольника
Все разделы по геометрии
Рейтинг: 0 / 5
Формула площади круга, диаметр
Круг это плоская фигура, все точки которой, расположены на любом расстоянии от определенной точки (центр круга) но не больше заданной длины (радиус).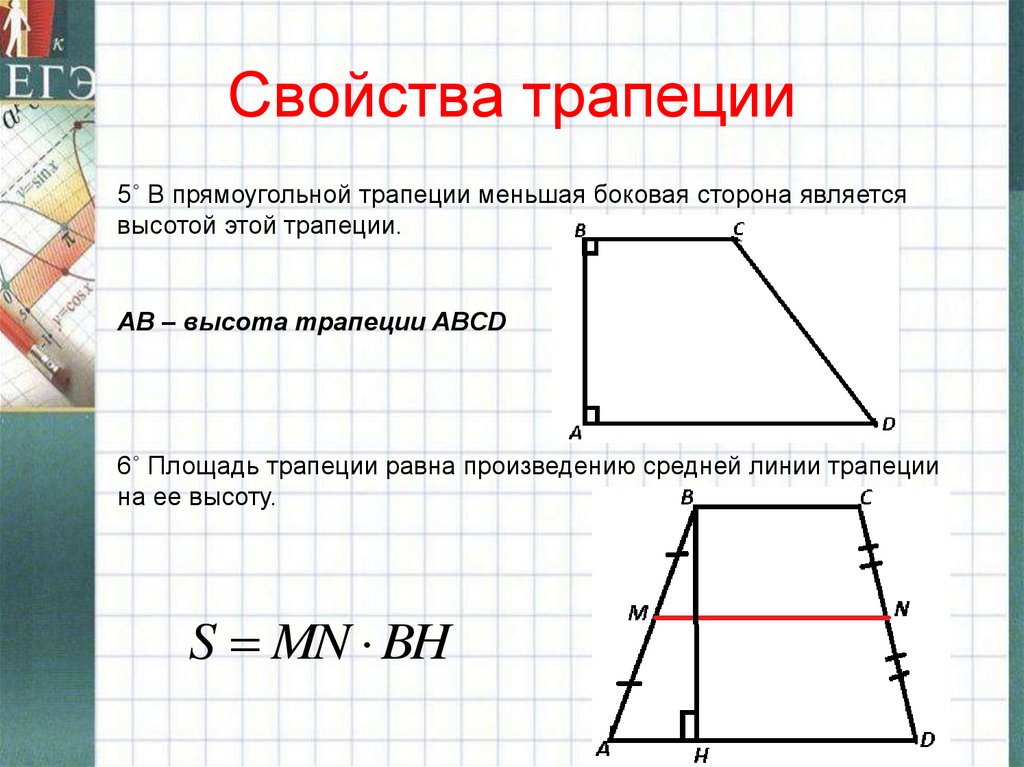
Радиус круга — отрезок, соединяющий центр окружности и любую, максимально удаленную от центра точку круга.
Диаметр круга — отрезок, соединяющий две любые точки максимально удаленные от центра круга и проходящий через этот центр. Диаметр, в два раза больше радиуса
Зная диаметр
или радиус круга или длину окружности, можно найти его площадь.
r — радиус круга
D — диаметр круга
π ≈ 3.14
Формула площади круга, (S):
Решения задач
на тему: Площадь круга
Калькулятор для расчета площади круга через радиус
Радиус окружности, r =
Количество знаков после запятой: 2124610F
Площадь круга, S =
Калькулятор для расчета площади круга через диаметр
Диаметр окружности, D =
Количество знаков после запятой: 2124610F
Площадь круга, S =
L — длина окружности
О — центр круга
π ≈ 3. 14
14
Формула площади круга если известна длина окружности, (S):
Решения задач
на тему: Площадь круга
Калькулятор для расчета площади круга через длину
Длина окружности, L =
Количество знаков после запятой: 2124610F
Площадь круга, S =
Рейтинг: 5 / 5
Площадь кольца равна — число π, умноженное на разницу квадратов, радиуса внешней окружности и радиуса внутренней окружности
R — радиус внешней окружности
r — радиус внутренней окружности
π ≈ 3.14
Формула площади кольца (S):
Калькулятор — вычислить, найти площадь кольца
Рейтинг: 1 / 5
R — радиус внешней окружности
r — радиус внутренней окружности
α — угол сектора AOB, в градусах
π ≈ 3.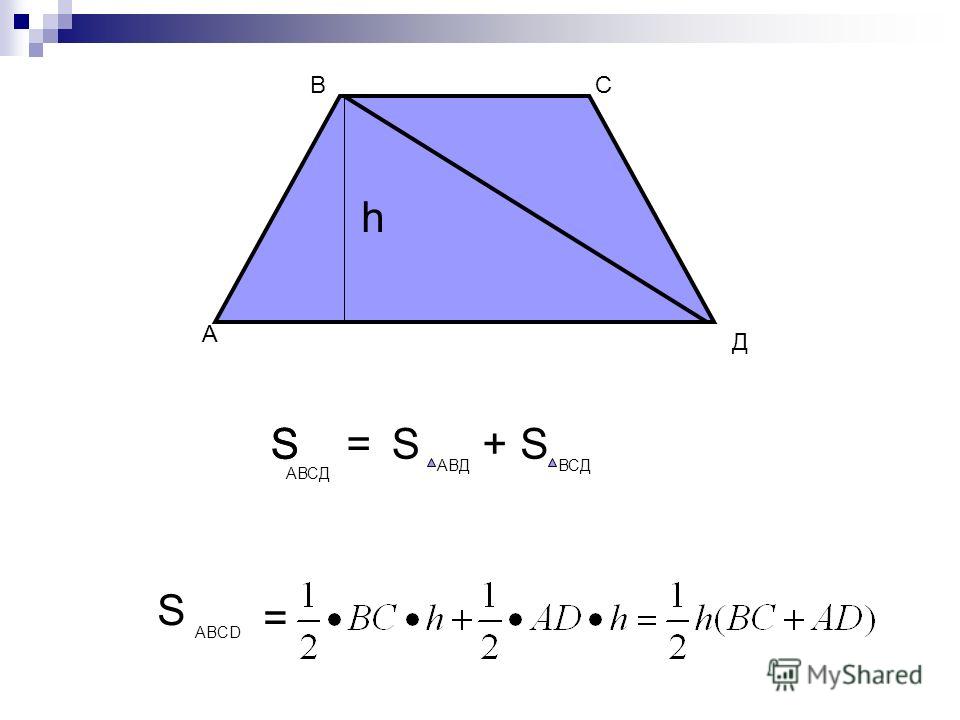 14
14
Формула площади сектора кольца (S):
Рейтинг: 0 / 5
R — радиус круга
α — угол сегмента в градусах
π ≈ 3.14
Формула площади сегмента круга (S), отсекаемая хордой AC:
Калькулятор для расчета длины дуги окружности :
Формулы для окружности и круга:
Длина хорды окружности
Высота сегмента круга
Все разделы по геометрии
Рейтинг: 5 / 5
Найти площадь сектора круга если даны радиус и длина дуги или радиус и центральный угол
r — радиус круга
L — длина дуги AB
α — угол сектора круга AOB в градусах
π ≈ 3.14
Формула площади сектора круга (S), через длину дуги (L):
Формула площади сектора круга (S), через угол (α):
Формулы для окружности и круга:
Длина хорды окружности
Высота сегмента круга
Все разделы по геометрии
Рейтинг: 0 / 5
Вычислить площадь ромба, зная: (диагонали) или (сторону и угол между ними) или (диагональ и угол между сторонами)
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
β — тупой угол
Формулы площади ромба через диагонали и углы между сторонами ( S ):
a — сторона ромба
h — высота
r — радиус вписанной окружности
Формула площади ромба через высоту или радиус вписанной окружности ( S ):
Рейтинг: 0 / 5
1. Формула площади параллелограмма через стороны и углы
Формула площади параллелограмма через стороны и углы
a, b — стороны параллелограмма
α, β — углы параллелограмма
Формула площади через стороны и углы параллелограмма, (S):
Калькулятор — вычислить, найти площадь параллелограмма:
2. Формула площади параллелограмма через сторону и высоту
a, b — стороны параллелограмма
Hb — высота на сторону b
Ha — высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):
3. Формула площади параллелограмма через диагонали и угол между ними
D — большая диагональ
d —меньшая диагональ
α, β — углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):
Калькулятор — вычислить, найти площадь параллелограмма:
D (большая диагональ)=
d (меньшая диагональ )=
α или β (угол в градусах)= ( sin α=sin β )
S=
Формулы для параллелограмма:
Как найти стороны параллелограмма
Как найти диагонали параллелограмма
Острый угол и тупой угол параллелограмма
Углы между диагоналями параллелограмма
Формула суммы квадратов диагоналей параллелограмма
Высота параллелограмма и угол пересечения высот
Свойства и длина биссектрисы параллелограмма
Периметр параллелограмма
Все формулы по геометрии
Рейтинг: 5 / 5
1. Формула площади трапеции через основания и высоту
Формула площади трапеции через основания и высоту
a — нижнее основание
b — верхнее основание
m — средняя линия
h — высота трапеции
Формула площади трапеции, (S ):
2. Формула площади трапеции через диагонали и угол между ними
d1, d2 — диагонали трапеции
α, β — углы между диагоналями
Формула площади трапеции, (S ):
3. Формула площади трапеции через четыре стороны
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
Формула площади трапеции, (S ):
Рейтинг: 5 / 5
Зная сторону
или диагональ квадрата, можно найти его площадь
a — сторона квадрата
c — диагональ
Формула площади квадрата через сторону a, (S):
Калькулятор — вычислить, найти площадь квадрата:
Формула площади квадрата через диагональ c, (S):
C (диагональ)=
S=
Рейтинг: 5 / 5
Зная длину
и ширину прямоугольника, можно вычислить его площадь
b — длина прямоугольника
a — ширина прямоугольника
Формула площади прямоугольника, (S):
Калькулятор — вычислить, найти площадь прямоугольника:
a (длина) =
b (ширина)=
S=
Рейтинг: 1 / 5
a — сторона многоугольника
n — количество сторон
Формула площади правильного многоугольника, (S):
Калькулятор — вычислить, найти площадь правильного многоугольника
Рейтинг: 0 / 5
Площадь трапеции по сторонам онлайн калькулятор.
 Как найти площадь трапеции
Как найти площадь трапецииТрапеция — это особый вид четырехугольника, у которого две противолежащие стороны параллельны друг другу, а две другие — нет. Трапецеидальную форму имеют различные реальные объекты, поэтому вам может понадобиться рассчитать периметр такой геометрической фигуры для решения повседневных или школьных задач.
Геометрия трапеции
Трапеция (от греч. «трапезион» — стол) — это фигура на плоскости, ограниченная четырьмя отрезками, два из которых параллельны, а два — нет. Параллельные отрезки носят название оснований трапеции, а непараллельные — боковых сторон фигуры. Боковые стороны и их углы наклона определяют вид трапеции, которая может быть разносторонней, равнобедренной или прямоугольной. Помимо оснований и боковых сторон, трапеция имеет еще два элемента:
- высота — расстояние между параллельными основаниями фигуры;
- средняя линия — отрезок, соединяющий середины боковых сторон.
Данная геометрическая фигура широко распространена в реальной жизни.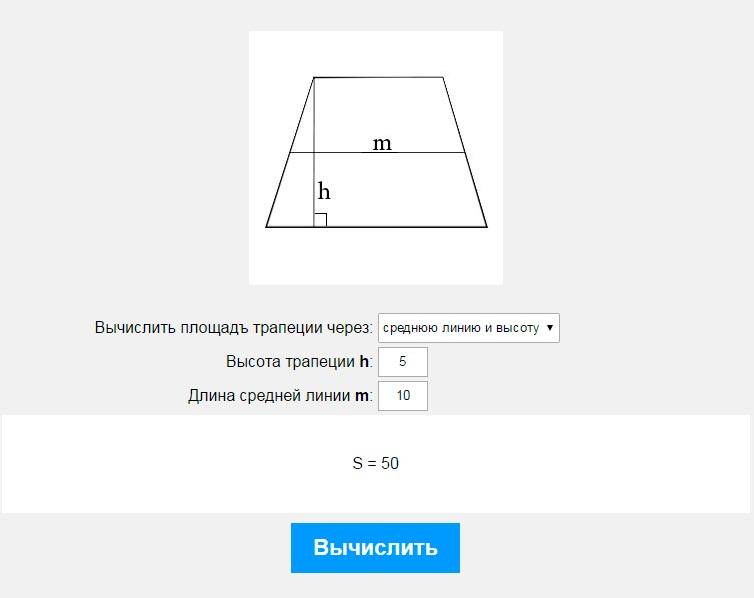
Трапеция в реальности
В повседневной жизни трапецеидальную форму принимают многие реальные предметы. Вы легко найдете трапеции в следующих сферах человеческой деятельности:
- дизайн интерьеров и декор — диваны, столешницы, стены, ковры, подвесные потолки;
- ландшафтный дизайн — границы газонов и искусственных водоемов, формы декоративных элементов;
- мода — форма одежды, обуви и аксессуаров;
- архитектура — окна, стены, основания зданий;
- производство — различные изделия и детали.
При столь широком использовании трапеций специалистам часто приходится вычислять периметр геометрической фигуры.
Периметр трапеции
Периметр фигуры — это числовая характеристика, которая рассчитывается как сумма длин всех сторон n-угольника. Трапеция — это четырехугольник и в общем случае все его стороны имеют разную длину, поэтому периметр рассчитывается по формуле:
P = a + b + c + d,
где a и c – основания фигуры, b и d – ее боковые стороны.
Несмотря на то, что при вычислении периметра трапеции нам нет нужды узнавать высоту, программный код калькулятора требует ввода этой переменной. Так как высота никак не влияет на вычисления, при использовании нашего онлайн-калькулятора вы можете ввести любое значение высоты, которое больше нуля. Рассмотрим пару примеров.
Примеры из реальной жизни
Платок
Допустим, у вас есть платок в форме трапеции, и вы хотите отделать его бахромой. Вам понадобится узнать периметр платка, чтобы не купить лишнего материала или не ходить в магазин два раза. Пусть ваш равнобедренный платок имеет следующие параметры: a = 120 см, b = 60 см, c = 100 см, d = 60 см. Вбиваем эти данные в онлайн-форму и получаем ответ в виде:
Таким образом, периметр платка составляет 340 см, и именно такой длины должна быть тесьма бахромы для его отделки.
Откосы
К примеру, вы решили сделать откосы для нестандартных металлопластиковых окон, которые имеют трапецеидальную форму. Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок. Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Следовательно, периметр трапециевидного окна составляет 390 см, и именно столько вам понадобится купить пластиковых панелей для формирования откосов.
Заключение
Трапеция — популярная в повседневности фигура, определение параметров которой может понадобиться в самых неожиданных ситуациях. Расчет периметров трапецией необходим многим профессионалам: от инженеров и архитекторов до дизайнеров и механиков. Наш каталог онлайн-калькуляторов позволит вам выполнить расчеты для любых геометрических фигур и тел.
Этот калькулятор рассчитал 2192 задачи на тему «Площадь трапеции»
ПЛОЩАДЬ ТРАПЕЦИИ
Выберете формулу вычисления площади трапеции, которую Вы планируете применить для решения поставленной перед Вами задачи:
Общая теория для вычисления площади трапеции.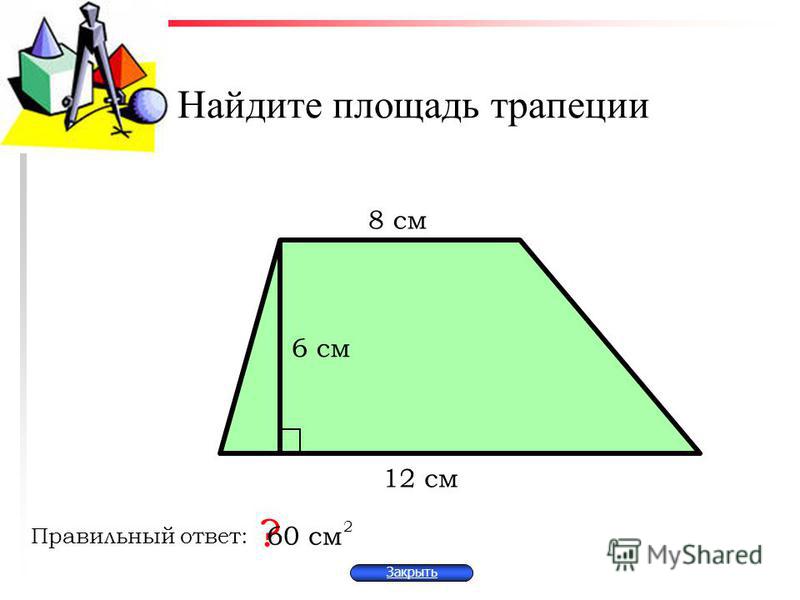
Трапеция — это плоская фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, и четырех отрезков (сторон), соединяющих попарно эти четыре точки, у которой две противоположные стороны параллельны (лежат на параллельных прямых), а две другие не параллельны.
Точки называются вершинами трапеции и обозначаются заглавными латинскими буквами.
Отрезки называются сторонами трапеции и обозначаются парой заглавных латинских букв соответственно вершинам, которые отрезки соединяют.
Две параллельные стороны трапеции называются основаниями трапеции .
Две не параллельные стороны трапеции называются боковыми сторонами трапеции .
Рисунок №1: Трапеция ABCD
На рисунке №1 представлена трапеция ABCD с вершинами A,B ,C, D и сторонами AB, BC, CD, DA.
AB ǁ DC — основания трапеции ABCD.
AD, BC — боковые стороны трапеции ABCD.
Угол, образованный лучами AB и AD, называется углом при вершине A. Обозначается он как ÐA или ÐBAD, или ÐDAB.
Обозначается он как ÐA или ÐBAD, или ÐDAB.
Угол, образованный лучами BA и BC, называется углом при вершине B. Обозначается он как ÐB или ÐABC, или ÐCBA.
Угол, образованный лучами CB и CD, называется углом при вершине C. Обозначается он как ÐC или ÐDCB, или ÐBCD.
Угол, образованный лучами AD и CD, называется углом при вершине D. Обозначается он как ÐD или ÐADC, или ÐCDA.
Рисунок №2: Трапеция ABCD
На рисунке №2 отрезок MN, соединяющий середины боковых сторон, называется средней линией трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме. То есть,.
Рисунок №3: Равнобедренная трапеция ABCD
На Рисунке №3, AD=BC.
Трапеция называется равнобедренной (равнобокой) , если ее боковые стороны равны.
Рисунок №4: Прямоугольная трапеция ABCD
На Рисунке №4 угол D — прямой (равен 90 о).
Трапеция называется прямоугольной, если угол при боковой стороне прямой.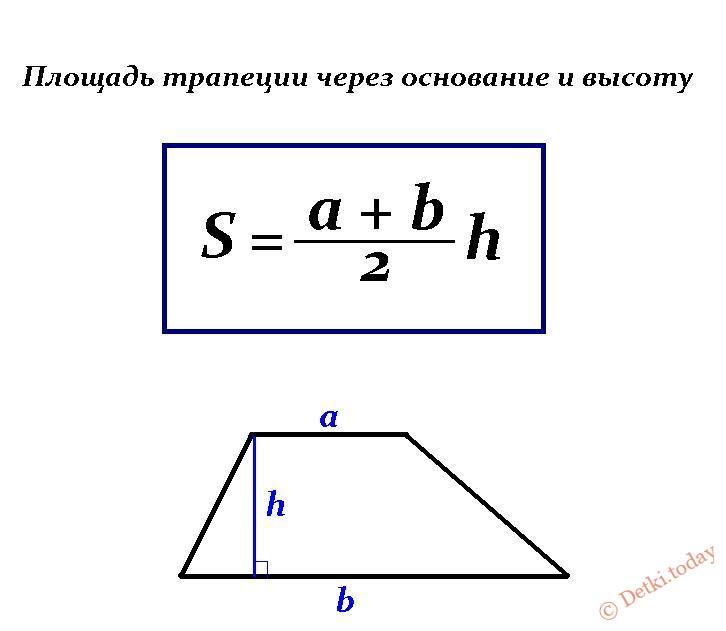
Площадью S плоской фигуры, к которым относится и трапеция, называется ограниченное замкнутое пространство на плоскости. Площадь плоской фигуры показывает величину этой фигуры.
Площадь обладает несколькими свойствами:
1. Она не может быть отрицательной.
2. Если дана некоторая замкнутая область на плоскости, которая составлена из нескольких фигур, не пересекающихся друг с другом (то есть, фигуры не имеют общих внутренних точек, но вполне могут касаться друг друга), то площадь такой области равна сумме площадей составляющих ее фигур.
3. Если две фигуры равны, то и площади их равны.
4. Площадь квадрата, который построен на единичном отрезке, равна единице.
За единицу измерения площади принимают площадь квадрата, сторона которого равна единице измерения отрезков.
При решении задач часто используются следующие формулы вычисления площади трапеции:
1. Площадь трапеции равна полусумме ее оснований умноженной на высоту:
2.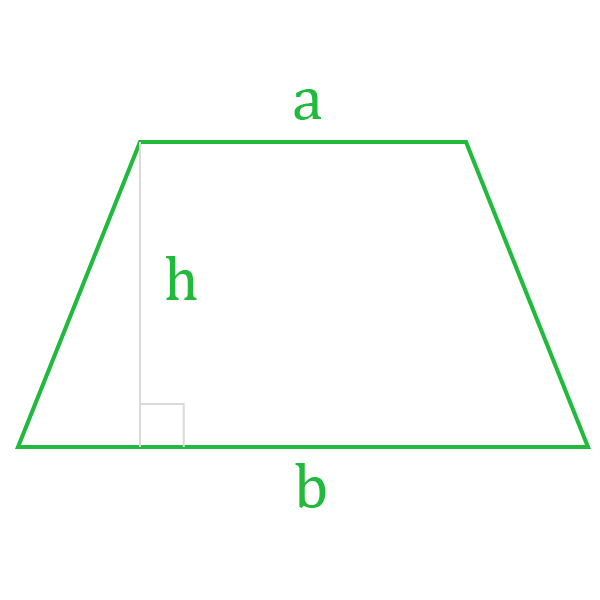 Площадь трапеции равна произведению ее средней линии на высоту:
Площадь трапеции равна произведению ее средней линии на высоту:
3. При известных длинах оснований и боковых сторон трапеции её площадь можно вычислить по формуле:
4. Возможно вычислить площадь равнобедренной трапеции при известной длине радиуса вписанной в трапецию окружности и известном значении угла при основании по следующей формуле:
Пример 1: Вычислить площадь трапеции с основаниями a=7, b=3 и высотой h=15.
Решение:
Ответ:
Пример 2: Найти сторону основания трапеции с площадью S=35 см 2 , высотой h=7см и вторым основанием b = 2 см.
Решение:
Для нахождения стороны основания трапеции воспользуемся формулой вычисления площади:
Выразим из данной формулы сторону основания трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 3: Найти высоту трапеции с площадью S=17 см 2 и основаниями a=30 см, b = 4 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 4: Вычислить площадь трапеции с высотой h=24 и средней линией m=5.
Решение:
Для нахождения площади трапеции воспользуемся следующей формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 5: Найти высоту трапеции с площадью S = 48 см 2 и средней линией m=6 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы высоту трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 6: Найти среднюю линию трапеции с площадью S = 56 и высотой h=4.
Решение:
Для нахождения средней линии трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы среднюю линию трапеции:
Таким образом, имеем следующее.
Для того чтобы чувствовать себя на уроках геометрии уверенно и успешно решать задачи, недостаточно выучить формулы. Их нужно в первую очередь понимать. Бояться, а тем более ненавидеть формулы — непродуктивно.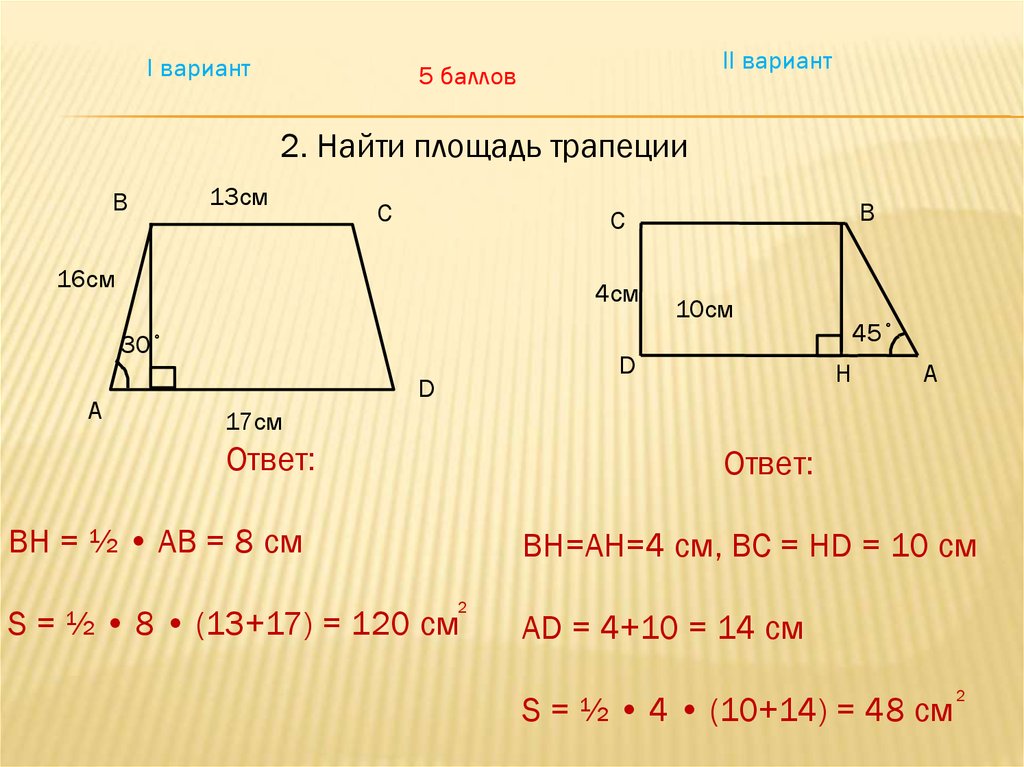 В этой статье доступным языком будут проанализированы различные способы поиска площади трапеции. Для лучшего усвоения соответствующих правил и теорем уделим некоторое внимание ее свойствам. Это поможет разобраться в том, как работают правила и в каких случаях следует применять те или иные формулы.
В этой статье доступным языком будут проанализированы различные способы поиска площади трапеции. Для лучшего усвоения соответствующих правил и теорем уделим некоторое внимание ее свойствам. Это поможет разобраться в том, как работают правила и в каких случаях следует применять те или иные формулы.
Определяем трапецию
Что это за фигура в целом? Трапецией называют многоугольник из четырех углов с двумя параллельными сторонами. Две другие стороны трапеции могут быть наклонены под различными углами. Ее параллельные стороны называют основаниями, а для непараллельных сторон применяют наименование «боковые стороны» или «бедра». Такие фигуры довольно часто встречаются в обыденной жизни. Контуры трапеции можно увидеть в силуэтах одежды, предметах интерьера, мебели, посуды и многих других. Трапеция бывает разных видов: разносторонняя, равнобокая и прямоугольная. Более детально их типы и свойства разберем далее в статье.
Свойства трапеции
Остановимся коротко на свойствах этой фигуры. Сумма углов, прилегающих к любой боковой стороне, всегда равняется 180°. Надо заметить, что все углы трапеции в сумме составляют 360°. У трапеции существует понятие средней линии. Если соединить середины боковых сторон отрезком — это и будет средняя линия. Ее обозначают m. У средней линии есть важные свойства: она всегда параллельна основаниям (мы помним, что основания также параллельны между собой) и равна их полусумме:
Сумма углов, прилегающих к любой боковой стороне, всегда равняется 180°. Надо заметить, что все углы трапеции в сумме составляют 360°. У трапеции существует понятие средней линии. Если соединить середины боковых сторон отрезком — это и будет средняя линия. Ее обозначают m. У средней линии есть важные свойства: она всегда параллельна основаниям (мы помним, что основания также параллельны между собой) и равна их полусумме:
Это определение обязательно надо выучить и понять, ведь это ключ к решению множества задач!
У трапеции всегда можно опустить высоту на основание. Высота — это перпендикуляр, часто обозначаемый символом h, который проведен из любой точки одного основания на другое основание или его продолжение. Средняя линия и высота помогут найти площадь трапеции. Подобные задачи являются самыми распространенными в школьном курсе геометрии и регулярно появляются среди контрольных и экзаменационных работ.
Самые простые формулы площади трапеции
Разберем две самые популярные и простые формулы, с помощью которых находят площадь трапеции. Достаточно умножить высоту на полусумму оснований, чтобы легко найти искомое:
Достаточно умножить высоту на полусумму оснований, чтобы легко найти искомое:
S = h*(a + b)/2.
В этой формуле a, b обозначают основания трапеции, h — высоту. Для удобства восприятия в этой статье знаки умножения отмечены символом (*) в формулах, хотя в официальных справочниках знак умножения обычно опускают.
Рассмотрим пример.
Дано: трапеция с двумя основаниями, равными 10 и 14 см, высота составляет 7 см. Чему равна площадь трапеции?
Разберем решение этой задачи. По этой формуле сначала нужно найти полусумму оснований: (10+14)/2 = 12. Итак, полусумма равняется 12 см. Теперь полусумму умножаем на высоту: 12*7 = 84. Искомое найдено. Ответ: площадь трапеции равна 84 кв. см.
Вторая известная формула гласит: площадь трапеции равна произведению средней линии на высоту трапеции. То есть фактически вытекает из предшествующего понятия средней линии: S=m*h.
Использование диагоналей для вычислений
Другой способ нахождения площади трапеции на самом деле не так уж сложен.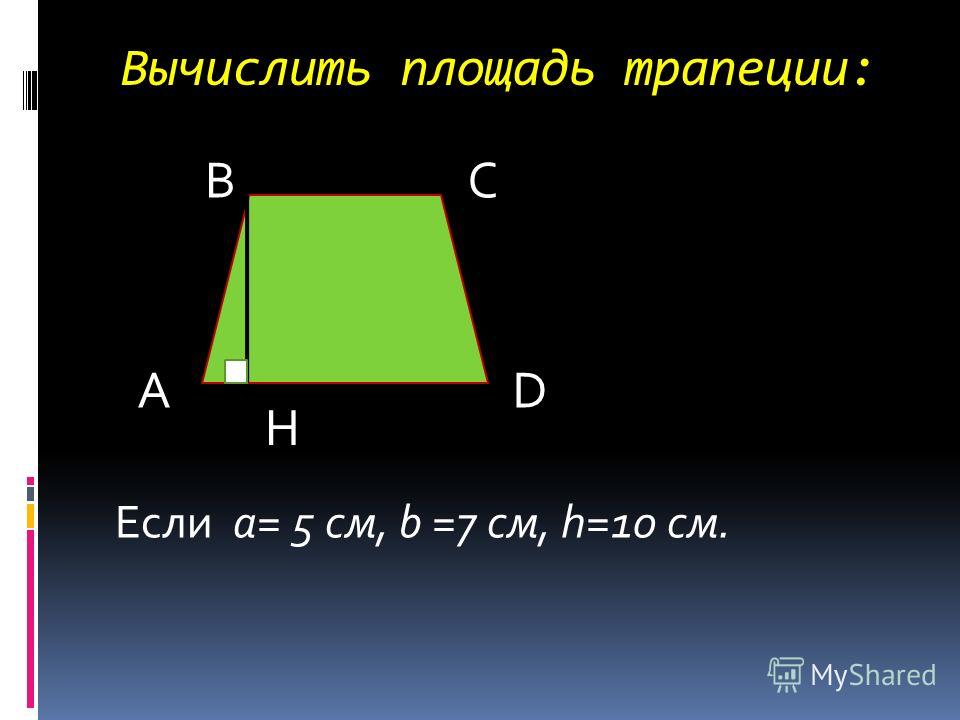 Он связан с ее диагоналями. По этой формуле для нахождения площади требуется умножить полупроизведение ее диагоналей (d 1 d 2) на синус угла между ними:
Он связан с ее диагоналями. По этой формуле для нахождения площади требуется умножить полупроизведение ее диагоналей (d 1 d 2) на синус угла между ними:
S = ½ d 1 d 2 sina.
Рассмотрим задачу, которая показывает применение этого способа. Дано: трапеция с длиной диагоналей равной соответственно 8 и 13 см. Угол a между диагоналями равняется 30°. Найти площадь трапеции.
Решение. Используя вышеприведенную формулу, легко вычислить требуемое. Как известно, sin 30° составляет 0,5. Следовательно, S = 8*13*0,5=52. Ответ: площадь равна 52 кв. см.
Ищем площадь равнобокой трапеции
Трапеция может быть равнобокой (равнобедренной). Ее боковые стороны одинаковы И углы при основаниях равны, что хорошо иллюстрирует рисунок. Равнобедренная трапеция имеет такие же свойства, что и обычная, плюс ряд особых. Вокруг равнобокой трапеции может быть описана окружность, и в нее может быть вписана окружность.
Какие же есть методики вычисления площади такой фигуры? Нижеприведенный способ потребует больших вычислений.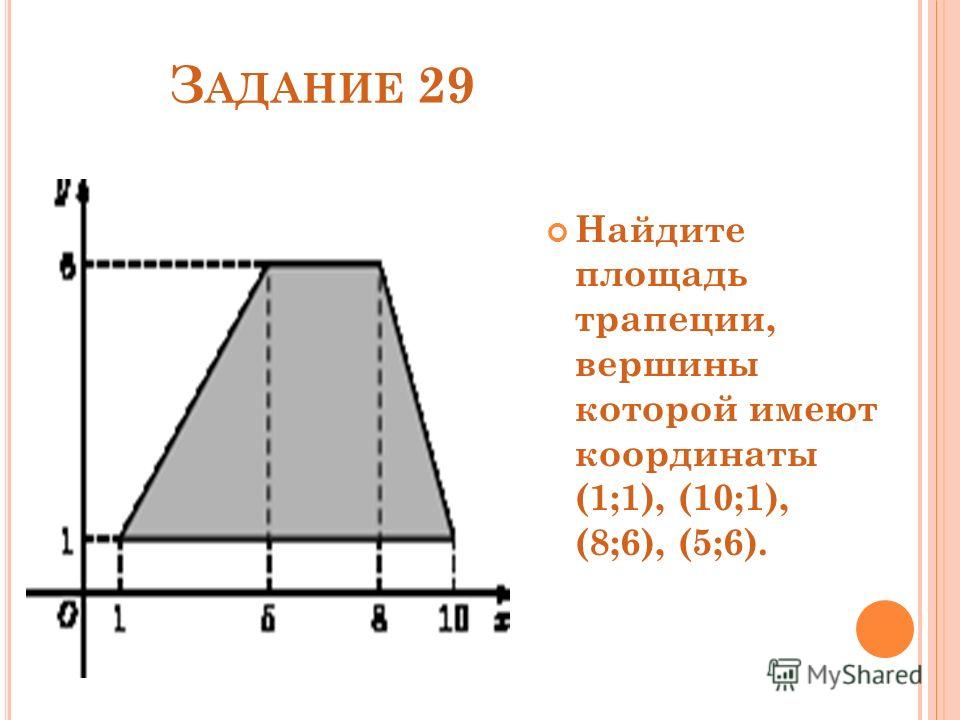 Для его применения нужно знать значения синуса (sin) и косинуса (cos) угла при основании трапеции. Для их расчетов требуются либо таблицы Брадиса либо инженерный калькулятор. Вот эта формула:
Для его применения нужно знать значения синуса (sin) и косинуса (cos) угла при основании трапеции. Для их расчетов требуются либо таблицы Брадиса либо инженерный калькулятор. Вот эта формула:
S = c *sin a *(a — c *cos a ),
где с — боковое бедро, a — угол при нижнем основании.
Равнобокая трапеция обладает диагоналями одинаковой длины. Верно и обратное утверждение: если у трапеции диагонали равны, то она является равнобедренной. Отсюда следующая формула, помогающая найти площадь трапеции — полупроизведение квадрата диагоналей на синус угла между ними: S = ½ d 2 sina.
Находим площадь прямоугольной трапеции
Известен частный случай прямоугольной трапеции. Это трапеция, у которой одна боковая сторона (ее бедро) примыкает к основаниям под прямым углом. Она имеет свойства обычной трапеции. Помимо этого, она обладает очень интересной особенностью. Разность квадратов диагоналей такой трапеции равняется разности квадратов ее оснований.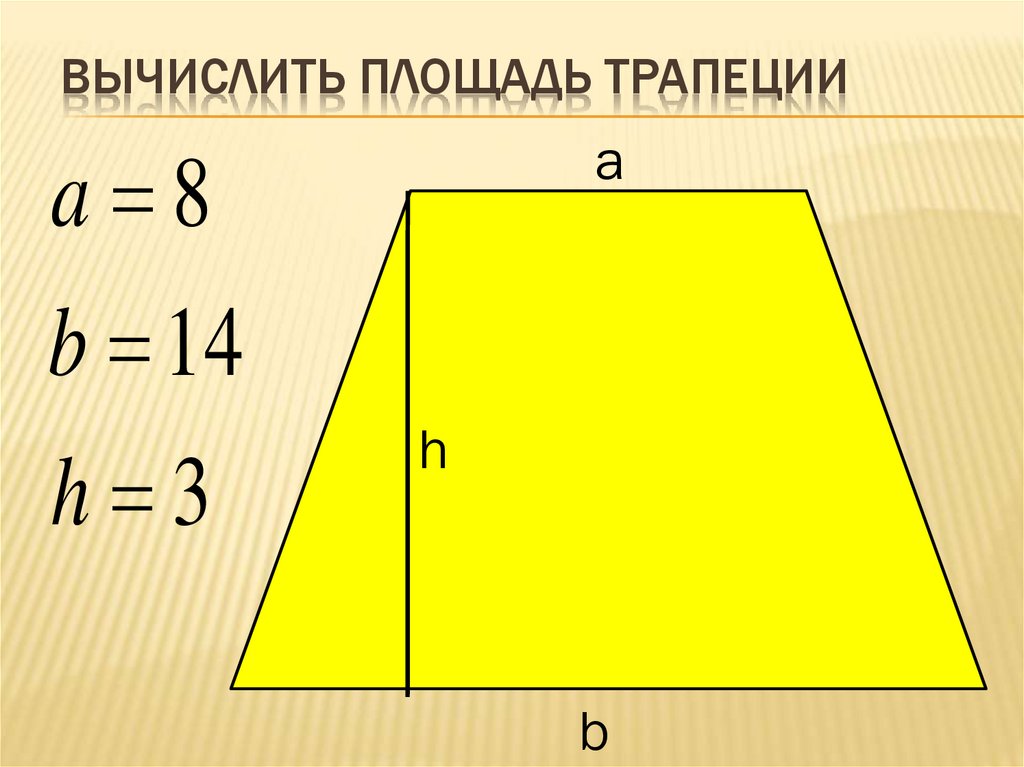 Для нее используют все ранее приведенные методики вычисления площади.
Для нее используют все ранее приведенные методики вычисления площади.
Применяем смекалку
Есть одна хитрость, которая может помочь в случае забывчивости специфических формул. Рассмотрим внимательнее, что представляет собой трапеция. Если мысленно разделить ее на части, то мы получим знакомые и понятные геометрические фигуры: квадрат или прямоугольник и треугольник (один или два). Если известны высота и стороны трапеции, можно воспользоваться формулами площади треугольника и прямоугольника, после чего сложить все полученные величины.
Проиллюстрируем это следующим примером. Дана прямоугольная трапеция. Угол C = 45°, углы A, D составляют 90°. Верхнее основание трапеции равно 20 см, высота равна 16 см. Требуется вычислить площадь фигуры.
Данная фигура очевидным образом состоит из прямоугольника (если два угла равны 90°) и треугольника. Так как трапеция прямоугольная, следовательно, ее высота равна ее боковой стороне, то есть 16 см. Имеем прямоугольник со сторонами 20 и 16 см соответственно. Рассмотрим теперь треугольник, угол которого равен 45°. Мы знаем, что одна его сторона составляет 16 см. Так как эта сторона является одновременно высотой трапеции (а нам известно, что высота опускается на основание под прямым углом), следовательно, второй угол треугольника равен 90°. Отсюда оставшийся угол треугольника составляет 45°. Следствием этого мы получаем прямоугольный равнобедренный треугольник, у которого две стороны одинаковы. Значит, другая сторона треугольника равна высоте, то есть 16 см. Осталось вычислить площадь треугольника и прямоугольника и сложить полученные величины.
Рассмотрим теперь треугольник, угол которого равен 45°. Мы знаем, что одна его сторона составляет 16 см. Так как эта сторона является одновременно высотой трапеции (а нам известно, что высота опускается на основание под прямым углом), следовательно, второй угол треугольника равен 90°. Отсюда оставшийся угол треугольника составляет 45°. Следствием этого мы получаем прямоугольный равнобедренный треугольник, у которого две стороны одинаковы. Значит, другая сторона треугольника равна высоте, то есть 16 см. Осталось вычислить площадь треугольника и прямоугольника и сложить полученные величины.
Площадь прямоугольного треугольника равна половине произведения его катетов: S = (16*16)/2 = 128. Площадь прямоугольника равняется произведению его ширины на длину: S = 20*16 = 320. Мы нашли требуемое: площадь трапеции S = 128 + 320 = 448 кв. см. Можно легко себя перепроверить, воспользовавшись вышеприведенными формулами, ответ будет идентичен.
Используем формулу Пика
Напоследок приведем еще одну оригинальную формулу, помогающую искать площадь трапеции.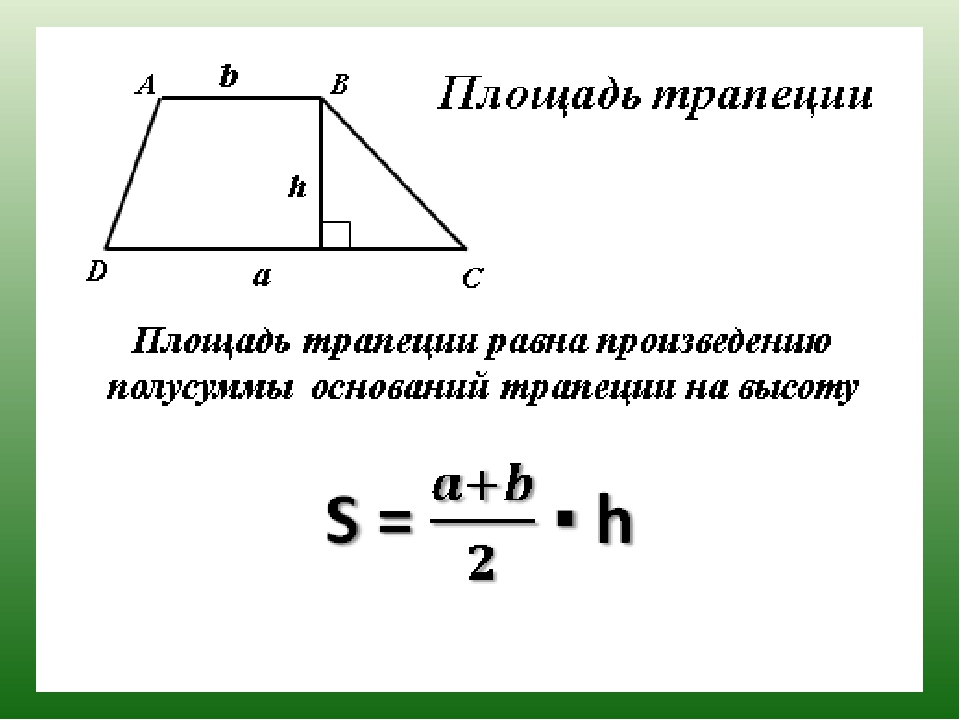 Она называется формулой Пика. Ею удобно пользоваться, когда трапеция нарисована на клетчатой бумаге. Подобные задачи часто встречаются в материалах ГИА. Выглядит она следующим образом:
Она называется формулой Пика. Ею удобно пользоваться, когда трапеция нарисована на клетчатой бумаге. Подобные задачи часто встречаются в материалах ГИА. Выглядит она следующим образом:
S = M/2 + N — 1,
в этой формуле M — количество узлов, т.е. пересечений линий фигуры с линиями клетки на границах трапеции (оранжевые точки на рисунке), N — количество узлов внутри фигуры (синие точки). Удобнее всего пользоваться ею при нахождении площади неправильного многоугольника. Тем не менее, чем больше арсенал используемых методик, тем меньше ошибок и лучше результаты.
Разумеется, приведенными сведениями далеко не исчерпываются типы и свойства трапеции, а также способы поиска ее площади. В этой статье дан обзор наиболее важных ее характеристик. В решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности.
Собранные воедино самые распространенные формулы помогут ученикам сориентироваться в разнообразных способах вычисления площади трапеции и более качественно подготовиться к тестам и контрольным работам по этой теме.
Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
1) , где AD и BC основания, а BH-высота трапеции. Доказательство: проведем диагональ BD и выразим площади треугольников ABD и CDB через полупроизведение их оснований на высоту:
, где DP – внешняя высота в
Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:
Вынесем за скобку
Что и требовалось доказать.
Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то
2) Применение общей формулы площади четырехугольника .
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению . Отсюда
Отсюда
3) Метод сдвига диагонали
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции.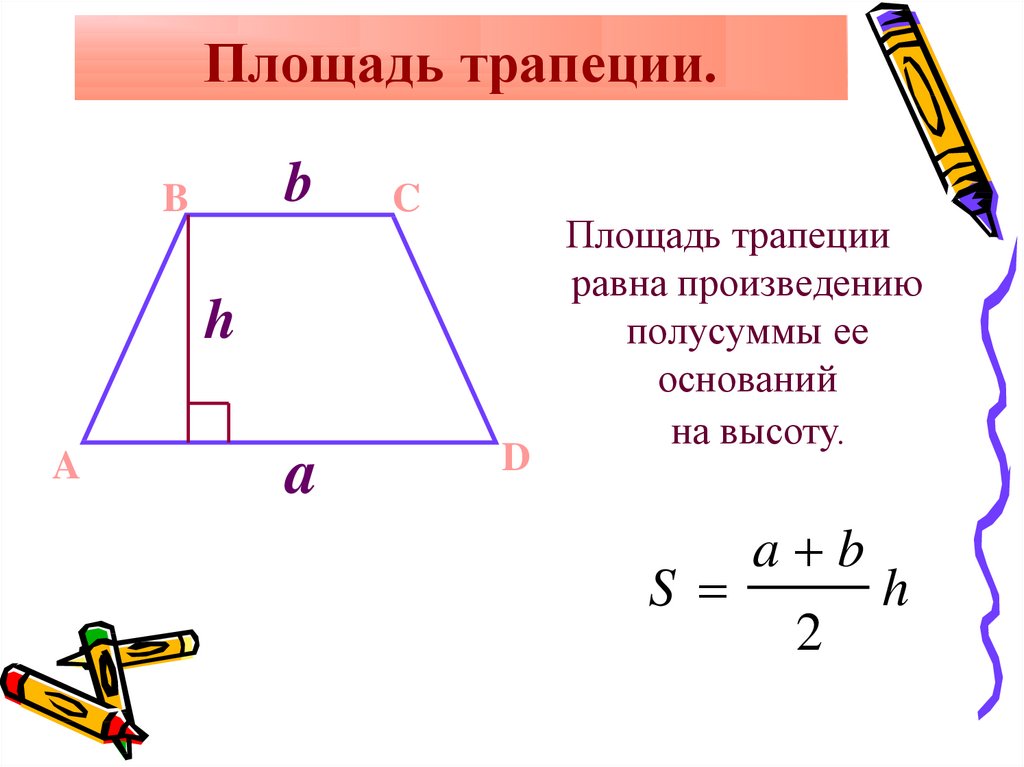 С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
Спецприемы репетитора по математике.
Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать. Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Доказательство: проведем высоты SM и SN в треугольниках BCS и ADS и выразим сумму площадей этих треугольников:
Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:
Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.
В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции.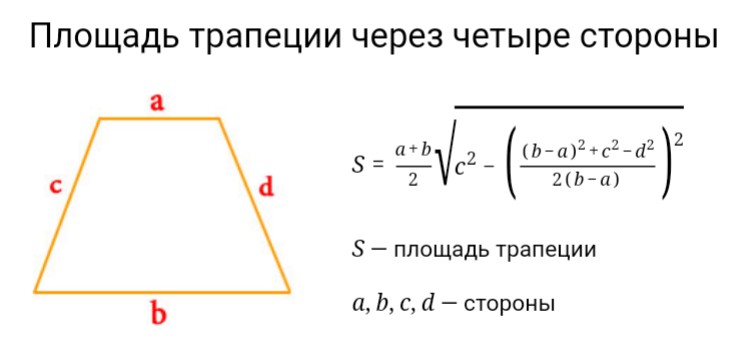 Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Задачи на площадь трапеции:
Замечание репетитора по математике : Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.
1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол .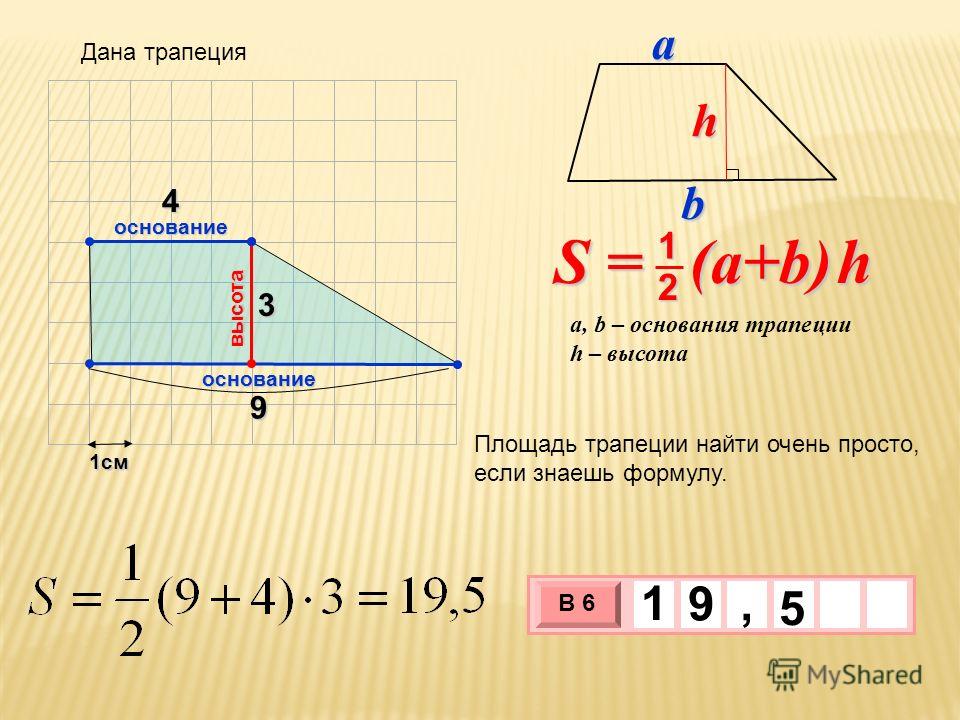 Найти площадь трапеции, если ее высота равна 6см.
Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см. Найдите расстояние до нее от середины противоположной боковой стороны.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).
Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.
Колпаков А.Н.
Репетитор по математике в Москве , подготовка к ЕГЭ в Строгино .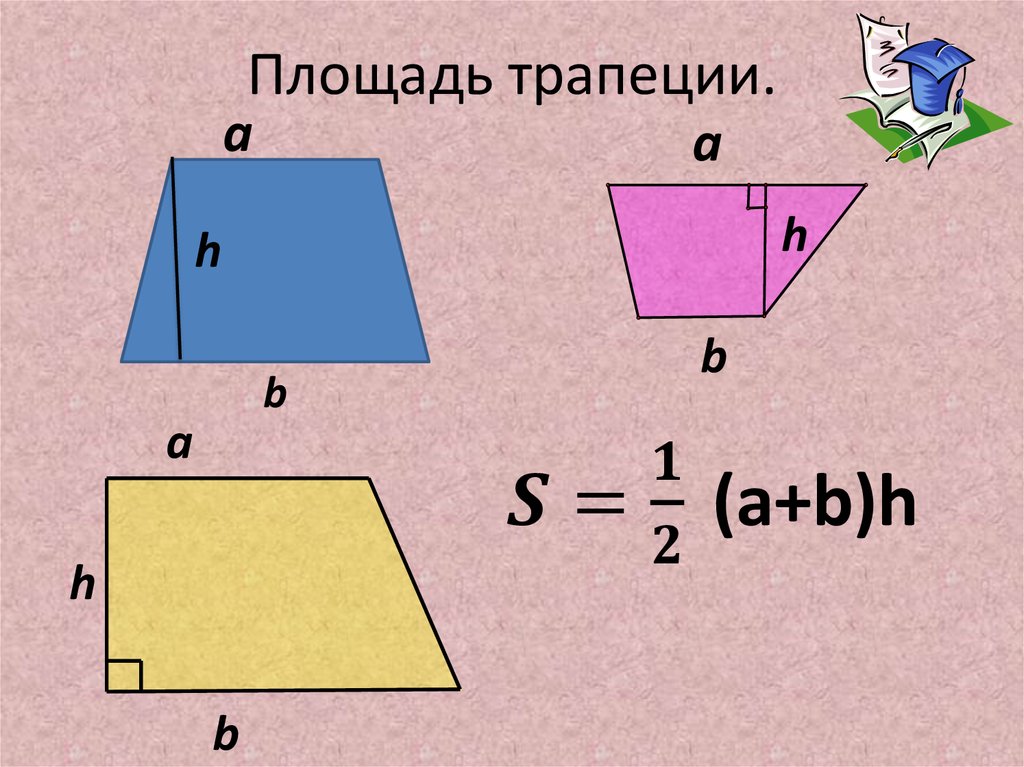
И . Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.
Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции. Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Как и у треугольников, у трапеция есть частные виды в виде равнобедренной (равнобокой) трапеции, у которой длина боковых сторон одинаковы и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.
Трапеции обладают некоторыми интересными свойствами:
- Средняя линия трапеции равна полусумме оснований и параллельна им.

- У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
- Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
- Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
- Если сумма углов, образованных сторонами трапеции у любого ее основания равна 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.
- Равнобедренную трапецию можно описать окружностью. И наоборот. Если в трапеция вписывается в окружность, значит она равнобедренная.
- Отрезок, проходящий через середины оснований равнобедренной трапеции будет перпендикулярен ее основаниям и представляет собой ось симетрии.
Как найти площадь трапеции .
Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается в виде выражения:
где S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота трапеции.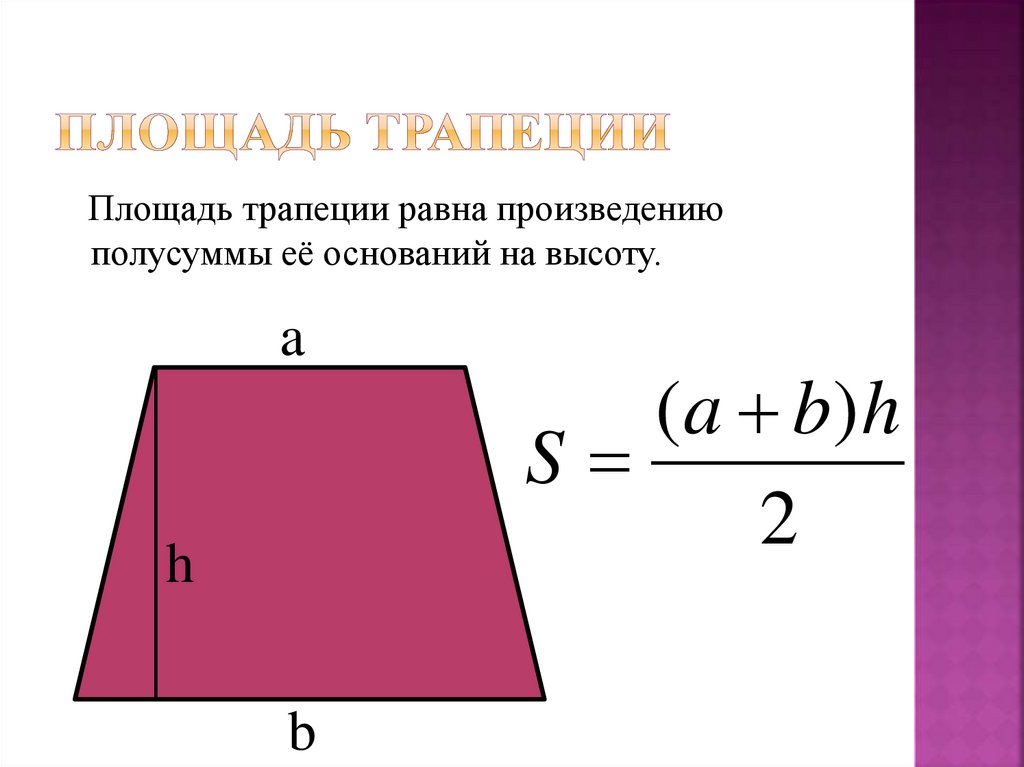
Понять и запомнить эту формулу можно следующим образом. Как следует из рисунка ниже трапецию с использованием средней линии можно преобразовать в прямоугольник, длина которого и будет равна полусумме оснований.
Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.
Есть еще одна простая формула для подсчета ее площади. Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.
В этом случае площадь трапеции может быть найдена по формуле:
S = ((a+b)/2)*√c 2 -((b-a) 2 +c 2 -d 2 /2(b-a)) 2
где S-площадь, a,b-основания, c,d-боковые стороны трапеции.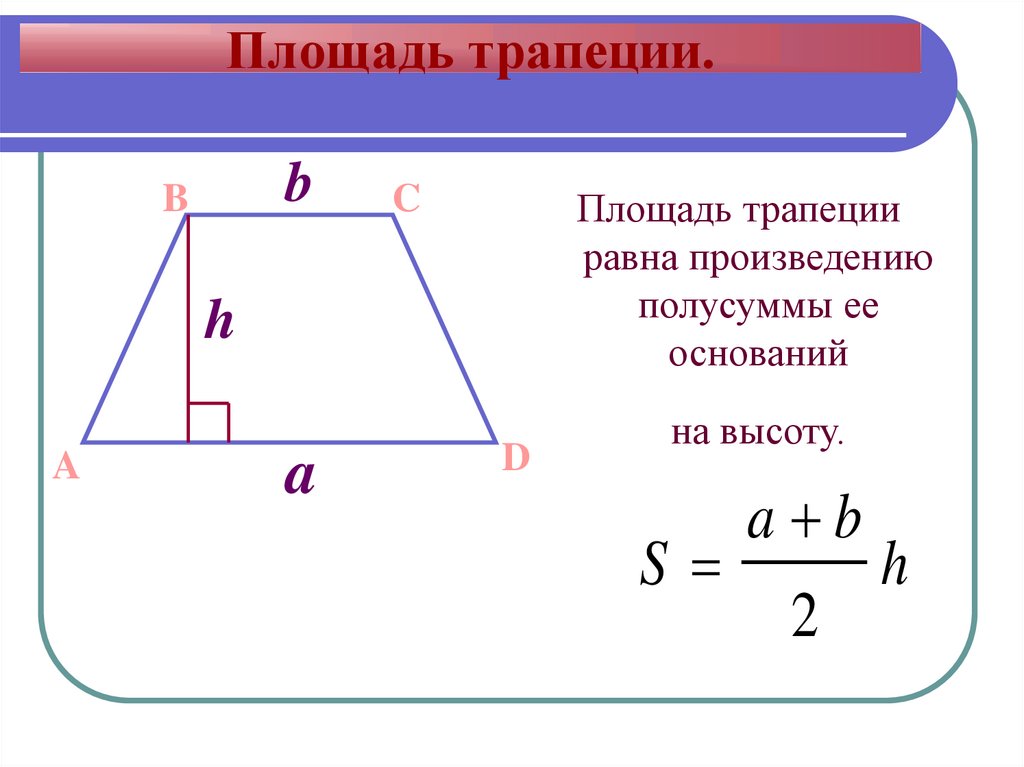
Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.
Как рассчитать площадь комнаты самостоятельно без ошибок
Если вы решили сделать ремонт в квартире или доме, в первую очередь необходимо выбрать материалы для отделки и понять, сколько же их нужно. Для этого нужно правильно рассчитать площадь всех поверхностей в квартире. Конечно, можно прибегнуть к помощи профессионалов, потратив при этом лишние деньги. А можно заняться этим самостоятельно. Тому, как рассчитать площадь комнаты разной формы, посвящена данная статья.
План комнаты, размер которой необходимо считать в два этапа путем сложения величинЧитайте в статье
- 1 Для чего необходимо знать площадь комнаты и что потребуется для расчетов?
- 2 Как высчитать квадратный метр?
- 3 Как посчитать площадь комнаты самостоятельно?
- 3.
 1 Как найти площадь прямоугольника?
1 Как найти площадь прямоугольника? - 3.2 Калькулятор расчета площади четырехугольного помещения
- 3.3 Как посчитать площадь треугольников (прямоугольных и других)?
- 3.3.1 Калькулятор расчета площади треугольного помещения
- 3.4 Расчет площади трапеции
- 3.5 Как вычислить площадь круга?
- 3.5.1 Расчет площади сегмента круга
- 3.
- 4 Как посчитать площадь комнаты: порядок действий
- 5 Как посчитать площадь стен?
- 6 Общие рекомендации
- 7 Заключение
Для чего необходимо знать площадь комнаты и что потребуется для расчетов?
В каких же случаях необходимо рассчитывать площадь комнаты?
- Конечно, в первую очередь для определения количества расходных материалов для ремонта. Многие закупают их с запасом, а излишки возвращают в магазин. Однако в данном случае теряется много времени, к тому же не все магазины предоставляют такую услугу. Поэтому целесообразней правильно высчитать площадь всех поверхностей перед покупками.

- Кроме того, зная площадь, проще распланировать свой бюджет. Ведь даже стоимость работ наемных работников в большинстве случаев зависит от того, сколько квадратных метров они должны обработать.
- Количество осветительных приборов также зависит от площади. Однако в большинстве случаев к сложным расчетам при выборе светильников не прибегают, данный вопрос обычно решается опытным путем.
- И последнее. Одна из главных величин в квартире – объем помещений (при этом необходимо площадь умножить на высоту), ведь в зависимости от него подбирают климатическое оборудование.
Важно! Обязательно проверьте площадь при покупке квартиры, особенно, если вы купили ее в новостройке. Ведь от нее зависит размер коммунальных платежей и зачастую стоимость самой жилплощади.
Например, застройщик (в случае долевого участия в строительстве) обязан возместить стоимость недостающих квадратных метров.
Таким образом, существует огромное количество причин, по которым необходимо правильно высчитать площадь помещения. Но с чего же начать? Сначала нужно подготовить измеряемое помещение и инструменты.
Измерения желательно проводить в полностью освобожденном помещении. Если такой возможности нет, расчистите хотя бы участки около стен, ведь именно вдоль них будут проводиться замеры.
Обязательно отодвиньте всю крупную мебель от стен, которые вы будете измерятьВажно! Если комната прямоугольная, перед началом замеров проверьте правильность ее формы. Для этого сравните противоположные диагонали. Если они равны, перед вами правильный равносторонний прямоугольник.
Итак, для определения площади помещения необходимы следующие приспособления:
- Рулетка. Конечно, электронное приспособление удобней, но оно имеет большую погрешность.
 Кроме того, такой рулеткой не измерить сложные формы, при работе с выступающими элементами также могут возникнуть проблемы. Поэтому оптимальный набор – простая рулетка и линейка. Главное – проверить их точность, так как многие старые или детские приспособления имеют приличную погрешность.
Кроме того, такой рулеткой не измерить сложные формы, при работе с выступающими элементами также могут возникнуть проблемы. Поэтому оптимальный набор – простая рулетка и линейка. Главное – проверить их точность, так как многие старые или детские приспособления имеют приличную погрешность. - Карандаш.
- Листок бумаги для вычислений и записи результатов.
- Калькулятор.
Кроме того, вам может понадобиться длинная линейка для проверки ровности стен.
Как высчитать квадратный метр?
В квадратных метрах в большинстве случаев вычисляется площадь любой поверхности. Так как рассчитать квадратный метр?
Для начала, если комната прямоугольная, необходимо измерить ее длину и ширину. При этом желательно использовать рулетку с нанесенными делениями сантиметров и миллиметров. Если вам удалось найти только линейку с футами, не беда, их легко можно перевести в квадратные метры.
Далее две полученные величины в сантиметрах переводятся в метры (сразу это сделать проще) путем деления на 100.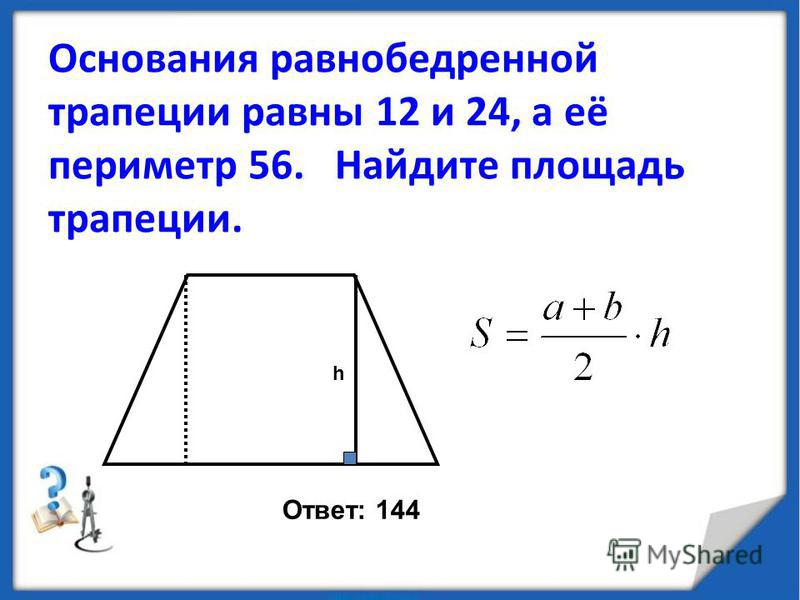 Далее две величины перемножаются, полученная величина и есть площадь комнаты в квадратных метрах. Если у вас футы, сначала перемножьте полученные значения, таким образом вы получите квадратные футы. Затем для перевода в м2 умножьте полученную величину на 0,093 (если измерения были сделаны в ярдах, умножьте результат на 0,84). В данном случае для расчета квадратных метров калькулятор – отличное решение.
Далее две величины перемножаются, полученная величина и есть площадь комнаты в квадратных метрах. Если у вас футы, сначала перемножьте полученные значения, таким образом вы получите квадратные футы. Затем для перевода в м2 умножьте полученную величину на 0,093 (если измерения были сделаны в ярдах, умножьте результат на 0,84). В данном случае для расчета квадратных метров калькулятор – отличное решение.
Интересно! В интернете существует множество онлайн калькуляторов квадратных метров для вычисления площади помещения. Если компьютер под рукой, такой способ будет самым быстрым.
Когда цифра получена, округлите ее до 2 знаков после запятой, более точное значение будет излишним.
Как посчитать площадь комнаты самостоятельно?
Как рассчитать площади всех помещений в квартире?
Идеальная комната прямоугольной формы – большая редкость. Как узнать площадь помещения с выступами, нишами или криволинейными скосами? Самое простое – измерить длины всех стен, а так же углы между ними, после чего начертить план вашей комнаты на листке бумаги (масштаб при этом, скорее всего, подойдет 1:100, то есть одному сантиметру на бумаге будет соответствовать один метр в помещении). Затем необходимо разделить помещение на правильные фигуры (прямоугольника, треугольники, круги и так далее), если это возможно, и пользуясь формулами расчета площади, определить квадратуру каждого участка.
Затем необходимо разделить помещение на правильные фигуры (прямоугольника, треугольники, круги и так далее), если это возможно, и пользуясь формулами расчета площади, определить квадратуру каждого участка.
Ниже приведены самые популярные фигуры, описания методик расчета которых, помогут ответить на вопрос: «Как вычислить площадь комнаты самостоятельно?».
Как найти площадь прямоугольника?
Как вычислить площадь прямоугольника самостоятельно? Комната правильной прямоугольной формы – наиболее простой случай. Для расчета площади прямоугольника достаточно перемножить его длину и ширину. Однако свои нюансы в такой ситуации тоже есть:
- После измерения одной из сторон мерят вторую необходимо строго перпендикулярно. В противном случае измерения могут получиться с существенной погрешностью.
- Чтобы избежать неточностей, меряйте обе параллельные стены, так как часто их длины несколько разные, а для точности желательно взять их среднее арифметическое.
 То есть сложить их значения и разделить на 2.
То есть сложить их значения и разделить на 2. - Не забудьте вычесть из полученной площади всевозможные выступы (или прибавить ниши).
Пример расчета площади простой прямоугольной комнатыИнтересно! В интернете существует множество программ для вычисления площади прямоугольника, онлайн калькулятор – самая простая и удобная из них.
Калькулятор расчета площади четырехугольного помещения
Как посчитать площадь треугольников (прямоугольных и других)?
В некоторых случаях углы комнаты сильно скошены. Тогда при обрисовке плана и разделении его на фигуры появляются элементы треугольной формы. Как вычислить площадь треугольников?
Старайтесь, чтобы все треугольники на вашей схеме быль прямоугольными. В противном случае, посчитать площадь треугольника будет сложнее, а результат будет с большей погрешностью.
Основные формулы расчета площади треугольниковПо сути, прямоугольный треугольник – это половина прямоугольника, поэтому, чтобы найти площадь прямоугольного треугольника, необходимо перемножить длины его катетов (сторон, прилегающих к прямому углу) и разделить полученную величину на 2.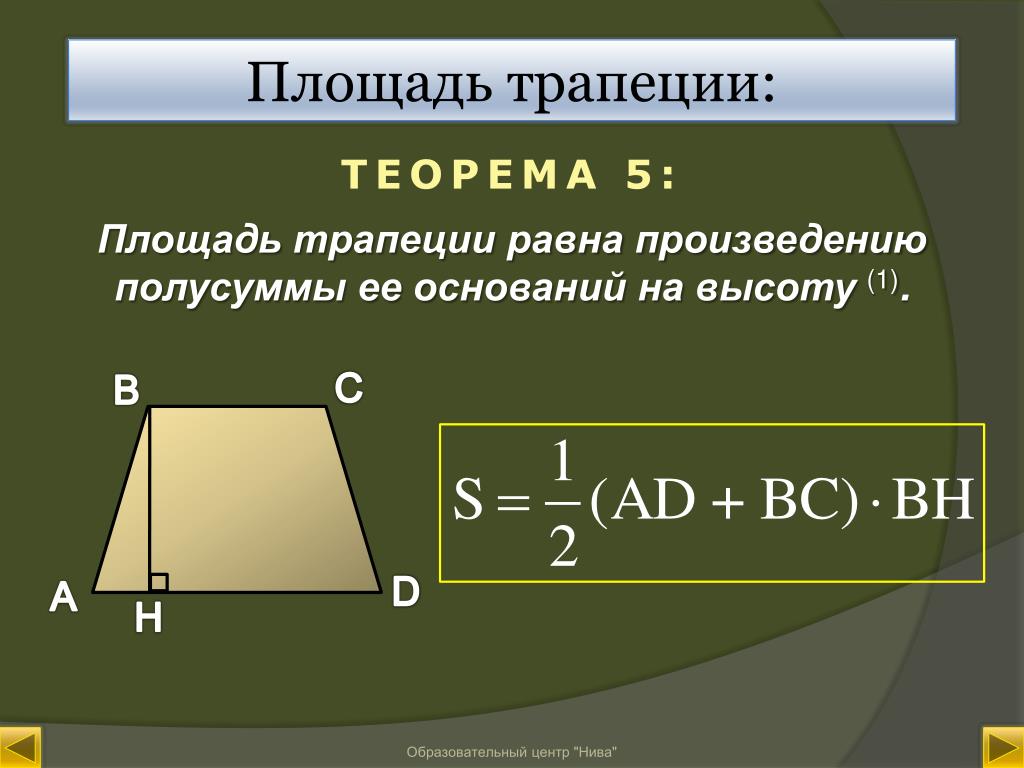 Если фигура оказалась всё-таки не прямоугольной, можно воспользоваться (в зависимости от того, какие величины известны) одной из следующих формул:
Если фигура оказалась всё-таки не прямоугольной, можно воспользоваться (в зависимости от того, какие величины известны) одной из следующих формул:
- S=a*h/2, где h – высота треугольника, а – сторона, к которой она опущена.
- S=a*a*sina/2. Данная формула подходит для равнобедренного треугольника (то есть с двумя одинаковыми сторонами), где а – длина одной из одинаковых сторон, а угол а – угол между одинаковыми сторонами.
- S=a*b*sina/2. Также формула для равнобедренного треугольника, а – одна из одинаковых сторон, b – третья сторона, угол а – угол между a и b.
Кроме того, любой треугольник можно попробовать разделить на несколько прямоугольных фигур. Для этого проведите линию из вершины к противоположной стороне фигуры, чтобы она образовала с ней прямой угол.
Калькулятор расчета площади треугольного помещения
Расчет площади трапеции
Трапеция – это фигура, имеющая четыре стороны, две из которых являются параллельными, а две – нет.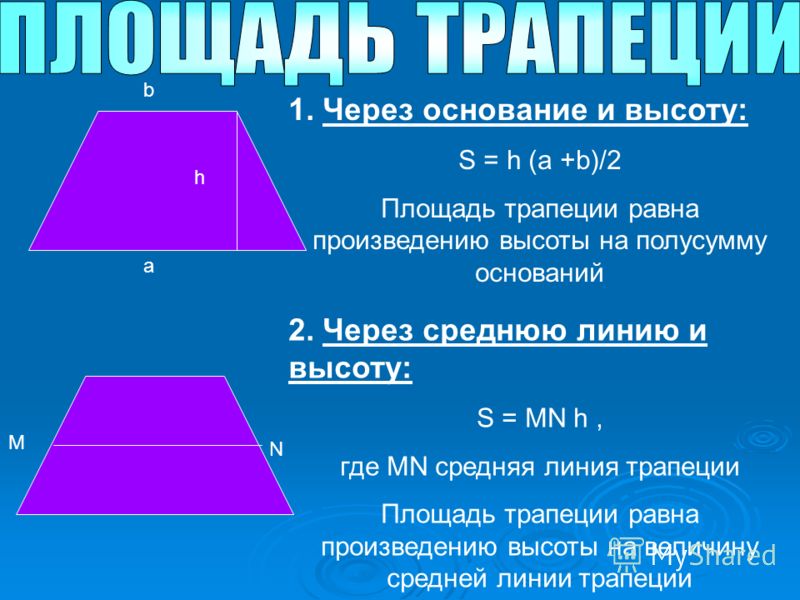 Как рассчитать площадь трапеции самостоятельно? Можно пойти двумя путями:
Как рассчитать площадь трапеции самостоятельно? Можно пойти двумя путями:
- Разделить трапецию на треугольники и прямоугольник (в некоторых случаях получится всего один треугольник + прямоугольник), высчитать площадь каждой фигуры, сложить их, тем самым рассчитав площадь трапеции.
- Воспользоваться несложной формулой: S= (a+b)*h/2, где а и b – параллельные стороны фигуры, h – высота (кратчайшее расстояние) между ними.
Формула для расчета является универсальной, то есть от направления и размера боковых граней ничего не меняется. Главное – правильно измерить высоту фигуры, для этого сделайте замеры в нескольких местах.
Как вычислить площадь круга?
В комнатах (особенно в гостиных) довольно часто бывают круглые выступы, поэтому важно уметь правильно рассчитать площадь круга. При этом главное – узнать радиус окружности. Для этого измерьте расстояние от края дуги до центра виртуального круга, проведя линию между самыми дальними точками фигуры.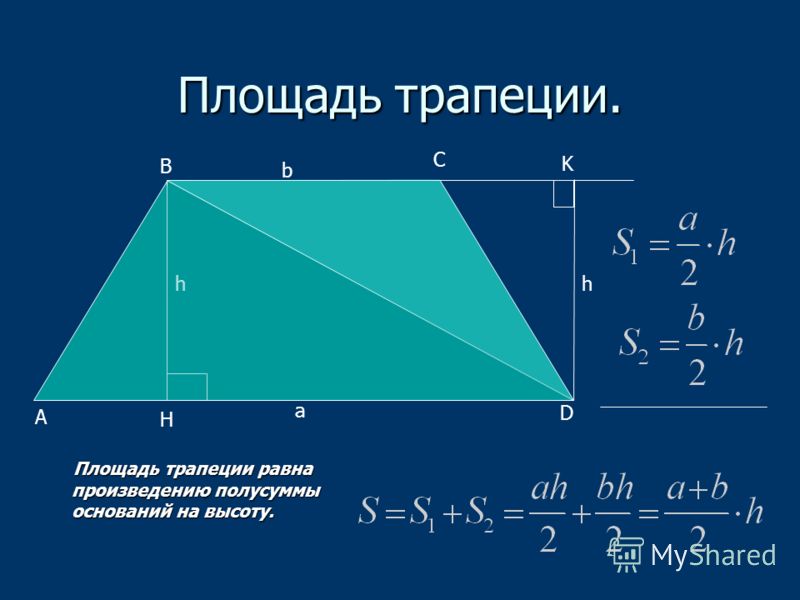
Теперь для расчета площади круга воспользуемся формулой: S=πR2, где π – постоянная величина 3,14, R – радиус окружности.
Схема кругаРасчет площади сегмента круга
Определение площади сегмента круга – задача сложнее. Для начала определимся, что же такое сегмент? Это часть круга, ограниченная хордой (линией, началом и концом которой случат точки от радиуса на окружности).
В первую очередь необходимо найти центр круга, чаще всего сделать это проще экспериментальным путем. Например, попросив друга стать на место предполагаемого центра, дать ему в руки один конец рулетки. Самому же описывать предполагаемую окружность. Таким образом, расчертив необходимый сегмент, можно приступать к расчету площади сектора круга. Формула довольно сложная:
Формула расчета площади сегмента кругаПоэтому целесообразней будет воспользоваться онлайн-расчетом в интернете.
Как посчитать площадь комнаты: порядок действий
Итак, что же нужно сделать, чтобы рассчитать площадь пола в комнате? Порядок действий:
- Подготовительный этап.
 Необходимо приготовить все инструменты и приспособления, а так же расчистить комнату.
Необходимо приготовить все инструменты и приспособления, а так же расчистить комнату. - Измерения. Измерьте длину всех стен в комнате. При этом обратите особое внимание на углы, если они не прямые, непременно запишите их значение.
- Запись результатов. Можно пойти двумя путями: начертить план на листке или нанести размеры непосредственно на пол (если комната находится в стадии черновой отделки).
- Вычисления. При этом если вычисления осуществляются путем расчета отдельных фигур, сложите их очень внимательно, ничего не забыв и следя за тем, чтобы фигуры не находили друг на друга. Основные формулы и порядок расчетов описаны выше, поэтому с данным пунктом проблем возникнуть не должно.
Важно! Измерьте каждую длину как минимум два раза, так вы сможете избежать неточностей и ошибок.
Пример:
Пример комнаты неправильной формыНа рисунке ниже представлена неровная комната. Как посчитать квадратные метры в данном случае? Необходимо выполнить следующий порядок действий:
- Находим площадь прямоугольника, не учитывая его скос в верхнем правом углу.
 Для этого длину 2,5 умножаем на ширину 1,75, получается 4,375 м2.
Для этого длину 2,5 умножаем на ширину 1,75, получается 4,375 м2. - Находим площадь скошенного участка, это прямоугольный треугольник, поэтому получается: 0,57*0,57/2=0,162.
- Вычитаем из первой величины вторую: 4,375-0,162=4,213 м2.
- Округляем до сантиметров: 4,21 м2.
Как посчитать площадь стен?
Ни один ремонт не проходит без замены обоев или покраски стен, ведь эта самая заметная поверхность любой комнаты. Для придания стенам привлекательного вида часто требуется провести несколько этапов ремонтных работ: выравнивание при помощи штукатурки и шпаклевки, грунтовка, финишная отделка (покраска, поклейка обоев, нанесение декоративной штукатурки). На все это требуется большое количество материалов, поэтому важно заранее знать, сколько их нужно и каких денег это будет стоять.
Для этого необходимо правильно рассчитать площади стен комнаты (калькулятор, рулетка, линейка и лист бумаги – все это понадобится вам для работы в обязательном порядке).
Порядок действий:
- Определяем периметр. Как рассчитать периметр комнаты самостоятельно и правильно? Главное – делать измерения не только по плинтусам у пола, но и в середине и в верхней части стены, так как в большинстве как современных, так и старых домов стены не отличаются идеальной ровностью. При этом может возникнуть проблема с определением длины криволинейного участка (например, части окружности). Конечно, можно воспользоваться специальными формулами для расчетов, но проще приложить плотно к стене гибкую рулетку и аккуратно зафиксировать ее показание. Все полученные величины необходимо сложить.
Измерения должны проводиться не только на одной высотеВажно! При расчете периметра обязательно пользуйтесь уровнем (особенно, когда проводите измерения в середине стены).
- Теперь необходимо измерить высоту помещения. Для этого опять же воспользуйтесь уровнем и начертите строго вертикальную линию на стене. Если уровня под рукой не оказалось, не беда, можно сделать вертикальный отвес: к нитке привязать что-либо тяжелое (например, болтик) а держать ее у потолка.
 Под действием силы тяжести нитка натянется вертикально вниз, а вы (или ваш помощник) сможете начертить вертикаль.
Под действием силы тяжести нитка натянется вертикально вниз, а вы (или ваш помощник) сможете начертить вертикаль. - Перемножьте полученные величины, это и будет площадью стен вашей комнаты.
Пример многоуровневого потолкаВажно! Если вы не уверены в ровности потолков, или в данном помещении он является многоуровневым, необходимо считать каждую стену по отдельности.
- Теперь необходимо вычесть из полученного значения площадь оконных и дверных проемов (делайте это по откосам). В некоторых случаях окна имеют круглую или треугольную формулу, тогда необходимо воспользоваться формулами, приведенными выше.
Общие рекомендации
Кроме всего вышесказанного стоит отметить еще несколько важных моментов, на которые стоит обратить внимание при измерении комнаты:
- Во время измерения дверных и оконных проемов не стоит надеяться на правильность их формы.
 Лучше несколько раз все перепроверить для исключения ошибок и погрешностей.
Лучше несколько раз все перепроверить для исключения ошибок и погрешностей. - При расчете расхода строительных материалов не забудьте о том, что некоторых из них понадобится несколько слоев, то есть полученный размер комнаты умножаем на несколько единиц перед покупками.
- При покупке обоев обратите внимание, нужно ли будет подгонять рисунок, если да, берите их с большим запасом. Специалисты рекомендуют даже однотонные обои брать с запасом, так как цвет разных партий несколько расходится, и докупить подходящий материал, возможно, будет сложно.
- При расчете высоты помещения необходимо знать, окончательная ли это высота пола, или он будет подниматься за счет выравнивания или покрытия. Данный момент очень важен, так как в некоторых случаях пол может подняться даже на 10-15 сантиметров из-за выравнивания слишком кривого пола, утепления, шумоизоляции и так далее.
Заключение
Измерение площади комнаты – процесс трудоемкий, но не сложный. Поэтому нет смысла вызывать специальную бригаду, при наличии минимального набора инструментов с этой задачей вполне можно справиться самостоятельно.
Поэтому нет смысла вызывать специальную бригаду, при наличии минимального набора инструментов с этой задачей вполне можно справиться самостоятельно.
Watch this video on YouTube
| Геометрия | Формы | Контакты и конфиденциальность | Геометрические калькуляторы | Немецкий: Geometriechner, Formen | ||||
| 1DЛиния, дуга окружности, парабола, спираль, кривая Коха
2D Правильные многоугольники: Равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, многоугольник, десятиугольник, десятиугольник, додекагон, шестиугольник, N-угольник, кольцо многоугольника Другие многоугольники: Круглые формы: Tetrahedron, Cube, Octahedron, Dodecahedron, Icosahedron Archimedean Solids: Catalan Solids: Johnson Solid: Круглые формы: | Anzeige Расчеты на трапеции. Trapezoid shape: Formulas: Сторона длина, высота, диагонали и периметр имеют одну и ту же единицу измерения (например, метр), площадь имеет эту единицу в квадрате (например, квадратный метр). Anzeige
Поделиться: © Jumk.de Веб-проекты | Онлайн калькуляторы Anzeige |
Калькулятор площади… Ваше полное руководство
Какой калькулятор площади следует использовать и почему?
Это окончательное руководство призвано ответить на этот вопрос и предоставить сборник лучших калькуляторов площади в Интернете и когда их использовать.
Наш сборник организован по вариантам использования, то есть по форме, площадь которой нужно найти, а затем перечислены в порядке наиболее часто используемых калькуляторов площади.
Найдите площадь круга
Найдите площадь треугольника
Найдите площадь трапеции
Найдите площадь четырехугольника
Найдите площадь параллелограмма
Найдите площадь неправильной формы
2 Площадь круга
Чтобы найти площадь идеального круга, вам понадобится одна из трех вещей:
Радиус
Прямая линия, идущая от центра круга к его краю.
Диаметр
Прямая линия, проходящая из стороны в сторону через центр окружностей.
Окружность
Линейное расстояние от края круга.
Если у вас есть хотя бы одно из этих измерений, перейдите по ссылке:
Математика — это весело
Площадь круга
Очень простой интерфейс, который определяет площадь круга при вводе радиуса, диаметра или длины окружности. Это отличный ресурс для правильных многоугольников, если вы знаете некоторые размеры.
Онлайн-калькулятор Keisan
Калькулятор площади круга
Если у вас есть радиус или диаметр круга, этот калькулятор площади предоставит как площадь, так и длину окружности. Отсутствие окружности круга в качестве входных данных немного снижает его полезность, но он так же точен, как и «Математика — это весело».
Отсутствие окружности круга в качестве входных данных немного снижает его полезность, но он так же точен, как и «Математика — это весело».
Calculator Soup
Circle Calculator
Чуть менее интуитивный, но похожий на Maths is Fun, Calculator Soup находит площадь круга при вводе радиуса, диаметра или длины окружности.
SketchAndCalc
Площадь нарисованного круга
SketchAndCalc предлагает другой подход. Если у вас есть только диаметр кругов или вы просто представляете себе пространство, которое окружность должна занимать внутри импортированного изображения или карты, SketchAndCalc может быть лучшим вариантом. Как только масштаб установлен, рисование круга в любом заданном масштабе (от нанометров до миль) позволит получить результаты площади.
Площадь треугольника
Как найти площадь треугольника зависит от того, что вы знаете о треугольнике.
Если у вас есть основание и высота треугольника, просто перемножьте их вместе и разделите на 2, и вы получите площадь (площадь = основание x высота / 2)
Если вы знаете длины сторон треугольника, вам нужно будет использовать Формула Герона или коснитесь длин:
Математика — это весело
Площадь треугольника по сторонам (формула Герона)
попал в наш список, потому что он, пожалуй, самый интуитивно понятный, обновляющий площадь и углы по мере изменения длины сторон.
Если вы знаете угол и длины двух сторон, перейдите к:
Open Math Reference
Площадь треугольника – метод «боковой угол стороны» (SAS)
Этот калькулятор площади треугольника из Open Math Reference предоставляет математическая формула в левом верхнем углу, которая обновляется по мере того, как вы корректируете длину линии и угол. Это похоже на то, как работает SketchAndCalc без отображения длины третьей стороны и оставшихся углов.
Если вам нужно вычислить площадь треугольника на изображении или представленном на карте, попробуйте:
SketchAndCalc
Нарисуйте треугольник на карте или изображении
Независимо от того, начинаете ли вы с пустой сетки, изображения или карты, нарисуйте свой треугольник, а затем переместите вершины в положение, соответствующее длине линий и углам, которые вам нужны. Вы также можете указать точную длину линий и отобразить углы при выборе вершины.
Соберите площадь треугольника вместе с его периметром в правом нижнем углу.
Площадь трапеции
Трапеция — это четырехсторонняя фигура, по крайней мере, с одним набором параллельных сторон, в отличие от четырехугольника, который является любой четырехсторонней фигурой.
Если вы хотите найти площадь трапеции, вам понадобятся две вещи:
Длины двух параллельных линий (идут горизонтально).
Высота фигуры (по вертикали).
Если у вас есть оба из них, перейдите к:
Онлайн-калькулятор Keisan
Калькулятор площади трапеции
Опять же, калькулятор трапеций в онлайн-калькуляторе Keisan не единственный, но нам нравится, что он чистый, простые входы.
Площадь четырехугольника
Четырехугольник — это любая четырехсторонняя фигура, независимо от углов или длин линий.
Чтобы вычислить площадь четырехугольника, вам понадобятся следующие шесть вещей:
Длины всех четырех сторон.
Два из четырех углов.
Если у вас есть все это, перейдите по адресу:
Онлайн-калькулятор Keisan
Калькулятор площади четырехугольника
Для нахождения площади четырехугольника требуется много входных данных. Если вы не знаете всех четырех длин и обоих углов, но имеете представление о том, как выглядит фигура, или у вас есть изображение, содержащее фигуру, вы можете нарисовать ее, используя:
Если вы не знаете всех четырех длин и обоих углов, но имеете представление о том, как выглядит фигура, или у вас есть изображение, содержащее фигуру, вы можете нарисовать ее, используя:
SketchAndCalc
Площадь неправильных форм
Прежде чем рисовать область четырехугольников, импортируйте ее изображение и задайте масштаб чертежа, рисуя по известной длине (согласно запросу в процессе импорта изображения).
Площадь параллелограмма
Параллелограмм — это любая фигура, у которой противоположные стороны равны по длине, параллельны друг другу и имеют равные по величине противоположные углы.
Итак, по определению, квадраты, прямоугольники и ромбы являются параллелограммами.
Найдите площадь параллелограмма, перемножив основание и высоту вместе, или перейдите к:
Омникалькулятор
Калькулятор площади параллелограмма
Если у вас есть длины сторон и угол параллелограмма, измените «Заданное» значение на: стороны + угол между
Калькулятор сторон параллелограмма и площади угла
Если вы знаете только длины линий вашего параллелограмма и не имеете углов, вам нужно нарисовать фигуру с помощью:
SketchAndCalc
Калькулятор площади параллелограмма
С помощью «инструмента рисования ограниченных линий» SketchAndCalc можно нарисовать идеальный параллелограмм. Отрегулируйте длину линий вручную, перемещая вершины, или просто выберите метку длины линии и введите желаемую длину.
Отрегулируйте длину линий вручную, перемещая вершины, или просто выберите метку длины линии и введите желаемую длину.
Площадь неправильных форм
Измерьте любую неправильную область на картах, изображениях или планах с помощью SketchAndCalc.
SketchAndCalc
Калькулятор нестандартной площади
Установите масштаб изображения с известной длиной или, в случае области карты, просто найдите адрес и начните рисовать периметр фигуры или фигур, которые вы хотите рассчитать.
Мы надеемся, что это руководство было полезным и сэкономило вам время. Если есть калькуляторы площади правильных или неправильных многоугольников, которые вы хотели бы видеть включенными, сообщите нам об этом.
рассчитайте площадь и периметр с помощью онлайн-калькулятора или формулы
трапеция представляет собой тип геометрической фигуры с четырьмя сторонами, но отличается от квадрата или прямоугольника тем, что только две стороны параллельны друг другу.
Из-за этого расчет площади трапеции требует использования другой формулы, чем обычное умножение основания на высоту. К счастью, наш онлайн-калькулятор позволяет вам получить площадь этой геометрической фигуры, просто введя длину наименьшего основания, наибольшего основания и высоту.
Разделы статей
- Как найти площадь трапеции
- Решенное упражнение по вычислению площади трапеции
- Классификация трапеций
- Периметр трапеции
- Вычислить медиану трапеции
- Сколько сторон у трапеции?
Как извлечь площадь трапеции
Для вычисления площади трапеции мы должны сложить длины оснований, то есть сторон, которые параллельны друг другу. Затем умножаем значение суммы на высоту трапеции и, наконец, делим результат на два.
Короче говоря, вы должны применить следующую математическую формулу , чтобы получить площадь трапеции:
Решенное упражнение по вычислению площади трапеции
Чтобы лучше понять приведенную выше формулу, давайте см. практический пример, как вычисляет площадь трапеции по длине ее сторон и ее высоте.
практический пример, как вычисляет площадь трапеции по длине ее сторон и ее высоте.
На предыдущем рисунке мы видим, что трапеция имеет следующие размеры:
- Верхняя база (b): 4 см
- Нижнее основание (B): 10 см
- Высота (в): 4 сантиметра
Этого достаточно, чтобы можно было вычислить площадь этой фигуры геометрической. Применим приведенную выше формулу и получим:
Площадь = (10 + 4) x 4 / 2 = 28 см 2
Помните, что когда мы говорим о площадях, результирующая единица должна быть возведена в квадрат.
Классификация трапеций
Трапеции могут быть разных типов Поэтому мы предлагаем вам классификацию по их сторонам.
Хотя существуют разные виды трапеций, формула расчета его площади одинакова для всех .
Равнобедренный треугольник
Наиболее часто в задачах по геометрии встречается равнобедренная трапеция, т. е. та, у которой имеет непараллельные стороны одинаковой длины .
е. та, у которой имеет непараллельные стороны одинаковой длины .
Прямоугольная трапеция
Существует также прямоугольная трапеция, у которой одна сторона перпендикулярна основаниям , что приводит к появлению двух прямых углов.
Разносторонняя трапеция
Наконец, мы находим разностороннюю трапецию, у которой все внутренних углов являются различными s, что также является результатом наличия сторон разной длины.
Периметр трапеции
Чтобы рассчитать периметр трапеции , просто добавьте длину ее четырех сторон, то есть:
Периметр = a + b + c + d
В случае периметра равнобедренной трапеции Поскольку стороны c и d точно равны, формулу можно упростить:
Периметр равнобедренной трапеции трапеция: a + b + 2c
Например, в решенном упражнении, которое мы видели ранее, у нас есть пример равнобедренной фигуры, поэтому мы можем вычислить ее периметр, используя предыдущую формулу:
Периметр = 10 + 4 + 2 + 2 х 5 = 24 сантиметра.
Легко, не правда ли?
Вычисление медианы трапеции
Медиана трапеции определяется как отрезок , соединяющий половины двух боковых сторон и параллельный двум основаниям . Чтобы рассчитать его длину, мы должны усреднить два основания, то есть мы должны применить следующую формулу:
Среднее = (Малое основание + большое основание) / 2
На изображении выше медиана будет FG сегмент.
Сколько сторон у трапеции?
Трапеция представляет собой четырехстороннюю фигуру :
- Две стороны параллельны и образуют основания трапеции. Расстояние между этими сторонами равно высоте.
- Две непараллельные стороны , которые могут образовывать разные углы с основаниями.
Nacho
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En Esta веб-те Ayudo hacer cálculos у преобразования sencillas дие кон-эль-Пасо-де-лос-Años се-нос-ха olvidado Cómo себе Hace. Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.
Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.
- Площадь пирамиды
- Площадь квадрата
- Площадь сферы
- Площадь круга
- Площадь прямоугольника
- Вычислить площадь и апофему пятиугольника трапеции
- Вычислить площадь треугольника
- Вычислить площадь цилиндра
- Вычислить площадь ромба
- Вычислить площадь и апофему правильного шестиугольника
- Вычислить сторону квадрата
- Додекаэдр
- Икосаэдр
- Ромбовид
- Круговой сектор
- Тетраэдр
Калькулятор площади трапеции | Вычислить площадь трапеции
✖Короткое основание трапеции — это более короткая сторона среди пары параллельных сторон трапеции. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | +10% -10% | ||
✖Длинное основание трапеции — это длинная сторона среди пары параллельных сторон трапеции. | А.Е. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | +10% -10% | |
✖height трапеции -это перпендикулярная расстояние между парами параллельных сторон трапеции. | 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | +10% -10% |
✖Площадь трапеции — это общее количество плоскостей, ограниченных границей трапеции. | AcreAcre (US Survey)AreArpentBarnCarreauCircular InchCircular MilCuerdaDecareDunamElectron Cross SectionHectareHomesteadMile (Roman)²Mile (Statute)²MuPingPlazaPyongRoodSabinSectionSquare AngstromSquare CentimeterSquare ChainSquare DecameterSquare DecimeterSquare FootSquare Foot (US Survey)Square HectometerSquare InchSquare KilometerSquare MeterSquare MicrometerSquare MilSquare MileSquare Mile (US Survey)Square MillimeterSquare NanometerSquare PerchSquare PoleSquare RodSquare Rod ( Исследование США) Square YardStremmaTownshipVaras Castellanas CuadVaras Conuqueras Cuad | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Площадь решения трапеции
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовую единицу
Короткое основание трапеции: 5 метров —> 5 метров Преобразование не требуется
Длинное основание трапеции: 15 метров —> 15 метров Преобразование не требуется
Высота трапеции: 8 метров —> 8 метров преобразование не требуется
ШАГ 2: Вычисление формулы
ШАГ 3: Преобразование результата в единицу измерения
80 Квадратный метр —> преобразование не требуется
< 7 Калькулятор площади< 3 Калькулятор площади трапецииФормула площади трапеции
Площадь трапеции = ((короткое основание трапеции+длинное основание трапеции)/2)*высота трапеции
A = ((B Short +B Long )/2)*h
Что такое Трапеция?
Трапеция – это четырехугольник с одной парой противоположных и параллельных сторон. Пару параллельных сторон называют основаниями трапеции, а пару непараллельных ребер — катетами трапеции. Из четырех углов трапеция обычно имеет 2 острых угла и 2 тупых угла, которые являются попарно дополнительными углами.
Пару параллельных сторон называют основаниями трапеции, а пару непараллельных ребер — катетами трапеции. Из четырех углов трапеция обычно имеет 2 острых угла и 2 тупых угла, которые являются попарно дополнительными углами.
Как рассчитать площадь трапеции?
Калькулятор площади трапеции использует Площадь трапеции = ((Короткое основание трапеции + Длинное основание трапеции)/2)*Высота трапеции для расчета площади трапеции. Формула площади трапеции определяется как общее количество заключенной плоскости по границе трапеции. Площадь трапеции обозначается символом A .
Как рассчитать площадь трапеции с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для площади трапеции, введите Короткое основание трапеции (B Короткая ) , Длинное основание трапеции (B Длинная ) и Высота трапеции (h) и нажмите кнопку расчета. Вот как можно объяснить вычисление площади трапеции с заданными входными значениями -> 80 = ((5+15)/2)*8 .
Вот как можно объяснить вычисление площади трапеции с заданными входными значениями -> 80 = ((5+15)/2)*8 .
Часто задаваемые вопросы
Что такое площадь трапеции?
Формула площади трапеции определяется как общее количество плоскостей, ограниченных границей трапеции, и представляется как A = ((B Short +B Long )/2)*h или Площадь трапеции = ((Короткое основание трапеции+Длинное основание трапеции)/2)*Высота трапеции . Короткое основание трапеции — это более короткая сторона среди пары параллельных сторон трапеции, длинное основание трапеции — это более длинная сторона среди пары параллельных сторон трапеции, а высота трапеции — это перпендикулярное расстояние между парой параллельных сторон трапеции. Трапеция.
Как рассчитать площадь трапеции?
Формула площади трапеции определяется как общее количество плоскостей, ограниченных границей трапеции, рассчитывается с использованием Площадь трапеции = ((короткое основание трапеции + длинное основание трапеции)/2)*высота трапеции . Чтобы вычислить площадь трапеции, вам нужно короткое основание трапеции (B короткое ) , длинное основание трапеции (B длинное ) и высота трапеции (h) . С помощью нашего инструмента вам нужно ввести соответствующее значение для короткого основания трапеции, длинного основания трапеции и высоты трапеции и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Чтобы вычислить площадь трапеции, вам нужно короткое основание трапеции (B короткое ) , длинное основание трапеции (B длинное ) и высота трапеции (h) . С помощью нашего инструмента вам нужно ввести соответствующее значение для короткого основания трапеции, длинного основания трапеции и высоты трапеции и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Сколько существует способов вычисления площади трапеции?
В этой формуле площадь трапеции использует короткое основание трапеции, длинное основание трапеции и высоту трапеции. Мы можем использовать 2 других способа (ов) для вычисления того же самого, которые заключаются в следующем:
- Площадь трапеции = центральная медиана трапеции * высота трапеции
- Площадь трапеции = ((периметр трапеции-(короткая катет трапеции+длинный катет трапеции))*высота трапеции)/2
Поделиться
Скопировано!
Калькулятор трапецеидального правила — найдите трапециевидную сумму и приближение
Онлайн-калькулятор трапециевидного правила поможет вам оценить площадь под графиком заданной функции, используя правило трапеций. Калькулятор площади свободной трапеции аппроксимирует интеграл в нескольких подынтервалах с пошаговыми вычислениями. Взгляните на правило трапеций и формулу суммы в приведенном ниже контексте.
Калькулятор площади свободной трапеции аппроксимирует интеграл в нескольких подынтервалах с пошаговыми вычислениями. Взгляните на правило трапеций и формулу суммы в приведенном ниже контексте.
Калькулятор по правилу трапеций использовал метод трапеций для оценки определенных интегралов.
Однако онлайн-калькулятор интегралов позволяет находить интегралы функций по рассматриваемой переменной.
Площадь трапеции(Изображение)
Теперь площадь трапеции определяется как:
Площадь = h/2 (a + b)
Где,
9n), \text { где} , Δa = (y-x)/n.$$- Разобьем отрезок на меньшие трапеции длины Δa.
- В подынтервалах последним является y, а первым — x, и вычисляем функции при этих значениях трапеций.
- Подставьте значения в формулу правила трапеций и просуммируйте полученные значения, чтобы получить оценочное значение.

Однако онлайн-калькулятор суммы Римана поможет вам аппроксимировать определенный интеграл и выборочные точки средних точек, трапеций, правых и левых конечных точек, используя конечную сумму. 95) = f(1) = 2√(1+sin3(1) = 1,2632$$
$$Δa/2 = 1/10$$
Наконец, просуммируйте вышеуказанные значения и умножьте на Δa/2
$$= 1/10 (1 + 2,0078 + 2,0582 + 2,1725 + 2,3402 + 1,2632)$$
$$= 1,0842$$
Как работает калькулятор правил трапеций? области с помощью метода трапеций, выполнив следующие шаги: Ввод:- Сначала введите функцию относительно различных переменных.0348
- Теперь подставьте верхний и нижний пределы.
- Затем добавьте необходимое количество трапеций.
- Нажмите кнопку «Рассчитать», чтобы увидеть результаты.
- Калькулятор трапециевидной формы отображает ввод и ответ в стандартной форме.
- Калькулятор площади трапеции предоставляет все конечные точки и сумму этих точек.

Правило Симпсона можно назвать параболическим правилом. Но правило трапеций можно назвать правилом трапеций.
Какое правило лучше трапециевидное или Симпсоны?Когда мы работаем с квадратичными функциями, правило Симпсонов обеспечивает наилучшую оценку, а правило трапеций обеспечивает наихудшее приближение. Кроме того, для тригонометрических функций метод Симпсона также дал наиболее точную оценку, а метод трапеций дал наименее точную оценку.
Заключение:Используйте этот бесплатный онлайн-калькулятор трапецеидального правила, который предназначен для исследователей, студентов, математиков и учителей. Эта удобная область калькулятора трапеций принимает интегральную функцию с верхним и нижним пределами и быстро обеспечивает 100% точное пошаговое решение.
Ссылка: Из источника Википедии: Правило трапеций, Численная реализация, Неравномерная сетка, Равномерная сетка.
Из источника Math 24: Суммы Римана, маленькие трапеции, определенный интеграл, правило трапеций.
Из источника LibreText: Численное интегрирование — средняя точка, трапеция, правило Симпсона, правило средней точки.
Момент инерции трапеции
Прыжки до
-Калькулятор
-Определения
СОДЕРЖА Главные оси
— Размеры
— Момент инерции масс
— Приложения
Поделитесь этим
См. также
Момент инерции трапеции
— Д-р Минас Э. Лемонис, доктор философии — Обновлено: 2 мая 2020 г.
Главная > 9 Момент инерции Этот инструмент вычисляет момент инерции I (второй момент площади) трапеции. У трапеции есть хотя бы одна пара параллельных сторон, называемых основаниями. Введите размеры формы «b», «a» и «h» ниже. Вычисленные результаты будут иметь те же единицы измерения, что и введенные вами. Пожалуйста, используйте согласованные единицы для любых входных данных.
b = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
h = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Results | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ищете другую ось? Больше информации?
РЕКЛАМА
Содержание
— Калькулятор
-Определения
-Параллельные оси Теорема
-Повернутые оси
-Основные оси
-Размеры
-Mass Moment of Inertia
-Применения
OF
9
-Приложения
OF
2
-Применения
OF
9
—
OF
2
—
OF
2 9018. можно найти, если всю площадь разделить на три меньших, A, B, C, как показано на рисунке ниже. Конечную область можно рассматривать как аддитивную комбинацию A+B+C.
 Следовательно, момент инерции I 93}{12} (3a+b) \end{split}
Следовательно, момент инерции I 93}{12} (3a+b) \end{split}Момент инерции относительно центральной оси x-x можно найти с помощью теоремы о параллельных осях (см. ниже). Однако сначала необходимо определить положение центроида, а точнее его вертикальное расстояние от нижнего основания (другими словами, его координату y 0 ). Это, в свою очередь, можно рассчитать, используя первые моменты площади трех подобластей A, B, C. Поскольку основания треугольных площадок А и С совпадают с основанием дна трапеции, получается следующее выражение:
\begin{split} y_{c} & = \frac{1}{A}\left( \frac{b_1 h}{2}\frac{h}{3} + {a h}\frac{h} {2} + \frac{(b-a-b_1) h}{2}\frac{h}{3}\right) \Rightarrow \\ y_{c} & = \frac{h}{3}\frac{2a +b}{a+b} \end{split}
где A — площадь трапеции, равная (a+b)h/2 .
Последнее выражение — это формула, которая дает расстояние до центра тяжести от нижнего основания.
Аналогичным образом можно найти момент инерции относительно осей y или y0 (перпендикулярных основаниям), а также произведение инерции. Однако формулировка простых уравнений для этих величин невозможна. 92
Однако формулировка простых уравнений для этих величин невозможна. 92
где I’ — момент инерции относительно произвольной оси, I — момент инерции относительно центральной оси, параллельной первой, d — расстояние между двумя параллельными осями и A — площадь форма (=bh/2 в случае треугольника).
Для произведения инерции Ixy теорема о параллельных осях принимает аналогичную форму:
I_{xy’} = I_{xy} + A d_{x}d_{y}
относительно центроидальных осей x,y и Ixy’ есть произведение инерции относительно осей, параллельных центроидальным x,y, имеющих смещения от них d_{x} и d_{y} соответственно.
Повернутые оси
Для преобразования моментов инерции от одной системы осей x,y к другой u,v, повернутой на угол φ, используются следующие уравнения:
\begin{split} I_u & = \frac{I_x+I_y}{2} + \frac{I_x-I_y}{2} \cos{2\varphi} -I_{xy} \sin{2\varphi} \\ I_v & = \frac{I_x +I_y}{2} — \frac{I_x-I_y}{2} \cos{2\varphi} +I_{xy} \sin{2\varphi} \\ I_{uv} & = \frac{I_x-I_y }{2} \sin{2\varphi} +I_{xy} \cos{2\varphi} \end{split}
где Ix, Iy — моменты инерции относительно начальных осей, а Ixy — произведение инерции. Iu, Iv и Iuv – соответствующие величины для вращающихся осей u,v. Произведение инерции трапеции обычно не равно нулю, если не существует симметрии, по любой из соответствующих осей.
Iu, Iv и Iuv – соответствующие величины для вращающихся осей u,v. Произведение инерции трапеции обычно не равно нулю, если не существует симметрии, по любой из соответствующих осей.
Калькулятор общего назначения для преобразования моментов инерции и произведения инерции любой 2D-формы из-за вращения оси доступен здесь.
Главные оси
В главных осях, повернутых на угол θ относительно исходных центроидальных осей x,y, произведение инерции становится равным нулю. Из-за этого любая ось симметрии формы также является главной осью. Моменты инерции относительно главных осей I_I, I_{II} называются главными моментами инерции и являются максимальным и минимальным для любого угла поворота системы координат. Если Ix, Iy и Ixy известны для произвольной центроидальной системы координат x,y, то главные моменты инерции и угол поворота θ главных осей можно найти, используя следующие выражения: 94 .
Массовый момент инерции
В физике термин момент инерции имеет другое значение.

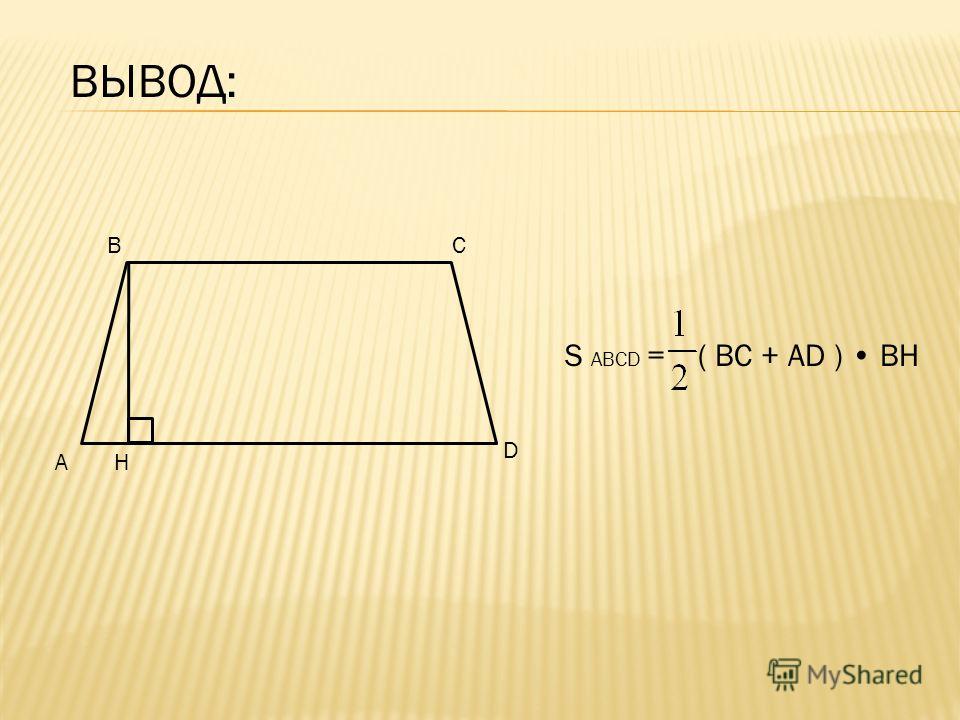

 1 переключится и на входе D триггера DD1.2 появится напряжение высокого уровня. Поэтому при нажатии очередной кнопки кода SA2 триггер DD1.2 изменяет свое состояние и подготавливает к переключению следующий триггер. В случае дальнейшего правильного набора последним сработает триггер DD2.2, и …
1 переключится и на входе D триггера DD1.2 появится напряжение высокого уровня. Поэтому при нажатии очередной кнопки кода SA2 триггер DD1.2 изменяет свое состояние и подготавливает к переключению следующий триггер. В случае дальнейшего правильного набора последним сработает триггер DD2.2, и …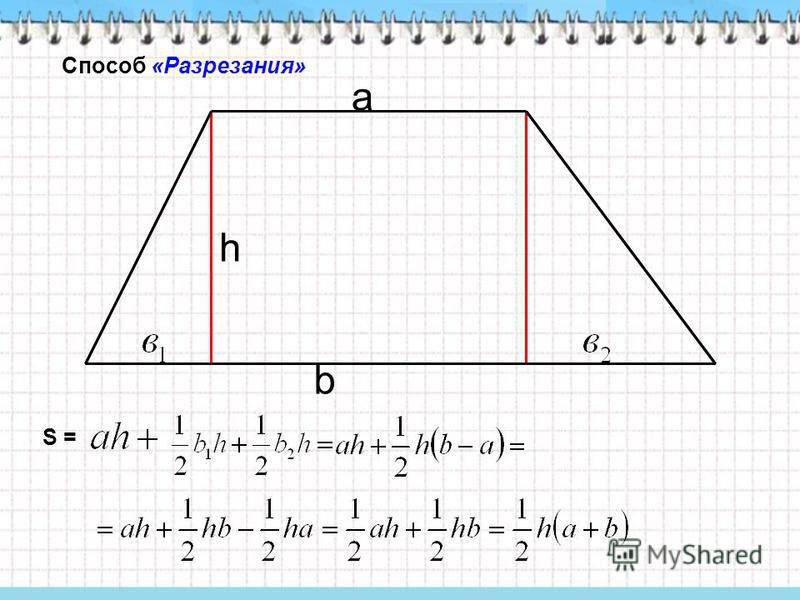 11.2017
11.2017 Также они наклонены к основанию под одним углом.
Также они наклонены к основанию под одним углом.






 Сколько бумаги требуется для крышки бака.
Сколько бумаги требуется для крышки бака.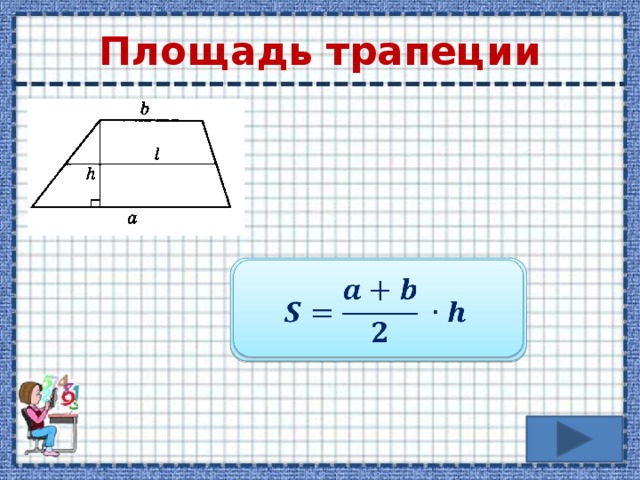 Переместите нижнюю половину треугольника рядом с верхней половиной, чтобы получился параллелограмм.Более короткая диагональ (a) становится основанием параллелограмма, а половина более длинной диагонали (b) становится высотой параллелограмма. Таким образом, площадь ромба равна a * b или произведению диагоналей, что является стандартной формулой для ромба.
Переместите нижнюю половину треугольника рядом с верхней половиной, чтобы получился параллелограмм.Более короткая диагональ (a) становится основанием параллелограмма, а половина более длинной диагонали (b) становится высотой параллелограмма. Таким образом, площадь ромба равна a * b или произведению диагоналей, что является стандартной формулой для ромба.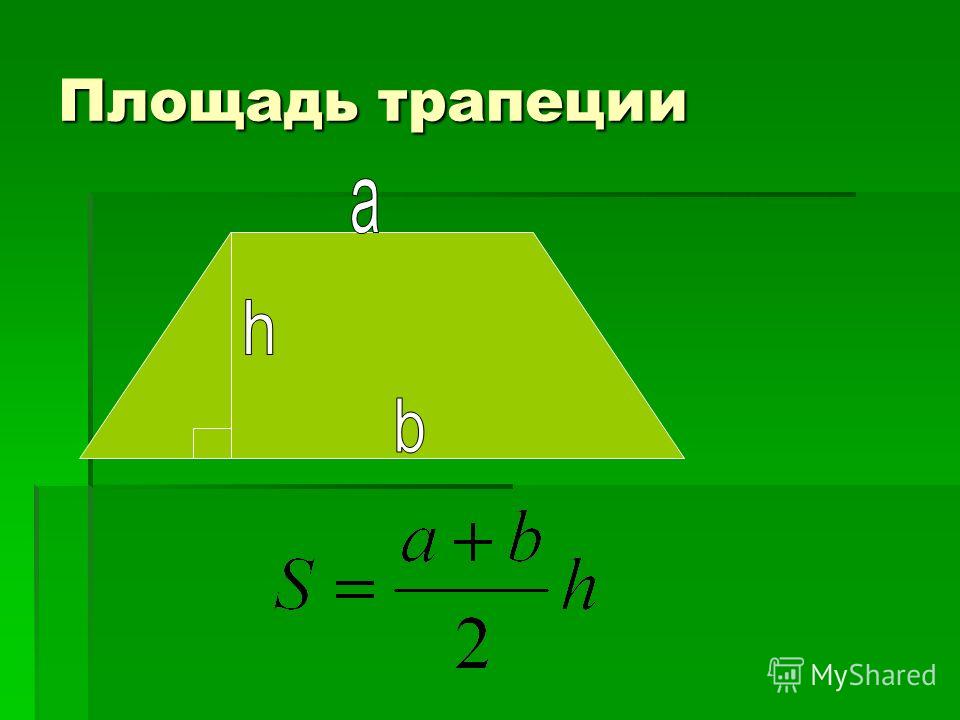
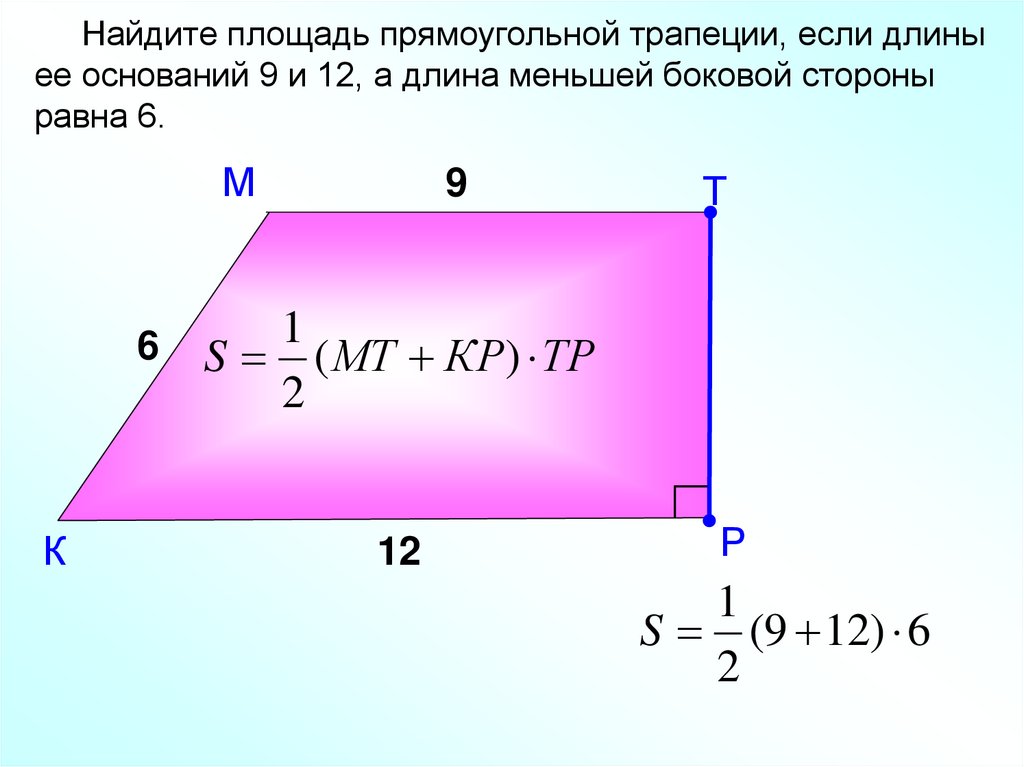 1 Как найти площадь прямоугольника?
1 Как найти площадь прямоугольника?
 Например, застройщик (в случае долевого участия в строительстве) обязан возместить стоимость недостающих квадратных метров.
Например, застройщик (в случае долевого участия в строительстве) обязан возместить стоимость недостающих квадратных метров. Кроме того, такой рулеткой не измерить сложные формы, при работе с выступающими элементами также могут возникнуть проблемы. Поэтому оптимальный набор – простая рулетка и линейка. Главное – проверить их точность, так как многие старые или детские приспособления имеют приличную погрешность.
Кроме того, такой рулеткой не измерить сложные формы, при работе с выступающими элементами также могут возникнуть проблемы. Поэтому оптимальный набор – простая рулетка и линейка. Главное – проверить их точность, так как многие старые или детские приспособления имеют приличную погрешность.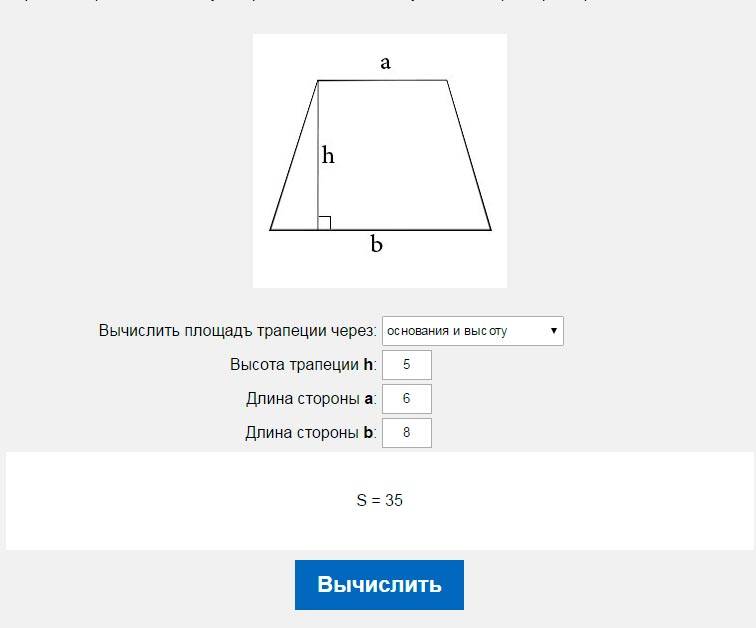 То есть сложить их значения и разделить на 2.
То есть сложить их значения и разделить на 2. Необходимо приготовить все инструменты и приспособления, а так же расчистить комнату.
Необходимо приготовить все инструменты и приспособления, а так же расчистить комнату.