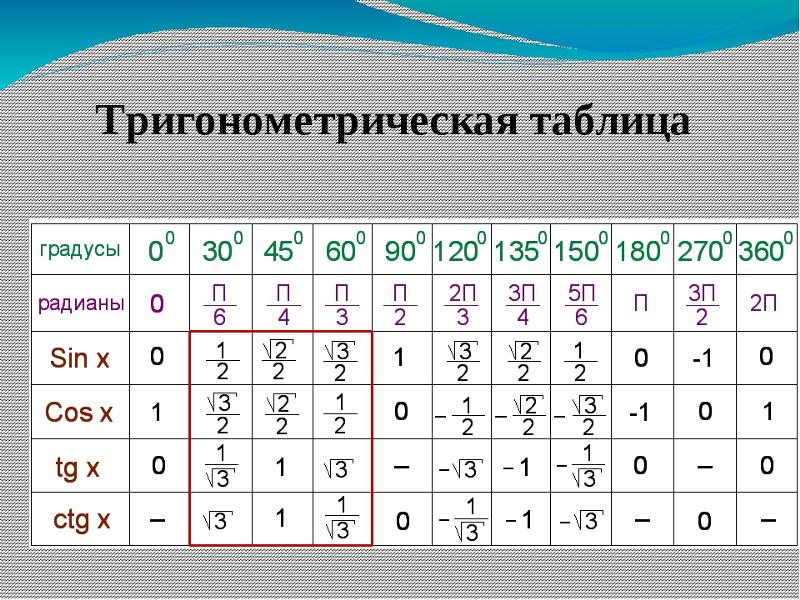
Значения синуса, косинуса и тангенса для углов 30, 45 и 60 градусов
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Значения синуса,
косинуса и тангенса
для углов
0
30 ,
0
45
и
0
60
Методическая разработка урока
по геометрии 8 класса
учителя ГБОУ СОШ № 277
города Санкт-Петербурга
Протасовой Светланы Михайловны
2. Цели урока
• Научить учащихся вычислять значениясинуса, косинуса и тангенса для углов
300, 450 и 600.

• Формировать навыки решения
прямоугольных треугольников,
используя синус, косинус и тангенс
острого угла.
3. Содержание
• Проверка домашнего задания• Устная работа
• Вычисление значений синуса, косинуса и
тангенса для углов 300, 450 и 600 в ходе
решения задач
• Таблица значений синуса, косинуса и
тангенса для углов 300, 450 и 600
• Решение задач
• Итоги урока
• Домашнее задание
4. Проверка домашнего задания
Дано:АВС
∠С=900
ВС=1
АС=2
Найти:
Sin A, cos A, tg A,
Sin B, cos B, tg B.
Ответ:
1
2
1
Sin A
; Cos A
; tg A .
2
5
5
2
1
2
Sin B
; Cos B
; tg B 2.
1
5
5
5. Проверка домашнего задания
Ответы к тесту:1) А
2) А
3) В
4) Б
5) Б
6. Устная работа
1. Сформулируйте теорему Пифагора дляпрямоугольного треугольника.
C2=a2+b2
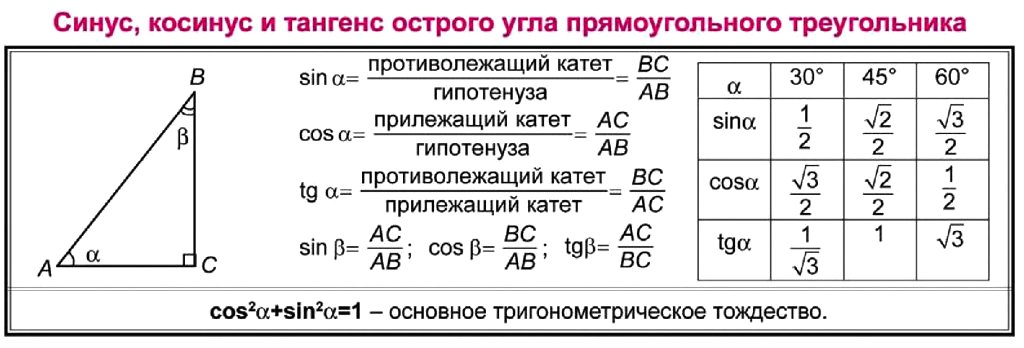
2.Что называют синусом, косинусом, тангенсом
острого угла прямоугольного треугольника?
3.
 Как найти площадь параллелограмма?
Как найти площадь параллелограмма?S=a∙h
4. Как найти катет прямоугольного треугольника,
лежащий напротив угла в 300?
7. Устная работа
Дано:АВС
∠С=900
ВС=5
АВ=13
Найти:
Sin A, cos A, tg A,
Sin B, cos B, tg B.
8. Решение задачи
По теореме Пифагора:АВ2=ВС2+АС2
АС2=169-25
АС2=144
АС=12
BC
5
SIN A=
SIN A
13
AB
COS A=
tg A=
AC
AB
BC
AC
12
COS A
13
tg A
5
12
SIN B =
AC
AB
COS B=
tg B =
BC
AB
AC
BC
12
SIN B
13
5
COS B
13
12
2
tg B
2
5
5
9. Устная работа
Дано:АВСD-параллелограмм
∠E=900
∠A=600
AE=4
ED=5
Найти:
SABCD.
10. Решение задачи
SABCD=BE·ADAD=4+5=9
AE=0,5∙AB => AB=8
По теореме Пифагора:
AB2=AE2+BE2
BE2=64-16=48
BE 48
S 9 48
∠ABE=300
Ответ: S
9 48
11.
 Вычисление значений синуса, косинуса и тангенса для углов 300, 450 и 600 в ходе решения задачДано:
Вычисление значений синуса, косинуса и тангенса для углов 300, 450 и 600 в ходе решения задачДано:АВС
∠А=300
∠С=900
Найти:
Sin A, cos A, tg A,
Sin B, cos B, tg B.
300
12. Решение задачи №1
ACAC
2
2
4X
3X
2
X
2
2
300
AC 3 X
BC X 1
SIN A
AB 2 X 2
COS A
tg A
AC
3X
3
AB
2X
2
BC
X
1
3
AC
3X
3 3
=> SIN
300
SIN B
=> COS 300 COS B
=> tg 300
tg B
AC
3X
3
=>
AB 2 X
2
BC
X
1
AB
2X
2
SIN 600
=> COS 600
AC
3X
3
3
BC
X
1
=> tg 600
13. Вычисление значений синуса, косинуса и тангенса для углов 300, 450 и 600 в ходе решения задач
Дано:АВС
∠А=450
∠С=900
Найти:
Sin A, cos A,
tg A.
450
14. Решение задачи №2
AB2
BC
2
AC
2
AB 2 x
450
BC
X
1
2
SIN A
=> SIN 450
AB
2
2X
2
AC
X
1
2 => COS 450
COS A
AB
2
2X
2
BC X
tg A
1
AC X
=> tg 450
15.
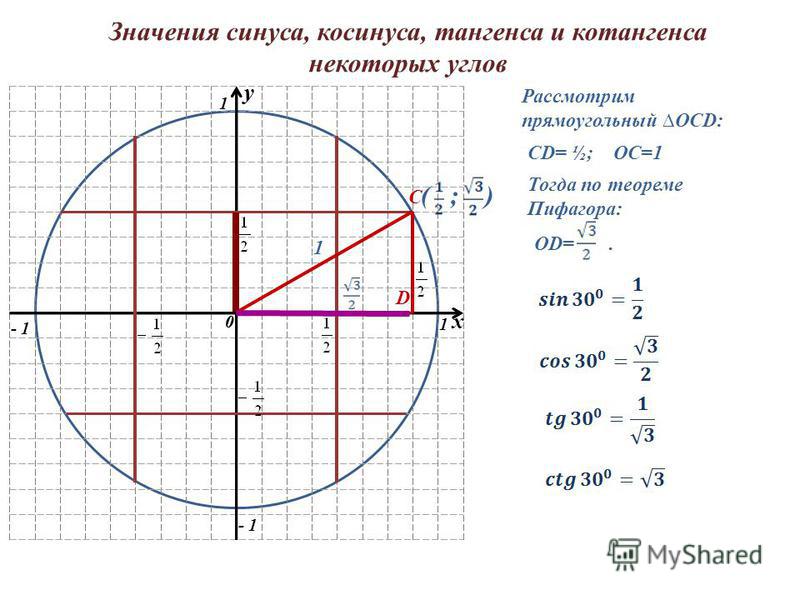 Таблица значений синуса, косинуса и тангенса для углов 300, 450 и 600sin
Таблица значений синуса, косинуса и тангенса для углов 300, 450 и 600sin 300
450
600
1
2
2
2
3
2
cos
3
2
2
2
tg
3
3
1
1
2
3
16. Решение задач
В прямоугольной трапеции основания равны6 и 11, меньшая боковая сторона равна 4.
Найдите синус, косинус и тангенс острого
угла трапеции.
Дано:
АВСD-трапеция
CD AD
CD=4
AD=11
BC=6
Найти:
Sin A, cos A, tg A.
17. Решение задачи №3
Проведем ВН ADBH=CD=4
AH=AD – HD=5
ABH-прямоугольный
ПО ТЕОРЕМЕ ПИФАГОРА:
АВ2=ВН2+АН2
AB 41
BH
4
4 41
SIN A
AB
41
41
AH
5
5 41
COS A
AB
41
41
BH 4
tg A
AH 5
ОТВЕТ: SIN A 4 41 ; COS A 5 41 ; tg A 4
41
41
5
18. Решение задач
В прямоугольном треугольникегипотенуза равна с, а один из острых
углов равен . Выразите второй
острый угол и катеты через с и и
найдите их значения, если с=24, а =600.

Дано:
АВС
∠А= =600
AВ=24
Найти:
∠В, АС, ВС,
Выразить через
и с.
19. Решение задачи №4
ABС-прямоугольный∠В=900-
∠В=300, так как =600
BC
3
SIN A
12 3
=> ВС=АВ∙SIN => BС=c∙SIN => BC 24
AB
2
COS A
AC
1
=> AС=АВ∙COS => AС=c∙COS =>AC 24 12
AB
2
Ответ: ∠В=900-
BС=c∙SIN
AС=c∙COS
∠В=300
АС=12
BC 12 3
20. Итоги урока
1. Как найти острый уголпрямоугольного треугольника, если
другой острый угол равен ?
2. Какая связь существует между
катетом, противолежащим ему
углом и гипотенузой?
21. Итоги урока
3. Как взаимосвязаны два катетапрямоугольного треугольника и
один из его острых углов?
4. Какая связь существует между
катетом, прилежащим к нему
острым углом и гипотенузой?
5. Для каких углов сегодня узнали
значения синуса, косинуса и
тангенса?
22. Домашнее задание
Выучить значения синуса, косинуса итангенса для углов 300, 450 и 600;
№ 595; № 597; № 598(б).
English Русский Правила
Примечание . В данной таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. Для обозначения дроби — символ «/». См. также полезные материалы: Для определения значения тригонометрической функции , найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т. Синус пи, косинус пи, тангенс пи и других углов в радианахПриведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах . Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан. Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны 180 градусам. Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180 . Примеры : 2. Косинус пи . 3. Тангенс пи Таблица значений синуса, косинуса, тангенса для углов 0 — 360 градусов (часто встречающиеся значения)
Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения. Таблица значений тригонометрических функций sin, cos, tg для наиболее популярных углов0, 15, 30, 45, 60, 90 … 360 градусов (цифровые значения «как по таблицам Брадиса»)
|
Урок: №55. Тема: «Синус, косинус, тангенс и котангенс произвольного угла. Значения синуса, косинуса, тангенса и котангенса углов». | Школа: Аксенгирская сш | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Дата: 24.01.2018г | ФИО учителя: Саламатова Куралай Мархабатовна | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Класс: 9Б Алгебра | Количество присутствующих: 8 | Количество отсутствующих: — | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
Цели обучения, которые будут достигнуты с помощью данного урока | * систематизировать и обобщить знания учащихся по теме «Синус, косинус, тангенс и котангенс произвольного угла. Значения синуса, косинуса, тангенса и котангенса углов». · * способствовать формированию умений и навыков использования основных формул тригонометрии для выполнения преобразований тригонометрических выражений; · * содействовать воспитанию интереса к математике, активности, мобильности, умения общаться | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Цели обучения | Все учащиеся смогут: решать примеры, задачи, уравнения | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Большинство учащихся будут уметь: самостоятельно осуществлять поиск информации ( в т.ч.Intenet), обрабатывать ее, строить аргументированный рассказ, отбирать главное в изучаемом материале | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Некоторые учащиеся смогут: развить речь ч/з подготовку сообщений, развитие коммуникативных свойств личности в результате работы в парах и группах, индивидуальных способностей и интересов. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Предыдущее обучение | Повторение изученного материала: Радианная и градусная мера угла | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
План урока | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Планируемые сроки | Планируемые действия | Ресурсы | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
Действия учителя | Действия ученика | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Начало урока /3 мин/ | Приветствует учащихся с целью создания благоприятной атмосферы урока Для создания обстановки психологического комфорта на уроке, снятие напряжения, включения учащихся в урок после шумной перемены, предлагаю тренинг «Улыбка». Проверка дом.задания: № 277 Активизация опорных знаний. Математический диктант. Вариант 1. Вариант 2 1. Углом какой четверти является угол a, если:
| Приветствуют учителя. Слушают, наблюдают, настраиваются на восприятие материала урока Улыбаются и приветствуют друг друга участвуют в тренинге Ответы:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
Середина урока /33 мин/ (осмысление) | Изучение нового материала Деятельность учащихся. Выполняют свою задачу (индивидуально или в паре): подбирают материал для проекта в Internet, библиотеке; решают тесты. Оформляют результаты работы в группах. Компетентностно-ориентированные задания (КОЗ) Информационная компетентность. Аспект – планирование и поиск информации (уровень2) Аспект – извлечение первичной информации (уровень 2) 4.Решение задач Тест Вариант 1. Часть А. А1. Найдите значение выражения: –3 cos 600 + 1/3 tg 450 A2. Какое из значений может принимать sin a? A3. Углом какой четверти является угол a, сos a0, tg a
A4. Вычислите значение выражения 2 sin2 450 + v3 ctg (–300). A5. Какое из данных выражений имеет отрицательное значение?
Часть В. В1. Найдите значение выражения 2cos 2a – 3 sin 3a при а = 300 Ответ:________________________________ В2. Найдите наибольшее значение выражения 4 – 2 cos a. Ответ:________________________________ В3. Найдите значение выражения tg (–4950) Ответ:________________________________ Часть С. С1. Углы треугольника пропорциональны числам 1, 2, 3. Найдите их градусные меры. Запишите ход решения на отдельном листе. Вариант 2. Часть А. А1. Найдите значение выражения: 1/5 sin 300 – 4 ctg 450 A2. Какое из значений может принимать cos a ? A3. Углом какой четверти является угол a, sin aa 0?
A4. Вычислите значение выражения v3 tg (–300) – 5 cos2 450 A5. Часть В. В1. Найдите значение выражения cos 3a – 2 sin 2a при а = 300 Ответ: ________________________________ В2. Найдите наибольшее значение выражения 5 – 3 sin a. Ответ: ________________________________ В3. Найдите значение выражения ctg (–6750) Ответ: ________________________________ Часть С. С1. Углы треугольника пропорциональны числам 2, 2, 5. Найдите их градусные меры. Запишите ход решения на отдельном листе. | Ученики отвечают на вопросы и решают задания Учащиеся определили свои роли и группируются в соответствии с ними в малые команды. Определяют долю участия каждого в подборе информации, в соответствии со своими интересами, определяют этапы разработки проекта, даты получения первых результатов. Ответы: Вариант 1 Часть А
Часть В
Часть С Ответ: 300, 600, 900 Вариант 2 Часть А
Часть В
Часть С Ответ: 400, 400, 1000 | ИД, учебник, ручки, тетрадь, карточки с заданием | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Конец урока /4мин/ | Завершение урока. Рефлексия Домашнее задание: §23 №278, №282 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Дополнительная информация | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Дифференциация. Как вы планируете поддерживать учащихся? Как вы планируете стимулировать способных учащихся? | Оценивание. Как вы планируете увидеть приобретенные знания учащихся? | Межпредметные связи. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
На уроке предусмотрено дифференцированное задание в групповой работе. Более способные учащиеся смогут проявить свои лидерские качества, проявить свои знания и умения | Оценивание пронизывает весь урок, предусмотрено оценивание индивидуальное, групповой работы и парной работы, а также взаимооценивание | В ходе раскрытия темы урока воспитание таких качеств личности как любознательность, порядочность | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рефлексия Были ли цели урока/цели обучения реалистичными? Что учащиеся сегодня изучили? На что направлено обучение Хорошо ли сработала запланированная дифференциация? Выдерживалось ли время обучения? Какие изменения из данного плана я реализовал и почему | Используйте пространство ниже, чтобы подвести итоги урока. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Цели урока были реалистичными, достижимыми, измеримыми. Учащиеся на уроке решали примеры, задачи, уравнения Атмосфера творческая, взаимопомощи, внимания и ответственности Нехватка времени на решение задач Было мало времени на обдумывания вопросов | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Итоговая оценка Какие два аспекта в обучении прошли хорошо (с учетом преподавания и учения)? 1: Деление на группы, оценивание индивидуальных ответов учащихся 2: Учатся друг у друга добывать и использовать полученные знания для реализации их в своей умственной деятельности Какие два обстоятельства могли бы улучшить урок (с учетом преподавания и учения)? 1: На рефлексию желательно отвести больше времени, чтобы учащиеся могли высказать побольше по обобщению темы урока 2: Размышляют вслух, выдвигают гипотезы и рассуждают Что я узнал(а) об учениках в целом или отдельных лицах? Класс активный, с положительной учебной мотивацией, учащиеся доброжелательные, организованные. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Синус, косинус и тангенс в четырех квадрантах
Синус, косинус и тангенс
Три основные функции в тригонометрии — это синус, косинус и тангенс.
Их легко вычислить:
Разделить длину одной стороны прямоугольного треугольника
на другую сторону
… но надо знать с каких сторон!
Для угла θ функции вычисляются следующим образом:
Синусоидальная функция: | sin( θ ) = Противоположность / Гипотенуза |
Функция косинуса: | cos( θ ) = Смежный / Гипотенуза |
Функция касания: | tan( θ ) = Противоположный / Смежный |
Пример: чему равен синус 35°?
Используя этот треугольник (длина только до одного десятичного знака): sin(35°) = противоположность / гипотенуза = 2,8/4,9 = 0,57. |
Декартовы координаты
Используя декартовы координаты, мы отмечаем точку на графике , как далеко вдоль и , как далеко вверх по :
Точка (12,5) находится на 12 ед. вдоль и на 5 ед. вверх.
Четыре квадранта
Когда мы включаем отрицательных значений , оси x и y делят пространство на 4 части:
Квадранты I, II, III и IV
(Нумерация против часовой стрелки)
- В квадранте I и x, и y положительны,
- в квадранте II x отрицательное (y все еще положительное),
- в квадранте III и x, и y отрицательны, а
- в квадранте IV x снова положительный, а y отрицательный.
Вот так:
| Квадрант | X (по горизонтали) | Y (вертикальный) | Пример |
|---|---|---|---|
| я | Положительный | Положительный | (3,2) |
| II | Отрицательный | Положительный | (−5,4) |
| III | Отрицательный | Отрицательный | (-2,-1) |
| IV | Положительный | Отрицательный | (4,−3) |
Пример: Точка «C» (−2,−1) находится на 2 единицы вперед в отрицательном направлении и на 1 единицу вниз (т. е. в отрицательном направлении).
е. в отрицательном направлении).
И x, и y отрицательны, так что точка находится в «Квадранте III»
Контрольный угол
Углы могут быть больше 90º
Но мы можем вернуть их ниже 90º, используя ось X в качестве точки отсчета.
Думайте, что «ссылка» означает «ссылка x»
Самый простой способ — сделать набросок!
Пример: 160º
Начните с положительной оси x и поверните на 160º
Затем найдите угол к ближайшей части оси x,
в данном случае 20º
Базовый угол для 160º равен 20°
Здесь мы видим четыре примера с опорным углом 30º:
Вместо эскиза можно использовать следующие правила:
| Квадрант | Контрольный угол |
| я | θ |
| II | 180º − θ |
| III | θ − 180º |
| IV | 360º − θ |
Синус, косинус и тангенс в Четыре квадранта
Теперь давайте посмотрим на детали прямоугольного треугольника с углом 30° в каждом из 4 квадрантов.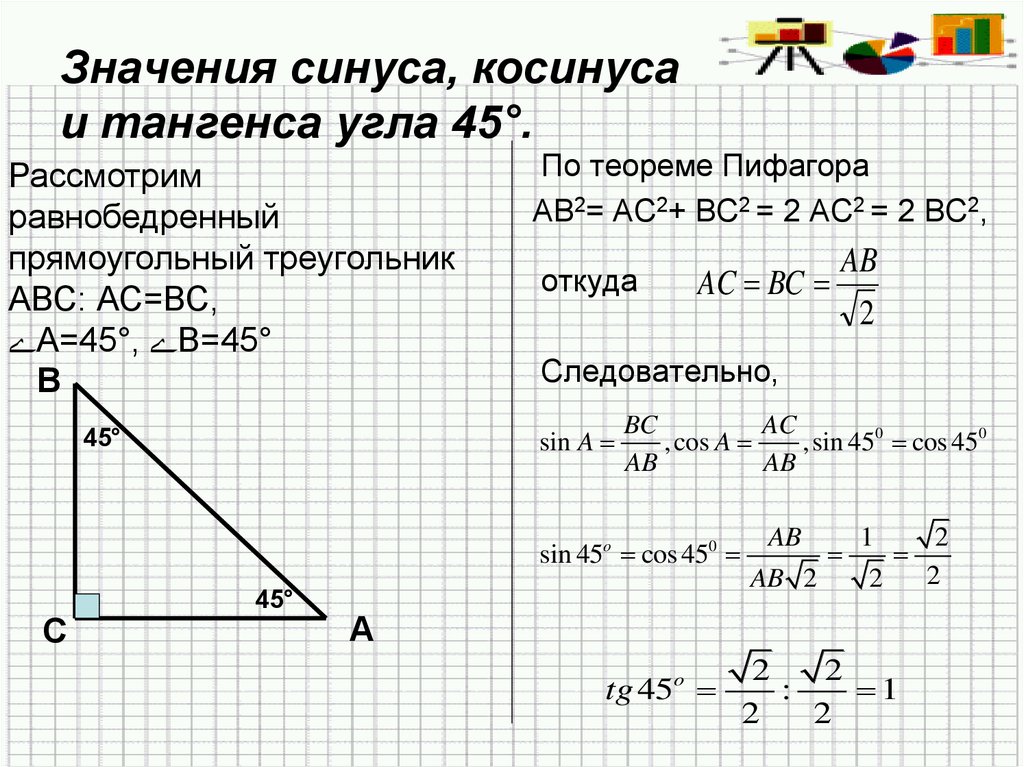
В квадранте I все в норме, а синус, косинус и тангенс положительны:
Пример: синус, косинус и тангенс угла 30°
Синус | sin(30°) = 1 / 2 = 0,5 |
Косинус | cos(30°) = 1,732 / 2 = 0,866 |
Касательная | тангенс (30°) = 1 / 1,732 = 0,577 |
Но в квадранте II направление x отрицательно , а косинус и тангенс становятся отрицательными:
Пример: синус, косинус и тангенс угла 150°
Синус | sin(150°) = 1/2 = 0,5 |
Косинус | cos(150°) = −1,732 / 2 = −0,866 |
Касательная | тангенс (150°) = 1 / -1,732 = -0,577 |
В квадранте III синус и косинус отрицательны:
Пример: синус, косинус и тангенс 210°
Синус | sin(210°) = −1 / 2 = −0,5 |
Косинус | cos(210°) = −1,732 / 2 = −0,866 |
Касательная | тангенс (210°) = −1 / −1,732 = 0,577 |
Примечание. Тангенс равен положительному числу , потому что деление отрицательного числа на отрицательное дает положительное значение.
Тангенс равен положительному числу , потому что деление отрицательного числа на отрицательное дает положительное значение.
В квадранте IV синус и тангенс отрицательны:
Пример: синус, косинус и тангенс 330°
Синус | sin(330°) = −1 / 2 = −0,5 |
Косинус | cos(330°) = 1,732 / 2 = 0,866 |
Касательная | тангенс (330°) = −1 / 1,732 = −0,577 |
Выкройка есть! Посмотрите, когда синус, косинус и тангенс положительны …
- Все три из них положительные в квадранте I
- Синус положительный только в Квадранте II
- Только тангенс положителен в квадранте III
- Косинус положителен только в Квадранте IV
Это можно показать еще проще:
На этом графике также отображается «ASTC».
Некоторым людям нравится запоминать четыре буквы ASTC по одному из следующих:
- Все студенты сдают химию
- Все учащиеся сдают математический анализ
- Все глупые коты Том
- Все станции к центральному
- A dd S сахар T o C офис
Может быть, вы могли бы придумать свой собственный. Или же просто помните ASTC.
Инверсия Sin, Cos и Tan
Что такое арксинус 0,5?
грех -1 (0,5) = ?
Другими словами, когда на графике ниже у равно 0,5, чему равен угол?
Существует много углов где y=0,5
Проблема в следующем: калькулятор выдаст вам только одно из этих значений …
… но всегда есть два значения между 0º и 360º
(и бесконечно много дальше):
| | Первое значение | Второе значение |
| Синус | θ | 180º − θ |
| Косинус | θ | 360º − θ |
| Касательная | θ | θ + 180º |
Теперь мы можем решить уравнения для под любым углом!
Пример: Решаем sin θ = 0,5
Получаем первое решение из калькулятора = sin -1 (0,5) = 30º (это в квадранте I)
Следующее решение: 180º − 30º = 150º (квадрант II)
Пример: вычислить cos θ = −0,85
Получаем первое решение из калькулятора = cos -1 (−0,85) = 148,2º (квадрант II)
Другое решение: 360º − 148,2º = 211,8º (квадрант III)
Возможно, нам потребуется изменить угол между 0º и 360º, прибавив или вычитая 360º
Пример.
 Решите тангенс θ
= -1,3
Решите тангенс θ
= -1,3Получаем первое решение из калькулятора = tan -1 (−1,3) = −52,4º
Это меньше 0º, поэтому прибавляем 360º: −52,4º + 360º = 307,6º (квадрант IV)
Другое решение: −52,4º + 180º = 127,6º (квадрант II)
3914, 3915, 3916, 3917, 3918, 3919, 3920, 3921, 3922, 3923
Упражнение: Прогулка по пустыне 2
Как вычисляются синус, косинус и тангенс?
Тригонометрия — это раздел математики, изучающий соотношение сторон и углов в треугольнике. С помощью тригонометрии возможно определение высоты больших гор или башен, а также в астрономии, она используется для определения расстояния между звездами или планетами и широко используется в физике, архитектуре и системах GPS-навигации. Тригонометрия основана на принципе, что «Если два треугольника имеют одинаковое множество углов, то их стороны находятся в одинаковом отношении» . Длина сторон может быть разной, но соотношение сторон одинаковое.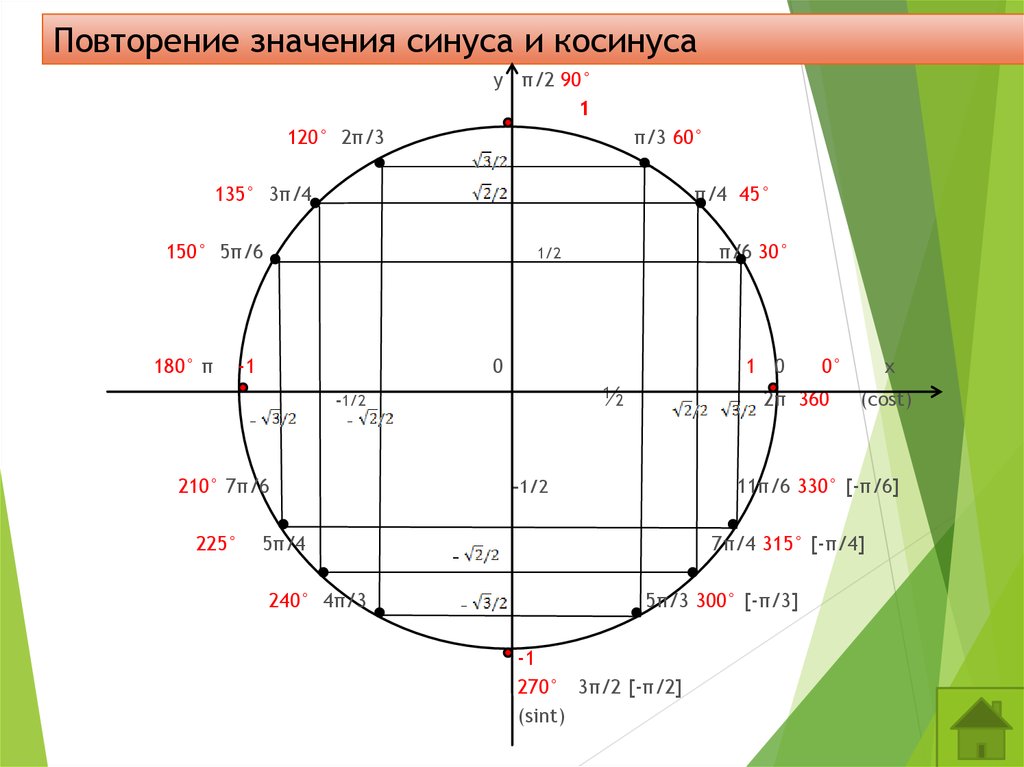
Прямоугольный треугольник
Тригонометрические отношения определены только для прямоугольного треугольника. В прямоугольном треугольнике есть угол 90 °, а два других угла меньше 90 °, относительно этих углов каждая сторона называется перпендикулярным основанием и гипотенузой. Давайте посмотрим, что такое перпендикуляр, основание и гипотенуза прямоугольного треугольника,
- Гипотенуза: Сторона, противоположная 90°. это самая большая сторона.
- Перпендикуляр: Сторона перед углом или напротив угла перпендикулярна.
- Основание: Основание — это одна из сторон, которая касается угла,
Примечание Гипотенуза никогда не может рассматриваться как основание или перпендикуляр.
В прямоугольном треугольнике угол, отличный от 90°, образован двумя сторонами, одна из которых является гипотенузой. другая сторона, которая содержит угол или касается угла, является основанием, а сторона, которая не касается угла, перпендикулярна.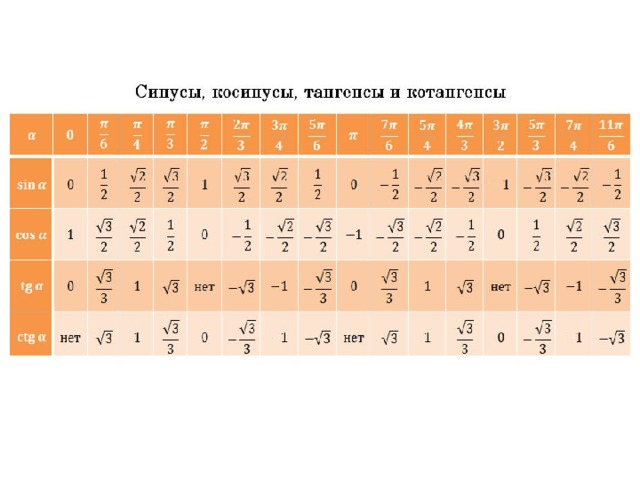
Как показано на диаграмме выше, для того же треугольника, если рассматривать угол 30°, перпендикуляром является сторона PQ, но если рассматривать угол 60°, перпендикуляром является сторона QR.
Тригонометрические функции
Тригонометрические функции также называются круговыми функциями или тригонометрическими отношениями. являются отношениями сторон прямоугольного треугольника, Они показывают отношения между углом и сторонами, и они являются основой тригонометрии . Существует шесть тригонометрических функций: синус, косинус, тангенс, косеканс, секанс, котангенс. Представления сторон для шести соотношений:
- sin A = Перпендикуляр / Гипотенуза
- cos A = Основание / Гипотенуза
- tan A = Перпендикуляр / Основание
- cot A = Основание / Перпендикуляр
- sec A = Гипотенуза / Основание
- cosec.
Как рассчитываются синус, косинус и тангенс?
Синус, косинус и тангенс, также называемые sin, cos и tan соответственно, являются наиболее часто используемыми тригонометрическими отношениями, остальные 3 являются обратными им.
- Sin – Синус угла A – это отношение длин перпендикуляра к гипотенузе.
sin A = Перпендикуляр / Гипотенуза
- Cos – Cos угла A – это отношение длины основания к гипотенузе.
cos A = Основание / Гипотенуза
- Тангенс – Тангенс угла А представляет собой отношение длин перпендикуляров к основанию.
желтовато-коричневый A = перпендикулярно / основание
Чтобы рассчитать эти отношения, найдите длину сторон треугольника и затем возьмите соответствующие отношения. Чтобы найти длину, если известна одна из сторон и угол, можно легко найти остальные стороны через синус, косинус и тангенс угла. Ниже приведены тригонометрические значения некоторых важных углов.
| углов (в градусах) | 0 ° | 30 ° | 45° | 60° | 90° |
| Sin θ | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| Cos θ | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| Tan θ | 0 | 1/√3 | 1 | √3 | ∞ |
| Cot θ | ∞ | √3 | 1 | 1/√3 | 0 |
| Sec θ | 1 | 2/√3 | √2 | 2 | ∞ |
| Cosec θ | ∞ | 2 | √2 | √ 3/2 | 1 |
Примеры задач
Вопрос 1: Рассмотрите следующий треугольник и ответьте на вопрос ниже?
Найдите значение SIN, COS и TAN для углы 30 °
Решение:
для угла 30 °
Perpendicular = 1CM, Base = √3cm, гипотенера = 2 CM.
Sin(30°) = (п/ч) = 1/2.
Cos(30°) = (ч/ч) = √3/2.
tan(30°) = (p/b) = 1/2.
Вопрос 2. Для той же фигуры в вопросе 1 найдите значение sin, cos и tan для угла 60°
Решение:
Для угла 60°
перпендикуляр = √3см, основание = 1см , гипотенуза = 2 см.
Sin(60°) = (п/ч) = √3/2.
Cos(60°) = (ч/ч) = 1/2.
тангенс (60°) = (p/b) = √3/1.
Вопрос 3: В прямоугольном треугольнике основание угла 30° равно 18 м. Найдите длину гипотенузы.
Решение:
Дано: Основание = 18 м
Cos = √3/2
B/H = √3/2
18/H = √3/2
) / √3
H = 12√3м
Вопрос 4. В прямоугольном треугольнике сторона, противоположная углу 30°, равна 14 м. Найдите длину гипотенузы.
Решение:
Дано: Перпендикуляр = 14 м
Sin 30 = 1/2
P/H = 1/2
14/H = 9 1/20005
Н = 14 × 2
Н = 28м.
Линейные значения тригонометрических функций. Темы по тригонометрии
Темы | Дом
17
Полный период sin θ
Полный период cos θ
Полный период загара θ
Проекции
ЗНАЧЕНИЕ ЛИНИИ тригонометрической функции — это прямая линия, длина которой представляет значение функции. Поскольку при изменении центрального угла значение линии становится своеобразным «графиком» функции. Это отличный способ для учащегося визуализировать и запомнить значения каждой функции, в частности синуса, косинуса и тангенса.
Строка значений
Пусть A — центр единичной окружности с радиусами AB, AD.
Из В опустить перпендикуляр ВС на AD.
Начертить радиус AF перпендикулярно DA; провести касательные DE, FG к окружности; то есть нарисуйте их под прямым углом к радиусам; (теорема 13)
и продлите AB до пересечения с этими касательными в точках E, G соответственно.
Тогда, поскольку AG — прямая, пересекающая параллельные прямые FG, AD, противоположные углы FGA, GAD равны. (теорема 8)
Следовательно, прямоугольные треугольники ACB, ADE, GFA подобны.
Теперь линейные значения функций угла θ выглядят следующим образом; чтобы избежать прокрутки, цифра ниже такая же:
| sin θ | = | СВ БА | = | ЦБ 1 | = CB. |
| , потому что θ | = | АС ВА | = | АС 1 | = AC. |
| желтовато-коричневый θ | = | Германия AD | = | Германия 1 | = Герм. |
| csc θ | = | АГ ФА | = | АГ 1 | = АГ.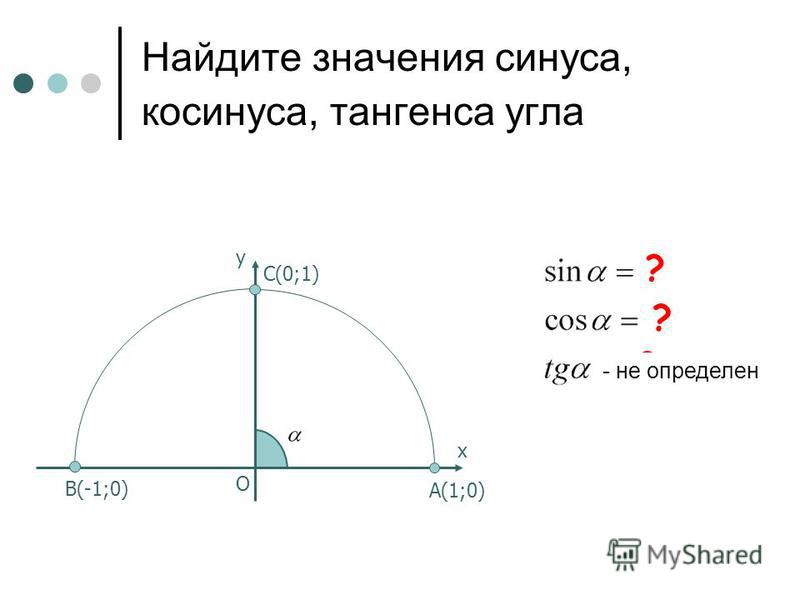 |
| сек θ | = | AE DA | = | АЕ 1 | = AE. |
| кроватка θ | = | ФГ ФЗ | = | ФГ 1 | = ФГ. |
Теперь мы понимаем, почему функция тангенса (DE) так называется: На самом деле это тангенс. Функция секанса (AE) является секансом. Он разрезает круг; от латинского secare резать.
Полный период sin θ
Теперь учащийся должен попытаться визуализировать, что происходит с CB, линейным значением sin θ, когда AB совершает полный оборот вокруг единичной окружности.
При θ = 0° точка B совпадает с D, так что CB обращается в нуль. sin 0° = 0,
По мере увеличения θ в первом квадранте CB также увеличивается, пока не достигнет своего максимального значения при 90°.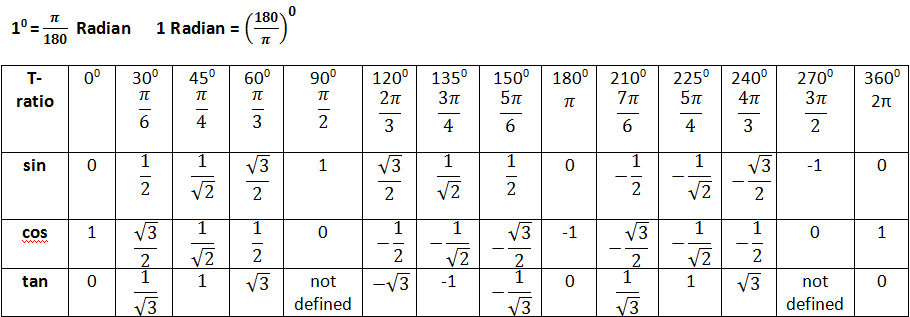 CB совпадает там с единичным радиусом AF, так что CB = AF. sin 90° = 1,
CB совпадает там с единичным радиусом AF, так что CB = AF. sin 90° = 1,
Когда θ, угол DAB, входит во второй квадрант (рис. 2), значение CB начинает уменьшаться. При 180° B совпадает с K, и CB снова обращается в нуль. sin 180° = 0,
В третьем квадранте (рис. 3) CB увеличивается, но синус в этом квадранте алгебраически отрицателен. При 270° CB совпадает с единичным радиусом AL. sin 270° имеет свой алгебраический минимум. sin 270° = −1.
Наконец, в четвертом квадранте (рис. 4) CB уменьшается до тех пор, пока B снова не совпадет с D. sin 360° = sin 0° = 0,
Пройдя один полный круг, sin θ прошел все возможные значения. Мы говорим, что sin θ завершил один период. Принято использовать меру в радианах и говорить, что период sin θ равен 2π.
Это означает, что каждые 2π радиан sin θ возвращается к тому же значению линии CB.
Для любого угла θ sin (θ + 2π) = sin θ.
Мы вернемся к этому в следующем разделе.
Кроме того, мы видим, что sin θ — значение линии CB — никогда не имеет значения больше 1, которое он имеет при 90°; или меньше -1, который он имеет при 270 °.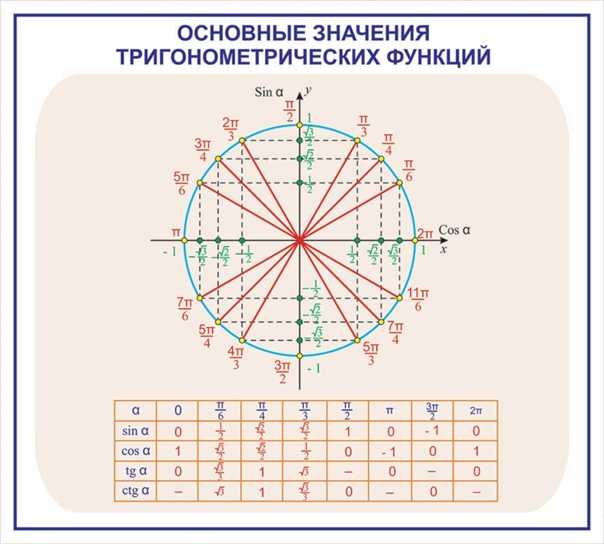
−1 ≤ sin θ ≤ 1,
Полный период cos θ
Строковое значение cos θ равно переменному току. Когда крайняя сторона AB вращается, конечная точка C перемещается вперед и назад по диаметру KD. При 0° AC совпадает с единичным радиусом AD, так что cos 0° = 1,
.При θ = 90° C совпадает с A, так что AC обращается в нуль. cos 90° = 0,
При θ = 180° C достигает K. AC = AK. cos 180 ° = -1.
При θ = 270° C возвращается в A. cos 270° = 0,
Наконец, при θ = 360° AC снова совпадает с единичным радиусом AD. cos 360° = 1,
Период cos θ также равен 2π.
cos θ (AC) также имеет максимальное значение 1 при 0° и минимальное –1 при 180°.
−1 ≤ cos θ ≤ 1,
Полный период загара θ
Значения тангенса θ, как и значения всех тригонометрических функций, регулярно повторяются.
Поскольку θ принимает значения от 0 до − или от 0 до , длина касательной DE не ограничена.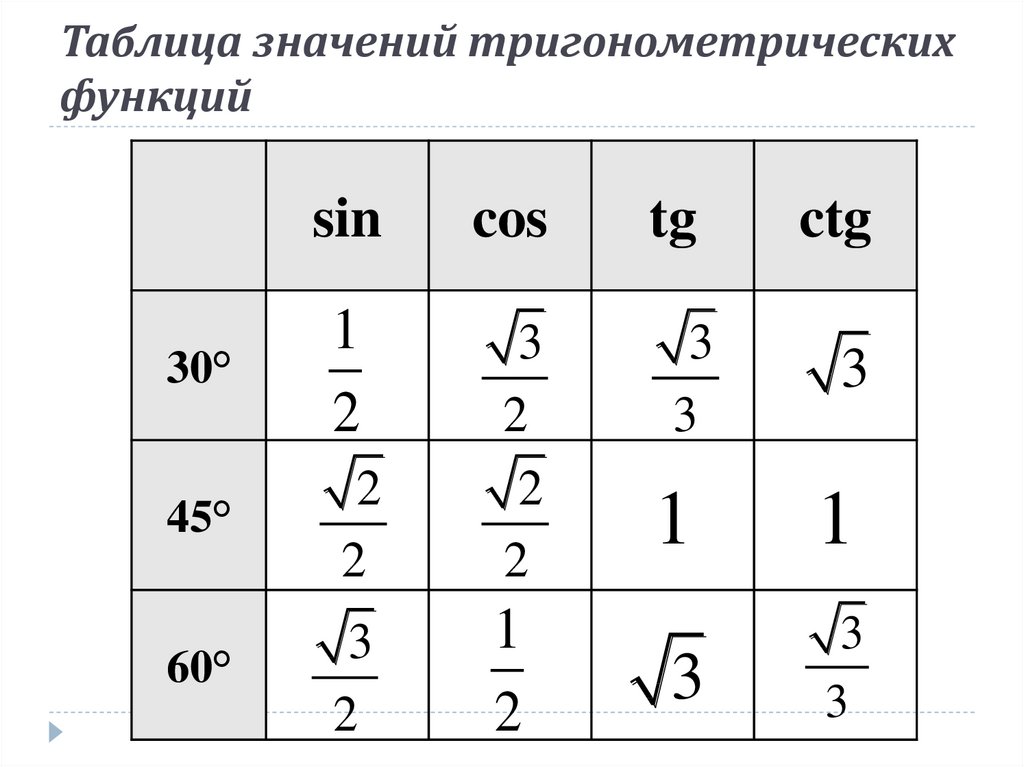 Он всегда параллелен и -ось. В квадранте IV тангенс отрицательный; в квадранте I положительный. Между − и tan θ принимает все возможные значения.
Он всегда параллелен и -ось. В квадранте IV тангенс отрицательный; в квадранте I положительный. Между − и tan θ принимает все возможные значения.
−∞
Интервал от − до составляет один полный период tan θ. Период — это расстояние между этими двумя точками: π.
График тригонометрической функции представляет собой ее линейное значение, построенное как координата y в зависимости от радианного угла x . См. следующую тему: Графики тригонометрических функций.
Проблема. Что из следующего возможно?
а) sin θ = .
Невозможно. Значения sin θ никогда не превышают 1,
.См. здесь.
б) cos θ = 2,058
Невозможно. Значения cos θ никогда не превышают 1,
.в) тангенс θ = 2,058
Возможно. Значения тангенса θ не ограничены.
См. здесь.
г) кроватка θ = 0,003
Возможно. Поскольку нет предела значениям тангенса θ, нет предела и значениям его обратной величины.
д) csc θ = ½
Невозможно. Поскольку значения sin θ должны быть меньше или равны 1, значения его обратной величины должны быть больше.
е) сек θ = 5
Возможно. Поскольку значения cos θ должны быть меньше или равны 1, значения его обратной величины должны быть больше.
Проекции
Прямая CD называется вертикальной проекцией прямой AB. (Прямые BD, AC проведены перпендикулярно CD. Это как если бы свет падал на AB, а CD — это тень.)
EF называется горизонтальной проекцией AB.
Теперь, если AB — единичный радиус, гипотенуза прямоугольного треугольника,
, то sin θ — его вертикальная проекция; cos θ, горизонтальная проекция.
Следующая тема: Графики тригонометрических функций
Темы | Дом
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2022 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
How to Calculate Values for the Six Trigonometric Functions
By: Mary Jane Sterling and
Updated: 07-09-2021
From The Book: Pre-Calculus Workbook For Dummies
Pre- Учебное пособие по исчислению для чайников
Исследовать книгу Купить на Amazon
В предварительном исчислении вам необходимо оценить шесть триггерных функций — синус, косинус, тангенс, косеканс, секанс и котангенс — для одного угла на единичной окружности. Для каждого угла на единичной окружности три других угла имеют аналогичные значения триггерной функции. Единственная разница в том, что знаки этих величин противоположны, в зависимости от того, в каком квадранте находится угол. Иногда угол не будет лежать на единичной окружности, и вам придется использовать свой калькулятор.
Иногда угол не будет лежать на единичной окружности, и вам придется использовать свой калькулятор.Если в вашем распоряжении нет единичного круга (например, если вы проходите тест), вы можете нарисовать картинку и найти нужные вам значения долгим путем.
Синус и косинус
Определение точки на плоскости косинуса в прямоугольном треугольникеПоскольку гипотенуза r всегда равна 1 в единичной окружности, значение x равно значению косинуса. И если вы вспомните альтернативное определение синуса,
, вы поймете, что y 9Значение 0021 — это значение синуса. Таким образом, любая точка на единичном круге всегда равна
. Разговор о том, чтобы сложить все части воедино!
В алфавитном порядке x предшествует y , а c предшествует s (другими словами, косинус предшествует синусу). Этот факт должен помочь вам вспомнить, какой из них есть какой.
Тангенс, котангенс, секанс и косеканс
Тангенс, котангенс, секанс и косеканс требуют немного больше усилий, чем синус и косинус. Для многих углов единичной окружности вычисление этих функций требует осторожной работы с дробями и квадратными корнями.
Для многих углов единичной окружности вычисление этих функций требует осторожной работы с дробями и квадратными корнями.Не забывайте всегда рационализировать знаменатель любой дроби в своем окончательном ответе. Кроме того, помните, что любое число, деленное на 0, не определено. Функции тангенса и секанса, например, не определены, когда значение косинуса равно 0. Точно так же значения котангенса и косеканса не определены, когда значение синуса равно 0.
Время для примера. Чтобы вычислить шесть тригонометрических функций 225 градусов с помощью единичного круга, выполните следующие действия:
Нарисуй картинку.
Когда вас просят найти триггерную функцию угла, вам не нужно каждый раз рисовать единичный круг. Вместо этого используйте свой ум, чтобы понять картину. Для этого примера 225 градусов на 45 градусов больше, чем 180 градусов. Нарисуйте треугольник 45-45-90 градусов только в третьем квадранте.
Введите длины катетов и гипотенуз.

Треугольник 45er, украшенный как рождественская елка
Используйте правила треугольника 45er. Координата точки в 225 градусов равна
На рисунке показан треугольник, а также вся информация для оценки шести триггерных функций.
Будьте осторожны! Используйте то, что вы знаете о положительных и отрицательных осях на координатной плоскости, чтобы помочь вам. Поскольку треугольник находится в третьем квадранте, оба значения x и y должны быть отрицательными.
Найдите синус угла.
Синус угла представляет собой значение y или вертикальную линию, которая проходит от точки на единичной окружности до x- ось. Для 225 градусов значение y равно
.Найдите косинус угла.
Значение косинуса равно x , поэтому оно должно быть
.Найдите тангенс угла.
Чтобы найти тангенс угла на единичной окружности, вы используете альтернативное определение тангенса:
С другой стороны,
, потому что в единичном круге значение y представляет собой синус, а 9Значение 0020 x — это косинус.
. Итак, если вы знаете синус и косинус любого угла, вы также знаете тангенс. (Спасибо, единичный круг!) Синус и косинус 225 градусов равны
Итак, если вы знаете синус и косинус любого угла, вы также знаете тангенс. (Спасибо, единичный круг!) Синус и косинус 225 градусов равныСледовательно, вы можете разделить синус на косинус, чтобы получить тангенс 225 градусов, который равен 1.
Найдите косеканс угла.
Косеканс любого угла равен
или r / y , используя определение точки в плоскости. Используя то, что вы определили на шагах 1,
Теперь вы можете делить 1 на
.Найдите секанс угла.
секанс любого угла равен
Потому что косинус 225 градусов тоже равен
найдено на шаге 4, секанс 225 градусов равен
Найдите котангенс угла.
Котангенс угла равен
Из шага 5 тангенс (225 градусов) = 1. Сокот (225 градусов) = 1/1 = 1. Легко как пирог (но не пи, что является совершенно другой темой).
Об этой статье
Эта статья взята из книги:
- Предварительное исчисление для чайников,
Об авторе книги:
Мэри Джейн Стерлинг преподавала алгебру, деловое исчисление, геометрию и конечную математику в Брэдли Университет в Пеории, штат Иллинойс, более 30 лет. Она является автором книг «Тригонометрия для чайников», и «Конечная математика для чайников».
Она является автором книг «Тригонометрия для чайников», и «Конечная математика для чайников».
Этот артикул находится в категории:
- Предварительное вычисление ,
Единица окружности: функции синуса и косинуса | Предварительный расчет II |
Чтобы определить наши тригонометрические функции, мы начнем с рисования единичной окружности с центром в начале координат и радиусом 1, как показано на рисунке 2. Угол (в радианах), который пересекает
ttt
, образует дугу длины
сс
. Используя формулу
s=rts=rts=rt
и зная, что
r=1r=1r=1
, мы видим, что для единичного круга ,
s=ts=ts=t
.
Напомним, что оси x- и y- делят координатную плоскость на четыре четверти, называемые квадрантами. Мы помечаем эти квадранты, чтобы имитировать направление положительного угла. Четыре квадранта обозначены I, II, III и IV.
Для любого угла
ttt
мы можем обозначить пересечение конечной стороны и единичного круга его координатами,
(х,у)\влево(х,у\вправо)(х,у)
. Координаты
xxx
и
yyy
будут выходами тригонометрических функций
f(t)=costf\left(t\right)=\cos tf(t)=cost
и
f(t)=sintf\left(t\right)=\sin tf(t)=sint
соответственно. Это означает
x=costx=\cos tx=cost
и
y=sinty=\sin ty=sint
.
Рис. 2. Единичная окружность с центральным углом
ttt
радианы
A Общее примечание: единица окружности
Единичная окружность имеет центр в точке
(0,0)\left(0,0\right)(0,0)
и радиус
111
. В единичном круге длина пересекаемой дуги равна радианной мере центрального угла
111
.
Пусть
(x,y)\left(x,y\right)(x,y)
будет концом на единичной окружности дуги длины дуги
ссс
. Координаты
(x,y)\left(x,y\right)(x,y)
этой точки можно описать как функции угла.
Определение функций синуса и косинуса
Теперь, когда мы пометили нашу единичную окружность, мы можем узнать, как координаты
(x,y)\left(x,y\right)(x,y)
относятся к длине дуги и углу .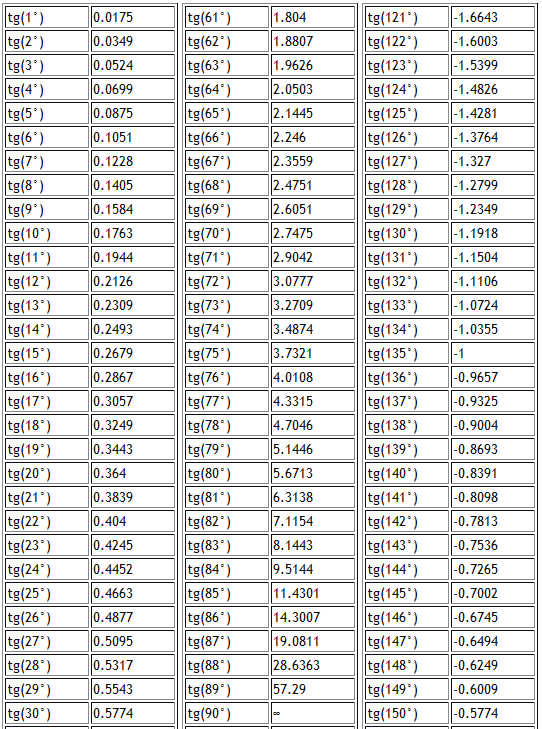 Функция синуса связывает действительное число
Функция синуса связывает действительное число
ttt
с y -координата точки пересечения соответствующего угла с единичной окружностью. Точнее, синус угла
ttt
равен y -значению конечной точки на единичной окружности дуги длиной
ttt
. На рисунке 2 синус равен
гггг
. Как и все функции, синусоидальная функция имеет вход и выход. Его вход является мерой угла; его вывод — y -координата соответствующей точки на единичной окружности.
Функция косинуса угла
ttt
равна x -значению конечной точки на единичной окружности дуги длиной
ttt
. На рисунке 3 косинус равен
xxx
.
Рисунок 3
Поскольку синус и косинус являются функциями, нам не всегда нужно записывать их в круглых скобках:
sint\sin tsint
равно 9{2}(cos(t))2
. Имейте в виду, что многие калькуляторы и компьютеры не распознают стенографию. Если вы сомневаетесь, используйте дополнительные скобки при вводе вычислений в калькулятор или компьютер.
A Общее примечание: функции синуса и косинуса
Если
ttt
является вещественным числом и точка
(x,y)\left(x,y\right)(x,y)
на единичной окружности соответствует углу
ttt
, тогда
cost=x\cos t=xcost=x
sint=y\sin t=ysint=y
Как: Дана точка
P(x,y)\left(x,y\right)(x,y)
на единичной окружности соответствующему углуttt
, найти синус и косинус.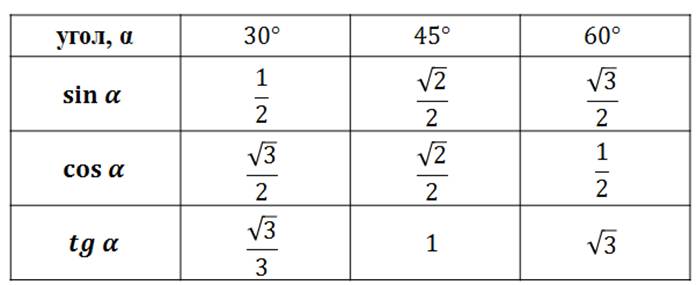
- Синус
ttt
равен y -координате точкиP:sint=yP:\sin t=yP:sint=y
. - Косинус
ttt
равен x -координате точкиP:cost=xP: \text{cos}t=xP:cost=x
.
Пример 1. Нахождение значений функции для синуса и косинуса
Точка
PPP
— это точка на единичной окружности, соответствующая углу
ttt
, как показано на рисунке 4. Найдите
cos(t)\cos \left(t\right)\\cos (t)
и
sin(t)\text{sin}\left(t\right)\\sin(t)
.
Рисунок 4
Решение
Мы знаем, что
cost\cos tcost
— это x — координата соответствующей точки на единичной окружности, а
sint\sin tsint
— это y — координата соответствующей точки на единичной окружности. Итак:
Итак:
x=cost=12y=sint=32\begin{array}{l}\begin{array}{l}\\ x=\cos t=\frac{1}{2}\ end{array}\qquad \\ y=\sin t=\frac{\sqrt{3}}{2}\qquad \end{array}\\x=cost=21y=sint=23
Попробуйте 1
Определенный угол
ttt
соответствует точке на единичной окружности
(−22,22)\left(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)\ \(−22
,22
)
, как показано на рисунке 5. Найдите
cost\cos tcost
и
sint\sin tsint
9
09.Рисунок 5
Решение
Нахождение синусов и косинусов углов на оси
Для квадрантных углов соответствующая точка на единичной окружности приходится на 9\circ \right)=1\end{массив}\\x=cost=cos(90∘)=0y=sint=sin(90∘)=1
Косинус 90° равен 0; синус 90° равен 1.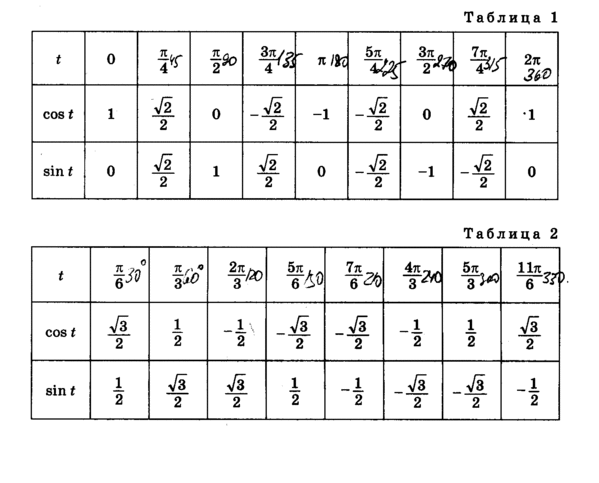
Попробуйте 2
Найдите косинус и синус угла
π\pi π
.
Раствор
Тождество Пифагора
Рисунок 7
Теперь, когда мы можем определить синус и косинус, мы узнаем, как они соотносятся друг с другом и с единичным кругом. Напомним, что уравнение для единичного круга имеет вид
9{2}t=1cos2t+sin2t=1, известное как Пифагорейская идентичность .
Мы можем использовать тождество Пифагора, чтобы найти косинус угла, если мы знаем синус, или наоборот. Однако, поскольку уравнение дает два решения, нам нужно дополнительное знание угла, чтобы выбрать решение с правильным знаком. Если мы знаем квадрант, в котором находится угол, мы можем легко выбрать правильное решение.
Общее примечание: Пифагорейская идентичность
9{2}t=1cos2t+sin2t=1
Как: Зная синус некоторого угла
ttt
и его положение в квадранте, найдите косинусttt
.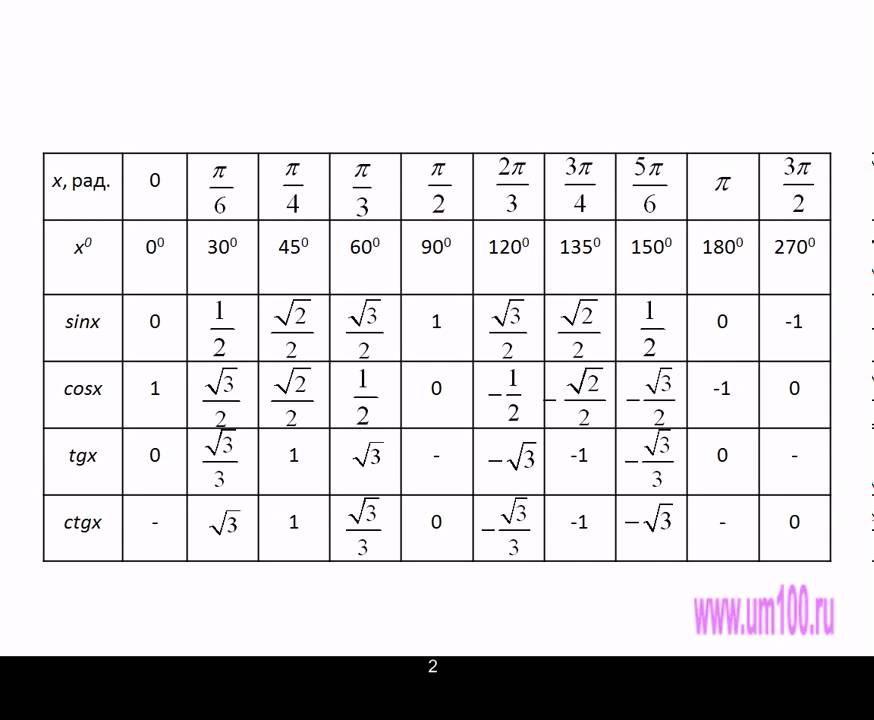
- Подставьте известное значение
sin(t)\sin \left(t\right)sin(t)
в тождество Пифагора. - Найдите
cos(t)\cos \left(t\right)cos(t)
. - Выберите решение с соответствующим знаком для значений x в квадранте, где находится
ttt
.
Пример 3. Нахождение косинуса по синусу или синуса по косинусу
Если
sin(t)=37\sin \left(t\right)=\frac{3}{7}\\sin(t)=73
и
ttt
находится во втором квадранте , найдите
cos(t)\cos\left(t\right)\\cos(t)
.
Решение
Если мы опустим вертикальную линию из точки на единичной окружности, соответствующей
ttt
, мы создадим прямоугольный треугольник, из которого мы можем увидеть, что тождество Пифагора — это просто один из случаев теоремы Пифагора. 9{2}\left(t\right)=\frac{40}{49}\qquad \\ \text{cos}\left(t\right)=\pm \sqrt{\frac{40}{49}} =\pm \frac{\sqrt{40}}{7}=\pm \frac{2\sqrt{10}}{7}\qquad \end{array}\\cos2(t)+sin2(t)= 1cos2(t)+499=1cos2(t)=4940cos(t)=±4940
9{2}\left(t\right)=\frac{40}{49}\qquad \\ \text{cos}\left(t\right)=\pm \sqrt{\frac{40}{49}} =\pm \frac{\sqrt{40}}{7}=\pm \frac{2\sqrt{10}}{7}\qquad \end{array}\\cos2(t)+sin2(t)= 1cos2(t)+499=1cos2(t)=4940cos(t)=±4940
=±740
=±7210
Поскольку угол находится во втором квадранте, мы знаем, что значение x- является отрицательным действительным числом, поэтому косинус также отрицателен. Итак,
cos(t)=−2107\text{cos}\left(t\right)=-\frac{2\sqrt{10}}{7}\\cos(t)=−7210
Попробуйте 3
Если
cos(t)=2425\cos \left(t\right)=\frac{24}{25}\\cos(t)=2524
и
ttt
находится в четвертом квадранте , найдите
sin(t)\text{sin}\left(t\right)\\sin(t)
.
Раствор
Нахождение синусов и косинусов специальных углов
Мы уже изучили некоторые свойства специальных углов, например преобразование радианов в градусы. Мы также можем вычислить синусы и косинусы специальных углов, используя 9Треугольник \circ 45∘−45∘−90∘
является равнобедренным, поэтому координаты x- и y соответствующей точки на окружности совпадают. Поскольку значения x- и y одинаковы, значения синуса и косинуса также будут равны.
Рисунок 9
В точке
t=π4t=\frac{\pi }{4}t=4π
, что составляет 45 градусов, радиус единичной окружности делит пополам первый квадрантный угол . Это означает, что радиус лежит вдоль линии 9{2}=\frac{1}{2}\\ \text{ }x=\pm \frac{1}{\sqrt{2}}\end{array}\\x2=21 x=±2
1
В квадранте I
x=12x=\frac{1}{\sqrt{2}}\\x=2
1
.
At
t=π4t=\frac{\pi }{4}t=4π
или 45 градусов,
(x,y)=(x,x)=(12,12)x=12 ,y=12cost=12,sint=12\begin{array}{l}\left(x,y\right)=\left(x,x\right)=\left(\frac{1} {\ sqrt {2}}, \ frac {1} {\ sqrt {2}} \ right) \ qquad \\ x = \ frac {1} {\ sqrt {2}}, y = \ frac {1} { \sqrt{2}}\qquad \\ \cos t=\frac{1}{\sqrt{2}},\sin t=\frac{1}{\sqrt{2}}\qquad \end{array} \\(х,у)=(х,х)=(2
1,2
1)x=2
1,y=2
1cost=2
1,sint=2
1
Если мы затем рационализируем знаменатели, мы получим
cost=1222=22sint=1222=22\begin{array}{l}\cos t=\frac{1}{\sqrt{2}}\frac {\ sqrt {2}} {\ sqrt {2}} \ qquad \\ = \ frac {\ sqrt {2}} {2} \ qquad \\ \ sin t = \ frac {1} {\ sqrt {2} }\frac{\sqrt{2}}{\sqrt{2}}\qquad \\ =\frac{\sqrt{2}}{2}\qquad \end{массив}\\cost=2
1 2
2
= 22
\circ 60∘
, как показано на рисунке 12.
Рисунок 11
Рисунок 12
Так как все углы равны, то и стороны равны. Вертикальная линия имеет длину2y2y2y
, и поскольку все стороны равны, мы также можем заключить, что
r=2yr=2yr=2y
или
y=12ry=\frac{1}{2} ry=21r
. Поскольку
sint=y\sin t=ysint=y
,
sin(π6)=12r\sin\left(\frac{\pi} {6}\right)=\frac{1} {2}r\\sin(6π)=21r
И так как
r=1r=1r=1
в нашем единичном круге ,
sin(π6)=12(1) =12\begin{array}{l}\sin \left(\frac{ \pi }{6}\right)=\frac{1}{2}\left(1\right)\qquad \\ \text{ }=\frac{1}{2}\qquad \end{array}\ \sin(6π)=21(1) =21
Используя тождество Пифагора, мы можем найти значение косинуса. {2}\left (\frac{\pi }{6}\right)=\frac{3}{4}\qquad & \text{Использовать свойство квадратного корня}.\qquad \\ \text{ }\cos \left(\frac {\pi} {6}\right)=\frac{\pm \sqrt{3}}{\pm \sqrt{4}}=\frac{\sqrt{3}}{2}\qquad & \text{ Поскольку }y\text{ положителен, выберем положительный корень}.\qquad \end{array}\\cos26π+sin2(6π)=1 cos2(6π)+(21)2=1 cos2(6π )=43 cos(6π)=±4 9\circ 60∘
{2}\left (\frac{\pi }{6}\right)=\frac{3}{4}\qquad & \text{Использовать свойство квадратного корня}.\qquad \\ \text{ }\cos \left(\frac {\pi} {6}\right)=\frac{\pm \sqrt{3}}{\pm \sqrt{4}}=\frac{\sqrt{3}}{2}\qquad & \text{ Поскольку }y\text{ положителен, выберем положительный корень}.\qquad \end{array}\\cos26π+sin2(6π)=1 cos2(6π)+(21)2=1 cos2(6π )=43 cos(6π)=±4 9\circ 60∘
. Теперь у нас есть равносторонний треугольник. Поскольку каждая сторона равностороннего треугольника
ABCABCABC
имеет одинаковую длину, и мы знаем, что одна сторона равна радиусу единичной окружности, все стороны должны иметь длину 1.
Рисунок 13
УголABDABDABD
равен 30°. Итак, если он двойной, угол
ABCABCABC
равен 60°.
BDBDBD
— серединный перпендикуляр к
ACACAC
, поэтому
ACACAC
разрезается пополам.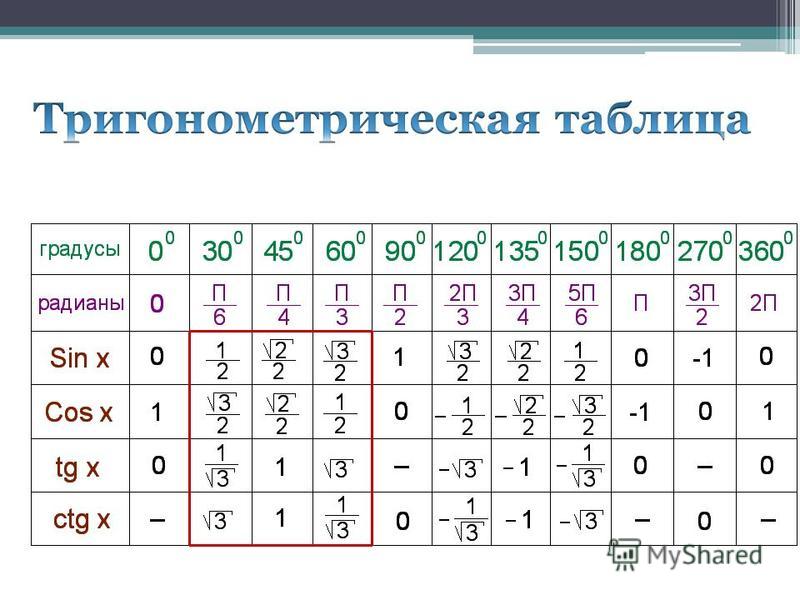 Это означает, что
Это означает, что
ADADAD
равно
12\frac{1}{2}21
радиусу или
12\frac{1}{2}21
. Обратите внимание, что
ADADAD
— это координата x точки
BBB
, которая находится на пересечении угла 60° и единичной окружности. Это дает нам треугольник
BADBADBAD
с гипотенузой 1 и стороной 9.{2}=\frac{3}{4}\\ \text{ }y=\pm \frac{\sqrt{3}}{2}\end{массив}\\41+y2=1 y2=1 −41 y2=43 y=±23
Поскольку
t=π3t=\frac{\pi }{3}t=3π
имеет конечную сторону в квадранте I, где координата y- положительна, мы выбираем
y=32y=\frac{ \sqrt{3}}{2}\\y=23
, положительное значение.
At
t=π3t=\frac{\pi }{3}\\t=3π
(60°),
(x,y)\left(x,y\right)(x ,у) 9\circ 60∘
равно
(12,32)\left(\frac{1}{2},\frac{\sqrt{3}}{2}\right)\\(21,23
)
, поэтому мы можем найти синус и косинус.
(x,y)=(12,32)x=12,y=32cost=12,sint=32\begin{массив}{l}\left(x,y\right)=\left (\ frac {1} {2}, \ frac {\ sqrt {3}} {2} \ right) \ qquad \\ x = \ frac {1} {2}, y = \ frac {\ sqrt {3} {2}\qquad \\ \cos t=\frac{1}{2},\sin t=\frac{\sqrt{3}}{2}\qquad \end{array}\\(x,y )=(21,23
)x=21,y=23
стоимость=21,sint=23
Теперь мы нашли значения косинуса и синуса для всех наиболее часто встречающихся углов в первом квадранте единичной окружности. В таблице ниже приведены эти значения.
В таблице ниже приведены эти значения.
| Уголок | 0 | π6\frac{\pi }{6}\\6π , или 30 | π4\frac{\pi }{4}\\4π , или 45° | π3\frac{\pi }{3}\\3π , или 60° | π2\frac{\pi }{2}\\2π , или 90° |
| Косинус | 1 | 32\frac{\sqrt{3}}{2}\\23 | 22\frac{\sqrt{2}}{2}\\22 | 12\frac{1}{2}\\21 | 0 |
| Синус | 0 | 12\frac{1}{2}\\21 | 22\frac{\sqrt{2}}{2}\\22 | 32\frac{\sqrt{3}}{2}\\23 | 1 |
На рисунке 14 показаны общие углы в первом квадранте единичной окружности.
Рисунок 14
Использование калькулятора для нахождения синуса и косинуса
Чтобы найти косинус и синус углов, отличных от специальных углов , обратимся к компьютеру или калькулятору. Имейте в виду : Большинство калькуляторов могут быть установлены в режим «градус» или «радиан», который сообщает калькулятору единицы измерения для входного значения. Когда мы оцениваем
cos(30)\cos \left(30\right)cos(30)
на нашем калькуляторе, он оценит это как косинус 30 градусов, если калькулятор находится в режиме градусов, или как косинус 30 радиан если калькулятор находится в радианном режиме.
Как: Зная угол в радианах, используйте графический калькулятор, чтобы найти косинус.
- Если в калькуляторе есть режимы в градусах и в радианах, установите его в режим в радианах.

- Нажмите клавишу COS.
- Введите значение угла в радианах и нажмите клавишу закрытия скобок «)».
- Нажмите ВВОД.
Пример 4. Использование графического калькулятора для нахождения синуса и косинуса
Вычислите
cos(5π3)\cos \left(\frac{5\pi }{3}\right)\\cos(35π)
с помощью графического калькулятора или компьютера.
Решение
Введите следующие нажатия клавиш:
COS (5 × π ÷ 3 ) ВВОД
cos(5π3)=0,5\cos \left(\frac{5\pi }{3}\right)=0,5\\cos(35π )=0,5
Анализ решения
Мы можем найти косинус или синус угла в градусах прямо на калькуляторе с режимом градусов. Для калькуляторов или программного обеспечения, использующего только режим радиан, мы можем найти знак 9\circ 20∘
, например, включив коэффициент преобразования в радианы как часть ввода:
SIN( 20 × π ÷ 180 ) ENTER
Попробуйте 4
Вычислите
sin(π3)\sin \left(\frac{\pi }{3}\right)\\sin(3π)
.
Раствор
Определение области значений и диапазона функций синуса и косинуса
Теперь, когда мы можем найти синус и косинус угла, нам нужно обсудить их области определения и диапазоны. Каковы области определения функций синуса и косинуса? То есть, каковы наименьшее и наибольшее числа, которые могут быть входными данными функций? Поскольку углы меньше 0 и углы больше
2π2\pi 2π
по-прежнему можно изобразить на единичной окружности и иметь действительные значения
x,yx,yx,y
и
rrr
, для углов нет нижнего или верхнего предела которые могут быть входными данными для функций синуса и косинуса. Входными данными для функций синуса и косинуса является поворот от положительной оси x , и это может быть любое действительное число.
Каковы диапазоны функций синуса и косинуса? Каковы наименьшее и максимальное возможные значения их выхода? Мы можем увидеть ответы, изучив единичный круг , как показано на рисунке 15. Границы координаты x равны
[−1,1]\left[-1,1\right][−1,1]
. Границы координаты y также равны
[−1,1]\left[-1,1\right][−1,1]
. Следовательно, диапазон функций синуса и косинуса составляет
[−1,1]\left[-1,1\right][−1,1]
.
Рисунок 15
Мы обсудили нахождение синуса и косинуса для углов в первом квадранте, но что, если наш угол находится в другом квадранте? Для любого заданного угла в первом квадранте существует угол во втором квадранте с таким же значением синуса. Поскольку значение синуса равно y -координата на единичной окружности, другой угол с тем же синусом будет иметь такое же значение y , но противоположное x -значение. Следовательно, его значение косинуса будет противоположно значению косинуса первого угла.
Следовательно, его значение косинуса будет противоположно значению косинуса первого угла.
Аналогично, в четвертом квадранте будет угол с тем же косинусом, что и исходный угол. Угол с тем же косинусом будет иметь то же значение x , но будет иметь противоположное значение y . Следовательно, его значение синуса будет противоположно значению синуса исходного угла.
Как показано на рисунке 16, угол
α\alpha α
имеет то же значение синуса, что и угол
ttt
; значения косинуса противоположны. Угол
β\beta β
имеет то же значение косинуса, что и угол
ttt
; значения синуса противоположны.
sin(t)=sin(α)andcos(t)=−cos(α)sin(t)=−sin(β)andcos(t)=cos(β)\begin {массив}{lll}\sin\left(t\right)=\sin\left(\alpha\right)\qquad & \text{and}\qquad & \cos \left(t\right)=-\cos \left(\alpha \right)\qquad \\ \sin \left(t\right)=-\sin \left(\beta \right)\qquad & \text{and}\qquad & \cos \left(t \right)=\cos \left(\beta \right)\qquad \end{array}sin(t)=sin(α)sin(t)=-sin(β)andandcos(t)=-cos (α)cos(t)=cos(β) 9\circ 90∘
, или
000
и
π2\frac{\pi }{2}2π
радиан.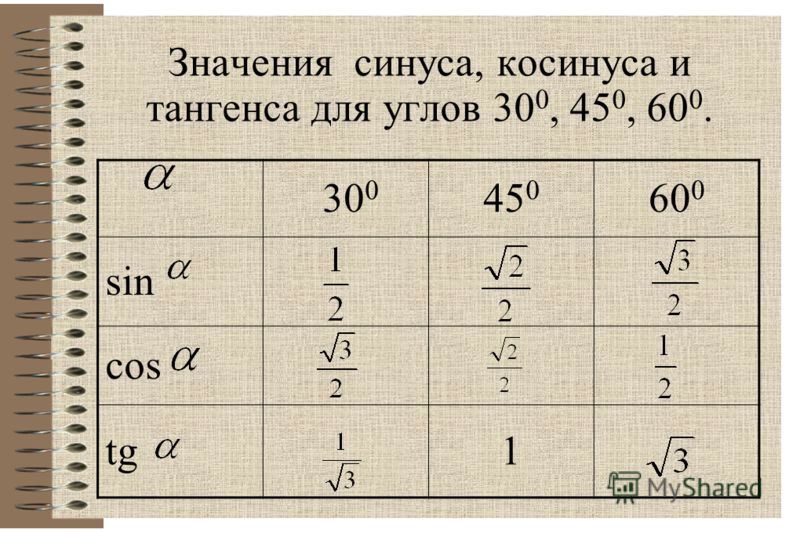 Как видно из рисунка 17, для любого угла в квадрантах II, III или IV существует исходный угол в квадрантах I.
Как видно из рисунка 17, для любого угла в квадрантах II, III или IV существует исходный угол в квадрантах I.
Рисунок 17
Как: Зная угол между
000
и2π2\pi 2π
, найдите его опорный угол.- Угол в первом квадранте является собственным опорным углом.
- Для угла во втором или третьем квадранте опорный угол равен 9\circ ∣(180∘−225∘)∣=∣−45∘∣=45∘
Попробуйте 5
Найдите опорный угол
5π3\frac{5\pi }{3}35π
.
Раствор
Использование опорных углов
Теперь давайте еще раз рассмотрим колесо обозрения, представленное в начале этого раздела. Предположим, всадник делает снимок, остановившись в двадцати футах над уровнем земли. Затем всадник вращается на три четверти круга. Какова новая высота всадника? Чтобы ответить на такие вопросы, как этот, нам нужно оценить функции синуса или косинуса при углах, превышающих 90 градусов или под отрицательным углом .
 Опорные углы позволяют вычислять тригонометрические функции для углов вне первого квадранта. Их также можно использовать для нахождения
Опорные углы позволяют вычислять тригонометрические функции для углов вне первого квадранта. Их также можно использовать для нахождения(x,y)\left(x,y\right)(x,y)
координат для этих углов. Мы будем использовать опорный угол угла поворота в сочетании с квадрантом, в котором лежит конечная сторона угла.
Использование опорных углов для оценки тригонометрических функций
Мы можем найти косинус и синус любого угла в любом квадранте, если знаем косинус или синус его опорного угла. Абсолютные значения косинуса и синуса угла такие же, как у опорного угла. Знак зависит от квадранта исходного угла. Косинус будет положительным или отрицательным в зависимости от знака числа 9.1446 x -значения в этом квадранте. Синус будет положительным или отрицательным в зависимости от знака значений и в этом квадранте.
Общее примечание: использование опорных углов для нахождения косинуса и синуса
Углы имеют косинусы и синусы с тем же абсолютным значением, что и их опорные углы.
 Знак (положительный или отрицательный) можно определить по квадранту угла.
Знак (положительный или отрицательный) можно определить по квадранту угла.Как: по заданному углу в стандартном положении найдите опорный угол, а также косинус и синус исходного угла.
- Измерьте угол между конечной стороной заданного угла и горизонтальной осью. Это опорный угол.
- Определите значения косинуса и синуса опорного угла.
- Присвойте косинусу тот же знак, что и значениям x в квадранте исходного угла.
- Присвойте синусу тот же знак, что и y -значения в квадранте исходного угла.
Пример 5. Использование опорных углов для нахождения синуса и косинуса 9\circ \right)sin(150∘)
. - Используя опорный угол, найдите
cos5π4\cos \frac{5\pi }{4}cos45π
иsin5π4\sin \frac{5\pi }{4}sin45π
.
Решение
- 150° находится во втором квадранте. Угол, который он образует с осью x , равен 180° − 150° = 30°, поэтому опорный угол равен 30°.
 \circ \right)=\frac{1}{2}cos(30∘)=23 9\circ \right)=\frac{1}{2}cos(150∘)=−23
\circ \right)=\frac{1}{2}cos(30∘)=23 9\circ \right)=\frac{1}{2}cos(150∘)=−23andsin(150∘)=21
5π4\frac{5\pi }{4}45π
находится в третьем квадранте. Его исходный угол равен5π4−π=π4\frac{5\pi }{4}-\pi =\frac{\pi }{4}45π−π=4π
. Косинус и синус числаπ4\frac{\pi }{4}4π
равны22\frac{\sqrt{2}}{2}22
. В третьем квадранте оба числаxxx
иyyy
отрицательны, поэтому: 2}}{2}\text{and}\sin\frac{5\pi}}{4}=-\frac{\sqrt{2}}{2}cos45π=−22 9\circ \right)sin(315∘).
б. Используйте опорный угол
−π6-\frac{\pi }{6}−6π
, чтобы найти
cos(−π6)\cos \left(-\frac{\pi }{6}\ right)cos(−6π)
и
sin(−π6)\sin \left(-\frac{\pi}{6}\right)sin(−6π)
.

Решение
Использование опорных углов для определения координат
Теперь, когда мы научились находить значения косинуса и синуса для специальных углов в первом квадранте, мы можем использовать симметрию и опорные углы, чтобы заполнить значения косинуса и синуса для остальных специальных углов на единичной окружности. Они показаны на рисунке 19.. Найдите время, чтобы узнать
(x,y)\left(x,y\right)(x,y)
координаты всех основных углов в первом квадранте.
В дополнение к изучению значений специальных углов, мы можем использовать эталонные углы, чтобы найти
(x, y)\left(x,y\right)(x,y)
координаты любой точки на единичной окружности, используя что мы знаем об опорных углах вместе с тождествами
x=costy=sint\begin{array}{l}x=\cos t\qquad \\ y=\sin t\qquad \end{ массив}x=costy=sint
Сначала находим опорный угол, соответствующий данному углу.
 Затем мы берем значения синуса и косинуса опорного угла
Затем мы берем значения синуса и косинуса опорного угла
Как сделать: Зная угол точки на окружности и радиус окружности, найдите
(x, y)\left(x,y\right)(x,y)
координат точки.- Найдите опорный угол, измерив наименьший угол к x -ось.
- Найдите косинус и синус опорного угла.
- Определите соответствующие знаки для
xxx
иyyy
в данном квадранте.
Пример 6. Использование единичного круга для поиска координат
Найдите координаты точки на единичной окружности под углом
7π6\frac{7\pi }{6}67π
.
Решение
Мы знаем, что угол
7π6\frac{7\pi }{6}67π
находится в третьем квадранте.
Сначала найдем опорный угол, измерив угол относительно оси x . Чтобы найти исходный угол угла, крайняя сторона которого находится в квадранте III, находим разность угла и
π\pi π
.
7π6−π=π6\frac{7\pi }{6}-\pi =\frac{\pi }{6}67π−π=6π
Далее найдем косинус и синус опорного угла:
cos(π6)=32sin(π6)=12\cos\left(\frac{\pi }{6}\right)=\frac{ \sqrt{3}}{2}\sin\left(\frac{\pi }{6}\right)=\frac{1}{2}cos(6π)=23
грех(6π)=21
Мы должны определить соответствующие знаки для x и y в данном квадранте. Поскольку наш исходный угол находится в третьем квадранте, где
xxx
и
yyy
отрицательны, то и косинус, и синус отрицательны.
cos(7π6)=−32sin(7π6)=−12\begin{array}{l}\cos\left(\frac{7\pi}}{6}\right)=-\frac{\sqrt {3}}{2}\qquad \\ \sin \left(\frac{7\pi }{6}\right)=-\frac{1}{2}\qquad \end{array}cos(67π )=−23
sin(67π)=−21
Теперь мы можем вычислить координаты
(x,y)\left(x,y\right)(x,y)
, используя тождества
x=cosθx=\cos \theta x=cosθ
и
y=sinθy=\sin \theta y=sinθ
.
Координаты точки:
(−32,−12)\left(-\frac{\sqrt{3}}{2},-\frac{1}{2}\right)(−23
,−21)
на единичной окружности.
Попробуйте 7
Найдите координаты точки на единичной окружности под углом 9{2}t=1cos2t+sin2t=1
Ключевые понятия
- Нахождение значений функции для синуса и косинуса начинается с рисования единичной окружности с центром в начале координат и радиусом в 1 единицу.

- Используя единичную окружность, синус угла
ttt
равен y -значению конечной точки на единичной окружности дуги длинойttt
, тогда как косинус углаttt
равен x -значение конечной точки. - Значения синуса и косинуса наиболее непосредственно определяются, когда соответствующая точка на единичной окружности попадает на ось.
- Когда известен синус или косинус, мы можем использовать тождество Пифагора, чтобы найти другой. Тождество Пифагора также полезно для определения синусов и косинусов специальных углов.
- Калькуляторы и программы для построения графиков полезны для нахождения синусов и косинусов, если известна правильная процедура ввода информации.
- Областью определения функций синуса и косинуса являются все действительные числа.
- Диапазон функции синуса и косинуса равен
[−1,1]\left[-1,1\right][−1,1]
. - Синус и косинус угла имеют то же абсолютное значение, что и синус и косинус исходного угла.

- Знаки синуса и косинуса определяются из значений x и y в квадранте исходного угла.
- Опорный угол угла — это угол размера,
ttt
,образованы концевой стороной угла
ttt
и горизонтальной осью. - Опорные углы можно использовать для нахождения синуса и косинуса исходного угла.
- Опорные углы также можно использовать для определения координат точки на окружности.
Глоссарий
- Функция косинуса
- x -значение точки на единичной окружности, соответствующей заданному углу
- Пифагорейская идентичность
- следствие теоремы Пифагора о том, что квадрат косинуса данного угла плюс квадрат синуса этого угла равен 1
- функция синуса
- y -значение точки на единичной окружности, соответствующей заданному углу
- единичный круг
- круг с центром в точке
(0,0)\влево(0,0\вправо)(0,0)
и радиусом
Раздел Упражнения
- 1.
 Опишите единичный круг.
Опишите единичный круг. - 2. Что представляют собой координаты x- и y- точек на единичной окружности?
3. Обсудите разницу между котерминальным углом и опорным углом.
4. Объясните, чем косинус угла во втором квадранте отличается от косинуса его опорного угла в единичной окружности.
5. Объясните, чем синус угла во втором квадранте отличается от синуса его исходного угла в единичной окружности.
В следующих упражнениях используйте заданный знак функций синуса и косинуса, чтобы найти квадрант, в котором находится конечная точка, определяемая
ttt
.6.
sin(t)<0\text{sin}\left(t\right)<0sin(t)<0
иcos(t)<0\text{cos}\left(t\right) )<0cos(t)<0
7.
sin(t)>0\text{sin}\left(t\right)>0sin(t)>0
иcos(t)>0\ cos \left(t\right)>0cos(t)>0
8.
sin(t)>0\sin\left(t\right)>0sin(t)>0
иcos(t)<0\cos \left(t\right)<0cos(t)<0
9.
sin(t)<0\sin\left(t\right)<0sin(t)<0
иcos(t)>0\cos \left(t\right)>0cos (t)>0
В следующих упражнениях найдите точное значение каждой тригонометрической функции.

10.
sinπ2\sin \frac{\pi }{2}sin2π
11.
sinπ3\sin \frac{\pi }{3}sin3π
12.
cosπ2\cos \frac{\pi }{2}cos2π
13.
cosπ3\cos \frac{\pi }{3}cos3π
14.
sinπ4\ sin \frac{\pi }{4}sin4π
15.
cosπ4\cos \frac{\pi }{4}cos4π
16.
sinπ6\sin \frac{\pi } π\cos \pi cosπ
20.
cos0\cos 0cos0 9\circ 135∘
28.
5π4\frac{5\pi }{4}45π
29.
2π3\frac{2\pi }{3}32π
30. 90\ frac{5\pi }{6}65π
31.
−11π3\frac{-11\pi }{3}3−11π
32.
−7π4\frac{-7\pi } {4}4−7π
33.
−π8\frac{-\pi }{8}8−π
Для следующих упражнений найдите исходный угол, квадрант конечной стороны и синус и косинус каждого угла. Если угол не является одним из углов единичной окружности, воспользуйтесь калькулятором и округлите его до трех знаков после запятой. 9\circ 150∘
42.
5π4\frac{5\pi }{4}45π
43.

7π6\frac{7\pi }{6}67π
44. 90\
frac{5\pi }{3}35π45.
3π4\frac{3\pi }{4}43π
46.
4π3\frac{4\pi }{3}34π
47.
2π3\frac{2\pi }{3}32π
48.
5π6\frac{5\pi }{6}65π
49.
7π4\frac{7\pi {4}47π
В следующих упражнениях найдите требуемое значение.
50. Если
cos(t)=17\text{cos}\left(t\right)=\frac{1}{7}cos(t)=71
иttt
находится в 4 -й квадрант, найдитеsin(t)\text{sin}\left(t\right)sin(t)
.51. Если
cos(t)=29\text{cos}\left(t\right)=\frac{2}{9}cos(t)=92
иttt
находится в 1 st квадрант, найдитеsin(t)\text{sin}\left(t\right)sin(t)
.52. Если
sin(t)=38\text{sin}\left(t\right)=\frac{3}{8}sin(t)=83 9\circ 120∘
.56. Найдите координаты точки на окружности радиусом 8, соответствующей углу
7π4\frac{7\pi }{4}47π
.57. Найдите координаты точки на окружности радиусом 16, соответствующей углу
5π9\frac{5\pi }{9}95π
.
58. Укажите область определения функций синуса и косинуса.
59. Укажите диапазон функций синуса и косинуса.
В следующих упражнениях используйте заданную точку на единичной окружности, чтобы найти значение синуса и косинуса числа 9.0005
ттт
.60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
В следующих упражнениях используйте для оценки графический калькулятор.
80.
sin5π9\sin \frac{5\pi }{9\circ sin310∘
90.
sin(11π3)cos(−5π6)\sin\left(\frac{11\pi}}{3}\right)\cos\left(\frac{-5\ pi }{6}\right)sin(311π)cos(6−5π)
91.
sin(3π4)cos(5π3)\sin \left(\frac{3\pi }{4 }\right)\cos \left(\frac{5\pi }{3}\right)sin(43π)cos(35π)
92.
sin(−4π3)cos(π2)\ sin \left(-\frac{4\pi }{3}\right)\cos \left(\frac{\pi }{2}\right)sin(-34π)cos(2π)
93.

sin(−9π4)cos(−π6)\sin\left(\frac{-9\pi }{4}\right)\cos \left(\frac{-\pi }{6}\right )грех(4−9π)cos(6−π)
94.
sin(π6)cos(−π3)\sin\left(\frac{\pi}{6}\right)\cos\left(\ frac{-\pi }{3}\right)sin(6π)cos(3−π)
95.
sin(7π4)cos(−2π3)\sin \left(\frac{7 \pi }{4}\right)\cos \left(\frac{-2\pi }{3}\right)sin(47π)cos(3−2π)
96.
cos(5π6 )cos(2π3)\cos \left(\frac{5\pi }{6}\right)\cos \left(\frac{2\pi }{3}\right)cos(65π)cos(32π )
97.
cos(−π3)cos(π4)\cos \left(\frac{-\pi }{3}\right)\cos \left(\frac{\pi }{4 }\right)cos(3−π)cos(4π)
98.
sin(−5π4)sin(11π6)\sin \left(\frac{-5\pi }{4}\right)\sin \left(\frac{11\pi }{6 }\right)sin(4−5π)sin(611π)
99.
sin(π)sin(π6)\sin \left(\pi \right)\sin \left(\frac{ \pi }{6}\right)sin(π)sin(6π)
Для следующих упражнений используйте этот сценарий: Ребенок садится в карусель, один оборот которой занимает одну минуту. Ребенок входит в точку
(0,1)\влево(0,1\вправо)(0,1)
, то есть строго на север. Предположим, что карусель вращается против часовой стрелки.
Предположим, что карусель вращается против часовой стрелки.100. Каковы координаты ребенка через 45 секунд?
101. Каковы координаты ребенка через 90 секунд?
102. Каковы координаты ребенка через 125 секунд?
103. Когда у ребенка появятся координаты
(0,707,−0,707)\влево(0,707,-0,707\вправо)(0,707,−0,707)
, если поездка длится 6 минут? (Ответов несколько.)104. Когда у ребенка появятся координаты
(−0,866, −0,5)\влево (-0,866, –0,5\вправо)(−0,866, −0,5)
если поездка длилась 6 минут?
Лицензии и атрибуты
Контент по лицензии CC, совместно используемый ранее
- Unit Circle Image. Автор : CK-12. Расположен по адресу : https://www.ck12.org/trigonometry/trigonometry-and-the-unit-circle/lesson/Trigonometric-Ratios-on-the-Unit-Circle-ALG-II/. Лицензия : CC BY-NC: Attribution-NonCommercial
Лицензионный контент CC, конкретное указание авторства
- Предварительный расчет.
 Автор : Колледж OpenStax. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]:1/Preface. Лицензия : CC BY: Атрибуция
Автор : Колледж OpenStax. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]:1/Preface. Лицензия : CC BY: Атрибуция
Все права защищены. Содержание
- Введение в тригонометрические функции с использованием углов. Автор : Mathispower4u. Лицензия : Все права защищены . Условия лицензии : Стандартная лицензия YouTube
Понимание синуса, косинуса и тангенса
Статью, объясняющую тригонометрические функции с использованием единичной окружности, можно найти здесь
Использование единичной окружности является стандартным способом определения и понимания тригонометрических функций в математике.
Я рекомендую сначала прочитать и понять эту статью. Позже, если вы захотите понять, как определяются тригонометрические функции для значений больше 90° или меньше 0°, прочтите другую статью.
Синус часто вводится следующим образом:
Что верно, но у большинства людей глаза стекленеют.
Проблема в том, что со времени, когда люди начали изучать треугольники, до того момента, когда люди разработали концепцию тригонометрических функций (синус, косинус, тангенс, секанс, косеканс и котангенс), прошло более 3000 лет.
Древние изучали треугольники. Одной из вещей, которые они сделали, было сравнение длин сторон треугольников:
Треугольник имеет три стороны, поэтому есть 6 различных способов сравнения сторон:
от А до В, от А до С, от В до С, от В до А, от С до А и от С до В
Обычно мы записываем их в виде дробей:
А А В В С С -, -, -, -, -, - Б В С А А Б
Они обнаружили, что если два треугольника имеют одинаковые отношения трех сторон, то треугольники имеют одинаковую форму — у них одинаковые внутренние углы, даже если размеры треугольников могут быть разными.
Это оказалось очень, очень полезным, потому что это означало, что если бы вы могли найти меньший треугольник, который имел бы ту же форму, что и большой треугольник, то вы могли бы изучить меньший треугольник и узнать что-то о большом треугольнике. Это работает и наоборот: если у вас есть очень маленький треугольник и вы можете найти больший треугольник, с которым легче работать, тогда вы можете изучить больший треугольник и узнать что-то о меньшем треугольнике. Эти типы треугольников называются подобных треугольников .
Это работает и наоборот: если у вас есть очень маленький треугольник и вы можете найти больший треугольник, с которым легче работать, тогда вы можете изучить больший треугольник и узнать что-то о меньшем треугольнике. Эти типы треугольников называются подобных треугольников .
Одним из первых применений этого было расчёт теней — использование теней для измерения вещей.
Предположим, вы хотите измерить высоту дерева, как бы вы это сделали?
Вы можете взобраться на дерево, неся веревку. Вы опускали веревку до тех пор, пока она не достигала земли, отмечали длину веревки, а затем измеряли длину веревки (после того, как вы спустились). К сожалению, это (1) медленно, (2) опасно (всегда есть риск падения) и (3) возможно неточно, так как не всегда есть возможность забраться на самую вершину дерева (стволы и ветки деревьев истончаются). близко к вершине, и они могут быть недостаточно прочными, чтобы поддержать вас на всем пути к вершине).
Вы можете срубить дерево и измерить его. Но если вы хотите сохранить дерево, срубить его не вариант (к тому же это довольно медленно).
Что делать, если вы хотите измерить высоту здания или скалы? Использование веревки сработает (при условии, что веревка достаточно длинная), но перерезать ее не получится.
Однако древние заметили, что дерево (или здание, или скала) образует одну сторону прямоугольного треугольника (будем считать, что дерево растет вертикально, а не под углом), его тень образует основание прямоугольного треугольника. треугольник и солнечные лучи образуют гипотенузу.
Если мы можем построить меньший прямоугольный треугольник с гипотенузой под тем же углом, что и солнечные лучи, то мы получим аналогичный треугольник. Затем мы можем измерить меньший (и подобный) треугольник и применить то, что мы знаем о нем, к большему треугольнику:
Поскольку большой и малый треугольник подобны, это означает, что отношения сторон одинаковы. Если у нас есть палка известной длины и мы поместим ее перпендикулярно земле (это сторона a маленького треугольника), она отбросит тень, и мы сможем измерить длину этой тени (это сторона b маленького треугольника). . Мы можем легко измерить длину тени, отбрасываемой деревом (это сторона B большого треугольника). Поскольку эти два треугольника подобны, мы знаем, что отношение a/b должно быть таким же, как отношение A/B.
Если у нас есть палка известной длины и мы поместим ее перпендикулярно земле (это сторона a маленького треугольника), она отбросит тень, и мы сможем измерить длину этой тени (это сторона b маленького треугольника). . Мы можем легко измерить длину тени, отбрасываемой деревом (это сторона B большого треугольника). Поскольку эти два треугольника подобны, мы знаем, что отношение a/b должно быть таким же, как отношение A/B.
ПРИМЕЧАНИЕ: не имеет значения, как рассчитывается соотношение: a/b или b/a, если оно рассчитывается одинаково для обоих треугольников.
Если наша измерительная линейка имеет высоту 2 м и отбрасывает тень длиной 1,25 м, отношение a/b равно 1,6. Поскольку треугольники подобны, мы знаем, что отношение A/B должно быть 1,6. Если дерево отбрасывает тень длиной 15 м, мы можем подставить это число в уравнение и записать A/15 = 1,6. Умножение обеих сторон на 15 дает нам: (A/15)*15 = 1,6*15. Умножая получаем А = 24, значит высота дерева 24м.
Обязательно попробуйте дома. Рассчитайте высоту вашего дома, измерив длину его тени и соотнеся ее с длиной известной меры (критерий (или измерительная линейка) подойдет — если у вас нет линейки или измерительной линейки, вы всегда можете использовать 12-дюймовая (30 см) линейка). Или измерьте высоту деревьев в вашем районе.
Рассчитайте высоту вашего дома, измерив длину его тени и соотнеся ее с длиной известной меры (критерий (или измерительная линейка) подойдет — если у вас нет линейки или измерительной линейки, вы всегда можете использовать 12-дюймовая (30 см) линейка). Или измерьте высоту деревьев в вашем районе.
Фалес из Милета использовал этот метод для измерения высоты Великой пирамиды (которой было уже около 2000 лет к тому времени, когда Фалес измерил ее высоту):
Фалес подождал, пока тень окажется на одной линии с одной гранью пирамиды, а затем измерил длину тени плюс половину длины основания, чтобы получить длину стороны B подобного треугольника. Очевидно, у него была мерная линейка, тень которой он также измерял.
В конце концов, кто-то понял, что вместо того, чтобы постоянно измерять стороны треугольника и вычислять отношения, можно создать справочную таблицу, в которой будут отношения для прямоугольных треугольников с разными углами.
Мы знаем, что треугольники подобны, если:
- отношения трех сторон одинаковы или
- все углы одинаковые или
- две стороны имеют одинаковое соотношение и один угол одинаковый (пока он не находится между двумя сторонами)
Мы можем сказать, подобны ли два прямоугольных треугольника, просто измерив один угол, если он не является квадратным (90°) углом. Поскольку сумма всех углов треугольника должна составлять 180°, мы можем легко найти 3 rd угол (180° – 90° – измеренный угол = оставшийся угол)
Поскольку сумма всех углов треугольника должна составлять 180°, мы можем легко найти 3 rd угол (180° – 90° – измеренный угол = оставшийся угол)
Любая другая справочная таблица требует, чтобы мы измеряли как минимум две стороны и вычисляли их отношение.
Самым ранним свидетельством того, что кто-то делал это, является Гиппарх из Никеи, который во 2 – веках до н. э. составил таблицу тригонометрических отношений (это были хорды, и они связаны с нашими тригонометрическими отношениями, но не совпадают с ними). Математика греков попала в Индию и была разработана индийскими математиками, затем их работы были переняты и развиты арабами, которые (к 9 в.-й -й век) разработал современное представление о шести тригонометрических функциях, которые мы используем, и имел справочные таблицы для прямоугольных треугольников с разными углами. Около 12 го или 13 го века работа арабов вернулась в Европу и была переведена с арабского языка на латынь, термин sinus (из которого мы получаем sine ) был переводом, используемым для арабского языка. слово джиба — оба из которых означают раза . Если бы ученые не перевели это слово, мы могли бы использовать джиба или джиб или что-то подобное вместо него.
слово джиба — оба из которых означают раза . Если бы ученые не перевели это слово, мы могли бы использовать джиба или джиб или что-то подобное вместо него.
Подробнее об истории тригонометрических функций можно прочитать здесь, здесь и здесь. [ ПРИМЕЧАНИЕ. это внешние ссылки, которые на момент написания этой статьи считались рабочими, безопасными и актуальными. Хотя время от времени я дважды проверяю ссылки, я не даю никаких гарантий относительно них. Я также ценю, когда мне сообщают, если ссылки не работают или больше недействительны.]
Когда мы спрашиваем, «Чему равен синус 30°?» ответ на самом деле не имеет ничего общего с углом. Угол описывает , о каком прямоугольном треугольнике идет речь, и , какие две стороны интересующего нас треугольника, но ответом является отношение длин этих двух сторон.
Лучше задать вопрос так:
«В прямоугольном треугольнике с углом 30° какое число получится, если разделить длину стороны, наиболее удаленной от угла, на длину гипотенузы?»
Сказать sin(30) , это более короткий способ выразить предыдущее (длинное) предложение:
Что нужно помнить:
- значение синуса всегда между 0 и 1 (точнее между -1 и 1)
- одна из сторон всегда гипотенуза (самая длинная сторона) и всегда знаменатель
- противоположная сторона может быть разрезана линией от рассматриваемого угла ( S ine и S liced оба начинаются с буквы С )
Когда мы спрашиваем, «Каков косинус 30°?» ответ на самом деле не имеет ничего общего с углом. Угол описывает , о каком прямоугольном треугольнике идет речь, и , какие две стороны интересующего нас треугольника – и ответом является отношение длин этих двух сторон.
Угол описывает , о каком прямоугольном треугольнике идет речь, и , какие две стороны интересующего нас треугольника – и ответом является отношение длин этих двух сторон.
Лучше задать вопрос так:
«В прямоугольном треугольнике с углом 30° какое число получится, если разделить длину стороны, ближайшей к углу, на длину гипотенузы?»
Сказать cos(30) , это более короткий способ выразить предыдущее (длинное) предложение:
Что нужно помнить:
- значение косинуса всегда между 0 и 1 (точнее между -1 и 1)
- одна из сторон всегда гипотенуза (самая длинная сторона) и всегда знаменатель
- соседней стороной является та, которая co соединена с углом ( Co синус и Co соединены, обе начинаются с Ко )
Когда мы спрашиваем «Какова тангенс 30°?» ответ на самом деле не имеет ничего общего с углом. Угол описывает , о каком прямоугольном треугольнике идет речь, и , какие две стороны интересующего нас треугольника – и ответом является отношение длин этих двух сторон.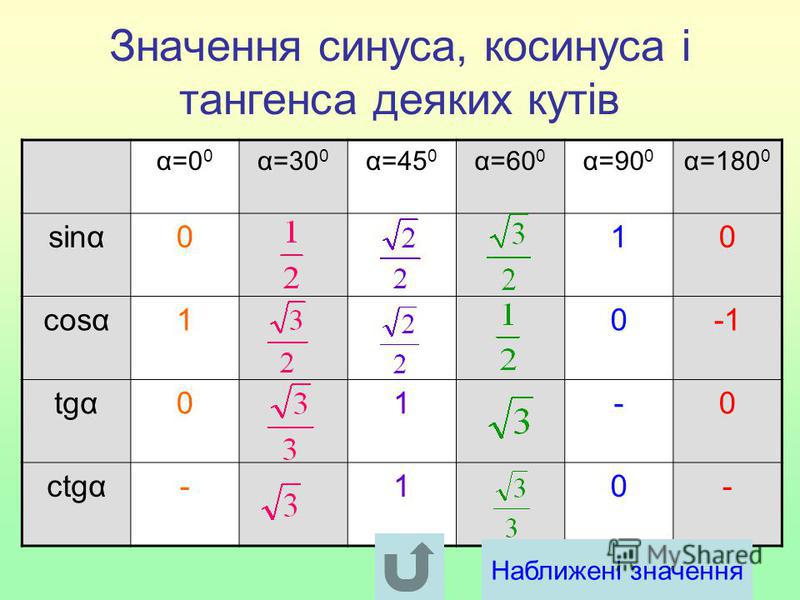
Лучше задать вопрос так:
«В прямоугольном треугольнике с углом 30° какое число получится, если разделить длину стороны, наиболее удаленной от угла, на длину стороны, ближайшей к углу?»
Сказать tan(30) , это более короткий способ выразить предыдущее (длинное) предложение:
ПРИМЕЧАНИЕ: тангенс совпадает с наклоном гипотенузы.
Это важно знать / помнить при изучении исчисления, и вы слышите о касательной к точке на кривой. На самом деле, каждый раз, когда вы слышите «касательная линия», это означает «наклон линии»
.Что нужно помнить:
- значение тангенса всегда между 0 и undefined (иногда, неточно, называют бесконечным ∞ – точнее сказать «наклон стремится к бесконечности»). Что касается синуса и косинуса, то он может быть положительным или отрицательным.
- гипотенуза не используется при вычислении тангенса
- тангенс совпадает с наклоном гипотенузы
- уклон всегда равен подъему, деленному на прогон (высота, деленная на длину)
- пробег (длина) — это сторона, соединенная с углом (если бы вы стояли там, где был угол, вы бы стояли сбоку)
- подъем (высота) — это сторона, наиболее удаленная от угла (если бы вы стояли там, где был угол, и смотрели в сторону, вы бы увидели, что она поднимается вверх)
Секанс, косеканс и котангенс — три другие тригонометрические функции, обратные первым трем тригонометрическим функциям.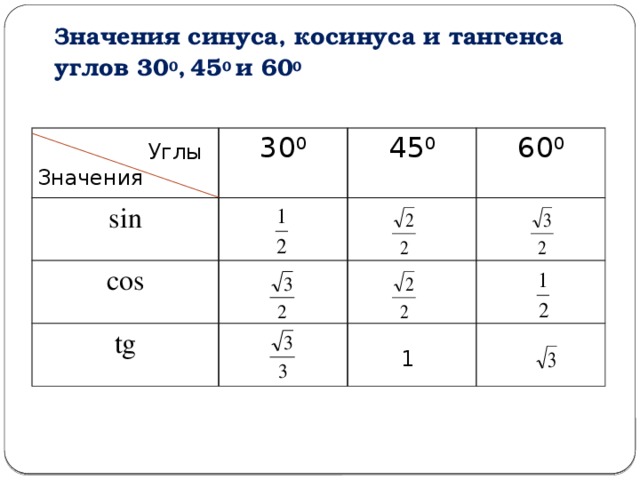
Котангенс
Это легко, это обратная тангенс. Вместо того, чтобы вычислять наклон гипотенузы, мы вычисляем обратную сторону наклона.
кроватка α = рядом/противоположно (или по ходу/подъему)
Секанс
Секанс равен , а НЕ обратному синусу . Секанс является обратным косинусом .
Мы инвертируем и , как мы вычисляем, и как мы называем функцию.
сек α = гипотенуза / соседнее
Косеканс
Косеканс равен , а НЕ обратному косинусу. Косеканс обратен синусу.
инвертируем оба как мы вычисляем и как мы называем функцию.
Часто прямоугольный треугольник рисуют так:
Однако треугольник и заданный угол можно нарисовать как угодно, поэтому важно правильно определить, какие стороны какие:
Гипотенуза зеленого цвета.
Соседняя сторона синего цвета.
Противоположная сторона красная.
В настоящее время математика, похоже, сосредоточена на обучении «математическим словам» — аббревиатурам или мнемоникам, помогающим запоминать понятия. Для тригонометрических функций используется следующее: SOH-CAH-TOA (произносится «сох ках ту ах»). Предполагается, что это поможет запомнить тригонометрическую функцию и какие стороны дают какой ответ.
SOH – S ine = O pposite ÷ H ypotenuse.
CAH – C осин = A djacent ÷ H ypotenuse.
TOA – T угол = O pposite ÷ A djacent.
Чтобы облегчить запоминание, буквы используются в качестве первых букв в причудливом предложении. Я создал эти два, потому что они используют омонимы (похожие по звучанию слова) для тригонометрических функций:
Представьте, что вы только что что-то купили и вам нужно заполнить некоторые документы:
S ign O ver H здесь.


 Далее, исходя из информации, которая была получена на предыдущем уроке, можно посчитать оставшийся тангенс, поделив найденный синус определенного угла на найденный косинус того же угла.
Далее, исходя из информации, которая была получена на предыдущем уроке, можно посчитать оставшийся тангенс, поделив найденный синус определенного угла на найденный косинус того же угла. Желательно, чтобы школьники знали о том, откуда появились данные значения и запомнили таблицы.
Желательно, чтобы школьники знали о том, откуда появились данные значения и запомнили таблицы.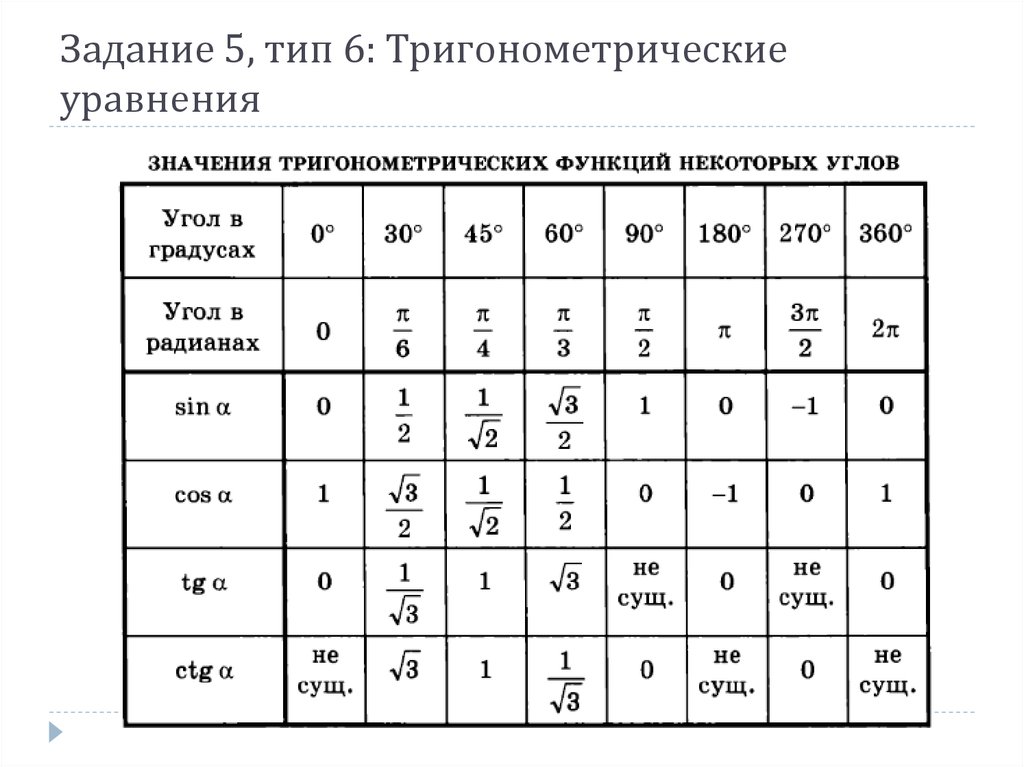 Перечислим их по порядку.
Перечислим их по порядку.
 Таким образом, и . Остается вычислить значения тангенса и котангенса, имеем и .
Таким образом, и . Остается вычислить значения тангенса и котангенса, имеем и . Они могут быть получены по определениям синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике с использованием теоремы Пифагора.
Они могут быть получены по определениям синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике с использованием теоремы Пифагора. Тогда по теореме Пифагора несложно проверить, что длины катетов равны . Теперь мы можем вычислить значения синуса, косинуса, тангенса и котангенса как отношение длин соответствующих сторон рассматриваемого прямоугольного треугольника. Имеем и .
Тогда по теореме Пифагора несложно проверить, что длины катетов равны . Теперь мы можем вычислить значения синуса, косинуса, тангенса и котангенса как отношение длин соответствующих сторон рассматриваемого прямоугольного треугольника. Имеем и .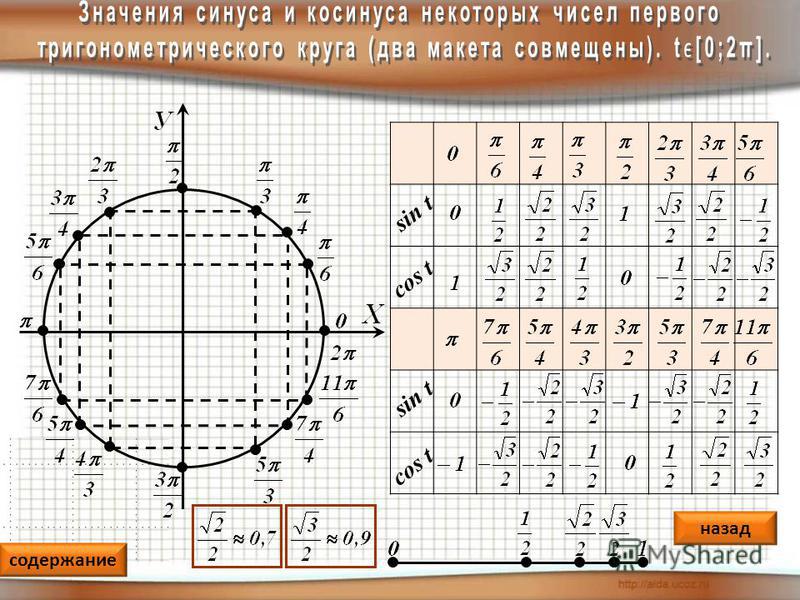 Если же аргумент тригонометрической функции, значение которой нам нужно найти, выходит за пределы от 0 до 90 градусов, то мы всегда при помощи формул приведения можем перейти к нахождению значения тригонометрической функции, аргумента которой будет в указанных пределах.
Если же аргумент тригонометрической функции, значение которой нам нужно найти, выходит за пределы от 0 до 90 градусов, то мы всегда при помощи формул приведения можем перейти к нахождению значения тригонометрической функции, аргумента которой будет в указанных пределах.
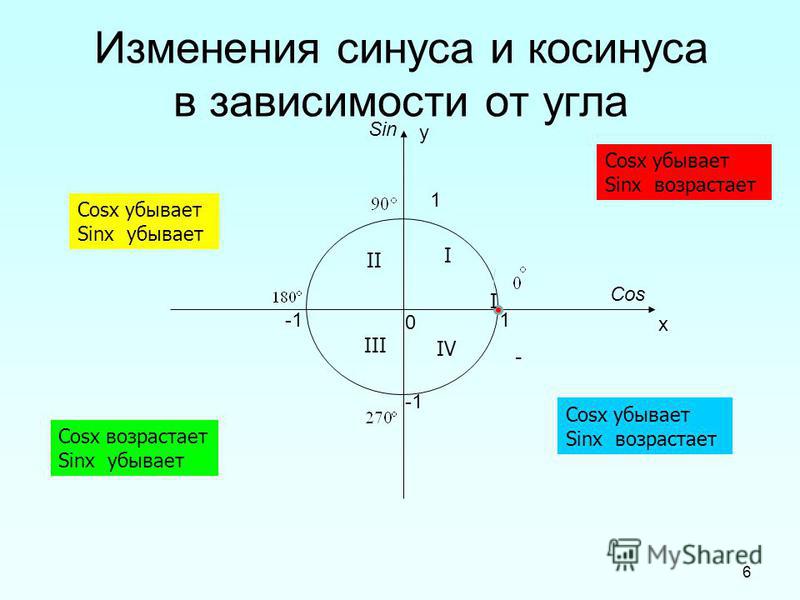

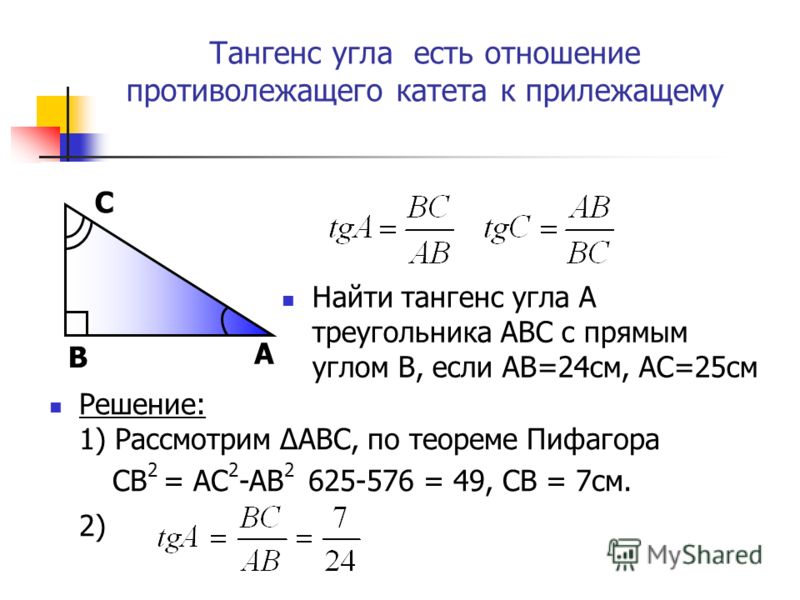

 Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях!
Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях!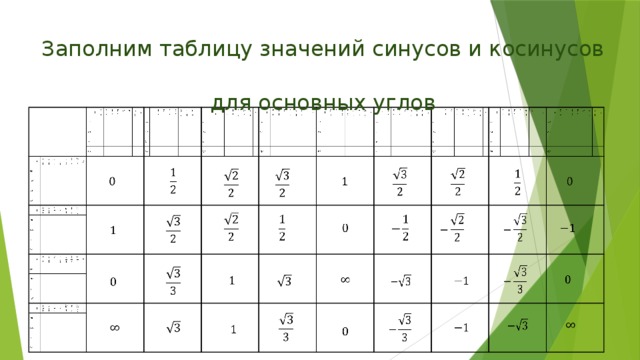 д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.
д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.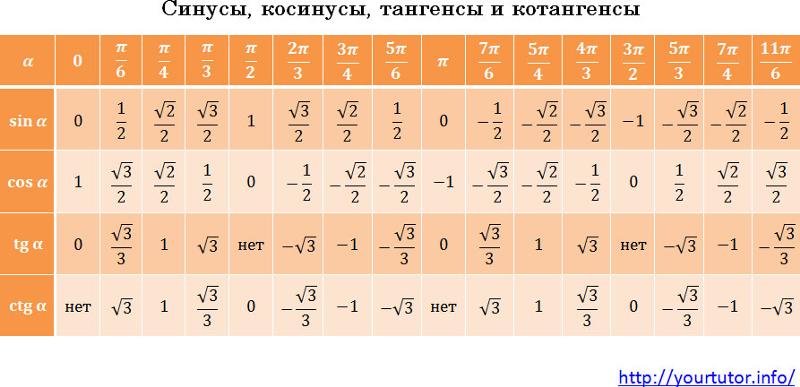
 Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.
Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач. Значения синуса, косинуса, тангенса и котангенса углов»
Значения синуса, косинуса, тангенса и котангенса углов»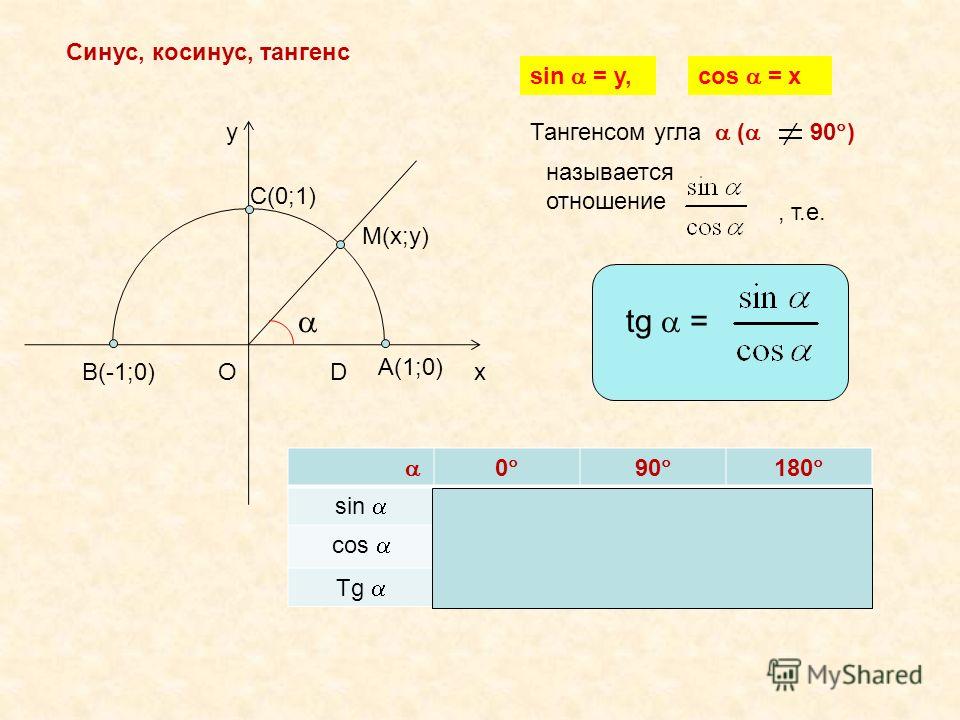
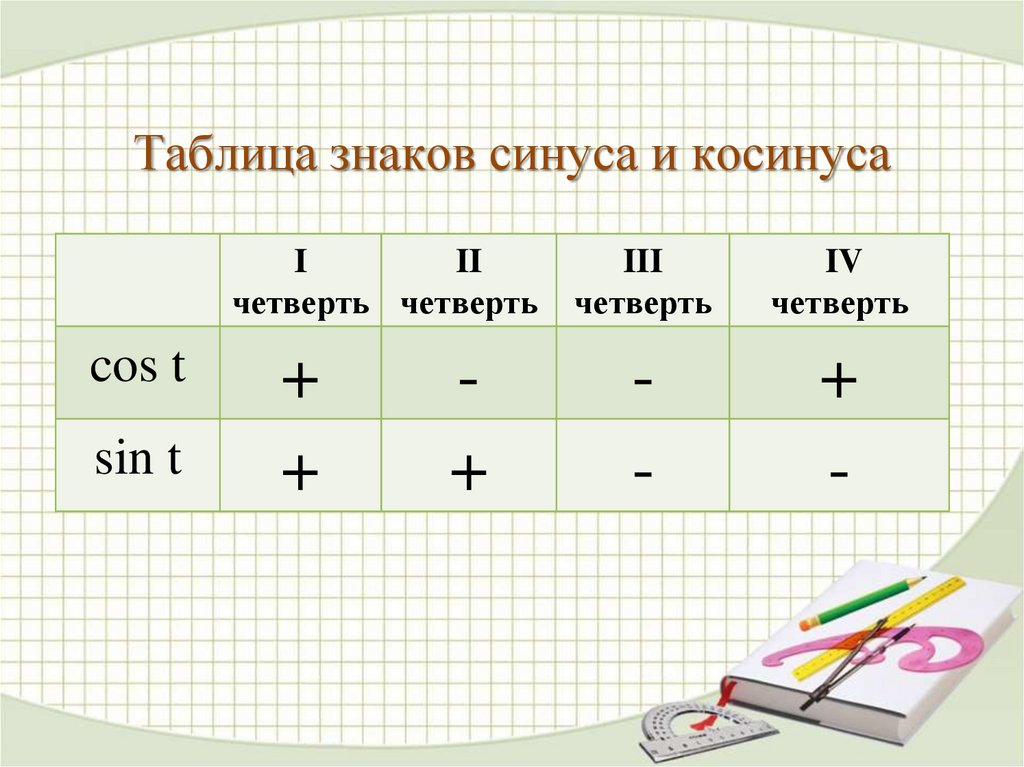
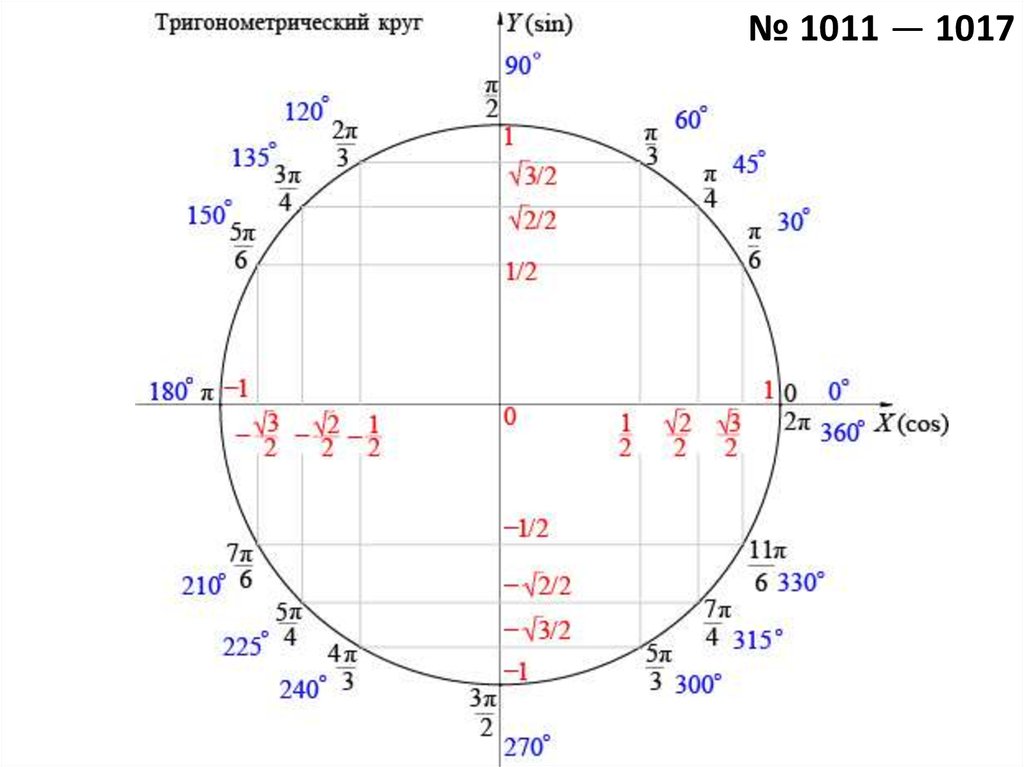

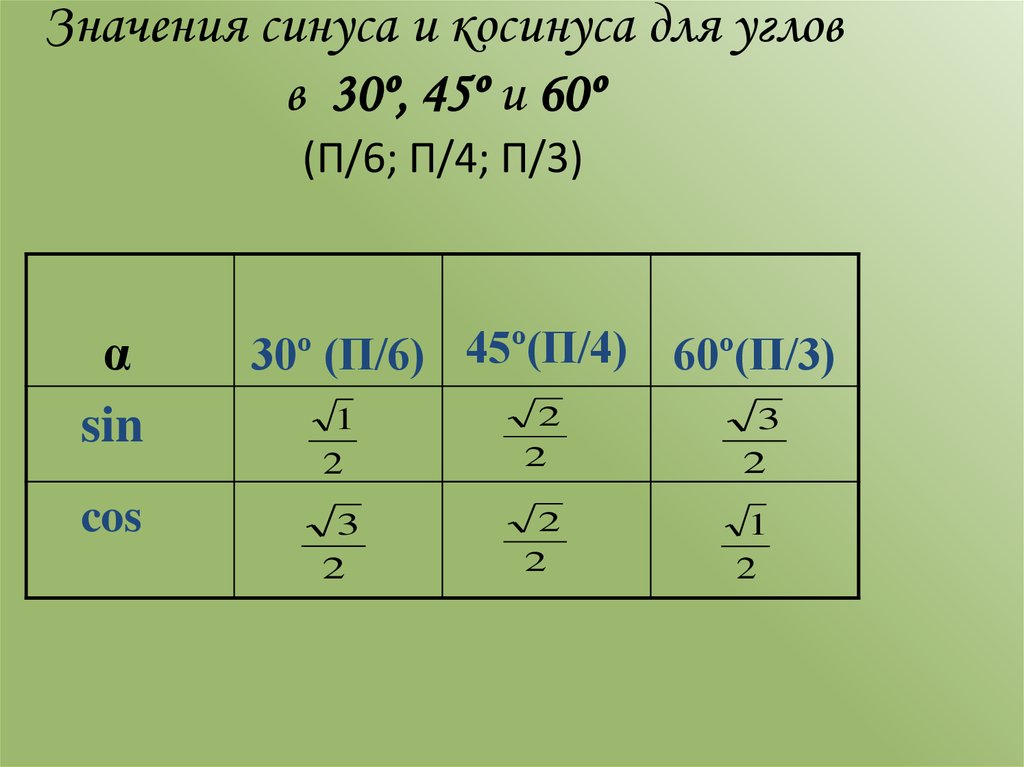 Какое из данных выражений имеет положительное значение?
Какое из данных выражений имеет положительное значение? Общая оценка работы класса, групп, отдельных учащихся.
Общая оценка работы класса, групп, отдельных учащихся. (Ответьте на самые актуальные вопросы об уроке из блока слева. )
(Ответьте на самые актуальные вопросы об уроке из блока слева. )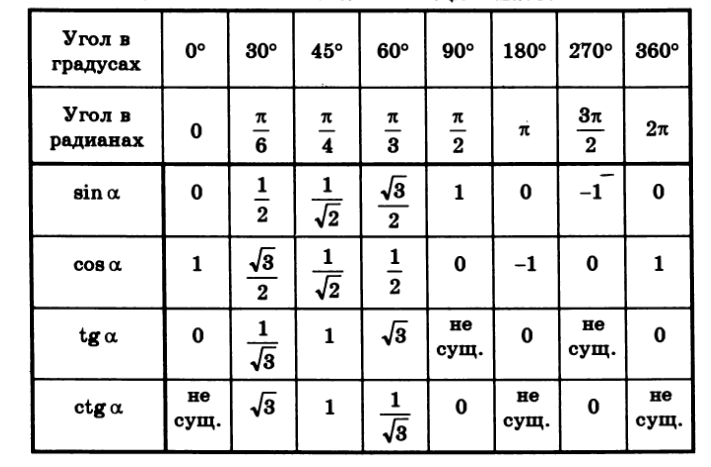 Есть несколько учащихся, намного опережающих большинство класса по уровню интеллектуального развития, которые всегда первыми поднимают руку, быстро мыслят и обладают самостоятельным критическим мышлением. Для этих учащихся следует ежеурочно продумывать индивидуальные виды заданий, более усложненные.
Есть несколько учащихся, намного опережающих большинство класса по уровню интеллектуального развития, которые всегда первыми поднимают руку, быстро мыслят и обладают самостоятельным критическим мышлением. Для этих учащихся следует ежеурочно продумывать индивидуальные виды заданий, более усложненные.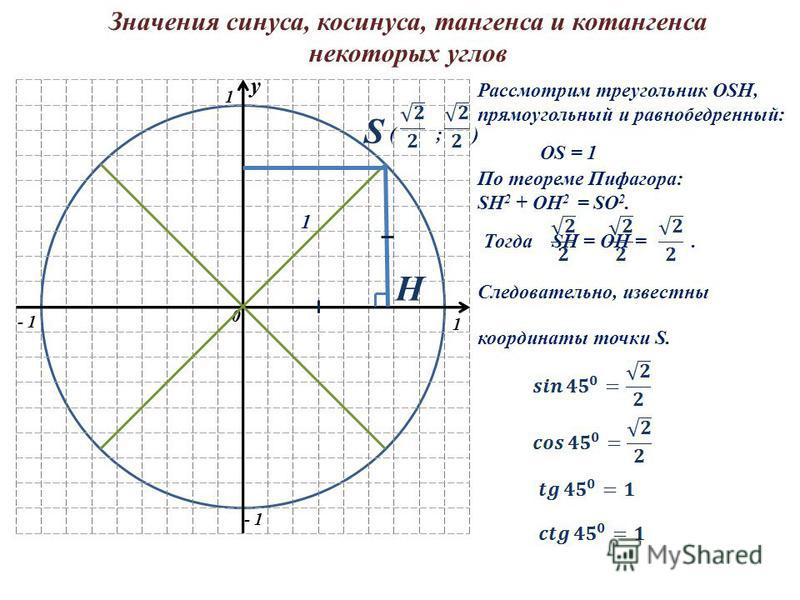 ..
.. 


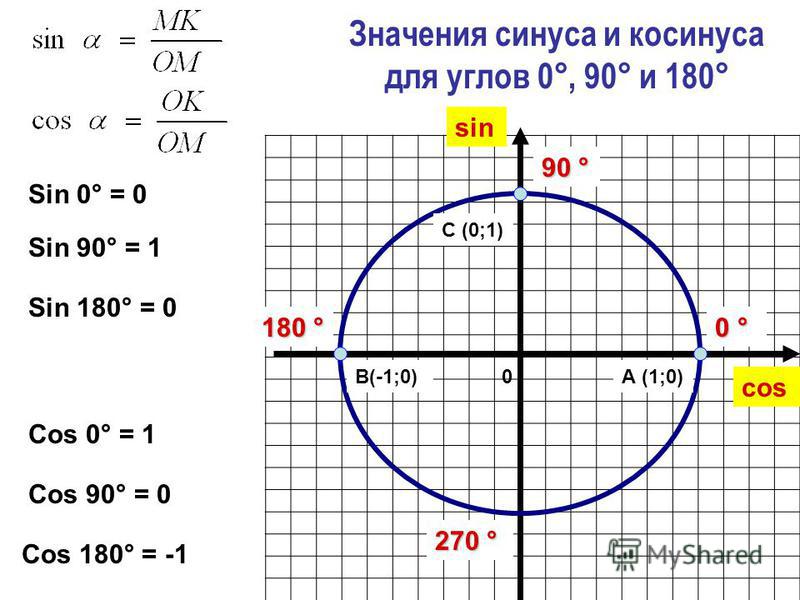 Итак, если вы знаете синус и косинус любого угла, вы также знаете тангенс. (Спасибо, единичный круг!) Синус и косинус 225 градусов равны
Итак, если вы знаете синус и косинус любого угла, вы также знаете тангенс. (Спасибо, единичный круг!) Синус и косинус 225 градусов равны
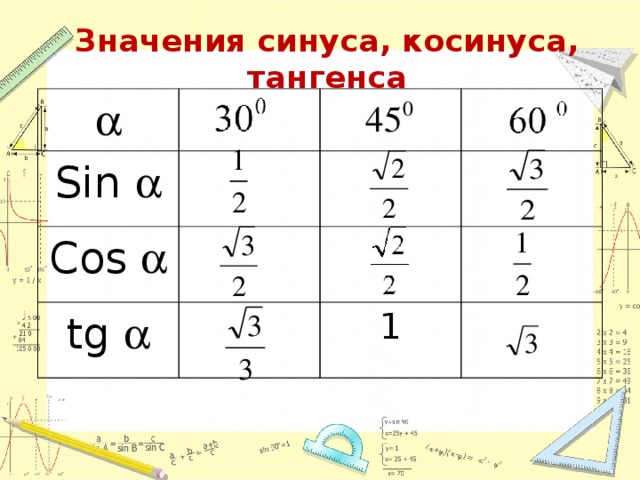 Опорные углы позволяют вычислять тригонометрические функции для углов вне первого квадранта. Их также можно использовать для нахождения
Опорные углы позволяют вычислять тригонометрические функции для углов вне первого квадранта. Их также можно использовать для нахождения Знак (положительный или отрицательный) можно определить по квадранту угла.
Знак (положительный или отрицательный) можно определить по квадранту угла.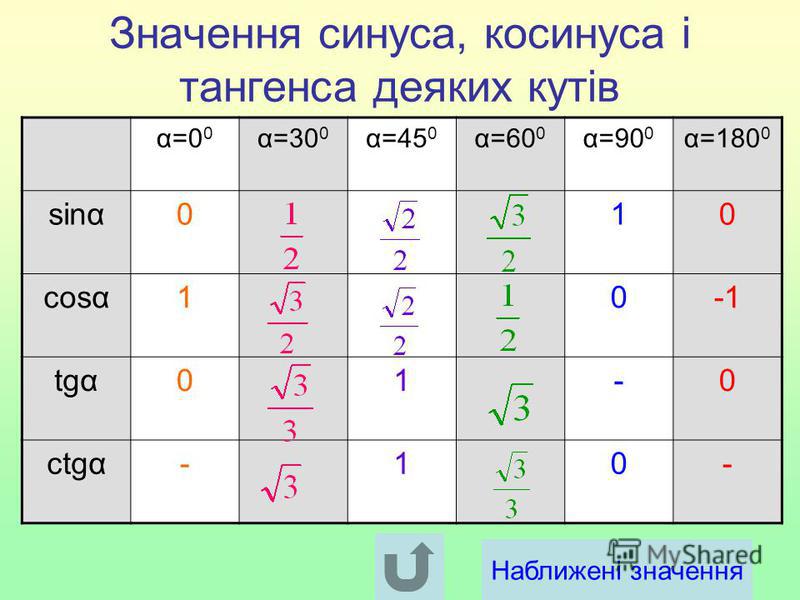 \circ \right)=\frac{1}{2}cos(30∘)=23 9\circ \right)=\frac{1}{2}cos(150∘)=−23
\circ \right)=\frac{1}{2}cos(30∘)=23 9\circ \right)=\frac{1}{2}cos(150∘)=−23
 Затем мы берем значения синуса и косинуса опорного угла
Затем мы берем значения синуса и косинуса опорного угла 
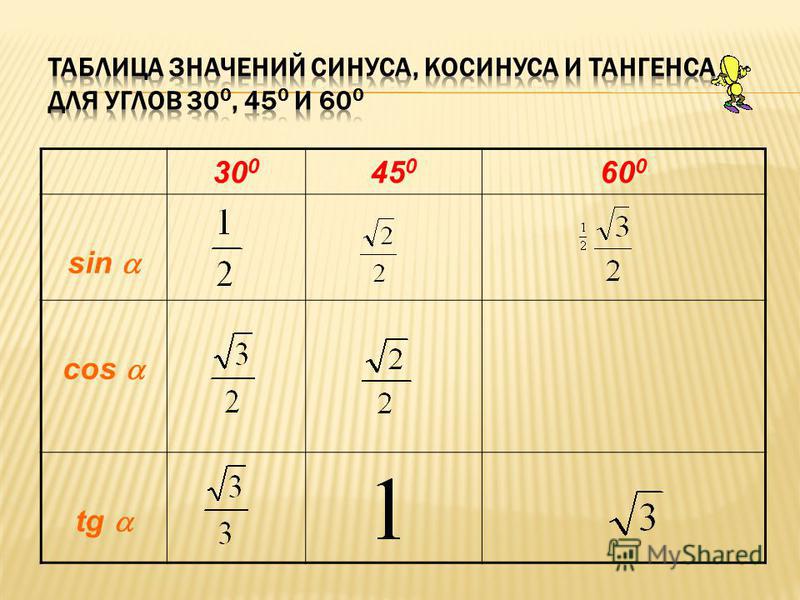
 Опишите единичный круг.
Опишите единичный круг.
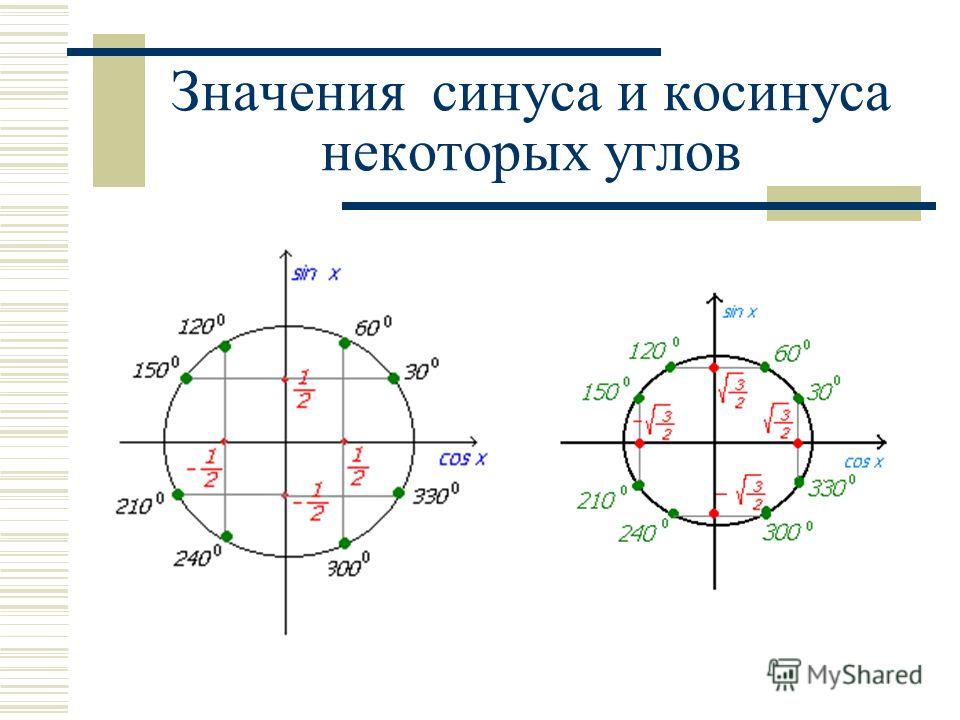


 Предположим, что карусель вращается против часовой стрелки.
Предположим, что карусель вращается против часовой стрелки. Автор : Колледж OpenStax. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]:1/Preface. Лицензия : CC BY: Атрибуция
Автор : Колледж OpenStax. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]:1/Preface. Лицензия : CC BY: Атрибуция