2 Пи р квадрат это формула • Вэб-шпаргалка для интернет предпринимателей!
Содержание
- 1 Содержание
- 2 История [ править | править код ]
- 3 Использование многоугольников [ править | править код ]
- 4 Доказательство Архимеда [ править | править код ]
- 4.1 Не больше [ править | править код ]
- 4.2 Не меньше [ править | править код ]
- 5 Доказательство перегруппировкой [ править | править код ]
- 6 Интегрирование [ править | править код ]
- 7 Быстрая аппроксимация [ править | править код ]
- 7.1 Метод удвоения Архимеда [ править | править код ]
- 7.2 Улучшение Снелла-Гюйгенса [ править | править код ]
- 7.3 Развитие формулы удваивания Архимеда [ править | править код ]
- 8 Аппроксимация случайными бросаниями [ править | править код ]
- 9 Конечная перегруппировка [ править | править код ]
- 10 Обобщения [ править | править код ]
- 10.1 Рекомендуем к прочтению
Для того чтобы найти площадь круга, существует формула, которую лучше запомнить:
S=πr 2 – это произведение числа пи на квадрат радиуса.
Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр или длину окружности .
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.
Данные онлайн калькуляторы предназначены для расчета площади круга. Вычисление происходит по приведенным выше геометрическим формулам, где π считается константой, округленной до 15-го знака после запятой.
Определение: Круг- это часть плоскости , ограниченная окружностью, круг является выпуклой фигурой.
Результат работы калькулятора также округляется до аналогичного разряда. Для использования калькулятора расчета площади круга необходимо ввести только значение радиуса, диаметра или окружности круга. Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.
Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.
Перевод радиан в градусы.
Ad = Ar * 180 / пи
Где Ad — угол в градусах, Ar — угол в радианах.
Перевод градусов в радианы.
Ar = Ad * пи / 180
Где Ad — угол в градусах, Ar — угол в радианах.
Длина окружности.
L = 2 * пи * R
Где L — длина окружности, R — радиус окружности.
Длина дуги окружности.
L = A * R
Где L — длина дуги окружности, R — радиус окружности, A — центральный угол, выраженный в радианах
Для окружности A = 2*пи (360 градусов), получим L = 2*пи*R.
Площадь треугольника.
S = (p * (p-a) * (p-b) * (p-c) ) 1/2
Где S — площадь треугольника, a, b, c — длины сторон,
p=(a+b+c)/2 — полупериметр.
Площадь круга.
S = пи * R 2
Где S — площадь круга, R — радиус круга.
Площадь сектора.
S = Ld * R/2 = (A * R 2 )/2
Где S — площадь сектора, R — радиус круга, Ld — длина дуги.
Площадь поверхности шара.
S = 4 * пи * R 2
Где S — площадь поверхности шара, R — радиус шара.
Площадь боковой поверхности цилиндра.
S = 2 * пи * R * H
Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.
Площадь полной поверхности цилиндра.
S = 2 * пи * R * H + 2 * пи * R 2
Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.
Площадь боковой поверхности конуса.
S = пи * R * L
Где S — площадь боковой поверхности конуса, R — радиус основания конуса, L — длина образующей конуса.
Площадь полной поверхности конуса.
S = пи * R * L + пи * R 2
Где S — площадь полной поверхности конуса, R — радиус основания конуса, L — длина образующей конуса.
Объем шара.
V = 4 / 3 * пи * R 3
Где V — объем шара, R — радиус шара.
Объем цилиндра.
V = пи * R 2 * H
Где V — объем цилиндра, R — радиус основания цилиндра, H — высота цилиндра.
Объем конуса.
V = пи * R * L = пи * R * H/cos (A/2) = пи * R * R/sin (A/2)
Где V — объем конуса, R — радиус основания конуса, L — длина образующей конуса, A — угол при вершине конуса.
Площадь круга с радиусом r равна πr 2 . Здесь символ π (греческая буква пи) обозначает константу, выражающую отношение длины окружности к её диаметру или площади круга к квадрату его радиуса. Поскольку площадь правильного многоугольника равна половине его периметра, умноженного на апофему (высоту), а правильные многоугольники стремятся к окружности при росте числа сторон, площадь круга равна половине длины окружности, умноженной на радиус (то есть 1 ⁄2 × 2πr × r).
Содержание
История [ править | править код ]
Современные математики могут получить площадь круга с помощью методов интегрирования или вещественного анализа. Однако площадь круга изучалась ещё в Древней Греции. Евдокс Книдский в пятом столетии до нашей эры обнаружил, что площади кругов пропорциональны квадратам их радиусов. [1] Великий математик Архимед использовал методы евклидовой геометрии, чтобы показать, что площадь внутри окружности равна площади прямоугольного треугольника, основание которого имеет длину окружности, а высота равна радиусу окружности, в своей книге Измерение круга [en] . Длина окружности равна 2 π r, а площадь треугольника равна половине основания на высоту, что даёт π r 2 . До Архимеда Гиппократ Хиосский первый показал, что площадь круга пропорциональна квадрату его диаметра в его попытках квадрирования гиппократовых луночек [2] Однако он не установил константу пропорциональности.
Использование многоугольников [ править | править код ]
Площадь правильного многоугольника равна половине периметра, умноженного на апофему (высоту). При увеличении числа сторон многоугольник стремится к окружности, а апофема стремится к радиусу. Это даёт основание считать, что площадь круга равна произведению половины длины окружности на радиус. [3]
При увеличении числа сторон многоугольник стремится к окружности, а апофема стремится к радиусу. Это даёт основание считать, что площадь круга равна произведению половины длины окружности на радиус. [3]
Доказательство Архимеда [ править | править код ]
Следуя Архимеду, сравним площадь круга с площадью прямоугольного треугольника, основание которого равно длине окружности, а высота равна радиусу. Если площадь круга не равна площади треугольника, она должна быть меньше или больше. Исключим оба варианта, что оставит только одну возможность — площади равны. Для доказательства будем использовать правильные многоугольники.
Не больше [ править | править код ]
Предположим, что площадь круга C больше площади треугольника T = 1 ⁄2cr. Пусть E означает превышение площади. Впишем [en] квадрат в окружность, чтобы все его четыре угла лежали на окружности. Между квадратом и окружностью четыре сегмента. Если общая их площадь G4 больше E, делим каждую дугу пополам, что превращает вписанный квадрат в восьмиугольник и образует восемь сегментов с меньшим общим зазором, G8. Продолжаем деление, пока общий зазор Gn не станет меньше E. Теперь площадь вписанного многоугольника Pn = C − Gn должна быть больше площади треугольника.
Продолжаем деление, пока общий зазор Gn не станет меньше E. Теперь площадь вписанного многоугольника Pn = C − Gn должна быть больше площади треугольника.
G_\P_&<>=C-G_\&<>>C-E\P_&<>>Tend>>»> E = C − T > G n P n = C − G n > C − E P n > T <displaystyle <eginE&<>=C-T\&<>>G_\P_&<>=C-G_\&<>>C-E\P_&<>>Tend>> G_\P_&<>=C-G_\&<>>C-E\P_&<>>Tend>»/>
Но это ведёт к противоречию. Для доказательства проведём высоту из центра окружности на середину стороны многоугольника, её длина h меньше радиуса окружности. Пусть каждая сторона многоугольника имеет длину s, сумма всех сторон составит ns, и эта величина меньше длины окружности. Площадь многоугольника состоит из n равных треугольников высоты h с основанием s, что даёт 1 ⁄2nhs.![]() Но h 1 ⁄2cr, получили противоречие.
Но h 1 ⁄2cr, получили противоречие.
Не меньше [ править | править код ]
Предположим, что площадь круга меньше площади треугольника. Пусть D означает разницу площадей. Описываем квадрат вокруг окружности, так что середины сторон лежат на ней. Если суммарный зазор между квадратом и окружностью G4 больше D, срезаем углы касательными, превращая квадрат в восьмиугольник и продолжаем такие отсечения пока площадь зазора не станет меньше D. Площадь многоугольника Pn должна быть меньше T.
G_\P_&<>=C+G_\&<> D = T − C > G n P n = C + G n C + D P n T <displaystyle <eginD&<>=T-C\&<>>G_\P_&<>=C+G_\&<> G_\P_&<>=C+G_\&<>
Это тоже приводит к противоречию. Каждый перпендикуляр, проведённый от центра круга к середине стороны, является радиусом, т.е. имеет длину r. А поскольку сумма сторон больше длины окружности, многоугольник из n одинаковых треугольников даст площадь, большую T. Снова получили противоречие.
Снова получили противоречие.
Таким образом, площадь круга в точности равна площади треугольника.
Доказательство перегруппировкой [ править | править код ]
Следуя Сато Мошуну [4] и Леонардо да Винчи [5] , мы можем использовать вписанные правильные многоугольники другим способом. Положим, мы вписали шестиугольник. Разрежем шестиугольник на шесть треугольников, делая сечения через центр. Два противоположных треугольника содержат общие диаметры. Сдвинем теперь треугольники, чтобы радиальные стороны стали смежными. Теперь пара треугольников образует параллелограмм, в котором стороны шестиугольника образуют две противоположные стороны длиной s. Две радиальные стороны становятся боковыми сторонами, а высота параллелограмма равна h (как в доказательстве Архимеда). Фактически, мы можем собрать все треугольники в один большой параллелограмм, располагая в ряд полученные параллелограммы (из двух треугольников). То же самое будет верно, если мы будем увеличивать число сторон. Для многоугольника с 2n сторонами параллелограмм будет иметь основание
Для многоугольника с 2n сторонами параллелограмм будет иметь основание
| многоугольник | параллелограмм | |||
|---|---|---|---|---|
| n | сторона | основание | высота | площадь |
| 4 | 1,4142136 | 2,8284271 | 0,7071068 | 2,0000000 |
| 6 | 1,0000000 | 3,0000000 | 0,8660254 | 2,5980762 |
| 8 | 0,7653669 | 3,0614675 | 0,9238795 | 2,8284271 |
| 10 | 0,6180340 | 3,0901699 | 0,9510565 | 2,9389263 |
| 12 | 0,5176381 | 3,1058285 | 0,9659258 | 3,0000000 |
| 14 | 0,4450419 | 3,1152931 | 0,9749279 | 3,0371862 |
| 16 | 0,3901806 | 3,1214452 | 0,9807853 | 3,0614675 |
| 96 | 0,0654382 | 3,1410320 | 0,9994646 | 3,1393502 |
| ∞ | 1/∞ | π | 1 | π |
Интегрирование [ править | править код ]
Используя интегралы, мы можем просуммировать площадь круга, разделив его на концентрические окружности подобно луковице. Площадь бесконечно тонкого «слоя» радиуса t будет равна 2 π t dt, то есть произведению длины окружности на толщину слоя. В результате получим элементарный интеграл для круга радиуса r.
Площадь бесконечно тонкого «слоя» радиуса t будет равна 2 π t dt, то есть произведению длины окружности на толщину слоя. В результате получим элементарный интеграл для круга радиуса r.
A r e a ( r ) = ∫ 0 r 2 π t d t = [ ( 2 π ) t 2 2 ] t = 0 r = π r 2 .
Визуализируем в R данные мониторинга температуры процессора Raspberry PI Zero W / Хабр
Для автоматического обновления данных в рамках небольшого проекта по визуализации погоды в регионах РФ используется скрипт на языке R, который выполняется по расписанию (ежедневно каждые три часа) на моём маленьком домашнем устройстве — Raspberry PI Zero W.
Маленький домашний помощник, работающий в режиме 24/7Исходные данные: cpu_temp.log
В этот раз мы будем визуализировать данные поминутного изменения температуры процессора Raspberry PI, которые сохраняются в специальным лог-файле c помощью bash-скрипта:
#!/bin/bash date +"%d.%m.%Y %T" | tr '\n' '\t' >> /home/pi/cpu_temp.log ; vcgencmd measure_temp| tr -d "temp=" | tr -d "'C" >> /home/pi/cpu_temp.log
Для запуска bash-скрипта по расписанию через cron была добавлена запись (каждую минуту):
*/1 * * * * ~/cpu_temp.sh
В результате выполнения скрипта данные о температуре процессора сохраняются в лог:
Эти данные мы и будем визуализировать с помощью R (cpu_temp.R), а на график вставим лого Raspberry PI: https://disk.yandex.ru/d/dP16Vwq9sH6RNQ
library(tidyverse)
library(readr)
library(geomtextpath)
library(glue)
library(here)
# Загружаем логотип Raspberry Pi
png <- magick::image_read("raspberrypi-logo.png")
img <- grid::rasterGrob(png, interpolate = TRUE)
# Загружаем данные (лог температуры)
cpu_temp <- read_delim(
"cpu_temp.log",
delim = "\t",
col_names = c("datetime", "cpu_temp"),
trim_ws = TRUE) %>%
mutate(datetime = lubridate::as_datetime(datetime,
"%d.%m.%Y %H:%M:%S",
tz = "Asia/Yekaterinburg"))
# Временной интервал для графика -- последние 3 часа из лога
last_datetime <- cpu_temp$datetime[length(cpu_temp$datetime)]
first_datetime <- last_datetime - lubridate::hours(3)
# Описательные для графика (мин, макс, среднее)
maxTempCPU <- max(cpu_temp$cpu_temp[between(cpu_temp$datetime,
first_datetime, last_datetime)])
minTempCPU <- min(cpu_temp$cpu_temp[between(cpu_temp$datetime,
first_datetime, last_datetime)])
meanTempCPU_period <-
round(mean(cpu_temp$cpu_temp[between(cpu_temp$datetime,
first_datetime, last_datetime)]), 1)
# для вставки лого
mt <- ceiling(max(cpu_temp$cpu_temp))
mt_min <- floor(min(cpu_temp$cpu_temp))
x_max <- last_datetime + lubridate::minutes(25)
x_min <- last_datetime + lubridate::minutes(10)
cpu_temp %>%
filter(between(datetime, first_datetime, last_datetime)) %>%
ggplot(aes(datetime, cpu_temp)) +
annotation_custom(
img,
ymin = mt ,
ymax = mt + 8.
25,
xmin = x_min,
xmax = x_max
) +
geom_texthline(
yintercept = mean(cpu_temp$cpu_temp),
size = 3.75,
linetype = "dashed",
linewidth = 0.25,
label = glue("Среднее за всё время: <b>{round(mean(cpu_temp$cpu_temp),1)}</b>°C"),
hjust = 0.985,
vjust = -0.2,
color = "gray70",
rich = TRUE
) +
geom_texthline(
yintercept = meanTempCPU_period,
size = 3.75,
linewidth = 0.25,
label = glue("Среднее за 3 часа: <b>{meanTempCPU_period}</b>°C"),
hjust = 0.985,
vjust = -0.2,
color = "gray70",
rich = TRUE
) +
geom_step(color = "gray10") +
scale_y_continuous(
breaks = seq(mt_min, mt + 1, 2),
limits = c(mt_min, mt + 1),
labels = c(as.character(seq(mt_min, mt - 1, 2)),
glue::glue("{mt + 1}°C"))
) +
scale_x_datetime(
"Время",
date_breaks = "30 min",
date_labels = "%H:%M",
expand = c(0.15, 0)
) +
labs(
title = "Температура процессора Raspberry Pi Zero W",
subtitle = glue(
"Поминутное изменение температуры за последние 3 часа\n",
"{format(first_datetime, format = '%d %b %H:%M')} - {format(last_datetime, format = '%H:%M')}",
" | Мин {minTempCPU}°C | Среднее {meanTempCPU_period}°C | Макс {maxTempCPU}°C"
),
x = "Время",
y = ""
) +
coord_cartesian(clip = "off") +
theme(text = element_text(family = "Open Sans"),
panel. background = element_blank(),
axis.title.x = element_text(size = 14),
plot.margin = margin(25, 30, 10, 12),
plot.title.position = "plot",
plot.subtitle = element_text(size = 12, color = "gray60"),
title = element_text(size = 16),
axis.text.y = element_text(size = 12),
axis.text.x = element_text(size = 12)
)
ggsave(
glue("img/cpu_temp_{format(last_datetime, '%d_%m_%Y_%H_%M')}.png"),
dpi = 300,
scale = 1.5
)
background = element_blank(),
axis.title.x = element_text(size = 14),
plot.margin = margin(25, 30, 10, 12),
plot.title.position = "plot",
plot.subtitle = element_text(size = 12, color = "gray60"),
title = element_text(size = 16),
axis.text.y = element_text(size = 12),
axis.text.x = element_text(size = 12)
)
ggsave(
glue("img/cpu_temp_{format(last_datetime, '%d_%m_%Y_%H_%M')}.png"),
dpi = 300,
scale = 1.5
)
Финальный график выглядит так:
Для запуска скрипта каждые три часа создадим задачу в cron:
0 */3 * * * Rscript /home/pi/cpu_temp/cpu_temp_pi.R
Полученный график будем отправлять себе в телеграм через телеграм-бота (см. отличный туториал по созданию ботов в R) для отправки личных уведомлений простой командой в конце нашего скрипта:
bot$sendPhoto(chat_id,
photo = glue("~/cpu_temp/img/cpu_temp_{format(last_datetime, '%d_%m_%Y_%H_%M')}.png")
)Сообщения с графиком от ботаPS: для быстрой установки R последней версии без необходимости компиляции основных пакетов рекомендую воспользоваться информацией из проекта R4Pi. 2
2
Оценивание показателей надёжности психометрических шкал теста neo PI-R при помощи численного ресамплинга Текст научной статьи по специальности «Прочие медицинские науки»
ОЦЕНИВАНИЕ ПОКАЗАТЕЛЕЙ НАДЁЖНОСТИ ПСИХОМЕТРИЧЕСКИХ ШКАЛ ТЕСТА NEO PI-R ПРИ ПОМОЩИ ЧИСЛЕННОГО РЕСАМПЛИНГА
© Кашпарова В.С.*, Синицын В.Ю/
Российский государственный аграрный университет -Московская сельскохозяйственная академия им. К.А. Тимирязева, г. Москва
Институт информационных наук и технологий безопасности Российского государственного гуманитарного университета, г. Москва
Сообщается о вычислении точечных и интервальных оценок различных показателей надёжности психометрических шкал теста NEO PI-R при помощи методов генерации повторных выборок.
Ключевые слова NEO PI-R, показатели надёжности психометрических шкал, альфа Кронбаха, коэффициенты Гуттмана, надёжность половинного расщепления, численный ресамплинг, рандомизация, бутст-реп, вычислительная среда R, язык программирования R.
Личностный опросник NEO PI-R создан с применением факторного анализа на основе широко известной концепции «Большая Пятерка» [1-2] и предназначен для оценки пяти общих аспектов личности (Нейротизм, Экстраверсия, Открытость опыту, Согласие и Сознательность). Каждый из этих доменов состоит из 6 личностных характеристик, измеряемых также средствами теста NEO PI-R. В России психолексические исследования показали, что имеется явное сходство между «Большой Пятеркой» и наиболее значимыми факторами, найденными на российской выборке [3].
Наши исследования связаны с русскоязычной версией теста NEO PI-R, подготовленной преподавателями и студентами РГГУ в 2000 году [4]. С использованием этой русскоязычной версии теста проведен опрос студентов РГГУ и подробно исследована структура данных анкетирования методами факторного анализа [5-6]. Факторы, ранжированные по убыванию процента объясняемой ими дисперсии, представляют собой Нейротизм, Сознательность, Экстраверсию, Согласие и Открытость опыту соответственно. Такая структура хорошо объясняется концепцией «Большой Пятерки». Порядок следования факторов, полученный нами для студентов РГГУ, отличается от последовательности факторов для американских респондентов [2], что согласуется с результатами А.Г. Шмелева и В.И. Похилько [3]. Для проверки
Такая структура хорошо объясняется концепцией «Большой Пятерки». Порядок следования факторов, полученный нами для студентов РГГУ, отличается от последовательности факторов для американских респондентов [2], что согласуется с результатами А.Г. Шмелева и В.И. Похилько [3]. Для проверки
* Профессор кафедры Иностранных языков Российского государственного аграрного университета — Московской сельскохозяйственной академии им. К.А. Тимирязева, кандидат филологических наук, доцент.
* Доцент кафедры Фундаментальной и прикладной математики Института информационных наук и технологий безопасности РГГУ, кандидат физико-математических наук, доцент.
устойчивости структуры «Большой Пятерки» были также использованы методы кластерного анализа. Получено множество классификаций подшкал теста NEO PI-R с помощью различных стратегий классификации и способов вычисления расстояния. С помощью пошаговых методов дискрими-нантного анализа решены задачи статистического распознавания подгрупп респондентов по полу, факультету и степени религиозной приверженности. Построены различные регрессионные модели, выявляющие взаимосвязи шкал, подшкал и элементов теста NEO PI-R, позволяющие прогнозировать одни психологические характеристики через другие.
Построены различные регрессионные модели, выявляющие взаимосвязи шкал, подшкал и элементов теста NEO PI-R, позволяющие прогнозировать одни психологические характеристики через другие.
Выполнен анализ надежности 5 шкал и 30 подшкал теста NEO PI-R, при котором показатели надежности были найдены как для всей группы респондентов, так и отдельно для юношей, девушек и студентов различных факультетов. Значения альфа Кронбаха для шкал находятся в пределах от 0,83 (Открытость опыту) до 0,92 (Нейротизм). Результаты вычислений позволили сделать вывод о том, что русскоязычная версия опросника NEO PI-R имеет хорошие характеристики надежности и является достаточно эффективным инструментом анализа общего психологического портрета личности [5-6].
Несмотря на то, что «Большая Пятерка» по существу не является частью какой-либо объяснительной модели когнитивной и эмоциональной активности, патологических процессов или процессов развития, важным и интересным представляется вопрос о построении новых психометрических шкал из элементов теста NEO PI-R, таких шкал, которые не были запланированы в первоначальной конструкции личностного опросника [7-9]. К настоящему моменту удалось построить из элементов опросника NEO PI-R множество шкал цинизма, подобных шкале Сноу [10]. Построенные шкалы содержат от шести до тридцати одного элемента теста NEO PI-R и имеют высокие показатели надежности (альфа Кронбаха от 0,82 до 0,85). При построении шкал цинизма было использовано специальное программное обеспечение, реализующее процедуры пошагового анализа надежности с включением и исключением элементов. Необходимо отметить, что в настоящий момент процедуры пошагового анализа надежности психометрических шкал не поддерживаются доступными статистическими системами, такими как SPSS и Statistica, поэтому были созданы программы на языке программирования R [14]. Актуальной также на наш взгляд является задача построения психометрических шкал личностных характеристик повинуемости [11-13].
К настоящему моменту удалось построить из элементов опросника NEO PI-R множество шкал цинизма, подобных шкале Сноу [10]. Построенные шкалы содержат от шести до тридцати одного элемента теста NEO PI-R и имеют высокие показатели надежности (альфа Кронбаха от 0,82 до 0,85). При построении шкал цинизма было использовано специальное программное обеспечение, реализующее процедуры пошагового анализа надежности с включением и исключением элементов. Необходимо отметить, что в настоящий момент процедуры пошагового анализа надежности психометрических шкал не поддерживаются доступными статистическими системами, такими как SPSS и Statistica, поэтому были созданы программы на языке программирования R [14]. Актуальной также на наш взгляд является задача построения психометрических шкал личностных характеристик повинуемости [11-13].
Для построения качественных новых психометрических шкал необходимо уметь более подробно исследовать их свойства надёжности как инструмента измерения. Известны различные характеристики надёжности психометрических шкал, которым посвящено большое количество работ классиков психометрики [15-18] и современных авторов [19]. Однако, интервальное оценивание характеристик надёжности психометрических шкал вызывает значительые трудности.
Однако, интервальное оценивание характеристик надёжности психометрических шкал вызывает значительые трудности.
Для отыскания и исследования доверительных интервалов таких характеристик надёжности как альфа Кронбаха, лямбда 6 Гуттмана и показатели надёжности половинного расщепления авторами были использованы современные методы численного ресамплинга: рандомизация, метод «складного ножа» и бутстреп [20]. Для всех шкал и подшкал теста NEO PI-R были найдены 95 % доверительные интервалы названных выше показателей надёжности. Для альфа Кронбаха и лямбда 6 Гуттмана результаты представлены в табл. 1. При вычислении генерировались псевдовыборки объёмом 1000 элементов каждая.
Таблица 1
Доверительные интервалы показателей надёжности (p = 0.95)
Название шкалы или подшкалы Nval Альфа Крошбаха L _ Me _ R Лямбда 6 Гуттмана L _ Me _ R
N Нейротизм 356 0.90 0.91 _ 0.92 0.94 0.95 0.95
N1 Тревожность 373 0.71 0.75 _ 0.79 0.71 _ 0.75 _ 0.79
N2 Враждебность 368 0. 64 0.69 _ 0.74 0.66 _ 0.71 _ 0.75
64 0.69 _ 0.74 0.66 _ 0.71 _ 0.75
№_Депрессивность 373 0.66 0.71 _ 0.75 0.67 _ 0.72 _ 0.75
N4 Застенчивость 371 0.54 0.60 _ 0.65 0.56 _ 0.62 _ 0.67
N5 Импульсивность 368 0.46 0.54 _ 0.61 0.47 _ 0.55 _ 0.62
N6 Уязвимость 373 0.70 0.75 _ 0.79 0.71 _ 0.76 _ 0.80
Е Экстраверсия 352 0.83 0.85 _ 0.87 0.90 _ 0.92 _ 0.93
Е1_Доброжелательность 372 0.67 0.71 _ 0.75 0.68 _ 0.73 _ 0.76
Е2 Общительность 370 0.64 0.69 _ 0.73 0.67 _ 0.71 _ 0.75
Е3 Настойчивость 370 0.70 0.75 _ 0.78 0.71 _ 0.75 _ 0.78
Е4 Активность 366 0.65 0.70 _ 0.74 0.67 _ 0.72 _ 0.76
Е5 Непоседливость 372 0.45 0.53 _ 0.60 0.47 _ 0.55 _ 0.62
Е6 Жизнерадостность 371 0.50 0.58 _ 0.65 0.55 _ 0.62 _ 0.68
О Открытость опыту 353 0.80 0.83 _ 0.85 0.88 _ 0.89 _ 0.91
О1 Фантазия 369 0.66 0.71 _ 0.75 0.69 _ 0.73 _ 0.77
О2 Эстетичность 370 0.72 0.76 _ 0.79 0.73 _ 0.76 _ 0.80
О3 Чувства 370 0.55 0.61 _ 0.67 0.57 0.62 0.67
О4_Действия 372 0.40 0.49 _ 0. 57 0.42 _ 0.50 _ 0.57
57 0.42 _ 0.50 _ 0.57
О5_Идеи 369 0.55 0.61 _ 0.67 0.59 _ 0.65 _ 0.69
О6 Ценности 371 0.30 0.41 _ 0.52 0.34 _ 0.44 _ 0.54
А Согласие 359 0.81 0.84 _ 0.87 0.89 _ 0.91 _ 0.92
А1_Доверие 371 0.74 0.78 _ 0.82 0.76 _ 0.79 _ 0.83
А2 Прямота 373 0.62 0.67 _ 0.72 0.63 _ 0.68 _ 0.72
А3 Альтруизм 369 0.59 0.66 _ 0.71 0.63 _ 0.69 _ 0.73
А4 Уступчивость 372 0.51 0.59 _ 0.65 0.52 _ 0.59 _ 0.65
А5 Скромность 370 0.66 0.71 _ 0.76 0.68 _ 0.73 _ 0.77
А6 Отзывчивость 373 0.41 0.50 _ 0.57 0.42 _ 0.50 _ 0.57
С Сознательность 354 0.88 0.89 _ 0.91 0.93 _ 0.94 _ 0.94
С1 Компетентность 372 0.53 0.61 _ 0.66 0.58 _ 0.64 _ 0.69
С2 Организованность 369 0.52 0.59 _ 0.65 0.55 _ 0.62 _ 0.67
С3 Ответственность 371 0.53 0.60 _ 0.65 0.57 _ 0.62 _ 0.67
С4 Целеустремленность 372 0.63 0.68 _ 0.72 0.64 _ 0.70 _ 0.73
С5 Самодисциплина 368 0.66 0.71 _ 0.76 0.67 _ 0.72 _ 0.76
С6 Осмотрительность 372 0.69 0.74 _ 0.78 0.71 0.75 0.79
Список литературы:
1. Costa P. T. Jr., & Widiger T. A. Personality disorders and the five-factor model of personality. — Washington, DC: American Psychological Association, 1994.
Costa P. T. Jr., & Widiger T. A. Personality disorders and the five-factor model of personality. — Washington, DC: American Psychological Association, 1994.
2. Piedmont R.L. The Revised NEO Personality Inventory: Clinical and Research Applications. — New York, Boston. Dordrecht, London: Kluwer Academic / Plenum Publishers, 1998.
3. Shmelyov A.G & Pokhil’ko VI. A taxonomy-oriented study of Russian personality-trait names // European Journal of Personality. — 1993. — № 7. — С. 1-17.
4. Воронов А.Я., Зайчикова Е.А., Синицын В.Ю. Некоторые кросс-культурные психологические различия российских и американских студентов // Ценностная и социальная идентичность российской гуманитарной интеллигенции: Тезисы всероссийской теоретико-методологической конференции. Москва, 26-27 апреля 2000 г. — М.: РГГУ 2000. — С. 120-123.
5. Синицын В.Ю., Кашпарова В.С. Психометрические свойства теста NEO PI-R и его применение для исследования психологического портрета студента // Психолого-педагогические исследования в системе образования: Материалы II Всероссийской научно-практической конференции: в 5 ч.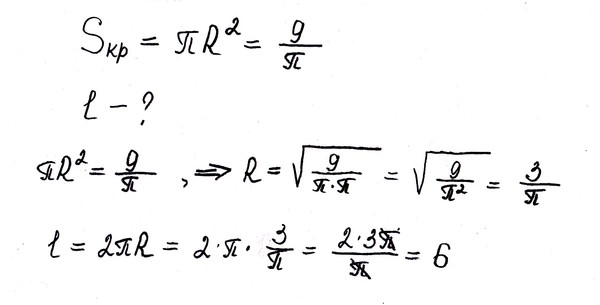 Ч. 4 / Акад. повышен. квалиф. и перепод. раб. обр.; Южно-Уральск. гос. ун-т; Че-ляб. гос. пед. ун-т; Челяб. ин-т доп. проф.-пед. образ. — М., Челябинск, 2004. -C. 31-34.
Ч. 4 / Акад. повышен. квалиф. и перепод. раб. обр.; Южно-Уральск. гос. ун-т; Че-ляб. гос. пед. ун-т; Челяб. ин-т доп. проф.-пед. образ. — М., Челябинск, 2004. -C. 31-34.
6. Воронов А.Я., Кашпарова В.С., Синицын В.Ю. Тест NEO PI-R как инструмент исследования психологического портрета студента // Материалы XVIII международной конференции «Применение новых технологий в образовании» («ИТ0-Троицк-2007»), 27-28 июня 2007 г. — Троицк, 2007. -С. 314 — 316.
7. Боровиков Д.В., Синицын В.Ю. От психолексических исследований и пятифакторной модели личности к статистическому конструированию новых психометрических шкал // Математика и её приложения: Сборник трудов IV Международной научной конференции «Математика. Образование. Культура»: в 3-х ч. Ч. 1, 21-24 апреля 2009 г., Россия, г. Тольятти. — Тольятти: ТГУ 2009. — С. 65-69.
8. Боровиков Д.В., Синицын В.Ю. Применение пошаговых методов анализа надёжности для построения новых психометрических шкал // Обозрение прикладной и промышленной математики. — М., 2009. — Т. 16, Вып. 3. -С. 455-456.
— М., 2009. — Т. 16, Вып. 3. -С. 455-456.
9. Кашпарова В.С., Синицын В.Ю. О построении новых психометрических шкал на основе многошкального личностного опросника NEO PI-R // Наука и современность. — 2013. — № 26-1. — С. 180-183.
10. Snow J. The Correlates and Psychometric Properties of a Scale of Cynicism. Thesis submitted to the Faculty of the Graduate School of the University of Maryland in partial fulfillment of the requirements for the degree of Master of Arts, 1995.
11. Воронов А.Я., Синицын В.Ю. Авторитаризм и цинизм студентов РГГУ как индикаторы ценностей молодого поколения российской гуманитарной интеллигенции // Ценностная и социальная идентичность российской гуманитарной интеллигенции: Тезисы всероссийской теоретико-методологической конференции, 26-27 апреля 2000 г. — М.: РГГУ 2000. — С. 115-117.
12. Воронов А.Я., Пионтковский Д.И., Синицын В.Ю. Роль некоторых личностных и демографических характеристик повинуемости официальной власти в современной России: ситуация призыва в армию осенью 1996 г. // «Новая» Россия: власть права и право власти: Материалы Российской межвузовской научной конференции, 28-29 ноября 1997 г. — М.: РГГУ, 1997. -С. 101-106.
// «Новая» Россия: власть права и право власти: Материалы Российской межвузовской научной конференции, 28-29 ноября 1997 г. — М.: РГГУ, 1997. -С. 101-106.
13. Воронов А.Я., Пионтковский Д.И., Синицын В.Ю. О повинуемости и сопротивлении власти в современной России (1990-е годы) // Объединенный научный журнал. — М.: Фонд правовых исследований, 2007. — № 8 (196). -С. 22-27.
14. Официальный сайт проекта R [Электронный ресурс]. — Режим доступа: http://www.r-project.org.
15. Cronbach L.J. Coefficient alpha and the internal strucuture of tests // Psy-chometrika. — 1951. — № 16. — P. 297-334.
16. Guttman L. A basis for analyzing test-retest reliability // Psychometrika. -1945. — № 10 (4). — P. 255-282.
17. Revelle W. Hierarchical cluster-analysis and the internal structure of tests // Multivariate Behavioral Research. — 1979. — № 14 (1). — P. 57-74.
18. Ten Berge J. M. F. & Zegers F. E. A series of lower bounds to the reliability of a test // Psychometrika. — 1978. — № 43 (4). — P. 575-579.
— 1978. — № 43 (4). — P. 575-579.
19. Zinbarg R. E., Revelle W., Yovel I. & Li W. Cronbach’s a, Revelle’s Д and McDonald’s m_h: Their relations with each other and two alternative conceptualizations of reliability // Psychometrika. — 2005. — № 70 (1). — P. 123-133.
20. Шитиков В.К., Розенберг Г.С. Рандомизация и бутстреп: статистический анализ в биологии и экологии с использованием R. — Тольятти: Кассандра, 2013. — 314 c.
Число Пи — значение, история, кто придумал
Все окружности похожи
Если сравнить окружности отличных друг от друга размеров, то можно заметить следующее: размеры разных окружностей пропорциональны. А это значит, что при увеличении диаметра окружности в некоторое количество раз, увеличивается и длина этой окружности в такое же количество раз. Математически это записать можно так:
| C2 | |||
| = | |||
| d1 | d2 | (1) |
где C1 и С2 – длины двух разных окружностей, а d1 и d2 – их диаметры.
Это соотношение работает при наличии коэффициента пропорциональности – уже знакомой нам константы π. Из отношения (1) можно сделать вывод: длина окружности C равна произведению диаметра этой окружности на независящий от окружности коэффициент пропорциональности π:
C = πd.
Также эту формулу можно записать в ином виде, выразив диаметр d через радиус R данной окружности:
С = 2πR.
Как раз эта формула и является проводником в мир окружностей для семиклассников.
Еще с древности люди пытались установить значение этой константы. Так, например, жители Месопотамии вычисляли площадь круга по формуле:
| C2 | |||
| S | = | , | |
| 12 |
где S – площадь круга, C – длина окружности (круга).
| (2πR)2 | ||
| πR2 | = | |
| 12 |
, откуда π = 3.
В древнем Египте значение для π было точнее. В 2000-1700 годах до нашей эры писец, именуемый Ахмесом, составил папирус, в котором мы находим рецепты разрешения различных практических задач. Так, например, для нахождения площади круга он использует формулу:
| 8 | 2 | |||||
| S | = | ( | d | ) | ||
| 9 |
Из каких соображений он получил эту формулу? – Неизвестно. Вероятно, на основе своих наблюдений, впрочем, как это делали и другие древние философы.
Вероятно, на основе своих наблюдений, впрочем, как это делали и другие древние философы.
По стопам Архимеда
— Какое из двух числе больше 22/7 или 3.14 ?
— Они равны.
— Почему ?
— Каждое из них равно π.
А. А. Власов. Из Экзаменационного билета.
Некоторы полагают, что дробь 22/7 и чисо π тождественно равны. Но это является заблуждением. Помимо вышеприведенного неверного ответа на экзамене (см. эпиграф) к этой группе можно также добавить одну весьма занимательную головоломку. Задание гласит: «переложите одну спичку так, чтобы равенство стало верным».
Решение будет таковым: нужно образовать «крышу» для двух вертикальных спичек слева, используя одну из вертикальных спичек в знаменателе справа. Получится визуальное изображение буквы π.
Многие знают, что приближение π = 22/7 определил древнегреческий математик Архимед. В честь этого часто такое приближение называют «Архимедовым» числом. Архимеду удалось не только установить приближенное значение для π, но также найти точность этого приближения, а именно – найти узкий числовой промежуток, которому принадлежит значение π. В одной из своих работ Архимед доказывает цепь неравенств, которая на современный лад выглядела бы так:
В одной из своих работ Архимед доказывает цепь неравенств, которая на современный лад выглядела бы так:
| 10 | 6336 | 14688 | 1 | |||||||||
| 3 | < | < | π | < | < | 3 | ||||||
| 71 | 1 | 1 | 7 | |||||||||
| 2017 | 4673 | |||||||||||
| 4 | 2 | |||||||||||
можно записать проще: 3,140 909 < π < 3,1 428 265. ..
..
Как видим из неравенств, Архимед нашел довольно-таки точное значение с точностью до 0,002. Самое удивительно то, что он нашел два первых знака после запятой: 3,14… Именно такое значение чаще всего мы используем в несложных расчетах.
Практическое применение
Едут двое в поезде:
− Вот смотри, рельсы прямые, колеса круглые.
Откуда же стук?
− Как откуда? Колеса-то круглые, а площадь
круга пи эр квадрат, вот квадрат-то и стучит!
Как правило, знакомятся с этим удивительным числом в 6-7 классе, но более основательно им занимаются к концу 8-го класса. В этой части статьи мы приведем основные и самые важные формулы, которые пригодятся вам в решении геометрических задач, только для начала условимся принимать π за 3,14 для удобства подсчета.
Пожалуй, самая известная формула среди школьников, в которой используется π, это – формула длины и площади окружности. Первая – формула площади круга – записывается так:
| πD2 | |
| S=πR2= | |
| 4 |
где S – площадь окружности, R – ее радиус, D – диаметр окружности.
Длина окружности, или, как ее иногда называют, периметр окружности, вычисляют по формуле:
С = 2 πR = πd,
где C – длина окружности, R – радиус, d – диаметр окружности.
Понятно, что диаметр d равен двум радиусам R.
Из формулы длины окружности можно легко найти радиус окружности:
| C | C | ||
| R= | = | ||
| 2π | d |
Обозначения для этих формул остаются те же.
Диаметр окружности можно найти по формуле:
| C | ||
| D= | =2R | |
| π |
где D – диаметр, С – длина окружности, R – радиус окружности.
Это базовые формулы, знать которые должен каждый ученик. Также иногда приходится вычислять площадь не всей окружности, а только ее части – сектора. Поэтому представляем вам её – формулу для вычисления площади сектора окружности. Выглядит она так:
| α | |||
| S | = | πR2 | |
| 360˚ |
где S – площадь сектора, R – радиус окружности, α – центральный угол в градусах.
Такое загадочное 3,14
И правда, оно загадочно. Потому что в честь этих магических цифр устраивают праздники, снимают фильмы, проводят общественные акции, пишут стихи и многое другое.
Например, в 1998 году вышел фильм американского режиссера Даррена Аронофски под названием «Пи». Фильм получил множество наград.
Каждый год 14 марта в 1:59:26 люди, интересующиеся математикой, празднуют «День числа Пи». К празднику люди подготавливают круглый торт, усаживаются за круглый стол и обсуждают число Пи, решают задачи и головоломки, связанные с Пи.
Вниманием это удивительное число не обошли и поэты, неизвестный написал:
Надо только постараться и запомнить всё как есть – три, четырнадцать, пятнадцать, девяносто два и шесть.
Давайте развлечемся!
Вашему вниманию предлагаются интересные ребусы с числом Пи. Разгадайте слова, какие зашифрованы ниже.
1. π р
2. π L
3. π k
Ответы: 1. Пир; 2. Надпил; 3. Писк.
Число Пи — справочные материалы
Чему равно число Пи
Как запомнить число Пи
Число Пи в Excel
Число Пи на клавиатуре и в Word
Фотографии числа Пи
2 пи r формула
Вход на сайт. Имя или Email:. Запомнить меня. Регистрация нового пользователя Забыли пароль?
Имя или Email:. Запомнить меня. Регистрация нового пользователя Забыли пароль?
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Расчет площади круга
- Длина окружности и площадь круга
- Площадь круга
- Длина окружности
- Периметр окружности
- Длина окружности круга
- Формулы перевода градусов в радианы, длин, площадей и объемов основных геометрических фигур
- Онлайн калькулятор.
Площадь круга
- 24. Длина окружности и площадь круга. Правила
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Что такое число Пи? Кто его изобрел и почему оно так важно
Расчет площади круга
Число Пи — математическая константа, которая выражает отношение длины окружности к её диаметру. Равна приблизительно 3, Некоторые могут подумать, раз это отношение обозначается греческой буквой, стало быть, его вывел некий греческий математик. На самом деле об этом история умалчивает.
Зато имеются данные о том, кто впервые использовал в своих работах это обозначение. Если сравнить окружности отличных друг от друга размеров, то можно заметить следующее: размеры разных окружностей пропорциональны.
А это значит, что при увеличении диаметра окружности в некоторое количество раз, увеличивается и длина этой окружности в такое же количество раз.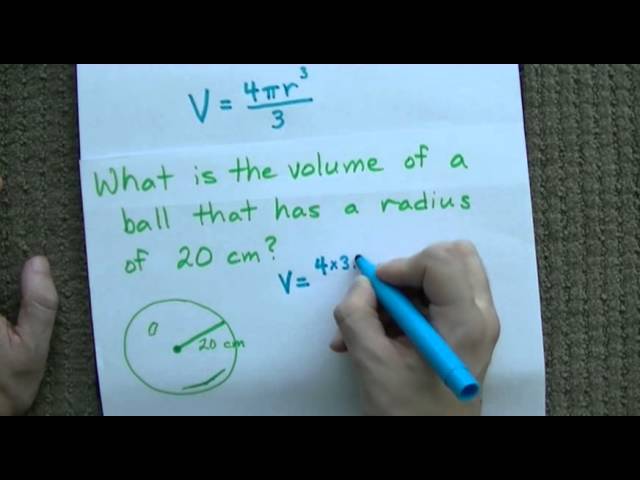 Математически это записать можно так:. Также эту формулу можно записать в ином виде, выразив диаметр d через радиус R данной окружности:. Еще с древности люди пытались установить значение этой константы.
Математически это записать можно так:. Также эту формулу можно записать в ином виде, выразив диаметр d через радиус R данной окружности:. Еще с древности люди пытались установить значение этой константы.
Так, например, жители Месопотамии вычисляли площадь круга по формуле:. В годах до нашей эры писец, именуемый Ахмесом, составил папирус, в котором мы находим рецепты разрешения различных практических задач. Так, например, для нахождения площади круга он использует формулу:.
Из каких соображений он получил эту формулу? Вероятно, на основе своих наблюдений, впрочем, как это делали и другие древние философы. Из Экзаменационного билета. Но это является заблуждением.
Помимо вышеприведенного неверного ответа на экзамене см. Задание гласит: «переложите одну спичку так, чтобы равенство стало верным». Решение будет таковым: нужно образовать «крышу» для двух вертикальных спичек слева, используя одну из вертикальных спичек в знаменателе справа. В честь этого часто такое приближение называют «Архимедовым» числом. В одной из своих работ Архимед доказывает цепь неравенств, которая на современный лад выглядела бы так:. Как видим из неравенств, Архимед нашел довольно-таки точное значение с точностью до 0, Именно такое значение чаще всего мы используем в несложных расчетах.
В одной из своих работ Архимед доказывает цепь неравенств, которая на современный лад выглядела бы так:. Как видим из неравенств, Архимед нашел довольно-таки точное значение с точностью до 0, Именно такое значение чаще всего мы используем в несложных расчетах.
Откуда же стук? Колеса-то круглые, а площадь круга пи эр квадрат, вот квадрат-то и стучит! Как правило, знакомятся с этим удивительным числом в классе, но более основательно им занимаются к концу 8-го класса. Первая — формула площади круга — записывается так:.
Это базовые формулы, знать которые должен каждый ученик. Также иногда приходится вычислять площадь не всей окружности, а только ее части — сектора. Поэтому представляем вам её — формулу для вычисления площади сектора окружности. Выглядит она так:.
И правда, оно загадочно. Потому что в честь этих магических цифр устраивают праздники, снимают фильмы, проводят общественные акции, пишут стихи и многое другое. Например, в году вышел фильм американского режиссера Даррена Аронофски под названием «Пи». Фильм получил множество наград. Каждый год 14 марта в люди, интересующиеся математикой, празднуют «День числа Пи». К празднику люди подготавливают круглый торт, усаживаются за круглый стол и обсуждают число Пи, решают задачи и головоломки, связанные с Пи.
Фильм получил множество наград. Каждый год 14 марта в люди, интересующиеся математикой, празднуют «День числа Пи». К празднику люди подготавливают круглый торт, усаживаются за круглый стол и обсуждают число Пи, решают задачи и головоломки, связанные с Пи.
Вниманием это удивительное число не обошли и поэты, неизвестный написал: Надо только постараться и запомнить всё как есть — три, четырнадцать, пятнадцать, девяносто два и шесть. Вашему вниманию предлагаются интересные ребусы с числом Пи. Разгадайте слова, какие зашифрованы ниже. Число Пи на клавиатуре и в Word. Число Пи — значение, история, кто придумал Число Пи — математическая константа, которая выражает отношение длины окружности к её диаметру.
Как раз эта формула и является проводником в мир окружностей для семиклассников. Понятно, что диаметр d равен двум радиусам R. Такое загадочное 3,14 И правда, оно загадочно. Давайте развлечемся!
Пир; 2. Надпил; 3. Добавьте Ваш комментарий.
Длина окружности и площадь круга
На нашем сайте собрано более бесплатных онлайн калькуляторов по математике, геометрии и физике. Не можете решить контрольную?! Мы поможем! Более 20 авторов выполнят вашу работу от руб!
Не можете решить контрольную?! Мы поможем! Более 20 авторов выполнят вашу работу от руб!
Пожалуй, самые важные в изучении тригонометрии формулы — sin пи на 2 = cos(2π) = 1, и sin(3 пи на 2) = cos(π) = –1. Я не только.
Площадь круга
Круг — геометрическое место точек плоскости, расстояние от которых до данной точки не больше, чем заданное ненулевое. Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки центра , лежащей в той же плоскости, что и кривая. Также круг можно определить как часть плоскости, ограниченную окружностью. Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади круга выражается числом заключающихся в него квадратных единиц. Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина. Копирование материалов с сайта возможно только с разрешения администрации портала и при наличие активной ссылки на источник.
Длина окружности
Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в 3,14 раза. Следовательно, формула длины окружности будет выглядеть так:. Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга. Формула нахождения площади круга :.
Окружность — это замкнутая линия, причем расстояние от любой точки, находящейся на этой линии, до центра окружности одинаково. Кругом является внутренняя часть окружности.
Периметр окружности
Круг — это геометрическая фигура, где точки плоскости имеют расстояние до определенной точки не более, чем заданное. Его окружность представляет собой замкнутую плоскую кривую, в которой все точки удалены на одинаковое расстояние от центра. Зачастую круг называют частью плоскости, которая ограничивается окружностью. Для абсолютно любой окружности ее длина и диаметр одинаковы. Наш калькулятор поможет вам вычислить периметр этой фигуры при помощи значения радиуса.
Длина окружности круга
Впишем в окружность правильный — угольник, пусть его периметр равен. Удвоим число его сторон, т. На рисунке удвоение сторон показано на примере стороны. При переходе от первого многоугольника ко второму каждая сторона заменяется суммой двух и хотя и меньших сторон, но , поэтому. Продолжая неограниченно процесс удвоения числа сторон, получим бесконечную возрастающую числовую последовательность периметров правильных вписанных в окружность многоугольников с общим членом :. Нетрудно представить себе, что при каждом новом удвоении числа сторон приращение периметра будет все меньшим и меньшим, то есть величина этого приращения стремится к нулю, а поэтому сам периметр при неограниченном увеличении стремится к некоторому постоянному числу — пределу.
Это число принято обозначать греческой буквой π («пи»). У этого числа за Площадь круга определяется по формуле S = π ⋅ R 2. R_all-audio.pro
Формулы перевода градусов в радианы, длин, площадей и объемов основных геометрических фигур
В этой статье: По длине окружности По площади круга По диаметру По площади сектора и центральному углу 6 Источники. Радиус круга — это расстояние от центра круга до любой точки, которая лежит на внешней окружности круга. В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту. Категории: Геометрия.
Радиус круга — это расстояние от центра круга до любой точки, которая лежит на внешней окружности круга. В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту. Категории: Геометрия.
Онлайн калькулятор. Площадь круга
ВИДЕО ПО ТЕМЕ: Сборник НОВЫХ серий #2017 — Смешарики. ПИН — код -Познавательные мультфильмы
Используя этот онлайн калькулятор, вы сможете найти площадь круга зная его радиус, диаметр или длину окружности. Воспользовавшись онлайн калькулятором для вычисления площади круга, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал. В онлайн калькулятор вводить можно числа или дроби 3, 0. Более подробно читайте в правилах ввода чисел. Если у вас возникли трудности с преобразованием единиц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади.
Пожалуй, в ответе на этот вопрос мне поможет пицца.
24. Длина окружности и площадь круга. Правила
Современные математики могут получить площадь круга с помощью методов интегрирования или вещественного анализа. Однако площадь круга изучалась ещё в Древней Греции. Евдокс Книдский в пятом столетии до нашей эры обнаружил, что площади кругов пропорциональны квадратам их радиусов. До Архимеда Гиппократ Хиосский первый показал, что площадь круга пропорциональна квадрату его диаметра в его попытках квадрирования гиппократовых луночек [2] Однако он не установил константу пропорциональности. Площадь правильного многоугольника равна половине периметра, умноженного на апофему высоту. При увеличении числа сторон многоугольник стремится к окружности, а апофема стремится к радиусу.
Круг — это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность. Отрезок, который соединяет центр круга с точками его окружности, называется радиусом.
Существуют также рабочие листы, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое pi r в квадрате?
Пир в квадрате — это формула площади круга.
Это связано с тем, что существует определенная зависимость между радиусом ( r ) круга и его площадью. 9{2}(1 . \mathrm{d} . \mathrm{p}) \end{выровнено}
Что такое pi r в квадрате?
Что такое пи?
\pi (произносится как пи) — греческая буква, обозначающая отношение длины окружности к ее диаметру.
Для всех кругов, если вы разделите длину окружности на длину диаметра, вы получите значение \pi.
Примечание : \pi — это иррациональное число, что означает, что его нельзя записать в виде дроби. Это неповторяющаяся десятичная дробь, имеющая приблизительное значение 3,1415…9.х ?], см. ниже.
Это неповторяющаяся десятичная дробь, имеющая приблизительное значение 3,1415…9.х ?], см. ниже.
Иногда на вопрос может потребоваться дать ответ «в пересчете на \pi».
3 \times \pi = 3 \pi (это ответ в виде числа pi)
5 \times \pi = 5 \pi (это ответ в виде числа pi)
17 \times \pi = 53,407… (это ответ не в терминах пи)
Как использовать пи в квадрате
Чтобы вычислить площадь круга:
- Найдите радиус круга. 92} для вычисления площади круга.
- Дайте ответ четко, используя правильные единицы измерения.
Как использовать пи г в квадрате
Рабочий лист в квадрате pi r
Получите бесплатный рабочий лист в квадрате pi r, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКОРО
ИксРабочий лист в квадрате pi r
Получите бесплатный рабочий лист в квадрате pi r, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы. 92
Включает рассуждения и прикладные вопросы. 92
Пример 5: расчет площади круга по длине окружности
Окружность имеет длину 12 см.
Вычислите его площадь.
Дайте ответ с точностью до 2 знаков после запятой.
Найдите радиус окружности.
Вопрос дает длину окружности, которая равна 2\pi r
Это означает, что вы можете найти радиус окружности по окружности, см. ниже:
Помните, что вопрос требует, чтобы вы дали ответ «в терминах \pi ’ ». Поэтому вы оставляете ответ в виде 10000 \pi
10000\pi
Площадь целого круга диаметром 20м. Вам нужна только площадь полукруга.
Полукруг имеет половину площади полного круга, поэтому ответ нужно разделить на два. Не забудьте сохранить его с точки зрения \pi .
\begin{aligned} &10000 \pi \div 2 \\\\ &5000\pi \end{aligned}
Помните, что вопрос требует, чтобы вы дали ответ на вопрос ‘в терминах 4 \pi ‘ . Поэтому вы оставляете ответ в виде 5000 \pi 92
Распространенные заблуждения
- Без использования радиуса
Чтобы найти площадь круга по формуле, необходимо знать радиус.
Вопрос может не дать вам радиус напрямую, поэтому нам нужно использовать предоставленную информацию, чтобы сначала найти радиус.
- Не включая правильные единицы измерения
При работе с площадью вы всегда должны указывать правильные единицы измерения в квадрате
92 и т. д.- Неверное округление
Эти вопросы часто предполагают округление. Вы должны округлять только в конце вопроса и до указанного количества знаков после запятой.
- Не дается ответ в пересчете на \pi
Иногда на вопрос может быть предложено дать ответ «в пересчете на \pi». Это означает, что вы не даете числовой ответ, который получается при умножении на \pi.
Напр.
6 \times \pi = 6\pi (это ответ в виде пи)
6 \times \pi = 18,8495592… (этот ответ не в виде пи)
- Неправильное использование калькулятора
Убедитесь, что вы знаете, как правильно использовать кнопку \pi на вашем калькуляторе.
- Градусы и радианы
Мы также можем измерять углы в радианах, однако на GCSE мы всегда будем измерять углы в градусах.
Практика ответов на вопросы в квадрате 92
\pi \times 10 \times 10 равно 314,15
…
Этот ответ правильно округлен до 1 знака после запятой и имеет правильные единицы измерения
Пир в квадрате Вопросы GCSE
1. Радиус круга равен 4,5 см
Определите площадь круга
Дайте правильный ответ до 3-х значащих цифр
(3 балла)
9000 Показать 9000 Показать ответ \pi \times 4. 5 \times 4.5 или 63,617… 92
5 \times 4.5 или 63,617… 92
Все еще застряли?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Узнайте больше о нашей программе повторения GCSE по математике.
Как доказать, что площадь круга равна pi r в квадрате?
Окружность – это замкнутая двумерная фигура, центр которой находится в том месте, где все точки плоскости равноудалены от нее. Каждая линия, проходящая через окружность, образует линию симметрии отражения. В дополнение к этому, он имеет вращательную симметрию вокруг центра для каждого угла. Некоторыми примерами кругов являются колеса, пицца, круглая площадка и т. д.
Свойства окружностей
Окружность характеризуется следующим набором свойств:
- Внешняя линия окружности расположена на равном расстоянии от центра.

- Диаметр круга делит его на две равные части.
- Окружности с равными радиусами конгруэнтны друг другу.
- Круги с разными радиусами похожи друг на друга.
- Диаметр окружности называется наибольшей хордой и равен удвоенному радиусу.
Части круга
Окружность представляет собой совокупность точек, расположенных на фиксированном расстоянии от центра окружности. Площадь круга считается мерой пространства или области, заключенной внутри круга.
- Радиус: Расстояние от центра до точки на границе. Обозначается буквой «r» или «R». Используется для определения длины окружности.
- Диаметр: Линия, проходящая через центр и конечные точки, лежащие на окружности. Обозначается буквой «d» или «D».
Формула диаметра: Формула диаметра круга представлена как удвоенный его радиус.
Диаметр = 2 × радиус
Другими словами,
D = 2R или D = 2R
Если диаметр круга известен, его Radius может быть вычислен как:
7777777777777777.r = d/2 или R = D/2
Как доказать, что площадь круга равна pi r в квадрате?
Доказательство:
Круг можно легко разделить на 16 равных секторов, расположенных следующим образом. Все сектора равны по площади. Это означает, что все сектора имеют одинаковую длину дуги. Если число секторов, вырезанных из круга, увеличить, параллелограмм в конечном итоге будет выглядеть как прямоугольник с длиной, эквивалентной πr, и шириной, эквивалентной r.
Площадь прямоугольника (А) также считается площадью круга. Следовательно,
- A = πr×r
- A = πr 2
Примеры вопросов
Вопрос 1. Найдите площадь круга, если его радиус равен 10 см? Используйте π = 3,14.
Решение:
Здесь нам нужно найти площадь круга,
Дано:
Радиус круга = 10 см
Как мы знаем, что
Площадь круга = πr 2
Площадь круга = 3,14 × 10 × 10
Площадь круга = 314 см .
Вопрос 2. Если диаметр круга равен 24 м, то найдите площадь круга? Используйте π = 3,14
Решение:
Здесь нам нужно найти площадь круга,
Дано:
Диаметр круга = 24 м
Радиус круга = 24/2
Радиус круга = 12 м
Как мы знаем, что
Площадь круга = πr 2
Площадь круга = 3,14 × 12 × 050 90 90 90 Площадь круга = 452,16 м 2
Следовательно,
Площадь круга равна 452,16 м 2 .
Вопрос 3. Если площадь круга 3850 см 2 то найдите радиус круга? Используйте π = 22/7.
Решение:
Здесь мы должны найти радиус круга, используя его площадь.
Дано:
Площадь круга = 3850 см 2
Как мы знаем, что
Площадь круга = πr 2
Область круга = 22/7 × R 2
.
3850 = 22/7 × r 2
r 2 = 3850 × 7/22
r 2 = 1225
r = √03 05 см 9 03 05 9 00005
Следовательно,
Радиус круга равен 35 см, если площадь круга равна 3850 см 2 .
Вопрос 4. Найти стоимость коврового покрытия круглого гимнастического зала радиусом 33 м из расчета 350 руб./м 2 ? Используйте π = 3,14.
Решение:
Здесь нужно найти стоимость коврового покрытия гимнастического зала,
Дано:
Радиус круглого гимнастического зала = 33 м
Поскольку мы знаем, что
Площадь круга = πr 2
Площадь круга = 3,14 × 33 2
Площадь круга = 3,14 × 9,33 × 34
5 Площадь круга M 2
Сейчас
Стоимость коврового покрытия = 350 × площадь круговой гимнастической зала
Стоимость коврового покрытия = ₹ 350 × 3419,46
Стоимость коврового покрытия = ₹ 1196811
,
Стоимость коврового покрытия = ₹ 1196811
,
Стоимость коврового покрытия = ₹ 1196811
,
Стоимость коврового покрытия = ₹ 1196811
,
.
2$. В чем проблема этого рассуждения?
Линии, расположенные рядом друг с другом, будут идти только прямо, как прямоугольник, поэтому вам придется развести их на одном из концов, чтобы получить круг, поэтому я думаю, что проблема где-то здесь. Может ли кто-нибудь объяснить проблему в рассуждениях выше?
- исчисление
- геометрия
- интуиция
- круги
- поддельные доказательства
$\endgroup$
7
$\begingroup$
92$. Но посмотрите, что произойдет, если вы сделаете так:Проблема в том, что полосы перекрываются, поэтому общая площадь $n$ полос больше площади круга. Если вы запустите анимацию (при необходимости перезагрузив страницу), вы можете убедиться, что в ограничении $n\rightarrow\infty$ половина каждой полосы вносит свой вклад в конечную область. (Обратите внимание, что при добавлении полос против часовой стрелки примерно половина каждой полосы закрывается последующими полосами.
92$.)
$\endgroup$
2
$\begingroup$
Проблема с этим рассуждением заключается в том, что при отображении площади прямоугольника путем деления длины и высоты прямоугольника на единицы измерения длины и высоты образуют квадраты. Вращение радиуса вокруг круга на заданное число градусов для разделения круга не дает квадратов; эти ломтики больше похожи на треугольники. Напомним, что площадь треугольника равна $\dfrac{bh}{2}$; математика немного сложнее, но вы можете провести здесь параллель площади круга и прямоугольника. При прочих равных условиях прямоугольник в два раза больше площади треугольника, поэтому площадь фигуры, разделенной на несколько конгруэнтных треугольников, будет равна половине площади фигуры, разделенной на такое же количество прямоугольников той же длины и высоты, что и треугольники.
Фактическая математика для доказательства площади круга очень тесно связана с этим, но включает дополнительную концепцию исчисления:
Для любого произвольного $n$ нарисуйте $n$-угольник (шестиугольник, восьмиугольник, и т.
д.) по окружности радиуса $r$. Каждая сторона этой фигуры будет иметь длину $s$ и $s*n > 2\pi r$; периметр n-угольника будет больше длины окружности (напомним, что $\pi = \dfrac{c}{d}, d=2r \следовательно, c=2\pi r$). Однако с увеличением $n$ $s$ уменьшается, и периметр n-угольника будет приближаться к окружности окружности. Это никогда не достигается ни для каких конечных n , но это достаточно близко, что позволяет нам определить то, что известно в исчислении как предел: $\lim_{n\to \infty}ns = 2\pi r$.
Теперь для каждой стороны n-угольника мы можем определить равнобедренный треугольник между вершинами стороны и центром окружности. Симметричные стороны этого треугольника имеют длину $l$, которая равна $>r$ (поскольку прямая соединяется с вершиной n-угольника вне круга), но подобно тому, как $ns$ приближается к $2\pi r$ , $l$ приближается к $r$ при $n\to \infty$. Этот равнобедренный треугольник с основанием $s$ и высотой $r$ можно разбить на два прямоугольных треугольника с основанием $s/2$ и высотой $r$.
2$.
КЭД.
$\endgroup$
$\begingroup$
ОК, значит, суть вашей интуиции заключается в том, чтобы связать область с длиной линии, необходимой для заполнения этой области. Это как штриховать картинку шариковой ручкой.
Возьмите свой пример с квадратом: в конце, когда вы нарисовали все свои линии, вы заштриховали всю область. Таким образом, если вы знаете, сколько чернил вы израсходовали из пера, вы знаете площадь — вы закрасили область более или менее равномерно, поэтому количество израсходованных чернил пропорционально площади.
Неравномерное затенение:
Однако, когда вы рисуете линии для своего круга, вы несколько раз проходите по центру. На самом деле в самом центре круга делается невероятно много, потому что каждая линия, которую вы рисуете, начинается или заканчивается там. Однако по краям круга ваши линии гораздо более разнесены.
Интуиция, которую вы используете, основана на идее, что вы равномерно затеняете область.
2$.
$\endgroup$
$\begingroup$
Вот аналогичный подход. Разделите радиус на $n$ равных частей и сформируйте концентрические окружности радиуса $0, \frac{r}{n}, \frac{2r}{n},…,r$. Подумайте о поперечном сечении луковицы. Затем оцените площадь, развернув каждый круг, аппроксимировав его площадь прямоугольной полосой, длина которой определяется внешним радиусом и шириной $\frac{r}{n}$, и сложите все вместе. Затем пусть $n \to \infty$, чтобы сделать приближение лучше. 92$, по желанию.
Обратите внимание, что $\frac{1}{2}$ появляется потому, что вы суммируете $1+ (1-\frac{1}{n})+ \cdots + \frac{1}{n}$. Если вы нарисуете линии длиной $1$, $1-\frac{1}{n}$ и т. д., наложенные друг на друга, вы увидите, что они приближаются к треугольнику. Площадь треугольника вдвое меньше, чем у «эквивалентного» прямоугольника. Это объясняет «исчезновение» 2 в формуле.
$\endgroup$
$\begingroup$
Для каждой фигуры типа квадрата или круга, которую при достаточно большом $n$ можно разбить на линии толщиной примерно $\frac{1}{n}$, можно найти функцию, которая присваивает каждому достаточно большому положительное целое число $n$ упорядоченная пара, первый компонент которой является одним таким разбиением его части с нулевой площадью перекрытия, а второй компонент которого является отношением длины к площади, где длина считается эквивалентной площади $\frac{1}{ в n}$ раз больше длины, так что когда $n$ приближается к $\infty$, незаполненная область разбиения приближается к нулю.
Это означает, что при приближении $n$ к $\infty$ площадь, соответствующая длине такого разбиения, должна приближаться к площади круга, если площадь, не заполненная разбиением, стремится к нулю, а площадь перекрытия остается равной нулю. Если вы возьмете разбиение на $2\pi n$, умноженное на число, приближающееся к 1 равноотстоящим линиям, идущим от края к центру толщины $\frac{1}{n}$, то это не тот случай, когда площадь перекрытия в расщепление равно нулю. 92. $$
Причина, по которой это не работает так, как вы изначально думали, заключается в том, чтобы добавить «утолщенные» радиусы по всему кругу, утолщенные радиусы перекрываются, и поэтому вы пересчитываете.
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie 92$$
Приведенная выше формула, пожалуй, самая известная, но ее редко понимают.
Хотя формула площади круга была известна еще в Древней Греции, ее обоснование совсем не просто. Так что это отличная тема, чтобы обогатить вопрос «Почему?» серии.
⭐️ Площадь круга – формула
Как видно выше – квадрат и круг одинаковой площади не связаны «как-то интуитивно просто». Более того, было даже показано, что квадратура круга (процедура, выполняемая с помощью циркуля и линейки без шкалы) невозможна! А вот и гениальная идея с прямоугольником. Прежде чем я расскажу вам, что это такое, давайте посмотрим, что на самом деле говорит формула π·r².
Значит, в круге радиуса r чуть больше 3 квадратов со стороной r.
⭐️ Площадь круга – доказательство анимацией
Я много работал над этой анимацией, надеюсь, она вам понравится. Дайте мне знать в комментариях 🙂
⭐️ Площадь круга — доказательство правильными многоугольниками
Примечание — следующее не является формальным доказательством, оно только иллюстрирует метод вывода, используемый древними греками (например, метод Архимеда и определение числа пи).
Видно, что длина окружности правильного n-угольника, описанного на окружности, равна
$$C_n=na$$
, а его площадь равна сумме площадей треугольников с основанием a и высотой, равной к радиусу окружности r.
$$A_n=n\frac{ar}{2}=\frac{nar}{2}$$
Замена
$$A_n=\frac{C_nr}{2}$$
Как n получается больше, Aₙ все больше и больше приближает площадь круга, а Cₙ приближает его окружность. На «предельном шаге» (бесконечно малом) получаем 92$$
⭐️ Площадь круга – формальное доказательство
Доказательство, которое я собираюсь представить, не будет основано на интегрировании уравнения окружности. Я собираюсь использовать последовательности, их пределы и теорему сжатия.
Теорема сжатия
Пусть даны три действительные последовательности aₙ, bₙ и cₙ. Если «почти везде» (т.е. опуская самое большее конечное число членов) существует отношение
$$a_n\leq b_n\leq c_n$$
и
$$\lim a_n = \lim c_n = g$$
затем
$$\lim b_n = g$$
Полезный предел
$$\lim_{x\to 0}\frac{\sin x}{x} = 1$$
Помню со школы , на уроках физики мой учитель неоднократно предполагал, что при малых x функция sin(x) может быть хорошо аппроксимирована x.
Это результат разложения sin(x) в ряд Тейлора — позвольте мне опустить объяснение. Однако я рассчитаю предел, используя правило Лопиталя. Позже это очень пригодится 🙂
$$\lim_{x\to 0}\frac{\sin x}{x}=\big(\frac{0}{0}\big)\text{ Правило Лопиталя} = $ $
$$=\lim_{x\to 0}\frac{(\sin x)\prime}{x\prime}=\lim_{x\to 0}\frac{\cos x}{1}=$ $
$ $ = \ frac {\ cos 0} {1} = \ frac {1} {1} = 1 $ $
$ $ \ lim_ {x \ to 0} \ frac {\ sin x} {x } = 1$$
⭐️ Площадь круга – доказательство
Рассмотрим правильный n-угольник, описанный на окружности и вписанный внутрь окружности. Назовем «Внешнюю область» областью описанного n-угольника и обозначим ее через Oₙ. Точно так же мы будем называть вписанную область n-угольника «Внутренней областью», обозначая ее Iₙ.
Очевидно
$$I_n\leq A\leq O_n$$
где A обозначает площадь круга.
На следующем шаге мы делим n-угольник на n-треугольников. Заметим, что таким образом весь угол также делился на n равных частей.
Площадь «внешнего треугольника» будет Tₙ, а площадь внутреннего треугольника tₙ.
$$O_n=nT_n$$
$$I_n=nt_n$$
Площадь «внешнего» треугольника определяем по
$$T_n=Br$$
а 92*грех(2*пи/п) скаляр > O(3,1) е1 = 5,196152422706632 скаляр > O(7,1) е2 = 3,371022331652701 скаляр > O(20,1) е3 = 3,1676888064
4 скаляр > O(1000,1) е4 = 3,14160298
56 скаляр > I(3,1) е5 = 1,2905676658 скаляр > I(7,1) е6 = 2,7364101886381045 скаляр > I(20,1) е7 = 3,0
943749474 скаляр > I(1000,1) е8 = 3,141571982779475Плюс график сходимости последовательностей
//Площадь круга.scg вар = п от = 3 до = 100 мин = пи-0,5 макси = пи+0,5 exp1 = О (n, 1) ехр2 = I(n,1) ехр3 = пи строка1 = 0 строка2 = 0 по = 1 курс = 1 93-89 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92 2pir – Подробное объяснение и подробные примеры
2pir – длина окружности.

Окружность (или периметр) круга равна общей длине границы круга . Окружность является линейной мерой, и ее единицы в основном задаются в сантиметрах, метрах или дюймах.
Окружность — это замкнутая круглая фигура, все точки на границе которой равноудалены от центра окружности. В геометрии нас интересует только вычисление площади и длины окружности. В этой теме мы обсудим 9{2}$.
Если мы разрежем круг, построим его по прямой и измерим его длину, то получим общую длину границы круга . Поскольку круг является замкнутой фигурой, и нам нужна формула для вычисления общей границы круга, здесь нам поможет формула.
Мы должны использовать важные элементы круга, используемые для расчета площади и длины окружности круга и этих важных элементов.
1. Центр окружности
2. Диаметр окружности
3. Радиус окружности
Центр окружности : Центром окружности является фиксированная точка окружности, расположенная на равном расстоянии от каждой точки на границе окружности.
Диаметр окружности : Диаметр окружности – это общее расстояние от одной точки окружности до другой точки при условии, что нарисованная линия пересекает центр окружности. Таким образом, это линия, которая касается разных концов или границ круга, проходя через центр. Он обозначается как «$\dfrac{r}{2}$».
Радиус круга : Радиус круга — это общее расстояние от любой точки на границе круга до центра круга и обозначается как «$r$».
Как доказать, что длина окружности равна 2pir
Длина окружности — это общая длина границы окружности, и ее нельзя вычислить с помощью линейки или шкалы, как это делается для других геометрических фигур. Круг имеет изогнутую форму , и мы должны использовать формулу для вычисления длины окружности. При выводе формулы 2pir в качестве длины окружности мы используем постоянное значение $\pi$ и переменное значение радиуса «$r$».
$\pi$ имеет постоянное значение $3,14159$ или $\dfrac{22}{7}$.
Значение $\pi$ равно отношению длины окружности к диаметру окружности .
$\pi = \dfrac{C}{D}$ (1)
Здесь
C = длина окружности
D = диаметр окружности Формула для диаметра
9003 окружности задается как:$D = \dfrac{r}{2}$
Таким образом, подставив значение «D» в уравнение «1»: 9{\dfrac{\pi}{2}}$
$L = 4r \dfrac{\pi}{2}$
$L = 2\pi r$.
Почему длина окружности 2pir, а не Pid?
Обычно мы используем $2\pi r$ вместо $\pi d$, поскольку окружность u обычно задается радиусом, а не диаметром . Заметим, что диаметр $d$ равен удвоенному радиусу, т. е. $d=2r$, поэтому можно написать $2\pi r = \pi d$, и обе формулы равноправны.
2pir Калькулятор
Для расчета длины окружности нам понадобится значение $\pi$ и радиус . Мы уже знаем, что значение $\pi$ задается как $\dfrac{22}{7}$, а значение радиуса либо задается, либо мы вычисляем его, если нам известна площадь круга.
Если нам дано значение диаметра вместо радиуса, мы сначала рассчитаем значение радиуса, используя формулу для диаметра окружности $D =\dfrac{r}{2}$.
Применение окружности круга
Вот несколько реальных применений длины окружности:
- Эта формула будет использоваться всякий раз, когда мы сталкиваемся с круглой формой в реальной жизни.
- Колесо считается одним из лучших изобретений в истории человечества. Формула длины окружности необходима при проектировании модели колеса.
- Формула используется при решении различных тригонометрических задач, особенно уравнений окружности.
- Ступица потолочного вентилятора имеет круглую форму, поэтому мы должны использовать эту формулу для расчета периметра ступицы.
- Различные формы монет, пуговиц и круглых часов — все это приложения окружности круга, и мы должны использовать эту формулу при разработке всего этого.
- Формула $2\pi r$ также используется при расчете средней скорости объекта, движущегося по круговой траектории.
Формула для расчета скорости объекта, движущегося по круговой траектории, имеет вид 2pir/t.
Пример 1:
Если радиус круга равен 20 см, какой будет длина окружности?
Решение:
Радиус окружности $= 20 см$
Длина окружности $= 2.\pi.r$
C $= 2 \pi . 20$
C $= 125,6$ см
Пример 2:
Если диаметр круга равен 24 см, какой будет длина окружности?
Решение:Диаметр $= 24$
Радиус окружности $= \dfrac{24}{2} = 12$
Длина окружности $= 2.\pi.r$
$ С = 2 \pi.12$
$C = 75,36 см$
Пример 3:
Периметр нити квадратной формы равен $250 см$. Если из той же нити сделать круг, какой будет окружность круга? Также необходимо рассчитать радиус и диаметр окружности.
Решение:
Мы знаем, что периметр квадратной нити = общему количеству нитей, использованных для создания квадрата . Это также будет равно длине окружности, потому что, если мы используем ту же нить для формирования окружности, длина окружности останется прежней.
Длина окружности $= 250$ см
$C = 2.\pi.r$
$250 = 2\times \pi \times r$
$r = \dfrac{250}{\pi \ раз r}$
Пример 4:
Разница между длиной окружности и диаметром футбольного мяча составляет $10$ см. Каков будет радиус футбольного мяча?
Решение:Пусть радиус футбольного мяча $= r$
Как указано в утверждении, длина окружности – диаметр $= 10$ см
Окружность футбольного мяча $= 2.\pi.r$
Диаметр футбольного мяча $= 2.r$
$2. \Пи . r – 2r = 10$
$r (2\pi – 2) = 10$
$r (4,28) = 10$
$r = \dfrac{10}{4,28} = 2,34$ см прибл.
Пример 5:
Пастух хочет построить круглую границу, чтобы защитить свой скот от гончих и хищников. Какова будет общая расчетная стоимость, если 30$-метровый радиус круговой границы оплачивается по $\$15$ за метр? 92 калькулятор также .
Практические вопросы:
- Колесо автомобиля имеет радиус $7$ метров.

 log ; vcgencmd measure_temp| tr -d "temp=" | tr -d "'C" >> /home/pi/cpu_temp.log
log ; vcgencmd measure_temp| tr -d "temp=" | tr -d "'C" >> /home/pi/cpu_temp.log

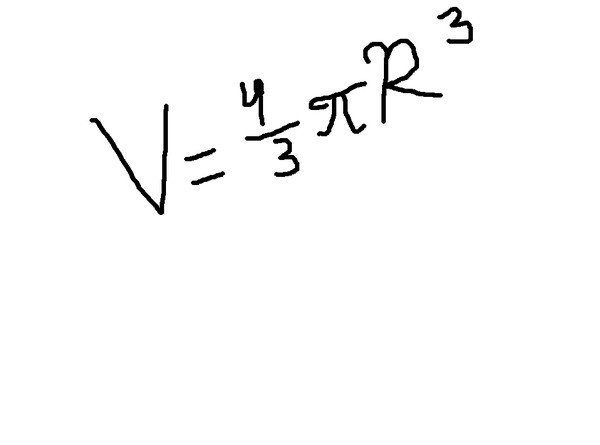 Площадь круга
Площадь круга


 3850 = 22/7 × r 2
3850 = 22/7 × r 2  2$. В чем проблема этого рассуждения?
2$. В чем проблема этого рассуждения? )
) д.) по окружности радиуса $r$. Каждая сторона этой фигуры будет иметь длину $s$ и $s*n > 2\pi r$; периметр n-угольника будет больше длины окружности (напомним, что $\pi = \dfrac{c}{d}, d=2r \следовательно, c=2\pi r$). Однако с увеличением $n$ $s$ уменьшается, и периметр n-угольника будет приближаться к окружности окружности. Это никогда не достигается ни для каких конечных n , но это достаточно близко, что позволяет нам определить то, что известно в исчислении как предел: $\lim_{n\to \infty}ns = 2\pi r$.
д.) по окружности радиуса $r$. Каждая сторона этой фигуры будет иметь длину $s$ и $s*n > 2\pi r$; периметр n-угольника будет больше длины окружности (напомним, что $\pi = \dfrac{c}{d}, d=2r \следовательно, c=2\pi r$). Однако с увеличением $n$ $s$ уменьшается, и периметр n-угольника будет приближаться к окружности окружности. Это никогда не достигается ни для каких конечных n , но это достаточно близко, что позволяет нам определить то, что известно в исчислении как предел: $\lim_{n\to \infty}ns = 2\pi r$. 2$.
2$. 2$.
2$. Это означает, что при приближении $n$ к $\infty$ площадь, соответствующая длине такого разбиения, должна приближаться к площади круга, если площадь, не заполненная разбиением, стремится к нулю, а площадь перекрытия остается равной нулю. Если вы возьмете разбиение на $2\pi n$, умноженное на число, приближающееся к 1 равноотстоящим линиям, идущим от края к центру толщины $\frac{1}{n}$, то это не тот случай, когда площадь перекрытия в расщепление равно нулю. 92.
$$
Это означает, что при приближении $n$ к $\infty$ площадь, соответствующая длине такого разбиения, должна приближаться к площади круга, если площадь, не заполненная разбиением, стремится к нулю, а площадь перекрытия остается равной нулю. Если вы возьмете разбиение на $2\pi n$, умноженное на число, приближающееся к 1 равноотстоящим линиям, идущим от края к центру толщины $\frac{1}{n}$, то это не тот случай, когда площадь перекрытия в расщепление равно нулю. 92.
$$ Хотя формула площади круга была известна еще в Древней Греции, ее обоснование совсем не просто. Так что это отличная тема, чтобы обогатить вопрос «Почему?» серии.
Хотя формула площади круга была известна еще в Древней Греции, ее обоснование совсем не просто. Так что это отличная тема, чтобы обогатить вопрос «Почему?» серии.
 Это результат разложения sin(x) в ряд Тейлора — позвольте мне опустить объяснение. Однако я рассчитаю предел, используя правило Лопиталя. Позже это очень пригодится 🙂
Это результат разложения sin(x) в ряд Тейлора — позвольте мне опустить объяснение. Однако я рассчитаю предел, используя правило Лопиталя. Позже это очень пригодится 🙂 Площадь «внешнего треугольника» будет Tₙ, а площадь внутреннего треугольника tₙ.
Площадь «внешнего треугольника» будет Tₙ, а площадь внутреннего треугольника tₙ.

 Значение $\pi$ равно отношению длины окружности к диаметру окружности .
Значение $\pi$ равно отношению длины окружности к диаметру окружности .
 Формула для расчета скорости объекта, движущегося по круговой траектории, имеет вид 2pir/t.
Формула для расчета скорости объекта, движущегося по круговой траектории, имеет вид 2pir/t.
