Онлайн калькулятор приведение кривой второго порядка к каноническому виду: Приведение кривой второго порядка к каноническому виду онлайн

Содержание

76. Приведение квадратичных форм к каноническому виду

Рассмотрим некоторое линейное преобразование А с матрицей .

Это симметрическое преобразование можно записать в виде:

Y1 = a11x1 + a12x2

Y2 = a12x1 + a22x2

Где у1 и у2 – координаты вектора в базисе .

Очевидно, что квадратичная форма может быть записана в виде

Ф(х1, х2) = х1у1 + х2у2.

Как видно, геометрический смысл числового значения квадратичной формы Ф в точке с координатами х1 и х2 – скалярное произведение .

Если взять другой ортонормированный базис на плоскости, то в нем квадратичная форма Ф будет выглядеть иначе, хотя ее числовое значение в каждой геометрической точке и не изменится. Если найти такой базис, в котором квадратичная форма не будет содержать координат в первой степени, а только координаты в квадрате, то квадратичную форму можно будет привести к каноническому виду.

Если в качестве базиса взять совокупность собственных векторов линейного преобразования, то в этом базисе матрица линейного преобразования имеет вид:

При переходе к новому базису от переменных х1 и х2 мы переходим к переменным и . Тогда:

Тогда .

Выражение называется Каноническим видом квадратичной формы. Аналогично можно привести к каноническому виду квадратичную форму с большим числом переменных.

Теория квадратичных форм используется для приведения к каноническому виду уравнений кривых и поверхностей второго порядка.

Пример. Привести к каноническому виду квадратичную форму

Ф(х1, х2) = 27.

Коэффициенты: а11 = 27, а12 = 5, а22 = 3.

Составим характеристическое уравнение: ;

(27 — l)(3 — l) – 25 = 0

L2 — 30l + 56 = 0

L1 = 2; l2 = 28;

Пример. Привести к каноническому виду уравнение второго порядка:

17×2 + 12xy + 8y2 – 20 = 0.

Коэффициенты а11 = 17, а12 = 6, а22 = 8. А =

Составим характеристическое уравнение:

(17 — l)(8 — l) — 36 = 0

136 — 8l — 17l + l2 – 36 = 0

L2 — 25l + 100 = 0

L1 = 5, l2 = 20.

Итого: — каноническое уравнение эллипса.

Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

Решение: Составим характеристическое уравнение квадратичной формы : при

Решив это уравнение, получим l1 = 2, l2 = 6.

Найдем координаты собственных векторов:

Полагая m1 = 1, получим n1 =

Полагая m2 = 1, получим n2 =

Собственные векторы:

Находим координаты единичных векторов нового базиса.

Имеем следующее уравнение линии в новой системе координат:

Каноническое уравнение линии в новой системе координат будет иметь вид:

Решение: Составим характеристическое уравнение квадратичной формы : при

Решив это уравнение, получим l1 = 1, l2 = 11.

Найдем координаты собственных векторов:

Полагая m1 = 1, получим n1 =

Полагая m2 = 1, получим n2 =

Собственные векторы:

Находим координаты единичных векторов нового базиса.

Имеем следующее уравнение линии в новой системе координат:

Каноническое уравнение линии в новой системе координат будет иметь вид:

4ху + 3у2 + 16 = 0

Коэффициенты: a11 = 0; a12 = 2; a22 = 3.

Характеристическое уравнение:

Корни: l1 = -1, l2 = 4.

Для l1 = -1 Для l2 = 4

M1 = 1; n1 = -0,5; m2 = 1; n2 = 2;

= (1; -0,5) = (1; 2)

Получаем: — каноническое уравнение гиперболы.

При использовании компьютерной версии “Курса высшей математики” возможно запустить программу, которая решает рассморенные выше примеры для любых начальных условий.

Для запуска программы дважды щелкните на значке:

В открывшемся окне программы введите коэффициенты квадратичной формы и нажмите Enter.

Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.

< Предыдущая		Следующая >

Векторная алгебра и аналитическая геометрия

Образовательные онлайн сервисы: теория и практика

Главная
Примеры
- Математический анализ
- Векторная алгебра и аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование
  Методы оптимизации
- Математика в экономике
  Экономическая статистика
Видео-уроки
- Математический анализ
- Векторная алгебра и Аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование. Методы оптимизации
Готовые работы
- Математический анализ
- Векторная алгебра и аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование
  Методы оптимизации
- Математика в экономике
  Экономическая статистика
- Другое
Контакты

Полезные материалы:

Учебники
Справочники
Онлайн калькуляторы

Помощь в решении
Онлайн занятия в Zoom

Векторы

Понятие вектора 4:24

Проекция вектора 3:12

Действия над векторами 5:56

Разложение вектора по векторам (базису) 14:54

Скалярное произведение векторов 4:23

Векторное произведение векторов 5:44

Векторное произведение векторов в координатной форме 7:08

Смешанное произведение векторов 3:59

Смешанное произведение векторов в координатной форме 5:44

Аналитическая геометрия на плоскости

Прямоугольная система координат 5:02

Полярная система координат 6:07

Простейшие задачи аналитической геометрии 7:17

Деление отрезка пополам. Середина отрезка 4:34

Деление отрезка в данном отношении 5:37

Длина отрезка. Расстояние между двумя точками 6:15

Уравнение линии 5:14

Уравнение прямой с угловым коэффициентом 5:25

Угол между прямыми 5:46

Уравнение прямой, проходящей через две точки 4:09

Общее уравнение прямой 5:52

Уравнение прямой в отрезках 3:02

Нормальное уравнение прямой 6:50

Расстояние от точки до прямой 5:36

Нахождение площади треугольника на плоскости 1:41

Квадратичные формы. Кривые 2 порядка

Окружность 5:07

Эллипс 8:00

Гипербола 8:16

Парабола 5:28

Общее уравнение кривой 2 порядка 3:46

Преобразование координат 6:59

Метод Лагранжа. Приведение квадратичной формы к каноническому и нормальному видам 6:27

Нахождение матрицы квадратичной формы в новом базисе 7:00

Приведение общего уравнения кривой к каноническому виду (без поворота осей) 9:25

Приведение общего уравнения кривой к каноническому виду (с поворотом осей) 11:05

Аналитическая геометрия в пространстве

Прямоугольная система координат в пространстве 6:25

Задать вопрос
Заказать помощь

ОТЗЫВЫ

+7-911-7987704

vk.

com/id286009794

Написать в Whatsapp

Написать в Viber

@matem96

Skype: matem96.ru

2 (1 + x)$, мы можем записать рациональную каноническую форму как:

$$R = \begin{bmatrix} 0 & 0 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{ bmatrix}$$

Есть несколько способов найти матрицу $P$, но мне нравится использовать операции над строками из разложения на инвариантные факторы. Если мы воспользуемся ими (сведем их к матрице, показанной выше), мы получим:

$$P = \begin{bmatrix} -2 & -6 & -18 \\ 0 & 0 & -8 \\ 1 &-1 &-7 \end{bmatrix}$$

9{-1} = \begin{bmatrix} 3 & 4 & 0 \\-1 & -3 & -2 \\ 1 & 2 & 1 \end{bmatrix} = A$$

Из комментариев и из Книга, которую вы упоминаете (которой у меня нет), должна была сработать, но я не уверен, так как хотел бы прочитать подробности. Есть несколько подходов к ним, и они не тривиальны и не уникальны.

Также обратите внимание на очень важное наблюдение о матрицах $P$ для жордановых и рациональных канонических форм: они не совпадают.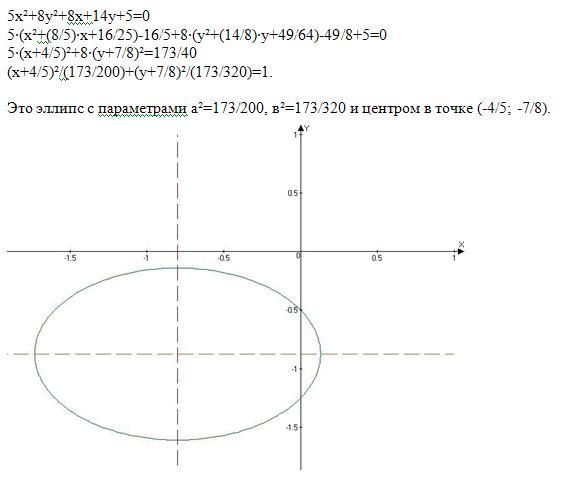

Другие ссылки, которые вы, возможно, захотите проверить:

Абстрактная алгебра, Даммит и Фут
Линейная алгебра, Эдвардс
Алгебра, Вивек Сахай, Бист Викас

Кривизна и радиус кривизны

Рассмотрим плоскую кривую, определяемую уравнением y = f ( x ). Предположим, что касательная проведена к кривой в точке M ( x , y ). Тангенс образует угол α с горизонтальной осью (рис. 1).

Рис. 1.

При смещении $\Delta s$ по дуге кривой точка $M$ перемещается в точку ${M_1}.$ Положение касательной также меняется: угол наклона касательной к положительной $x-\text{оси}$ в точке ${M_1}$ будет равен $\alpha + \Delta\alpha.$ Таким образом, при движении точки на расстояние $\Delta s,$ касательная поворачивается на угол $\Delta\alpha.$ (Предполагается, что угол $\alpha$ увеличивается при вращении против часовой стрелки.)

Абсолютное значение отношения $\frac{{\Delta \alpha}}{{\Delta s}}$ называется средней кривизной дуги $M{M_1}. $ В пределе как \ (\Delta s \to 0,\) получаем кривизну кривой в точке $M:$

\[K = \lim\limits_{\Delta s \to 0} \left| {\ frac {{\ Delta \ alpha}} {{\ Delta s}}} \ right |. \]

Из этого определения следует, что кривизна в точке кривой характеризует скорость вращения касательной кривой в этой точке. 92}}} = 1\] в его вершинах.

Раствор.

Очевидно, достаточно найти кривизну эллипса в точках $A\left( {a,0} \right)$ и $B\left( {0,b} \right)$ (рис. \ (2\)), так как из-за симметрии кривой кривизна в двух противоположных вершинах эллипса будет одинаковой.

Рис. 2.

Для расчета кривизны удобно перейти от канонического уравнения эллипса к уравнению в параметрической форме:

9{\ frac {3} {2}}}}} = 2, \; \; R = \ frac {1} {K} = \ frac {1} {2}. \]

Пример 3.

Найти кривизну и радиус кривизны кривой \[y = \cos mx\] в точке максимума.