Binary Конвертер — конвертация между системами исчисления онлайн
Powered by aspose.com and aspose.cloud
Попробуйте другие приложения
Легко конвертируйте между системами исчисления!
Binary Конвертер — это бесплатное онлайн-приложение и полезный инструмент для программистов, разработчиков, инженеров, математиков и многих других, который поможет повысить вашу производительность. Он обеспечивает быстрый способ поиска представлений чисел в десятичном, двоичном, восьмеричном и шестнадцатеричном виде.Наш Binary Конвертер быстрый, понятный и простой в использовании. Преобразование происходит в реальном времени. Вы можете преобразовать десятичное число в двоичное, десятичное в восьмеричное, десятичное в шестнадцатеричное, двоичное в восьмеричное, двоичное в шестнадцатеричное и двоичное в десятичное. Наше браузерное приложение работает на всех платформах, включая Windows, Linux, Mac OS, Android и iOS. Вам не требуется регистрация, установка плагинов или программного обеспечения.
Так что сэкономьте свое драгоценное время и выполняйте преобразования между двоичными, десятичными и другими системами исчисления онлайн!Как использовать Binary Конвертер
- Сначала вы должны ввести десятичное значение, например 452, в верхнем текстовом поле.
- Затем нажмите кнопку «Конвертировать».
- Вы сразу получаете результат в двоичной, шестнадцатеричной и восьмеричной системах.
- Можно выбрать новую пару систем исчисления для преобразования или выполнить преобразование наоборот.
FAQ
- Что такое двоичное число?Десятичная система счисления с основанием десять имеет десять возможных значений — 0,1,2,3,4,5,6,7,8 или 9 — для каждого разрядного значения.
Напротив, двоичная система счисления представляет собой позиционную систему с основанием 2 и имеет два возможных значения, представленных как 0 или 1 для каждого разряда. Поскольку двоичная система может быть легко реализована в цифровой электронике, она используется во всех современных компьютерах и другом цифровом оборудовании, например, в мобильных телефонах. Таким образом, поскольку двоичная система является внутренним языком электроники, разработчики должны понимать, как конвертировать из десятичной в двоичную. - Как работает двоичный код?Практически все современные технологии и компьютеры используют двоичную систему из-за простоты ее реализации в цифровых схемах с использованием логических вентилей. Гораздо проще разработать оборудование, которое должно обнаруживать только два состояния: «OFF» и «ON». 0 и 1 в двоичном коде означают «OFF» или «ON» соответственно. В транзисторе «0» означает отсутствие потока электроэнергии, а «1» означает, что току разрешено течь. Таким образом, числа физически представлены внутри вычислительного устройства, что позволяет выполнять вычисления.
- Что такое восьмеричная система?Восьмеричная система (oct) — это позиционная система исчисления по основанию 8. Для обозначения любого числа используются цифры от 0 до 7. Восьмеричная система используется в цифровом оборудовании.
- Что такое шестнадцатеричная система?Шестнадцатеричная система счисления (hex) — это система исчисления с основанием 16. Она используется в современных цифровых технологиях, информатике и математике.
Напротив, двоичная система счисления представляет собой позиционную систему с основанием 2 и имеет два возможных значения, представленных как 0 или 1 для каждого разряда. Поскольку двоичная система может быть легко реализована в цифровой электронике, она используется во всех современных компьютерах и другом цифровом оборудовании, например, в мобильных телефонах. Таким образом, поскольку двоичная система является внутренним языком электроники, разработчики должны понимать, как конвертировать из десятичной в двоичную.
В транзисторе «0» означает отсутствие потока электроэнергии, а «1» означает, что току разрешено течь. Таким образом, числа физически представлены внутри вычислительного устройства, что позволяет выполнять вычисления.Быстрый и простой Binary Конвертер
Введите десятичное значение в верхнем поле ввода текста. Затем нажмите кнопку «Конвертировать» и сразу получите результат конвертации!Конвертируйте с любого устройства
Конвертер работает со всех платформ, включая Windows, Linux, Mac OS, Android и iOS. Все файлы обрабатываются на наших серверах.Качество Binary Конвертера
Все данные обрабатываются с помощью API-интерфейсов Aspose, которые используются многими компаниями из списка Fortune 100 в 114 странах.
Затем нажмите кнопку «Конвертировать» и сразу получите результат конвертации!© Aspose Pty Ltd 2001-2023. All Rights Reserved.
- Privacy Policy
- Terms of Service
- Contact
Программирование на калькуляторе / Хабр
Здравствуйте, хабражители. Думаю, многие из вас слышали о программируемых калькуляторах (а некоторые даже использовали их). Как ни странно, здесь я не нашел ни одной статьи, рассказывающей о такой интересной вещи, и поэтому решил восполнить этот пробел и рассказать об основах программирования на калькуляторах.
Некоторое время назад я нашел у себя в кладовке старый «Электроника МК-61», принадлежавший моему папе. Естественно, я не мог упустить такой шанс освоить не совсем «стандартное» программирование на калькуляторе. (В случае, если у вас нет программируемого калькулятора, вы можете скачать эмулятор здесь)
Память
Прежде всего необходимо понять, как устроена память в этом калькуляторе. В распоряжении пользователя имеется 4 стековых регистра: X, Y, Z, T. Содержимое регистра X всегда показывается на экране (в режиме расчетов), ввод чисел тоже идет в него. По сути, стековая память после включения калькулятора выглядит так:
T 0 Z 0 Y 0 X 0
Для помещения чего-либо в стек используется клавиша [В↑]. Она копирует содержимое регистра X в регистр Y, значение регистра Y в Z, Z в T, а значение, находившееся в T теряется. То есть, если перед нажатием на кнопку [В↑] в регистрах были значения
T 5 Z 8 Y 14,5 X 6
,
то после значения станут
T 8 Z 14,5 Y 6 X 6
Кроме того существует команда, позволяющая циклически сдвинуть все значения регистров: T в Z, Z в Y, Y в X, X в T.
[F] [.].Команда [] меняет содержимое регистров X и Y местами.
Команда [CX] стирает содержимое регистра X.
Помимо стековой памяти, в калькуляторе есть 15 адресуемых регистров (RG0-RGE). Для работы с ними используются клавиши [X→П] и [П→X]. Первая команда помещает содержимое регистра X в соответствующий адресуемый регистр. Например, последовательность команд [4] [X→П] [0] помещает в регистр RG0 число 4. Вторая команда, как вы уже догадались, копирует содержимое адресуемого регистра в регистр X. То есть [П→X] [0] поместит в X число 4.
Важно помнить, что после выключения калькулятора значения всех регистров стираются.
Расчеты
Главное, что необходимо знать перед началом расчетов — в МК-61 используется обратная польская нотация (ОПН). Если нам нужно совершить какую-либо унарную операцию, она совершается над числом, находящимся в регистре X.
[2] [В↑] [3] [+]. При этом значения регистров меняются следующим образом:До всех операций:
T 8 Z 14,5 Y 6 X 0
После нажатия клавиш [2] [В↑] [3]:
T 14,5 Z 6 Y 2 X 3
После нажатия [+]:
T 14,5 Z 14,5 Y 6 X 5
Попробуем провести чуть более сложные вычисления, например, (15 + 2 / 5) * 7 + 10. В ОПН это выражение можно записать так: 15 2 5 / + 7 * 10 +. Для того, чтобы это посчитать на калькуляторе, мы должны нажать клавиши:
Программирование
Так, ну а это уже интереснее :).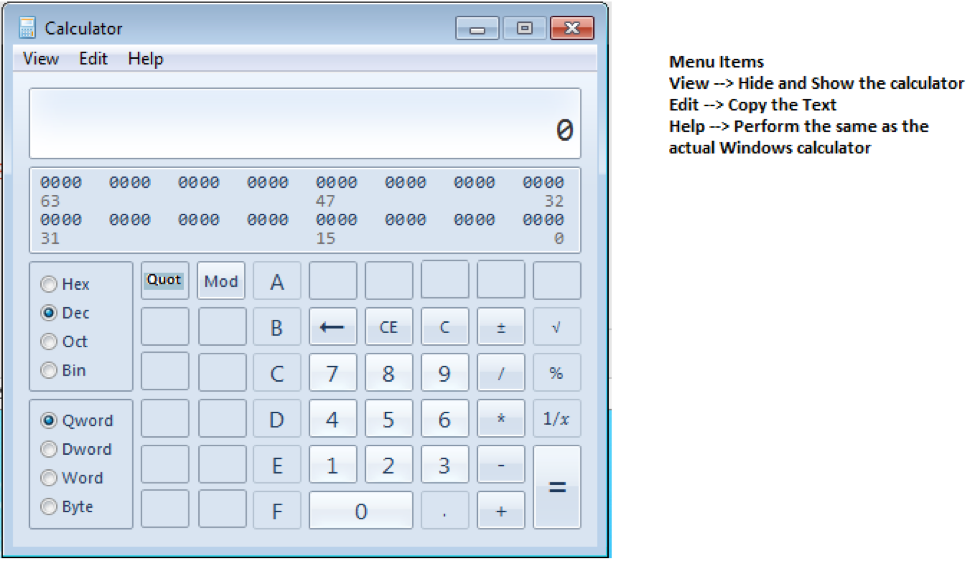
Для перехода в режим программирования нужно нажать [F] [ВП]. На дисплее появятся 00. Это означает номер текущей команды. Вообще, программа в МК-61 представляет собой последовательность команд, необходимых для решения задачи. Обычно это арифметические операции, цифры, иногда специальные коды циклов и ветвлений. Всего программа может состоять не более чем из 105 команд, которые нумеруются от 00 до 99. Для ввода команды необходимо нажать соответствующую ей клавишу. Вот таблица соответствия кодов и клавиш калькулятора:
В режиме программирования видно 3 последних введенных операции. Например
02 01 0E 06 на дисплее означает:06— адрес следующей вводимой команды0E, 01, 02— три последовательные команды, расположенные соответственно по адресам 03, 04, 05.
Основы
Разберем простейшую задачу нахождения площади круга по формуле πr2.
Для того, чтобы калькулятор решил эту задачу, введем следующие команды в режиме программирования ([F] [ВП]) (будем считать что радиус окружности находится в регистре RG1):
// Первые две цифры — адрес команды, потом нажимаемые клавиши 00 [П→X] [1] // Вызываем значение регистра RG1 в регистр X (61) 01 [F] [*] // Возводим в квадрат радиус (22) 02 [F] [+] // Вызываем в X пи (20) 03 [*] // Перемножаем содержимое X и Y (12) 04 [С/П] // Специальная команда для останова (без нее программа не остановится) (50)
Вот и все. Теперь мы должны перейти в режим вычислений с помощью команды [F] [/-/], а затем нужно нажать клавишу [В/О] для перехода к началу программы. Занесем число 5 в регистр RG1 ([5] [X→П] [1]) и нажмем [С/П] для начала выполнения. После того, как калькулятор пройдет все шаги, на экране должно появиться число 78,539815 — площадь круга с радиусом 5.
Безусловный и условный переходы
С помощью команды [БП] (51) можно осуществить безусловный перезод (goto) по нужному адресу.
Для этого в режиме программирования нужно нажать [БП] а затем две цифры адреса, по которому мы хотим перейти. Когда калькулятор при выполнении программы дойдет до этого оператора, он продолжит выполнение уже с команды по указанному адресу. Например:
... 10 [F] [-] // 21 11 [БП] // 51 12 [4] [2] // Адрес перехода (42) ... 42 [+] // 10
В данном случае после шага 12 калькулятор перейдет сразу к шагу 42.
Условный переход гораздо полезнее. Для осуществления условного перехода существует 4 команды: [X >= 0], [X < 0], [X = 0] и [X != 0]. С помощью этих команд проверяют содержимое регистра X на выполнения условия. В случае, если условие не выполняется, управление переходит к адресу, указанному после оператора, иначе (если условие выполняется) адрес игнорируется и программа продолжает нормально выполняться далее. Например:
... 09 [F] [*] // 22 10 [F] [ШГ←] // "if (X == 0)" (5E) 11 [4] [2] // В случае, если условие ложно, переходим по адресу 42 (42) 12 [+] // В случае, если X = 0 (10) ... 42 [4] // 04
Циклы
Циклы можно реализовать с помощью команд условного перехода, но, кроме того, для организации циклов в МК-61 используются команды L0-L3 ([F] [П→X], [F] [X→П], [F] [БП] и [F] [ПП]). Эти команды оперируют с содержимым регистров RG0-RG3 соответственно. При каждом выполнении команды цикла из содержимого соответствующего регистра вычитается 1 и производится сравнение с нулём. Если содержимое регистра не равно нулю, происходит переход по адресу, записанному после команды цикла, если равно, то происходит переход к команде, следующей за адресом перехода цикла. Чтобы было понятнее, посмотрим на примере. Будем считать факториал числа, находящегося в регистре X.
// В RG0 будем хранить счетчик цикла, в RG1 произведение. 00 [X→П] [0] // Заносим значение X в RG0 - инициализируем счетчик цикла (40) 01 [1] // Заносим 1 в X (01) 02 [X→П] [1] // Инициализируем единицей значение RG1 - произведение (41) 03 [П→X] [1] // Заносим в стек текущее значение произведения (61) 04 [П→X] [0] // Заносим в стек текущее значение счетчика цикла (60) 05 [*] // Перемножаем их (12) 06 [X→П] [1] // Заносим результат в произведение (41) 07 [F] [П→X] // L0 - уменьшаем счетчик на единицу и проверяем на равенство нулю.
Если не равен... (5Г)
08 [0] [3] // ...переходим к команде по адресу 03... (03)
09 [С/П] // ...иначе - останов (50)Заключение
Конечно, эта статья — далеко не полное руководство по программированию на МК-61. Интересующимся в более глубоком освоении этой темы рекомендую почитать инструкцию (pdf, 6 MB) к этому замечательному калькулятору.
Ссылки
- Инструкция по эксплуатации МК-61 (pdf, 6 MB)
- Интересный сайт о программировании микрокалькуляторов
- Статья в Википедии о МК-61
- Графические игры на МК-61
Программатор Калькулятор | Преобразование номера
Получить расширение Chrome
Преобразование числа из одного основания в другое основание
Побитовый калькулятор
Побитовые операторы AND, OR, XOR, NOT, NAND, NOR, ShiftЧто такое программатор калькулятор | Для чего используется преобразование базовых чисел?
- Преобразование любого числа из одной системы счисления в другую систему счисления
- Преобразование из базы 2 в базу 10
- Преобразование из базы 2 в базу 16
- Преобразование из базы 2 в базу 8
- Преобразование из базы 10 в базу 2
- Преобразование из базы 10 в базу 16
- Преобразование из 10-кратного в 8-ричное
- Преобразование из шестнадцатеричной системы счисления в двоичную.
- Преобразование из шестнадцатеричной системы счисления в десятичную.
- Преобразование из шестнадцатеричной системы счисления в восьмерочную.
- Преобразование из базы 8 в базу 2
- Преобразование из базы 8 в базу 10
- Преобразование из базы 8 в базу 16
- Преобразование Hex в ASCII, кодирование и перевод символов, букв, слов, предложений.
- Преобразовывать текст ASCII в шестнадцатеричный, кодировать и переводить символы, буквы, слова, предложения.
- Преобразование двоичных файлов в ASCII, кодирование и перевод символов, букв, слов, предложений.
- Преобразование текста ASCII в двоичный, кодирование символов, букв, слов, предложений.
- Преобразовывать десятичные числа в ASCII, кодировать и переводить символы, буквы, слова, предложения.
- Преобразовывать текст ASCII в десятичный, кодировать и переводить символы, буквы, слова, предложения.
- Двоичные операции — добавить, мул, под, div, ехр
- Побитовые операции — AND, OR, XOR, NOT, NAND, NOR, сдвиг битов
- Операции битового сдвига — сдвиг влево, сдвиг вправо
- Побитовые операции — И биты
- Побитовые операции — биты И-НЕ
- Побитовые операции — биты НЕ-ИЛИ
- Побитовые операции — НЕ биты
- Побитовые операции — биты ИЛИ
- Побитовые операции — XNOR биты
- Побитовые операции — биты XOR
Преобразование системы счисления
Преобразование системы счисления касается операций по изменению основания чисел. Например, чтобы изменить десятичное число с основанием 10 на двоичное число с основанием 2.
Мы также можем выполнять арифметические операции, такие как сложение, вычитание, умножение в системе счисления.
Основы счисления
В базовой системе счисления числа представлены цифрами (0-9) и буквами основного латинского алфавита (от «A» до «Z» = 26 букв). В конвертере входная числовая база должна состоять только из цифр [0-9] и букв [A-Z].
Преобразование общих оснований
Преобразование между различными основаниями счисления на самом деле очень просто, но обоснование этого может на первый взгляд показаться немного запутанным. Хотя тема различных систем счисления может показаться вам тривиальной, доступность компьютеров и компьютерной графики увеличила потребность в информации о том, как работать с различными (не десятичными) системами счисления.
Базовые имена систем счисления
- 1 — унарный
- 2 — двоичный
- 3 — тройной / тройной
- 4 — четвертичный
- 5 — пятерка / пятерица
- 6 — шестнадцатеричный / шестнадцатеричный
- 7 — семеричный / семеричный
- 8 — восьмеричный / восьмеричный / восьмеричный / восьмеричный
- 9 — нонарный / нотариальный / нотариальный
- 10 — десятичная/десятичная
- 11 — недесятичный / недесятичный / недесятичный
- 12 — дюжинальный / двенадцатеричный / двенадцатеричный
- 13 — трехзначный/троичный/трехдесятичный
- 14 — тетрадесятеричный / квадродесятичный / квадродесятичный
- 15 — пятидесятичный / пятидесятичный
- 16 — шестнадцатеричный / шестнадцатеричный / шестнадцатеричный
- 17 — семеричный/семидесятичный
- 18 — восьмидесятеричный/десятичный восьмеричный
- 19 — недесятичный / новодесятичный / десятичный
- 20 — десятичный / бидесятеричный / бидесятеричный
- 21 — недесятеричные / недесятеричные
- 22 — двенадцатидесятичный
- 23 — трехдесятиричный
- 24 — четверично-десятичный / четырехдесятичный
- 26 — шестнадцатеричный / шестидесятеричный
- 27 — семидесятеричный
- 28 — восьмерично-десятичный
- 29 — новодесятичный
- 30 — тройничный / тройничный
- 31 — тройная
- 32 десятеричный (уже популярное название для этой базы)
- 33 три семеричных числа
- 34 дважды
- 35 недвухвечерний
- 36 шестнадцатеричный / шестидесятеричный
Лучшие инструменты
Самые популярные инструменты
Бесплатный онлайн-калькулятор, программируемый калькулятор и калькулятор математических выражений
Что такое Hicalc Онлайн создать программу с удобным интерфейсом для вычислений и поделиться с другими людьми, а также предложить онлайн-калькулятор математических выражений. Зачем нужен HicalcДля пользователя:
Для программиста:
|
