2.1.2. Соответствие. Функция
Соответствие между множествами А и В – это множество, представляющее собой некоторое подмножество их декартова произведения
.
Полное соответствие между множествами А и В – это множество, равное их декартовому произведению
.
Если то говорят, что соответствуетв соответствии , (или они находятся в соответствии Р). Обозначается:или,,.
Соответствие предполагает, что некоторым элементам множества A (возможно, всем) поставлены в соответствие некоторые элементы множества B.
Соответствие, как
и декартово произведение, можно изобразить
графически в виде решетки или в виде
векторной диаграммы.
Пусть имеются множества и. Декартово произведение будет представлять собой следующую последовательность
.
Из нее можно взять любые компоненты, которые и будут представлять собой соответствие из А в В, например
,,.
График соответствия для данных множеств представлен на рис. 2.2.
В виде векторной диаграммы соответствия представлены на рис. 2.3.
Образ элемента в множествепри соответствии– множество всех , соответствующих элементу.Обозначается .
Прообраз
элемента
в множествепри соответствии–
множество всех
,
соответствующих элементу.Обозначается
.
Таким образом, если ,
то образ ,
а–прообраз .
Область определения соответствия Р (обозначается или) – множество таких ,для которых существует образ.
Область значений соответствия Р (обозначается или) – множество таких ,для которых существует прообраз.
Всюду определенное соответствие – соответствие, при котором выполняется равенство . В противном случае соответствие называется частичным.
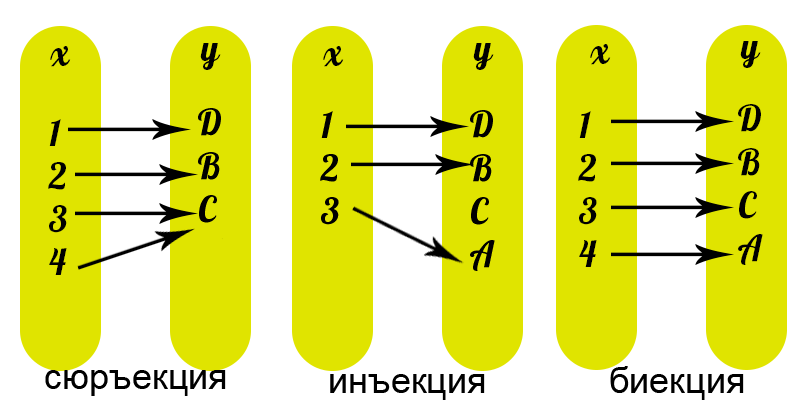
Сюръективное соответствие (сюръекция) – соответствие, при котором выполняется равенство .
Инъективное соответствие (инъекция)
Функциональное соответствие (функция) – соответствие , при котором образом любого элемента из множества является единственный элемент из множества (соответствие не содержит пар с одинаковыми первыми и различными вторыми координатами).
Взаимнооднозначное соответствие – соответствие, которое функционально и инъективно, то есть или .
Биекция (1-1 соответствие) – соответствие, которое всюду определено, сюръективно, функционально и инъективно.
Отображение в – соответствие, которое всюду определено и функционально.
Отображение на – соответствие, которое всюду определено, функционально и сюръективно.
Равномощные
множества – множества, между которыми можно
установить биекцию.
Счетное множество – множество, равномощное множеству натуральных чисел.
Континуальное множество – множество, равномощное множеству действительных чисел отрезка .
Пример 2.6.
Дано соответствие между (осью абсцисс) и (осью ординат) в виде круга радиуса
Образом в данном соответствии для числа 4 (ось абсцисс) является единственное число 2 (ось ординат), образом числа 3 является уже отрезок [1, 3] оси ординат.
Прообразом отрезка [1, 3] (ось ординат) является отрезок [2, 4] (ось абсцисс).
Данное соответствие не является
функциональным,
поскольку для такого соответствия
необходимо, чтобы образом любого элемента
из множества
являлся единственный элемент из
множества
.
Здесь множество это множество всех действительных чисел
(ось
абсцисс), каждому из которых может
соответствовать не единственный образ
из множества – множества всех действительных чисел
(ось
ординат).
Примером функционального соответствия на том же рис. 2.4 могут служить дуги окружности, координаты которых каждой единственной точке на оси абсцисс ставят в соответствие единственную точку на оси ординат. В частности это могут быть дуги ,или.
Отметим,
что в общем случае для задания соответствия
необходимо указать не только множество
,
но и множества
,
то есть указать,подмножеством
какого прямого произведения является
.
В данном примере тот же круг
задает и другое соответствие:между
отрезком [2,
4] и
отрезком [1, 3]. При этом по некоторым свойствам
соответствия
и×отличаются: так второе соответствие в
отличие от первого всюду определено и
сюръективно, то есть и .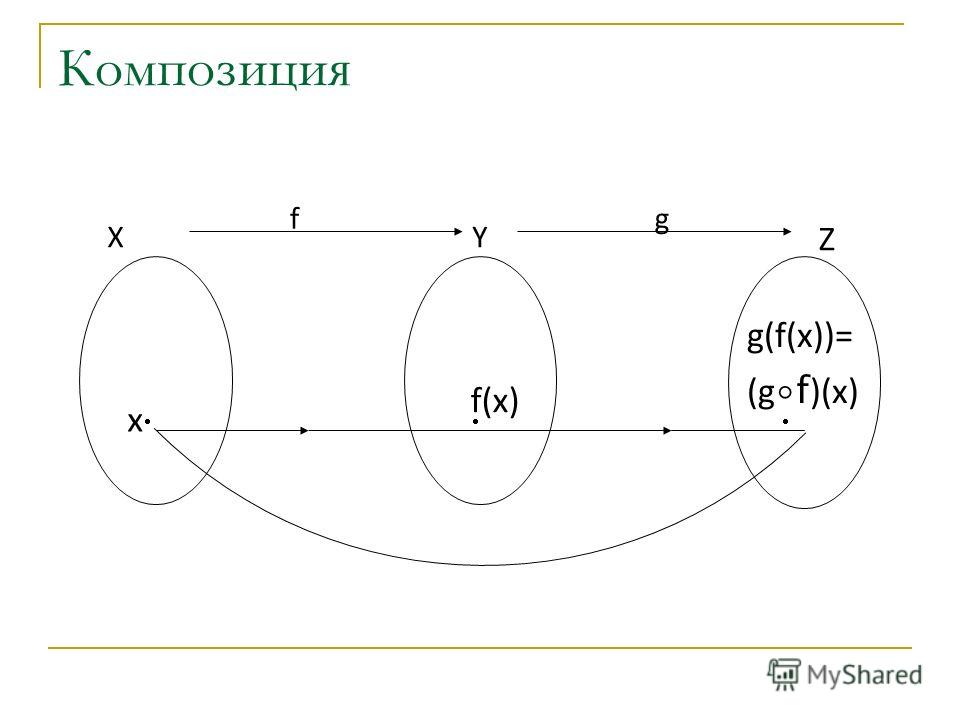
Учитывая это, соответствие необходимо
было бы определять как тройку множеств
,
и тогда не было бы необходимости
оговариваться, что один круг может
задавать два соответствия, поскольку
это и так было бы ясно из-за различия
троек
и.
Однако такие оговорки обычно делаются
редко, так как либо множества
ясны из контекста, либо различия в из
выборе не влияют на исследуемые свойства
соответствия. Поэтому определение
соответствия через тройку множеств
здесь использоваться не будет.
Пример 2.7.
Соответствие в виде словаря. Например, русско-английский словарь устанавливает соответствие между множеством русских и английских слов. Это соответствие не функционально, так как одному русскому слову обычно ставится в соответствие несколько английских слов. Кроме того, оно практически никогда не является полностью определенным, так как всегда можно найти русское слово, не содержащееся в данном словаре.
Пример 2.
8.
Соответствие в виде шахматной позиции.
Конкретная позиция на шахматной доске представляет собой взаимнооднозначное соответствие между множеством оставшихся на доске фигур и множеством занятых ими полей.Пример 2.9.
Соответствие в виде кодирования. Кодирование букв азбукой Морзе, представление чисел в различных системах исчисления, секретные шифры, входящие и исходящие номера в деловой переписке, различные классификации и др. – являются соответствиями между кодируемыми объектами и присваиваемым им кодами.
Данные соответствия обычно обладают всеми свойствами взаимнооднозначного соответствия, кроме одного – сюръективности (), которое в некоторых случаях может не выполняться.
Так единственность
образа и прообраза в кодировании
гарантирует однозначность шифровки и
дешифровки. Отсутствие сюръективности
означает, что не всякий код имеет смысл,
то есть соответствует какому-либо
объекту.
Соответствия, отображения, функции множеств
Пусть заданы множества А и В. Тогда Соответствием между А и В называется подмножество . О паре говорят, что B соответствует A при соответствии G. При этом Пр1G называется областью определения, а Пр2G – областью значений соответствия G. Таким образом, соответствие, обозначаемое G, представляет собой тройку множеств
G = (A, B, G ),
Где, зачастую, А — называется Областью отправлений, В — Областью прибытия, G — Графиком соответствия.
Если Пр1G=А, то соответствие называется Всюду определенным, а если Пр2G=В – Сюръективным.
Рис.1.12. Геометрические представления (а) не всюду определенного и не сюръективного соответствия, (б) – всюду определенного, (в) – сюръективного, А={A1,A2,A3,A4}, B={b1,b2,b3}.
На рис.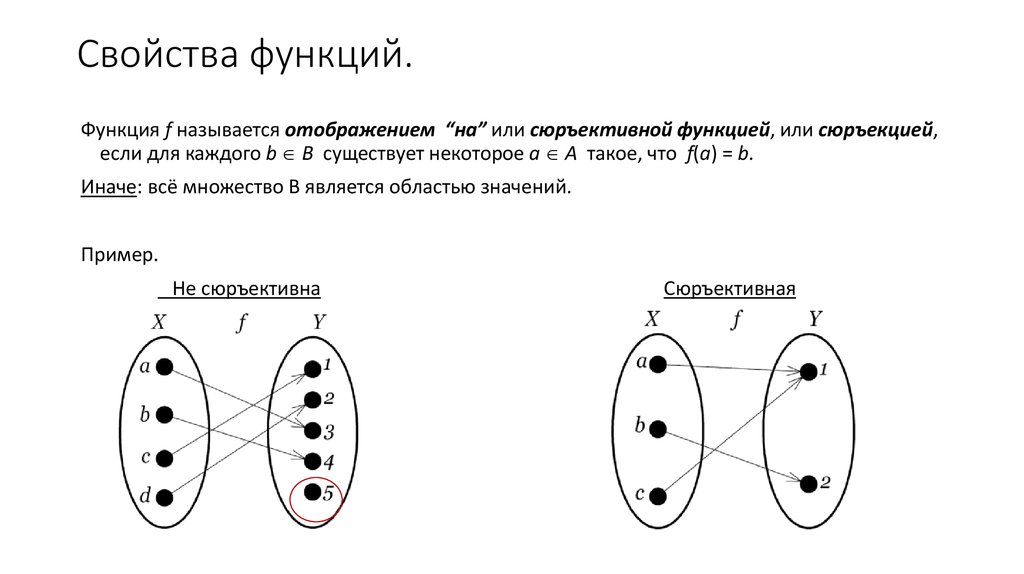
1.12. представлены примеры соответствий. Множество всех BÎВ, соответствующих элементу АÎА, называется образом при соответствии G. Например, для рис. 1.12.а {B1,B2}Ì В является образом А2ÎА. Одновременно множество всех АÎА, которым соответствует BÎВ, называются прообразом B в А. Так, на рис. 1.12.б {A1,A2,A3}ÌA является прообразом B2ÎВ. Если С Í ПР1G, то образом С является объединение образов всех элементов С. Аналогично определяется прообраз множества D для любого DÍПр2G.
Соответствие называется Функциональным, если образом любого элемента из Пр1G является единственный элемент из Пр2G. Таким является соответствие, представленное на рис.1.12.в.
Если соответствие g=(A, B,G) одновременно всюду определено, сюръективно, функционально и прообразом любого элемента из Пр2G является единственный элемент из Пр1G, то оно называется
Взаимно однозначным.Для примера рассмотрим на плоскости круг (рис.
1.13.)
. (1.53)
Рис.1.13. Пример соответствия, заданного кругом
Полагаем, что Х, уÎR и соответствие G зададим неравенством (1.53), тогда GÍRxR. Очевидно, что Х=3 соответствует единственное значение У=1, однако значению Х=2 соответствует УÎ[0;2]. Т. к. Пр1G=[1;3]ÌR, Пр2G=[0;2]ÌR, то соответствие не всюду определено и не сюръективно.
Если же А=[1;3], B=[0;2], то GÍ[1;3]x[0;2] и Пр1G=A, Пр2G=В и соответствие становится всюду определенным и сюръективным, но в связи с неединственностью образов для ХÎ(1;3) оно не является функциональным.
Если взять А=[1;3],B=[1;2], а в качестве G использовать только дугу окружности АВС, то каждому X будет соответствовать единственное значение Y и, очевидно, соответствие будет всюду определенным, сюръективным и функциональным, но не взаимно однозначным.
Для взаимной однозначности нужно взять A=[1;2], B=[1;2], а соответствие задать четвертью окружности АВ (или BC), для которой для каждого Y прообразом является единственное значение X.
В качестве другого примера можно рассмотреть англо-русский словарь, устанавливающий соответствие английских и русских слов. Такое соответствие не является функциональным (так как одному английскому слову соответствует в общем случае несколько русских), не полностью определено и не сюръективно (так как словарь содержит лишь часть действующих языков).
Пусть задано соответствие g=(A, B,G), GÍAxB. Если соответствие h=(B, A,H), HÍBxA таково, что тогда и только тогда, когда , то соответствие H (или Н) называется обратным к G (или G) и обозначается :
G-1=(B, A,G-1), G-1ÍBxA
Геометрическая интерпретация прямого и обратного соответствий представлены на рис.1.14, откуда с очевидностью следует, что (g-1)-1=g.
Б
Рис.1.14. Геометрическое представление прямого (a) и обратного (б) соответствий
Рассмотрим теперь два соответствия:
G=(A, B,G), GÍAxB;
H=(B, C,H), HÍBxC,
Где Пр2G=Пр1H.
Тогда каждому АÎПр1GÍA cоответствует некоторый образ из Пр2G, а каждому элементу из образа A соответствует образ C из Пр2HÍC.
Таким образом, каждому АÎПр1GÍA соответствует образ из Пр2HÍC и мы получим Композицию соответсвий
Графически иллюстрация композиции соответствий представлена на рис.1.15., для которых можем записать:
Рис.1.15. Геометрическое представление композиции соответствий
Очевидно, что композицию соответствий можно распространить и на произвольное число соответствий.
Функциональное соответствие между А и В называют функцией F и пишут:
F:А®В,
Или более привычно
И называют аргументом, а – значением функции.
Полностью определенная функция F:А®В называется Отображением А в В. Образ А при отображении f обозначается F(A) для . Если соответствие при этом сюръективно, то говорят, что имеет место отображение А на В. Если, например, F(A) состоит из одного элемента, то F называется функцией-константой.
Функции f и g Равны, ели равны их области определения (пусть это множество DÍA) и для любых АÎD f(A)=g(A).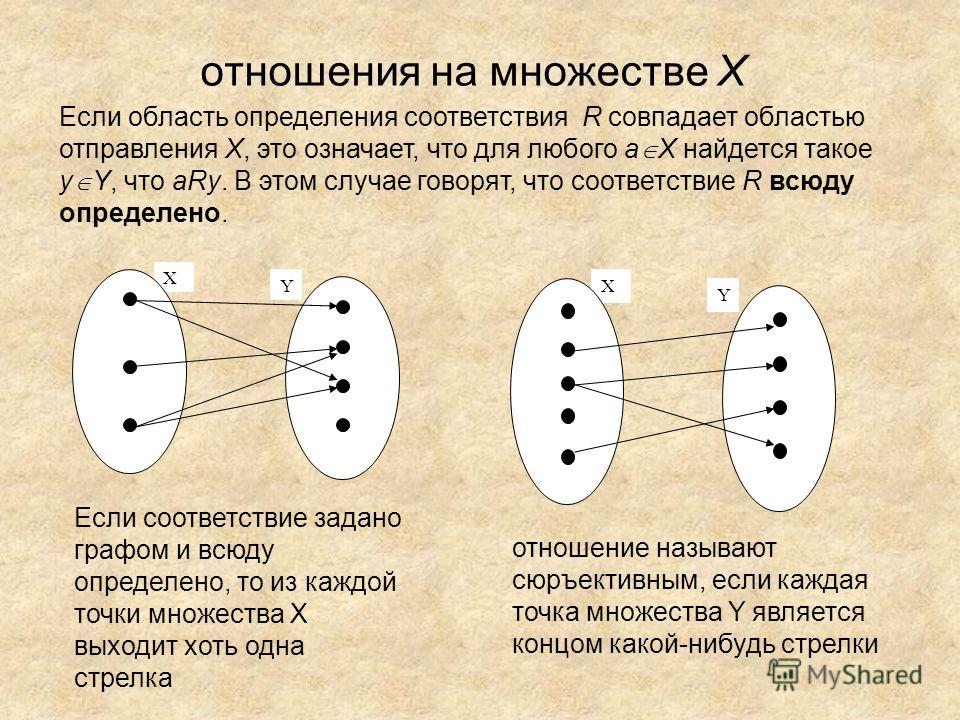
Функции типа
Называются N-местными функциями. Примером таких функций могут служить сложение и умножение действительных чисел на R. Это так называемые 2-х местные функции типа R2®R.
Еcли соответствие, обратное к функции F:A®B, является функциональным, то оно называется Функцией, обратной к F И обозначается .
Например, для соответствие F:X®Y, где F(X)=sinX, является взаимооднозначным, а, следовательно, существует обратное соответствие или обратная функция .
Как и для соответствий, для функций f:A®B, g:B®C можно ввести функцию H: A®C, которая называется Композицией F и G и обозначается , если имеет место равенство:
H(X)=G(F(X)), XÎA.
Пусть задана функция f:A®B, тогда она называется Инъективной
Если для существует АÎА такой, что , то функция F:A®B называется Сюръективной, а если функция F одновременно сюръективна и инъективна, то она называется Биективной и задает Взаимно однозначное Соответствие между А и В.
Например, о функциях F:R®R можно сказать, что:
Функция f(x)=10x инъективна, но не сюръективна;
Функция f(x)=x3-x сюръективна, но не инъективна;
Функция f(x)=5х-1 биективна.
В соответствии с введенными определениями можем утверждать, что отображение имеет обратное отображение тогда и только тогда, когда F – биективно. Очевидно, что это же справедливо для функций. Заметим также, что композиция двух биективных функций есть биективная функция.
Отображение eA:A®A называется Тождественным отображением множества А в себя, если для любого АÎА eA(A)=A.
Можно для инъективных функций отметить свойства:
А для биективных функций:
.
В более широком смысле Отображением Называют соответствие (X, Y, Г), Г Í X x Y, являющееся всюду определенным, т. е. Пр1Г=Х. В этом случае каждому хÎХ отображение Г ставит в соответствие некоторое подмножество Y, т. е.:
Очевидны простейшие свойства отображений:
A) если то:
Б) если то: .
Поскольку отображение является частным случаем соответствия, то для отображения имеют место введенные для соответствий понятия обратного отображения и композиции отображений.
Рассмотрим подробнее отображения и их свойства. Графическая интерпретация отображения Представлена на рис. 1.16.
Рис. 1.16. Иллюстрация отображения
Пример 1.4. Пусть множества натуральных чисел. Каждому поставим в соответствие число Тогда: , и т. д. Очевидно, что соответствие, заданная подобным образом, является отображением где или иногда пишут
Если рассмотреть отображение то Образом, Или Изображением Множества Является множество
Которое изображено на рисунке 1.17.
Рис. 1.17. Иллюстрация образа
Для примера 1.4. образом множества Является множество
Композиция двух отображений и это отображение обозначаемое ○ или иначе Иллюстрация композиции представлена на рис. 1.18.
Рис. 1.18.Иллюстрация композиции отображений
Из определения отображения очевидно, что поскольку должно быть: где И .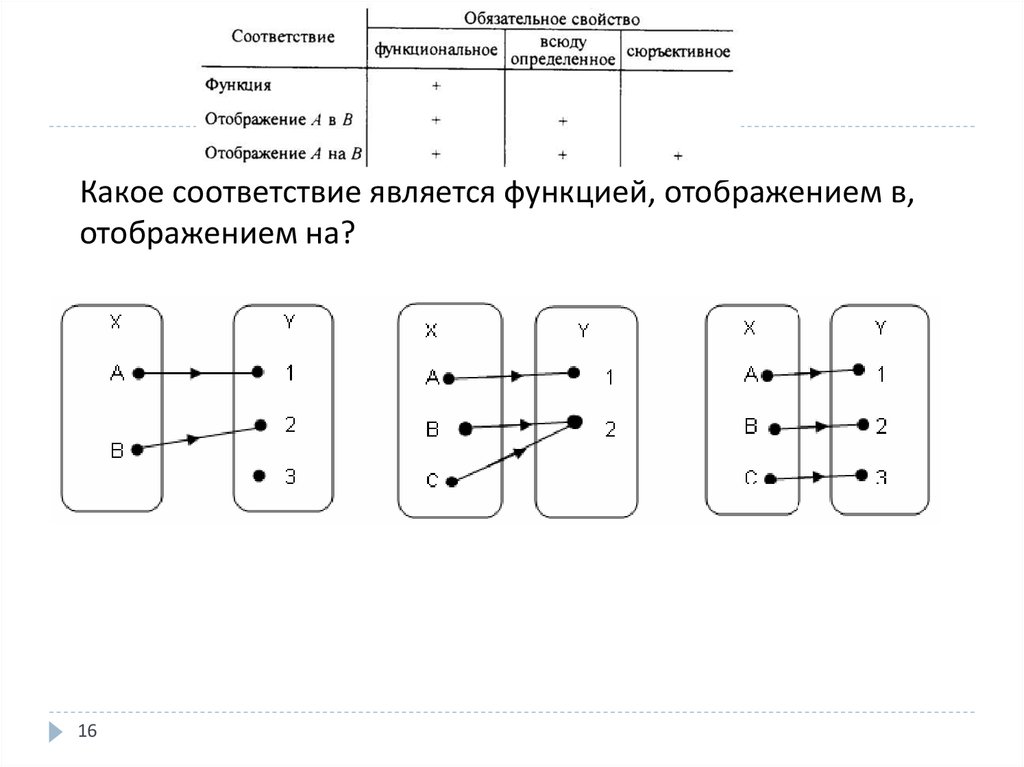
Пример 1.5. Пусть Множество людей, {январь, февраль,…}- множество месяцев года, Рассмотрим отображение, в котором ассоциируем каждого человека из с месяцем, в котором он родился и отображение , в котором каждому месяцу ставим в соответствие его номер от 1 до 12.
Тогда:
.
Точно так же можно получить композицию нескольких отображений. Можно только заметить, что в общем случае:
Отметим некоторые свойства отображений. Отображения и равны тогда и только тогда, когда каждый имеет один и тот же образ для обоих отображений, т. е.
Отображение Является инъекцией тогда и только тогда, когда двум разным элементам из Соответствуют разные элементы из , т. е.
Инъекция
Или иначе
Инъекция
Из последнего с очевидностью следует, что для инъективных отображений Справедливо (если И — конечные):
Пример 1.6. Пусть а отображение задано формулой . Такое отображение является инъекцией (см.
рис. 1.19.)
Рис. 1.19. Иллюстрация примера 1.6
Можно отметить, что композиция иньекций И есть инъекция. Действительно:
А отсюда следует, что
Отображение сюръективно тогда и только тогда, когда для каждого Существует хоть один элемент Такой, что Т. е.
Сюръекция
Или иначе
Сюръекция
Если И -конечные множества, то
Сюръекция
Пример 1.7. а отображение Определяется операция Взятие целой части действительного числа Тогда является сюръекцией, причем каждому соответствует бесконечное множество Например и т. д.
Заметим, что композиция сюръекций есть сюръекция. Действительно для сюръективных отображений и имеем:
и
Но тогда
Сюръекция.
Отображение называется биективным, если оно иньективно и сюръективно, т. е. взаимно однозначно (рис. 1.20). В этом случае видно, что для конечных множеств И
Рис. 1.20. Иллюстрация биективного отображения
Композиция двух биекций есть биекция.
Это следует с очевидностью из предыдущих утверждений о композициях иньекций и сюръекций.
Обратное отображение для отображения определим следующим образом. Отображение такое что причем каждая пара , т. е.:
Но Есть отображение, если каждому элементу соответствует единственный элемент — С другой стороны Нас Отображения и каждому соответствует единственный Следоватально является биективным, т. е. взаимно-однозначным отобржением.
Вывод. Если — обратное отображение, то Является биекцией.
Пример 1.8. Отображение , задано функцией обратным отображением есть и
Композиция прямого и обратного отображений, является с очевидностью инвариантным (тождественным) отображением, т. е.
Тождественное отображение Это отображение, для которого справедливо Из этого следует
Пример 1.9. Пусть Моноид, т. е. множество всех подмножеств множества Е. Отображение Определим для любого множества Как взятие дополнения
Но тогда для обратного отображения получим
Откуда
Частным, но достаточно важным случаем отображения, является случай совпадения X и Y, т.
е. отображения Г:Х®Х. При этом отображение Х самого в себя определяется парой (Х, Г), где ГÍХ2. Изучением таких отображений занимается, например, теория графов.
Примером графа может служить генеалогическое дерево (рис. 1.16), указывающее связь поколений. В этом графе точки – это люди, а стрелки указывают на «родительство».
Использование композиции отображений Г и Г позволяет записать и, если для графа на рис. 1.21. ГХ – множество детей, то Г2Х – множество внуков .
Г(ГХ)=Г2Х
Рис.1.21. Генеалогическое дерево, представленное графом
В общем случае для любого
Г k х=Г(Г k -1х), (1.54)
А введя по определению
Г0х=х, (1.55)
Можем для отрицательных k ввести соотношение
Г — k х=Г-1(Г –(k –1)х), (1.56)
Которое следует из (1.54) и (1.55)
Г0х=Г(Г-1х)=ГГ-1х,
Где Г-1 представляет собой обратное отображение.
На графе рис. 1.14 Г-1Х – родители элемента Х, Г-2Х – прародители
Для обозначения некоторых специальных видов отображений, заданных на одном и том же множестве или на разных, применяют также термин «отношение», которые мы рассмотрим в следующем разделе. Рассматривая отображение F:X®Y как функцию, мы не накладывали на множество Х каких либо ограничений. Однако чаще всего мы работаем с функциями действительных переменных – одно или многоместными, которые производят отображения R®R или Rn®R.
Вместе с тем, в задачах управления системами многочисленны случаи, когда из всех видов управления (читай «из определенного класса функций времени») требуется выбрать то, которое доставит некоторому показателю качества управления наилучшее (оптимальное) значение. Таким образом, множество Х в этом случае есть некоторое множество (класс) функций, а Y –множество действительных чисел.
Тогда можем записать отображение
J:M(F(T))®R, (1.
57)
Где M(f(t)) – множество действительных функций некоторого класса (кусочно-непрерывные, непрерывные, гладкие и т. п.). Такое отображение называется Функционалом, который записывается как J=J[f(t)]. Примерами функционалов могут служить следующие выражения:
1. , где yÎM1- множество интегрируемых на функций;
2. , где yÎM2 – множество дифференцируемых на функций.
Действительно для У1=sinX и Y2=-X3 получим:
Еще одним специфическим отображением является Оператор. Оператором L называется отображение
L:X®Y,
В котором X и Y являются множествами функций с элементами X(t) и Y(t), так что элементами множества L являются пары (X(t),y(t)). Говорят, что оператор L преобразует функцию X(t) в функцию
Представителем операторов является оператор дифференцирования , который можно записать, например, .
В задачах управления роль оператора часто выполняет сама управляемая система (рис.
1.22), преобразующая по некоторому закону L входной сигнал Х(t).
Рис.1.22. Представление управляемой системы в виде оператора,
Как понимать инъективные функции, сюръективные функции и биективные функции
Один из способов думать о функциях
Функции легко рассматривать как способ сопоставления чисел из одного набора с числами
другой. Например, функция f(x)=x+3 — это просто способ сказать, что я сопоставляю
сложить число 1 с числом 4, число 2 с числом 5 и т. д. Другой пример
будет функцией абсолютного значения, которая соответствует как -4, так и +4 числу +4. Думать о
выполняет функции сватов.
Функции могут быть «инъективными» (или «один к одному»)
Инъективная функция — это сваха, которая не из Юты. Полиамурных матчей не бывает
как и функция абсолютного значения, есть только однозначные совпадения, такие как f(x)=x+3 .
Возьмем два набора чисел A и B. Допустим, мы знаем, что между ними существует инъективная функция.
Это означает, что мы знаем, что каждое число в A имеет единственное уникальное совпадение в B. Но мы не знаем,
в B есть какие-то числа, которые «не учитываются» и ни с чем не сопоставляются. Если вы думаете
об этом, это подразумевает, что размер набора A должен быть меньше или равен размеру набора B.
Это важное следствие инъективных функций, и это одна из причин, по которой они часто встречаются.
Пример: f(x) = x! (факториальная функция)
где оба набора A и B являются набором всех положительных целых чисел (1, 2, 3…).
Почему это инъективно: все в множестве A соответствует чему-то в B, потому что факториалы дают только положительные целые числа. И не существует повторяющихся совпадений, потому что 1!
Функции могут быть «сюръективными» (или «на»)
Существуют также сюръективные функции. Сюръективные функции — это свахи, которые следят за тем, чтобы они
найти совпадение для всего набора B, и кто не против использовать для этого полиаморию.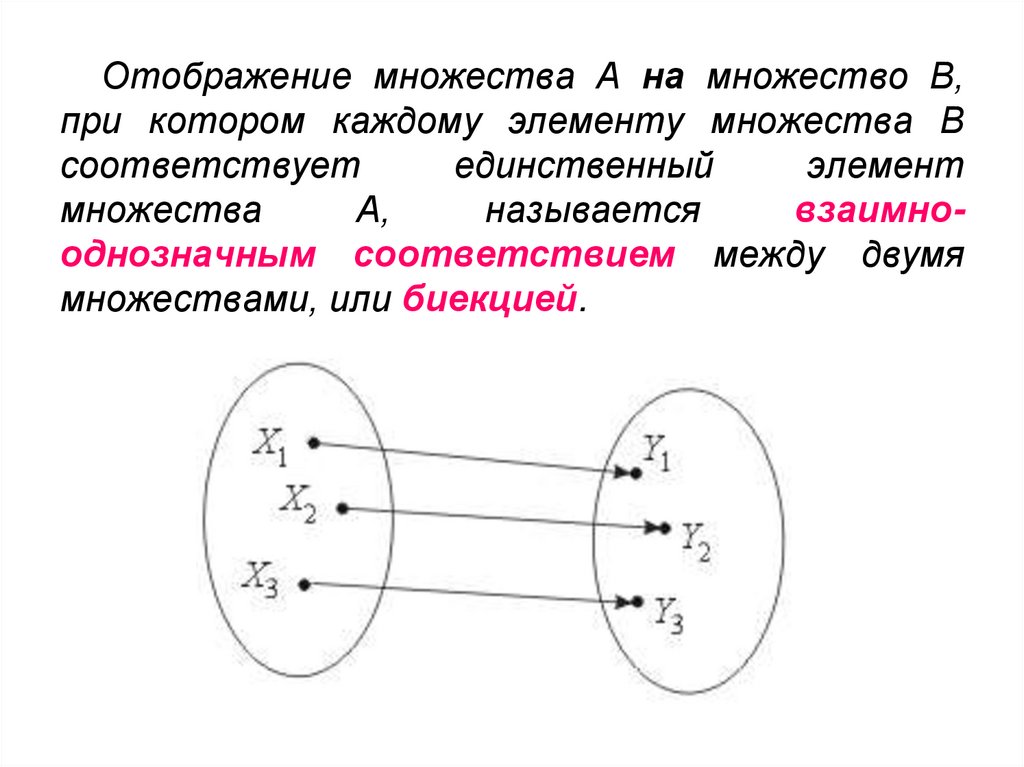
Итак, если вы знаете
между наборами A и B существует сюръективная функция, что означает, что каждое число в B соответствует
одно или несколько чисел в A. Опять же, если подумать, это означает, что размер множества A
должен быть больше или равен размеру множества B. Еще одно важное следствие.
Пример: f(x) = x 2 где A — множество действительных чисел, а B — множество неотрицательных
вещественные числа.
Почему это сюръективно: все множество B совпадает, потому что у каждого неотрицательного действительного числа есть действительное число который возводится в квадрат (а именно, его квадратный корень). Обратите внимание, что в этом примере полиамория распространен, потому что почти все числа в B имеют 2 совпадения с A (положительное и отрицательное квадратный корень).
Биективные функции
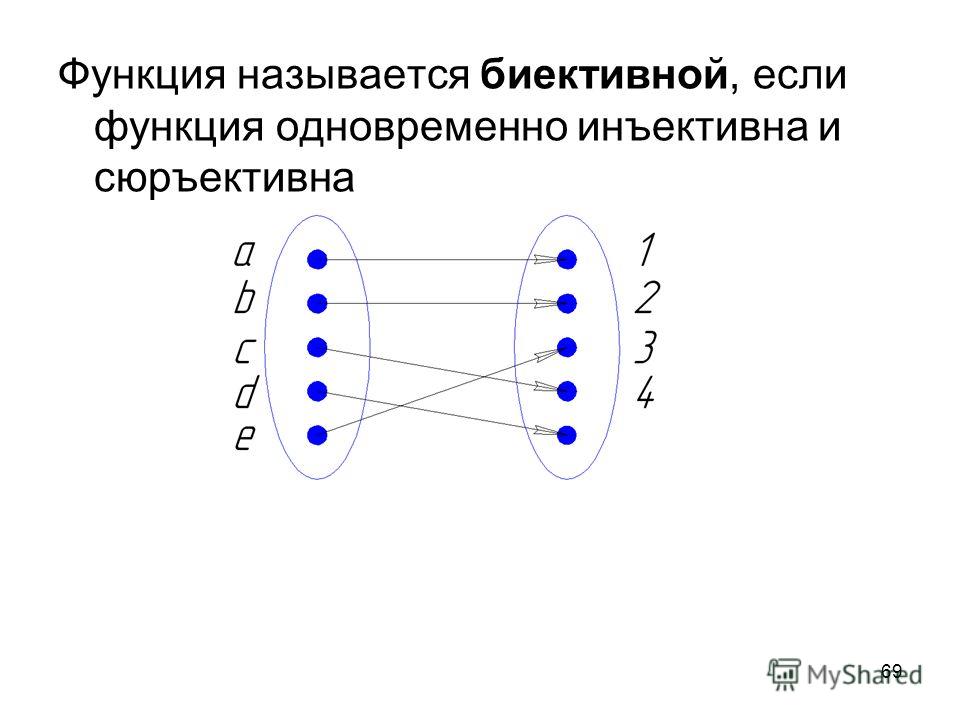
Наконец, биективная функция является одновременно инъективной и сюръективной. Если биективное
существует функция между A и B, то вы знаете, что размер A меньше или равен B
(из-за инъективности), и что размер A также больше или равен B (из-за того, что
сюръективный).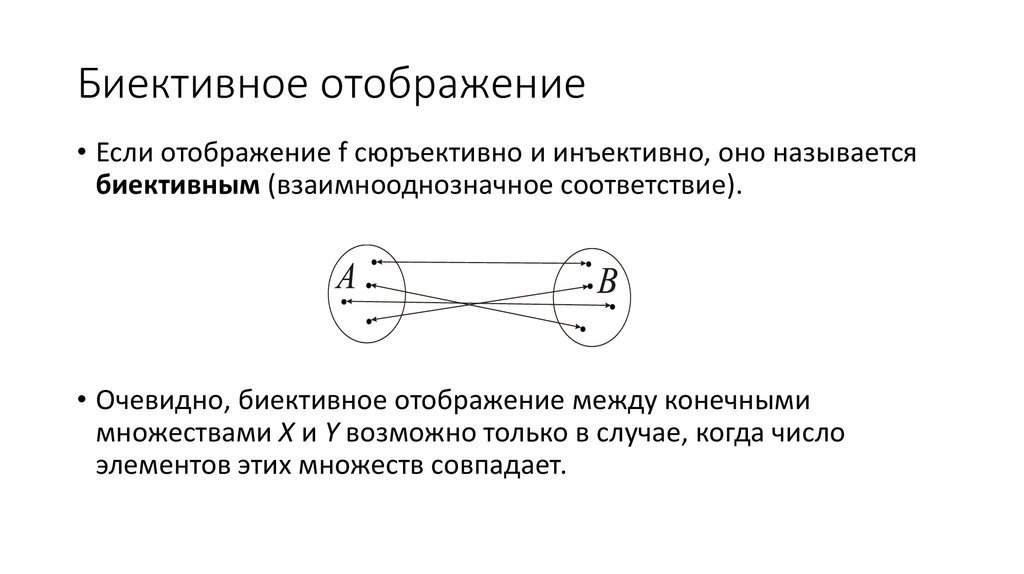
Тогда единственная возможность состоит в том, что размер A должен быть в точности равен
размер B. Так же, как если значение x меньше или равно 5, а также больше или
равно 5, то может быть только 5.
Пример: f(x) = 2x , где A — множество целых чисел, а B — множество четных целых чисел.
Почему оно биективно: все числа A совпадают с числами B, потому что каждое целое число при удвоении становится четным. Этот матч
уникальным, потому что когда мы берем половину любого конкретного четного числа, существует только один возможный
результат. Это делает функцию инъективной. Функция также сюръективна, потому что
ничего в B не «осталось», то есть нет четного целого числа, которое не может быть найдено
удвоение некоторого другого целого числа. Поскольку функция сопоставления одновременно инъективна и сюръективна,
это означает, что он биективен, и, следовательно, и A, и B имеют одинаковый размер. Если
вы думаете о том, что содержат А и В, интуиция приведет к предположению, что В может
быть вдвое меньше A.
Но, как ни удивительно, интуиция здесь оказывается ошибочной. И это
приводит к нашему выводу…
Как это относится к бесконечным множествам
Итак, для любых двух множеств, между которыми можно найти биективную функцию, вы знаете множества точно такого же размера. Даже бесконечные множества. Вот как Георг Кантор смог показать какие бесконечные множества были одного размера. Он нашел биекции между ними.
Кантор смог показать, какие бесконечные множества строго меньше других, с помощью демонстрируя, как любая возможная инъективная функция, существующая между ними, по-прежнему остается непревзойденной числа во втором наборе. Другими словами, любая функция, которая использовала все A однозначно сопоставление с B все еще не использовало все B. Следовательно, B должен быть больше по размеру.
Кантор показал, что существует бесконечное число размеров бесконечных множеств! Но возможно, я приберегу эту замечательную часть математики для другого раза.
Различия между инъективной функцией и сюръективной функцией
В математике функции широко используются для определения и описания определенных отношений между множествами и другими математическими объектами.
Кроме того, функции можно использовать для наложения математических структур на множества.
Если никакие два компонента домена не указывают на одно и то же значение в совместном домене, функция является инъективной. Функция сюръективна, если каждый элемент в области определения указывает по крайней мере на один элемент в области определения. Если функция обладает как инъективными, так и сюръективными свойствами.
Инъекция A→B сопоставляет A с B, что позволяет найти копию A внутри B. Сюръекция A→B сопоставляет A с B в том смысле, что изображение охватывает всю ширину B. Sur” – это латинское фраза, означающая «выше» или «выше», например, «избыток» или «обзор».
Инъективные и сюръективные функции
Инъективные функции
Инъективная функция или функция «один к одному» — это функция, которая отображает различные элементы одной области в различные элементы другой области.
Таким образом, рассмотрим f как функцию, областью определения которой является множество A.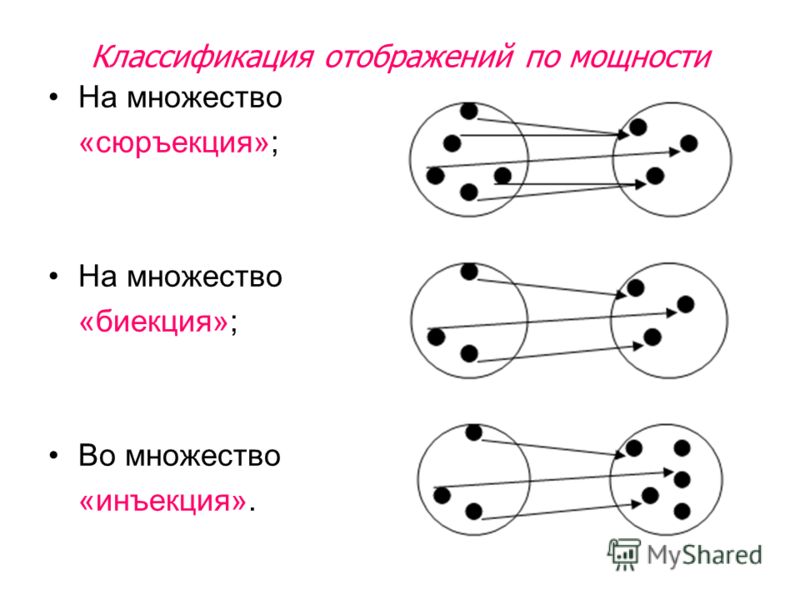
Если для всех x и y в A функция называется инъективной.
Предположим, что f(x) = f(y), а затем докажите, что x = y.
Предположим, что x не равно y, и продемонстрируем, что f(x) не равно f. (Икс).
Субъективные функции
Сюръективная функция (также сюръективная или онто-функция) в математике — это функция f, которая отображает элемент x в каждый элемент y; то есть для любого y существует такой x, что f(x) = y. Другими словами, каждый элемент кодового домена функции является образом хотя бы одного элемента домена функции.
Если каждый элемент кодового домена отображается хотя бы в один элемент домена, кодовый домен является сюръективным или на. Другими словами, каждый элемент кодомена имеет непустой прообраз. Функция сюръективна, если ее образ совпадает с кодовым доменом.
Если диапазон f равен кодовой области f, функция f : A → B сюръективна, или on.RB в каждой функции с диапазоном R и кодовой областью B.
Чтобы продемонстрировать, что данная функция сюръективна, мы должны установить, что Б Р; поэтому R = B будет истинным.
Differences of injective and surjective functions
Injective functions | Surjective functions |
An injective function is one in which each element of Y is transferred to at most один элемент X. |
Сюръективная функция — это функция, которая отображает каждый элемент Y в некоторый (т. е. хотя бы один) элемент X. |
Функция является однозначной или инъективной, если она не отображает два разных элемента домена в один и тот же элемент диапазона. |
Два простых качества, которыми могут обладать функции, оказываются чрезвычайно полезными. Если кодовый домен функции также является ее диапазоном, функция является онтогенной или сюръективной. |
функция f инъективна, если из a1a2 следует f(a1)≠f(a2) |
Если f равно своему диапазону, функция f:A→B сюръективна (на). Альтернативно, для любого bB существует некоторый aA такой, что f(a)=b. Это означает, что для любого y в B существует некоторый x в A, такой что y=f (x). |
Определить приемистость в заданной области. | Определение сюръективности домена. |
|
|
Пример: f:N→N,f(x)=3x является инъективным.
f:N→N,f(x)=x2 инъективно. |
Пример: f:N→N,f(x)=x+2 является сюръективным выражением. f:R→R,f(x)=x2 не является сюръективным, поскольку никакое действительное целое число не имеет отрицательного квадрата. |
Заключение
В этой статье мы делаем вывод, что Injective также известен как «One-to-One».