Онлайн калькулятор синуса, косинуса, тангенса и котангенса
- Подробности
Калькулятор онлайн вычисляет тригонометрические функции для любого значения угла α заданного в градусах: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec), косеканс (cosec), версинус (синус-верзус) (versin), коверсинус (косинус-верзус) (vercos), гаверсинус (половина от синус-верзус) (haversin), экссеканс (exsec), экскосеканс (excsc).
Вычислить значения синуса и косинуса для стандартных значений углов можно с помощью тригонометрической окружности (тригонометрического круга). Например по тригонометрическому кругу можно найти значение синуса 45 градусов, косинуса 60 градусов или косинуса 90 градусов.
Вычислить значения для тангенсов и котангенсов можно с помощью
| Дано: | Решение: | |||||
| Значение угла α, град. | ||||||
Прямые тригонометрические функции | sin(α) | = | синус | = | вычисление синуса угла | |
| cos (α) | = | косинус | = | вычисление косинуса угла | ||
Производные тригонометрические функции | tg (α) | = | тангенс | = | вычисление тангенса угла | |
| сtg (α) | = | котангенс | = | вычисление котангенса угла | ||
Прочие тригонометрические функции | sec (α) | = | секанс | = | вычисление секанса угла | |
| cosec (α) | = | косеканс | = | вычисление косеканса угла | ||
| versin (α) | = | версинус | = | вычисление версинуса угла | ||
| vercos (α) | = | коверсинус | = | вычисление коверсинуса угла | ||
| haversin (α) | = | гаверсинус | = | вычисление гаверсинуса угла | ||
| exsec (α) | = | экссеканс | = | вычисление экссеканса угла | ||
| excsc (α) | = | экскосеканс | = | вычисление экскосеканса угла | ||
| округление до 12345 знаков после запятой | ||||||
| Тригонометрические функций на единичной окружности | Тригонометрический круг (тригонометрическая окружность) |
Тригонометрическая таблица основных значений синусов, косинусов, тангенсов и котангенсов.
| α | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
| sin(α) | 0 | 1/2 | √2/2 | √3/2 | 1 | √3/2 | √2/2 | 1/2 | 0 | -1/2 | -√2/2 | -√3/2 | -1 | -√3/2 | -√2/2 | -1/2 | 0 |
| cos(α) | 1 | √3/2 | √2/2 | 1/2 | 0 | -1/2 | -√2/2 | -√3/2 | -1 | -√3/2 | -√2/2 | -1/2 | 0 | 1/2 | √2/2 | √3/2 | 1 |
| tg(α) | 0 | √3/3 | 1 | √3 | — | -√3 | -1 | -√3/3 | 0 | √3/3 | 1 | √3 | — | -√3 | -1 | -√3/3 | 0 |
| ctg(α) | — | √3 | 1 | 0 | -√3/3 | -1 | -√3 | — | √3 | 1 | √3/3 | 0 | -√3/3 | -1 | -√3 | — | |
| α | 0 | π/6 | π/4 | π/3 | π/2 | 2π/3 | 3π/4 | 5π/6 | π | 7π/6 | 5π/4 | 4π/3 | 3π/2 | 5π/3 | 7π/4 | 11π/6 | 2π |
I.
Для справки:
- тригонометрические функции
- — элементарные функции, которые возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе (или, что равнозначно, зависимость хорд и высот от центрального угла (дуги) в круге). Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение тригонометрических функций было расширено, их аргументом теперь может быть произвольное вещественное или даже комплексное число. Наука, изучающая свойства тригонометрических функций, называется тригонометрией.
Основные тригонометрические функции:
- синус угла α
- обозначается sin(α) — отношение длины противоположного этому углу катета к гипотенузе;
- косинус угла α
- обозначается cos(α) — отношение прилежащего этому углу катета к гипотенузе.
Остальные тригонометрические функции можно выразить через синус и косинус:
- тангенс
- обозначается tg(α) — отношение длины противоположного углу катета к прилежащему катету;
- котангенс
- обозначается ctg(α) — отношение длины прилежащего к углу катета к противоположному катету;
- секанс
- обозначается sec(α) — отношение длины гипотенузы к прилежащему к углу катету;
- косеканс
- обозначается cosec(α) — отношение длины гипотенузы к противоположному катету.
Редко используемые тригонометрические функции:
- версинус
- обозначается versin(α) — единица минус косинус угла α;
- коверсинус
- обозначается vercos(α) — единица минус синус угла α;
- гаверсинус
- обозначается haversin(α) — половина версинуса угла α;
- экссеканс
- обозначается exsec(α) — секанс угла α минус единица;
- экскосеканс
- обозначается excsc(α) — косеканс угла α минус единица.
II. Примечание:
- Округление результатов расчета выполняется до указанного количества знаков после запятой (по умолчанию — округление до сотых).
- Блок исходных данных выделен желтым цветом, блок промежуточных вычислений выделен голубым цветом, блок решения выделен зеленым цветом.
ФорумСпециалистыО нас
Ссылка для цитирования в списке литературы: CAE-CUBE: [Электронный ресурс]. URL: https://premierdevelopment.ru/ (дата обращения ) | premierdevelopment.ru, все права защищены, 2015 - 2021 e-mail: Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра. |
Функция косинуса: онлайн калькулятор, формулы, график
Функция {$ main.types[data.type] $}
Введите угол α{$ main.angles[data.
Результат расчёта
{$ data.type $}(α) = {$ result[0]|number:data.round $}
Введите {$ data.type $}(α){$ main.angles[data.angle2] $}
Результаты расчёта
- {$ result[1] $}
- {$ result[2] $}
Округлять до {$ data.round $} {$ Plural(data.round, [‘знака’, ‘знаков’, ‘знаков’]) $} после запятой
Косинус — тригонометрическая функция, которая геометрически определяется как соотношение прилежащего катета к гипотенузе. Как и все тригонометрические функции, косинус нашел широчайшее применение в науке.
История вопроса
Тригонометрия как наука возникла еще в Древней Индии, когда ученые разработали таблицу соотношений катетов и гипотенуз и их численных значений для основных углов. Термин «косинус» — сравнительно молодой, так как изначально ученые пользовались только синусом и тангенсом угла.
Complementry sinus, он же дополнительный синус, он же косинус — это просто синус угла, смещенного на 90 градусов. Именно поэтому для расчета соотношений прилежащего к углу катета и гипотенузы использовался синус смещенного угла, что упрощало расчеты.
Геометрически косинус — это соотношение прилежащего катета к гипотенузе. Прилежащий катет — это сторона прямоугольного треугольника, которая вместе с гипотенузой образует рассматриваемый угол. Как и любая тригонометрическая функция, изначально косинус рассчитывался только для углов. Для любого значения угла косинус имеет строго определенное значение и никогда не изменяется. С развитием математической науки тригонометрические функции были расширены на всю числовую ось, и сегодня легко взять косинус не только целого числа, но также вещественного и даже комплексного.
Определение косинуса
Итак, есть прямоугольный треугольник, катеты которого обозначаются как A и B, а гипотенуза как C. Из определения косинуса мы получаем, что для заданного угла AC его соотношение прилежащего катета и гипотенузы будет равно cosAC = A/C.
Изначально косинусы рассчитывались только для прямоугольных треугольников, однако с развитием математической науки косинусы прочно вошли в расчеты и сейчас используются для любых треугольников. Одним из таких примеров является теорема косинусов — теорема евклидовой геометрии, которая расширяет теорему Пифагора на любые плоские треугольники.
Теорема косинусов
Для любого треугольника справедливо равенство:
a2 = b2 + c2 — 2b × c × cosA,
где угол A — это угол, противолежащий стороне a.
Данное уравнение правдиво для любых плоских треугольников и при помощи него легко определить угол или одну из сторон. Если угол A — прямой, то выражение 2b×c×cosA обращается в ноль, так как cos90 = 0. Следовательно, напротив прямого угла лежит наибольшая сторона или гипотенуза, а теорема косинусов превращается в классическую теорему Пифагора:
a2 = b2 + c2,
где a — гипотенуза.
Использование косинусов
В повседневной жизни тригонометрические функции не находят применения.
Вся бытовая математика находится на уровне математических познаний древних греков, когда для простейших расчетов используются элементарные арифметические функции и рациональные соотношения. Однако большая часть современных технологий функционирует с использованием различных тригонометрических функций. К примеру, для определения мощности электротехнических приборов используется косинус фи — косинус угла между векторными значениями тока и напряжения. Еще пример: через тригонометрические функции легко перевести геодезические углы в привычные нам координаты на земной поверхности.
Наша программа представляет собой онлайн-калькулятор, который позволяет рассчитывать значения основных тригонометрических функций углов, выраженных в градусах или радианах. Для использования калькулятора требуется выбрать в меню программы требуемую функцию и ввести величину угла в градусах. Калькулятор вычисляет и обратную функцию арккосинуса. Если требуется определить угол по известному значению косинуса, введите значение функции в ячейку «Косинус» и выполните расчет.
Программа мгновенно выдаст значение угла. Рассмотрим пару примеров использования калькулятора.
Примеры из жизни
Вычисление углов
Пусть в задаче по геометрии дан треугольник со сторонами A = 3 см, B = 4 см и C = 5 см. Требуется найти значения всех углов. На первый взгляд это сложная задача, однако мы знаем, что 3, 4 и 5 — это классическая пифагорова тройка, следовательно, известны значения катетов и гипотенуз. Очевидно, что угол AB = 90 градусов, так как катеты всегда образуют прямой угол. Теперь мы можем найти углы AC и BC. Косинус угла численно равен дроби, в числителе которой стоит прилежащий катет, а в знаменателе — гипотенуза. Прилежащие катеты — это образующие угол катеты, следовательно, cosAC = A/C и cosBC = B/C. Подсчитаем численные значения:
- cosAC = A/C = 3/5 = 0,6;
- cosBC = B/C = 4/5 = 0,8.
Теперь определим соответствующие углы при помощи нашего калькулятора. Углы с такими значениями косинусов равны соответственно 53,13 и 36,87 градуса.
Правильность решения легко проверить, сложив величины углов:
90 + 53,13 + 36,87 = 180.
Расчет косинусов
Прямая задача определения численных значений функций — это вычисление косинуса в зависимости от величины угла. Для такой задачи можно использовать таблицу Брадиса — четырехзначные таблицы значений тригонометрических функций для целочисленных величин углов. Вычислим значения косинусов для основных углов. Для этого введем значения в ячейки «Косинус»:
- cos30 = 0,866;
- cos45 = 0,707;
- cos60 = 0,5;
- cos90 = 0;
- cos120 = –0,5;
- cos150 = — 0,866;
- cos180 = — 1.
Это основные значения косинусов для стандартных величин углов треугольника. В целом значения тригонометрических функций периодически повторяются каждые 360 градусов.
Заключение
Тригонометрия — определенно важный раздел математики, функции которого повсеместно используются в современных технологиях. Наши калькуляторы прекрасно подходят для элементарных расчетов по геометрии и тригонометрии.
Синус Косинус Тангенс Калькулятор — Бесплатный Калькулятор Тригонометрии
Синус Косинус Тангенс являются основными функциями тригонометрии и основаны на прямоугольном треугольнике.
Что такое калькулятор синусо-косинуса-тангенса?
«Калькулятор синуса, косинуса, тангенса» — это онлайн-инструмент, который помогает вычислить значения синуса, косинуса и тангенса для заданного угла тета. Этот онлайн-калькулятор синуса, косинуса и тангенса поможет вам вычислить значения синуса, косинуса и тангенса для заданного угла тета за несколько секунд.
Калькулятор синус-косинуса-тангенса
ПРИМЕЧАНИЕ. Введите угол до трех цифр
Как использовать Калькулятор синус-косинуса-тангенса?
Чтобы найти значения синуса, косинуса и тангенса для заданного тета-угла, выполните следующие действия:
- Шаг 1: Выберите из раскрывающегося списка отношение синуса, косинуса и тангенса для заданного тета-угла. .
- Шаг 2: Введите угол тета (в градусах) в данное поле ввода.
- Шаг 3: Нажмите кнопку «Вычислить» , чтобы найти значения синуса, косинуса и тангенса для заданного угла тета.
- Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и найти значения синуса, косинуса и тангенса для различных углов.
.Как найти отношение синус-косинуса-тангенса?
Функция синуса определяется как отношение длины противоположной стороны к длине гипотенузы в прямоугольном треугольнике. Синус — это тригонометрическая функция угла. Он обозначается как sinθ, где θ – угол между двумя сторонами.
Функция косинуса определяется как отношение длины прилежащей стороны к длине гипотенузы в прямоугольном треугольнике. Косинус – это тригонометрическая функция угла. Он обозначается как cosθ, где θ – угол между двумя сторонами.
Касательная функция определяется как отношение длины противоположной стороны к длине смежной стороны прямоугольного треугольника.
Тангенс — это тригонометрическая функция угла. Он обозначается как tanθ, где θ – угол между двумя сторонами.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Забронировать бесплатный пробный урок
Пример 1:
Найдите значение синуса, если θ = 45°?
Решение:
Дано θ = 45°
sin 45° = 1 / √2
= 0,71
Пример 2:
Найдите значение косинуса, если θ = 60°?
Решение:
Дано θ = 60°
cos 60° = 1 / 2
Пример 3: Найдите значение тангенса, если θ = 45°?
Решение:
Дано θ = 45°
tan 45° = 1
перейти к слайдуперейти к слайдуперейти к слайду
Точно так же вы можете попробовать калькулятор синуса, косинуса, тангенса, чтобы найти значения синуса, косинуса и тангенса для следующего:
- θ = 60°
- θ = 150°
- Функция синуса
- Функция косинуса
- Касательная функция
Рабочие листы по математике и визуальная программа
Калькулятор sin онлайн — Расчет sin — производная — первообразная — предел
Sin, расчет онлайн
Резюме:
Тригонометрическая функция sin для вычисления синуса угла в радианах,
градусов или градианов.
sin online
Описание:
Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить синус , косинус и касательная угла через одноименные функции.
Синус тригонометрической функции отметил грех , позволяет рассчитать синус угла онлайн , можно использовать разные угловые единицы: градус, градус и радианы, которые по умолчанию являются угловыми единицами.
- Расчет синуса
- Таблица специальных синусоидальных значений
- Основные свойства
Вычисление синуса угла в радианах
Калькулятор синуса позволяет с помощью функции sin вычислить онлайн синус синус угла в радианах, сначала нужно
выберите нужную единицу, нажав на кнопку параметров расчетного модуля.
После этого можно приступать к расчетам.
Чтобы вычислить синус онлайн от `pi/6`, введите sin(`pi/6`), после вычисления результат `1/2` возвращается.
Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.
Вычислить синус угла в градусах
Чтобы вычислить синус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить синус 90, введите sin(90). результат 1 возвращается.
Вычислить синус угла в градусах
Чтобы вычислить синус угла в градианах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить синус 50, введите sin(50), после вычисления,
возвращается результат `sqrt(2)/2`.
Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.
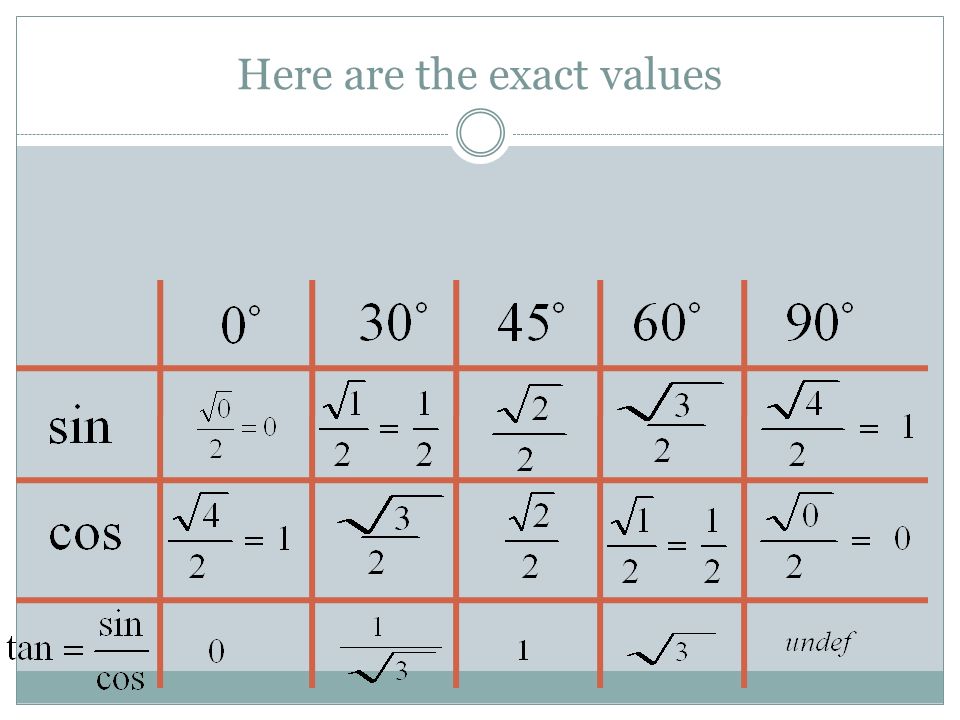
Синус допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот таблица общих синусоидальных значений :
| sin(`2*pi`) | `0` |
| sin(`pi`) | `0` |
| sin(`pi/2`) | `1` |
| sin(`pi/4`) | `sqrt(2)/2` |
| sin(`pi/3`) | `sqrt(3)/2` |
| sin(`pi/6`) | `1/2` | sin 902(*) pi/3`) | `sqrt(3)/2` |
| sin(`3*pi/4`) | `sqrt(2)/2` |
| sin(`5*pi/ 6`) | `1/2` |
| sin(`0`) | `0` |
| sin(`-2*pi`) | `0` |
| sin(`-pi`) | `0` | sin `pi) | `-1` |
| sin(`-pi/4`) | `-sqrt(2)/2` |
| sin(`-pi/3`) | `-sqrt(3) )/2` |
| sin(`-pi/6`) | `-1/2` |
| sin(`-2*pi/3`) | `-sqrt(3)/2 ` |
| sin(`-3*pi/4`) | `-sqrt(2)/2` |
| sin(`-5*pi/6`) | `-1/2` |
`AA x в RR, k в ZZ`,
- `sin(-x)= -sin(x)`
- `sin(x+2*k*pi)=sin(x)`
- `sin(pi-x)=sin(x) `
- `sin(pi+x)=-sin(x)`
- `sin(pi/2-x)=cos(x)`
- `sin(pi/2+x)=cos(x) `
Производная синуса равна cos(x).
Первообразная синуса равна -cos(x).
Функция sine является нечетной функцией, для каждого действительного x `sin(-x)=-sin(x)`. Следствием для кривой, представляющей синусоидальную функцию, является то, что она допускает начало отсчета как точку симметрии.
Калькулятор имеет решатель, который позволяет решать уравнение с синусом формы cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `грех(х)=1/2` или `2*sin(x)=sqrt(2)` с этапами расчета.
Синтаксис:
sin(x), где x — мера угла в градусах, радианах или градах.
Примеры:
sin(`0`), возвращает 0
Производная синус :
Чтобы дифференцировать функцию синуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции синуса
производная sin(x) is производная(`sin(x)`)=`cos(x)`
Первообразная синуса :
Калькулятор первообразной позволяет вычислить первообразную функции синуса.
Первопроизводная sin(x) является первообразной(`sin(x)`)=`-cos(x)`
Предел синуса :
Калькулятор предела позволяет вычислить пределы функции синуса.
предел sin(x) это limit(`sin(x)`)
Обратная функция синуса :
обратная функция синуса представляет собой функцию арксинуса, отмеченную арксинусом.
График синуса :
Графический калькулятор может отображать функцию синуса в заданном интервале.
Свойство функции синуса:
Функция синуса является нечетной функцией.
Вычислить онлайн с sin (sine)
См. также
Список связанных калькуляторов:
- Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
- Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.