Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
05.15
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Найдите гипотенузу прямоугольного треугольника,если периметр равен 24 см,а площадь 24 см2
геометрическая прогрессия (bn) задана условиями: b1= 1/2, bn+1=3bn.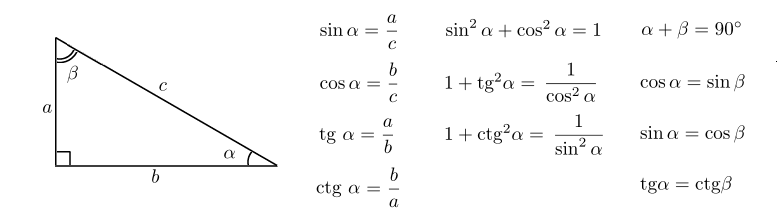
—+—+—=30 Заполните пустые места используя данные числа (1,3,5,7,9,11,13,15) Одно и тоже число можно использовать несколько раз.
Площадь равнобедренного треугольника равна 81 корень 3 .Длина боковой стороны равна 18.Найти косинус угла ,лежащего напротив основания треугольника , если известно что этот угол тупой
Точка D на стороне AB треугольника ABC выбрана так,что AD =AC.Известно что треугольник CAB=10 и треугольник ACB=166.Найдите угол DCB ответ дайте в градусах
Пользуйтесь нашим приложением
Решение | Есть синус | Тригонометрия: треугольники к функциям
Выйти из полноэкранного режима
Наиболее знакомыми нам тригонометрическими функциями являются синус и косинус.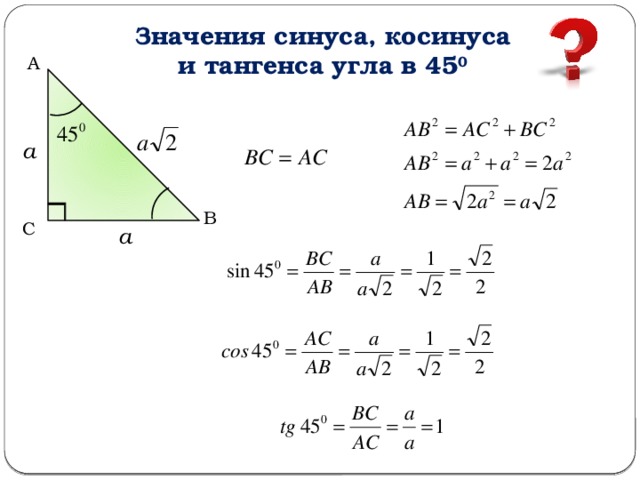
Из них мы можем получить тангенс, а также обратные секанс, косеканс и котангенс. В прошлом математики также использовали множество других тригонометрических функций. Некоторые из них проиллюстрированы ниже.
Найдите следующие длины через \(\sin\theta\) и \(\cos \theta\).
\(ОБ\)
\(АВ\)
\(BC\) (это было известно как стихов синуса или стихов из \(\theta\), написанных \(\mathop{\mathrm{versin}}\theta\))
Треугольник \(OAB\) прямоугольный, с прямым углом при \(B\) и гипотенузой длины \(1\), поэтому мы видим, что \[OB = \cos\theta.\]
Аналогично, мы имеем \(AB = \sin\theta.\)
Поскольку окружность является единичной окружностью, мы знаем, что \(OC = 1\) и, следовательно, \[BC = OC — OB = 1 — \ cos \theta.\] Это говорит нам о том, что \(\mathop{\mathrm{versin}}\theta = 1 — \cos \theta.\)
\(ОД\)
\(CD\) (это было известно как exsecant от \(\theta\), написанное \(\mathop{\mathrm{exsec}}\theta\))
Треугольник \(OAD\) прямоугольный, с прямым углом при \(A\) и \(\угол DOA = \theta\), а сторона \(OA\) имеет длину \(1 \), поэтому мы находим, что \(\cos\theta = \dfrac{1}{OD},\) поэтому \[OD = \dfrac{1}{\cos\theta}.
\]
Следовательно, мы имеем \ [CD = OD-OC = \dfrac{1}{\cos\theta} — 1 = \sec\theta — 1.\] Это означает, что мы можем написать \(\mathop{\mathrm{exsec}}\theta = \ сек\тета — 1.\)
\(AD\)
\(AE\)
Снова взглянув на треугольник \(OAD\), мы находим, что \[AD = \tan\theta = \dfrac{\sin\theta}{\cos\theta}.\]
Мы можем рассмотреть треугольник \(AOE \), который имеет прямой угол при \(A\) и угол \(\theta\) при \(E\). Сторона \(AO\) имеет длину \(1\), поэтому мы видим, что \(\tan\theta = \dfrac{1}{AE},\) и, следовательно, \[AE = \cot\theta = \ dfrac{\cos\theta}{\sin\theta}.\]
\(AG\)
\(GO\)
\(FG\) (это было известно как покрытый синус или покрывающий синус из \(\theta\), написанный \(\mathop{\mathrm{coversin}}\theta\) или \(\ mathop {\ mathrm {обложки}} \ тета \) или \ (\ mathop {\ mathrm {cvs}} \ тета \))
Треугольник \(AGE\) имеет прямой угол в точке \(G\) и угол \(\theta\) в точке \(E\), и мы только что видели, что его гипотенуза имеет длину \(\cot\theta\ ).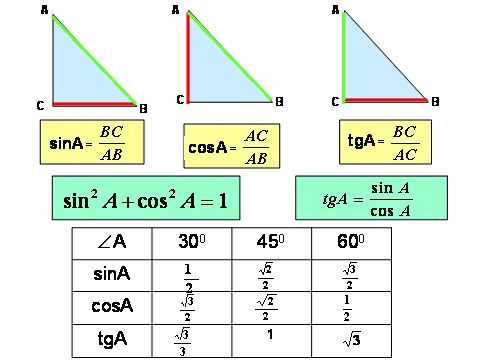
Итак, \[AG = \cot\theta \sin\theta = \cos\theta.\]
Четырехугольник \(ABOG\) является прямоугольником, так как все его углы прямые, поэтому \[GO = AB = \sin\theta.\]
Круг имеет радиус \(1\), поэтому \[FG = FO — GO = 1 — \sin\theta.\] Поэтому \(\mathop{\mathrm{coversin}}\theta = 1 — \sin\theta.\)
- \(EF\) (это было известно как экзосеканс от \(\theta\), записанный \(\mathop{\mathrm{excosec}}\theta\) или \(\mathop{\mathrm{excsc}}\theta\))
Длину \(EO\) можно найти, используя прямоугольный треугольник \(DOE\), у которого есть угол \(\theta\) (в точке \(E\)). Мы знаем, что \(OD = \sec\theta\), поэтому имеем \[EO = \dfrac{\sec\theta}{\tan\theta} = \dfrac{1}{\sin\theta}.\ ]
Тогда мы имеем \[EF = EO — 1 = \dfrac{1}{\sin\theta} — 1.\] Следовательно, мы можем написать \(\mathop{\mathrm{excosec}}\theta= \cosec \ тета -1.\)
Сможете ли вы найти на диаграмме отрезки, имеющие следующие длины?
косинус или веркосинус из \(\theta\), записанный как \(\mathop{\mathrm{vercos}}\theta\), который определяется как \[\mathop{\mathrm {vercos}}\theta = 1 + \cos\theta.
\]Покрытый косинус или каверкосинус от \(\theta\), записанный как \(\mathop{\mathrm{covercos}}\theta\), который определяется как \[\mathop{\mathrm{covercos}}\theta = 1 + \sin\theta.\]
\]Поскольку окружность имеет радиус \(1\) и \(OB = \cos\theta\), отрезок \(BH\) имеет длину \(1 + \cos\theta\).
Точно так же \(GJ\) имеет длину \(1 + \sin\theta\).
Мы знаем, что \(\cos\theta = \sin\left(\dfrac{\pi}{2} — \theta\right)\).
Как связаны версин и каверсин?
Как связаны веркозин и каверкозин?
У нас есть
\[\начать{выравнивать*}
\mathop{\mathrm{coversin}}\left(\dfrac{\pi}{2} — \theta\right) &= 1 — \sin\left(\dfrac{\pi}{2} — \theta\right ) \\
&= 1 — \cos\тета\\
&= \mathop{\mathrm{версин}}\тета.
\конец{выравнивание*}\]
Точно так же у нас есть
\[\начать{выравнивать*}
\mathop{\mathrm{covercos}}\left(\dfrac{\pi}{2} — \theta\right) &= 1 + \sin\left(\dfrac{\pi}{2} — \theta\right ) \\
&= 1 + \cos\тета\\
&= \mathop{\mathrm{vercos}}\тета.