Онлайн калькулятор суммы ряда: Найти сумму ряда online

alexxlab / / Разное

ВТБ кредитный калькулятор, калькулятор кредита онлайн расчет в 2023 году.

Дата платежаОстаток долгаНачисление %Платеж в
основной долг		Сумма платежа
07.04.2023100 000,00373,701 486,061 859,76
07.05.202398 513,94356,271 503,491 859,76
07.06.202397 010,45362,531 497,231 859,76
07.07.202395 513,22345,421 514,341 859,76
07.08.202393 998,88351,271 508,491 859,76
07.09.202392 490,39345,641 514,121 859,76
07.10.202390 976,27329,011 530,751 859,76
07.11.202389 445,52334,261 525,501 859,76
07. 12.202387 920,02317,961 541,801 859,76
07.01.202486 378,22322,791 536,961 859,76
07.02.202484 841,26317,051 542,711 859,76
07.03.202483 298,55291,201 568,561 859,76
07.04.202481 729,99305,421 554,331 859,76
07.05.202480 175,66289,951 569,811 859,76
07.06.202478 605,85293,751 566,011 859,76
07.07.202477 039,84278,611 581,151 859,76
07.08.202475 458,69281,991 577,771 859,76
07.09.202473 880,92276,091 583,671 859,76
07.10.202472 297,26261,461 598,301 859,76
07. 11.202470 698,96264,201 595,561 859,76
07.12.202469 103,40249,911 609,851 859,76
07.01.202567 493,55252,221 607,541 859,76
07.02.202565 886,01246,221 613,541 859,76
07.03.202564 272,47216,941 642,821 859,76
07.04.202562 629,65234,051 625,711 859,76
07.05.202561 003,94220,621 639,141 859,76
07.06.202559 364,80221,851 637,911 859,76
07.07.202557 726,89208,771 650,991 859,76
07.08.202556 075,90209,551 650,201 859,76
07.09.202554 425,69203,391 656,371 859,76
07. 10.202552 769,32190,841 668,921 859,76
07.11.202551 100,40190,961 668,801 859,76
07.12.202549 431,60178,771 680,991 859,76
07.01.202647 750,61178,441 681,311 859,76
07.02.202646 069,30172,161 687,601 859,76
07.03.202644 381,70149,801 709,951 859,76
07.04.202642 671,75159,461 700,291 859,76
07.05.202640 971,45148,171 711,591 859,76
07.06.202639 259,86146,711 713,041 859,76
07.07.202637 546,82135,791 723,971 859,76
07.08.202635 822,85133,871 725,891 859,76
07. 09.202634 096,96127,421 732,341 859,76
07.10.202632 364,62117,041 742,711 859,76
07.11.202630 621,91114,431 745,321 859,76
07.12.202628 876,58104,431 755,331 859,76
07.01.202727 121,25101,351 758,411 859,76
07.02.202725 362,8594,781 764,981 859,76
07.03.202723 597,8779,651 780,111 859,76
07.04.202721 817,7681,531 778,231 859,76
07.05.202720 039,5472,471 787,291 859,76
07.06.202718 252,2568,211 791,551 859,76
07.07.202716 460,7059,531 800,231 859,76
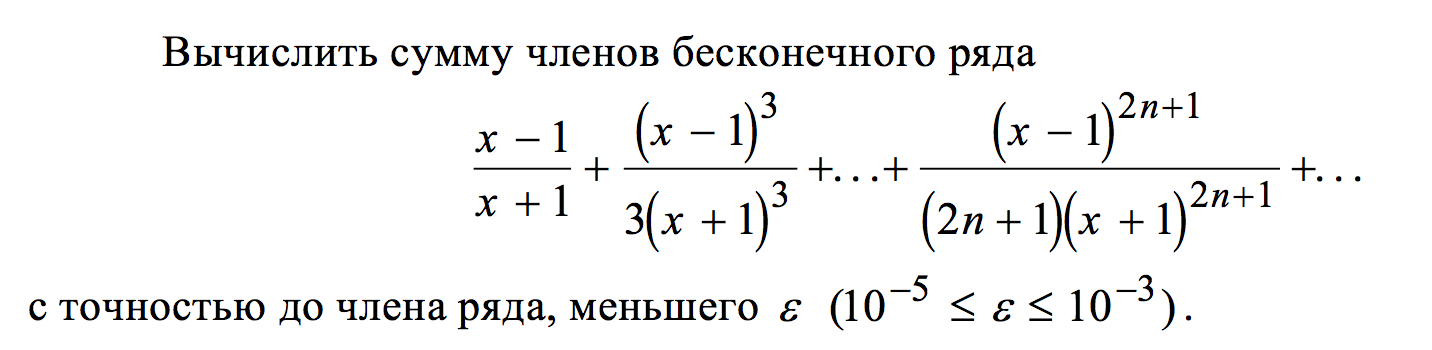07. 08.202714 660,4754,791 804,971 859,76
07.09.202712 855,5048,041 811,721 859,76
07.10.202711 043,7839,941 819,821 859,76
07.11.20279 223,9634,471 825,291 859,76
07.12.20277 398,6726,761 833,001 859,76
07.01.20285 565,6720,801 838,961 859,76
07.02.20283 726,7113,931 845,831 859,76
07.03.20281 880,886,581 880,881 887,46

Показать полностью

Скачать

6.2.3. Вычисление суммы ряда по общей формуле

Одной из основных областей применения циклов с условием являются приближенные математические вычисления, например, вычисление суммы ряда и решение нелинейных уравнений. Изучим особенности программной реализации некоторых из этих задач и начнем с задачи вычисления суммы бесконечного сходящегося ряда.

Рассмотрим ряд

,

где n= 1, 2, 3,… Требуется найти сумму ряда в некоторой заранее заданной точкеxс определенной точностью ε.

Исходными данными для этой задачи являются значение xи необходимая точность вычислений ε. Параметр «точность вычислений» означает, что слагаемые, которые по модулю меньше точности, считаются несущественными и в общую сумму не включаются. Для ввода исходных данных будем использовать функциюInputBox. Результатом программы является значение накопленной суммы. Но для проверки правильности вычислений мы будем еще выводить значение левой части выражения, номер и значение последнего слагаемого, вошедшего в сумму. Для вывода результатов будем использовать окно списка с именемlstA.

Для решения этой задачи нам потребуется организовать цикл с условием. На каждом шаге цикла мы будем по общей формуле вычислять значение очередного слагаемого и прибавлять его к общей сумме. Как только очередное слагаемое станет меньше заданной точности, мы закончим выполнение цикла.

Рассмотрим особенности программной реализации этого алгоритма. Для решения задачи нам потребуются следующие переменные: x– точка, в которой вычисляется сумма ряда,eps– требуемая точность вычислений,summa– искомая сумма ряда,slag– очередное слагаемое. Все эти переменные имеют рациональный тип данных. Для повышения точности наших вычислений будем использовать типDouble.

Dim x, summa, slag, eps As Double

Для вычисления факториала, стоящего в знаменателе дроби, заведем переменную f, которая будет иметь целый тип с максимально возможной емкостью –ULong.

Dim f As ULong

Так как для вычисления факториала необходимо организовать цикл, то нам потребуется специальная переменная – счетчик i. Заметим, что формула общего члена ряда зависит от номера слагаемого –n. Поэтому при решении задачи нам потребуется переменная для хранения номера очередного слагаемого.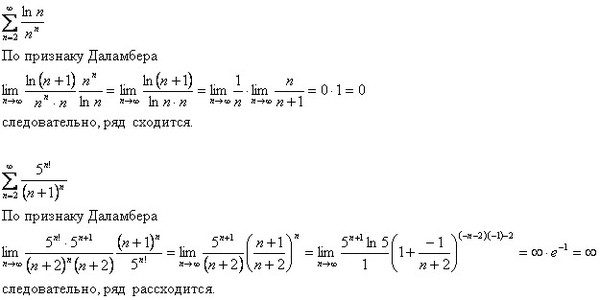 Назовем ееn. Она будем иметь целый тип данных.

Dim n, i As Integer

Работа программы начинается с очистки окна списка от ее предыдущих результатов.

lstA.Items.Clear()

Вводим исходные данные.

x = Val(InputBox(«Введите точку»))

eps = Val(InputBox(«Введите точность»))

Задаем начальные значения. Начальное значение суммы равно нулю. Номер текущего слагаемого тоже равен нулю, так как никакого слагаемого на данный момент времени мы не вычислили.

summa = 0

n = 0

Организуем основной цикл.

Do

На каждом шаге цикла будем вычислять очередного слагаемое. При этом его номер будет на единицу больше, чем на предыдущем шаге.

n += 1

Начинаем вычислять значение очередного слагаемого. Первым шагом будет вычисление факториала, стоящего в знаменателе дроби.

f = 1

For i = 2 To 2 * n — 1

f *= i

Next

Затем по общей формуле вычисляем само слагаемое, заменяя факториал на уже найденное значение. (2 * n — 1) / f

Полученное слагаемое добавляем к общей сумме.

summa += slag

Проверяем, если модуль слагаемого меньше заданной точности, то дальнейшие вычисления не приведут к заметным изменениям результата, и выполнение цикла можно завершить.

Loop Until Math.Abs(slag) <= eps

Выводим в окно списка полученную сумму, значение выражения, стоящего в левой части равенства, номер и значение последнего слагаемого.

lstA.Items.Add(«summa=» + Str(summa))

lstA.Items.Add(«sin(x)=» + Str(Math.Sin(x)))

lstA.Items.Add(«n=» + Str(n))

lstA.Items.Add(«Последнее слагаемое =» + Str(slag))

Полный текст программы представлен в приложении 17. Пример работы программы приведен на рис. 31. Исходные данные для этого случая: x = 1,eps = 1e-4 = 10-4.

Рис. 31.Пример работы программы вычисления суммы ряда по общей формуле

{\ малое n = 10} потому что (пи * х / 10)} $ $

$${\large45,34,20,23,34,42}$$

$${\large154 230 243 454}$$

Содержание:

  • Калькулятор суммирования с сигма-нотацией (Σ)
  • Что такое суммирование?
  • Формула записи суммирования
  • Типы суммирования
  • Как оценить суммирование?

Дайте нам отзыв

✎

✉

Калькулятор суммирования с сигма-нотацией (Σ)

Калькулятор суммирования — это онлайн-инструмент, который вычисляет сумму заданного ряда. Он может найти простую сумму чисел, а также сумму сигма-обозначения любой функции. Этот калькулятор записи суммирования также показывает расчет с шагами.

Что такое суммирование?

Суммирование — это процесс сложения последовательности чисел любого типа. Помимо чисел, можно суммировать и другие типы значений, такие как функции, матрицы и векторы.

Суммирование обозначается греческой буквой Сигма обозначение Σ .

Формула записи суммы

Уравнение для нахождения суммы ряда приведено ниже.

Где,

  • i — начальное значение, а
  • n — верхний предел.

Типы суммирования

Существует два типа суммирования.

  1. Простое суммирование
  2. Sigma notation

992
Название типа Заявление Экспрессия . Его также можно назвать алгебраической суммой чисел или величин. 1+2+3+4=10
Сигма-нотация

Сигма-нотация используется для оценки суммы функции путем размещения нижнего и верхнего предельных значений.

Нижний предел суммирования называется индексом данного выражения. В то время как верхний предел называется конечной точкой данного выражения.

Проблемы с сигма-представлением также могут быть решены с помощью нашего калькулятора суммы рядов для известной функции, такой как x 9n\left[f\left(x\right)\right]}$$

Как оценить суммирование?

Для расчета записи суммирования следуйте приведенному ниже примеру.

Пример 1:

Найдите сумму первых 10 простых чисел

Решение

Шаг 1: Запишите первые 10 простых чисел вместе со знаком сложения между ними.

2 + 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 + 29

Шаг 2: Теперь оцените сумму ряда простых чисел.

2 + 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 + 29 = 129

Следовательно, сумма первых 10 простых чисел равна 129.

Пример 2:

3 Для функции

(x + 2) 2 с верхним пределом 10 и исходное значение 4.

Решение:

99

Решение:

999

:

999

:

9002 99

.Шаг 1: Прежде всего, давайте определим значения.

x = 4, n = 10

Шаг 2: Поместите заданную функцию в уравнение суммирования.

Шаг 3: Подставьте значения ряда в приведенное выше уравнение.

Шаг 4: Упростите уравнение.

Калькулятор суммирования — ∑ Sigma Notation Solver

Онлайн-калькулятор суммирования поможет вам определить сумму указанных чисел, рядов или функций. Кроме того, сигма-калькулятор проверяет, сошелся ряд или нет. Давайте начнем понимать, как вычислить суммирование и сумму сигма.

Что такое суммирование?

В математике суммирование — это процесс сложения любых чисел, называемых слагаемыми или сложениями, в результате чего получается сумма или итог. Другими словами, сумма последовательности называется рядом, определяющим математическую операцию «+». Для обозначения суммирования используется символ «Σ».

Существует два типа суммирования последовательностей, известных как бесконечные и конечные наборы последовательностей.

Конечная последовательность имеет верхний предел и нижний предел (начальное и конечное значения), и бесконечные последовательности будут продолжаться бесконечно. Калькулятор суммирования использует как начальное, так и конечное значение для расчета результатов. 9n i= n(n + 1) / 2

В уравнении суммирования «i» — это начальное значение, а n — конечный предел.

Что такое сигма-нотация?

Обозначение сигма представлено символом S, который является производным от греческой заглавной буквы S. Обозначение сигма (S) сообщает нам значения добавленной последовательности. Типичное значение последовательности показано справа от символа сигмы и математических значений сигмы.

Переменная нотации сигма представлена ​​индексом, расположенным под символом сигма. Индекс обычно представлен i.

Индекс показан как упрощенное выражение для i = 1. Индекс предполагает, что значения последовательности начинаются со значения в правой части уравнения и заканчиваются значением над сигма-нотацией.

Начальное значение записи называется нижним пределом записи суммирования.

Точка, в которой останавливается суммирование, называется верхним пределом суммирования.

Как рассчитать сумму? 99 5n + 3

Где n — это заполнитель целого числа и суммирование выражения 5n + 3 с целыми числами от 0 до 9.

Поскольку нижний предел или начальное значение равен 0, а верхний предел или конечное значение равен 9, последовательность через 0, 1, 2, 3, 4,…, 9. Мы подставим 0 в выражение, затем добавим результат подстановки 1 в выражение, так что треть, пока мы не добавим результат подстановки нашего конечного целого числа 9 в выражение.

Как работает суммирующий калькулятор?

Используйте этот калькулятор сигма, чтобы быстро вычислить сумму заданных выражений чисел в заданном диапазоне, выполнив следующие действия:

Ввод:
  • Сначала выберите метод расчета: простая сумма или сумма сигма.
  • Если вы выбрали простую сумму, введите числа или серии через запятую.
  • При выборе формата сигма введите уравнение с начальным и конечным значениями.
  • Нажмите кнопку расчета, чтобы увидеть сумму константы и чисел.

Вывод:
  • Калькулятор суммирования отображает сумму заданного числа и общего количества введенных функций или рядов.
  • Калькулятор сигма обеспечивает пошаговые расчеты для заданного уравнения с начальным и конечным значениями.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *