Задачу линейного программирования решить симплексным методом: Симплекс-метод онлайн

Симплексный метод решения задач линейного программирования

Симплексный метод – это метод последовательного улучшения плана. Этим методом можно решать задачи линейного программирования с любым количеством переменных и ограничений.

Этот метод включает в себя три основные этапа:

1. Построение начального опорного плана.

2. Правило перехода к лучшему (точнее, нехудшему) решению.

3. Критерий проверки найденного решения на оптимальность.

При симплексном методе выполняются вычислительные процедуры (итерации) одного и того же типа в определенной последовательности до тех пор, пока не будет получен оптимальный план задачи или станет ясно, что его не существует.

1) Построение начального опорного плана.

Данную задачу линейного программирования необходимо сначала привести к каноническому виду; при этом правые части ограничений должны быть неотрицательными.

Признаком возможности построения начального опорного плана служит наличие в каждом ограничении-равенстве с неотрицательной правой частью базисной переменной.

Базисной называют плановую переменную, которая входит только в одно уравнение (а в другие не входит), и при этом имеет коэффициент, равный единице.

Пусть задача линейного программирования приведена к каноническому виду, и все уравнения системы ограничений имеют свою базисную переменную. Приравняв базисные переменные к соответствующим правым частям ограничений, а остальные переменные к нулю, получим опорное или базисное решение задачи.

Пример. Для данной задачи линейного программирования найти начальный опорный план (базисное решение).

max

Решение. Изменим знаки второго и третьего неравенств на противоположные, умножив каждое из них на –1. Система ограничений теперь будет такой:

В каждом ограничении слева добавим положительную переменную , соответственно запишем канонический вид задачи:

max

.

Переменные базисные. Приравниваем их к правым частям ограничений:Все остальные переменные – свободные, приравниваем их к нулю:

Запишем теперь начальный опорный план

(0; 0; 0; 0; 16; 4; 0).

2) Составление симплексных таблиц. Критерий оптимальности.

Симплексный метод удобно применять, используя построение симплексных таблиц. Первая симплексная таблица, соответствующая начальному плану, имеет вид:

Базис		В			…
					…
					…
					…
…	…	…	…	…	…	…
					…
					…

Здесь приняты следующие обозначения.

Столбец «Базис» – это базисные переменные.

Столбец «» – это коэффициенты при базисных переменных в целевой функции.

Столбец «В» – правые части ограничений;

–коэффициенты при переменных в ограничениях;

–коэффициенты при переменных в целевой функции.

Последняя строка в таблице () – это проверочная или оценочная строка.

–значение целевой функции, соответствующее построенному начальному плану. Его находят так: каждый элемент столбца умножают на соответствующий элемент столбца В и произведения складывают, т.е.

.

–называют оценками или симплексными разностями и находят так: элементы столбца умножают на соответствующие элементы столбца, складывают результаты и вычитают.

Например,

.

Оценки () базисных переменных всегда равны нулю.

Признак оптимальности опорного плана состоит в следующем:

Опорный план будет оптимальным тогда и только тогда, когда все оценки

для задачи на max и

для задачи на min.

Если критерии оптимальности не выполняются, то нужно перейти к нехудшему опорному плану, т.е. исключить из базиса некоторую переменную и ввести вместо нее новую из числа свободных переменных.

Переменная, которую нужно ввести в базис, соответствует той оценке , которая не удовлетворяет условию оптимальности. Если таких оценок несколько, то среди них выбирают наибольшую по абсолютной величине и соответствующую ей переменную вводят в базис. Столбец с этой переменной называютразрешающим.

Для определения переменной, которую нужно вывести из базиса, поступают так: элементы столбца В делят только на положительные элементы разрешающего столбца и находят симплексные отношения .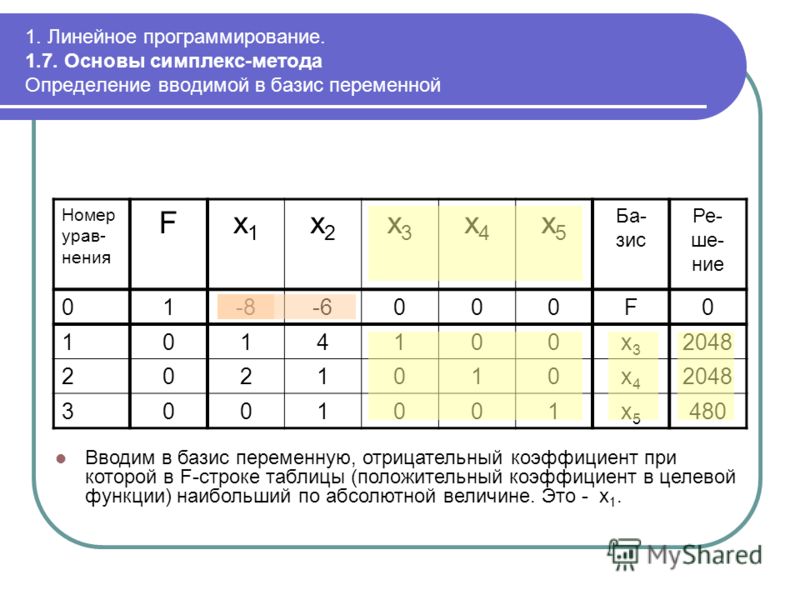 Выбирают изнаименьшее. Оно называет ту переменную, которую нужно ввести в базис. Соответствующая строка таблицы называетсяразрешающей.

На пересечении разрешающего столбца и разрешающей строки находится разрешающий элемент.

Теперь начинаем заполнять следующую таблицу. Покажем этот процесс на конкретном примере.

Пример. Решить симплексным методом задачу линейного программирования.

max

Решение. 1) Приводим задачу к каноническому виду, т.е. из ограничений неравенств делаем равенства.

max

2) Определяем базисные переменные – это .

3) Заполняем первую таблицу

Базис		В	2	3	0	0	0	0
	0	18	1	3	1	0	0	0
	0	16	2	1	0	1	0	0
	0	5	0	1	0	0	1	0
	0	21	3	0	0	0	0	1	–
		0	–2	–3	0	0	0	0

Здесь ине удовлетворяют условию оптимальности, т.  к. они меньше нуля. Выбираем среди них большее по модулю. Это. Следовательно, столбец переменной– разрешающий. Значит, в новый базис нужно ввести переменную.

Находим :;;

Наименьшее из этих чисел – это число 5, что соответствует строке базисной переменной . Значит, строка базисной переменной– разрешающая, следовательно, из базиса нужно вывести переменную. Элемент=1 – разрешающий. Новый базис:.

Заполнение следующей таблицы начинаем со столбцов «Базис» и «». Потом заполняем разрешающую строку, разделив каждый ее элемент на разрешающий, т.е. на 1. Все элементы разрешающего столбца будут нулями, кроме разрешающего, который всегда равен 1. Столбцы подпереписываем без изменения, т. к. эти переменные остались в базисе. Остальные элементы новой таблицы находим по правилу прямоугольника. Например, элементнайдем из прямоугольника

=

Или элемент =из прямоугольника

Оценки для новой таблицы можно находить по этому же правилу.

Вцелом, решение данной задачи симплексным методом в виде таблиц будет иметь вид

Базис		В	2	3	0	0	0	0
	0	18	1	3	1	0	0	0	6
	0	16	2	1	0	1	0	0	16
	0	5	0	1	0	0	1	0	5
	0	21	3	0	0	0	0	1	–
		0	–2	–3	0	0	0	0	таб. 1
	0	3	1	0	1	0	–3	0	3
	0	11	2	0	0	1	–1	0	5,5
	3	5	0	1	0	0	1	0	–
	0	21	3	0	0	0	0	1	7
		15	–2	0	0	0	3	0	таб. 2

Базис		В	2	3	0	0	0	0
	2	3	1	0	1	0	–3	0	–
	0	5	0	0	–2	1	5	0	1
	3	5	0	1	0	0	1	0	5
	0	12	0	0	–3	0	9	1
		21	0	0	2	0	–3	0	таб. 3
	2	6	1	0	–0,2	0,6	0	0
	0	1	0	0	–0,4	0,2	1	0
	3	4	0	1	0,4	–0,2	0	0
	0	3	0	0	0,6	–1,8	0	1
		24	0	0	0,8	0,6	0	0	таб. 4

Оценочная строка четвертой таблицы показывает, что получен оптимальный план, так как все.

–это значения из столбца В, т.е.,,,.

Свободные (небазисные) переменные .

Итак, = (6; 4; 0; 0; 1; 3),

= = 24.

Примечание: При переходе от таблицы к таблице для контроля сравнивают , которое должно быть не меньше предыдущего для задачи на максимум и не больше предыдущего – для задачи на минимум.

При использовании симплексного метода возможны следующие случаи.

1) Если в оценочной строке симплекс-таблицы оценка = 0 соответствует свободной переменной, то это означает, что ЗЛП имеет не единственный оптимальный план.

2) Если при переходе от одного опорного плана к другому в разрешающем столбце нет положительных элементов, то это означает, что целевая функция ЗЛП является неограниченной и оптимальных планов не существует.

Задания для самостоятельной работы.

Определить оптимальный план задач, используя симплексный метод решения задач линейного программирования:

а)

max

б)

min

Симплексный метод решения задач линейного программирования

При решении задачи линейного программирования можно поступить следующим образом найти любое из таких «вершинных» решений — не обязательно оптимальное — и принять его за исходный пункт расчетов. Такое решение и будет базисным. Если оно окажется оптимальным, расчет на этом закончен, если нет — последовательно проверяют, не будут ли оптимальными соседние вершинные точки ту из них, в которой план эффективнее, принимают снова за исходную точку и так, последовательно проверяя на оптимальность аналогичные вершины, приходят к искомому оптимуму. На этом принципе строятся т. н. симплексный метод решения задач линейного программирования, а также ряд других способов, объединенных  [c.26]
После того, как задача сформулирована в терминах линейного программирования, решение ее состоит в применении того или иного расчетного алгоритма. Наиболее распространенными методами решения задач линейного программирования являются симплексный (или метод последовательного улучшения плана), распределительный и индексный. Существует также ряд приближенных методов решения, разработанных для отдельных видов задач (пример решения задачи методом линейного программирования дан ниже).  [c.153]

СИМПЛЕКСНЫЙ МЕТОД ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ — наиболее универсальный и распространенный за рубежом метод решения задач линейного программирования. С. м. л. п. довольно сложен по расчетной процедуре, и это затрудняет его использование при ручном счете. Однако известны алгоритмы для решения задач при помощи этого метода на электронных вычислительных машинах, что открывает ему путь для практич. применения.  [c.21]

В настоящей главе рассматриваются общие методы решения задач линейного программирования, к которым относятся симплексный метод и метод обратных матриц. Указанными методами может быть решена любая задача линейного программирования.  [c.294]

Вторым этапом моделирования экономических процессов является выбор наиболее рационального математического метода для решения задачи. Например, для решения задач линейного программирования известно много методов симплексный, потенциалов и др. Лучшей моделью является не самая сложная и самая похожая на реальное явление или процесс, а та, которая позволяет получить самое рациональное решение и наиболее точные экономические оценки. Излишняя детализация затрудняет построение модели, часто не дает каких-либо преимуществ в анализе экономических взаимосвязей и не обогащает выводов. Излишнее укрупнение модели приводит к потере существенной экономической информации и иногда даже к неадекватному отражению реальных условий.  [c.105]

Как мы уже отмечали, графические методы, описанные в предыдущих разделах, приемлемы только в отношении задач с не более чем двумя неизвестными (например, х и у). В большинстве практических ситуаций число неизвестных может быть гораздо большим. Симплексный метод — один из наиболее известных подходов к решению задач линейного программирования через алгебраические методы. Симплексный метод применяется в самых разнообразных компьютерных программах, предназначенных для решений таких задач.  [c.279]

Т Определение. Симплексный метод — математический подход к решению задач линейного программирования. Это стандартный метод решения задач с более чем двумя переменными. А  [c.279]

Суть этого алгоритма [92] состоит в соединении основной схемы итеративного алгоритма решения соответствующей нецелочисленной задачи с идеей доводки его до целочисленного методом случайного поиска. Итеративный алгоритм, основанный на идее известного метода Брауна— Робинсона решения матричных игр, дает возможность получить приближенное решение задачи линейного программирования при небольших затратах машинного времени. Проведенные эксперименты доказывают, что в применении к некоторым классам задач линейного программирования итеративные алгоритмы могут конкурировать с симплексными [92].  [c.190]

Таким образом, построение календарного графика работы поточной линии с непрерывным регламентом выполнения операций заключается в решении задачи Б». Эта задача является линейно-программистской и, следовательно, может быть решена любым из существующих методов линейного программирования. Особенностью этой задачи является то, что в ней большинство коэффициентов при неизвестных в каждом из неравенств равны нулю. Так, в неравенствах (32), (33) только три коэффициента положительны, в неравенстве (34)—один, а в неравенстве (35) — два. Это обстоятельство упрощает решение задачи и позволяет решать задачи как вручную, так и на электронных вычислительных машинах (ЭВМ) относительно больших размеров. При небольшой размерности (на поточной линии выполняется порядка 10—15 операций) задача может быть решена вручную. При этом работник, имеющий некоторый навык в решении задач линейного программирования, может решить ее примерно за 1—1,5 часа. При решении задач больших размерностей (предмет проходит обработку через 30—50 операций) необходимо использовать ЭВМ. Внедряемая в настоящее время на промышленных предприятиях страны ЭВМ Минск-22 с успехом может использоваться для решения этих задач. Для реализации алгоритма может быть взята стандартная программа решения задач симплексным методом.  [c.48]

Решение задач линейного программирования осуществляется с помощью симплексного метода (с использованием, как правило, пакета прикладных программ). При этом реализуются следующие этапы  [c.16]

Решение задачи линейного программирования симплексным методом проводится в два этапа. Сначала находится начальное базисное решение, а затем проводится направленный перебор базисных решений для получения оптимального плана.  [c.49]

Транспортные задачи обычно связаны с анализом доставки товаров от разных источников по различным направлениям. Так, у предприятия может иметься несколько складов, предназначенных для отправки товаров в различные точки страны. В этом случае необходимо принять решение относительно оптимального способа передвижения этих товаров, с тем чтобы минимизировать затраты, время на перевозку и задействованные при этом ресурсы. Такого рода задача относится к отдельному типу задач линейного программирования. Мы имеем ряд ограничений, скажем, потребности точек назначения и наличие возможностей, и хотим минимизировать затраты. Поэтому мы можем сформулировать транспортную задачу как задачу линейного программирования и далее применить для получения решения симплексный метод. Однако в том, что касается перевозок, ограничения даются в особой форме, и целесообразен упрощенный метод решения.  [c.288]

В этой главе мы рассмотрели приемы линейного программирования при решении задач оптимизации. Типичный пример — максимизация прибыли предприятия за счет определения соответствующей номенклатуры производства. Кроме того, задачи линейного программирования могут быть направлены на минимизацию переменных, в частности затрат. Выражение, которое необходимо оптимизировать, называется объективной функцией. Эта функция высчитывается при наличии ряда ограничений. Одна из самых больших трудностей при решении такого рода задач состоит в исходной постановке задачи, когда необходимо определить ограничения, представить их в виде неравенств и выдать выражение объективной функции. При решении простых задач только с двумя переменными можно применить графический метод. Для более сложных задач применяется симплексный метод.  [c.304]

Ниже даются постановка основной задачи линейного программирования, описание симплексного метода решения и пример применения этого метода для выбора оптимального варианта размещения наливных станций, грузооборота, прикрепления к ним потребителей.  [c.179]

Разработан целый ряд вычислительных приемов, позволяющих решать на ЭВМ задачи линейного программирования, насчитывающие сотни и тысячи переменных, неравенств и уравнений. Среди них наибольшее распространение приобрели методы последовательного улучшения допустимого решения (см. Симплексный метод, Базисное решение), а также декомпозиционные методы решения крупноразмерных задач, методы динамического программирования и др. Сама разработка и исследование таких методов — развитая область вычислительной математики.  [c.172]

Р. А. 3 в я г и н а. Программа реализации на М-20 модифицированного симплексного метода для решения общей задачи линейного программирования.— Оптимальное планирование. Новосибирск, 1954, вып. 1.  [c.222]

При решении общей задачи линейного программирования симплексным методом для составления исходной программы необходимо, как рассматривалось выше, найти базисное решение.  [c.315]

При решении задач симплексным методом линейного программирования моделирование заключается в составлении системы линейных уравнений и неравенств, каждое из которых выражает одно из заданных в условии задачи ограничений в виде функций определяемых переменных.  [c.34]

Симплексный метод — один из основных методов линейного программирования. Он универсален и наиболее приспособлен к решению широкого круга экономических задач. С его помощью можно провести оптимизацию производственной программы, и уровня использования производственной мощности, осуществить оптимальную загрузку оборудования, оптимальное составление смесей, оптимальное оперативно-календарное планирование и др.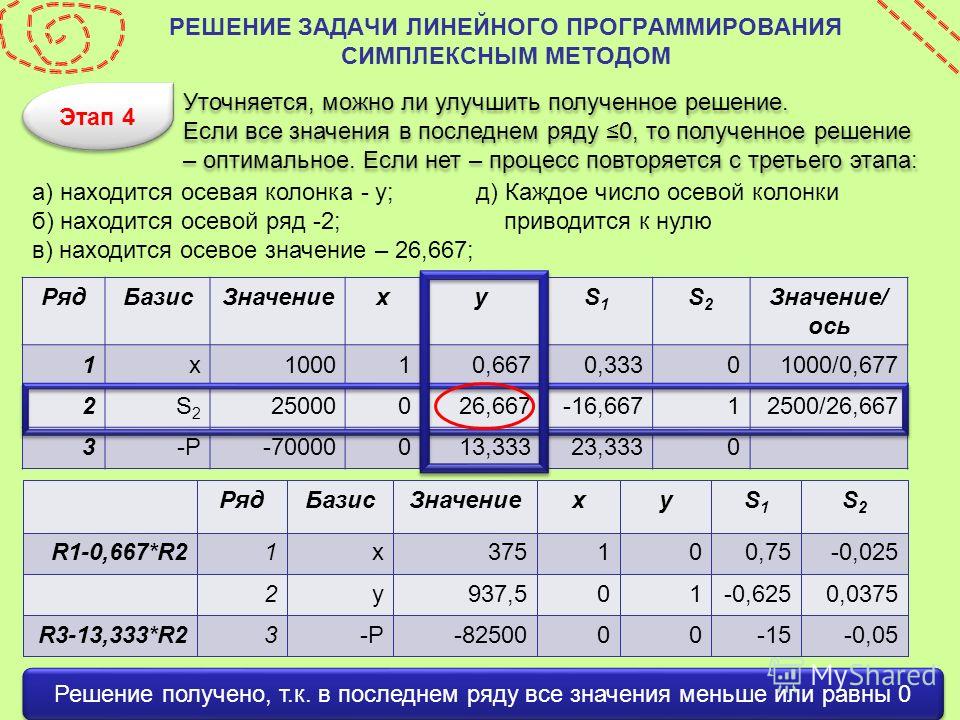  [c.122]

Математическое обеспечение модели основывается на симплексном методе линейного программирования и реализуется пакетом прикладных программ ЭВМ. В расчетах использованы нормативная база и показатели (ограничения) по конкретному производственному объекту. Изложим процедуру оптимизации производственной программы с выделением в ней дополнительного задания в рамках принятого годового плана. В табл. 7 приводится исходная информация решения задачи.  [c.64]

За рубежом применяются различные методы Л. п. Большинство авторов считает основным т. н. симплексный метод линейного программирования. Другие методы обычно трактуются как модификация симплексного метода. Однако некоторые из них имеют самостоятельное значение, обладают собственными расчетными приемами и сферой применения. Таков, в частности, распределительный метод линейного программирования, нашедший широкое применение в решении ряда задач. Симплексный и распределительный методы Л. п. основаны на различном подходе к определению отправного варианта и на разных способах изменения значений переменных в процессе улучшения последовательных вариантов. Неодинакова и сфера возможного применения этих 2 методов. Симплексный метод, будучи по технике вычислений несколько более громоздким и сложным, является более универсальным он применим к решению любых задач Л. п. Распределительный метод проще в технич. отношении, но имеет более узкую сферу применения (наиболее часто он применяется для составления оптимальных планов перевозок).  [c.398]

Симплексный метод является универсальным методом линейного программирования. Основы этого метода были сформулированы американским ученым Дж. Данцигом в 1949 г. Симплексный метод получил свое название из геометрического толкования одной из первых задач, решенных этим методом. В этой задаче переменные были неотрицательны, а их сумма равнялась единице  [c.296]

Задача об использовании оборудования. Ход решения задач симплексным методом рассмотрим на примере загрузки оборудования, который был использован в одной из предыдущих глав, при изложении графического метода линейного программирования.  [c. 298]

СИМПЛЕКСНЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (симплекс-метод) [simplex method] — вычислительная процедура, основанная на принципе последовательного улучшения решений — перехода от одной базисной точки (см. Базисное решение) к другой, для которой значение целевой функции больше (эти операции фиксируются в симплексной таблице). Доказано, что если оптимальное решение существует, то оно обязательно будет найдено через конечное число шагов (за исключением т.н. вырожденной задачи, при которой возможно явление «зацикливания», т.е. многократного возврата к одному и тому же положению). Название метод получил от термина » -мерный симплекс». Геометрическая интерпретация метода состоит в последовательном движении по верши) шм симплекса.  [c.322]

А. А. 3 о т о в а. Решение задач линейного программирования симплексным методом на ЦВМ ( Минск-12 ).— Вопросы вычисл. техники. Ростов-на-Дону, 1965.  [c.222]

ВЫРОЖДЕННАЯ ЗАДАЧА [degenerate problem] — задача линейного программирования, в которой при разложении вектора ограничений В (обозначения см. в ст. «Линейноепрограммирование») по некоторому базису а]х. … ат по крайней мере один коэффициент оказывается равным нулю. Такая ситуация затрудняет решение задачи симплексным методом, вызывая явление «зацикливания», при котором одно и то же множество базисных решений будет периодически повторяться, а оптимальный план никогда не будет достигнут.  [c.59]

См. также Ассортиментные задачи, Базисное решение, Блочное программирование, Булево линейное программирование, Ведущий столбец, Ведущая строка, Вершина допустимого многогранника, Вырожденная задача, Гомори способ, Граничная точка, Двойственная задача, Двойственность в линейном программировании, Дифференциальные ренты, Дополняющая нежесткостъ, Жесткость и нежесткость ограничений ЛП, Задача диеты, Задача о назначениях, Задача о раскрое, Задачи размещения, Исходные уравнения, Куна— Таккера условия, Множители Лагранжа, Область допустимых решений, Опорная прямая, Оптимальное распределение ресурсов, Распределительные задачи, Седловая точка, Симплексная таблица, Симплексный метод, Транспортная задача.  [c.173]

СИМПЛЕКСНАЯ ТАБЛИЦА (СИМПЛЕКС-ТАБЛИЦА) [simplex table] — матрица, служащая средством перебора допустимых базисных решений (невырожденной) задачи линейного программирования при ее решении симплексным методом. Образуется из матрицы коэффициентов системы уравнений линейного программирования, приведенной к «канонической форме»75 последовательное ее преобразование по т.н. симплексному алгоритму позволяет за ограниченное количество шагов (итераций) получать искомый результат — план, обеспечивающий экстремальное значение целевой функции.  [c.322]

Некоторые из них не связаны непосредственно с алгоритмом симплексного метода, как, например, метод потенциалов для решения транспортной задачи другие же в качестве составных элементов используют вычислительные процедуры симплексного метода. В качестве примера последних можно привести метод Гомори (метод отсечений) для решения задач линейного целочисленного программирования.  [c.524]

РАЗРЕШАЮЩИХ МНОЖИТЕЛЕЙ МЕТОД — один из методов линейного программирования, разработанный в 1939 сов.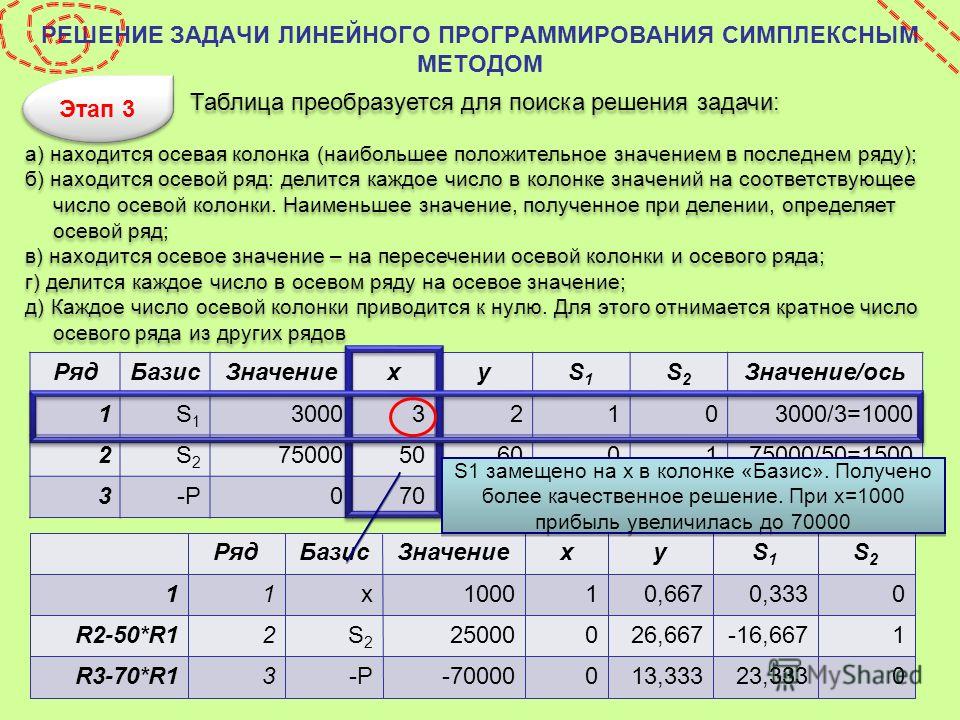 ученым Л. В. Канторовичем. Является универсальным методом, применимым для решения любых задач линейного программирования. Р. м. м. предвосхитил идеи, положенные Дж. Данцигом в основу известного симплексного метода линейного программирования, разработанного на десятилетие позднее. Р. м. м. был развит Л. В. Канторовичем в ряд методов, применимых для решения различных частных задач линейного программирования.  [c.401]

РАСПРЕДЕЛИТЕЛЬНЫЙ МЕТОД ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ — упрощающая модификация более универсального симплексного метода линейного программирования, применимая для решения лишь нек-рого класса задач линейного программирования. Типичным примером задач этого класса являются т. и. транспортная задача линейного программирования (см. Перевозок план оптимальный) и задачи, формально-математически приводимые к той же модели.  [c.405]

Е. Д. М я к и ш е в а. Стандартная программа для решения общей задачи линейного программирования симплексным методом с модификацией Г. Зойтендейк (ЭВМ М-20). — Стандартные программы решения задач матем. программирования. Вычисл. центр Московского гос. ун-та, 1964, вып. 3.  [c.222]

А. П. М е р е н к О Ё. Решение общей задачи линейного программирования модифицированным симплексным методом, (Библиотека программ для БЭСМ-2М, вып. я-1). М., 1965,  [c.223]

П. А. А х м е т о в. Программа мультипликативного алгоритма симплексного метода для решения общих задач линейного программирования (на ЭВМ БЭСМ-ЗМ ).— Стандартные программы. М., 1967.  [c.223]

Вычислительным методом для решения такой задачи служит типовой алгоритм методов линейного программирования, в том числе симплексного метода, т. е. метода последовательного улучшения производственной программы с помощью итерирования. За исходную точку расчетов принимается некоторый план производства по каждому изделию и затем в последовательном порядке изменяются значения прироста переменных.  [c.266]

линейное программирование — Решение задачи минимизации с использованием симплекс-метода

спросил 2 года 10 месяцев назад

Изменено 2 года, 10 месяцев назад

Просмотрено 10 тысяч раз

$\begingroup$

Существует способ решения задачи минимизации симплекс-методом, когда нужно просто умножить целевую функцию на знак -ve и затем решить ее симплекс-методом. Все, что вам нужно сделать, это снова умножить найденное максимальное значение на знак -ve, чтобы получить требуемое максимальное значение исходной задачи минимизации. Мой вопрос: есть ли какое-либо условие, которое должно быть выполнено в ограничениях задачи оптимизации, чтобы использовать этот метод?

• линейное программирование
• симплекс

$\endgroup$

5

$\begingroup$

Это не имеет никакого отношения даже к линейному программированию. Это простой математический факт:

$$\min \left( f \left( x \right) \right) = — \max \left( -f \left( x \right) \right)$$

что все еще сохраняется, когда вы ограничиваете область определения функции ограничениями (фактически до выпуклого многогранника в случае LP).

$\endgroup$

1

$\begingroup$

Единственные требования к ограничениям, о которых я знаю, при использовании симплексного алгоритма для решения задачи минимизации (и максимизации) включают в себя переменные резерва и избытка, где это необходимо, и переменные решения должны быть неотрицательными. . Ниже приведен пример, иллюстрирующий, как сформулировать решаемую задачу с помощью симплексного алгоритма и как включить в формулировку переменные резерва и избытка. \begin{align}\min&\quad z = 2x_1 — 3x_2\\\text{s.t.}&\quad x_1+x_2 \leq 4\\&\quad x_1-x_2 \geq 6\\&\quad x_1,x_2 \ geq 0\end{выравнивание}

Оптимальное решение для этого было бы там, где $ z = 2x_1-3x_2$ является наименьшим, но эквивалентно можно сказать, что оптимальное решение было бы там, где $ -z = -2x_1+3x_2$ было бы наибольшим. Это делается, поскольку симплекс-алгоритм используется для решения задач максимизации, и формулировка теперь выглядит следующим образом: \begin{align}\max&\quad-z = -2x_1 + 3x_2\\\text{s.t.}&\quad x_1+x_2 \leq 4\\&\quad x_1-x_2 \geq 6\\&\quad x_1,x_2 \geq 0\end{align}

Мы добавляем резервную переменную $s_1$ к первому ограничению, которое теперь становится $x_1 +x_2 +s_1 = 4$. Аналогично для второго ограничения мы добавляем избыточную переменную $s_2$, и теперь ограничение становится $x_1-x_2 + s_2= 6$.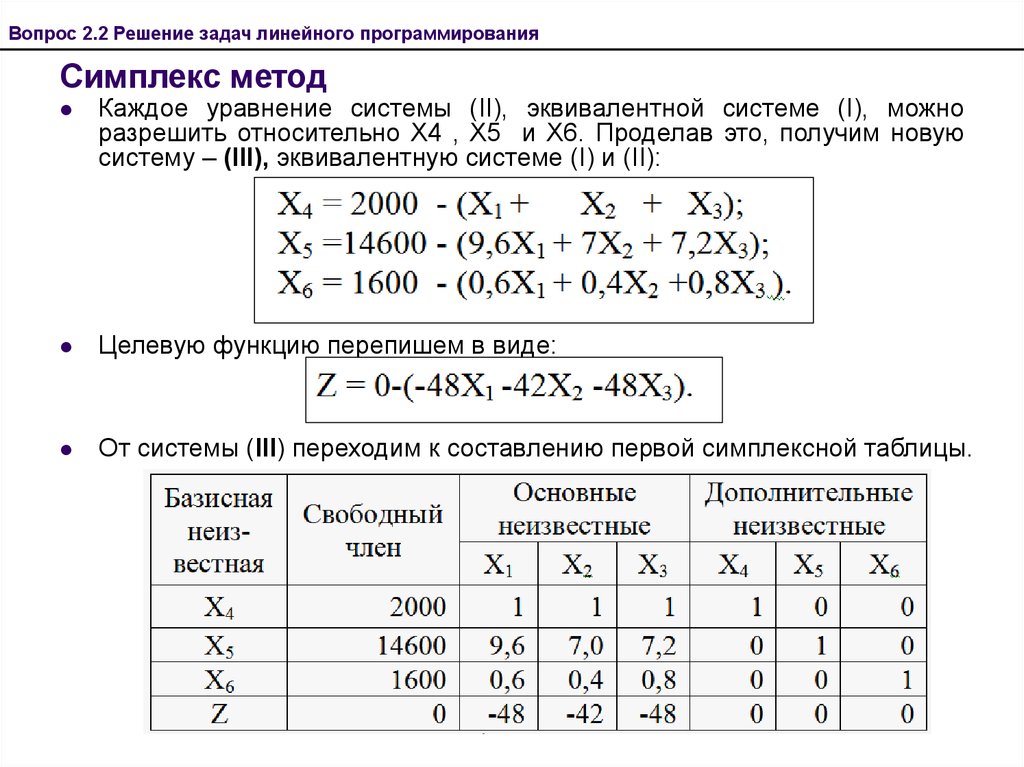

Формулировка, которая теперь находится в стандартной форме для решения с использованием симплексного алгоритма, выглядит следующим образом: \begin{align}\max&\quad-z = -2x_1 + 3x_2\\\text{s.t.}&\quad x_1 +x_2 +s_1 = 4\\&\quad x_1-x_2 + s_2= 6\\&\quad x_1,x_2 \geq 0\\&\quad s_1,s_2 \geq 0.\end{align}

$\endgroup$

Зарегистрируйтесь или войдите

Зарегистрироваться через Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Раздел 4.3 Вопрос 5. Часто задаваемые вопросы по математике

Симплекс-метод можно применить к приложению пивоварни, разработанному ранее в этой главе.

Пример 4    Найти оптимальный уровень производства

Задача линейного программирования для крафтовой пивоварни:

, где x ₁ — количество бочек светлого эля, а x ₂ — количество бочек портера. Используйте симплекс-метод, чтобы найти уровень производства, который максимизирует прибыль.

Решение В примере 1 мы добавили резервные переменные и нашли начальную симплексную таблицу для этой стандартной задачи максимизации.

Исходная симплексная таблица представляет собой матрицу 4 x 7,

Самая отрицательная запись в строке индикатора равна -100. Эта запись означает, что сводной столбец является первым столбцом в таблице. Частные, сформированные из последнего столбца и опорного столбца,

указывают, что третья строка является сводной.

Третью строку необходимо умножить на ¹ / _23,8 , чтобы изменить точку опоры на 1. последний столбец округляются до десятых.

Теперь нам нужно использовать три операции со строками, чтобы поместить нули в оставшуюся часть сводного столбца.

Отрицательное число в строке индикатора говорит нам о том, что второй столбец будет новым сводным столбцом.

Чтобы найти новую опорную точку, составьте частные из последнего столбца и второго столбца. Частные для отдельных строк:

Числа, показанные в частном, округлены, а вычисленная сумма округлена до ближайшего целого числа. Это не влияет на наш выбор опорной строки. Если частные близки друг к другу, несите больше десятичных знаков, чтобы не выбрать неправильную сводную строку из-за округления. Новый пивот — 0,544 в первой строке, во втором столбце.

Новая опорная точка изменяется на 1 путем умножения первой строки таблицы на ¹ / _0,544 :

Мы используем три операции со строками, чтобы поместить нули в оставшуюся часть опорной колонки:

Поскольку в строке индикатора нет отрицательных чисел, мы можем прочитать решение из этой таблицы.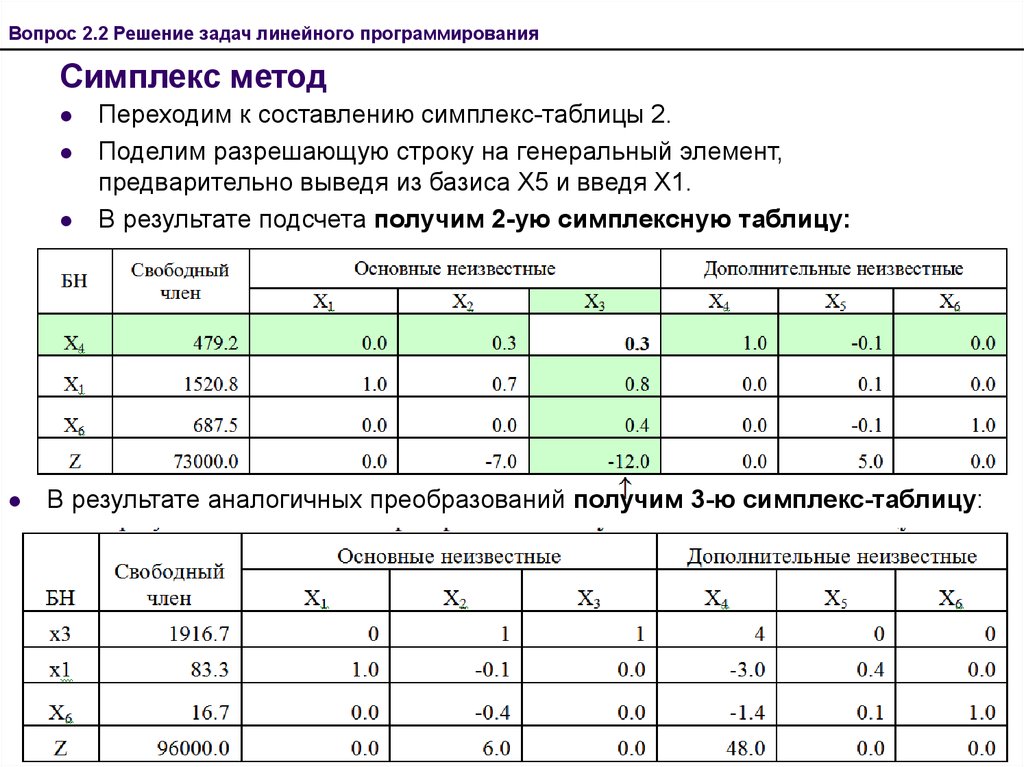 Если мы охватим неосновные переменные s ₁ и s ₂ , мы увидим, что решение, соответствующее этой таблице, равно ( x ₁ , x ₂ ) = (35,328,2, 14 671,8) и P = 4,706,563,7 или приблизительно 35 328 баррелей из бледного ALE и 14 672 батров из $ 4,66.

---

 

Пример 3 и пример 4 имеют две решающие переменные и также были выполнены графически в разделе 4.2. В следующем примере мы применяем симплекс-метод к задаче с тремя переменными решения. Задачи с более чем двумя решающими переменными невозможно решить с помощью графических методов, представленных в разделе 4.2.

Пример 5      Найти оптимальный инвестиционный портфель

Инвестирование в акции и взаимные фонды — это компромисс. Мы хотим максимизировать деньги, которые мы получаем от инвестиций, но управляем риском потери денег при неудачных инвестициях. Как правило, инвестиции с более высокой доходностью являются более рискованными, а инвестиции с более низкой доходностью менее рискованными.

Инвесторы используют несколько статистических данных для количественной оценки отдачи от своих инвестиций. Например, такие веб-сайты, как Yahoo Financial, рассчитывают такие показатели, как средняя норма прибыли. Это число указывает на общую прибыль инвестора от инвестиций в годовом исчислении за определенный период времени. Чем выше средняя норма прибыли, тем больше прибыли вы получите от дивидендов или продажи акций или взаимного фонда.

Есть также несколько мер риска, доступных для инвесторов. Один широко используемый индикатор называется бета. Бета акций или взаимных фондов рассчитывается с помощью регрессионного анализа. Детали анализа не важны для наших целей. Однако понимание того, что говорит вам бета-версия, является важным инструментом инвестирования.

Бета-версия акций или взаимных фондов измеряет волатильность цены инвестиции по отношению к некоторому контрольному показателю, такому как S&P 500 или промышленный индекс Доу-Джонса. Бета, равная 1, указывает на то, что цена инвестиции будет меняться вместе с изменениями эталона. Бета меньше 1 указывает на то, что цена инвестиции менее волатильна, чем эталон. Другими словами, изменения эталона будут больше, чем изменения цены инвестиции. Бета больше 1 указывает на то, что цена инвестиции более волатильна, чем эталон. В этом случае изменения эталона будут меньше, чем изменения цены инвестиции.

Предположим, инвестор заинтересован в инвестировании в три разных паевых инвестиционных фонда. Фонды, их средний годовой доход за пять лет и значения коэффициента бета показаны (по состоянию на 31 июля 2010 г.) в таблице ниже:

Фонд TIIRX имеет самую высокую норму дохода и самый низкий коэффициент бета. У фонда TCMVX самая низкая доходность и самая высокая бета. На первый взгляд может показаться, что инвестор должен вложить все свои деньги в TIIRX, поскольку это принесет наибольшую прибыль и наименьший риск.

У каждого инвестора свои требования к инвестициям, и в этом случае инвестор хочет диверсифицировать свои активы. Это означает, что инвестор хочет снизить общий риск, инвестируя в несколько широких категорий акций. TIIRX стремится инвестировать 80% своих средств в ценные бумаги, которые предлагают долгосрочную доходность. Он инвестирует около 20% в небольшие компании, которые предлагают возможность роста. Хотя это может показаться хорошим сочетанием, инвестор желает, чтобы сумма инвестиций в TCMVX и TIERX составляла не менее 25% от суммы, инвестированной в TIINX.

Если у инвестора есть 100 000 долларов для инвестирования, и он хочет, чтобы средневзвешенная бета не превышала 1, сколько инвестор должен вложить в каждый из трех фондов, чтобы их доход был максимальным?

Решение Хорошей отправной точкой для задач линейного программирования являются переменные. В этой задаче мы хотим найти сумму денег, которую нужно инвестировать в каждый фонд. Имеет смысл определить переменные следующим образом:

M : сумма денег, вложенная в фонд Mid Cap Value Fund.
G : сумма денег, инвестированная в Фонд роста и доходов.
E : сумма денег, вложенная в Международный фонд акций

Мы хотим получить максимальную отдачу от инвестиций. Доходность инвестиций определяется путем умножения вложенной суммы на среднегодовую доходность. Поскольку M , G и E представляют суммы вложенных денег, 0,0172 M , 0,0288 G и 0,0267 E представляют доход от этих сумм. Целевая функция представляет собой сумму этих сумм или

где R — общий доход.

Три элемента информации могут помочь нам записать ограничения. Во-первых, у инвестора есть 100 000 долларов для инвестирования. Это означает, что сумма сумм, вложенных в каждый фонд, должна быть меньше или равна 100 000 или

. % от того, что инвестируется в Фонд роста и дохода. Ориентируясь на слово «сумма» и словосочетание «25% от», пишем

Слово «сумма» означает, что мы должны сложить два количества, а фраза «25% от» означает, что мы должны умножить количество на 0,25.

Последняя часть информации диктует, что инвестор «желает, чтобы средневзвешенная бета не превышала 1». Средневзвешенное значение говорит нам, что нам нужно сложить некоторые члены, а затем разделить на общую сумму. Взвешенная сумма риска записывается как 1,16 M + 0,93 G + 1,04 E . Термин «взвешенный» указывает на присутствие переменной в каждом терме. Если бы мы просто сложили бета-значения, каждый из них внес бы «равный» вклад в сумму, поскольку каждый появляется в своем собственном термине. Умножая значение бета на сумму, инвестированную в соответствующий фонд, мы взвешиваем бета на сумму инвестиций. Если мы это сделаем, то фонд с большой суммой в нем внесет больший вклад в сумму, чем фонд с очень небольшими вложениями. Чтобы усреднить взвешенную сумму, мы делим ее на общую сумму инвестиций или на 9.0083 М + Г + Е . Ограничение

отражает желание инвестора, чтобы средневзвешенная бета не превышала 1.

Если добавить неотрицательные ограничения, задача линейного программирования примет вид

Эта задача линейного программирования не находится в стандартной максимальной форме.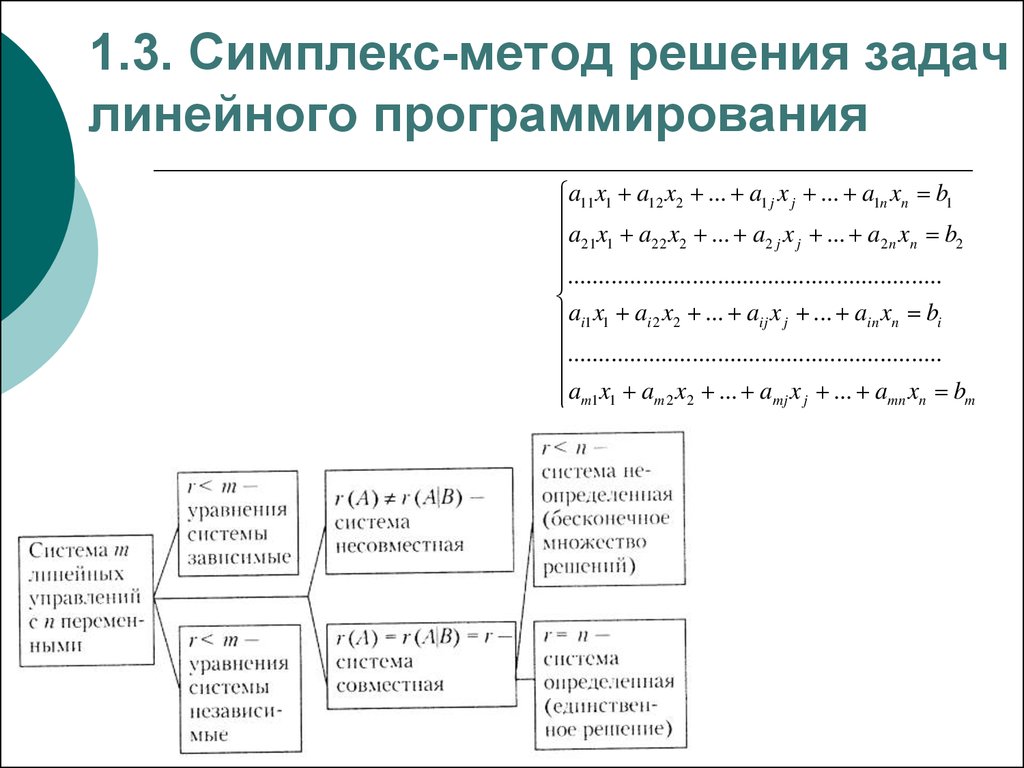 так как второе и третье ограничения не имеют вида

b ₁ x ₁ + b ₂ x ₂ +… + B _N x _N ≤ C

, где B ₁ , B 2 , , , и , , , , . чисел и c ≥ 0. Немного алгебры меняет эти ограничения на правильную форму.

Если мы начнем со второго ограничения и вычтем M и E с обеих сторон, мы получим неравенство

0 ≥ 0,25 G – M – E

Переверните неравенство и измените порядок членов, чтобы получить

– M + 0,25 G – E  ≤ 0

5 9000. Это неравенство имеет правильный вид.

If we start with the third inequality and multiply both sides by M + G + E we are left with

1.16 M + 0. 93 G + 1.04 E  ≤ M + Г + Е

Соберите все члены в левой части, чтобы получить

0,16 M – 0,07 G + 0,04 E  ≤ 0

С помощью этих модификаций мы можем записать стандартную задачу максимизации a

:

Теперь, когда задача представлена ​​в стандартной форме, мы можем добавить к ограничениям резервные переменные и записать исходную симплексную таблицу.

Целевая функция должна быть переписана со всеми членами слева от знака равенства или

-0,0172 M – 0,0288 G – 0,0267 E + R = 0

Обратите внимание, что переменные записываются в определенном порядке. Поскольку термины будут соответствовать столбцам в таблице, нам нужно использовать этот порядок для каждого уравнения, которое мы пишем.

Добавить переменные SLACK S ₁ , S ₂ и S ₃ .0002

Объедините эти уравнения с уравнением целевой функции, чтобы получить

Из этой исходной симплексной таблицы нам нужно выбрать опорный столбец и строку. Чтобы найти сводную колонку, найдите самую отрицательную запись в строке индикатора внизу. Запись -0,0288 является самой отрицательной записью, поэтому второй столбец является сводным столбцом.

Частные для выбора сводной строки находятся путем деления записей в последнем столбце на соответствующие записи в опорной колонке,

Помните, что частное с отрицательным числителем или знаменателем игнорируется, поэтому частное для третьей строки даже не вычисляется. Вторая строка содержит наименьшее частное, поэтому точка опоры равна 0,25 во второй строке, втором столбце.

Чтобы изменить опорную точку на 1, умножьте вторую строку на ¹ / _0,25 или 4:

При изменении опорной точки необходимы операции со строками, чтобы изменить другие числа в опорной колонке на нули.

После первой итерации симплекс-метода в строке индикатора все еще есть отрицательное число. Эта таблица не соответствует оптимальному решению, поэтому мы должны выбрать первый столбец в качестве опорного столбца и определить новую опорную строку.