Онлайн калькулятор уравнение плоскости проходящей через 3 точки: Онлайн калькулятор. Уравнение плоскости

Содержание

Уравнение плоскости.

Навигация по странице:

Плоскость — определение
Общее уравнение плоскости
Уравнение плоскости в отрезках
Уравнение плоскости, проходящей через точку, перпендикулярно вектору нормали
Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой

Онлайн калькулятор. Уравнение плоскости.

Определение. Плоскость — есть поверхность, полностью содержащая, каждую прямую, соединяющую любые её точки.

Любую плоскость можно задать уравнением плоскости первой степени вида

A x + B y + C z + D = 0

где A, B и C не могут быть одновременно равны нулю.

Уравнение плоскости в отрезках

Если плоскость пересекает оси OX, OY и OZ в точках с координатами (a, 0, 0), (0, b, 0) и (0, 0, с), то она может быть найдена, используя формулу уравнения плоскости в отрезках

x	+	y	+	z	= 1
a		b		c

Уравнение плоскости, проходящей через точку, перпендикулярно вектору нормали

Чтобы составить уравнение плоскости, зная координаты точки плоскости M(x₀, y₀, z₀) и вектора нормали плоскости n = {A; B; C} можно использовать следующую формулу.

A(x — x₀) + B(y — y₀) + C(z — z₀) = 0

Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой

Если заданы координаты трех точек A(x₁, y₁, z₁), B(x₂, y₂, z₂) и C(x₃, y₃, z₃), лежащих на плоскости, то уравнение плоскости можно найти по следующей формуле

x — x₁	y — y₁	z — z₁	= 0
x₂ — x₁	y₂ — y₁	z₂ — z₁
x₃ — x₁	y₃ — y₁	z₃ — z₁

Аналитическая геометрия: Вступление и оглавлениеРасстояние между двумя точками.

Середина отрезка. Координаты середины отрезка.Уравнение прямой.Уравнение плоскости.Расстояние от точки до плоскости.Расстояние между плоскостями.Расстояние от точки до прямой на плоскости.Расстояние от точки до прямой в пространстве.Угол между плоскостями.Угол между прямой и плоскостью.

Онлайн калькуляторы. Аналитическая геометрия. Декартовые координаты.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

найти уравнение плоскости проходящей через точку перпендикулярно плоскости

Вы искали найти уравнение плоскости проходящей через точку перпендикулярно плоскости? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и написать уравнение плоскости проходящей через точку, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз.

И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «найти уравнение плоскости проходящей через точку перпендикулярно плоскости».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как найти уравнение плоскости проходящей через точку перпендикулярно плоскости,написать уравнение плоскости проходящей через точку,написать уравнение плоскости проходящей через точку перпендикулярно вектору,написать уравнение плоскости проходящей через точку перпендикулярно плоскости,написать уравнение плоскости проходящей через точку перпендикулярно прямой,напишите уравнение плоскости проходящей через точку перпендикулярно плоскости,общее уравнение плоскости проходящей через точку перпендикулярно плоскости,плоскость проходит через точку,составить общее уравнение плоскости проходящей через точку перпендикулярно,составить общее уравнение плоскости проходящей через точку перпендикулярно плоскости,составить уравнение плоскости перпендикулярной плоскости,составить уравнение плоскости проходящей через точки перпендикулярно плоскости,составить уравнение плоскости проходящей через точку и перпендикулярно плоскости,составить уравнение плоскости проходящей через точку и перпендикулярной плоскости,составить уравнение плоскости проходящей через точку перпендикулярно,составить уравнение плоскости проходящей через точку перпендикулярно плоскостям,составить уравнение плоскости проходящей через точку перпендикулярно прямой,уравнение плоскости перпендикулярной прямой,уравнение плоскости перпендикулярной прямой и проходящей через точку,уравнение плоскости проходящей через 2 точки перпендикулярно плоскости,уравнение плоскости проходящей через точку и перпендикулярной прямой,уравнение плоскости проходящей через точку перпендикулярно плоскости,уравнение плоскости проходящей через точку перпендикулярно прямой,уравнение плоскости через точку перпендикулярно плоскости.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и найти уравнение плоскости проходящей через точку перпендикулярно плоскости. Просто введите задачу в окошко и нажмите «решить» здесь (например, написать уравнение плоскости проходящей через точку перпендикулярно вектору).

Где можно решить любую задачу по математике, а так же найти уравнение плоскости проходящей через точку перпендикулярно плоскости Онлайн?

Решить задачу найти уравнение плоскости проходящей через точку перпендикулярно плоскости вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.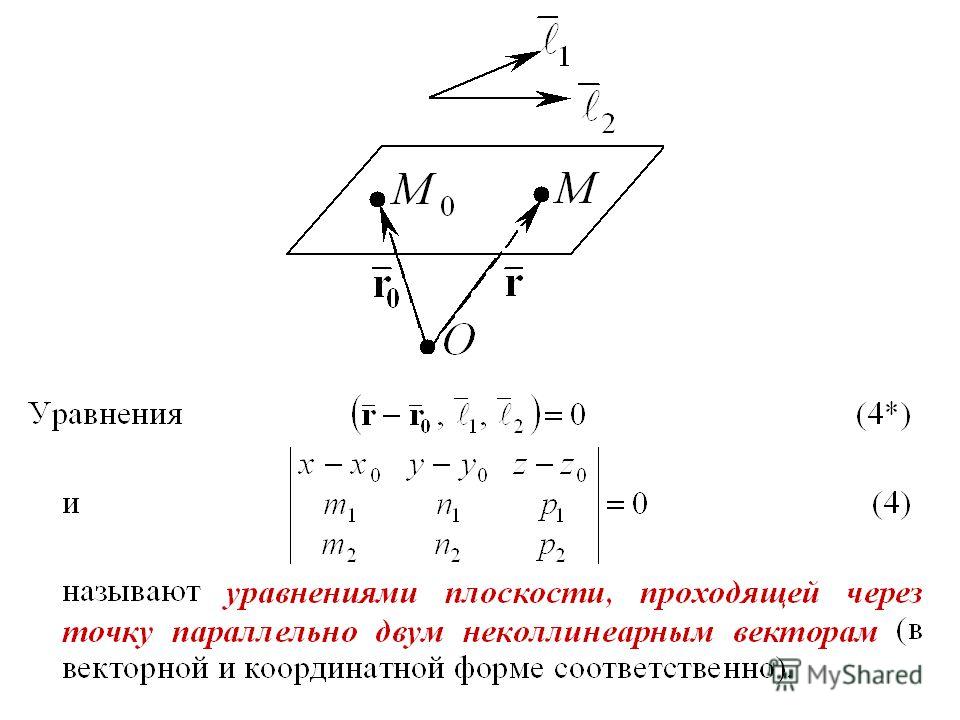

Калькулятор уравнений по 3 точкам

Введите 3 точки, чтобы составить квадратное уравнение:

Как работает калькулятор уравнения по 3 точкам?

Формирует квадрат из 3 введенных точек.
Этот калькулятор имеет 3 входа.

Какие 4 формулы используются в 3-точечном калькуляторе уравнений?

Δ = (a * f * k) + (b * g * i) + (c * e * j) — (c * f * i) — (a * g * j) — (b * e * k)
а числитель = (d * f * k) + (b * g * l) + (c * h * j) — (c * f * l) — (d * g * j) — (b * ч*к)
b числитель = (a * h * k) + (d * g * i) + (c * e * l) — (c * h * i) — (a * g * l) — (d * e * л)
(а*ж*л) + (б*ч*и) + (д*е*й) — (д*ж*я) — (а*ч*й) — (б*е*л )

Чтобы узнать больше о математических формулах, ознакомьтесь с нашим досье формул

Какие 4 понятия учитываются в 3-точечном калькуляторе уравнений?

Трехточечное уравнение

Уравнение параболы, проходящей через 3 двумерные точки

Уравнение

утверждение, объявляющее, что два математических выражения равны

точка

точное положение в пространстве, не имеющее ни длины, ни ширины, ни толщины некоторые примеры расчетов для 3-точечного калькулятора уравнений?

(1,2)(3,4)(5,6)

3-точечный калькулятор видео

Электронная почта: [email protected]
Тел.: 800-234-2933

Математическая тревога
судоку
Информационный бюллетень о недобросовестном преимуществе
Биографии математиков
Подкаст цены за клик

Математические Мемы
Глоссарий по математике
Предметы
бейсбольная математика

Друзья
Связаться с нами
Вакансии учителя математики
Политика в отношении файлов cookie
Политика конфиденциальности

Нахождение уравнения плоскости — Криста Кинг Математика

Формулы уравнения плоскости

Уравнение плоскости задается формулой

???a(x-x_1)+b(y-y_1)+c(z-z_1)=0???

где ???\langle{a},b,c\rangle??? числа направления от вектора нормали к плоскости.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Прочитайте больше.

Даны три точки на плоскости ???P(P_1,P_2,P_3)???, ???Q(Q_1,Q_2,Q_3)??? и ???R(R_1,R_2,R_3)???, мы можем найти уравнение плоскости по

, используя точки для создания двух векторов

???\vec{PQ}=\langle( Q_1-P_1),(Q_2-P_2),(Q_3-P_3)\rangle???

???\vec{PR}=\langle(R_1-P_1),(R_2-P_2),(R_3-P_3)\rangle???,

получение перекрестного произведения ???\vec {ПК}??? и ???\vec{PR}??? чтобы получить вектор нормали к плоскости

???\vec{PQ}\times\vec{PR}=\begin{vmatrix}\bold i&\bold j&\bold k\\PQ_1&PQ_2&PQ_3\\PR_1&PR_2&PR_3\end{vmatrix}=\bold i\begin{ vmatrix}PQ_2&PQ_3\\PR_2&PR_3\end{vmatrix}-\bold j\begin{vmatrix}PQ_1&PQ_3\\PR_1&PR_3\end{vmatrix}+\bold k\begin{vmatrix}PQ_1&PQ_2\\PR_1&PR_2\end{vmatrix}???

???=\жирный i(PQ_2PR_3-PQ_3PR_2)-\жирный j(PQ_1PR_3-PQ_3PR_1)???

???+\жирный k(PQ_1PR_2-PQ_2PR_1)???

, а затем вставить заданные точки и вектор нормали в формула для уравнения плоскости.

Имея три точки, лежащие на плоскости, мы воспользуемся специальной формулой, чтобы найти уравнение плоскости

Пройти курс

Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого. 🙂

Учить больше

Нахождение плоскости по трем точкам, лежащим в плоскости

Пример

Найдите уравнение плоскости, проходящей через заданные точки.

???Р(1,0,2)???

???Q(2,-1,3)???

???R(1,-1,2)???

Начнем с заданных точек ???P???, ???Q??? и ???Р??? найти два вектора ???\vec{PQ}??? и ???\vec{PR}??? которые лежат в плоскости.

???\vec{PQ}=\left\langle(2-1),(-1-0),(3-2)\right\rangle???

???\vec{PQ}=\left\langle1,-1,1\right\rangle???

???\vec{PR}=\left\langle(1-1),(-1-0),(2-2)\right\rangle???

???\vec{PR}=\left\langle0,-1,0\right\rangle???

Мы начнем с использования заданных точек P, Q и R, чтобы найти два вектора PQ и PR, которые лежат в плоскости.