Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Саша, Юра и Олег вместе сделали для новогодних гирлянд 48 бумажных фонариков. Олег сделал 12 фонариков. Сколько фонариков сделал Саша, если он сделал на 6 фонариков меньше, чем Юра?
Олег сделал 12 фонариков. Сколько фонариков сделал Саша, если он сделал на 6 фонариков меньше, чем Юра?
5 класс Жучка тяжелее кошки в 3 раза, мышка легче кошки в 10 раз, репка тяжелее мышки в 60 раз. Во сколько раз репка тяжелее Жучки? Ответ Обоснуйте Помогите пожалуйста
помогите плиз , решить задачу!!! в первой связке на 56 шаров больше, чем во второй. сколько шаров в каждой связке, если во второй связке в 5 раз меньше шаров, чем в первой?
Помогите с Географией1 определите поясное время в якутске если в самаре 16 часов2 где поясное время больше и на сколько : в красноярске или в москве 3 определите поясное время в симферополе если
решить задачу уменьшаемое на 24 больше разности, вычитаемое на 32 меньше уменьшаемого запишите равенство с таким уменьшаемым ,
Пользуйтесь нашим приложением
Питон | Функция math.cos()
Сохранить статью
- Уровень сложности: Средний
- Последнее обновление: 20 мар, 2019
Улучшить статью
Сохранить статью
В Python математический модуль содержит ряд математических операций, которые можно легко выполнить с помощью модуля.
math.cos() Функция возвращает косинус значения, переданного в качестве аргумента. Значение, переданное в эту функцию, должно быть в радианах.Синтаксис: Math.cos (x)
Параметр:
x: значение, которое должно быть передано в COS ()Возврат: Возвращает косинус. 1:
importmath
a=math.pi/6
Печать ("Значение косинуса PI / 6 IS:", конец="")
") (
369") (
369").)
Вывод:
Значение косинуса пи/6: 0,8660254037844387
Код #2:
импортматематика
importnumpy as np
importmatplotlib.pyplot as plt
in_array=np.linspace(-(2*np.pi),2*np.pi,20)
out_array=[]
foriinrange(len(in_array)):
out_array.append(math.cos(in_array[i]))
I+=1
339239003
.0026
("\nout_array : ", out_array)
plt.plot(in_array, out_array, color='red', marker="o")
plt.title("math.cos()")
plt.xlabel("X")
plt.ylabel(
"Y")
plt.show()Output:
in_array : [-6.28318531 -5.62179738 -4.96040945 -4.29
3 -3.6376336 -2.97624567
-2.31485774 -1.65346982 -0.99208189 -0.33069396 0.33069396 0.99208189
1.65346982 2.31485774 2.97624567 3.6376336 4.293 4.96040945
5.62179738 6.28318531]out_array : [1.0, 0.7891405093963934, 0.2454854871407988, -0.40169542465296987, -0.8794737512064891, -0.9863613034027223, -0.6772815716257412, -0.08257934547233249, 0.5469481581224268, 0.9458172417006346, 0.9458172417006346, 0.5469481581224268, -0.0825793454723316, -0.6772815716257405, -0.9863613034027223, -0.8794737512064893, -0.40169542465296987, 0.2454854871407988, 0.7891405093963934, 1.0]
Related Статьи
Что нового
Мы используем файлы cookie, чтобы обеспечить вам максимальное удобство просмотра нашего веб-сайта.
Используя наш сайт, вы подтверждаете, что вы прочитали и поняли наши Политика в отношении файлов cookie и Политика конфиденциальности
BIONINF 501 Модуль 4 (Оптимизация)
Похоже, что Юнь-Вей Шан и Ю-Хуан Цю утверждают, что локальные минимумы существуют в 4-м измерении при (-0,77565923, 0,61309337, 0,38206285, 0,14597202) в «Примечании к Расширенная функция Розенброка». Авторы использовали приличный градиент в качестве метода, чтобы найти это, однако я не могу воспроизвести их результаты с помощью этого метода.
Моя оценка экстремумов чрезвычайно близка к теоретическим аналогам, указанным как (1, 1, 1, 1). 92) } # начальное предположение для первых минимумов initial_x_rb <- c(0, 0, 0, 0) #начальное условие, функция, метод x_optimal_rb <- optim(initial_x_rb, f_rb, method="BFGS") # выполняет минимизацию x_min_rb <- x_optimal_rb$par # x_min содержит значения домена, при которых достигается (локальный) минимум x_min_rb # критическая точка/вектор
## [1] 0.9999755 0.9999517 0.9998969 0.9997934
# значение первого экстремума целевой функции x_optimal_rb$значение 92 возврат (с (z1)) } # это начальное предположение обеспечивает глобальные минимумы soll_mb<-solnp(c(10,10), fun = f_mb, ineqfun = eqn1, ineqLB = -Inf, ineqUB = 25)## ## Iter: 1 fn: 5.1975 Pars: 2.84730 2.98609 ## Iter: 2 fn: 3.7293 Pars: -0.31540 -0.18946 ## Iter: 3 fn: -2.0772 Pars: -1.57019 -1.05530 ## Iter: 4 fn: -105.7839 Pars: -3.04970 -1.55482 ## Iter: 5 fn: -106.7645 Pars: -3.13025 -1.58214 ## Iter: 6 fn: -106.7645 Pars: -3.13025 -1.58214 ## solnp--> Завершено за 6 итераций 92) z2 = (x[1] %% 4) + (x[2]/2) г3 = х[3] возврат (с (z1, z2, z3)) } фунт = с(-1000,-1000,-1000) уб = с(1000,1000,100) lh <- c(-Inf, -Inf, -Inf) # проверяется нижняя граница, и она не меняется при c = -100 и c = -1000 гм <- с(50, 1,5, Inf) # это первоначальная догадка, использующая максимальный диапазон в пределах заданных ограничений x0 <- c(49.

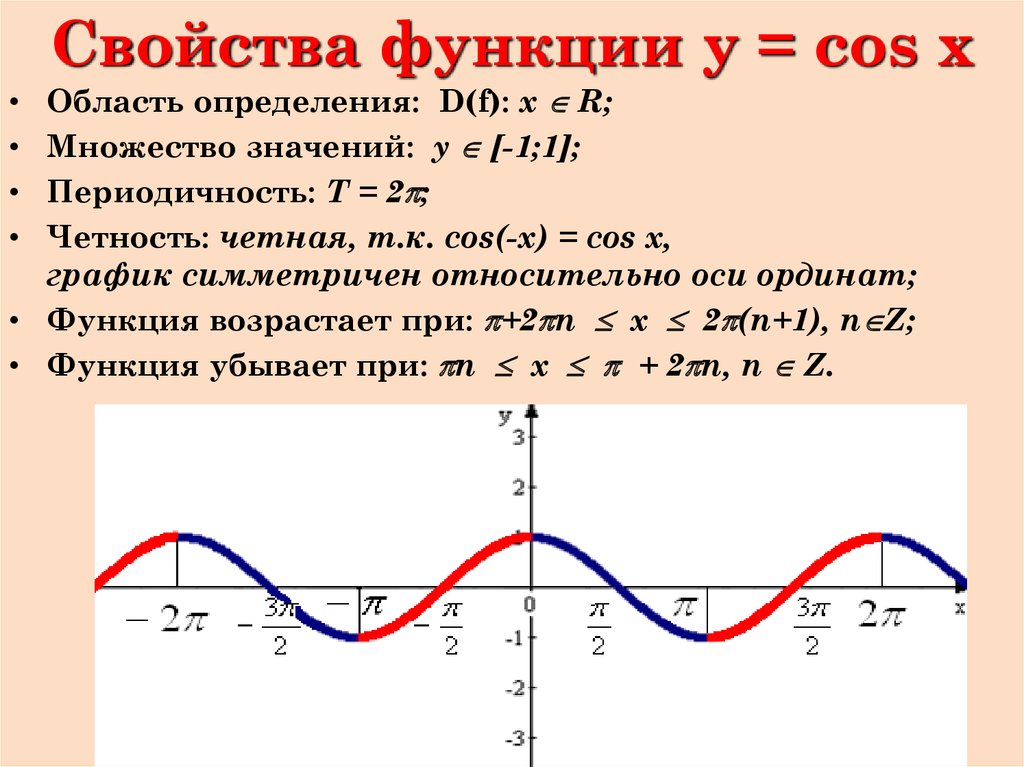
 Период равен периоду косинуса и равен 2 пи
Период равен периоду косинуса и равен 2 пи
 )
)  append(math.cos(in_array[i]))
append(math.cos(in_array[i])) 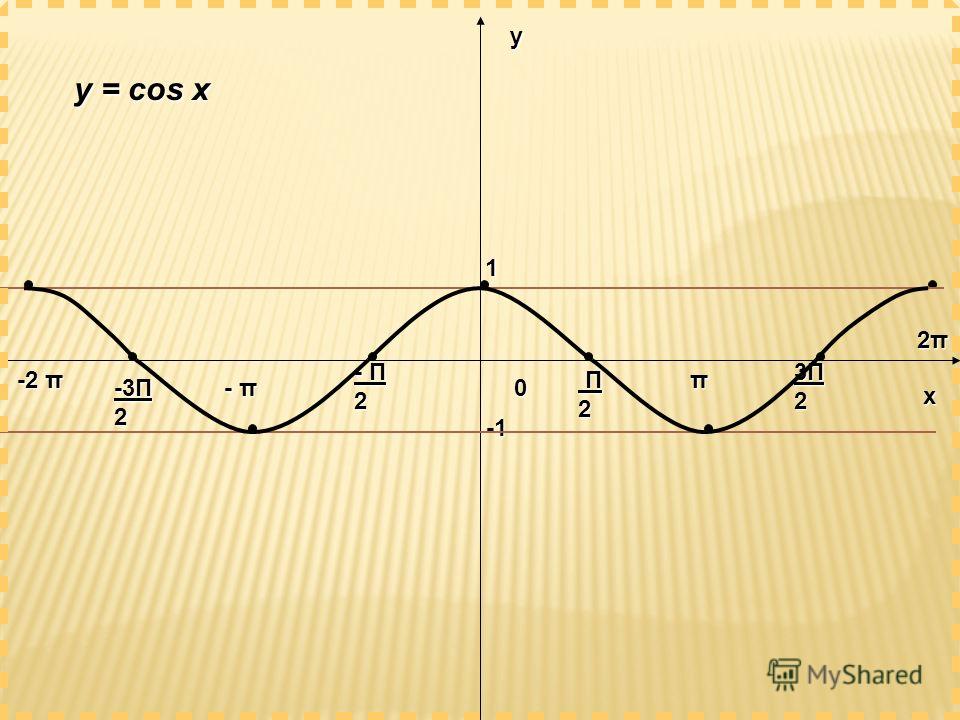 ylabel(
ylabel( 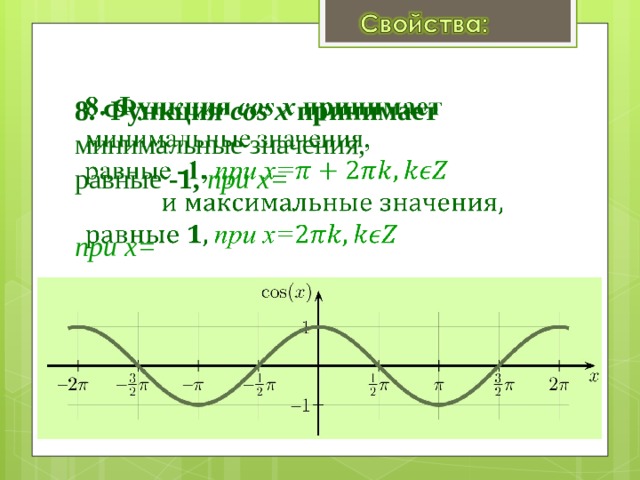 Используя наш сайт, вы
подтверждаете, что вы прочитали и поняли наши Политика в отношении файлов cookie и Политика конфиденциальности
Используя наш сайт, вы
подтверждаете, что вы прочитали и поняли наши Политика в отношении файлов cookie и Политика конфиденциальности  9999755 0.9999517 0.9998969 0.9997934
9999755 0.9999517 0.9998969 0.9997934