Калькулятор таблицы частот — MathCracker.com
Решатели Статистика
Инструкции: Используйте этот калькулятор таблицы частот, чтобы построить таблицу частот, связанную с образцом, представленным в форме ниже. Образец должен быть разделен запятыми или пробелами:
Значения X (через запятую или пробел) =
Имя случайной переменной (необязательно)
Compute Relative Frequencies
Compute Cumulative Frequencies
Таблица частот соответствует организованной таблице, которая содержит различные значения, которые есть в выборке, вместе с частотами этих значений (сколько раз каждое значение появляется в выборке).
Как правило, частотная таблица может быть представлена столбчатой диаграммой (гистограммой частот), чтобы получить четкое представление о распределении переменной.
Таблица относительных частот
Часто бывает полезно выразить частоты, чтобы нормализовать их и узнать, какая доля (процент) частот связана с каждым значением. Такие относительные частоты также можно изобразить и представить в виде гистограммы ( гистограмма относительной частоты ).
Режим этого образца — 3, потому что 3 — наиболее повторяющееся значение.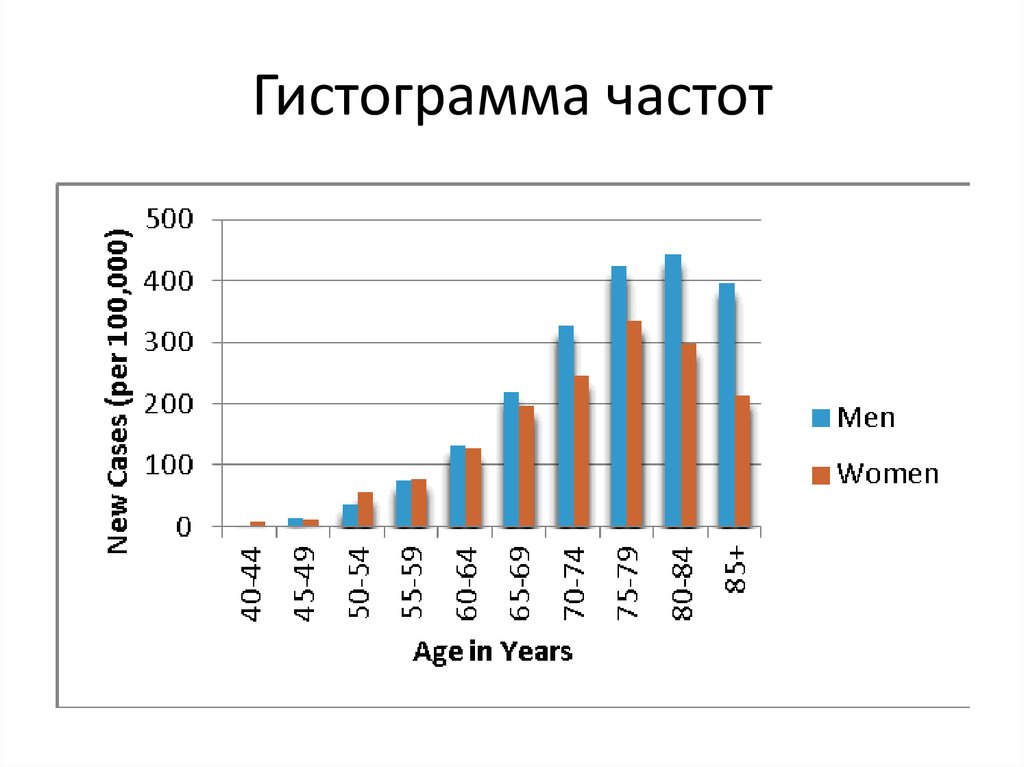
Действительно, значение 3 встречается в выборке четыре раза, больше, чем любое другое число.
Кумулятивная таблица частот
Кроме того, полезно построить совокупные частоты, чтобы увидеть, сколько накоплено (в терминах совокупных частот) по отношению к общему количеству частот.
Обратите внимание, что вместо этого для работы с классами вы можете использовать это создатель гистограммы вместо.
Базовый пакет статистики Кумулятивная таблица частот Калькулятор таблицы частот Создатель графиков Инструмент построения графиков Таблица относительных частот Калькулятор статистики Статистический решатель
Контрольная работа по математической статистике (матстат)
Чтобы узнать наличие других готовых вариантов или заказать авторское
решение Вашей работы со скидкой – перейдите по кнопке “Купить” и
нажмите “Связаться” (указывайте артикул работы)
ВАРИАНТ 1
Задание 1.
Рассчитать и построить гистограмму относительных частот по сгруппированным данным, где mi – частота попадания вариант в промежуток (xi;xi+1].
| i | xi<X<=xi+1 | mi |
| 1 | 2-4 | 5 |
| 2 | 4-6 | 8 |
| 3 | 6-8 | 16 |
| 4 | 8-10 | 12 |
| 5 | 10-12 | 9 |
Задание 2. Найти несмещенную выборочную дисперсию на основании данного распределения выборки.
| -6 | -2 | 3 | 6 | |
| 12 | 14 | 16 | 8 |
Задание 3. Проверить нулевую гипотезу о том, что заданное значение a0 = 10 является математическим ожиданием нормально распределенной случайной величины при 5%-м уровне значимости для двусторонней критической области, если в результате обработки выборки объема n = 10 получено выборочное среднее =12, а выборочное среднее квадратичное отклонение равно s1 = 1.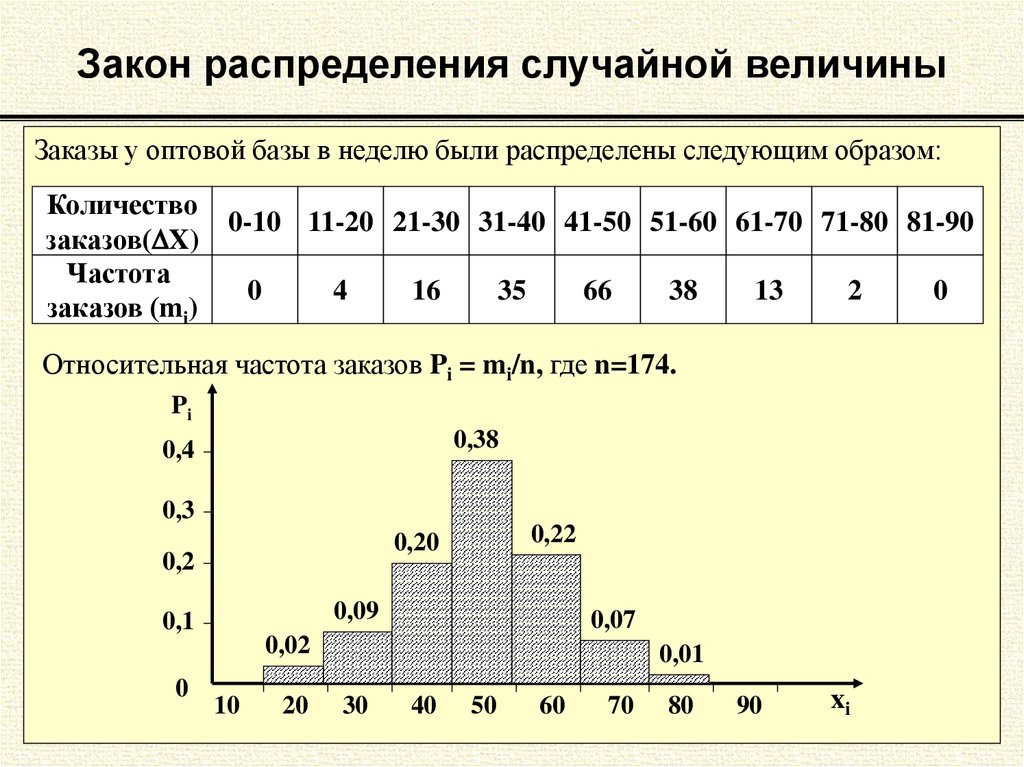
Задание 4. При уровне значимости α = 0,1 проверить гипотезу о равенстве дисперсий двух нормально распределенных случайных величин X и Y на основе выборочных данных при альтернативной гипотезе .
| xi | ni | yi | mi |
| 142 | 3 | 140 | 5 |
| 145 | 1 | 146 | 3 |
| 146 | 2 | 147 | 2 |
| 148 | 2 | 151 | 2 |
Задание 5. Найти выборочное уравнение линейной регрессии Y на X на основании корреляционной таблицы.
| X Y | 10 | 15 | 20 | 25 | 30 | 35 |
| 15 | 6 | 4 | ||||
| 25 | 6 | 8 | ||||
| 35 | 21 | 2 | 5 | |||
| 45 | 4 | 12 | 6 | |||
| 55 | 1 | 5 |
Задание 6.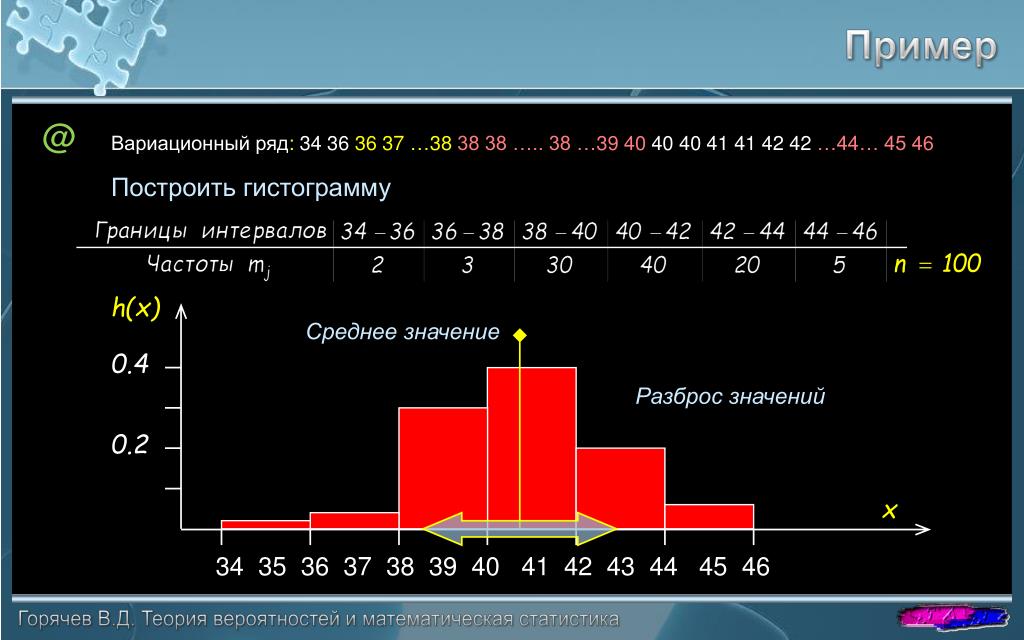
При уровне значимости α = 0,05 методом дисперсионного анализа проверить нулевую гипотезу о влиянии фактора на качество объекта на основании пяти измерений для трех уровней фактора.
| номер фактора | Ф1 | Ф2 | Ф3 |
| 1 | 24 | 18 | 22 |
| 2 | 16 | 14 | 15 |
| 3 | 12 | 10 | 16 |
| 4 | 5 | 4 | 12 |
| 5 | 6 | 16 | 8 |
1.6.2 — Гистограммы | СТАТ 500
Если имеется много точек данных и мы хотели бы увидеть распределение данных, мы можем представить данные с помощью гистограммы частот
Гистограмма похожа на гистограмму, но предназначена для количественных данных.
Для создания гистограммы данные необходимо сгруппировать по интервалам классов. Затем создайте подсчет, чтобы показать частоту (или относительную частоту) данных в каждом интервале. Относительная частота — это частота в определенном классе, деленная на общее количество наблюдений. Столбцы имеют ширину, равную интервалу классов, и высоту, соответствующую частоте (или относительной частоте).
Пример гистограммы
Джессика взвешивается каждую субботу в течение последних 30 недель. В таблице ниже показан ее зарегистрированный вес в фунтах.
135 | 137 | 136 | 137 | 138 | 139 |
140 | 139 | 137 | 140 | 142 | 146 |
148 | 145 | 139 | 140 | 142 | 143 |
144 | 143 | 141 | 139 | 137 | 138 |
139 | 136 | 133 | 134 | 132 | 132 |
Создайте гистограмму ее веса.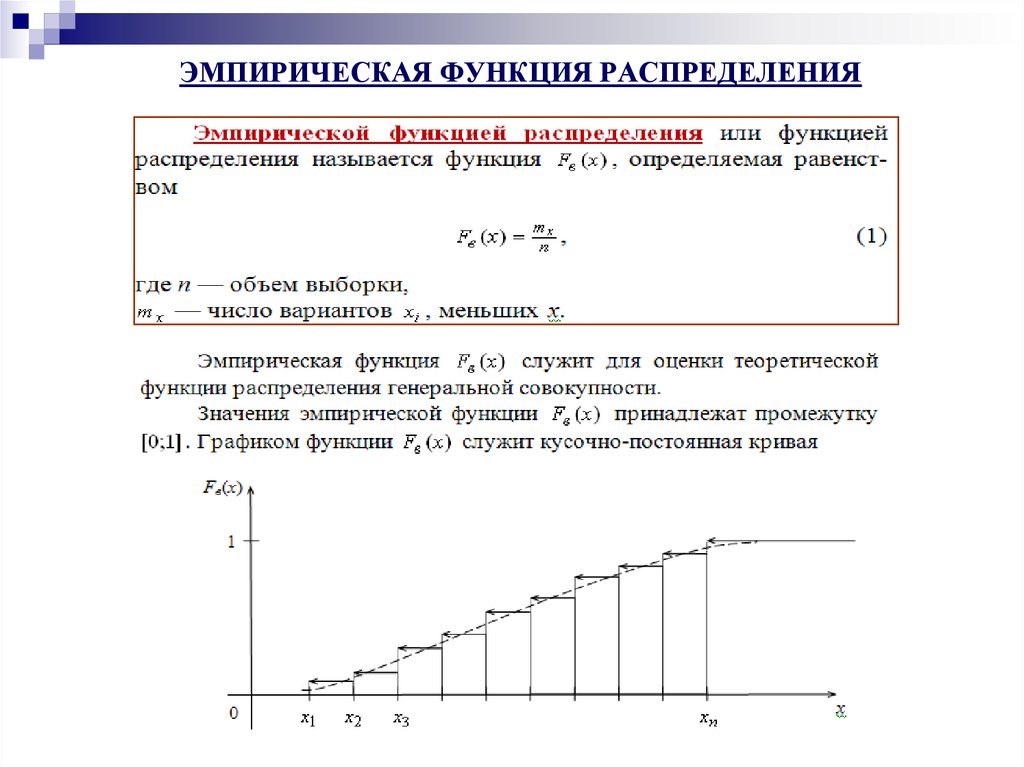
Ответ
Для гистограмм обычно требуется от 5 до 20 интервалов. Поскольку диапазон данных составляет от 132 до 148, удобно иметь класс шириной 2, так как это даст нам 9 интервалов.
- 131,5-133,5
- 133,5-135,5
- 135,5-137,5
- 137,5-139,5
- 139,5-141,5
- 141,5-143,5
- 143,5-145,5
- 145,5-147,5
- 147,5-149,5
Причина, по которой мы выбрали конечные точки как 0,5, состоит в том, чтобы избежать путаницы, принадлежит ли конечная точка интервалу слева от нее или интервалу справа от нее. Альтернативой является указание соглашения о конечной точке. Например, Minitab включает левую конечную точку и исключает правую конечную точку.
Имея интервалы, можно построить таблицу частот, а затем построить гистограмму частот или получить гистограмму относительных частот, чтобы построить гистограмму относительных частот. Следующая гистограмма создается программой Minitab, когда мы указываем средние точки для определения интервалов в соответствии с интервалами, выбранными выше.
Если мы не укажем среднюю точку для определения интервалов, Minitab по умолчанию выберет другой набор интервалов классов, что приведет к следующей гистограмме. В соответствии с соглашением о включении левой и исключении правой конечной точки наблюдение 133 включено в класс 133-135.
Обратите внимание, что разные значения интервалов классов приведут к разным гистограммам. Гистограммы относительной частоты строятся почти так же, как гистограмма частоты, за исключением того, что вертикальная ось представляет относительную частоту, а не частоту. Для визуального сравнения распределения двух наборов данных лучше использовать относительную частоту, а не частотную гистограмму, поскольку для всех относительных частот используется одна и та же вертикальная шкала — от 0 до 1.
Minitab: гистограммы Раздел
Как создать гистограмму в Minitab:
- Щелкните График > Гистограмма
- Выберите Простой .
- Введите столбец с вашей переменной
- Нажмите OK .
Статистика: Сила данных! Аналитический график: Суммарная частота
Заархивированное содержимое
Информация, обозначенная как заархивированная, предоставляется для справочных, исследовательских или учетных целей. На него не распространяются веб-стандарты правительства Канады, и он не изменялся и не обновлялся с момента архивирования. Пожалуйста, свяжитесь с нами, чтобы запросить формат, отличный от доступных.
- Пример 1 – Дискретные переменные
- Пример 2 – Непрерывные переменные
- Другие расчеты совокупной частоты
Суммарная частота используется для определения количества наблюдений, лежащих выше (или ниже) определенного значения в наборе данных. Кумулятивная частота рассчитывается с использованием таблицы распределения частот, которая может быть построена из диаграмм стеблей и листьев или непосредственно из данных.
Совокупная частота рассчитывается путем добавления каждой частоты из таблицы распределения частот к сумме ее предшественников. Последнее значение всегда будет равно сумме по всем наблюдениям, так как все частоты уже будут добавлены к предыдущей сумме.
Дискретные или непрерывные переменные
Переменные в любом расчете могут характеризоваться присвоенным им значением. Дискретная переменная состоит из отдельных неделимых категорий. Между переменной и ее соседом не может существовать никаких значений. Например, если вам нужно будет наблюдать за посещаемостью класса, зарегистрированной изо дня в день, вы можете обнаружить, что в классе учатся 29 учащихся в один день и 30 учащихся в другой. Однако посещаемость студентов не может быть между 29и 30. (Просто нет места для наблюдения каких-либо значений между этими двумя значениями, так как нет возможности иметь 29 с половиной студентов.)
Не все переменные характеризуются как дискретные. Некоторые переменные (такие как время, рост и вес) не ограничиваются фиксированным набором неделимых категорий.
Эти переменные называются непрерывными переменными , и они делятся на бесконечное число возможных значений. Например, время можно измерять в дробных частях часов, минут, секунд и миллисекунд. Таким образом, вместо того, чтобы закончить гонку за 11 или 12 минут, жокей и его лошадь могут пересечь финишную черту за 11 минут 43 секунды.
Важно знать разницу между двумя типами переменных, чтобы правильно рассчитать их кумулятивную частоту.
Начало страницы
Пример 1. Дискретные переменные
Общее число скалолазов в Лейк-Луизе, Альберта, было зарегистрировано за 30-дневный период. Результаты следующие:
31, 49, 19, 62, 24, 45, 23, 51, 55, 60, 40, 35 54, 26, 57, 37, 43, 65, 18, 41, 50, 56 , 4, 54, 39, 52, 35, 51, 63, 42.
- Используйте эти дискретные переменные для:
- настройте график стеблей и листьев (см. раздел о графиках стеблей и листьев) с дополнительными столбцами, помеченными Частота, Верхнее значение и Суммарная частота
- выяснить частоту наблюдений для каждого ствола
- найти верхнее значение для каждого штока
- рассчитать кумулятивную частоту путем сложения чисел из столбца Частота
- записать все результаты на график
- Постройте график, используя ось Y (или вертикальную линию) для совокупной частоты и ось X (или горизонтальную линию) для количества людей, занимающихся скалолазанием.
Ответы:
- Количество скалолазов колеблется от 4 до 65. Для построения графика стеблей и листьев данные лучше всего сгруппировать по классам с интервалом 10.
Каждый интервал может быть расположен в столбце Stem . Числа в этом столбце представляют собой первое число в пределах интервала класса. (например, Стебель 0 представляет интервал 0–9, Стебель 1 представляет интервал 10–19 и т. д.)
В столбце Leaf указано количество наблюдений, лежащих в пределах каждого интервала класса. Например, в Stem 2 (интервал 20–29) три наблюдения, 23, 24 и 26, представлены как 3, 4 и 6.
В столбце Частота указано количество наблюдений, найденных в пределах интервала класса. Например, в Ствол 5 найдено 9 листьев (или наблюдений); в Стержень 1 их всего два.
Используйте столбец Частота для расчета совокупной частоты.
- Сначала добавьте число из столбца Частота к предыдущему. Например, в Stem 0 у нас есть только одно наблюдение и нет предшественников. Суммарная частота равна единице.
1 + 0 = 1
- Однако в Stem 1 есть два замечания. Добавьте эти два к предыдущей кумулятивной частоте (один), и в результате получится три.
1 + 2 = 3
- В стержне 2 есть три наблюдения. Добавьте эти три к предыдущей кумулятивной частоте (три), и общая (шесть) будет кумулятивной частотой для Ствола 2.
3 + 3 = 6
- Продолжайте эти вычисления, пока не сложите все числа в столбце Частота .
- Запишите результаты в столбце Суммарная частота .
Верхнее значение 9В столбце 0233 перечислены наблюдения (переменные) с наибольшим значением в каждом из интервалов класса. Например, в Stem 1 два наблюдения 8 и 9 представляют переменные 18 и 19. Верхнее значение этих двух переменных равно 19.
Таблица 1. Совокупная частота ежедневных подсчетов скалолазов, зарегистрированных в Лейк-Луизе, Альберта, 30-дневный период0 4 1 4 1 1 8 9 2 19 1 + 2 = 3 2 3 4 6 3 26 3 + 3 = 6 3 1 5 5 7 9 5 39 6 + 5 = 11 4 0 1 2 3 5 9 6 49 11 + 6 = 17 5 0 1 1 2 4 4 5 6 7 9 57 17 + 9 = 26 6 0 2 3 5 4 65 26 + 4 = 30 - Сначала добавьте число из столбца Частота к предыдущему.
- Поскольку эти переменные являются дискретными, используйте верхние значения при построении графика. Нанесите точки, чтобы сформировать непрерывную кривую, называемую оживой.
Всегда маркируйте график кумулятивной частотой, соответствующей количеству сделанных наблюдений, на вертикальной оси. Отметьте горизонтальную ось другой переменной (в данном случае, общим количеством скалолазов), как показано ниже:
Например, в Stem 0 у нас есть только одно наблюдение и нет предшественников. Суммарная частота равна единице.
Совокупная частота ежедневных подсчетов скалолазов, зарегистрированных в Лейк-Луизе, Альберта, 30-дневный период
Нанесите точки, чтобы сформировать непрерывную кривую, называемую оживой.Следующую информацию можно получить из графика или таблицы:
- 11 из 30 дней 39 или менее человек поднялись на скалы вокруг озера Луиз
- 13 из 30 дней 50 или более человек поднялись на скалы вокруг озера Луиз
Когда используется непрерывная переменная, как расчет кумулятивной частоты, так и построение графика требуют несколько иного подхода, чем тот, который используется для дискретной переменной.
К началу страницы
Пример 2. Непрерывные переменные
За 25 дней высота снежного покрова на горе Уистлер, Британская Колумбия, составила был измерен (с точностью до сантиметра) и записан как , 249, 245, 254, 243, 235, 231, 257.
- Используйте приведенные выше непрерывные переменные для:
- настроить таблицу частотного распределения
- найти частоту для каждого интервала класса
- найти конечную точку для каждого интервала класса
- рассчитать кумулятивную частоту путем сложения чисел из столбца Частота
- записать все результаты в таблицу
- Используйте информацию, полученную из таблицы распределения частот, для построения графика кумулятивной частоты.
Ответы:
- Высота снежного покрова варьируется от 209 см до 266 см. Для составления таблицы частотного распределения данные лучше всего сгруппировать в интервалы классов по 10 см каждый.
В столбце Глубина снега указан каждый 10-сантиметровый интервал класса от 200 до 270 см.
В столбце Частота записывается количество наблюдений, попадающих в определенный интервал. Этот столбец представляет наблюдения в столбце Tally , только в числовой форме.
Столбец Конечная точка работает так же, как столбец Верхнее значение в упражнении 1, за исключением того, что конечная точка представляет собой наибольшее число в интервале, независимо от фактического значения каждого наблюдения. Например, в интервале классов 210–220 фактическое значение двух наблюдений равно 217 и 219.. Но вместо 219 используется конечная точка 220.
В столбце Суммарная частота указано общее количество каждой частоты, добавленной к предыдущей.
Таблица 2. Высота снежного покрова, измеренная на горе Уистлер, Британская Колумбия, 25-дневный период. 200 0 200 до < 210 1 210 1 210 до < 220 2 220 3 220 до < 230 3 230 6 230 до < 240 5 240 11 240 до < 250 7 250 18 250 до < 260 5 260 23 260 до < 270 2 270 25 - Поскольку переменная является непрерывной, при построении графика используются конечные точки каждого интервала класса. Нанесенные точки соединяются, образуя оживу.
Помните, что кумулятивная частота (количество сделанных наблюдений) указана на вертикальной оси Y, а любая другая переменная (глубина снега) отмечена на горизонтальной оси X, как показано на рисунке 2.
Нанесенные точки соединяются, образуя оживу.Следующая информация может быть получена из графика или таблицы:
- ни один из 25 дней не имел высоты снежного покрова менее 200 см
- в один из 25 дней снег имел высоту менее 210 см
- два из 25 дней снег имел глубину 260 см и более
Начало страницы
Другой расчет, который можно получить с помощью таблицы частотного распределения, — это относительное частотное распределение . Этот метод определяется как процент наблюдений, попадающих в каждый интервал класса. Относительную кумулятивную частоту можно найти, разделив частоту каждого интервала на общее количество наблюдений. (Дополнительную информацию см. в разделе «Распределение частот» в главе «Организация данных».