10 класс. Алгебра. Тригонометрические функции. Тригонометрические функции числового аргумента. — Тангенс и котангенс.
Комментарии преподавателяТангенс и котангенс
На предыдущем уроке мы вспомнили определение синуса и косинуса. Дадим определение тангенса и котангенса.
Рассмотрим числовую окружность в координатной плоскости. Дано произвольное число Ему соответствует единственная точка на окружности. У точки есть две координаты (рис. 1).
Координату назвали косинусом числа координату синусом числа
Тангенсом числа называется отношение синуса к косинусу Котангенсом называется отношение косинуса к синусу .
Определим связь между тангенсом и котангенсом.
Линии синусов и косинусов – это координатные оси. Линией тангенсов является касательная к окружности в точке A, параллельная оси y, линией котангенсов – касательная в точке B, параллельная оси  2).
2).
Вычислим тангенсы и котангенсы основных углов.
|
|
|||||
|
1 |
|||||
|
1 |
0 |
Значения тангенса и котангенса угла найдем из прямоугольного равнобедренного треугольника (рис.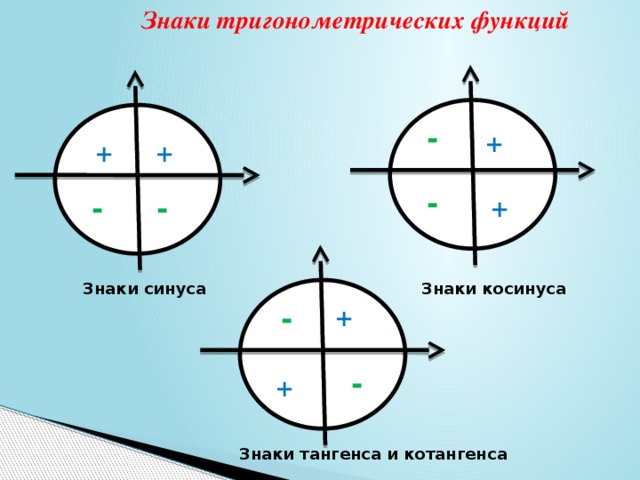 3):
3):
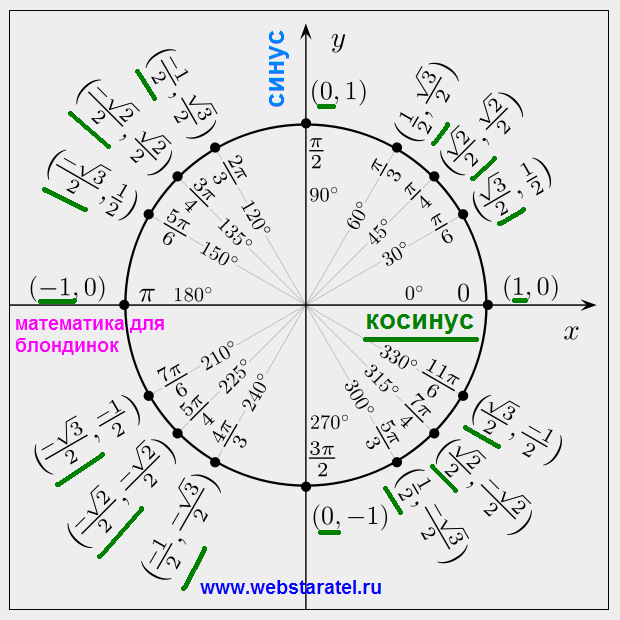
Изобразим полученные значения тангенсов на числовой окружности (рис. 4).
Пример 1. Найти
Решение (рис. 5).
Пример 2. Решить уравнение
Решение:
Найдем на линии тангенсов точку проведём прямую через эту точку и начало координат и получим две точки пересечения с окружностью – (рис. 6).
Ответ:
Пример 3. Решить уравнение
Решение (рис. 7).
Ответ:
Мы рассмотрели функции тангенса и котангенса, стандартные задачи, составили таблицу значений тангенса и котангенса, решили простейшие тригонометрические уравнения.
ИСТОЧНИК
http://interneturok.ru/ru/school/algebra/10-klass/trigonometricheskie-funkcii/tangens-i-kotangens-2
http://www. uchportal.ru/load/0-0-0-30453-20
uchportal.ru/load/0-0-0-30453-20
http://uslide.ru/images/22/28466/960/img5.jpg
http://cs403029.vk.me/v403029067/698e/VNFMdw7VrfI.jpg
ЗНАКИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ — Без Сменки
30 июня, 2022
1 мин
Многие выражения, содержащие синусы и косинусы становятся значительно проще, если пользоваться надежным инструментом — тригонометрическим кругом. А для этого нужно три простых шага и запомнить их: один раз сделал, запомнил и заслуженная пара баллов в кармане.
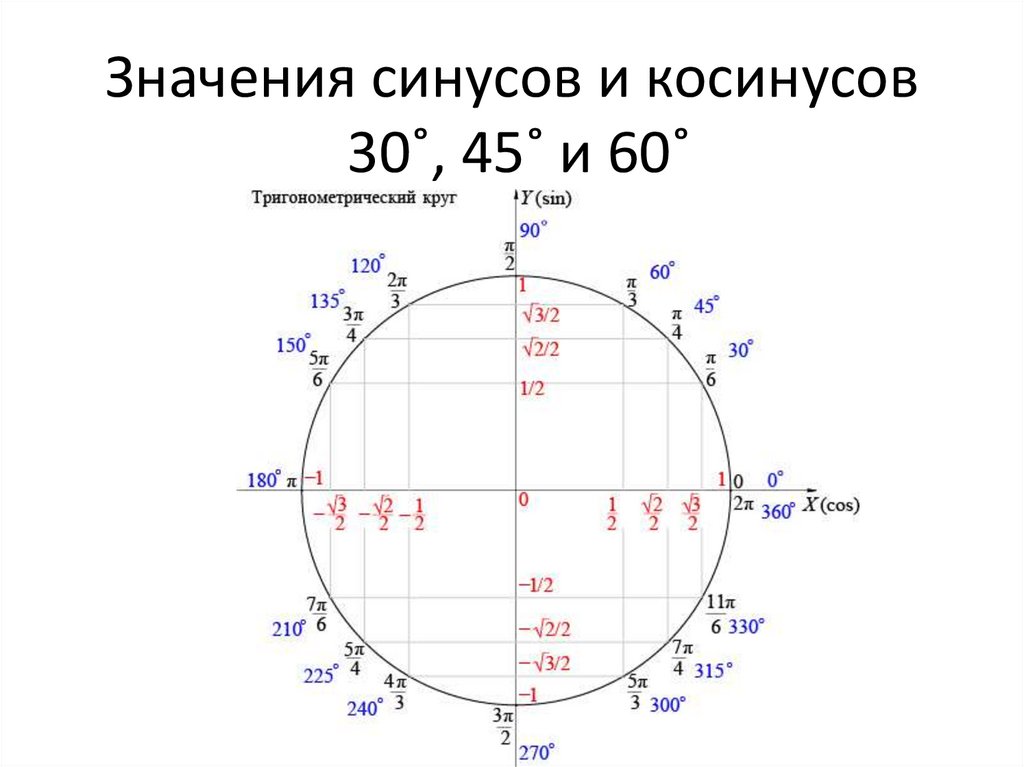
💁🏼♀ Разделим тригонометрический круг на 4 четверти, или квадранта. Первая четверть соответствует интервалу углов 0<α<90, вторая четверть соответствует углам 90<α<180, третья четверть лежит в интервале 180<α<270, и, наконец, четвертая четверть находится в интервале 270<α<360.
✅ Знаки тригонометрических функций зависят от того, в какой четверти находится угол. Синус положительный в первой и второй, косинус в первой и четвертой, а тангенс и котангенс одинаково положительны в первой и третьей.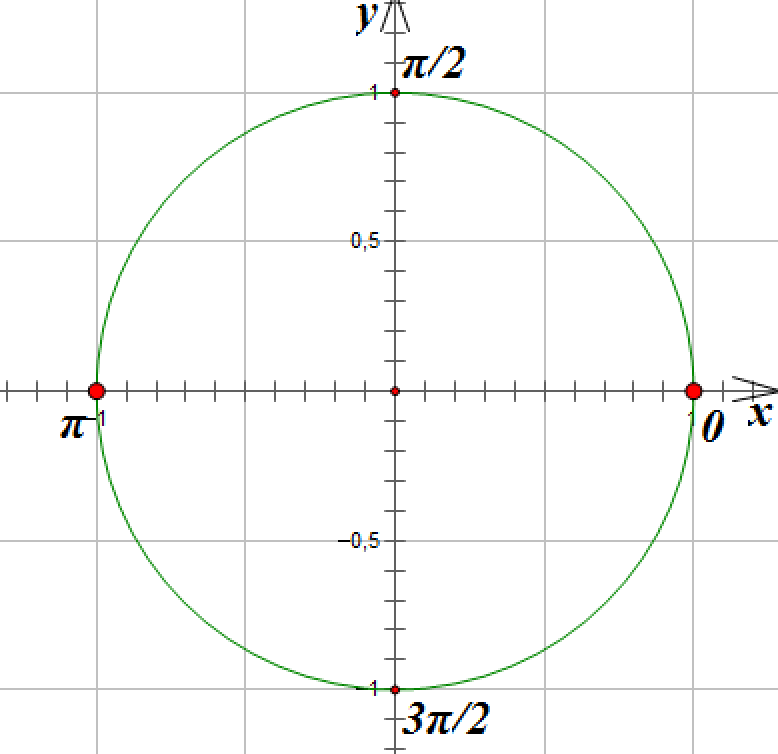 На картинке указаны знаки тригонометрических функций, которые смело можно сохранять.
На картинке указаны знаки тригонометрических функций, которые смело можно сохранять.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Редакция Без Сменки
Честно. Понятно. С душой.
+ Подписаться
Редакция Без Сменки
07 июня, 2022
1 мин
Био 🦠
Типы нервных систем
Эволюция шла вперёд полным ходом и нервная система постоянно видоизменялась в пользу большей. ..
..
Редакция Без Сменки
06 июня, 2022
1 мин
Англ 🇬🇧
Разница между quick и fast
Англичане, остановитесь!!! Хватит придумывать слова с одинаковым значением и потом говорить, что…
Редакция Без Сменки
10 июня, 2022
1 мин
Био 🦠
Проводящая система сердца
Возможно, вы не слышали такого словосочетания, но точно знаете из прошлого шага, что сердце…
Редакция Без Сменки
03 октября, 2022
1 мин
Химические запоминалки
Химические термины можно учить не только методом зубрёжки, но и с помощью специальных фраз. …
…
Редакция Без Сменки
16 марта, 2022
1 мин
Ист 🤴
Расселение восточных славян (карта)
Выделяют западных (поляки, чехи, словаки), южных (болгары, сербы, хорваты) и восточных славян….
ФУНКЦИИ ТАНГЕНСА И КОТАНГЕНСА – ТРИГОНОМЕТРИЯ
функция тангенсаВ тригонометрии прямоугольного треугольника (только для острых углов) тангенс определяется как отношение противолежащего катета к прилежащему. Определение единичной окружности: tanθ=y/x или tanθ=sinθ/cosθ. Функция тангенса отрицательна, когда синус или косинус, но не оба, отрицательны: второй и четвертый квадранты. Тангенс также равен наклону стороны терминала.
Функция тангенса — это старая математическая функция. Он был упомянут в 1583 году Томасом Финке, который ввел слово « tangens » на латыни. Эдмунд Гюнтер (1624 г.) использовал обозначение « tan », а Иоганн Генрих Ламберт (1770 г.) открыл представление этой функции в виде непрерывной дроби.
Он был упомянут в 1583 году Томасом Финке, который ввел слово « tangens » на латыни. Эдмунд Гюнтер (1624 г.) использовал обозначение « tan », а Иоганн Генрих Ламберт (1770 г.) открыл представление этой функции в виде непрерывной дроби.
Функция тангенса используется в математике, точных науках и технике.
- Домен: все действительные числа, кроме π/2 + kπ, k ∈ Z.
- Диапазон: все действительные числа (R)
- Период: π
- x-отрезки: x = kπ, k ∈ Z.
- y-отрезки: y = 0
- Симметрия: поскольку tan(-x) = – tanx, то tan x является нечетной функцией, и ее график симметричен относительно начала координат.
- Интервалы: за один период и от -π/2 до π/2, тангенс х увеличивается.
- Вертикальные асимптоты: x = π/2 + kπ, k ∈ Z.
Касательная функция соответствует y-координатам точек на касательной оси.

Пример: Найдите домен и диапазон ƒ (x) = tan 3x + 4.
Решение: Домен: 3x ≠ π/2 + kπ дает нам x ≠ π/6 kπ/3, k ∈ Z.
Итак, область определения равна {x | x ∈ R, x ≠ π/6 + kπ/3, k ∈ Z}.
Диапазон: tan 3x ∈ R, поэтому диапазон равен (-∞, ∞).
В прямоугольном треугольнике котангенс угла равен длине прилежащей стороны, деленной на длину противолежащей стороны. В формуле это сокращается до просто « кроватка ». Поскольку он редко используется, его можно заменить производными от более распространенных трех: sin, cos и tan.
Котангенс можно получить двумя способами: cot x = 1/tan x и cot x = cos x / sinx. Функция котангенса является обратной функцией функция тангенса .
Как и другие тригонометрические функции, котангенс может быть представлен в виде отрезка, связанного с единичной окружностью .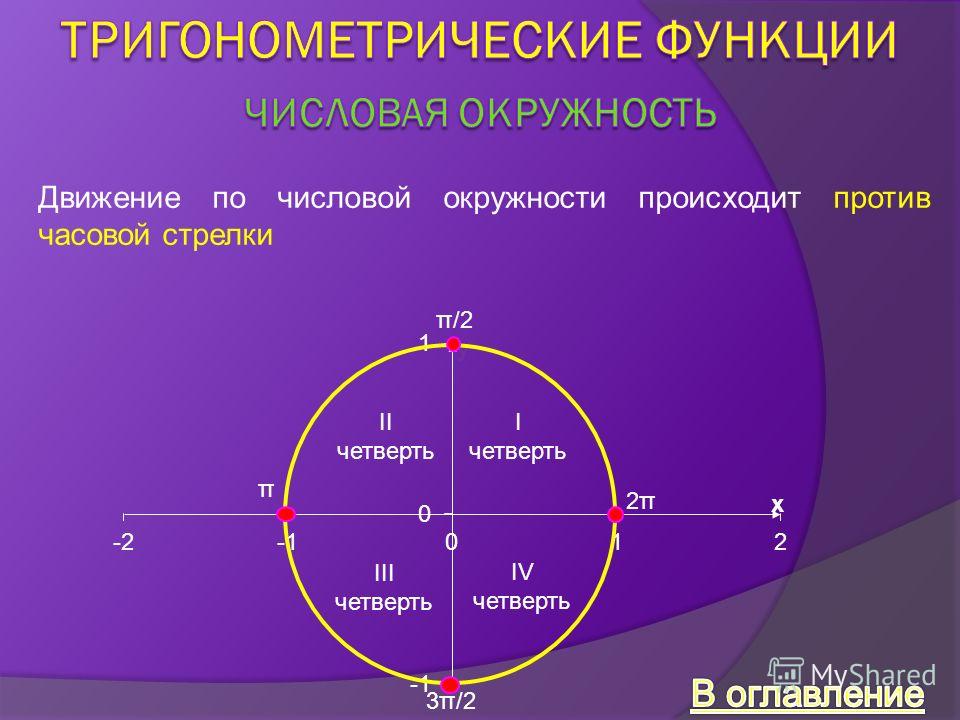 На диаграмме показан котангенс угла поворота θ от сорока пяти градусов (измерен против часовой стрелки от положительной оси x ). Отрезок линии AF (показан красным) является котангенсом и лежит на прямой, касательной к окружности в точке A . Отрезок PF является продолжением отрезка OP (и, кстати, также является секансом ). Помните, что точка P – это точка на окружности единичного круга, чьи координаты
На диаграмме показан котангенс угла поворота θ от сорока пяти градусов (измерен против часовой стрелки от положительной оси x ). Отрезок линии AF (показан красным) является котангенсом и лежит на прямой, касательной к окружности в точке A . Отрезок PF является продолжением отрезка OP (и, кстати, также является секансом ). Помните, что точка P – это точка на окружности единичного круга, чьи координаты
- Домен: все действительные числа, кроме kπ, k ∈ Z.

- Диапазон: все действительные числа
- Период: π
- точки пересечения x: x = π/2 + kπ, k ∈ Z.
- Симметрия: так как cot(-x) = – cot(x), то cot x является нечетной функцией и ее график симметричен относительно начала координат.
- Интервалы: за один период и от 0 до π, cot x уменьшается.
- Вертикальные асимптоты: x = kπ, k ∈ Z.
Функция котангенса соответствует x-координатам точек на оси котангенса.
Так:
Нравится Загрузка…
6.1.1 Тригонометрические функции
Исчисление одной действительной переменной автора Pheng Kim VingГлава 6: Тригонометрические функции и их обратные значения Раздел 6.1.1: Тригонометрические функции |
6.
|
Возврат
К содержанию
Перейти к проблемам и решениям
1. Тригонометрические отношения |
словесный знак. Аналогично соотношения:
Три отношения синуса, косинуса и
тангенс — это первичных тригонометрических отношений . Есть также три других
отношения.
Это котангенс , секанс и косеканс , обозначаемые cot ,
сек и csc соответственно. Они определяются как
обратные числа
тангенс, косинус и синус соответственно, и, таким образом, называются обратными
тригонометрические соотношения .
Слово тригонометрия происходит от греческого
слова: три , что означает три, гоно , что означает угол, и метрия ,
что означает измерение.
Произвольные треугольники
Рис. 1.3
Тригонометрические соотношения в произвольном треугольнике. |
Рис. 1.4
Тригонометрические соотношения в произвольном треугольнике. |
Перейти Проблемы и решения Вернуться к началу страницы
2. |
Степень
Рассмотрим окружность радиусом r с центром в начале координат 0 оси x и пересекающую ее положительную сторону 9 A 9026 . См. рис. 2.1.
Разделим окружность круга на 360 равных частей или дуг,
начиная с А . Рассмотрим угол,
вершина
находится в центре круга
и который пересекает одну из дуг. Ясно, что длина дуги зависит от
значение r ,
но размер угла нет. Величина этого угла составляет единицу
измерение углов и называется
степень. Итак, степень , обозначаемый градусом или или , определяется как
быть равным одной 360-й части окружности
круг.
Предположим, что угол пересекает
дуга окружности с центром в ее вершине такая, что
длина дуги r 360
длина окружности, где r — неотрицательное
настоящий номер. Тогда мера этого угла равна r o . Вот почему
Тогда мера этого угла равна r o . Вот почему
угол, соединяющий любую окружность, равен 360 o , что перехват любого
полукруг имеет размеры 180 o , а прямой угол
меры 90 o .
Град
Аналогично, если мы разделим окружность
окружности на 400 равных дуг, то получим еще одну единицу измерения
углы, называемые град . Таким образом, град определяется как одна 400-я часть
окружность круга.
Радиан
Рис. 2.2
|
|
Conversion From Degree To Radian And Vice Versa
Example 2.
 1
1
Solution
EOS
Omission Of Единица радианы Запись
Примечание 2.1
Единицы измерения углов
определяются с использованием не обычных единиц длины, таких как метр, а элементов
из
круг как одна 360-я часть окружности для степени или радиуса для
радиан. См. также Проблема и решение 1.
Перейти Проблемы и решения Вернуться к началу страницы
3. Единичный круг |
Перейти Проблемы и решения Вернуться к началу страницы
4. |
Для единичного круга радиан мера центрального угла равна длине дуги, на которую опирается.
Любое действительное число можно рассматривать как радианную меру угол со знаком.
|
Линия ОА называется начальным плечом и линией OP концевой рычаг уголка x . Мы говорим
что x заканчивается в
квадрант, где находится конечное плечо; например, если конечное плечо находится в 3-м
квадрант, то мы говорим, что x заканчивается
в
3-й квадрант.
Размеры уголков
Углы:
|
Перейти к проблемам и решениям Вернуться к началу Страница
5. |
В части 1 мы определили синус,
косинус, тангенс, котангенс, секанс и косеканс острых углов, используя
прямоугольный треугольник,
и они называются тригонометрическими отношениями. Теперь мы собираемся расширить их до
все углы, используя единичный круг, и
они называются тригонометрическими функциями . Для остальной части этого
разделе, каждая окружность представляет собой единичную окружность с центром в начале координат
система координат uv , A это точка (1, 0), а B является точкой (0, 1), если не указано иное.
Перейти к проблемам и решениям Вернуться к началу Страница
6. Функции синуса и косинуса |
Пусть x будет острым
угол, OP его концевое плечо и ( u , v )
координаты Р .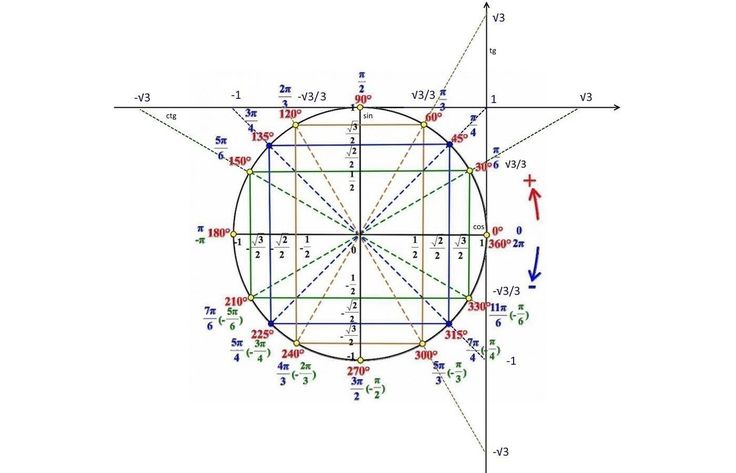 См. рис. 6.1. У нас есть грех x = UP / OP =
См. рис. 6.1. У нас есть грех x = UP / OP =
v /1 = v and cos x = OU / OP = u /1 = u . Продолжим синус и
косинус на все углы следующим образом. Пусть x будет любым углом ,
OP его конечным плечом и ( u , v ) координаты P .
Тогда синус и косинус числа x определены
следующим образом:
sin x = v ,
|
Обратите внимание, что синус отложен по вертикальной оси v , а косинус — по горизонтальной оси u .
Каждому вещественному числу x соответствует уникальное значение v = грех х . Следовательно,
это отображение является функцией. Это называется синус
Это называется синус
функция . Его домен R .
Его диапазон равен [1, 1], потому что v -координата P всегда попадает в [1, 1] независимо от того,
какое значение
x имеет. Точно так же у = cos x определяет функция косинуса , домен которой равен R , а диапазон также равен [1, 1].
Обоснование Расширения
Мы только что обосновали распространение синуса на все углы,
положительный или 0 или отрицательный.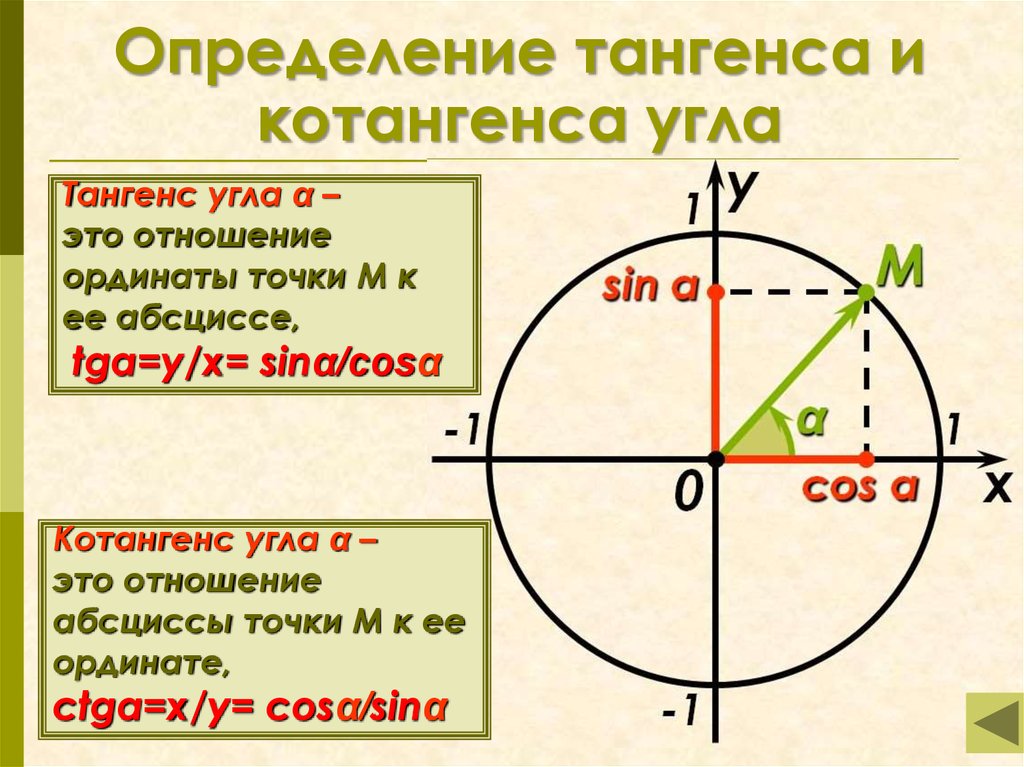 Обоснование расширения
Обоснование расширения
косинус аналогичен.
Пример 6.1
Покажите, что:
Рис. 6.4
EOS
Перейти к проблемам и решениям Вернуться к началу Страница
7. Функции тангенса и котангенса |
Пусть x будет любым угол. Расширенная функция тангенса и функция котангенса являются
определяется тангенсом x = (sin х )/(поскольку х )
и детская кроватка x = 1/(загар x ) = (cos x )/(sin х ) соответственно.
оставлен как проблема и решение 3. Случаи для остальные два квадранта подобны ему. У нас есть:
|
Обратите внимание, что касательная проходит по вертикальной оси z и котангенс находится на горизонтальной оси w .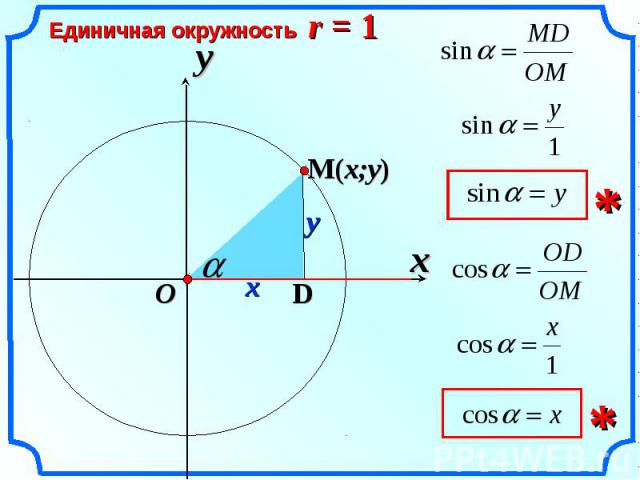
Перейти к проблемам и решениям Вернуться к началу Страница
8. Функции секанса и косеканса |
Пусть x быть любой угол . Расширенная функция секанса и функция косеканса определяются как sec x = 1/(cos x ) и
csc x = 1/(sin x )
соответственно.
остается как Проблема и Решение 4. Случаи
ибо оставшиеся два квадранта подобны ему. У нас есть:
|
Рис. 8.1
|
Обратите внимание, что секанс (= 1/косинус) находится на горизонтальной оси u (такой же, как косинус) и косеканс (= 1/синус) находится на вертикали
v -ось (то же, что и синус).
Перейти к проблемам и решениям Вернуться к началу Страница
9. Тригонометрические или круговые функции |
Тригонометрические функции синус, косинус, тангенс, котангенс,
секанс и косеканс определяются с помощью окружности.
По этой причине их также называют 9.0025 круговые функции . Они определены
используя единичный круг, как показано на рис. 9.1.
Рис. 9.1
|
Вернуться к началу страницы
Проблемы и решения |
1. Объяснить
почему длины дуг окружностей в нормальных единицах длины, таких как метр, не могут
использоваться в качестве меры
Объяснить
почему длины дуг окружностей в нормальных единицах длины, таких как метр, не могут
использоваться в качестве меры
углов, если только единичный круг (окружность
радиуса 1) принимается к использованию. См. также замечание 2.1.
Раствор
Вернуться на вершину страницы
0012Решение
Возвращение на вершину страницы
3. Предположим угла x .
заканчивается во 2-м квадранте. См. рисунок ниже. Покажи этот загар х = z и кроватка х = х . Также
см. обсуждение после уравнения. [7.1] и [7.2].
Решение
Прямоугольные треугольники OPU и ОЗА являются
похожий.

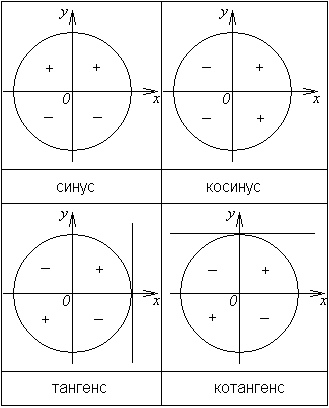
 1.1
1.1 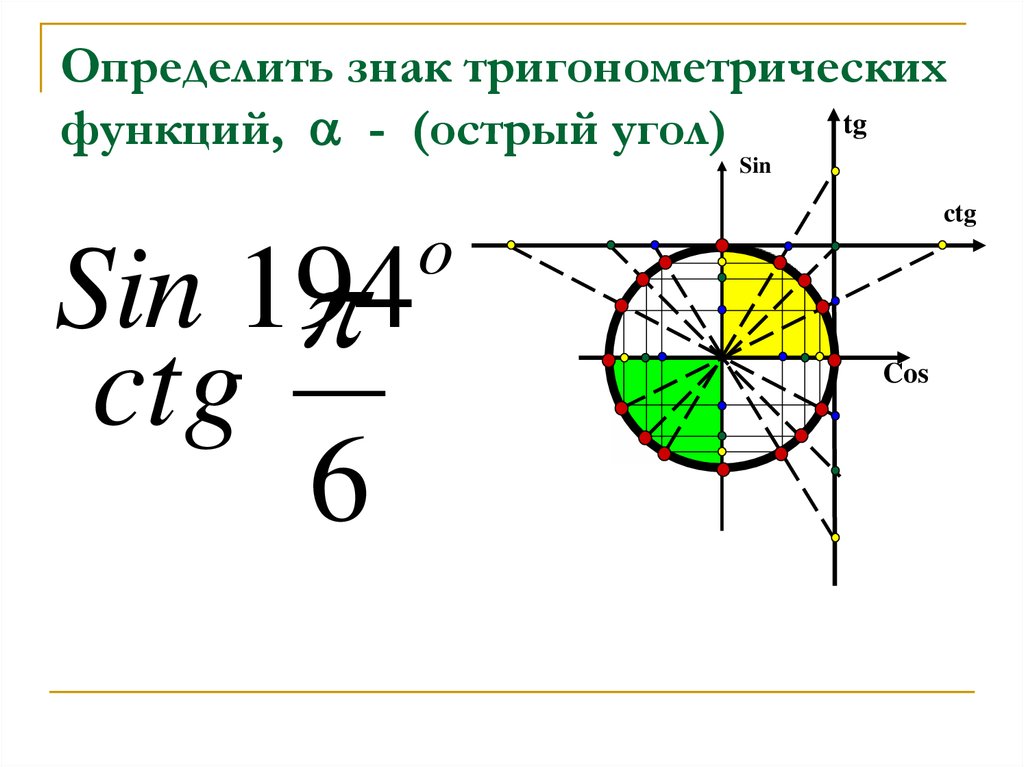 Радианная мера
Радианная мера  Углы и единичная окружность
Углы и единичная окружность  Тригонометрические функции
Тригонометрические функции