Сочетание размещение перестановка задачи: Размещения и сочетания — урок. Алгебра, 11 класс.

35 Элементы комбинаторики-перестановки,размещения, сочетания

В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).

Рождение комбинаторики как раздела математикисвязано с трудами Б. Паскаля и П. Ферма по теории азартных игр. Большой вклад в развитие комбинаторных методов внесли Г.В. Лейбниц, Я. Бернулли и Л. Эйлер.

Французский философ, писатель, математик и физик Блез Паскаль (1623–1662) рано проявил свои выдающиеся математические способности. Круг математических интересов Паскаля был весьма разнообразен. Паскаль доказал одну из основных теорем проективной геометрии (теорема Паскаля), сконструировал суммирующую машину (арифмометр Паскаля), дал способ вычисления биномиальных коэффициентов (треугольник Паскаля), впервые точно определил и применил для доказательства метод математической индукции, сделал существенный шаг в развитии анализа бесконечно малых, сыграл важную роль в зарождении теории вероятности. В гидростатике Паскаль установил ее основной закон (закон Паскаля). “Письма к провинциалу” Паскаля явились шедевром французской классической прозы.

Готфрид Вильгельм Лейбниц (1646–1716) — немецкий философ, математик, физик и изобретатель, юрист, историк, языковед. В математике наряду с И. Ньютоном разработал дифференциальное и интегральное исчисление. Важный вклад внес в комбинаторику. С его именем, в частности, связаны теоретико-числовые задачи.

Готфрид Вильгельм Лейбниц имел мало внушительную внешность и поэтому производил впечатление довольно невзрачного человека. Однажды в Париже он зашел в книжную лавку в надежде приобрести книгу своего знакомого философа. На вопрос посетителя об этой книге книготорговец, осмотрев его с головы до ног, насмешливо бросил: “Зачем она вам? Неужели вы способны читать такие книги?” Не успел ученый ответить, как в лавку вошел сам автор книги со словами: “Великому Лейбницу привет и уважение!” Продавец никак не мог взять втолк, что перед ним действительно знаменитый Лейбниц, книги которого пользовались большим спросом среди ученых.

В дальнейшем важную роль будет играть следующая

Лемма. Пусть в множестве элементов, а в множестве—элементов. Тогда число всех различных пар, гдебудет равно.

Доказательство. Действительно, с одним элементом из множества мы можем составитьтаких различных пар, а всего в множествеэлементов.

Пусть у нас есть множество из трех элементов . Какими способами мы можем выбрать из этих элементов два?.

Определение. Размещениями множества из различных элементов поэлементовназываются комбинации, которые составлены из данныхэлементов поэлементов и отличаются либо самими элементами, либо порядком элементов.

Число всех размещений множества из элементов поэлементов обозначается через(от начальной буквы французского слова “arrangement”, что означает размещение), гдеи.

Теорема. Число размещений множества из элементов поэлементов равно

Доказательство. Пусть у нас есть элементы . Пусть— возможные размещения. Будем строить эти размещения последовательно. Сначала определим— первый элемент размещения. Из данной совокупностиэлементов его можно выбратьразличными способами. После выбора первого элементадля второго элементаостаетсяспособов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем:

Пример. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов?

Решение. Искомое число трехполосных флагов:

Определение. Перестановкой множества из элементов называется расположение элементов в определенном порядке.

Так, все различные перестановки множества из трех элементов — это

Очевидно, перестановки можно считать частным случаем размещений при .

Число всех перестановок из элементов обозначается(от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле

Пример. Сколькими способами можно расставить 8 ладей на шахматной доске так, чтобы они не били друг друга?

Решение. Искомое число расстановки 8 ладей

по определению!

Определение. Сочетаниями из различных элементов поэлементов называются комбинации, которые составлены из данныхэлементов поэлементов и отличаются хотя бы одним элементом (иначе говоря,-элементные подмножества данного множества изэлементов).

Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из элементов поэлементов в каждом обозначается(от начальной буквы французского слова “combinasion”, что значит “сочетание”).

Числа

Все сочетания из множества по два —.

.

Перестановки и комбинации — Подготовка к тесту Каплана

Имея дело с перестановками и комбинациями, вы, по сути, пытаетесь найти количество различных результатов при заданном наборе элементов и ряде ограничений. Разница между перестановкой и комбинацией просто зависит от того, имеет ли значение порядок. Позвольте мне проиллюстрировать это примером. Предположим, у вас есть три продукта: яблоки, бананы и морковь. Если бы вас попросили выбрать только два из них, сколько было бы вариантов? Если вы получили 3, это правильный ответ. У вас есть яблоки и бананы, яблоки и морковь, бананы и морковь. это комбинация . Однако, если бы я сказал вам, что порядок, в котором вы едите пищу, имеет значение, у вас было бы больше возможностей, потому что вместо яблок и бананов вы также должны учитывать бананы и яблоки. Последний — это перестановка .
 

Листинг

То, что я сделал ранее, когда я перечислил 3 варианта, называется, что неудивительно, listing . Но есть метод листинга, чтобы убедиться, что вы не упустите ни одной возможности. У каждого свой метод, позвольте мне поделиться своим. Если у меня есть четыре элемента — a, b, c и d — и я должен выбрать 2:

• Шаг 1

  Возьмите первый элемент a и объедините его с b. Затем идите вниз по списку и комбинируйте его с c и d , чтобы получить всего три возможности:

  ab, ac, ad .

• Шаг 2

  Возьмите второй элемент b и объедините его с остальным списком. Не объединяйте его с a , потому что вы уже сделали это на шаге 1. Таким образом, вы получите: bc, bd

• Шаг 3

  Продолжайте делать то же самое для следующего элемента в списке, а именно c . За c в списке стоит только одно — d . Так что здесь только 1 вариант: cd

• Шаг 4

  Продолжайте, пока не доберетесь до предпоследнего предмета. В этом случае вы уже достигли этого на шаге 3. Подсчитайте ваши варианты: ab, ac, ad, bc, bd, cd

Древовидная диаграмма

Если вы заметили, перечисление — хороший метод для определения комбинаций. Древовидная диаграмма — это графический метод, который помогает вам с перестановкой. Используя предыдущий пример с 4 элементами, вот древовидная диаграмма, которая иллюстрирует количество способов перестановки элементов.

Если вы посмотрите на последнюю строку древовидной диаграммы и подсчитаете количество ящиков, вы увидите, что существует 12 возможных способов переставить 2 элемента из 4. Каждый элемент можно комбинировать с 3 другими вещами. Другой способ увидеть это состоит в том, что у вас есть два пробела, которые нужно заполнить ___ и ___. Глядя на первое место, у вас есть 4 возможных предмета, которые вы могли бы разместить там. Глядя на вторую ячейку, у вас есть 3 возможных предмета, которые вы могли бы разместить там, так как вы уже поместили 1 предмет в первую ячейку.

Таким образом, имеется 4 x 3 = 12 упорядоченных возможностей.
 

Метод мышления «пространство и количество вариантов заполнения этого пространства» по существу является фундаментальным принципом подсчета. Принцип гласит, что:

Давайте посмотрим, понимаете ли вы принцип на небольшом примере.
Сколькими способами можно расположить эти буквы: T A N G O.
Вы получили 120?
Представьте себе пять пробелов ___   ___   ___   ___   ___
У вас есть 5 возможных букв для первого пробела, и когда это будет сделано, у вас будет 4 возможных символа для второго пробела, 3 буквы для третьего пробела и так далее.
Значит, ответ 5*4*3*2*1 или 120!
 

После того, как вы выяснили, использовать ли перестановку или комбинацию, на самом деле очень мало работы нужно сделать, если вы знаете формулы для перестановки и комбинации или если вы знаете, где функция скрыта на вашем калькуляторе.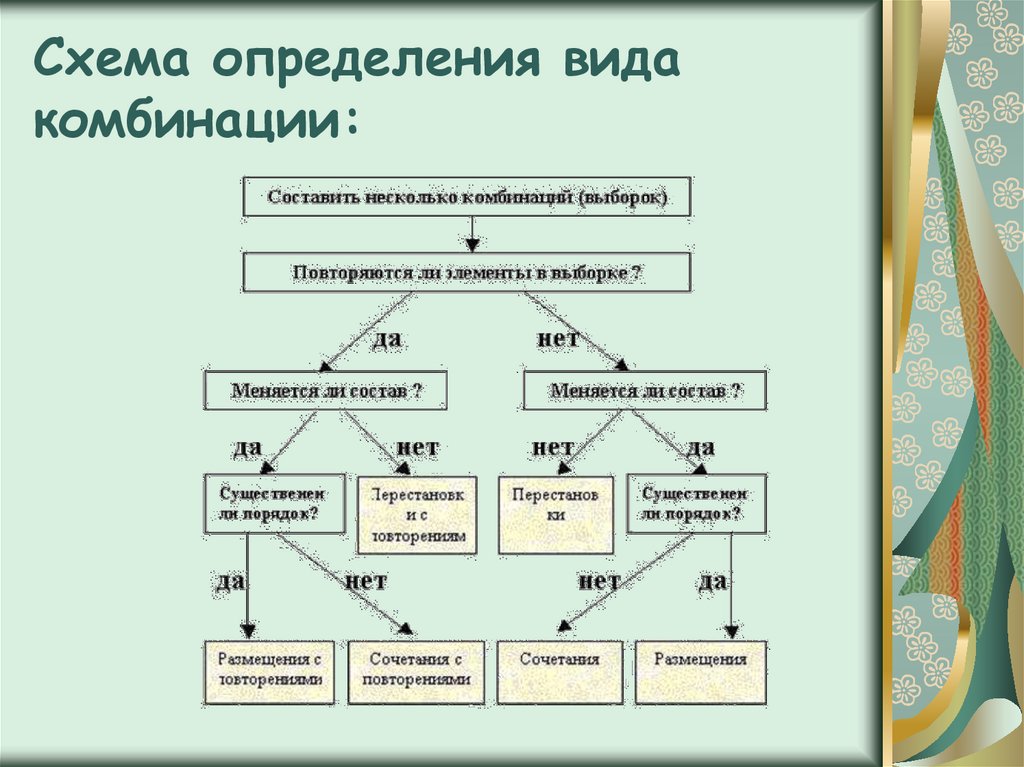

Как упоминалось ранее, перестановка используется, когда важен порядок, и комбинация, когда вы просто хотите выбрать, но не упорядочить элементы. Давайте погрузимся прямо в формулы, а затем рассмотрим несколько примеров.

Перестановка

Количество способов перестановки r объектов из n объектов равно

n P r =n!/(n-r)! где н! = n * (n-1) * (n-2) * … * (2) * (1)

Объединение

Количество способов объединения r объектов из n объектов равно

n C r = n!/r!(n-r)!

Обратите внимание, что 0! определяется как 1.

Пример 1

Сколькими способами можно расположить 4 буквы из следующих F R I E N D?

ДРУГ состоит из 6 разных букв, и, поскольку порядок букв имеет значение, вы должны использовать формулу перестановки. Непосредственное применение формулы дает ответ:

6 P 4 = 6!/(6-4)! – 6!/2! – 360

Вы можете перепроверить это, используя фундаментальный принцип подсчета, который мы рассмотрели в Части I. Начертить древовидную диаграмму тоже можно, но она может немного запутаться по мере того, как дерево становится все больше и больше.

Пример 2

Если есть 3 основных блюда и 5 десертов, сколькими способами можно выбрать 1 основное блюдо и 2 десерта? Обратите внимание, что в вопросе ничего не говорится о порядке, в котором едят основные блюда и десерты, поэтому вы знаете, как использовать принцип комбинирования. Поскольку вы выбираете первые блюда и десерты отдельно, вам нужно применить формулу комбинации дважды.

Во-первых, чтобы выбрать 1 блюдо из 3, мы применяем формулу 3 C

1 = 3!/1!(3-1)! – 3!/1!2! – 3

Далее, чтобы выбрать 2 десерта из 5, применяем формулу 5 C 2 = 5!/2!(5-2)! – 5!/2!3! – 10

Тогда, поскольку для каждого блюда есть 10 возможных комбинаций из 2-х десертов и есть 3 способа выбрать 1 блюдо, чтобы получить общее количество возможностей, мы берем 3*10 = 30.

Что, если вопрос бросает вам кривую и просит вас переставить что-то, что имеет повторяющийся элемент. Например, сколько существует способов расположения букв A G H A S T?

Буква «А» повторяется дважды, поэтому сначала нужно представить, что буквы различны, и найти количество возможных вариантов. Затем разделите это значение на 2! потому что «А» повторяется дважды.

AGHAST состоит из 6 букв, и если мы переставим все буквы местами, то получим 6!

Поскольку A повторяется, мы делим 6! на 2! чтобы получить ответ 360

Предположим, вас попросили переставить только 4 из 6 букв из AGHAST, тогда вы должны сделать 6 P 4 как обычно и разделить этот ответ на 2! так как A повторяется. Ответ должен быть 180.

Понимание перестановок и комбинаций

При решении задач «Шесть сигм» часто важно рассчитать вероятность того, что произойдет комбинация событий или упорядоченная комбинация событий. Понимание некоторых основных концепций вероятности дает практикам инструменты для прогнозирования событий или комбинаций событий. Это обеспечивает хорошую основу для понимания распределения вероятностей, доверительных интервалов и проверки гипотез. Перестановки и комбинации — две важные концепции для создания этой основы.

Но перестановки и комбинации вызывают много путаницы: «Какой из них какой?» и «Какой из них я использую?» являются общими вопросами.

Перестановки

Если я покупаю салат на обед, это может быть смесь листьев салата, помидоров, моркови и редиски. Меня не особо волнует, в каком порядке кладут овощи в миску. Меня волнует только то, что у меня есть салат из листьев салата, помидоров, моркови и редиски. Салат может состоять из «моркови, помидоров, редиски и салата» или «редиса, помидоров, моркови и салата». Для меня это все тот же салат.

Как насчет PIN-кода для моего банковского счета? «ПИН-код моей учетной записи — 8-9-10». Если я хочу получить доступ к своему банковскому счету через банкомат, мне нужно позаботиться о порядке этих цифр. «10-9-8» не будет получать доступ к моей учетной записи. Как и «9-10-8». Должно быть ровно 8-9-10. Порядок важен.

Детали имеют значение для перестановок – каждая мелочь. Для перестановки красный/желтый/зеленый отличается от зеленого/желтого/красного. Порядок важен, и его необходимо соблюдать.

Комбинации

С комбинациями гораздо проще договориться – детали не так важны. В комбинации красный/желтый/зеленый выглядит так же, как зеленый/желтый/красный.

Перестановки предназначены для списков (где порядок имеет значение), а комбинации — для групп (где порядок не имеет значения). Другими словами: перестановка — это упорядоченная комбинация.

Примечание. «Комбинированный» замок на самом деле следует называть «перестановочным», потому что порядок, в котором вы ставите числа, имеет значение. Настоящий «комбинированный» замок открывается с использованием либо 10-17-23, либо 23-17-10. На самом деле, любая комбинация из 10, 17 и 23 откроет настоящий «комбинационный» замок.

Перестановки: Детали, Детали, Детали

Перестановки — это все возможные способы расположения элементов множества. Мы будем заботиться о каждой мельчайшей детали, включая порядок каждого элемента.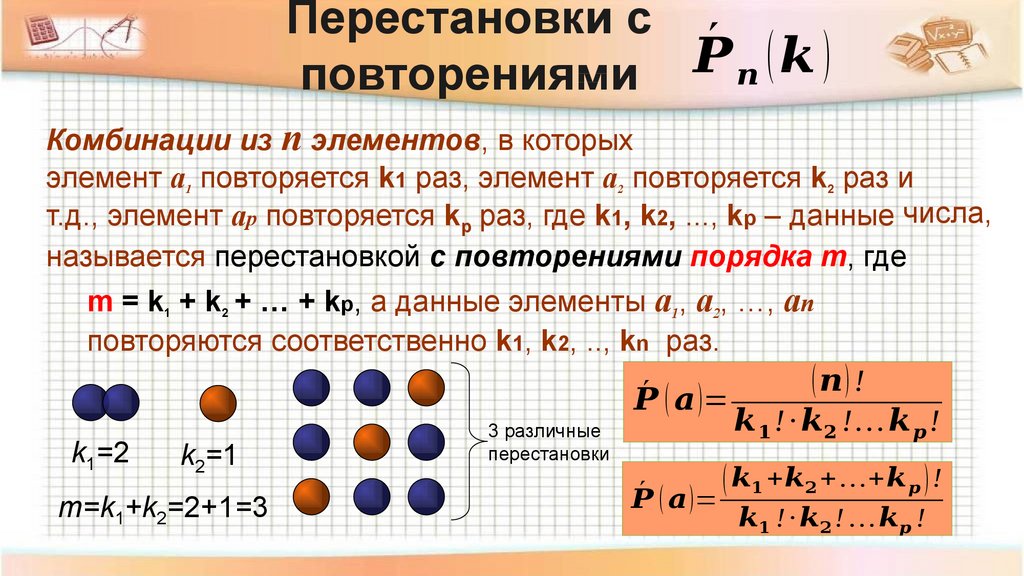 Перестановки рассматривают различные упорядоченные расположения как разные ответы.
Допустим, у нас есть пять человек, участвующих в конкурсе барбекю: Энди, Боб, Чарли, Дэвид и Эрик.

Сколькими способами мы можем наградить ленты за первое, второе и третье место (синюю, красную и желтую) среди 5 участников?

Поскольку важен порядок вручения лент, нам нужно использовать перестановки.

Вот разбивка:

• Голубая лента: Есть пять вариантов: A B C D E. Допустим, А выигрывает синюю ленту.
• Красная ленточка: Осталось четыре варианта: B C D E. Допустим, B выиграет красную ленточку.
• Желтая лента: Осталось три варианта: C D E. Допустим, C выиграет желтую ленту.

В этом примере мы выбрали определенных людей для победы, но на самом деле это не имеет значения. Важно лишь то, что мы понимаем, что сначала у нас было пять вариантов, затем четыре, а потом три. Всего вариантов было 5 × 4 × 3 = 60 . Пришлось заказывать трех человек из пяти. Для этого мы начинали со всех пяти вариантов, затем убирали их по одному (четыре, потом три и т. д.), пока не кончились ленты.

Пятифакториал (пишется 5!) это: 5! = 5 × 4 × 3 × 2 × 1 = 120 .

Но 120 слишком много! Это сработало бы, если бы у нас было пять лент. Но мы этого не делаем; у нас есть три ленты. Нам нужно только 5 × 4 × 3 (общее количество вариантов). Как заставить факториал «остановиться» на 3? Нам нужно избавиться от 2 × 1. Что мы называем 2 × 1? 2-факториал! Это то, что осталось после того, как мы выберем трех победителей из пяти участников.

Если разделить 5! на 2!, получаем: 5! / 2! = (5 × 4 × 3 × 2 × 1) / (2 × 1) = 5 × 4 × 3 = 60  (поскольку 2 × 1 в числителе и знаменателе компенсируют друг друга).

Лучше (проще) записать это так: 5! / (5 – 3)!

Это говорит: «Используйте первые три числа из 5!»

В более общем смысле, если у нас всего n предметов и мы хотим выбрать k в определенном порядке, мы получим:
n! / (н – к)!

А это формула перестановки: Количество способов заказать k элементов из n предметов:
P(n,k) = n! / (н – к)!

Комбинации: Заказ не требуется

У каждого из нас есть спокойный родственник. Ничто их не беспокоит. Они просто живут своей жизнью, как будто ничего не имеет значения.

Комбинации — беспечные родственники перестановок. Порядок для них не имеет значения. Вы можете смешать заказ, и они все равно будут счастливы. Мир кажется им одинаковым, упорядочен он или нет.

Допустим, вместо того, чтобы награждать синей, красной и желтой ленточками за наш конкурс барбекю, мы награждаем тройку лучших ленточками «участника». Сколькими способами я могу наградить тремя лентами участника пять человек?

В этом случае порядок не имеет значения. Если я подарю ленточку участника Энди, Бобу и Чарли, это будет то же самое, что подарить ленточку участника Чарли, Энди и Бобу. В любом случае, все они будут одинаково разочарованы.

Минуточку! Энди/Боб/Чарли = Чарли/Боб/Энди. У нас тут есть повторы. Не обращайте на это внимания, давайте просто подсчитаем, сколькими способами мы можем переставить трех человек.

У нас есть три варианта для первого лица, два для второго и только один для последнего.