ОГЭ по математике, базовый уровень. Системы неравенств
- Альфашкола
- Статьи
- ОГЭ по математике, базовый уровень. Системы неравенств
Условие
Решите неравенство:
Решение
Проанализируем данное неравенство. Неравенство состоит из двух частей:
(х2 + 4х – 5) и \( \sqrt{x+2} \)
При этом, выражение:
\( \sqrt{x+2} \) > 0
будет всегда, по свойству квадратного корня.
Отсюда следует, что первая часть неравенства также будет всегда:
х2 + 4х – 5> 0
Таким образом, мы получаем систему неравенств:
Решим систему неравенств:
Первое неравенство системы, возведем в квадрат обе части:
\( \sqrt{x+2} \) > 0 <=> х + 2 > 0 <=> х > — 2
Второе неравенство системы:
х2 + 4х – 5> 0
Представим в виде квадратного уравнения и найдем корни:
х2 + 4х – 5 = 0
D = 36
х1 = — 5
х2 = 1
Представим решение системы в графическом виде (Рис.
1):
Рис.1
Решением системы является множество:
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Полина Андреевна Чаплина
Репетитор по математике
Стаж (лет)
Образование:
Кубанский Государственный Университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Юлия Сергеевна Слива
Репетитор по математике
Стаж (лет)
Образование:
Кубанский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Виолетта Грантовна Саркисян
Репетитор по математике
Стаж (лет)
Образование:
Тбилисский Государственный Педагогический Университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ЕГЭ по математике (базовый уровень)
- Репетитор по геометрии
- Подготовка к олимпиадам по химии
- Репетитор по русскому языку для подготовки к ОГЭ
- Подготовка к олимпиадам по английскому языку
- Репетитор для подготовки к ЕГЭ по истории
- Репетитор для подготовки к ВПР по обществознанию
- Репетитор по биологии для подготовки к ОГЭ
- Репетитор по географии для подготовки к ЕГЭ
- Репетитор по информатике для подготовки к ОГЭ
Похожие статьи
- Площадь поверхности конуса
- Графики кубических функций
- Как перевести центнеры в граммы?
- Как округлить число до десятых?
- ЕГЭ по математике, базовый уровень.
Задачи с прикладным содержанием (вариант 1) - Задачи на движение по прямой (вариант 4)
- Откуда появляются ночные кошмары и почему это нельзя игнорировать
- Что из математики реально пригодится в жизни?
Задачи с прикладным содержанием (вариант 1)Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
01Математика — 8 класс. Алгебра — Понятие решения системы смешанных линейных неравенств
Для того чтобы проверить, какие из значений переменной \(\displaystyle x\) являются решением системы неравенств, подставим каждое из значений в систему неравенств.
\(\displaystyle x=0\) решение
Подставляя в систему линейных неравенств значение переменной \(\displaystyle x=\color{blue}{0}{ \small ,}\) получаем:
\(\displaystyle \left\{\begin{aligned}\color{blue}{0}&\le 6{\small , }\\\color{blue}{0}&\ge -3{\small .
}\end{aligned}\right.\)
Каждое из неравенств в системе верно (\(\displaystyle \color{blue}{0}\le 6\) – верно и \(\displaystyle \color{blue}{0}\ge -3\) – верно).
Значит, \(\displaystyle x=0\) является решением данной системы неравенств.
\(\displaystyle x=-8\) не является решением
Подставляя в систему линейных неравенств значение переменной \(\displaystyle x=\color{blue}{-8}{\small ,}\) получаем:
\(\displaystyle \left\{\begin{aligned}\color{blue}{-8}&\le 6{\small , }\\\color{blue}{-8}&\ge -3{\small .}\end{aligned}\right.\)
Второе неравенство в системе неверно, так как \(\displaystyle \color{blue}{-8}< -3{\small .}\)
Следовательно, \(\displaystyle x=-8\) не является решением данной системы неравенств.
\(\displaystyle x=5\) решение
Подставляя в систему линейных неравенств значение переменной \(\displaystyle x=\color{blue}{5}{ \small ,}\) получаем:
\(\displaystyle \left\{\begin{aligned}\color{blue}{5}&\le 6{\small , }\\\color{blue}{5}&\ge -3{\small .
}\end{aligned}\right.\)
Каждое из неравенств в системе верно (\(\displaystyle \color{blue}{5}\le 6\) – верно и \(\displaystyle \color{blue}{5}\ge -3\) – верно).
Значит, \(\displaystyle x=5\) является решением данной системы неравенств.
\(\displaystyle x=7\) не является решением
Подставляя в систему линейных неравенств значение переменной \(\displaystyle x=\color{blue}{7}{\small ,}\) получаем:
\(\displaystyle \left\{\begin{aligned}\color{blue}{7}&\le 6{\small , }\\\color{blue}{7}&\ge -3{\small .}\end{aligned}\right.\)
Первое неравенство в системе неверно, так как \(\displaystyle \color{blue}{7}> 6{ \small .}\)
Следовательно, \(\displaystyle x=7\) не является решением данной системы неравенств.
\(\displaystyle x=6\) решение
Подставляя в систему линейных неравенств значение переменной \(\displaystyle x=\color{blue}{6}{ \small ,}\) получаем:
\(\displaystyle \left\{\begin{aligned}\color{blue}{6}&\le 6{\small , }\\\color{blue}{6}&\ge -3{\small .
}\end{aligned}\right.\)
Каждое из неравенств в системе верно (\(\displaystyle \color{blue}{6}\le 6\) – верно и \(\displaystyle \color{blue}{6}\ge -3\) – верно).
Значит, \(\displaystyle x=6\) является решением данной системы неравенств.
Ответ: \(\displaystyle x=0{ \small ,}\,x=5 \) и \(\displaystyle x=6{\small .} \)
Видео с вопросами: Написание системы неравенств, описывающих область на графике
Стенограмма видео
Найдите систему неравенств, которая образует треугольник, показанный на графике.
Напомним, что система неравенств — это список различных неравенств, образующих определенную область. Когда нам дана область, как в этом вопросе, первое, что нужно сделать, это найти уравнение каждой линии, которая образует границу области. В этом вопросе нам нужно найти три разных неравенства, так как на графике показаны три линии. Первая линия, не являющаяся пунктирной, наклонена вниз слева направо и проходит через начало координат.
Вторая линия наклонена вверх слева направо. Это пунктирная линия. И он проходит через шесть по оси 𝑦. Наконец, у нас есть третья линия, тоже не пунктирная. И наклоняется вниз слева направо.
Сначала мы найдем уравнение каждой из этих трех линий, а затем подумаем о неравенстве, представленном заштрихованной частью. Прежде чем мы начнем с первой линии, нам нужно запомнить общую форму уравнения прямой линии: 𝑦 равно 𝑚𝑥 плюс 𝑏, где 𝑚 — наклон или градиент линии, а 𝑏 — 𝑦-отрезок. Если мы посмотрим на первую линию, давайте найдем наклон этой линии. Наклон линии можно найти по превышению над пробегом или по изменению 𝑦 над изменением 𝑥. Итак, глядя на этот треугольник, который мы нарисовали под первой линией, изменение 𝑦 будет отрицательным, а изменение 𝑥 будет равным единице. Следовательно, наклон отрицателен один к одному. А это равно отрицательной единице.
Далее, чтобы найти 𝑦-перехват, ищем место, где он пересекает 𝑦-ось. И это будет на нуле, на нуле. Таким образом, значение 𝑦 будет равно нулю.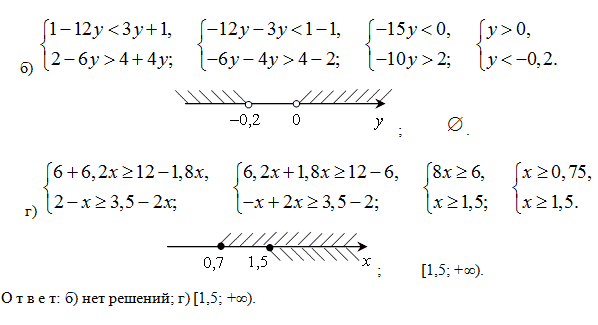
Теперь, когда у нас есть наклон и 𝑦-перехват, мы можем подставить это в уравнение прямой. 𝑦 равно отрицательной единице 𝑥 плюс ноль. И, конечно же, мы можем упростить это, чтобы получить 𝑦 равно отрицательному 𝑥.
Теперь давайте посмотрим, как найти наклон и 𝑦-пересечение второй строки. Мы можем нарисовать треугольник в любом месте на этой линии, чтобы помочь нам найти наклон, но часто бывает полезно найти целые значения для 𝑥- и 𝑦-координат. Линия проходит через координату минус два, два и минус один, четыре. На этот раз изменение 𝑦 или рост будет равно двум, а изменение 𝑥 или пробегу будет единице. Таким образом, наклон равен двум на один, что равно двум. Всегда полезно проверить, поскольку эта линия идет вверх слева направо, тогда у нас должен быть положительный наклон, который мы действительно нашли.
Затем нам нужно найти 𝑦-пересечение этой прямой, поэтому мы ищем точку пересечения прямой с 𝑦-осью. Поскольку это происходит, когда 𝑦-значение равно шести, то 𝑦-перехват равен шести.
Подставляя обе эти части информации в общее уравнение прямой линии, мы получаем, что 𝑦 равно двум 𝑥 плюс шесть. Теперь мы можем расчистить место, чтобы найти уравнение третьей строки. Начнем еще раз с определения наклона третьей линии. Эта линия проходит через точку один, восемь, а также через точку два, минус два. Таким образом, подъем этой линии будет равен минус 10. И мы видим, что он на восемь единиц выше оси 𝑥 и на две единицы ниже. Пробег будет один. Таким образом, наклон, который является подъемом над бегом, может быть записан как минус 10 на единицу, что упрощается до просто минус 10.
В качестве быстрой проверки этого значения, эта линия круче, чем две другие линии, поэтому мы можем ожидать, что абсолютное значение наклона будет больше. А затем он имеет наклон вниз слева направо, что указывает на то, что наклон будет отрицательным значением. Когда мы затем найдем 𝑦-перехват этой строки, вы можете заметить, что у нас возникнет проблема. На самом деле мы не можем видеть, где линия пересекает ось 𝑦.
Следовательно, нам понадобится другой способ найти уравнение этой прямой.
Эта форма линии, 𝑦 минус 𝑦 субединица равна 𝑚 умноженная на 𝑥 минус 𝑥 субединица, часто называется формой точечного наклона линии. Когда у нас есть координата или упорядоченная пара 𝑥 под единицей, 𝑦 под единицей и мы знаем наклон 𝑚, мы можем заполнить эти значения в этой форме точка-наклон, чтобы найти уравнение линии. Мы уже установили, что точка один, восемь лежит на прямой. Таким образом, один и восемь могут быть нашими значениями 𝑥 sub one и 𝑦 sub one. И мы знаем, что 𝑚, наклон, равен отрицательному значению 10. Таким образом, мы можем записать форму точки-наклона и заполнить значения. 𝑦 минус восемь равно минус 10, умноженному на 𝑥 минус один.
Если мы распределим минус 10 по скобкам, то получим минус 10𝑥. И тогда у нас будет отрицательное 10, умноженное на отрицательное, что дает нам положительное значение 10. Мы можем изолировать 𝑦-переменную в левой части, добавив восемь к обеим частям этого уравнения.
Итак, у нас будет 𝑦 равно отрицательному 10𝑥 плюс 18. Теперь мы нашли три уравнения этих трех прямых. Теперь мы можем взять каждую линию по очереди, чтобы определить область и то, как она соотносится с уравнением этой линии.
Если у нас есть линия без точек, это будет означать, что значения также могут лежать на этой линии. Другими словами, мы рассматриваем неравенства больше или равно или меньше или равно. Треугольник или заштрихованная область находится над первой линией. Таким образом, это представляет все значения, где 𝑦 больше отрицательного 𝑥. И помните, нам также нужно включить те значения, где 𝑦 равно отрицательному 𝑥. Итак, первое неравенство. Если бы область была заштрихована ниже этой линии, то неравенство было бы 𝑦 меньше или равно отрицательному 𝑥.
Для второй строки мы знаем, что уравнение 𝑦 равно двум 𝑥 плюс шесть. Но обратите внимание, что эта линия пунктирная, поэтому наше неравенство не будет включать значения, где 𝑦 равно двум 𝑥 плюс шесть. Заштрихованная область находится ниже этой линии, поэтому она представляет все значения, где 𝑦 меньше двух 𝑥 плюс шесть.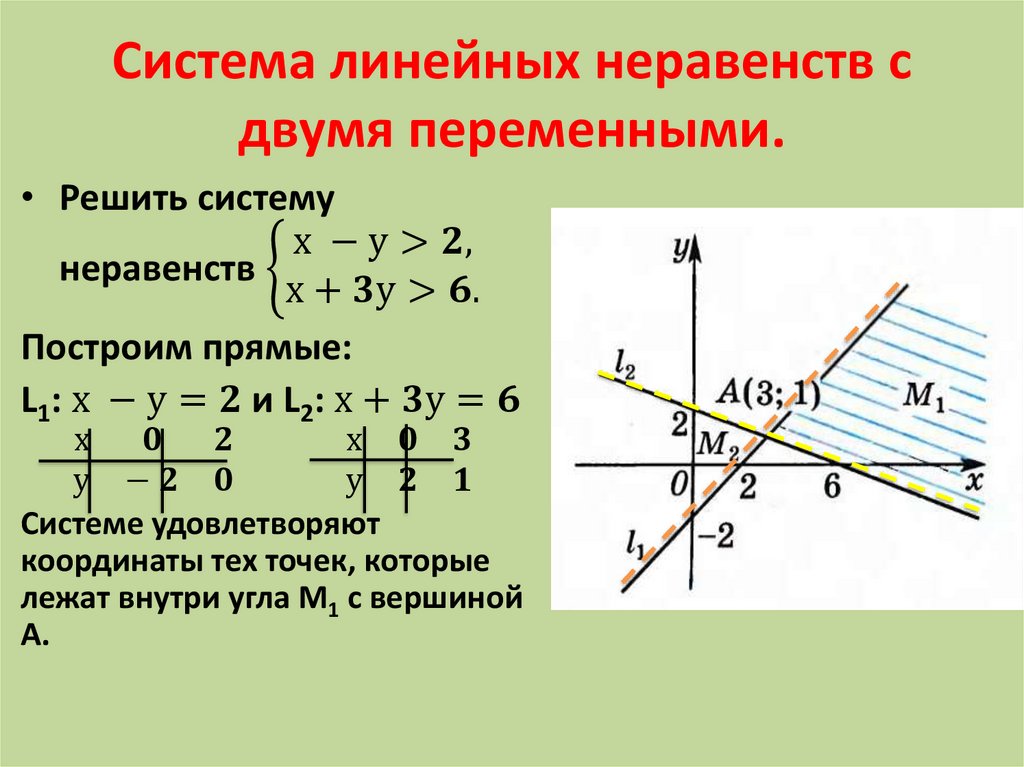
И это наше второе неравенство. Наконец, у нас есть третья строка с уравнением 𝑦 равно минус 10𝑥 плюс 18. Треугольник и заштрихованная область находятся ниже этой линии, но будет ли это знак меньше или меньше или равно?
Ну, так как у нас сплошная линия, а не пунктирная, значит, нам нужно включить и те значения, где 𝑦 равно минусу 10𝑥 плюс 18. Итак, наше третье неравенство. Таким образом, мы можем дать ответ, что эта система неравенств состоит из неравенств 𝑦 меньше двух 𝑥 плюс шесть, 𝑦 больше или равно отрицательному 𝑥 и 𝑦 меньше или равно отрицательному 10𝑥 плюс 18. И это не имеет значения, в каком порядке мы пишем эти неравенства.
Системы неравенств | Суперпроф
Типы систем линейных неравенств
Набор из двух или более линейных неравенств образует систему линейных неравенств.
Существуют два вида систем линейных неравенств:
- Система линейных неравенств с одной переменной
- Система линейных неравенств с двумя переменными
Система линейных неравенств с одной переменной изображается на числовой прямой, тогда как система линейных неравенств с двумя переменными изображается на оси координат.
В этой статье мы найдем множество решений системы линейных неравенств с двумя переменными.
Лучшие репетиторы по математике
Поехали
Как решаются системы линейных уравнений
Мы знаем, что системы линейных уравнений решаются одним из трех методов — подстановкой, исключением и построением графика. Системы уравнений могут быть легко решены без построения графика с помощью метода замены или исключения. Однако неравенства в системах линейных неравенств могут иметь разные знаки, поэтому поиск решения с помощью построения графика иногда является единственным, а в большинстве случаев наилучшим вариантом.
Количество решений в системах линейных неравенств
Система неравенств может иметь ноль, одно или несколько решений. Нулевое решение означает, что не существует ни одной упорядоченной пары, удовлетворяющей обоим неравенствам. Одно решение означает, что только одна упорядоченная пара (x, y) попадает в область решений графа. Множество решений означает, что в область решения графа попадает более одной упорядоченной пары (x, y).
Система линейных неравенств с двумя переменными содержит два линейных неравенства в одной системе. В этой статье мы увидим, как решить систему линейных неравенств с двумя переменными на примерах.
Пример 1
Найдите множество решений следующей системы линейных неравенств с двумя переменными.
Решение
Следуйте следующей пошаговой процедуре, чтобы решить приведенную выше систему неравенств.
Шаг 1. Постройте график первого неравенства
Сначала постройте график неравенства . Чтобы построить график неравенства, нам нужно сначала построить таблицу значений и .
| х | у |
|---|---|
| -1 | 2 |
| 0 | 3 |
| 1 | 4 |
| 2 | 5 |
| 3 | 6 |
We will construct the график путем построения значений из таблицы в координатной плоскости, как уравнения.
Поскольку неравенство строгое, т. е. оно имеет знак больше, поэтому мы будем использовать пунктирную линию для его представления на оси координат. График неравенства будет выглядеть так:
Как видите, неравенство имеет знак больше, поэтому мы представим его знак, заштриховав область над пунктирной линией.
Шаг 2. Нарисуйте график второго неравенства
Теперь нарисуйте график второго неравенства. Но для построения графика нам нужно сначала построить таблицу и значения.
| x | y |
|---|---|
| -2 | -4 |
| -1 | -3 |
| 0 | -2 |
| 1 | -1 |
| 2 | 0 |
Строитель Опять же, поскольку неравенство является строгим, мы будем использовать пунктирную линию для его представления.
Шаг 3. Затенение области решения
Постройте графики обоих неравенств в одной плоскости и выделите решение.
Решающая часть графика закрашена голубым цветом. Вы можете видеть, что графики обоих неравенств параллельны. Если бы мы решали систему уравнений и график был параллельным, то это означало бы, что система уравнений не имеет решения. Но это не относится к системе неравенств, потому что они имеют знаки больше, меньше, больше, чем равно и меньше, чем равно. Их решение лежит выше или ниже прямой, в отличие от систем уравнений, решения которых строго лежат на прямой.
Шаг 4. Проверка набора решений путем подстановки
Теперь мы возьмем несколько упорядоченных пар из области решений и посмотрим, удовлетворяют ли они обоим неравенствам. Из заштрихованной области на графике выше видно, что (1,6) и (-2,4) являются частью решения.
Сначала заменитель (1,6) в обеих неравенствах, таких как это:
Следовательно, упорядоченная пара (1,6) верна для обоих неравенств.
Аналогично, проверьте упорядоченную пару (-2,4), например:
Вы также можете взять другие упорядоченные пары в затененной зоне и проверить их, заменив в неравенство.
Пример 2
Найдите множество решений следующей системы линейных неравенств с двумя переменными.
Найдите репетитора по математике на Superprof.
Решение
Следуйте следующему пошаговому решению, чтобы решить приведенную выше систему неравенств. Поскольку приведенная выше система неравенств не имеет формы пересечения наклона, мы сначала преобразуем их в эту форму, выделив переменную в левой части неравенства.
Шаг 1. Преобразование неравенства в форму пересечения наклона
Форма пересечения наклона линейных уравнений . Преобразуйте неравенство в форму пересечения наклона линейных функций алгебраическим способом. Чтобы изолировать переменную в левой части, обе части неравенства нужно разделить на 2.
Шаг 2. Постройте график неравенства
Для построения графика неравенства мы сначала построим таблицу.
| x | y |
|---|---|
| -2 | 0 |
| -1 | 1 |
| 0 | 2 |
| 1 | 3 |
| 2 | 4 |
| 3 | 5 |
Теперь, нанеся эти значения, мы построим такой график:
Заштрихованная область над пунктирной линией представляет собой решение неравенства.
Шаг 3. Преобразуйте второе неравенство в форму пересечения наклона
Чтобы преобразовать его в форму пересечения наклона, разделите обе части на 3
Вычтите 2 из обеих частей неравенства, чтобы получить неравенство в виде пересечения наклона:
Шаг 4. Постройте график неравенства
To graph the inequality, first, you need to construct a table like this:
| x | y |
|---|---|
| -2 | -4 |
| -1 | -3 |
| 0 | -2 |
| 1 | -1 |
| 2 | 0 |
| 3 | 1 |
Using the values from the table, construct a graph вот так:
Поскольку знак неравенства меньше нуля, мы заштриховали область под пунктирной линией.
Шаг 5. Постройте систему уравнений и заштрихуйте область решения
На оси координат нет области, которая перекрывается обоими неравенствами.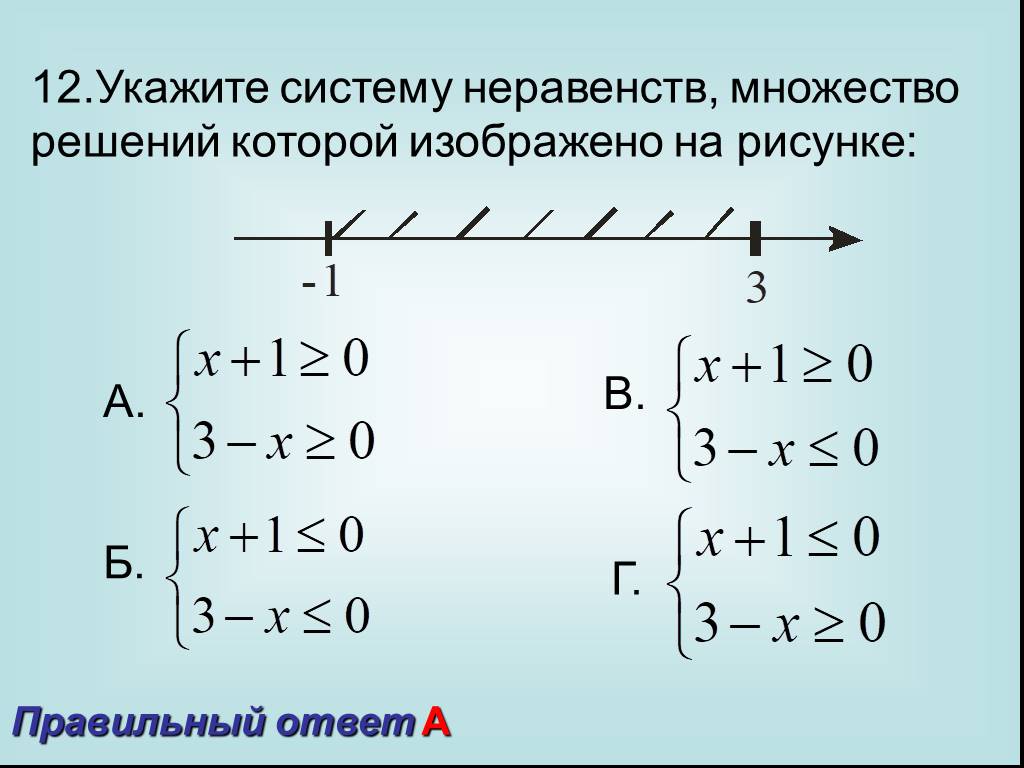
Следовательно, система неравенств не имеет решения. На приведенном ниже графике показана эта ситуация:
Вы можете видеть, что ни одна область не заштрихована, потому что нет решения.
Пример 3
Найдите множество решений следующей системы линейных неравенств с двумя переменными.
Решение
Сначала мы упростим приведенные выше неравенства, а затем изобразим их в виде графика, чтобы найти набор решений.
Шаг 1. Упростите неравенство
Разделите обе части неравенства на -2, чтобы выделить левую часть неравенства:
Мы знаем, что если обе части неравенства умножить или разделить на числа, знак неравенства меняется. В приведенном выше неравенстве знак больше или равно изменился на меньше или равно.
Step 2- Graph the inequality
To graph the inequality, first, we need to create a table of and values like this:
| x | y |
|---|---|
| -2 | — 10 |
| -1 | -7 |
| 0 | -4 |
| 1 | -1 |
| 2 | 2 |
Now, plot these values on the оси координат, чтобы получить такой график.
Вы можете видеть, что для построения графика этого неравенства используется сплошная прямая линия, потому что знак неравенства был меньше или равен.
Step 3- Graph the second inequality
To graph the inequality, first, you need to construct a table like this:
| x | y |
|---|---|
| -2 | -1 |
| -1 | 0 |
| 0 | 1 |
