Онлайн калькулятор уравнение прямой: Онлайн калькулятор. Уравнение прямой проходящей через две точки

Решить уравнение прямой онлайн

Решение функций

Одной из простейших геометрических фигур является прямая, представляющая бесконечную линию.

Любую прямую на плоскости в системе координат Оху можно выразить уравнением вида: A x + B y + C = 0, где коэффициенты А,В,С являются действительными числами, отметим, что А и В не могут равняться 0 одновременно, в противном случае уравнение примет вид: 0 + 0 + С = 0, что не имеет смысла.

Если один из коэффициентов равен 0, уравнение считается неполным.

1. При А = 0 общее уравнение будет неполным и примет вид Вy + С = 0, прямая в данном случае будет параллельна оси Ох.
2. При В = 0 неполное уравнение Ах + С = 0 задает прямую, параллельную оси Оy.
3. При С = 0 уравнение Ах + Вy = 0 задает прямую, которая пройдет через начало координат.
4. При А = С = 0 прямая будет совпадать с Ох.
5. При В = С = 0 прямая совпадает с осью Оу.

Уравнение прямой можно представить в разном виде в зависимости от исходных условий.

Уравнение прямой на плоскости

Через две не совпадающие произвольные точки на плоскости можно провести только одну прямую.

Если через 2 точки на плоскости с координатами М₁ (х₁;у₁), М₂ (х₂;у₂) провести прямую, ее уравнение можно представить в таком виде: (x — x₁) /( x₂ — x₁) = (y — y₁) /( y₂ — y₁)

Уравнение прямой в пространстве

Формула для прямой, проходящей через 2 заданные точки в прямоугольной системе координат Oxyz в 3-х-мерном пространстве, примет вид:
(x — x₁) /( x₂ — x₁) = (y — y₁) / ( y₂ — y₁) = (z — z₁) / ( z₂ — z₁), координаты 2-х точек в пространстве: М₁ (х₁,y₁,z₁), М₂ (х₂,y₂,z₂).

Уравнение прямой по точке и угловому коэффициенту

Общее уравнение прямой A x + B y + C = 0 можно представить в виде: y = — Ах/В — С/В.

А / В обозначим k, а — С / В обозначим b, тогда получим уравнение прямой с угловым коэффициентом: y = kх + b.

Например, дана точка М1 (х₁,y₁), уравнение прямой с заданным угловым коэффициентом: (у — у₁) = k (х — х₁).

Уравнение прямой в отрезках

Пусть прямая пересекает оси Ох и Оy в точках (а,0) и (0,b). С помощью формулы уравнения прямой в отрезках находим прямую: х / а + у / b = 1.

Воспользовавшись онлайн калькулятором, вы сможете быстро получить искомое уравнение прямой.

Предыдущая Угол наклона прямой

Следующая Прямая параллельная исходной

Уравнение прямой проходящей через две точки на плоскости. Онлайн калькулятор.

Онлайн калькулятор составляет уравнение прямой проходящей через 2 точки на плоскости. Подробное решение с пояснением.

Введите координаты точки A

Введите координаты точки B

Вывод формулы уравнения прямой по двум точкам

Воспользуемся уравнением прямой с угловым коэффициентом

y=kx+b

Так как точки A(x₁, y₁) и B(x₂, y₂) лежат на одной прямой то мы можем составить систему уравнений. Решив эту систему найдём коэффициенты k и b.

y₁=kx₁+b

y₂=kx₂+b

Вычтем из второго первое

y₂-y₁=kx₂-kx₁

Подставим k в первое и выведем b

Подставим выведенные значения k и b в уравненение прямой y=kx+b

Перенесём y₁ влево.

Разделим уравнение на y₂-y₁

Мы получили уравнение прямой по двум точкам

Общее уравнение прямой на плоскости

Ax+By+C=0

Уравнение вида Ax+By+C=0 где A и B одновременно не равны 0 определяет прямую.

Частные случаи общего уравнения прямой

	Значения коэффициентов	Уравнение прямой	Положение прямой
1	A≠0, B≠0, C=0	Ax+By=0	Прямая проходит через начало координат
2	A=0, B≠0, C≠0	By+C=0 ⇒ y=-C/B	Прямая будет параллельна оси x
3	A≠0, B=0, C≠0	Ax+C=0 ⇒ x=-C/A	Прямая будет параллельна оси y
4	A=0, B≠0, C=0	By=0 ⇒ y=0	Прямая будет совпадать с осью x
5	A≠0, B=0, C=0	Ax=0 ⇒ x=0	Прямая будет совпадать с осью y

Уравнение прямой с угловым коэффициентом

y=kx+d

Уравнение вида y=kx+d, где k является угловым коэффициентом а d некоторым числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой непараллельной оси y.

k — угловой коэффициент равный k=tg(α)

Подставим координаты точки A(0, d) в уравнение y=kx+d. Получится d=k×0+d, отсюда мы можем сделать вывод что прямая вида y=kx+d проходит через точку A(0, d).

Уравнение прямой в отрезках

x/a+y/b=1

Уравнение вида x/a+y/b=1, где a и b некоторые числа отличные от нуля, называют уравнением прямой в отрезках. Величины чисел a и b являются длинами отрезков отсекаемых этой прямой от осей ox и oy. Длины отрезков считаются от начала координат.

Знак − означает, что длину отрезка необходимо откладывать в отрицательном направлении координатной оси.

Приведение общего уравнения прямой к уравнению прямой в отрезках.

Ax+By+C=0

Возьмём общее уравнение прямой Ax+By+C=0 в котором все коэффициенты A, B и C не равны 0. Перенесём C вправо

Ax+By=-C

Разделим уравнение на -C

Преобразуем

Приведение общего уравнения прямой к уравнению прямой с угловым коэффициентом.

Ax+By+C=0

Возьмём общее уравнение прямой Ax+By+C=0 в котором все коэффициенты A, B и C не равны 0. Перенесём C и Ax вправо

By=-Ax-C

Разделим уравнение на B

y=-Ax/B-C/B

Составить уравнение прямой проходящее через две точки A(3, 5) и B(-5, -5)

Составить уравнение прямой проходящее через две точки A(-2, -4) и B(-8, 4)

Составить уравнение прямой проходящее через две точки A(-9, 10) и B(-3, 4)

Составить уравнение прямой проходящее через две точки A(-6, -2) и B(9, 9)

Составить уравнение прямой проходящее через две точки A(9, -10) и B(1, 9)

Калькулятор прямолинейной амортизации

Базовый калькулятор

Прямолинейная амортизация

Стоимость актива:

долл. США

Стоимость спасения:

долл. США

Срок полезного использования (годы):

. Поместите в эксплуатацию:

месяц:

январь.0003

Условное обозначение:

Полный месяцСередина месяцаСередина кварталаПолугодие

Округление до долларов:

Показать:

Только амортизацияПолная таблица

Ответ:

Распечатать расписание

Стоимость: 11 000,00 долларов США, утилизация: 1 000,00 долларов США
Срок службы: 5 лет, соглашение: полный месяц
Первый год: 8 мес.

Как этот калькулятор может быть лучше?

Поделитесь этой ссылкой для ответа: help
Вставьте эту ссылку в электронное письмо, текст или социальные сети.

Получить виджет для этого калькулятора

© Calculator Soup

Поделитесь этим калькулятором и страницей

Калькулятор Используйте

Используйте этот калькулятор для расчета простой линейной амортизации основных средств. Создайте и распечатайте графики амортизации.

Входы

Стоимость активов

первоначальная стоимость вашего актива или амортизируемая стоимость; сумма, необходимая для подготовки актива к использованию по назначению

Ликвидационная стоимость

стоимость актива в конце срока его полезного использования; также известная как остаточная стоимость или стоимость брака

Срок полезного использования

ожидаемое время, в течение которого актив будет продуктивным для ожидаемой цели

Введен в эксплуатацию

выберите месяц и введите год начала использования актива по назначению

Год

введите 1 или 4 цифры; введите год из четырех цифр, чтобы использовать фактические годы ИЛИ введите 1, чтобы перечислить годы, используя цифры от 1 до последнего года

Конвенция

выберите Соглашение о полном месяце, середине месяца, середине года или середине квартала; если вы не знаете, оставьте его на обычном Full-Month

Образец полного графика амортизации

Стоимость: 11 000,00 долларов США, утилизация: 1 000,00 долларов США
Срок службы: 5 лет, условность: полный месяц
Первый год: 8 месяцев

Формула прямолинейной амортизации

Прямолинейный расчет, как следует из названия, представляет собой прямолинейное снижение стоимости активов.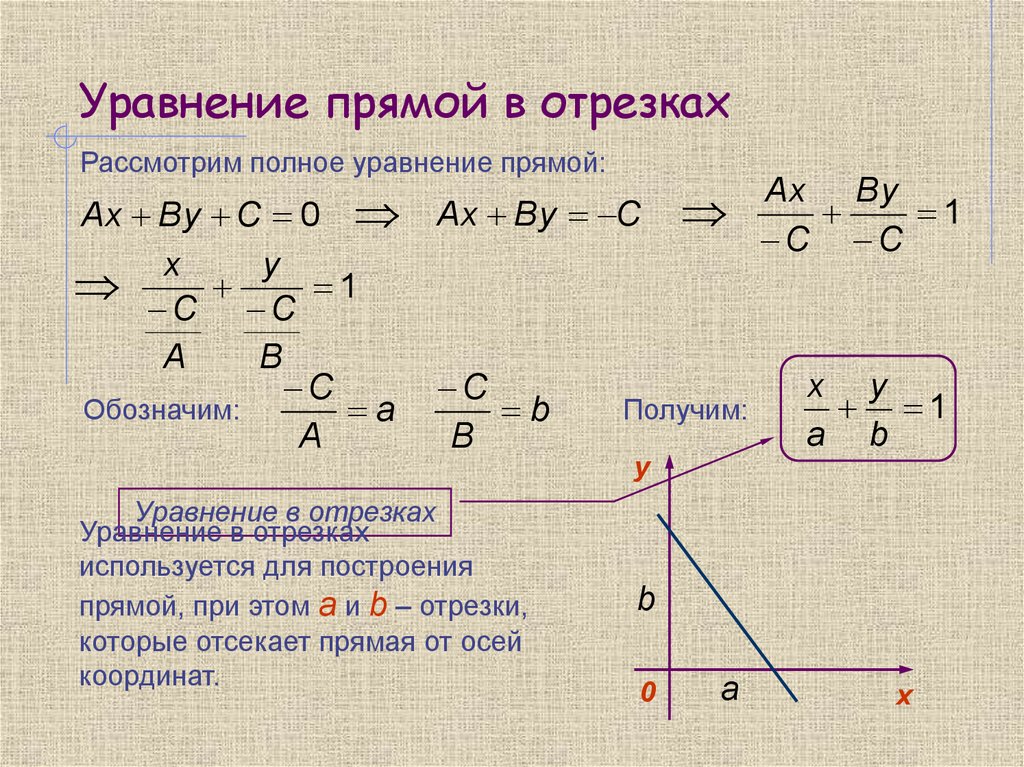

Амортизация актива распределяется равномерно в течение всего срока службы.

• Амортизация за любой период = ((Стоимость — Остаток) / Срок службы)
• Амортизация за неполный год, когда первый год состоит из M месяцев, принимается как:
  • Амортизация за первый год = (M / 12) * ((Стоимость — Спасение) / Срок службы)
  • Амортизация за прошлый год = ((12 — М) / 12) * ((Стоимость — Остаток) / Срок службы)
  • А, срок службы, например, 7 лет будет амортизироваться через 8 лет.

Пример равномерной амортизации

Предположим, что актив для бизнеса стоит 11 000 долларов США, будет иметь срок службы 5 лет и ликвидационную стоимость 1000 долларов США.

• Амортизация за любой 12-месячный период = ((11 000 – 1 000 долларов США) / 5 лет) = 10 000 долларов США / 5 лет = 2 000 долларов США в год.

Эквивалент функций Microsoft® Excel®: SLN

Эквивалентная функция Excel для прямолинейного метода: SLN(cost,salvage,life) рассчитает амортизационные отчисления за любой период. Более ускоренный метод амортизации см., например, в нашем Калькулятор амортизации по методу двойного уменьшаемого остатка.

(Microsoft® и Excel® являются зарегистрированными товарными знаками корпорации Microsoft)

 

Подписаться на CalculatorSoup:

Строка в калькуляторе стандартной формы

Инструкции: Воспользуйтесь этим калькулятором, чтобы найти уравнение прямой в стандартной форме с указанием всех шагов. Для этого необходимо предоставить информацию о строку, которую вы хотите привести к стандартной форме.

У вас есть несколько способов сделать это. Вы можете указать: (1) как наклон, так и точку пересечения по оси Y, (2) вы может предоставить любое линейное уравнение (например: \(2x + \frac{1}{5}y = 3 + 2x\)), (3) вы можете указать наклон и точку, через которую проходит линия, или (4) вы может указать две точки, где линия проходит.

Подробнее об этом уравнении прямой в калькуляторе стандартной формы

Это уравнение прямой в калькуляторе уравнений стандартной формы позволит вам определить уравнение одним из четырех способов, которые вы предпочитаете: и он покажет вам все необходимые шаги.

Как найти уравнение прямой? Итак, первое, что нужно сделать, это определить линейное уравнение. Для этого вы можете либо предоставить уравнения напрямую или иным образом, в зависимости от имеющейся у вас информации, вы можете предоставить:

(1) наклон и точка пересечения с осью y.

Или (2) наклон и одна точка, через которую проходит линия,

или (3) вы можете указать две точки, через которые проходит линия.

Какой способ вы будете использовать для определения вашего уравнения, будет зависеть от того, какая информация у вас есть.

Каков формат линейного уравнения в стандартной форме?

Говорят, что линейное уравнение имеет стандартную форму, если оно имеет следующую структуру:

\[а х + по = с\]

Затем ваша цель состоит в том, чтобы определить стандартную формулу формы и найти константы a, b и c, которые ее определяют.

Как решить стандартную форму на калькуляторе?

С этим калькулятором все, что вам нужно сделать, это ввести информацию для определения уравнения, среди четырех различных вариантов.

Зачем нужна стандартная форма

Определенные специфические формы уравнения происходят из традиции, но обычно потому, что полезно использовать специфическую форму.

В случае стандартного форме, удобно иметь его в виде \(a x + by = c\), потому что, подставив \(x=0\), легко вычислить y-перехват, и подставив \(y=0\), легко вычислить точку пересечения по оси x.

Кроме того, стандартная форма обычно используется в качестве предпочтительного формата при решении одновременных системы линейных уравнений.

Может ли этот решатель работать с дробными линейными уравнениями?

Одна из замечательных особенностей этого калькулятора заключается в том, что все коэффициенты, которые вы используете для определения уравнения, могут быть любыми. общее числовое выражение, содержащее дроби.

Чтобы увидеть пример того, как этот калькулятор работает с дробными линейными уравнениями, посмотрите пример ниже.

Пример: расчет уравнения прямой

Предположим, что у вас есть линия, проходящая через точку \(\left( \frac{1}{3}, \frac{2}{3}\right)\) с наклоном \(m = \frac{1}{ 2}\). Найдите стандартную форму линии.

Ответ:

Первоначально предоставленная информация о линии состоит в том, что наклон равен \(\displaystyle m = \frac{1}{2}\), а линия проходит через точку \(\displaystyle \left( \frac{1}{ 3}, \frac{2}{3}\right)\)

Следовательно, с имеющейся у нас информацией мы можем напрямую построить форму точки-наклона линии, которая равна

\[\displaystyle y — y_1 = m \left(x — x_1\right)\]

, а затем подставить известные значения \(\displaystyle m = \frac{1}{2}\) и \(\displaystyle \left( x_1, y_1 \right) = \left( \frac{1}{3) }, \frac{2}{3}\right)\), получаем

\[\displaystyle y-\frac{2}{3} = \frac{1}{2} \left(x-\frac{1}{3}\right)\]

Теперь нам нужно расширить правую часть уравнения, распределив наклон, так что мы получим \[\displaystyle y = \frac{1}{2} x + \frac{1}{2} \left(-\frac{1}{3}\right) + \frac{2}{3}\]

и упрощая получаем что \[\displaystyle y=\frac{1}{2}x+\frac{1}{2}\]

Передача независимой переменной в левую часть уравнения приводит к следующему стандартному виду линии:

\[\displaystyle -\frac{1}{2}x+y=\frac{1}{2}\]

Заключение : На основании предоставленных данных делаем вывод, что уравнение прямой в стандартной форме имеет вид \(\displaystyle -\frac{1}{2}x+y=\frac{1}{2}\).